Assessment and Management of Small Yellow Croaker (Larimichthys polyactis) Stocks in South Korea
Abstract
1. Introduction
2. Materials and Methods
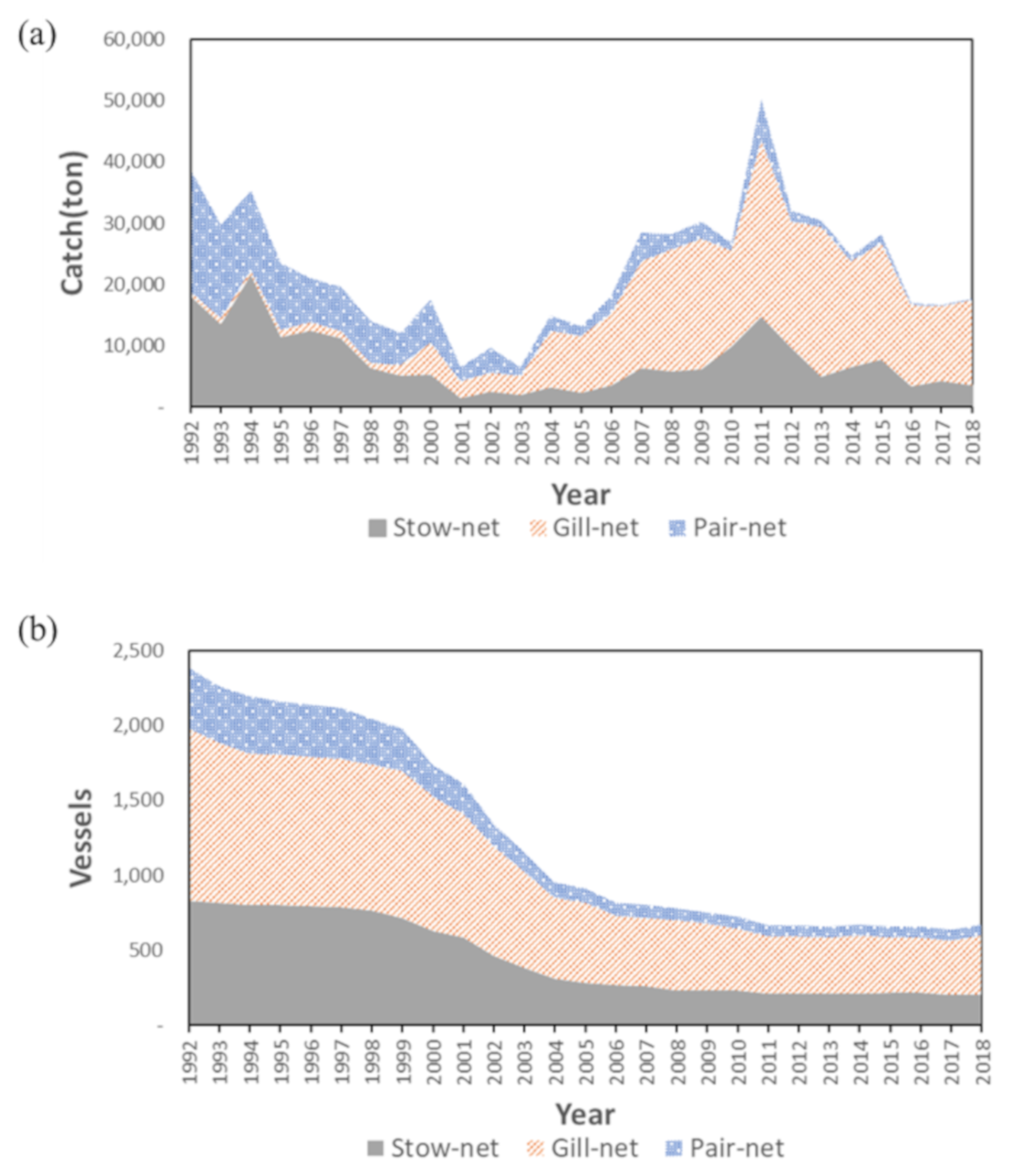
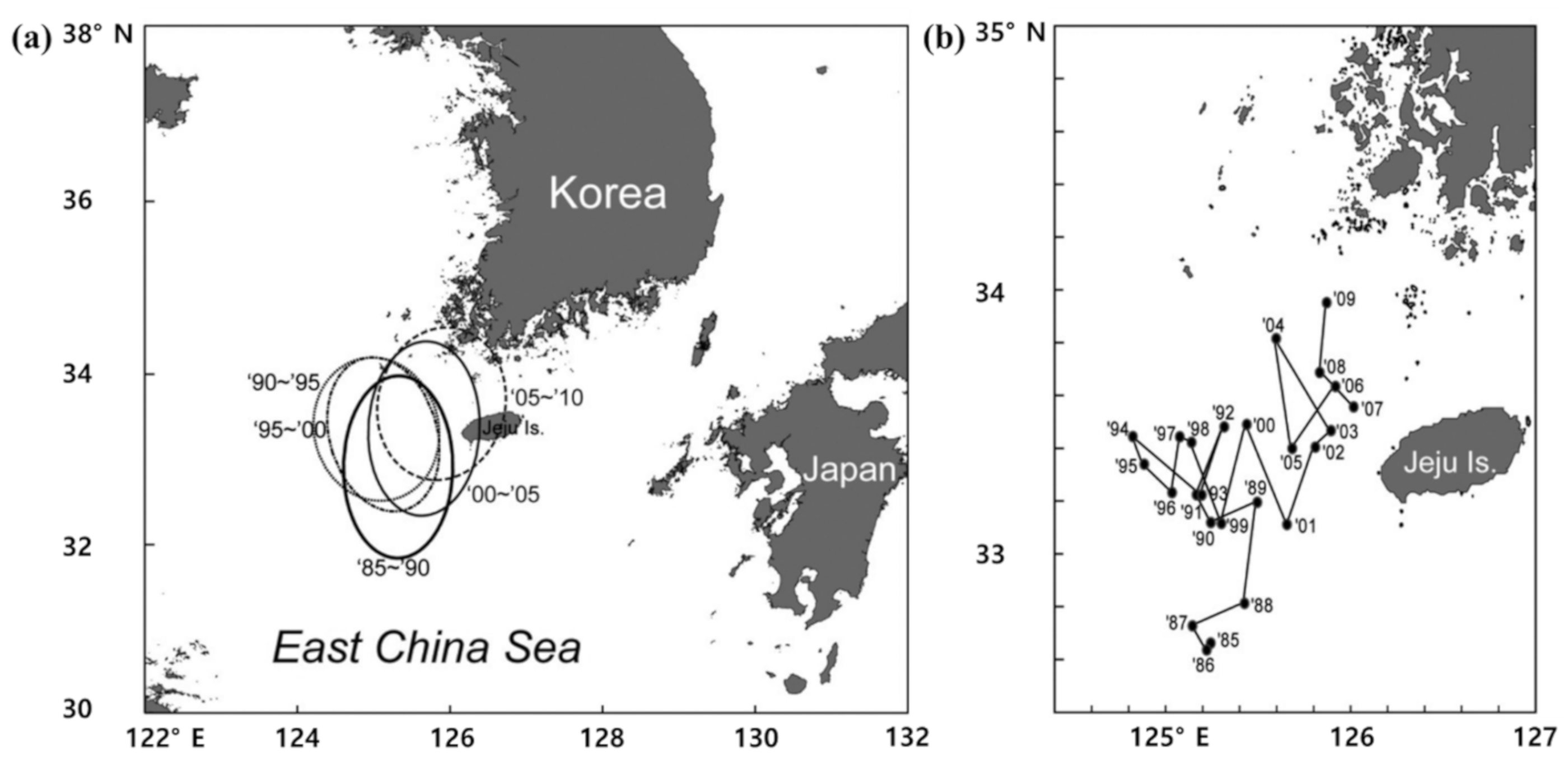
2.1. Data
2.2. Generalized Linear Model for CPUE Standardization
2.3. Surplus Production Model
2.4. Bayesian State-Space Model
Model Implementation and Comparison
3. Results
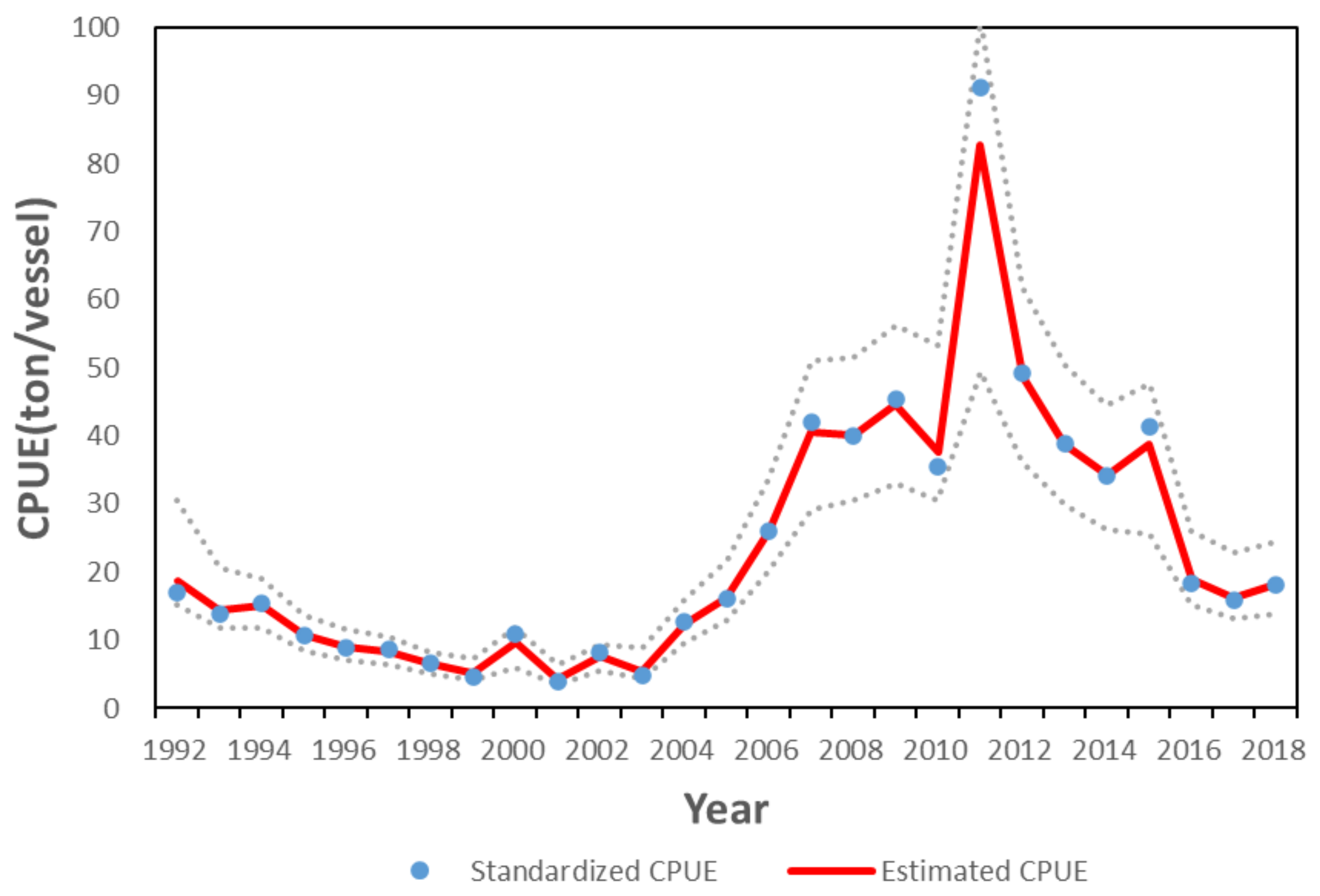
3.1. GLM Analysis Results and Model Comparison
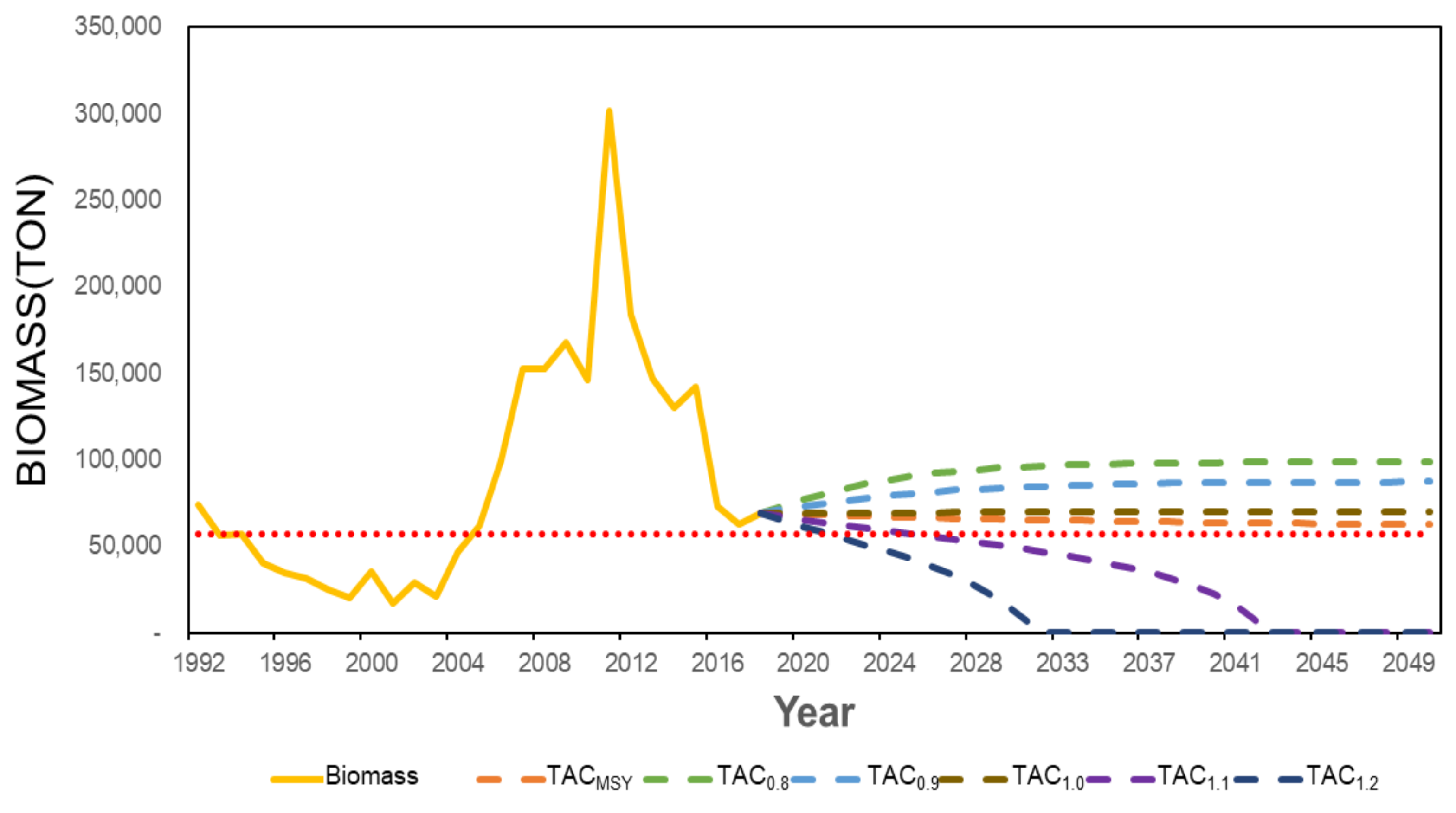
3.2. Analysis of Appropriate TAC Levels
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Variable | Coefficient | Std. Error | t-Statistics | p-Value |
|---|---|---|---|---|
| (Intercept) | 0.294 | 0.316 | 0.931 | 0.357 |
| year1993 | −0.042 | 0.4 | −0.106 | 0.916 |
| year1994 | 0.072 | 0.4 | 0.179 | 0.858 |
| year1995 | −0.069 | 0.4 | −0.172 | 0.865 |
| year1996 | −0.153 | 0.4 | −0.383 | 0.703 |
| year1997 | −0.208 | 0.4 | −0.52 | 0.605 |
| year1998 | −0.444 | 0.4 | −1.112 | 0.272 |
| year1999 | −0.377 | 0.4 | −0.944 | 0.350 |
| year2000 | 1.818 | 0.46 | 3.952 | 0.000 *** |
| year2001 | 0.836 | 0.46 | 1.817 | 0.076 . |
| year2002 | 1.496 | 0.46 | 3.252 | 0.002 ** |
| year2003 | 1.17 | 0.46 | 2.543 | 0.014 * |
| year2004 | 2.145 | 0.46 | 4.663 | 0.000 *** |
| year2005 | 2.724 | 0.437 | 6.231 | 0.000 *** |
| year2006 | 3.272 | 0.437 | 7.484 | 0.000 *** |
| year2007 | 3.769 | 0.437 | 8.619 | 0.000 *** |
| year2008 | 3.631 | 0.437 | 8.305 | 0.000 *** |
| year2009 | 3.761 | 0.437 | 8.603 | 0.000 *** |
| year2010 | 3.549 | 0.437 | 8.118 | 0.000 *** |
| year2011 | 4.547 | 0.437 | 10.399 | 0.000 *** |
| year2012 | 3.855 | 0.437 | 8.818 | 0.000 *** |
| year2013 | 3.516 | 0.437 | 8.043 | 0.000 *** |
| year2014 | 3.448 | 0.437 | 7.886 | 0.000 *** |
| year2015 | 3.658 | 0.437 | 8.367 | 0.000 *** |
| year2016 | 2.76 | 0.437 | 6.312 | 0.000 *** |
| year2017 | 2.638 | 0.437 | 6.034 | 0.000 *** |
| year2018 | 2.752 | 0.437 | 6.294 | 0.000 *** |
| pair_trawl | 3.189 | 0.245 | 13.029 | <2e−16 *** |
| stow_net | 2.509 | 0.245 | 10.249 | 0.000 *** |
| pair_trawl:move23 | −2.023 | 0.395 | −5.124 | 0.000 *** |
| stow_net:move23 | −2.601 | 0.395 | −6.59 | 0.000 *** |
| pair_trawl:move24 | −4.065 | 0.307 | −13.248 | <2e−16 *** |
| stow_net:move24 | −3.042 | 0.307 | −9.912 | 0.000 *** |
References
- Lee, S.G.; Midani, A.R. National comprehensive approaches for rebuilding fisheries in South Korea. Mar. Policy 2014, 45, 156–162. [Google Scholar] [CrossRef]
- National Institute of Fisheries Science. Fishes of the Pacific Ocean; National Institute of Fisheries Science: Busan, Korea, 2015.
- Park, J.M. Historical consideration of Production and using of a croaker. Korean J. Agric. Hist. 2010, 9, 197–222. [Google Scholar]
- Choi, M.J.; Kim, D.H. Comparing surplus production models for selecting effective stock assessment model: Analyzing potential yield of East Sea, Republic of Korea. Ocean Polar Res. 2019, 41, 183–191. [Google Scholar]
- Choi, M.J.; Kim, D.H.; Choi, J.H. Comparative analysis of stock assessment models for analyzing potential yield of fishery resources in the West Sea, Korea. J. Korean Soc. Fish. Ocean Technol. 2019, 55, 206–216. [Google Scholar] [CrossRef]
- Korean Statistical Information Service. Available online: http://kosis.kr/ (accessed on 18 January 2020).
- National Institute of Fisheries Science. Target Fish Species of Fisheries Resources Recovery Project. Available online: https://www.nifs.go.kr/page?id=rec_fish (accessed on 5 February 2020).
- Kim, D.H. Evaluating the TAC policy in the sandfish stock rebuilding plan. J. Fish. Bus. Adm. 2015, 46, 29–39. [Google Scholar] [CrossRef]
- Kim, D.Y.; Lee, J.S.; Kim, D.H. A study on establishing the performance evaluation system of the fish stock rebuilding plans. J. Fish. Bus. Adm. 2011, 42, 15–29. [Google Scholar]
- National Law Information Center. Enforcement Decree of the Fisheries Resources Management Act. Available online: http://www.law.go.kr (accessed on 5 February 2020).
- Jeong, M.J.; Nam, J.O. Effectiveness analysis on comb pen shell based on TAC system. J. Fish. Bus. Adm. 2016, 47, 15–33. [Google Scholar] [CrossRef][Green Version]
- Sim, S.H.; Lee, J.S.; Oh, S.Y. An analysis of the effects in the TAC system by analyzing catch of TAC target species. Ocean Polar Res. 2020, 42, 157–169. [Google Scholar]
- Korea Fisheries Resources Agency. TAC Introduction. Available online: https://www.fira.or.kr/fira/fira_030601.jsp (accessed on 5 February 2020).
- National Institute of Fisheries Science. Resource Status and Restoration Recommendation of Fisheries Resources in 2017; National Institute of Fisheries Science: Busan, Korea, 2017.
- Sim, S.H.; Nam, J.O. A Stock Assessment of yellow croaker using bioeconomic model: A case of single species and multiple fisheries. Ocean Polar Res. 2015, 37, 161–177. [Google Scholar] [CrossRef]
- Zhang, C.I.; Kim, S.; Yoon, S.B. Stock assessment and management implications of small yellow croaker in Korean waters. Korean J. Fish. Aquat. Sci. 1992, 25, 282–290. [Google Scholar]
- Clarke, R.P.; Yoshimoto, S.S.; Pooley, S.G. A bioeconomic analysis of the Northwestern Hawaiian Islands lobster fishery. Mar. Resour. Econ. 1992, 7, 115–140. [Google Scholar] [CrossRef]
- Millar, R.B.; Meyer, R. Non-linear state space modelling of fisheries biomass dynamics by using Metropolis-Hastings within-Gibbs sampling. J. R. Stat. Soc. C Appl. 2000, 49, 327–342. [Google Scholar] [CrossRef]
- Polacheck, T.; Hilborn, R.; Punt, A.E. Fitting surplus production models: Comparing methods and measuring uncertainty. Can. J. Fish. Aquat. Sci. 1993, 50, 2597–2607. [Google Scholar] [CrossRef]
- Bolker, B. Ecological Models and Data in R; Princeton University Press: Princeton, NJ, USA, 2008; pp. 233–242. [Google Scholar]
- Chaloupka, M.; Balazs, G. Using Bayesian state-space modelling to assess the recovery and harvest potential of the Hawaiian green sea turtle stock. Ecol. Model. 2007, 205, 93–109. [Google Scholar] [CrossRef]
- Meyer, R.; Millar, R.B. BUGS in Bayesian stock assessments. Can. J. Fish. Aquat. Sci. 1999, 56, 1078–1087. [Google Scholar] [CrossRef]
- Choi, M.J.; Kim, D.H.; Lee, H.W.; Seo, Y.I.; Lee, S.I. Assessing stock biomass and analyzing management effects regarding the black scraper (Thamnaconus modestus) using Bayesian state-space model. Ocean Polar Res. 2020, 42, 63–76. [Google Scholar]
- McAllister, M.K.; Pikitch, E.K.; Punt, A.E.; Hilborn, R. A Bayesian approach to stock assessment and harvest decisions using the sampling/importance resampling algorithm. Can. J. Fish. Aquat. Sci. 1994, 51, 2673–2687. [Google Scholar] [CrossRef]
- Otsuyama, K.; Kitakado, T. Bayesian state-space production models for the Indian Ocean bigeye tuna (Thunnus Obesus) and their predictive evaluation. IOTC 2016, WPTT18-19. [Google Scholar]
- Parker, D.; Winker, H.; da Silva, C.; Kerwath, S. Bayesian state-space surplus production model JABBA assessment of Indian Ocean black marlin (Makaira indica) stock. IOTC 2018, WPB16-15. [Google Scholar]
- Winker, H.; Carvalho, F.; Kapur, M. JABBA: Just another Bayesian biomass assessment. Fish. Res. 2018, 204, 275–288. [Google Scholar] [CrossRef]
- McAllister, M.K.; Pikitch, E.K.; Babcock, E.A. Using demographic methods to construct Bayesian priors for the intrinsic rate of increase in the Schaefer model and implications for stock rebuilding. Can. J. Fish. Aquat. Sci. 2001, 58, 1871–1890. [Google Scholar] [CrossRef]
- Millar, R.B. Reference priors for Bayesian fisheries models. Can. J. Fish. Aquat. Sci. 2002, 59, 1492–1502. [Google Scholar] [CrossRef]
- Van Dongen, S. Prior specification in Bayesian statistics: Three cautionary tales. J. Theor. Biol. 2006, 242, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Dick, E.J.; MacCall, A.D. Depletion-based stock reduction analysis: A catch-based method for determining sustainable yields for data-poor fish stocks. Fish. Res. 2011, 110, 331–341. [Google Scholar] [CrossRef]
- Dowling, N.A.; Smith, D.C.; Knuckey, I.; Smith, A.D.; Domaschenz, P.; Patterson, H.M.; Whitelaw, W. Developing harvest strategies for low-value and data-poor fisheries: Case studies from three Australian fisheries. Fish. Res. 2008, 94, 380–390. [Google Scholar] [CrossRef]
- Free, C.M.; Jensen, O.P.; Wiedenmann, J.; Deroba, J.J. The refined ORCS approach: A catch-based method for estimating stock status and catch limits for data-poor fish stocks. Fish. Res. 2017, 193, 60–70. [Google Scholar] [CrossRef]
- Zhou, S.; Punt, A.E.; Ye, Y.; Ellis, N.; Dichmont, C.M.; Haddon, M.; Smith, D.C.; Smith, A.D. Estimating stock depletion level from patterns of catch history. Fish 2017, 18, 742–751. [Google Scholar] [CrossRef]
- Gelman, A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Punt, A.E.; Hilborn, R. Fisheries stock assessment and decision analysis: The Bayesian approach. Rev. Fish Biol. Fish. 1997, 7, 35–63. [Google Scholar] [CrossRef]
- Thorson, J.T.; Cope, J.M. Uniform, uninformed or misinformed? The lingering challenge of minimally informative priors in data-limited Bayesian stock assessments. Fish. Res. 2017, 194, 164–172. [Google Scholar] [CrossRef]
- Maunder, M.N. Is it time to discard the Schaefer model from the stock assessment scientist’s toolbox? Fish. Res. 2003, 1, 145–149. [Google Scholar] [CrossRef]
- Schaefer, M.B. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. IATTC Bull. 1954, 1, 23–56. [Google Scholar]
- Fox Jr, W.W. An exponential surplus-yield model for optimizing exploited fish populations. T. Am. Fish. Soc. 1970, 99, 80–88. [Google Scholar] [CrossRef]
- Hinton, M.G.; Maunder, M.N. Methods for standardizing CPUE and how to select among them. Collect Vol. Sci. Pap. ICCAT 2004, 56, 169–177. [Google Scholar]
- Kimura, D.K. Standardized measures of relative abundance based on modelling log (CPUE), and their application to Pacific Ocean perch (Sebastes alutus). ICES J. Mar. Sci. 1981, 39, 211–218. [Google Scholar] [CrossRef]
- Gavaris, S. Use of a multiplicative model to estimate catch rate and effort from commercial data. Can. J. Fish. Aquat. Sci. 1980, 37, 2272–2275. [Google Scholar] [CrossRef]
- Kim, D.Y.; Kim, B.H. Restructuring of the off-shore otter trawl fishery in Korea. J. Fish. Mar. Sci. Edu. 2004, 16, 124–141. [Google Scholar]
- Lee, D.W.; Choi, K.H.; Kang, S. Changes of fishing ground of the large pair trawl fishery off Korean Waters. Korean J. Fish. Aquat. Sci. 2013, 46, 917–922. [Google Scholar]
- Seo, Y.I.; Oh, T.Y.; Cha, H.K.; Kim, B.Y.; Jo, H.S.; Jeong, T.Y.; Lee, Y.W. Change of relative fishing power index from technological development in the small yellow croaker drift gillnet fishery. J. Korean Soc. Fish. Ocean Technol. 2019, 55, 198–205. [Google Scholar] [CrossRef]
- Nishida, T.; Bigelow, K.; Mohri, M.; Marsac, F. Comparative study on Japanese tuna longline CPUE standardization of yellowfin tuna (Thunnus albacares) in the Indian Ocean based on two methods: General linear model (GLM) and habitat-based model (HBM)/GLM combined. IOTC Proc. 2003, 6, 48–69. [Google Scholar]
- Shono, H. Application of the Tweedie distribution to zero-catch data in CPUE analysis. Fish. Res. 2008, 93, 154–162. [Google Scholar] [CrossRef]
- Lim, Y.N.; Kim, H.Y.; Kim, D.H. Predicting changes in fishing conditions for the small yellow croaker Larimichthys polyactis based on expansions of the Yellow Sea bottom cold water. Korean J. Fish. Aquat. Sci. 2014, 47, 419–423. [Google Scholar]
- Best, J.K.; Punt, A.E. Parameterizations for Bayesian state-space surplus production models. Fish. Res. 2020, 222, 105411. [Google Scholar] [CrossRef]
- Coppola, G.; Pascoe, S. A surplus production model with a nonlinear catch-effort relationship. Mar. Resour. Econ. 1998, 13, 37–50. [Google Scholar] [CrossRef]
- Karim, E.; Qun, L.; Hasan, S.J.; Ali, M.Z.; Hoq, M.E.; Mahmud, M.Y. Maximum sustainable yield estimates of marine captured shrimp fishery of the Bay of Bengal, Bangladesh by using surplus production model. Thalassas 2020, 36, 471–480. [Google Scholar] [CrossRef]
- Haddon, M. Modelling and Quantitative Methods in Fisheries; CRC Press: New York, NY, USA, 2010; pp. 285–333. [Google Scholar]
- Kim, D.H. Bayesian Statistics Using R and WinBUGS; Freedom Academy: Paju, Korea, 2013; pp. 87–248. [Google Scholar]
- Ntzoufras, I. Bayesian Modeling Using WinBUGS; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 698, p. 520. [Google Scholar]
- Martell, S.; Froese, R. A simple method for estimating MSY from catch and resilience. Fish 2013, 14, 504–514. [Google Scholar] [CrossRef]
- Gilks, W.R.; Wild, P. Adaptive rejection sampling for Gibbs sampling. J. R. Stat. Soc. C Appl. 1992, 41, 337–348. [Google Scholar] [CrossRef]
- Kéry, M.; Schaub, M. Bayesian Population Analysis using WinBUGS: A Hierarchical Perspective; Academic Press: Cambridge, UK, 2011; p. 55. [Google Scholar]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS-a Bayesian modelling framework: Concepts, structure, and extensibility. Stat. Comput. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Neal, R.M. Markov Chain Monte Carlo Methods Based on ‘Slicing’ the Density Function. 1997, pp. 1–27. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.48.886&rep=rep1&type=pdf (accessed on 17 February 2020).
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Thomas, A.; Best, N.; Lunn, D. WinBUGS User Manual. 2003, pp. 1–60. Available online: https://www.mrc-bsu.cam.ac.uk/wp-content/uploads/manual14.pdf (accessed on 15 March 2020).
- Punt, A.E.; Hilborn, R. Bayesian Stock Assessment Methods in Fisheries: User’s Manual; Food and Agriculture Organization: Rome, Italy, 2001; pp. 1–68. [Google Scholar]
- Pella, J.J.; Tomlinson, P.K. A generalized stock production model. IATTC Bull. 1969, 13, 416–497. [Google Scholar]
- Chen, Y.; Shan, X.; Wang, N.; Jin, X.; Guan, L.; Gorfine, H.; Yang, T.; Dai, F. Assessment of fish vulnerability to climate change in the Yellow Sea and Bohai Sea. Mar. Freshw. Res. 2020, 71, 729–736. [Google Scholar] [CrossRef]
- Shan, X.; Li, X.; Yang, T.; Sharifuzzaman, S.M.; Zhang, G.; Jin, X.; Dai, F. Biological responses of small yellow croaker (Larimichthys polyactis) to multiple stressors: A case study in the Yellow Sea, China. Acta Oceanol. Sin. 2017, 36, 39–47. [Google Scholar] [CrossRef]

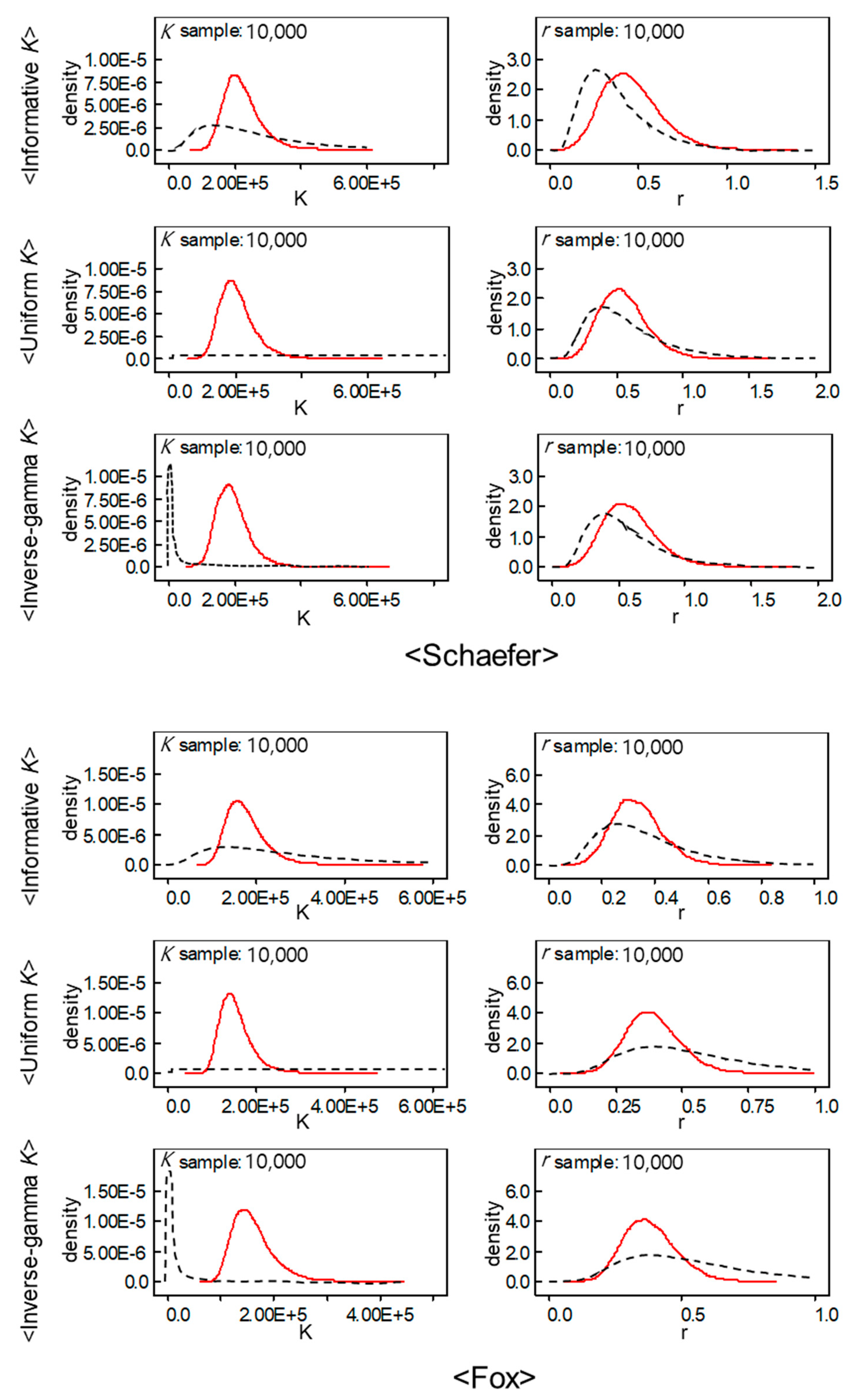

| Parameter | Informative Prior Distribution | Non-Informative Prior Distribution | |
|---|---|---|---|
| Uniform | Inverse-Gamma | ||
| r | Lognormal (−1.1, 0.512) | Lognormal (−0.69, 0.512) | Lognormal (−0.69, 0.512) |
| K | Inverse-lognormal (12.38, 0.752) | Uniform (10,000–100,000,000) | Inverse-gamma (0.01, 0.01) |
| q | Inverse-gamma (1,1) | Inverse-gamma (1,1) | Inverse-gamma (1,1) |
| Inverse-gamma (3.79, 0.01) | Inverse-gamma (3.79, 0.01) | Inverse-gamma (3.79, 0.01) | |
| Inverse-gamma (1.71, 0.01) | Inverse-gamma (1.71, 0.01) | Inverse-gamma (1.71, 0.01) | |
| Parameter | Schaefer | Fox | ||||
|---|---|---|---|---|---|---|
| Informative K | Non-Informative K | Informative K | Non-Informative K | |||
| Lognormal K | Uniform | Inverse-Gamma | Log-Normal K | Uniform | Inverse-Gamma | |
| r | 0.4469 | 0.5426 | 0.5703 | 0.3273 | 0.3854 | 0.3738 |
| K (ton) | 214,100 | 198,700 | 187,600 | 169,700 | 148,500 | 154,900 |
| q | 2.03E-04 | 2.31E-04 | 2.46E-04 | 2.35E-04 | 2.72E-04 | 2.63E-04 |
| MSY (maximum sustainable yield) | 23,920 | 26,954 | 26,747 | 20,433 | 21,054 | 21,301 |
| B2018/BMSY | 0.85 | 0.82 | 0.82 | 1.24 | 1.22 | 1.21 |
| 1.16E-04 | 1.13E-04 | 1.10E-04 | 1.33E-04 | 1.46E-04 | 1.43E-04 | |
| 0.03117 | 0.03382 | 0.03559 | 0.01848 | 0.01402 | 0.01473 | |
| R2 | 0.96 | 0.96 | 0.95 | 0.99 | 0.99 | 0.99 |
| DIC (deviance information criterion) | 149.599 | 150.050 | 150.953 | 142.938 | 139.631 | 139.226 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, M.-J.; Kim, D.-H. Assessment and Management of Small Yellow Croaker (Larimichthys polyactis) Stocks in South Korea. Sustainability 2020, 12, 8257. https://doi.org/10.3390/su12198257
Choi M-J, Kim D-H. Assessment and Management of Small Yellow Croaker (Larimichthys polyactis) Stocks in South Korea. Sustainability. 2020; 12(19):8257. https://doi.org/10.3390/su12198257
Chicago/Turabian StyleChoi, Min-Je, and Do-Hoon Kim. 2020. "Assessment and Management of Small Yellow Croaker (Larimichthys polyactis) Stocks in South Korea" Sustainability 12, no. 19: 8257. https://doi.org/10.3390/su12198257
APA StyleChoi, M.-J., & Kim, D.-H. (2020). Assessment and Management of Small Yellow Croaker (Larimichthys polyactis) Stocks in South Korea. Sustainability, 12(19), 8257. https://doi.org/10.3390/su12198257






