Measuring Operational Performance of Major Chinese Airports Based on SBM-DEA
Abstract
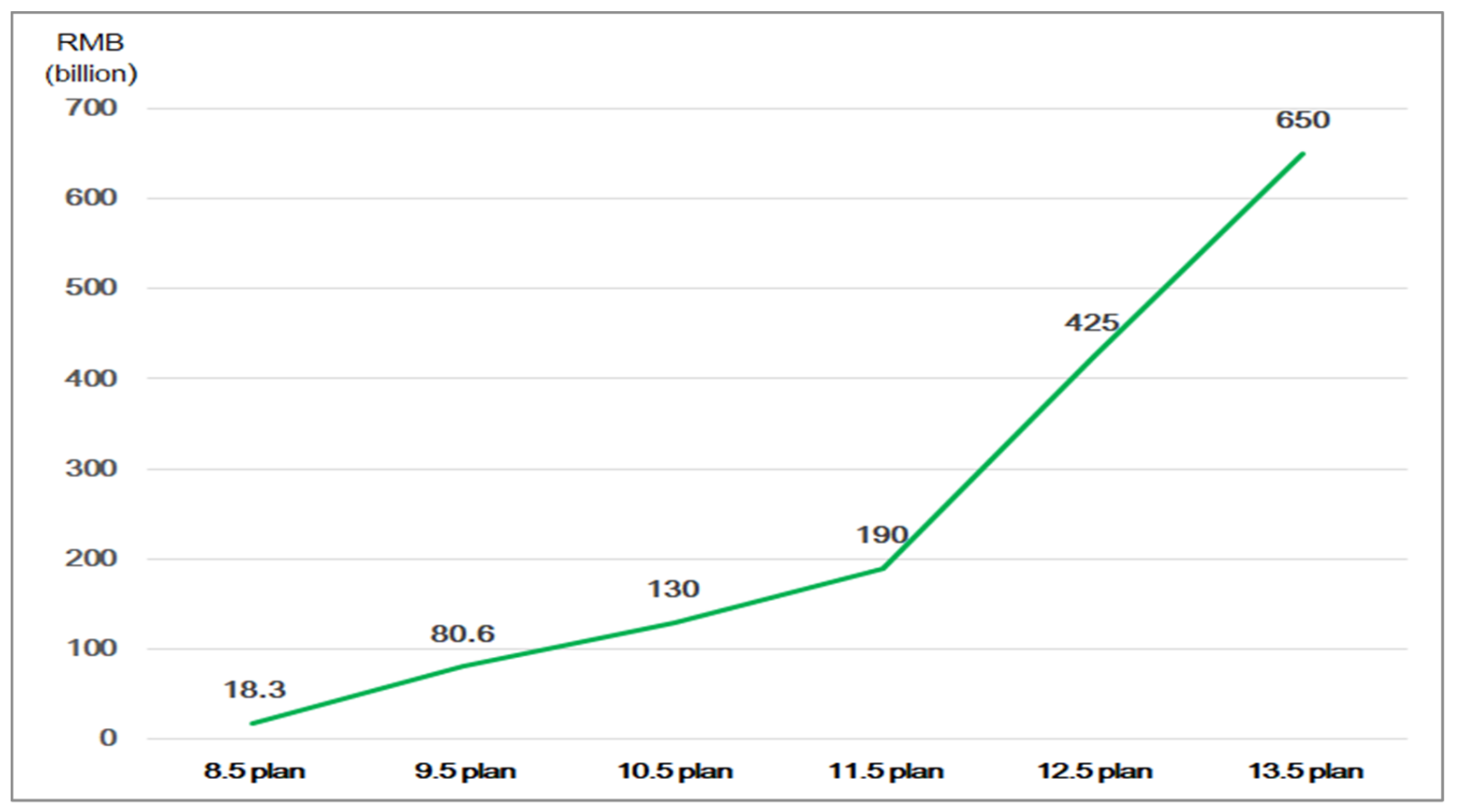
1. Introduction
2. Literature Review and Theoretical Background
3. Methodology and Empirical Tests
3.1. SBM-DEA
3.2. Efficiency Decomposition
4. Empirical Result and Its Implications
4.1. Descriptive Statistics on Data
4.2. Airport Operational Efficiency and Rectified Efficiency
4.3. Airport Operational Efficiency Based on Regional Heterogeneity
4.4. Airport Operational Efficiency with Projection for Delay Rate
4.5. Decomposition of Efficiency and Benchmark Information
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Song, M.G.; Yeo, G.T. Analysis of the Air Transport Network Chacteristics of Major Airports. Asian J. Shipp. Logist. 2017, 33, 117–125. [Google Scholar] [CrossRef]
- Choi, Y. The Asian Values of Guānxì as an Economic Model for Transition toward Green Growth. Sustainability 2018, 10, 2150. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, H.; Wang, Q. Impact of high-speed rail on China’s Big Three airlines. Transp. Res. Part A Policy Pract. 2017, 98, 77–85. [Google Scholar] [CrossRef]
- Yu, Y.; Choi, Y.; Wei, X.; Chen, Z. Did China’s regional transport industry enjoy better carbon productivity under regulations? J. Clean. Prod. 2017, 165, 777–787. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, H. International Transportation and Global Logistics; Chekyeon Publishing Co.: Seoul, Korea, 2018; pp. 34–35. [Google Scholar]
- Choi, Y. Challenges of Asian Models and Values for Sustainable Development. Sustainability 2019, 11, 1497. [Google Scholar] [CrossRef]
- Coto-Millán, P.; Casares-Hontañón, P.; Inglada, V.; Agüeros, M.; Pesquera, M.Á.; Badiola, A. Small is beautiful? The impact of economic crisis, low cost carriers, and size on efficiency in Spanish airports (2009–2011). J. Air Transp. Manag. 2014, 40, 34–41. [Google Scholar] [CrossRef]
- Bazargan, M.; Vasigh, B. Size versus efficiency: A case study of US commercial airports. J. Air Transp. Manag. 2003, 9, 187–193. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Gillen, D.; Lall, A. Developing measures of airport productivity and performance: An application of data envelopment analysis. Transp. Res. Part E Logist. Transp. Rev. 1997, 33, 261–273. [Google Scholar] [CrossRef]
- Lin, L.; Hong, C. Operational performance evaluation of international major airports: An application of data envelopment analysis. J. Air Transp. Manag. 2006, 12, 342–351. [Google Scholar] [CrossRef]
- Lam, S.W.; Low, J.M.; Tang, L.C. Operational efficiencies across Asia Pacific airports. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 654–665. [Google Scholar] [CrossRef]
- Liu, D. Measuring aeronautical service efficiency and commercial service efficiency of East Asia airport companies: An application of Network Data Envelopment Analysis. J. Air Transp. Manag. 2016, 52, 11–22. [Google Scholar] [CrossRef]
- Carlucci, F.; Cirà, A.; Coccorese, P. Measuring and Explaining Airport Efficiency and Sustainability: Evidence from Italy. Sustainability 2018, 10, 400. [Google Scholar] [CrossRef]
- Fung, M.K.Y.; Wan, K.K.H.; Van Hui, Y.; Law, J.S. Productivity changes in Chinese airports 1995–2004. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 521–542. [Google Scholar] [CrossRef]
- Chi-Lok, A.Y.; Zhang, A. Effects of competition and policy changes on Chinese airport productivity: An empirical investigation. J. Air Transp. Manag. 2009, 15, 166–174. [Google Scholar] [CrossRef]
- Yan, H.E.; Zhang, Y. The Operating Performance of Chinese International Airports—DEA-based Evaluation and Optimization. Logist. Sci-Tech 2011, 5, 4–7. [Google Scholar]
- Zou, B.; Kafle, N.; Chang, Y.-T.; Park, K. US airport financial reform and its implications for airport efficiency: An exploratory investigation. J. Air Transp. Manag. 2015, 47, 66–78. [Google Scholar] [CrossRef]
- Hong, S.-J.; Jeon, M. The Technical Efficiency of French Regional Airports and Low-Cost Carrier Terminals. Sustainability 2019, 11, 5107. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, P. Toward green IT: Modeling sustainable production characteristics for Chinese electronic information industry, 1980–2012. Technol. Forecast. Soc. Chang. 2015, 96, 62–70. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.; Wang, H. Energy and CO2 emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. Oper. Res. 2012, 221, 625–635. [Google Scholar] [CrossRef]
- Choi, Y.; Yu, Y.; Lee, H. A Study on the Sustainable Performance of the Steel Industry in Korea Based on SBM-DEA. Sustainability 2018, 10, 173. [Google Scholar] [CrossRef]
- Choi, Y.; Yang, F.; Lee, H. On the Unbalanced Atmospheric Environmental Performance of Major Cities in China. Sustainability 2020, 12, 5391. [Google Scholar] [CrossRef]
- Fan, L.; Wu, F.; Zhou, P. Efficiency measurement of Chinese airports with flight delays by directional distance function. J. Air Transp. Manag. 2014, 34, 140–145. [Google Scholar] [CrossRef]
- Chen, Y.; Jing, C. Chinese medium and large airports operational efficiency study based on three-stage SBM-DEA with Undesirable output. Technol. Ind. 2020, 20, 101–107. [Google Scholar]
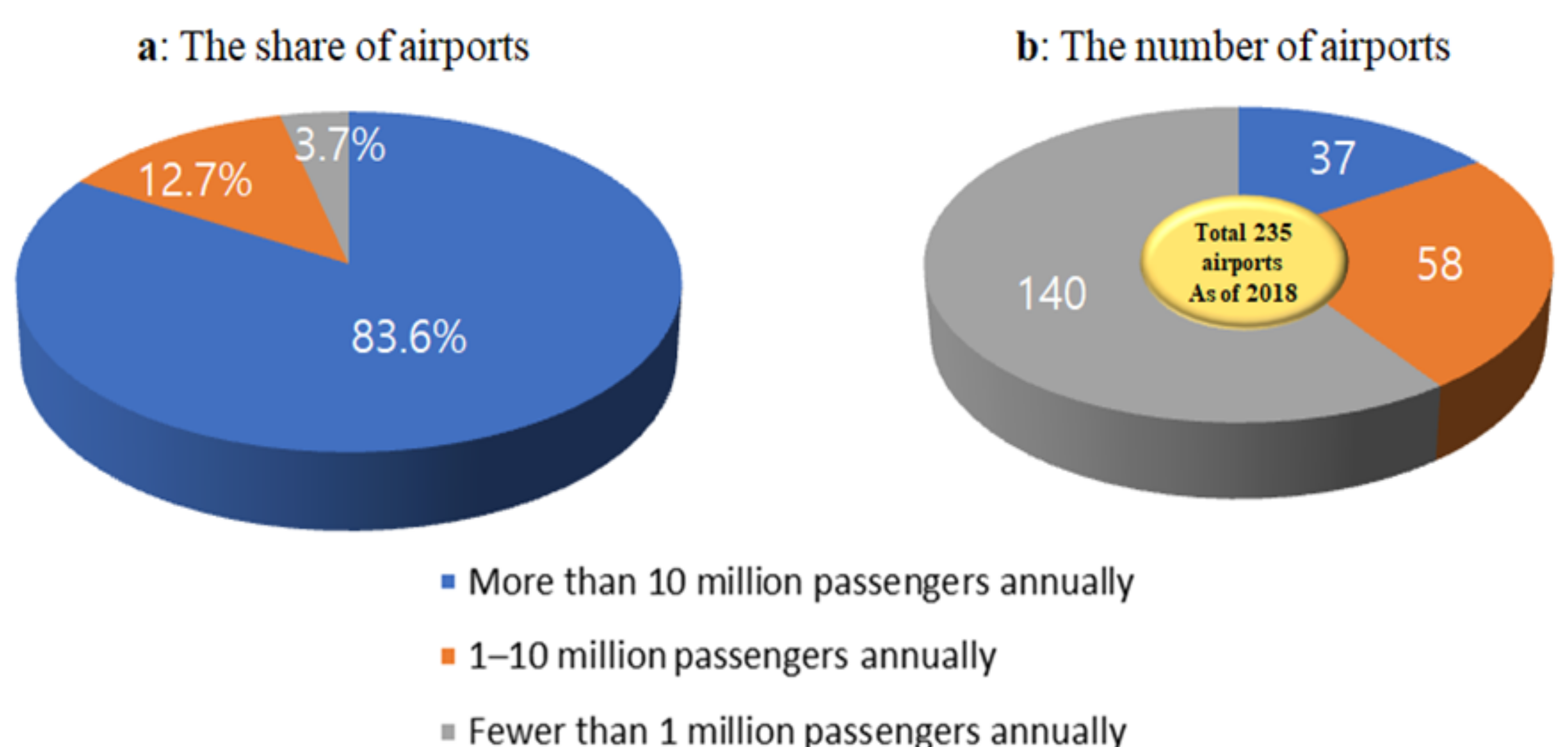
| Authors | Analysis Target | Period | Input | Output | Model |
|---|---|---|---|---|---|
| Gillen and Lall [10] | 21 airports in the U.S. | 1989–1993 | (1) number of runways (2) number of gates (3) terminal area (4) number of employees (5) number of baggage collection belts (6) number of public parking spots | (1) number of passengers (2) pounds of cargo (3) air carrier movements (4) commuter movements | DEA |
| Lin and Hong [11] | world’s 20 hub airports | 2003 | (1) employees (2) check-in counters (3) number of runways (4) parking spaces (5) baggage collection belts (6) number of aprons (7) boarding gates (8) terminal area | (1) movements (2) passengers (3) cargo | DEA |
| Lam, Low, and Tang [12] | 11 major airports in Asia Pacific | 2001–2005 | (1) labor (2) capital (3) soft input (4) trade value | (1) aeronautic movements (2) passengers (3) tons of cargo | DEA |
| Liu [13] | 10 East Asian airports | 2009–2013 | (1) runway area (2) staff costs (3) other operating costs | (1) passengers and cargo (2) operating revenues | Network DEA |
| Carlucci, Cirà, and Coccorese [14] | 34 Italian airports | 2006–2016 | (1) labor costs (2) invested capital (3) other expenses | (1) passenger movement (2) cargo (3) aircraft movements (4) revenue | DEA |
| Fung, Wan, Van Hui, and Law [15] | 25 regional airports in China | 1995–2004 | (1) length of runway(s) (2) terminal size | (1) passenger throughput (2) cargo throughput (3) aircraft movement | DEA, Malmquist index |
| Chi-Lok and Zhang [16] | 25 Chinese airports | 1995–2006 | (1) runway length (2) terminal size | (1) passenger volume (2) cargo volume (3) aircraft movement | DEA, regression |
| He and Zhang [17] | 30 Chinese airports | 2008 | (1) terminal area (2) width of mooring | (1) passenger volume (2) freight volume (3) aircraft movement | DEA |
| Zou, B. et al. [18] | 42 primary US airports | 2009–2012 | (1) labor cost (2) materials cost (3)capital cost | (1) passenger enplanements (2) cargo (3) aircraft operations (4) non-aeronautical revenue (5) delay | Two-staged DEA |
| Seock-Jin Hong and Minjun Jeon [19] | 99 French airports | 2006–2012 | (1) employees (2) labor costs (3) debt (4) subsidization (5) operational costs | (1) passenger (2) cargo (3) aircraft movements (4) revenue (5) net profit | DEA Malmquist |
| Variable | Type | Unit | Mean | Max | Min | Std. Dev. |
|---|---|---|---|---|---|---|
| Terminal Area | Input | 10,000 | 33.1 | 140.4 | 5.5 | 31.9 |
| Length of Runway | Input | m | 5532.4 | 15,000 | 3200 | 2838.3 |
| Freight | output | ton | 418,075.4 | 3,824,279.9 | 31,511.6 | 700,118.3 |
| Passengers | output | person | 27,127,735.7 | 100,983,290 | 6,130,384 | 19,845,769.8 |
| Aircraft movement | output | EA | 95,126.7 | 295,135 | 24,754 | 60,693.6 |
| Delay | output | % | 30.6 | 49.3 | 17.1 | 7.7 |
| Decision-Making Unit (DMU) | 2016 | 2017 | 2018 | 2019 | Average |
|---|---|---|---|---|---|
| Shanghai Pudong | 0.823 | 1.000 | 1.000 | 1.000 | 0.956 |
| Beijing Capital | 0.904 | 0.876 | 1.000 | 1.000 | 0.945 |
| Qingdao Liuting | 0.861 | 0.886 | 1.000 | 1.000 | 0.937 |
| Harbin Taiping | 0.837 | 0.844 | 1.000 | 1.000 | 0.920 |
| Shenzhen Bao’an | 0.771 | 0.827 | 0.939 | 1.000 | 0.884 |
| Xiamen Gaoqi | 0.710 | 0.743 | 1.000 | 0.893 | 0.837 |
| Chengdu Shuangliu | 0.638 | 0.682 | 0.807 | 1.000 | 0.782 |
| Guangzhou Baiyun | 0.555 | 0.605 | 0.690 | 1.000 | 0.713 |
| Xi’an Xianyang | 0.446 | 0.529 | 0.818 | 1.000 | 0.698 |
| Ningbo Lishe | 0.521 | 0.593 | 0.685 | 0.694 | 0.623 |
| Hangzhou Xiaoshan | 0.504 | 0.582 | 0.653 | 0.676 | 0.604 |
| Dalian Zhoushuizi | 0.477 | 0.556 | 0.594 | 0.651 | 0.570 |
| Haikou Meilan | 0.447 | 0.536 | 0.634 | 0.648 | 0.566 |
| Shanghai Hongqiao | 0.501 | 0.504 | 0.561 | 0.599 | 0.541 |
| Kunming Changshui | 0.408 | 0.449 | 0.486 | 0.495 | 0.460 |
| Sanya Phoenix | 0.398 | 0.440 | 0.485 | 0.503 | 0.457 |
| Hohhot Baita | 0.314 | 0.385 | 0.450 | 0.510 | 0.415 |
| Shenyang Taoxian | 0.356 | 0.388 | 0.430 | 0.483 | 0.414 |
| Jinan Yaoqiang | 0.339 | 0.363 | 0.450 | 0.498 | 0.413 |
| Urumchi Diwopu | 0.308 | 0.371 | 0.426 | 0.484 | 0.397 |
| Guiyang Longdongbao | 0.308 | 0.371 | 0.426 | 0.484 | 0.397 |
| Zhengzhou Xinzheng | 0.327 | 0.362 | 0.389 | 0.399 | 0.369 |
| Nanjing Lukou | 0.326 | 0.363 | 0.374 | 0.388 | 0.363 |
| Lanzhou Zhongchuan | 0.269 | 0.299 | 0.319 | 0.377 | 0.316 |
| Taiyuan Wusu | 0.255 | 0.291 | 0.335 | 0.349 | 0.308 |
| Changsha Huanghua | 0.251 | 0.272 | 0.307 | 0.344 | 0.294 |
| Nanning Wuxu | 0.264 | 0.288 | 0.314 | 0.325 | 0.298 |
| Chongqing Jiangbei | 0.272 | 0.277 | 0.296 | 0.319 | 0.291 |
| Fuzhou Changle | 0.271 | 0.279 | 0.305 | 0.303 | 0.290 |
| Tianjin Binhai | 0.262 | 0.304 | 0.311 | 0.279 | 0.289 |
| Nanchang Changbei | 0.180 | 0.200 | 0.304 | 0.391 | 0.269 |
| Wenzhou Longwan | 0.241 | 0.245 | 0.270 | 0.278 | 0.259 |
| Hefei Xinqiao | 0.206 | 0.233 | 0.262 | 0.317 | 0.255 |
| Changchun Longjia | 0.220 | 0.237 | 0.234 | 0.250 | 0.235 |
| Wuhan Tianhe | 0.189 | 0.199 | 0.229 | 0.251 | 0.217 |
| Zhuhai Jinwan | 0.135 | 0.164 | 0.212 | 0.233 | 0.186 |
| Shijiazhuang Zhengding | 0.126 | 0.125 | 0.142 | 0.159 | 0.138 |
| Average | 0.411 | 0.450 | 0.517 | 0.556 | 0.482 |
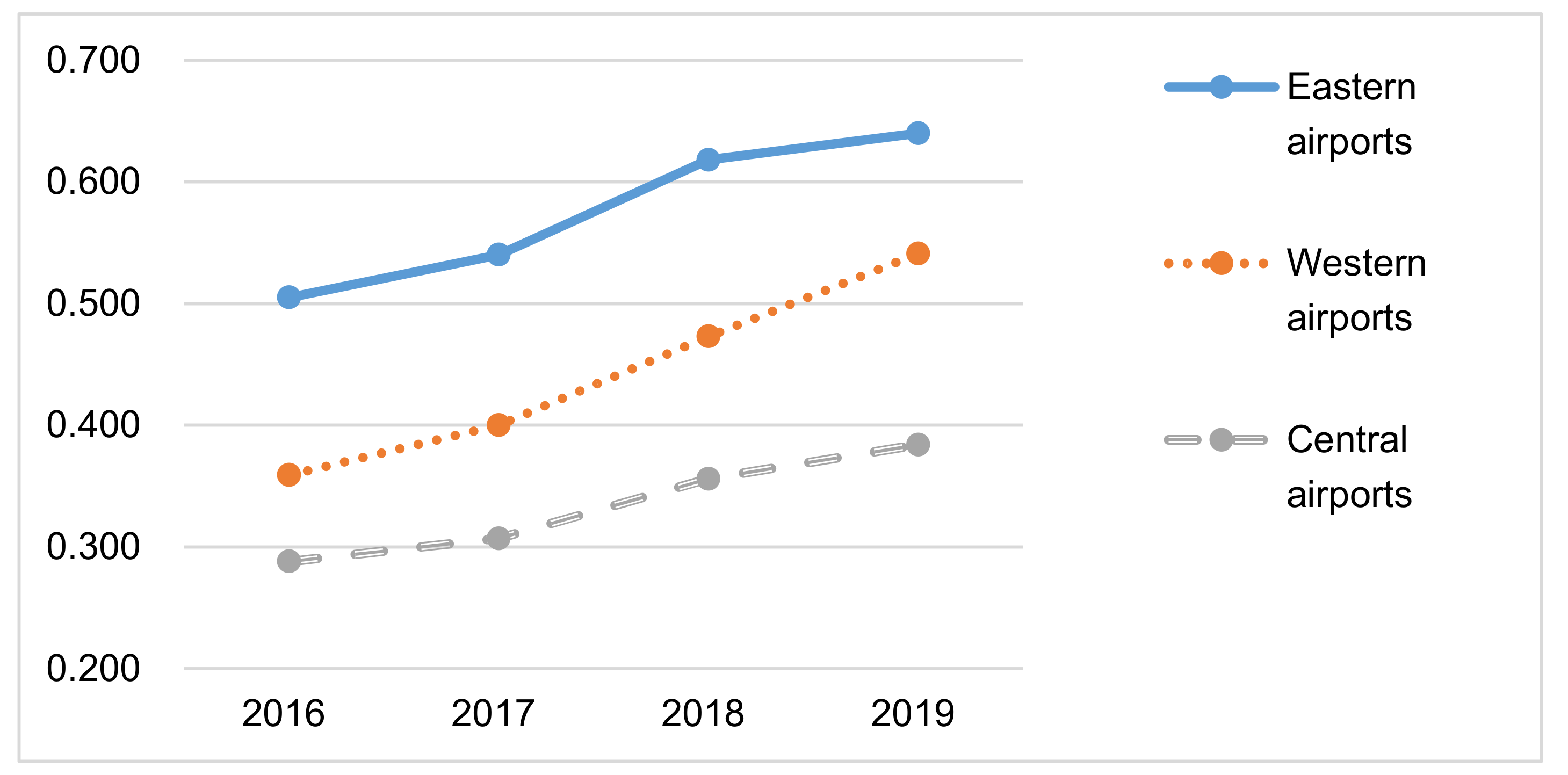
| Region | Obs | 2016 | 2017 | 2018 | 2019 | Average |
|---|---|---|---|---|---|---|
| Western | 9 | 0.359 | 0.401 | 0.473 | 0.541 | 0.443 |
| Central | 8 | 0.288 | 0.307 | 0.356 | 0.384 | 0.334 |
| Eastern | 20 | 0.505 | 0.540 | 0.618 | 0.640 | 0.571 |
| Test | Hypothesis | p-value | ||||
| Kruskal–Wallis | Western=Central=Eastern | 24.360 | 0.000 | |||
| DMU | 2016 | 2017 | 2018 | 2019 | Average | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Target | Slack | Target | Slack | Target | Slack | Target | Slack | Target | Slack | |
| Shanghai Pudong | 24.3 | −23.3 | 46.6 | 0 | 27.3 | 0 | 25.5 | 0 | 30.9 | −5.8 |
| Beijing Capital | 30.9 | −8.4 | 31.5 | −15.7 | 30.2 | 0 | 29.2 | 0 | 30.5 | −6.0 |
| Qingdao Liuting | 25.2 | 0.0 | 29.2 | −5.2 | 28.9 | 0.0 | 31.3 | 0.0 | 28.7 | −1.3 |
| Harbin Taiping | 20.4 | 0.0 | 26.7 | −6.3 | 27 | 0 | 29.9 | 0 | 26.0 | −1.6 |
| Shenzhen Bao’an | 20.5 | −14.4 | 22.9 | −13 | 24.7 | −1.2 | 26.3 | 0 | 23.6 | −7.2 |
| Xiamen Gaoqi | 26.5 | −14.4 | 27 | −22.3 | 35.4 | 0 | 28.7 | −13.7 | 29.4 | −12.6 |
| Chengdu Shuangliu | 20.5 | −4 | 23.6 | −7.7 | 22.8 | 0 | 21.9 | 0 | 22.2 | −2.9 |
| Guangzhou Baiyun | 30.1 | −5.9 | 32.1 | −4.6 | 26.9 | 0 | 21.5 | 0 | 27.7 | −2.6 |
| Xi’an Xianyang | 17.7 | 0 | 26.2 | 0 | 17.7 | 0 | 18.7 | 0 | 20.1 | 0.0 |
| Ningbo Lishe | 11.8 | −20.1 | 13.6 | −31.7 | 16.4 | −16.5 | 17.5 | −29.6 | 14.8 | −24.5 |
| Hangzhou Xiaoshan | 18.1 | −20.8 | 25.1 | −21.2 | 17.1 | −15 | 17.8 | −21.8 | 19.5 | −19.7 |
| Dalian Zhoushuizi | 11.8 | −9.7 | 16.6 | −9.4 | 17 | −3.9 | 19.5 | −5.1 | 16.2 | −7.0 |
| Haikou Meilan | 11.6 | −11.2 | 17.2 | −15 | 21.2 | −3.9 | 21.4 | −4.4 | 17.9 | −8.6 |
| Shanghai Hongqiao | 16.9 | −25.9 | 18.1 | −23.5 | 19.6 | −1.2 | 21.4 | −0.4 | 19.0 | −12.8 |
| Kunming Changshui | 19.6 | −5.1 | 22.1 | −10.8 | 23.2 | −1.2 | 21 | 0 | 21.5 | −4.3 |
| Sanya Phoenix | 14.9 | −12.3 | 19.1 | −16.2 | 20.7 | −7.5 | 21 | −7.8 | 18.9 | −11.0 |
| Hohhot Baita | 13.2 | −8.1 | 17.5 | −14.7 | 19.9 | −4.9 | 21.9 | −15.9 | 18.1 | −10.9 |
| Shenyang Taoxian | 6.6 | −18.1 | 7.9 | −28.4 | 8.9 | −23.4 | 9.7 | −24.6 | 8.3 | −23.6 |
| Jinan Yaoqiang | 7.2 | −14.3 | 11.6 | −17.2 | 14.9 | −5.1 | 15.8 | −11.6 | 12.4 | −12.1 |
| Urumchi Diwopu | 11.6 | −15.9 | 13.2 | −11.4 | 15 | −2.2 | 16.2 | −8.8 | 14.0 | −9.6 |
| Guiyang Longdongbao | 8 | −18.1 | 10.1 | −22.1 | 11.1 | −16.3 | 12.7 | −16.3 | 10.5 | −18.2 |
| Zhengzhou Xinzheng | 8.9 | −16.7 | 10.6 | −20.4 | 11.4 | −14.5 | 11.7 | −15.7 | 10.7 | −16.8 |
| Nanjing Lukou | 10.2 | −33.3 | 11.3 | −33.3 | 12 | −22.2 | 12.7 | −28.7 | 11.6 | −29.4 |
| Lanzhou Zhongchuan | 9.2 | −9.9 | 12.8 | −14.6 | 14.6 | −8.1 | 17.3 | −10.6 | 13.5 | −10.8 |
| Taiyuan Wusu | 8.4 | −9.7 | 13.7 | −17.7 | 15.7 | −8.8 | 15.8 | −15.6 | 13.4 | −13.0 |
| Changsha Huanghua | 9.1 | −20 | 11.5 | −21 | 13.6 | −11.1 | 16.3 | −12.3 | 12.6 | −16.1 |
| Nanning Wuxu | 5.1 | −22.7 | 6 | −34.7 | 6.4 | −24.3 | 6.6 | −25.3 | 6.0 | −26.8 |
| Chongqing Jiangbei | 15 | −6.2 | 15.6 | −10.1 | 16.3 | −3.7 | 17.2 | −2.8 | 16.0 | -5.7 |
| Fuzhou Changle | 5.3 | −23.2 | 5.4 | −35.2 | 6.0 | −24.3 | 6.1 | −34.0 | 5.7 | −29.2 |
| Tianjin Binhai | 7.8 | −20.9 | 9.2 | −27.7 | 9.7 | −18.2 | 9.1 | −26.6 | 9.0 | −23.4 |
| Nanchang Changbei | 3.6 | −18.3 | 4.9 | −28.1 | 7.9 | −18.8 | 7.8 | −23.3 | 6.1 | −22.1 |
| Wenzhou Longwan | 3.7 | −22.4 | 4.0 | −40.1 | 4.7 | −30.2 | 5.0 | −38.8 | 4.4 | −32.9 |
| Hefei Xinqiao | 3.5 | −22.4 | 4.1 | −35.5 | 4.8 | −29.7 | 6.5 | −35.0 | 4.7 | −30.7 |
| Changchun Longjia | 4.0 | −17.9 | 4.7 | −32.5 | 5.0 | −26.7 | 5.4 | −28.8 | 4.8 | −26.5 |
| Wuhan Tianhe | 9.5 | −17.1 | 10 | −22.1 | 10.2 | −13.1 | 11 | −15 | 10.2 | −16.8 |
| Zhuhai Jinwan | 5.8 | −36.9 | 4.1 | −42.1 | 7.2 | −19.7 | 8.3 | −24.4 | 6.4 | −30.8 |
| Shijiazhuang Zhengding | 3.7 | −20.9 | 7.6 | −35.6 | 4.9 | −25.5 | 4.9 | −32.6 | 5.3 | −28.7 |
| Average | 13.0 | −15.4 | 16.0 | −20.2 | 16.1 | −10.8 | 16.5 | −14.3 | 15.4 | −15.2 |
| DMU | 2016 | 2017 | 2018 | 2019 | Average | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PTAOE | SE | PTAOE | SE | PTAOE | SE | PTAOE | SE | PTAOE | SE | |
| Shanghai Pudong | 0.906 | 0.998 | 0.881 | 0.994 | 1.000 | 1.000 | 1.000 | 1.000 | 0.947 | 0.998 |
| Beijing Capital | 0.678 | 0.941 | 0.695 | 0.981 | 0.870 | 0.928 | 1.000 | 1.000 | 0.811 | 0.963 |
| Qingdao Liuting | 0.561 | 0.989 | 0.617 | 0.980 | 0.690 | 0.999 | 1.000 | 1.000 | 0.717 | 0.992 |
| Harbin Taiping | 1.000 | 0.837 | 0.909 | 0.929 | 1.000 | 1.000 | 1.000 | 1.000 | 0.977 | 0.942 |
| Shenzhen Bao’an | 1.000 | 0.861 | 0.912 | 0.972 | 1.000 | 1.000 | 1.000 | 1.000 | 0.978 | 0.958 |
| Xiamen Gaoqi | 0.829 | 0.992 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.957 | 0.998 |
| Chengdu Shuangliu | 0.785 | 0.982 | 0.837 | 0.988 | 0.951 | 0.987 | 1.000 | 1.000 | 0.893 | 0.989 |
| Guangzhou Baiyun | 0.858 | 0.520 | 0.535 | 0.989 | 1.000 | 0.818 | 1.000 | 1.000 | 0.848 | 0.832 |
| Xi’an Xianyang | 0.874 | 0.812 | 0.891 | 0.833 | 1.000 | 1.000 | 1.000 | 0.893 | 0.941 | 0.885 |
| Ningbo Lishe | 1.000 | 0.521 | 1.000 | 0.593 | 1.000 | 0.685 | 1.000 | 0.694 | 1.000 | 0.623 |
| Hangzhou Xiaoshan | 0.729 | 0.654 | 0.746 | 0.746 | 1.000 | 0.594 | 0.901 | 0.722 | 0.844 | 0.679 |
| Dalian Zhoushuizi | 0.533 | 0.946 | 0.592 | 0.984 | 0.668 | 0.978 | 0.681 | 0.993 | 0.619 | 0.975 |
| Haikou Meilan | 0.659 | 0.677 | 0.660 | 0.812 | 1.000 | 0.634 | 0.848 | 0.764 | 0.792 | 0.722 |
| Shanghai Hongqiao | 0.517 | 0.968 | 0.521 | 0.968 | 0.701 | 0.800 | 0.715 | 0.837 | 0.614 | 0.893 |
| Kunming Changshui | 0.436 | 0.936 | 0.458 | 0.981 | 0.512 | 0.949 | 0.560 | 0.884 | 0.492 | 0.938 |
| Sanya Phoenix | 0.558 | 0.551 | 0.600 | 0.618 | 0.907 | 0.469 | 1.000 | 0.484 | 0.766 | 0.531 |
| Hohhot Baita | 0.541 | 0.627 | 0.529 | 0.686 | 0.764 | 0.589 | 0.656 | 0.759 | 0.623 | 0.665 |
| Shenyang Taoxian | 1.000 | 0.314 | 0.516 | 0.747 | 1.000 | 0.450 | 0.615 | 0.829 | 0.783 | 0.585 |
| Jinan Yaoqiang | 0.604 | 0.660 | 0.600 | 0.732 | 0.649 | 0.747 | 0.660 | 0.763 | 0.628 | 0.726 |
| Urumchi Diwopu | 1.000 | 0.356 | 0.702 | 0.553 | 0.818 | 0.526 | 1.000 | 0.483 | 0.880 | 0.480 |
| Guiyang Longdongbao | 0.386 | 0.846 | 0.400 | 0.904 | 0.451 | 0.862 | 0.457 | 0.874 | 0.424 | 0.872 |
| Zhengzhou Xinzheng | 0.360 | 0.499 | 0.378 | 0.527 | 0.521 | 0.585 | 0.572 | 0.683 | 0.458 | 0.574 |
| Nanjing Lukou | 0.363 | 0.897 | 0.399 | 0.909 | 0.424 | 0.882 | 0.430 | 0.903 | 0.404 | 0.898 |
| Lanzhou Zhongchuan | 0.617 | 0.436 | 0.428 | 0.698 | 0.463 | 0.690 | 0.493 | 0.766 | 0.500 | 0.648 |
| Taiyuan Wusu | 0.371 | 0.836 | 0.381 | 0.837 | 1.000 | 0.342 | 0.413 | 0.865 | 0.541 | 0.720 |
| Changsha Huanghua | 0.306 | 0.819 | 0.324 | 0.841 | 0.363 | 0.846 | 0.392 | 0.878 | 0.346 | 0.846 |
| Nanning Wuxu | 1.000 | 0.255 | 0.426 | 0.682 | 0.491 | 0.681 | 0.484 | 0.721 | 0.600 | 0.585 |
| Chongqing Jiangbei | 0.472 | 0.559 | 0.490 | 0.587 | 0.540 | 0.582 | 0.549 | 0.592 | 0.513 | 0.580 |
| Fuzhou Changle | 0.363 | 0.568 | 0.388 | 0.600 | 0.443 | 0.591 | 0.489 | 0.647 | 0.421 | 0.602 |
| Tianjin Binhai | 0.335 | 0.812 | 0.307 | 0.902 | 0.407 | 0.728 | 0.430 | 0.742 | 0.370 | 0.796 |
| Nanchang Changbei | 0.417 | 0.650 | 0.409 | 0.682 | 0.462 | 0.659 | 0.448 | 0.677 | 0.434 | 0.667 |
| Wenzhou Longwan | 0.322 | 0.813 | 0.361 | 0.842 | 0.375 | 0.829 | 0.337 | 0.828 | 0.349 | 0.828 |
| Hefei Xinqiao | 0.425 | 0.567 | 0.413 | 0.592 | 0.474 | 0.569 | 0.483 | 0.576 | 0.449 | 0.576 |
| Changchun Longjia | 0.235 | 0.805 | 0.243 | 0.819 | 0.285 | 0.803 | 0.306 | 0.819 | 0.267 | 0.812 |
| Wuhan Tianhe | 0.445 | 0.495 | 0.428 | 0.554 | 0.453 | 0.517 | 0.473 | 0.529 | 0.450 | 0.524 |
| Zhuhai Jinwan | 0.219 | 0.618 | 0.265 | 0.619 | 0.341 | 0.621 | 0.353 | 0.660 | 0.295 | 0.630 |
| Shijiazhuang Zhengding | 0.265 | 0.475 | 0.252 | 0.498 | 0.292 | 0.485 | 0.309 | 0.514 | 0.280 | 0.493 |
| Average | 0.594 | 0.705 | 0.554 | 0.789 | 0.684 | 0.741 | 0.677 | 0.794 | 0.627 | 0.757 |
| Airport | RTS | Airport | RTS | ||
|---|---|---|---|---|---|
| Beijing Capital | CRS | Beijing Capital19(1.000000) | Nanning Wuxu | IRS | Shanghai Pudong18(0.187176); Shenzhen Bao’an19(0.054494) |
| Changchun Longjia | IRS | Shanghai Pudong18(0.195755) | Ningbo Lishe | IRS | Harbin Taiping19(0.580003); Shanghai Pudong18(0.007460) |
| Changsha Huanghua | IRS | Harbin Taiping19(0.258628); Shanghai Pudong18(0.312977) | Qingdao Liuting | CRS | Qingdao Liuting 19(1.000000) |
| Chengdu Shuangliu | CRS | Chengdu Shuangliu19(1.000000) | Sanya Phoenix | IRS | Harbin Taiping19(0.518708); Qingdao Liuting19(0.091059); Shanghai Pudong18(0.095369) |
| Dalian Zhoushuizi | IRS | Qingdao Liuting19(0.506938); Shanghai Pudong18(0.077388); Shenzhen Bao’an19(0.057721) | Shanghai Hongqiao | IRS | Shanghai Pudong19(0.106039); Shenzhen Bao’an19(0.709640) |
| Fuzhou Changle | IRS | Shanghai Pudong18(0.223351) | Shanghai Pudong | CRS | Shanghai Pudong19(1.000000) |
| Guangzhou Baiyun | CRS | Guangzhou Baiyun19(1.000000) | Shenzhen Bao’an | CRS | Shenzhen Bao’an19(1.000000) |
| Guiyang Longdongbao | IRS | Beijing Capital18(0.020047); Qingdao Liuting19(0.063486); Shenzhen Bao’an19(0.386065) | Shenyang Taoxian | IRS | Shanghai Pudong18(0.071972); Shenzhen Bao’an19(0.294502) |
| Harbin Taiping | CRS | Harbin Taiping19(1.000000) | Shijiazhuang Zhengding | IRS | Shanghai Pudong18(0.180212) |
| Haikou Meilan | IRS | Qingdao Liuting19(0.555693); Shanghai Pudong19(0.075054); Shenzhen Bao’an19(0.081226) | Taiyuan Wusu | IRS | Harbin Taiping19(0.455343); Shanghai Pudong18(0.081177) |
| Hangzhou Xiaoshan | IRS | Shanghai Pudong19(0.265953); Shenzhen Bao’an19(0.418153) | Tianjin Binhai | IRS | Shanghai Pudong18(0.332550) |
| Hefei Xinqiao | IRS | Harbin Taiping19(0.062757); Shanghai Pudong18(0.170089) | Wenzhou Longwan | IRS | Shanghai Pudong18(0.182839) |
| Hohhot Baita | IRS | Harbin Taiping19(0.722788); Shanghai Pudong18(0.010568) | Urumchi Diwopu | IRS | Harbin Taiping19(0.300731); Shanghai Pudong18(0.265034) |
| Jinan Yaoqiang | IRS | Harbin Taiping19(0.401150); Shanghai Pudong18(0.140069) | Wuhan Tianhe | IRS | Shanghai Pudong18(0.402404) |
| Kunming Changshui | IRS | Beijing Capital18(0.059523); Shanghai Pudong19(0.328773); Shenzhen Bao’an19(0.411288) | Xi’an Xianyang | CRS | Xi’an Xianyang19(1.000000) |
| Lanzhou Zhongchuan | IRS | Harbin Taiping19(0.493920); Shanghai Pudong18(0.091491) | Xiamen Gaoqi | IRS | Beijing Capital18(0.066600); Qingdao Liuting19(0.393833); Xiamen Gaoqi 18(0.406367) |
| Nanchang Changbei | IRS | Harbin Taiping19(0.087919); Shanghai Pudong18(0.188279) | Zhengzhou Xinzheng | IRS | Shanghai Pudong18(0.428688) |
| Nanjing Lukou | IRS | Shanghai Pudong18(0.465277) | Zhuhai Jinwan | IRS | Harbin Taiping19(0.156814); Shanghai Pudong18(0.130375) |
| Chongqing Jiangbei | IRS | Shanghai Pudong18(0.630748) | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Wen, H.; Lee, H.; Yang, H. Measuring Operational Performance of Major Chinese Airports Based on SBM-DEA. Sustainability 2020, 12, 8234. https://doi.org/10.3390/su12198234
Choi Y, Wen H, Lee H, Yang H. Measuring Operational Performance of Major Chinese Airports Based on SBM-DEA. Sustainability. 2020; 12(19):8234. https://doi.org/10.3390/su12198234
Chicago/Turabian StyleChoi, Yongrok, Hua Wen, Hyoungsuk Lee, and Hang Yang. 2020. "Measuring Operational Performance of Major Chinese Airports Based on SBM-DEA" Sustainability 12, no. 19: 8234. https://doi.org/10.3390/su12198234
APA StyleChoi, Y., Wen, H., Lee, H., & Yang, H. (2020). Measuring Operational Performance of Major Chinese Airports Based on SBM-DEA. Sustainability, 12(19), 8234. https://doi.org/10.3390/su12198234






