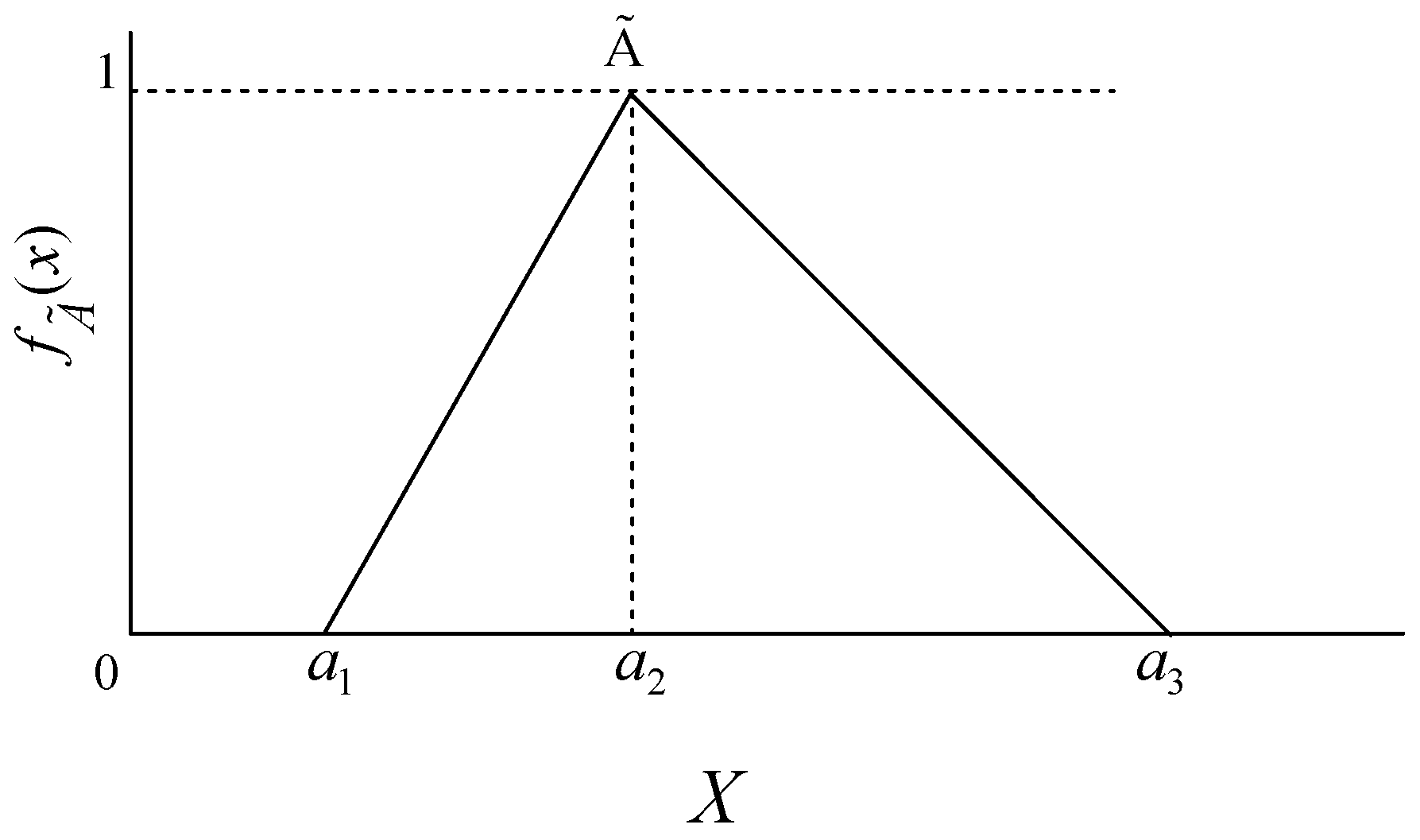1. Introduction
Concrete is a workable plastic mixture of cement, water, fine aggregates, and coarse aggregates in controlled proportions, for use in the construction industry [
1]. The concrete mixture parameters and water/cement (w/c) ratio affect the workability, strength, and durability, while the concrete mixture factors, namely, ratio of fine aggregate to cement (FA/c) and ratio of fine aggregate to total aggregate (FA/T) have an impact on concrete quality. There are other numerous concrete mixture factors such as cement type; minimum and maximum cement content; strength of cement; types, shape, and size of aggregates; aggregates grading; ratio of coarse aggregate and cement (CA/c); characteristics of concrete in green or hardened state; cost of concrete, etc., that influence the overall quality of concrete.
There are numerous methods to design the concrete mixture. The present study has considered three mixture design techniques, viz., the American Concrete Institute (ACI), Department of Energy (DOE), and Fineness Modulus (FM) mix design methods that have potentiality to include sustainable aspects in their design procedure; two advanced and one conventional concrete mixture design method are taken as alternatives in the MCDM model. The American Concrete Institute (ACI) mix design method considers workability, consistency, strength, and durability. The main principles of the ACI method are that the w/c ratio is inversely proportional to the design strength, the bulk volume of coarse aggregate per unit volume of concrete depends on the aggregate maximum size, and fine aggregate grading. The basic assumption made by the Department of Energy (DOE) mix design method is that the strength of the concrete is governed by the water/cement ratio. The other principles of the DOE method are that fine aggregate proportion varies with aggregate maximum size and water/cement ratio. The Fineness Modulus (FM) method for concrete mix design is based on the principle that the strength of the concrete depends on the water/cement ratio and the relative proportions of fine and coarse aggregate, such that the combined aggregate needs the least amount of cement paste for full compaction. This mixture method has not directly dealt with sustainability, though it takes care about environment aspects in its design approach.
The proper proportioning of constituents of concrete with sustainable qualitative performance can make concrete manufacturing sustainable. To prepare a concrete mixture with sustainable criteria, a proper mix design method, the most acceptable concrete mixture parameters, and optimum proportions of concrete ingredients are needed. The requirements of the concrete mixture may change due to material product characteristics having social, economic, and environmental constraints. The socioeconomic characteristics of sustainable criteria in the context of concrete include improvement to quality of life and cost reduction through high quality concrete properties and additional quality control personnel, optimum materials, and long life of produced concrete. The environmental characteristics of sustainable criteria in the context of concrete include lower CO
2 emission and natural resources consumption through optimum cement and water use in concrete production. Concrete mixture factors such as water/cement (w/c) ratio, density, ratio of fine aggregate to cement (FA/c), ratio of coarse aggregate and cement (CA/c), and cost of concrete may be used to satisfy the socioeconomic indicators of sustainable concrete. Concrete mixture factors such as water/cement (w/c) ratio, density, ratio of fine aggregate and total aggregate (FA/T), ratio of total aggregate to cement (T/c), and ratio of fine aggregate to cement (FA/c) can be used to satisfy the environmental indicators of sustainable concrete. Proper concrete proportioning along with optimum ratios of ingredients results in high durability of structures [
2] and helps to resolve the environment and socioeconomic issues. Alam et al. [
3] identified the factors concerning the quality of concrete production and pointed out that a proper concrete mix is one of the key factors which affects the quality of concrete. Ahmad [
4] studied concrete mixture proportion from the quality of concrete point of view and suggested that there exists an optimum ratio of fine aggregate and total aggregate (FA/T) and cement/fine aggregate (c/FA) ratio for improved quality. Zavadskas et al. [
5] emphasized that the application of Multicriteria Decision-Making (MCDM) techniques have great potential and sustainable decision-making in structural engineering, design, and building technology. An extensive body of literature is available in which MCDM approaches are used to tackle the selection of the right stackholder, the best practice or option, an optimum measure of right materials in concrete construction project management, and sustainable construction engineering. Zavadskas et al. [
6] present a summary of published research related to the application of basic decision-making frameworks and processes, along with advanced MCDM techniques for sustainability in the construction engineering discipline. A broader review of MCDM approaches and their applications in civil engineering are due to Kabir et al. [
7]. Stojcic et al. [
8] discussed the application of MCDM for sustainability in the engineering field. Monghasemi et al. [
9] introduced a new MCDM model to optimize the construction time, construction cost, and construction quality of projects. Alhumaidi [
10] proposed an MCDM technique considering a multi-attribute fuzzy weighted average approach for project contractor selection. Taylon et al. [
11] used a hybrid fuzzy Analytic Hierarchy Process (fuzzy-AHP) and fuzzy TOPSIS MCDM technique for assessing the selection criteria and risk criteria of construction projects. Hamdia et al. [
12] develop the reinforced cement concrete (RCC) building damage assessment criteria using the fuzzy analytic hierarchy process. The application of the MCDM technique to structural retrofitting procedures for buildings and bridges repairs is due to Caterino et al. [
13] and Rashidi et al. [
14]. They conclude that technique for order preference by similarity to ideal solution (TOPSIS) and the methodology of VIKOR (Vlse Kriterijumska Optimizacija I Kompromisno Resenje in Serbian) are more suitable for selecting retrofit procedures. Zhao et al. [
15] propose a coupled MCDM method, intervalued trapezoidal intuitionistic fuzzy number (IVTIFN), and a TOPSIS method to support the selection of pipe materials in building projects. The Fuzzy extended analytical hierarchy process (FEAHP) technique is proposed by Akadiri et al. [
16] for ranking building materials. Falqi et al. [
17] apply a TOPSIS method in a fuzzy environment for siliceous material management for sustainable concrete construction. Ahmed et al. [
18] propose a hybrid MCDM approach to select a concrete mixture design method for the production of high-performance concrete. Bera et al. [
19] suggested multi-attribute decision-making (MADM) to choose an appropriate proportion of silty sand and artificial clay for soil stabilization based on a mixing design approach.
It is clear from the literature review that a number of applications of MCDM techniques in construction industries for the incorporation of sustainability in various construction engineering processes and management are available. However, MCDM techniques’ application related to sustainable concrete quality management through a sustainable concrete design process is scarce. The present study is a contribution to the application of a MCDM technique to develop a concrete mixture design process for sustainable concrete quality management. Potential concrete design methods and mixture factors considering environmental and social–economic sustainable issues in a multicriteria selection problem of the concrete design process, particularly suitable for sustainable concrete quality management, are proposed. The criteria, namely workability, strength, and durability, and sub-criteria, namely water/cement (w/c) ratio, density, ratio of fine aggregate to cement (FA/c), ratio of coarse aggregate and cement (CA/c), ratio of fine aggregate and total aggregate (FA/T), and cost of concrete are so selected to satisfy the technical, environmental, and socioeconomic indicators of sustainable concrete, along with design mix methodology requirements.
The fuzzy TOPSIS approach, which has demonstrated its applicability in different fields, is applied by developing a concrete mixture design process to produce sustainable quality concrete, taking into account concrete mixture design methods that have the potential to adapt sustainability and prevailing concrete mixture factors that require the environmental and socioeconomic aspects of sustainability. The rating of concrete mixture design methods and concrete mixture factors is based on the decision-maker’s weighted criteria. The reason for choosing the fuzzy TOPSIS method is to select the best alternative to evaluate the most suitable and unsuitable alternative together.
2. Multicriteria Decision-Making Based on Fuzzy Sets Theory
Zadeh [
20] introduced the theory of fuzzy sets to describe linguistic concepts in the decision-making process with a view to reducing human judgment complexity. Bellman and Zadeh [
21] developed a fuzzy MCDM approach to tackle the lack of precision and uncertainty, and to assign significance to the weights of the parameters and to the ratings of alternatives for the assessment criteria [
22]. The study simplifies the important fuzzy concept by modifying the fuzzy concept.
“Let X be the universe of discourse, . A fuzzy set of X is a set of order pairs , where , is the membership function of , and stands for the membership degree” of in .
The
-cut
and strong
-cut
of the fuzzy set
in the universe of discourse,
X is defined by [
20]
“A fuzzy set
of the universe of discourse
X is convex if and only if every
is convex, that is
is a closed interval of
. It can be written as”
“The triangular fuzzy number (TFN) introduced by Zadeh [
20] can be defined as a triplet
and the membership function of the fuzzy number”
is defined as in
Figure 1.
According to Chen’s vertex method [
23], the difference between the fuzzy numbers
and
, which are parameterized by the triplets
and
, respectively, and can be calculated as
3. Fuzzy TOPSIS Method
A linear weighting technique, the TOPSIS method was first introduced in the crisp version by Chen and Hwang [
24], with reference to Hwang and Yoon [
25]. In MCDM, the criteria may be of varying significance and therefore, require different weights [
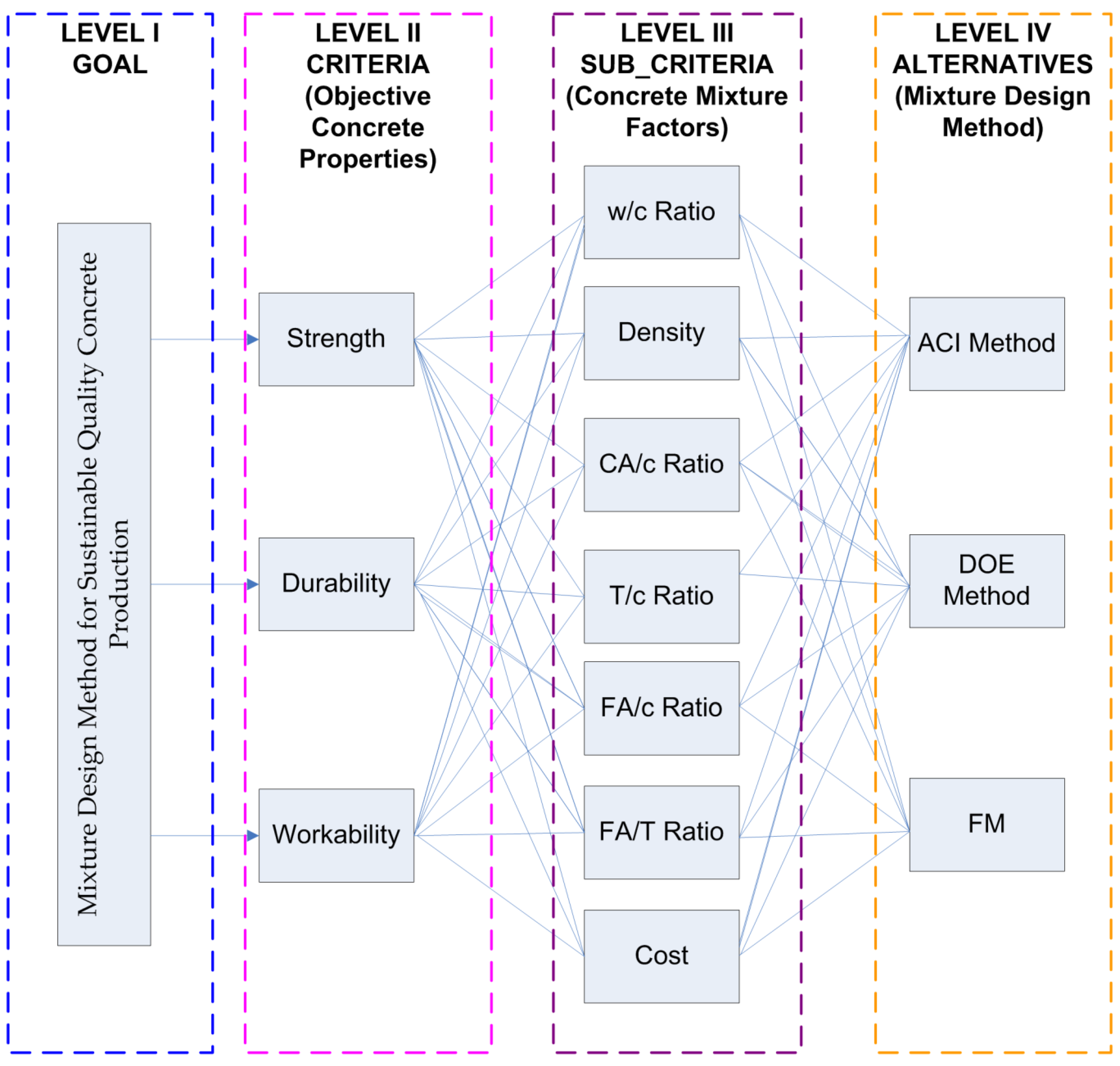
26]. The weights can be allocated using a range of methods, for example, analytic hierarchy process (AHP), analytic network process (ANP), entropy analysis, eigenvector method, etc. The proposed TOPSIS approach in the fuzzy environment is implemented to the problem of selecting an effective mix design method for the production of quality concrete. Problem formulation defines the goals of the problem, the assessment criteria, the decision-makers, and their classes. The framed problem, consisting of a four-level hierarchy, namely, goal (level 1), criteria (level 2—objective properties for sustainable quality concrete), sub-criteria (level 3—significant mixture parameters for sustainable quality concrete), and alternatives (level 4—popular mixture design methods effective for sustainable quality concrete), is depicted in
Figure 2. Three potential concrete mixture design methods for sustainability, the Department of Energy (DOE) method, the American Concrete Institute (ACI) method, and the Fineness Modulus (FM) method, with objective properties such as strength, workability, and durability, etc., required for sustainable quality concrete are considered in the model framework. The seven mixture factors, which include the proposed dominant mix factors for the production of sustainable quality concrete, i.e., environmental and socioeconomic aspects, namely density (environmental criteria), the cost, ratio of water and cement (w/c), ratio of total aggregate and cement (T/c), ratio of coarse aggregate and cement (CA/c), ratio of fine aggregate and cement (FA/c), and ratio of fine aggregate/total aggregate (FA/T) (socioeconomic criteria) are taken into consideration.
The problem criteria (objective properties) and sub-criteria (concrete mixture factors for sustainability quality concrete) are selected based on the opinion of experts and published literature [
27,
28,
29,
30,
31,
32] related to the design of concrete mixture. Helmi [
32] reported that the mix design process plays a significant role in comparing different sub-criteria of strength, workability, and durability, viz., “ratios of CA/c, T/c, w/c density, FA/T, FA/c” and the cost of determining an appropriate mixture design method for quality concrete production. The published data with international mix design methods for concrete mixture and mixture proportion factors to obtain quality concrete are presented in
Table 1.
The decision-makers’ group (consisting of five concrete technology and quality management experts, and consultants) was asked to judge and rank the selected seven dominant concrete mixture factors based on sustainability issues. The set questionnaire was given to the decision-makers’ group for their opinion, as shown in
Appendix A and
Appendix B. Initially, they were supplied seven questions about criteria rating using five linguistic variables [
33], namely very high, high, medium, low, and very low, along with TFN, as given in
Appendix A, reflecting the importance weights of performance criteria to judge the ability of the mix design method to produce sustainable quality concrete. In order to rank the mix design methods for concrete quality management, furthermore, the adopted criteria were used to assess the output of each mix design method for sustainable concrete quality management using Zelany’s notion [
34] i.e., “displaced ideal separated away from the ideal solution the least”. As per Hwang and Yoon [
25], in order to fix problems with MCDM, the selected alternative should not only have the shortest distance from the positive ideal reference point (PIRP), but also the longest distance from the negative ideal reference point (NIRP). Using Chen’s [
23] method, another set of questionnaires, as shown in
Appendix B, comprising seven questions each for the mixture design method alternatives, i.e.,
A1,
A2, …,
An, is given, in order to rate their individual capabilities concerning various sub-criteria already set aside. The overall performance of each mixture design method was assessed based on their sustainable performance and the opinion of experts collected earlier in linguistic variables viz., very good, good, fair, poor, and very poor, along with triangular fuzzy numbers. This method’s algorithm is defined in the following section.
3.1. Fuzzy Decision Matrix Construction for a Sustainable Quality Concrete Production Problem
Given m alternatives for the mix design method, selection criteria (
n), and expert group (k) comprising decision-makers (DM), a typical fuzzy multicriteria group decision-making shipper problem can be expressed in matrix format as below.
“where
A1,
A2, …,
Am are the alternatives to be chosen,
C1,
C2, …,
Cn denote the evaluation criteria for preferential mix design method, and
represents the rating of alternative
Ai with respect to criterion
Cj evaluated by k decision-makers”. Since the interpretation of the preferential mix design approach depends on an individual’s expertise, this study uses the mean value method to combine fuzzy output score
for
k decision-makers with the same assessment criteria, i.e.,
“where
is the rating of alternative
Ai with respect to criterion
Cj evaluated by the
kth decision-maker and
”.
3.2. Fuzzy Decision Matrix Normalization for a Sustainable Quality Concrete Production Problem
The various criteria needed to choose a preferred mix design method are quantified in various units; therefore, they need normalization. The current case utilizes the linear scales transform normalization function to maintain the characteristics that normalized TFN ranges should be included in [0, 1]. If
indicates the normalized fuzzy decision matrix [
25]
where
3.3. Weighted Normalized Fuzzy Decision Matrix Construction for a Sustainable Quality Concrete Production Problem
Given the different weight of each criterion, it is possible to determine the weighted normalized decision matrix by multiplying the importance weights of evaluation criteria and values in the normalized fuzzy decision matrix. The weighted normalized matrix of decisions is defined by
where
represents the importance weight of criterion
obtained through
“where
k is the number of members in a decision-makers’ group and
represents the fuzzy weight of
jth criteria assessed by
kth decision-makers”.
3.4. FPIRP and FNIRP Determination
The fuzzy positive ideal reference point (FPIRP, A+) and a fuzzy negative ideal reference point (FNIRP, A−) in the interval [0, 1] can be represented as,
where
and
,
3.5. Determination of Each Concrete Mixture Construction Process Distances to FPIRP and FNIRP
Estimation of each concrete mixture construction process distance to FPIRP and FNIRP can be carried out respectively as:
“where,
, denotes the distance measurement between two fuzzy numbers,
represents the distance of alternative
Ai from FPIRP, and
is the distance of alternative
Ai from FNIRP”.
3.6. Development of Closeness Coefficient (CC) and the Potential Alternatives Order
When the CC is calculated, all the potential alternative orders may be identified, permitting decision-makers to choose the most realistic alternative. Each alternative’s closeness coefficient is determined as
An alternative with index approaching 1 indicates that the alternative is close to the fuzzy positive ideal reference point and far from the fuzzy negative ideal reference point. A high closeness index value suggests better performance of the alternative Ai.
5. Discussion
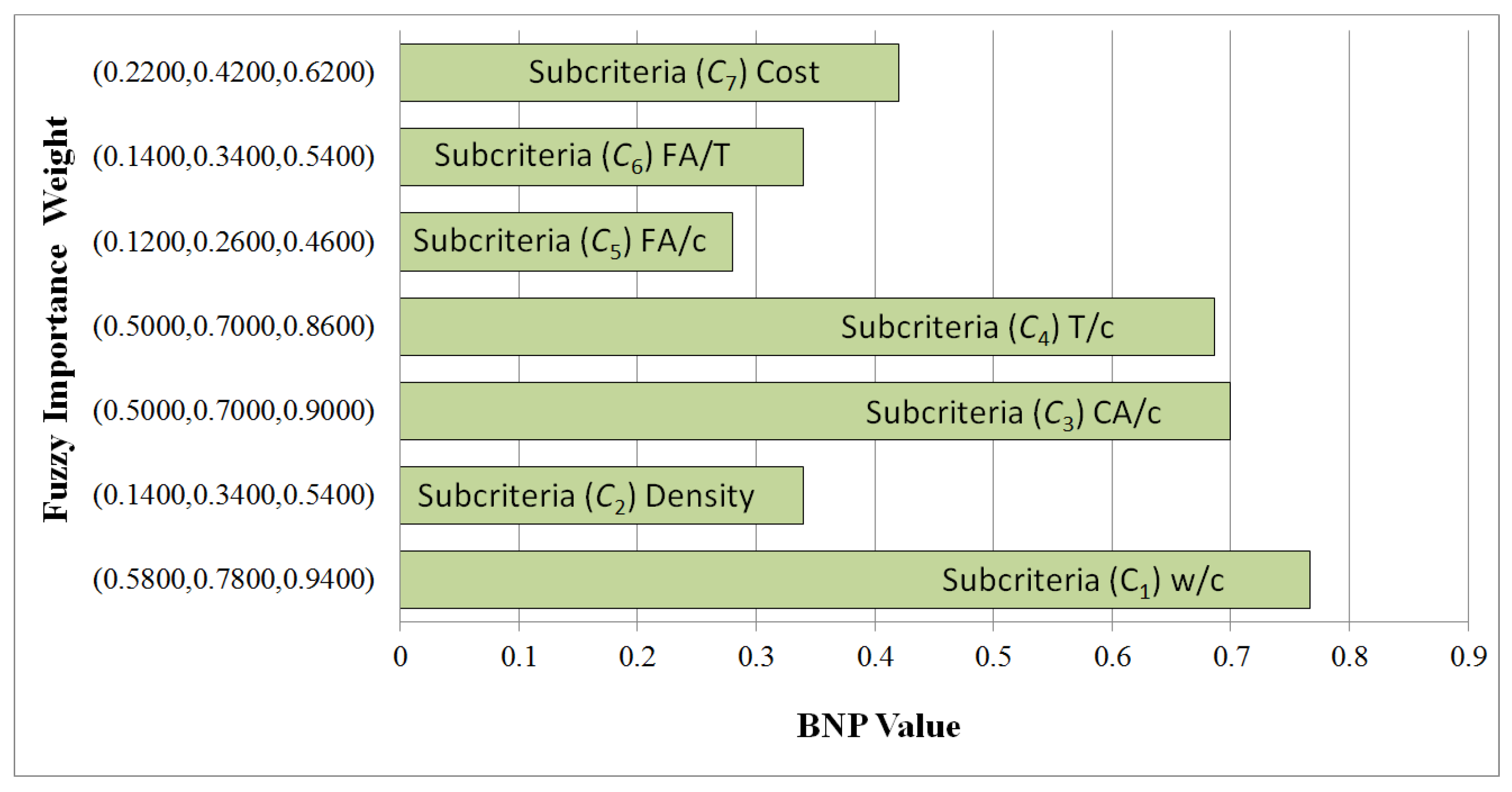
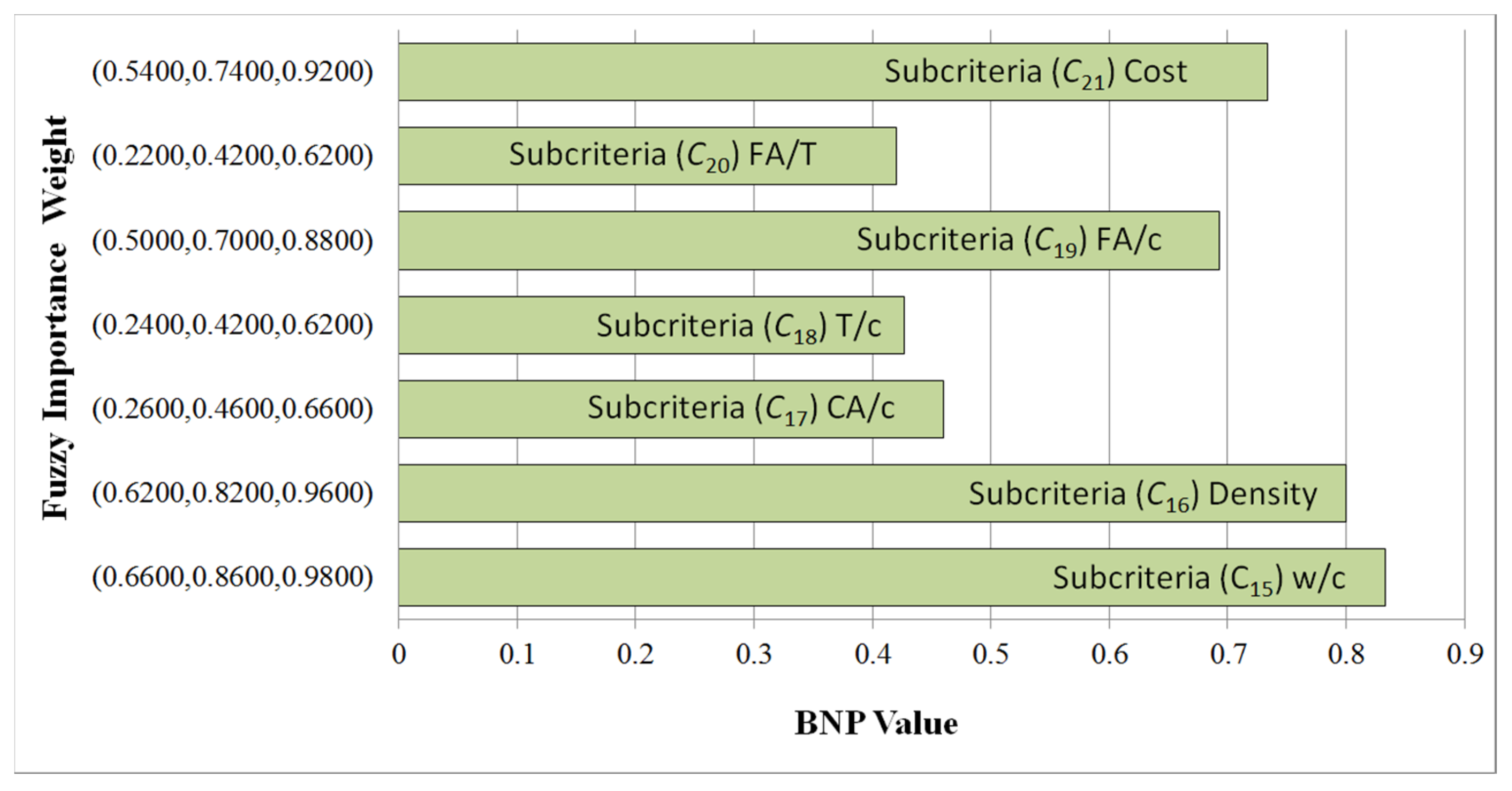
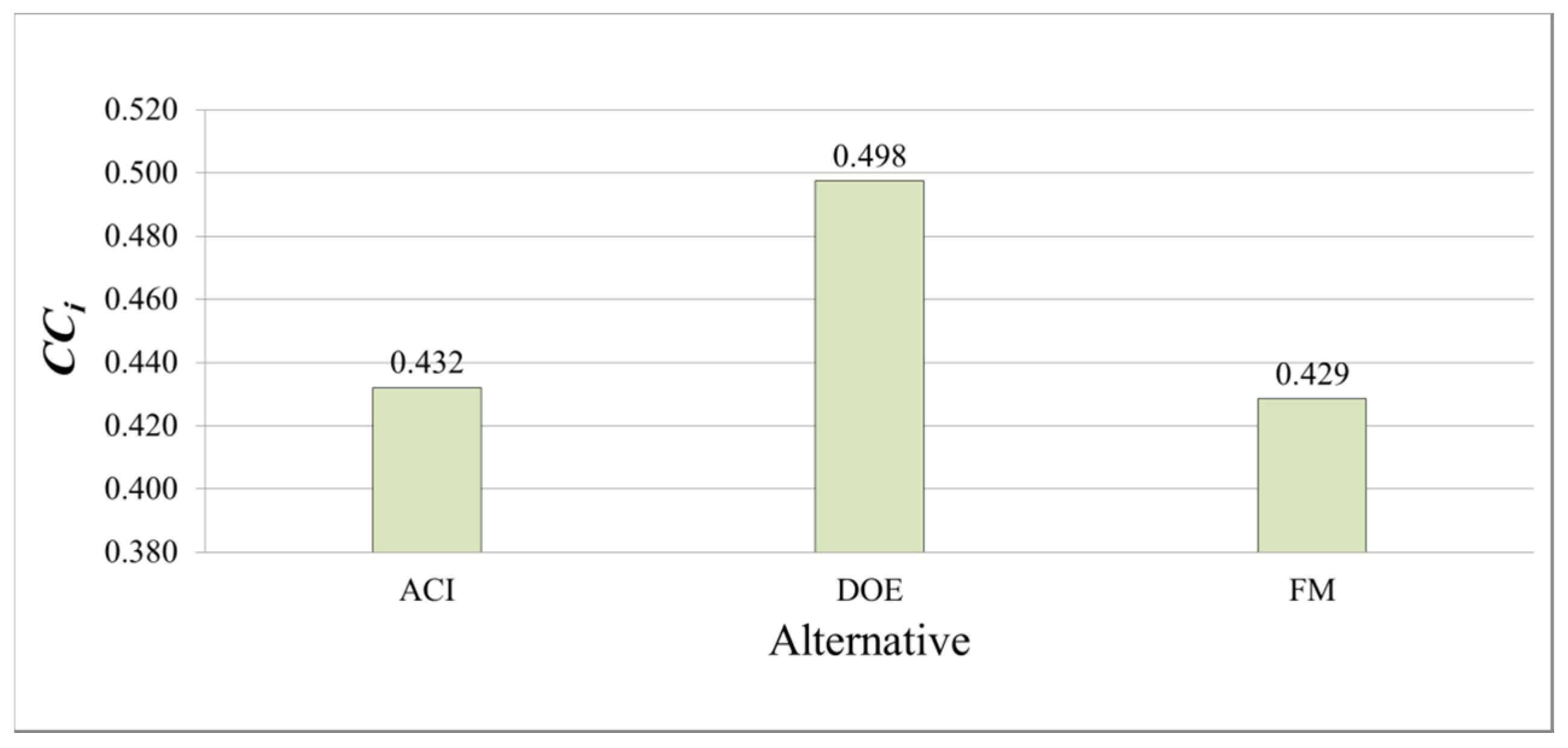
The result of the fuzzy TOPSIS method is implemented to select the concrete mix design technique with the most potential for sustainable concrete quality management considering objective properties and dominant concrete mixture factors considering socioeconomic and environmental aspects. The dominant concrete mixture factors for concrete considering socioeconomic and environmental issues are taken from the published literature and expert opinions. Fuzzy TOPSIS may provide an ideal solution to the issue of selecting the most possible method of developing concrete mixtures to achieve the goal of sustainable concrete. The ideal approach refers to having an alternative, a set of criteria, and sub-criteria having optimum performance (high potential for sustainable performance of concrete), whereas the negative ideal solution is just contrary, possessing the poorest performance (least potential for sustainable performance of concrete). Those that have the shortest distance from FPIRP and the farthest from FNIRP are the best options or decisions. Optimally, the closeness coefficient (CC) of mixture design methods close to 1 has the shortest distance from the FPIRP and the highest distance from FNIRP. In other words, a large closeness coefficient attained for any mixing design method provides better sustainable performance. It is evident that the CC value is governed by the criteria weight provided by decision-makers and the performance established by each mixture design method against the respective criteria.
After observing the importance weight ranking of the sub-criteria with respect to criteria (objective properties, namely workability, strength, and durability) for alternative (mixture design methods) selection for quality management, it is revealed that among sub-criteria (concrete mixture factors), the water and cement (w/c) ratio of the concrete mix ingredients is the most influential factor in the concrete mix design procedure suitable for sustainable quality concrete development. The proposed model outputs are also consistent with the results of Neville [
1] and Yurdakul [
31] related to sustainable concrete quality. Another more dominant concrete mixture factor for sustainable concrete quality is density. This seems consistent as sustainable concrete quality will depend on the density of concrete. The sub-criteria (concrete mixture factors) found to be least influential for quality concrete mixture includes the fine aggregate/cement ratio and the fine aggregate/total aggregate ratio. This seems acceptable as fine aggregate has no known relationship with the cement content and total aggregate content. The Department of Energy (DOE) method has a maximum value of CC (0.4975), so this method has the potential to design a concrete mixture for sustainable high-quality concrete. Other methods have similar CC value (0.4322 and 0.4285) and have equal potential for the design of a sustainable quality concrete mixture. The results of the MCDM model suggested above are also consistent with Helmy’s [
32] conclusion that the DOE mixture design method produced a mix with the lowest cement content and gave the most environmentally effective method among all the concrete mixtures found from the other mix design methods (ACI method and others).