Seasonality Effect Analysis and Recognition of Charging Behaviors of Electric Vehicles: A Data Science Approach
Abstract
1. Introduction
2. Methods
2.1. Regression Models
2.1.1. Quassi-Poisson Regression
2.1.2. Random Forest Regression
2.2. Classification Models
3. Data Preparation
4. Case Analysis
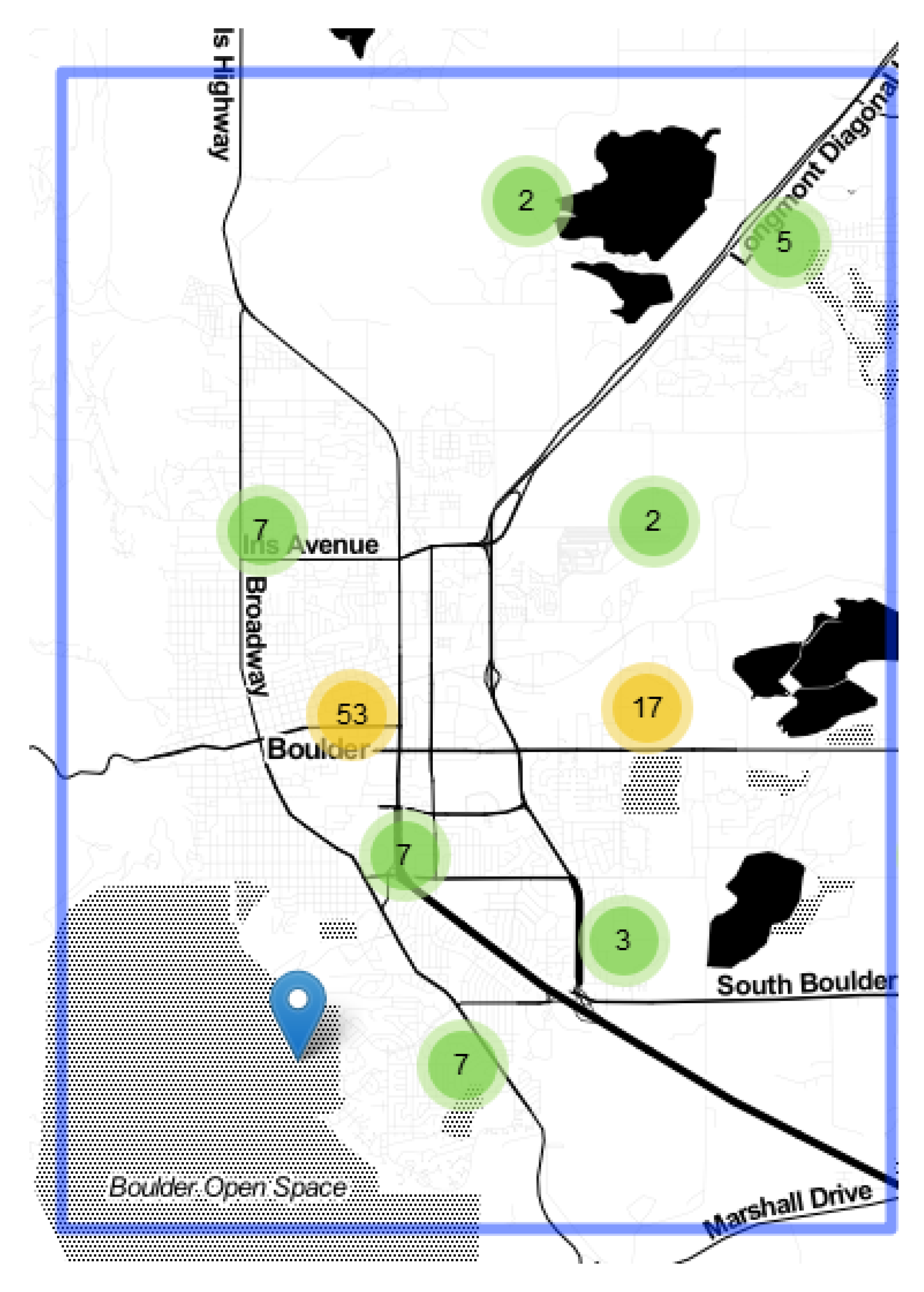
4.1. EVs Charging Stations in Boulder
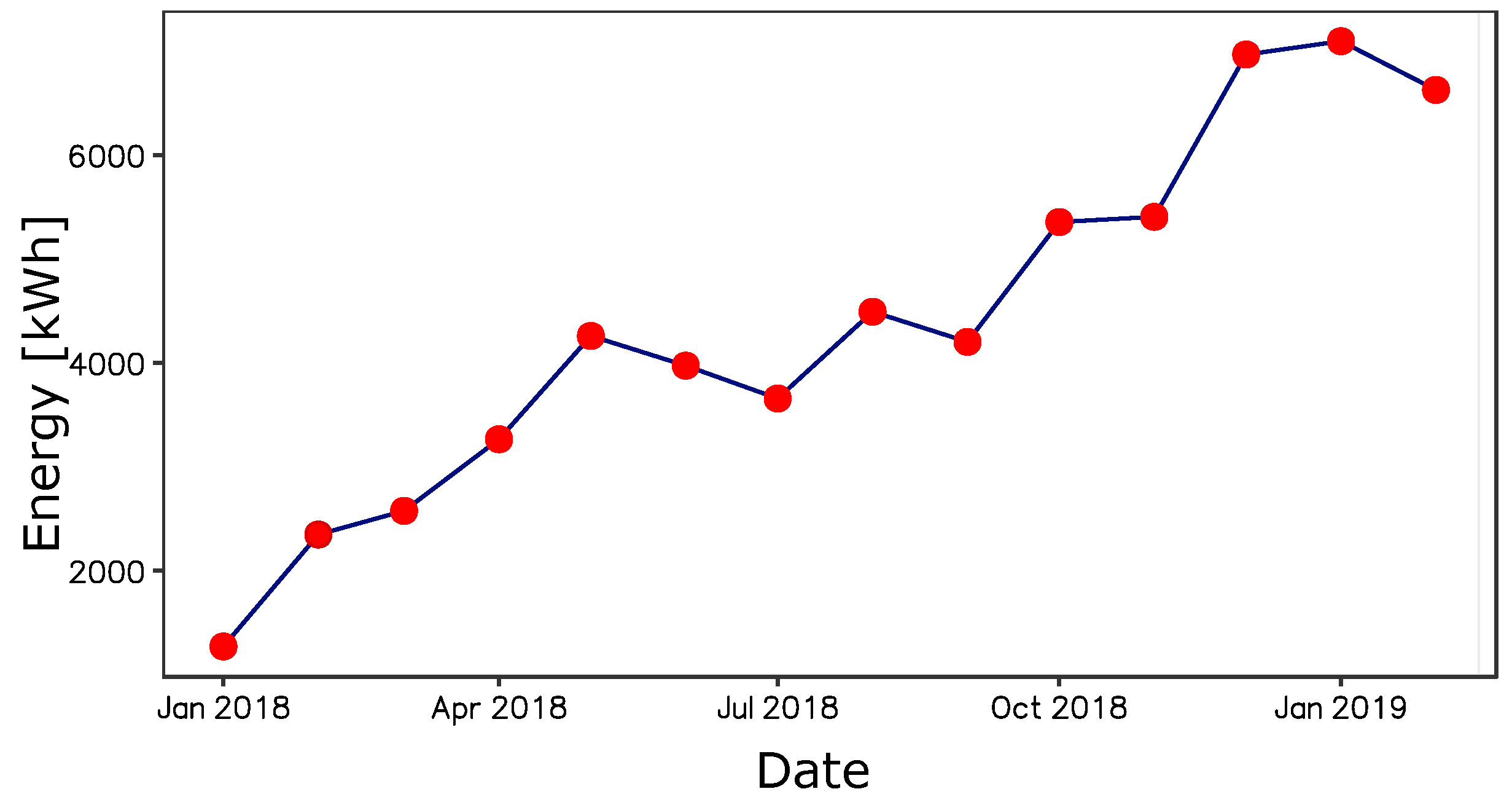
4.2. Exploratory Analysis
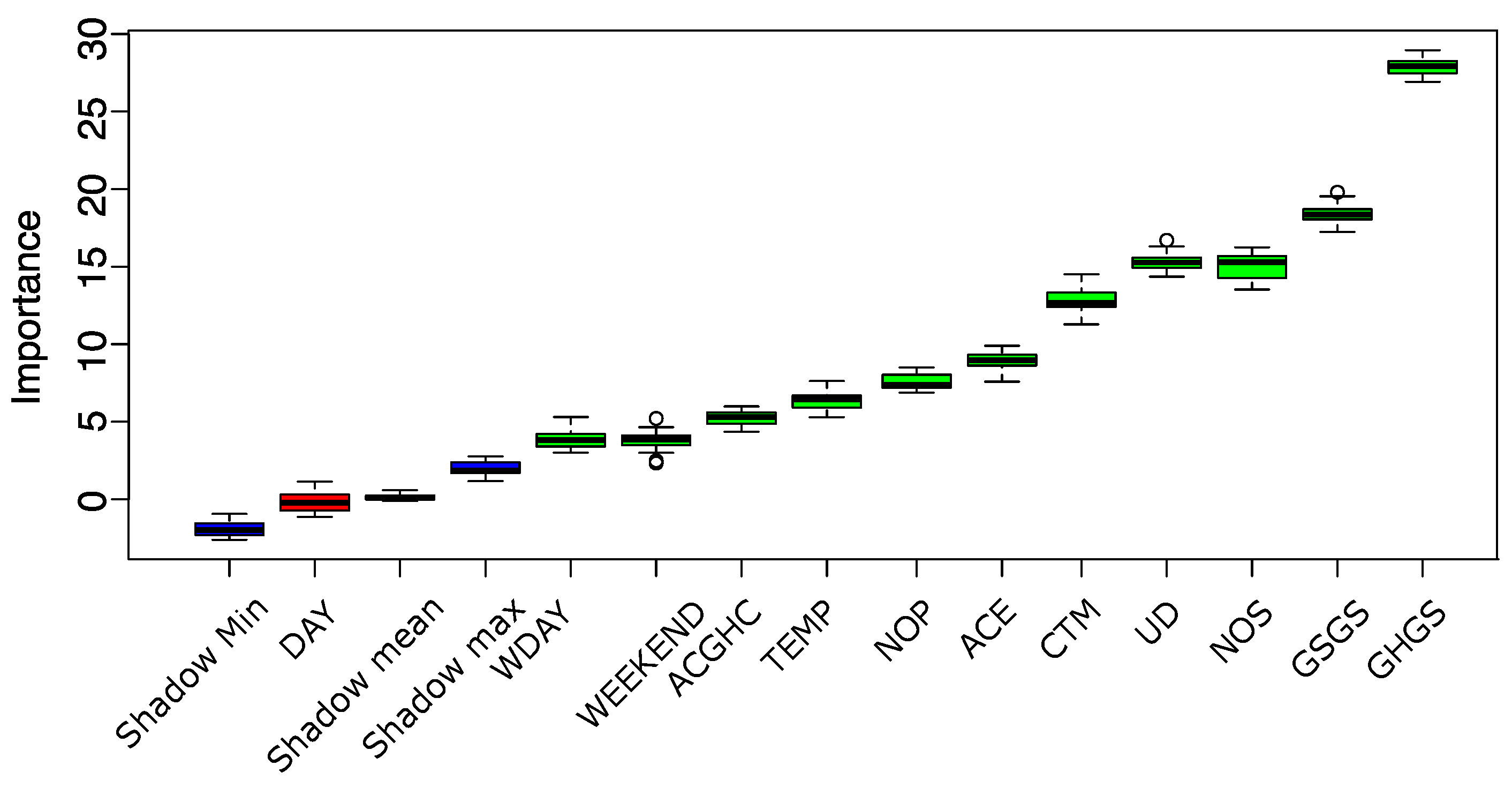
4.3. Feature Importance
- First, it duplicates the dataset, and rearrange the values in each column. These values are called shadow features. Then, it trains a classifier on the dataset. By this means, this model provides an idea of the importance through the accuracy for each of the features of the dataset. The higher the score, the better or more important.
- Then, the algorithm checks for each of your real features if they are importance. Each feature is evaluated through the Z-score i.e., the number of standard deviations from the mean a data point is. Then, the importance of each feature is depends on whether the feature has a higher score than the maximum score of the shadow features. If they do, they are taken into account. These are called hits. Next, another iteration is performed. After a predefined set of iterations, the algorithm provides with a table of these hits.
- At every iteration, the model compares the Z-scores of the shuffled copies (shadows features) and the original variables to see if the latter outperformed the former. If so, then the algorithm marks the feature as important. In summary, the algorithm validates the importance of the feature by comparing with random shuffled copies, fact that boost up the robustness.
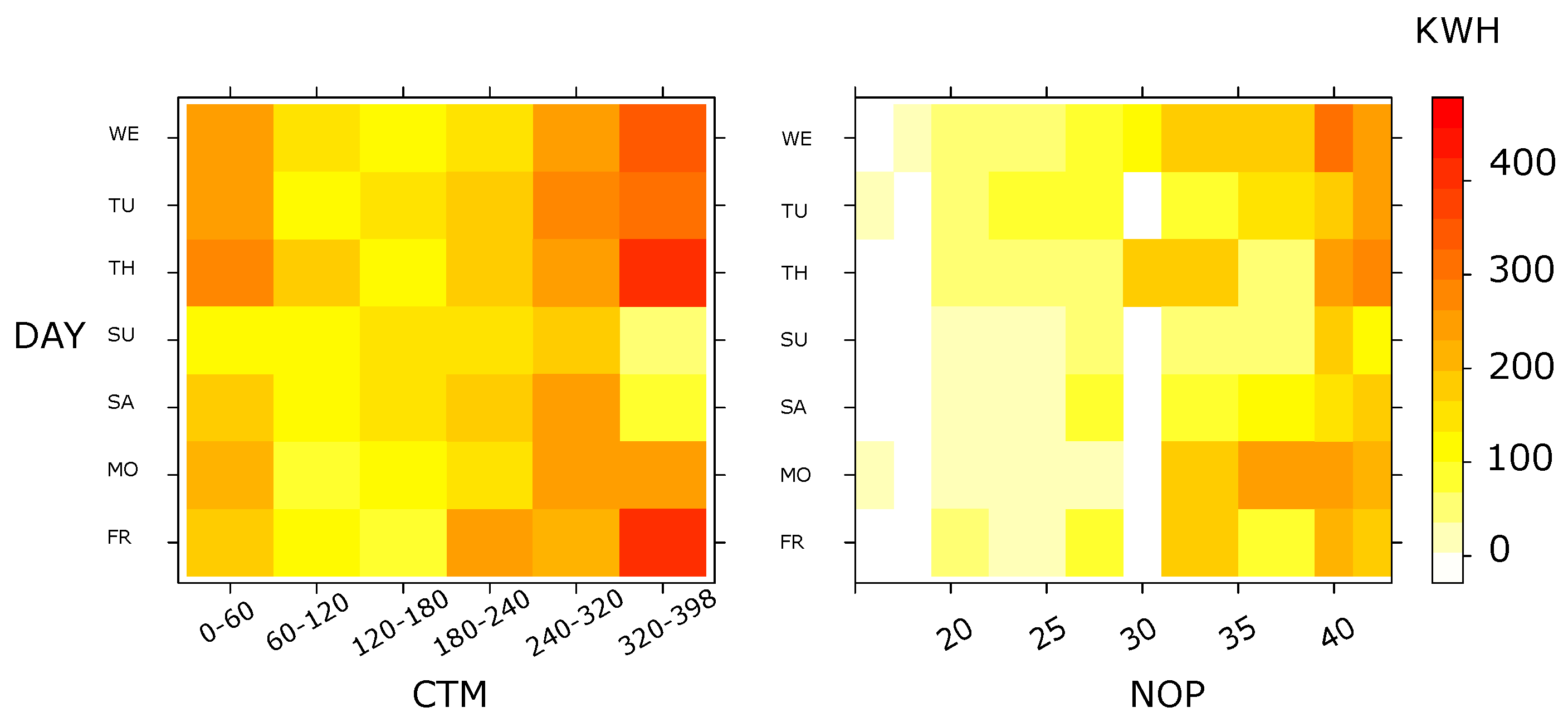
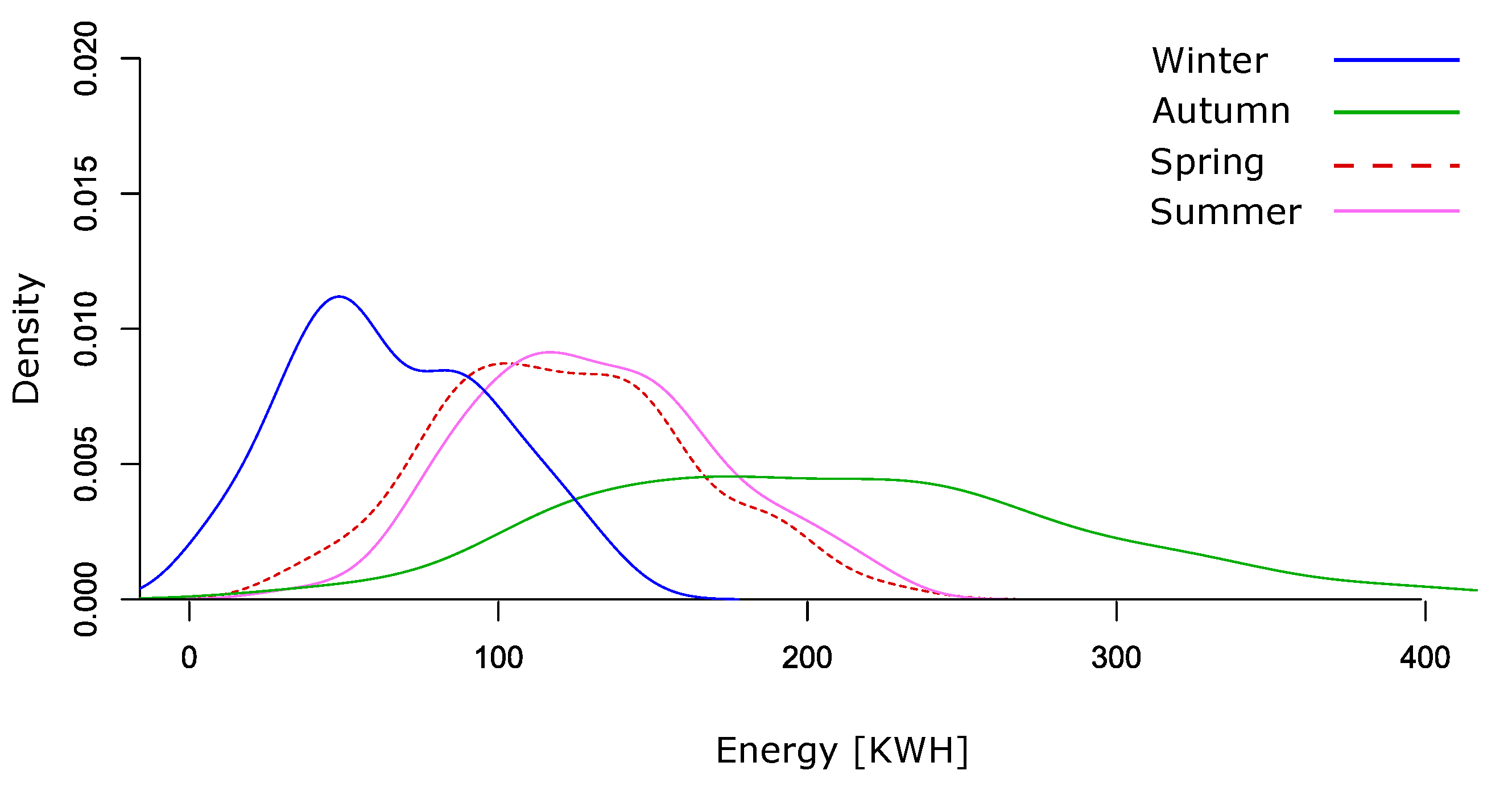
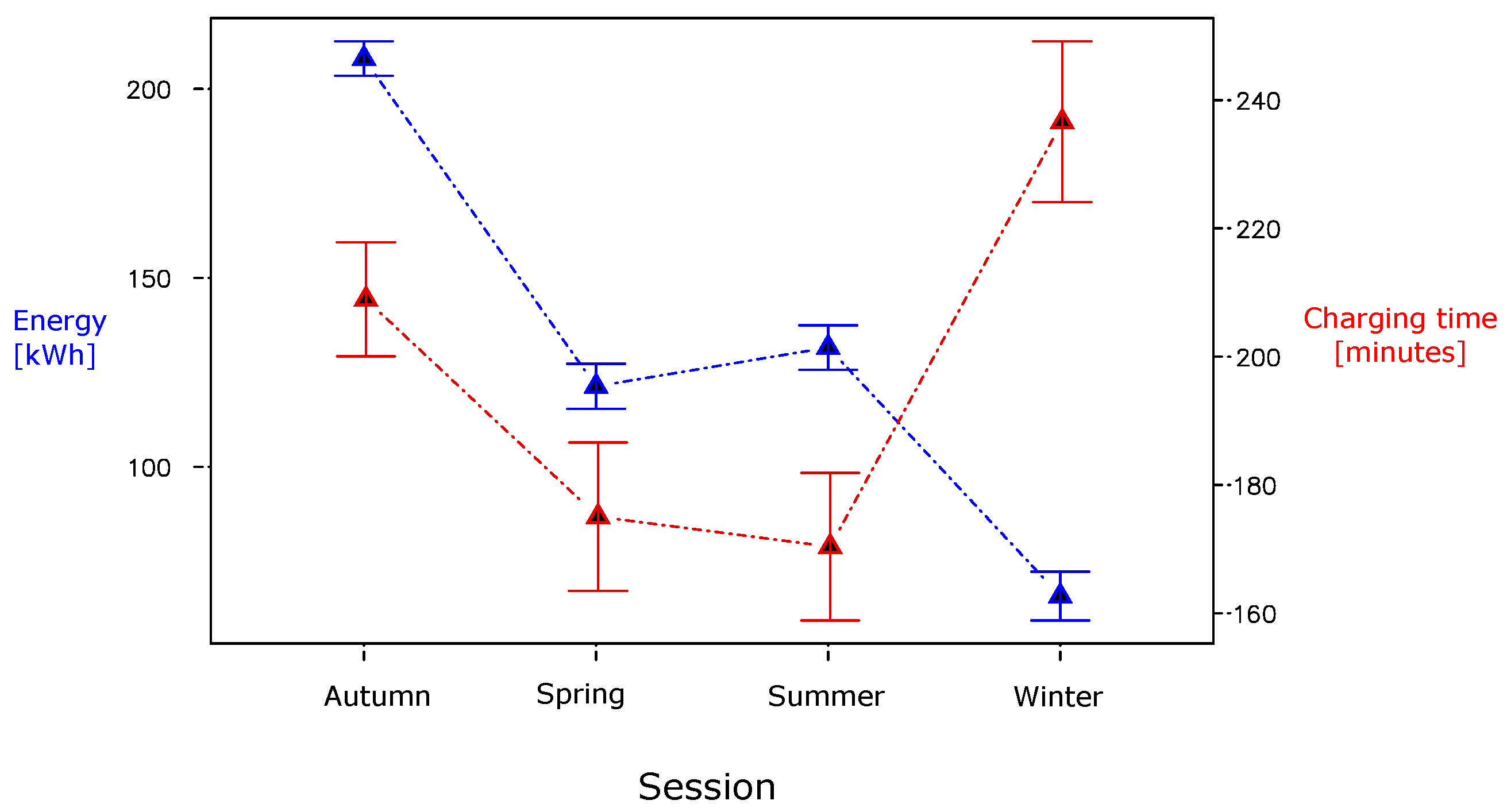
4.4. Analysis per Season
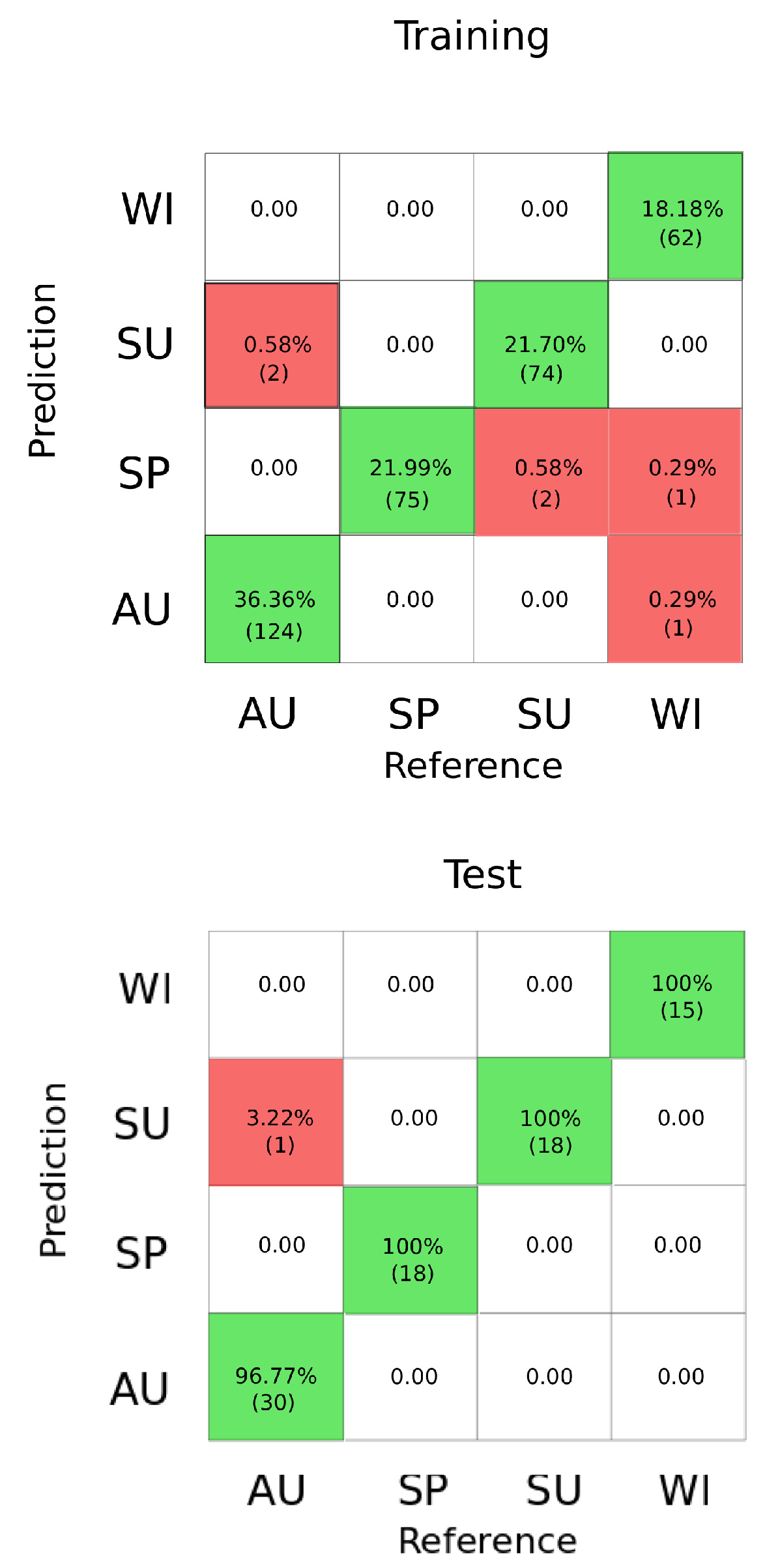
4.5. EVs Charging Load Classification per Season
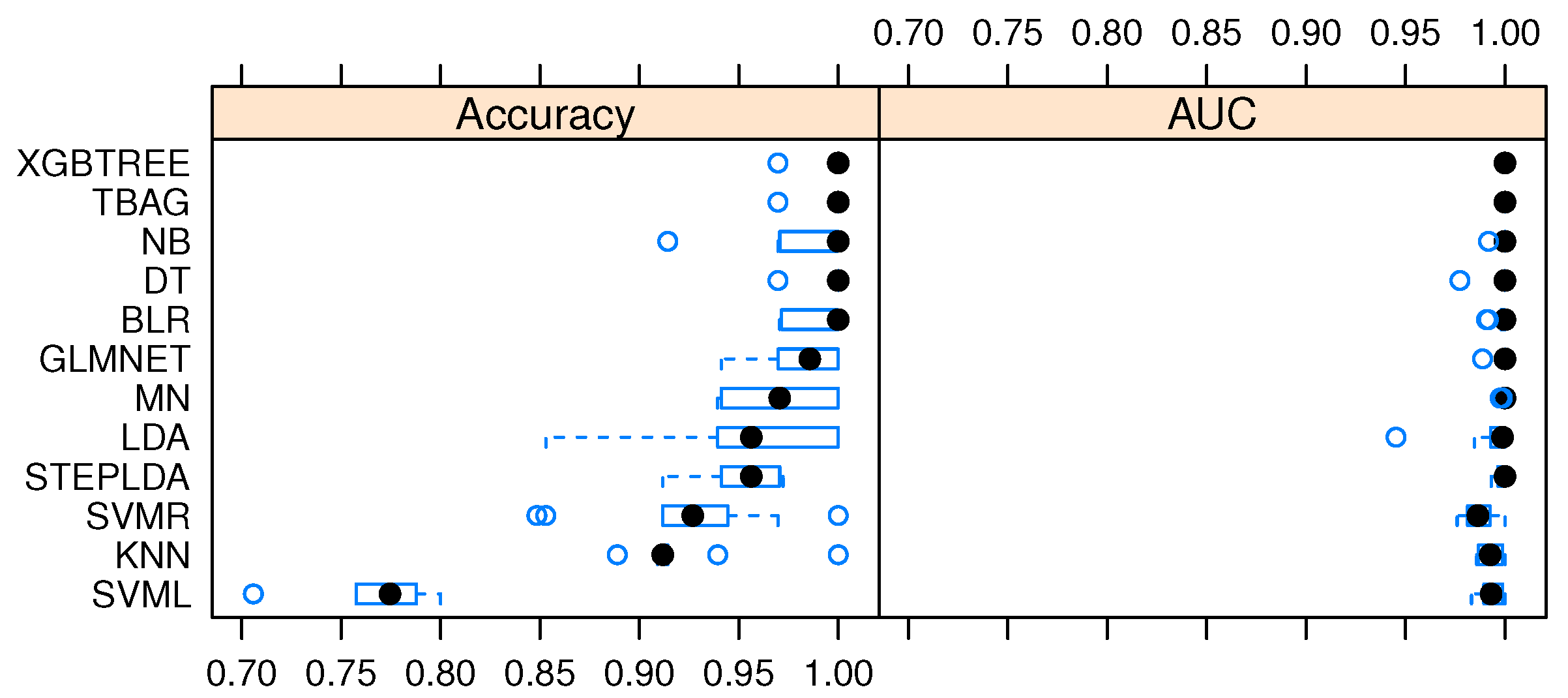
4.6. Performance Metrics for Classification
4.6.1. Accuracy
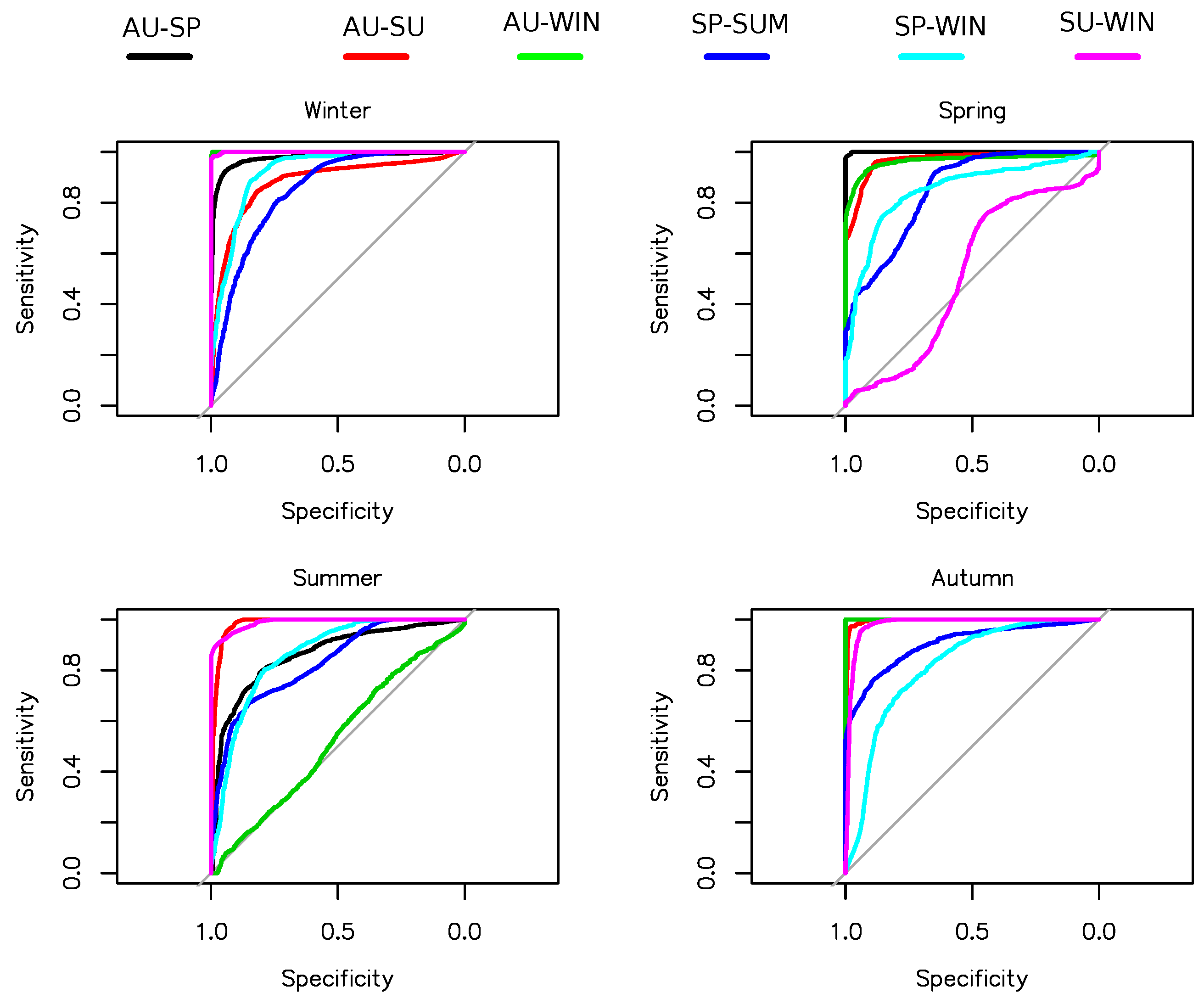
4.6.2. Receiver Operating Characteristic
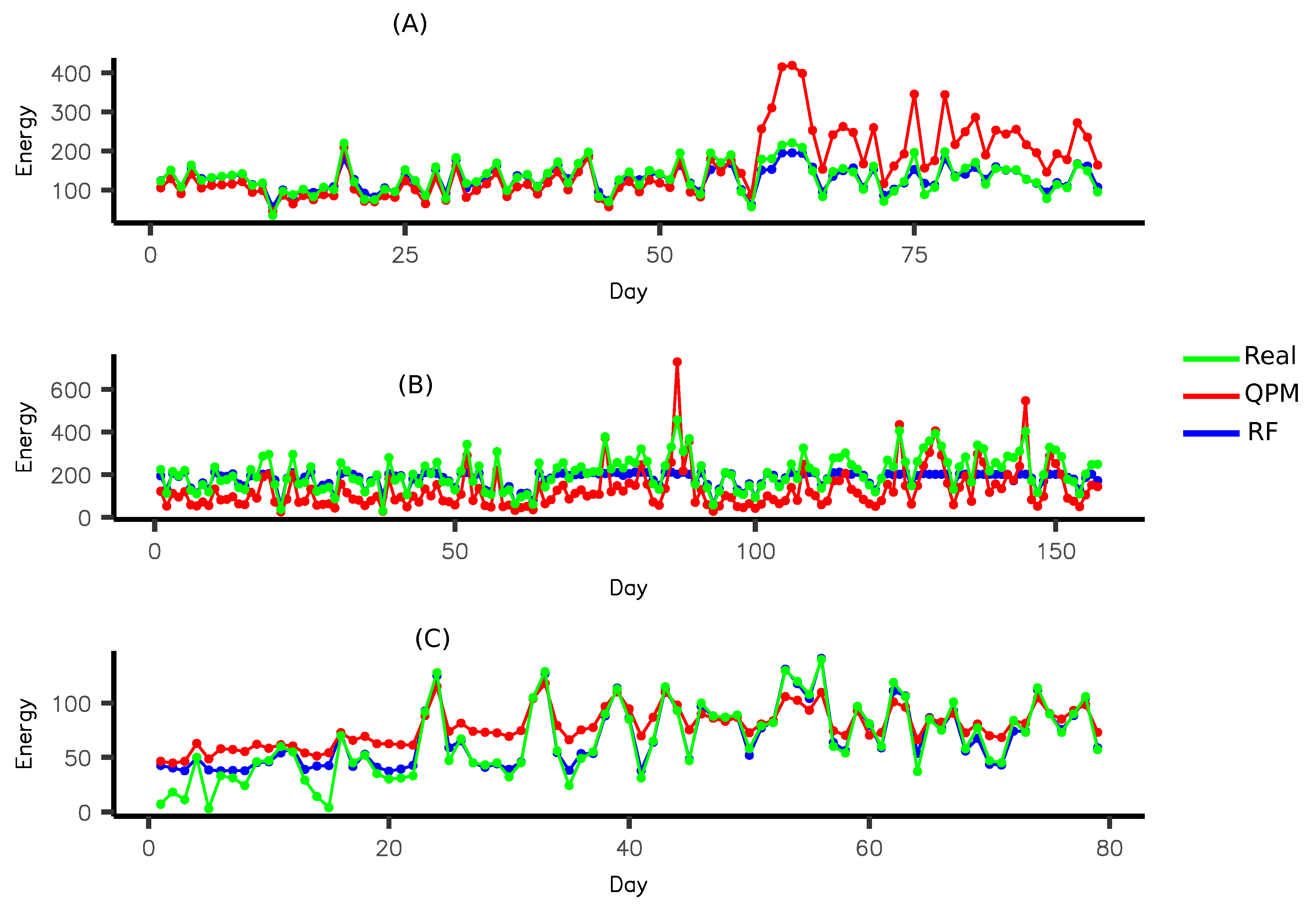
4.7. EVs Charging Load Prediction
- Case I: We used the data from spring (Training) to forecast the data in summer (Test)
- Case II: We joined the data from spring and summer (Training) to forecast the data in autumn (Test)
- Case III: We joined data from spring, summer and autumn (Training), to forecast the data in winter (Test)
4.8. Performance Metrics for Regression
5. Results and Discussion
5.1. Statistical Analysis
5.2. Classification
5.3. Regression
6. Conclusions
- This paper shows that EVs’ energy consumption can be forecasted and discriminated from seasons using machine learning tools with high accuracy.
- The statistical analysis proved that the seasonality shapes significantly charging behaviors within a 95% compatibility interval. In winter, the EV load is the lowest and the charging time is the maximum, meanwhile, in fall, the demand reaches its maximum value and the charging time is more moderate than winter but higher than Spring and Summer.
- From forecast results, both models were able to predict EVs load on the established scenarios. However, RF provided better global performance reaching MAPE up to 0.08%, and an RMSE of 2.27.
- Twelve classification models were trained and tested to select the one that maximizes the accuracy and the ROC. All the models showed an acceptable performance during the training and test stage. Despite, GLMNET with (, ) as final parameters was the method that provided the best classification performance according to mean accuracy and ROC. These results suggest that the seasonality effect powerfully shapes charging behaviors, and this fact is related to our findings from the exploratory analysis carried out that charging time and the temperature are inversely correlated.
Author Contributions
Funding
Conflicts of Interest
References
- Ayman, E.R. Toward a Sustainable More Electrified Future: The Role of Electrical Machines and Drives. IEEE Electrif. Mag. 2019, 7, 49–59. [Google Scholar]
- Wu, G.; Zhang, X.; Dong, Z. Powertrain architectures of electrified vehicles: Review, classification and comparison. J. Frankl. Inst. 2015, 352, 425–448. [Google Scholar] [CrossRef]
- Guirong, Z.; Henghai, Z.; Houyu, L. The Driving Control of Pure Electric Vehicle. Procedia Environ. Sci. 2011, 10, 433–438. [Google Scholar] [CrossRef]
- Langbroek, J.H.; Franklin, J.P.; Susilo, Y.O. The effect of policy incentives on electric vehicle adoption. Energy Policy 2016, 94, 94–103. [Google Scholar] [CrossRef]
- Cozzi, L. World Energy Outlook 2018. In International Energy Agency; Technical Report; IEA: Paris, France, 2019. [Google Scholar]
- Tamai, G. What Are the Hurdles to Full Vehicle Electrification? [Technology Leaders]. IEEE Electrif. Mag. 2019, 7, 5–11. [Google Scholar] [CrossRef]
- Mega, V.P. The Paths to Decarbonisation Through Cities and Seas. In Eco-Responsible Cities and the Global Ocean; Springer: Berlin, Germany, 2019; pp. 121–166. [Google Scholar]
- IEA; UNSD; WHO. Tracking SDG 7: The Energy Progress Report 2019; IRENA: Washington, DC, USA, 2019. [Google Scholar]
- Anastasiadis, A.G.; Kondylis, G.P.; Polyzakis, A.; Vokas, G. Effects of Increased Electric Vehicles into a Distribution Network. Energy Procedia 2019, 157, 586–593. [Google Scholar] [CrossRef]
- Haustein, S.; Jensen, A.F. Factors of electric vehicle adoption: A comparison of conventional and electric car users based on an extended theory of planned behavior. Int. J. Sustain. Transp. 2018, 12, 484–496. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Badri, A.; Parvania, M. A survey on mobile energy storage systems (MESS): Applications, challenges and solutions. Renew. Sustain. Energy Rev. 2014, 40, 161–170. [Google Scholar] [CrossRef]
- Dominguez, J.; Dante, A.; Agbossou, K.; Henao, N.; Campillo, J.; Cardenas, A.; Kelouwani, S. Optimal Charging Scheduling of Electric Vehicles based on Principal Component Analysis and Convex Optimization. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 935–940. [Google Scholar]
- Shahidinejad, S.; Filizadeh, S.; Bibeau, E. Profile of charging load on the grid due to plug-in vehicles. IEEE Trans. Smart Grid 2012, 3, 135–141. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Demand response as a load shaping tool in an intelligent grid with electric vehicles. IEEE Trans. Smart Grid 2011, 2, 624–631. [Google Scholar] [CrossRef]
- Zhao, Y.; Che, Y.; Wang, D.; Liu, H.; Shi, K.; Yu, D. An optimal domestic electric vehicle charging strategy for reducing network transmission loss while taking seasonal factors into consideration. Appl. Sci. 2018, 8, 191. [Google Scholar] [CrossRef]
- Boston, D.; Werthman, A. Plug-in Vehicle Behaviors: An analysis of charging and driving behavior of Ford plug-in electric vehicles in the real world. World Electr. Veh. J. 2016, 8, 926–935. [Google Scholar] [CrossRef]
- Ul-Haq, A.; Azhar, M.; Mahmoud, Y.; Perwaiz, A.; Al-Ammar, E.A. Probabilistic modeling of electric vehicle charging pattern associated with residential load for voltage unbalance assessment. Energies 2017, 10, 1351. [Google Scholar] [CrossRef]
- Taylor, J.W.; McSharry, P.E. Short-term load forecasting methods: An evaluation based on european data. IEEE Trans. Power Syst. 2007, 22, 2213–2219. [Google Scholar] [CrossRef]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Hong, T.; Xie, J.; Black, J. Global energy forecasting competition 2017: Hierarchical probabilistic load forecasting. Int. J. Forecast. 2019, 35, 1389–1399. [Google Scholar] [CrossRef]
- Liang, Y.; Niu, D.; Hong, W.C. Short term load forecasting based on feature extraction and improved general regression neural network model. Energy 2019, 166, 653–663. [Google Scholar] [CrossRef]
- Ganguly, A.; Goswami, K.; Mukherjee, A.; Sil, A.K. Short-Term Load Forecasting for Peak Load Reduction Using Artificial Neural Network Technique. In Advances in Computer, Communication and Control; Springer: Singapore, 2019; pp. 551–559. [Google Scholar]
- Franke, T.; Krems, J.F. Understanding charging behaviour of electric vehicle users. Transp. Res. Part F Traff. Psychol. Behav. 2013, 21, 75–89. [Google Scholar] [CrossRef]
- Chen, L.; Nie, Y.; Zhong, Q. A model for electric vehicle charging load forecasting based on trip chains. Trans. China Electrotech. Soc. 2015, 30, 216–225. [Google Scholar]
- Wang, H.; Wang, B.; Fang, C.; Li, W.; Huang, H. Charging Load Forecasting of Electric Vehicle Based on Charging Frequency. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; p. 062008. [Google Scholar]
- Gerossier, A.; Girard, R.; Kariniotakis, G. Modeling and Forecasting Electric Vehicle Consumption Profiles. Energies 2019, 12, 1341. [Google Scholar] [CrossRef]
- Alegre, S.; Míguez, J.V.; Carpio, J. Modelling of electric and parallel-hybrid electric vehicle using Matlab/Simulink environment and planning of charging stations through a geographic information system and genetic algorithms. Renew. Sustain. Energy Rev. 2017, 74, 1020–1027. [Google Scholar] [CrossRef]
- Mao, D.; Tan, J.; Liu, G.; Wang, J. Location Planning of Fast Charging Station considering its Impact on the Power Grid Assets. arXiv 2019, arXiv:1903.10149. [Google Scholar]
- Zhang, H.; Hu, Z.; Song, Y.; Xu, Z.; Jia, L. A prediction method for electric vehicle charging load considering spatial and temporal distribution. Autom. Electr. Power Syst. 2014, 38, 13–20. [Google Scholar]
- Ahmad, A.; Hassan, M.; Abdullah, M.; Rahman, H.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Jiao, R.; Zhang, T.; Jiang, Y.; He, H. Short-Term Non-Residential Load Forecasting Based on Multiple Sequences LSTM Recurrent Neural Network. IEEE Access 2018, 6, 59438–59448. [Google Scholar] [CrossRef]
- Abbasi, R.A.; Javaid, N.; Ghuman, M.N.J.; Khan, Z.A.; Rehman, S.U. Short Term Load Forecasting Using XGBoost. In Workshops of the International Conference on Advanced Information Networking and Applications; Springer: Berlin, Germany, 2019; pp. 1120–1131. [Google Scholar]
- Yan, D.; O’Brien, W.; Hong, T.; Feng, X.; Gunay, H.B.; Tahmasebi, F.; Mahdavi, A. Occupant behavior modeling for building performance simulation: Current state and future challenges. Energy Build. 2015, 107, 264–278. [Google Scholar] [CrossRef]
- Khatoon, S.; Singh, A.K. Effects of various factors on electric load forecasting: An overview. In Proceedings of the 2014 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014; pp. 1–5. [Google Scholar]
- Amara, F.; Agbossou, K.; Dubé, Y.; Kelouwani, S.; Cardenas, A. Estimation of temperature correlation with household electricity demand for forecasting application. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 3960–3965. [Google Scholar]
- Rijal, H.; Humphreys, M.; Nicol, F. Adaptive thermal comfort in Japanese houses during the summer season: Behavioral adaptation and the effect of humidity. Buildings 2015, 5, 1037–1054. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Ren, F. Learning customer behavior for effective load forecasting. IEEE Trans. Knowl. Data Eng. 2018, 31, 938–951. [Google Scholar] [CrossRef]
- Wang, D.; Sun, Z. Big data analysis and parallel load forecasting of electric power user side. Proc. CSEE 2015, 35, 527–537. [Google Scholar]
- Wu, X.; He, J.; Zhang, P.; Hu, J. Power system short-term load forecasting based on improved random forest with grey relation projection. Autom. Electr. Power Syst. 2015, 39, 50–55. [Google Scholar]
- Dudek, G. Short-term load forecasting using random forests. In Intelligent Systems’ 2014; Springer: Berlin, Germany, 2015; pp. 821–828. [Google Scholar]
- Electric Vehicle Charging Stations: Energy Consumption & Savings. Available online: https://bouldercolorado.gov/open-data/electric-vehicle-charging-stations/ (accessed on 16 May 2020).
- Colorado Energy Office. Colorado Energy Office Annual Report 2017–2018; Technical report; Colorado Energy Office: Denver, CO, USA, 2015.
- Toor, W.; Salisbury, M. Boulder Electric Vehicle Infrastructure and Adoption Assessment. In Southwest Energy Efficiency Project; Technical report; Southwest Energy Efficiency Project (SWEEP): Denver, CO, USA, 2015. [Google Scholar]
- Colorado Energy Office. Colorado’s electric vehicle roadmap. In Regional Air Quality Council; Technical report; Colorado Energy Office: Denver, CO, USA, 2020. [Google Scholar]
- Dowds, J.; Hines, P.; Farmer, C.; Watts, R.; Letendre, S. Plug-in Hybrid Electric Vehicle Research Project: Phase Two Report; Technical report; UVM Transportation Research Center: Burlington, VT, USA, 2010. [Google Scholar]
- Vassileva, I.; Campillo, J. Adoption barriers for electric vehicles: Experiences from early adopters in Sweden. Energy 2017, 120, 632–641. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Meyer, N.; Whittal, I.; Christenson, M.; Loiselle-Lapointe, A. The impact of driving cycle and climate on electrical consumption and range of fully electric passenger vehicles. In Proceedings of the EVS26 International Battery, Hybrid, and Fuel Cell Electric Vehicle Symposium, Los Angeles, CA, USA, 6–9 May 2012; pp. 1–11. [Google Scholar]
- Reyes, J.R.M.D.; Parsons, R.V.; Hoemsen, R. Winter happens: The effect of ambient temperature on the travel range of electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4016–4022. [Google Scholar] [CrossRef]
- How Do Extremely Cold Temperatures Affect the Range Of An Electric Car? Available online: https://www.fleetcarma.com/electric-car-range-in-bitter-cold/ (accessed on 16 December 2013).
- Sovacool, B.K.; Noel, L.; Kester, J.; de Rubens, G.Z. Reviewing Nordic transport challenges and climate policy priorities: Expert perceptions of decarbonisation in Denmark, Finland, Iceland, Norway, Sweden. Energy 2018, 165, 532–542. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a World Beyond “p < 0.05”. Am. Stat. 2019, 73, 1–19. [Google Scholar]

| Data Name | Description | Symbol |
|---|---|---|
| Date | Date EV charging station ports were used. | |
| Number of sessions | Number of times the charging ports were used on the listed date. | NOS |
| Unique drivers | Number of unique individual drivers using the charging station on the particular listed date. | UD |
| Number of ports | The total number of city-owned EV charging ports for the particular listed date. | NOP |
| Energy [kWh] | The amount of energy that has been dispensed by the charging stations on the particular listed date. | KWH |
| Accumulated energy [MWh] | The sum of all energy that has been dispensed by the charging stations since the beginning of 2018 up to the listed date. | ACE |
| GHG savings [Kg] | Estimated emissions avoided based on the energy dispensed and gasoline saved by the charging stations on the listed date. | GHGS |
| Accumulated GHG [Kg] | The sum of all GHG savings frpm the beginning of 2018 up to the listed date. | ACGHC |
| Charging time [Min] | The number of minutes any vehicle was plugged in and actively charging on the particular listed date. | CTM |
| Gasoline savings [Gal] | ,Estimated gallons of gasoline saved based on charging time on the paticular listed date. | GSGS |
| Mean temperature * | Diary ambient temperature | TEMP |
| Day | Indicates the current day i.e., monday, thursday, and so on. | DAY |
| Weekday * | 1/0 indicates whether it is a weekday | WDAY |
| Weekend * | 1/0 indicates whether it is a weekend | WEEK |
| Seasonality * | From Winter to Autumn | SEAS |
| Model | Min Acc | Mean Acc | Max Acc | Min AUC | Mean AUC | Max AUC |
|---|---|---|---|---|---|---|
| SVML | 0.7058 | 0.7653 | 0.8 | 0.9831 | 0.9934 | 1 |
| SVMR | 0.8484 | 0.9236 | 1 | 0.9759 | 0.9868 | 1 |
| KNN | 0.8888 | 0.9213 | 1 | 0.9857 | 0.9927 | 1 |
| LDA | 0.8529 | 0.9530 | 1 | 0.9452 | 0.9914 | 1 |
| STEPLDA | 0.9117 | 0.9530 | 0.97 | 0.9930 | 0.9981 | 1 |
| MN | 0.9393 | 0.9705 | 1 | 0.9975 | 0.9996 | 1 |
| NB | 0.9142 | 0.9854 | 1 | 0.9912 | 0.9991 | 1 |
| DT | 0.9696 | 0.9969 | 1 | 0.9773 | 0.9977 | 1 |
| XGBTREE | 0.9696 | 0.9969 | 1 | 1 | 1 | 1 |
| GLMNET | 0.9411 | 0.9822 | 1 | 0.9887 | 0.9997 | 1 |
| BLR | 0.9705 | 0.9912 | 1 | 0.9907 | 0.9980 | 1 |
| TBAG | 0.9696 | 0.9969 | 1 | 1 | 1 | 1 |
| Model | Target Season | AUC |
|---|---|---|
| GLMNET | WIN | 0.9376 |
| SP | 0.8587 | |
| SU | 0.8413 | |
| AU | 0.9489 | |
| XGBOOST | WIN | 0.8237 |
| SP | 0.8307 | |
| AU | 0.7806 | |
| WIN | 0.8082 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dominguez-Jimenez, J.A.; Campillo, J.E.; Montoya, O.D.; Delahoz, E.; Hernández, J.C. Seasonality Effect Analysis and Recognition of Charging Behaviors of Electric Vehicles: A Data Science Approach. Sustainability 2020, 12, 7769. https://doi.org/10.3390/su12187769
Dominguez-Jimenez JA, Campillo JE, Montoya OD, Delahoz E, Hernández JC. Seasonality Effect Analysis and Recognition of Charging Behaviors of Electric Vehicles: A Data Science Approach. Sustainability. 2020; 12(18):7769. https://doi.org/10.3390/su12187769
Chicago/Turabian StyleDominguez-Jimenez, Juan A., Javier E. Campillo, Oscar Danilo Montoya, Enrique Delahoz, and Jesus C. Hernández. 2020. "Seasonality Effect Analysis and Recognition of Charging Behaviors of Electric Vehicles: A Data Science Approach" Sustainability 12, no. 18: 7769. https://doi.org/10.3390/su12187769
APA StyleDominguez-Jimenez, J. A., Campillo, J. E., Montoya, O. D., Delahoz, E., & Hernández, J. C. (2020). Seasonality Effect Analysis and Recognition of Charging Behaviors of Electric Vehicles: A Data Science Approach. Sustainability, 12(18), 7769. https://doi.org/10.3390/su12187769








