Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures
Abstract
1. Introduction
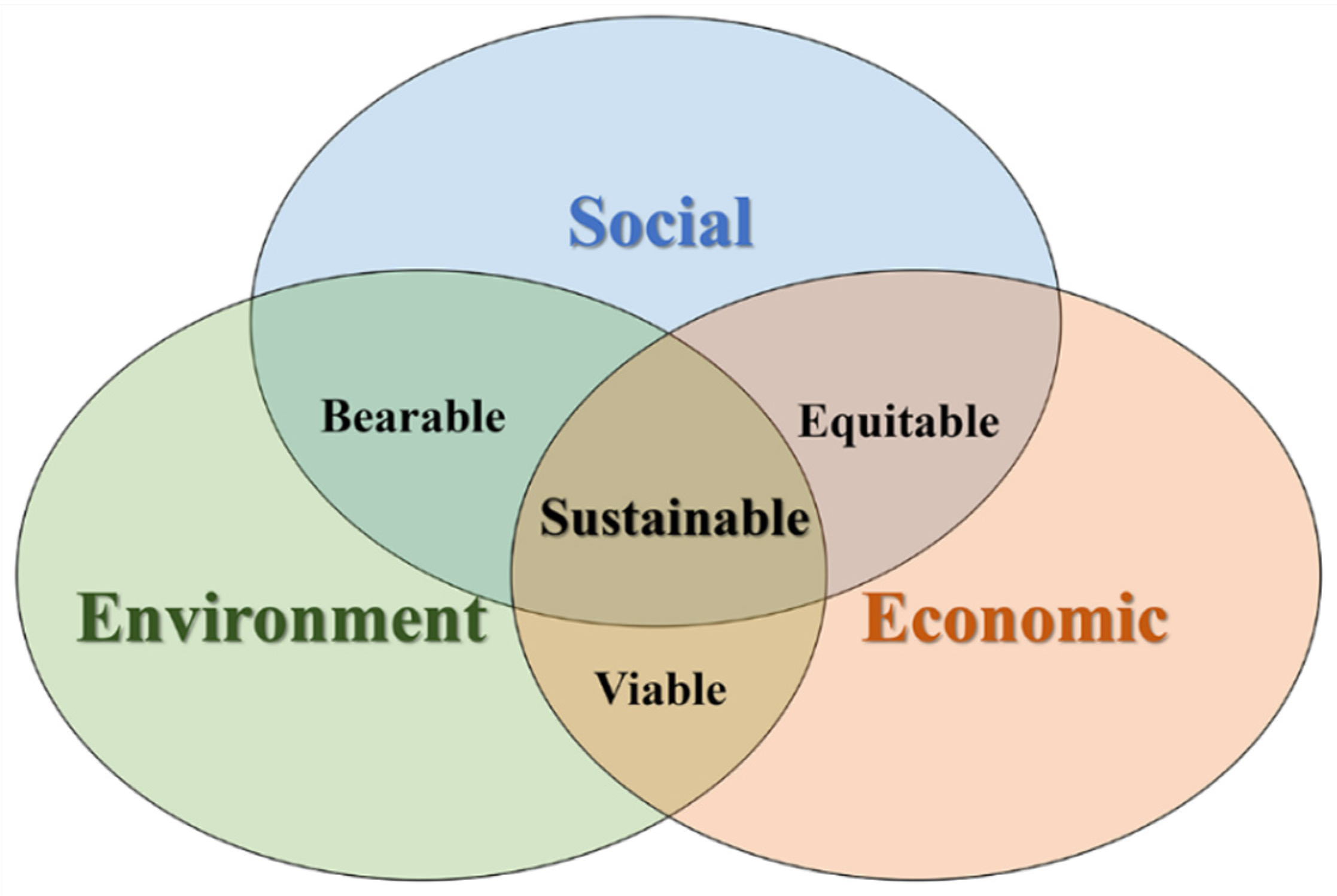
1.1. Sustainable Development
1.2. Renewable Energy
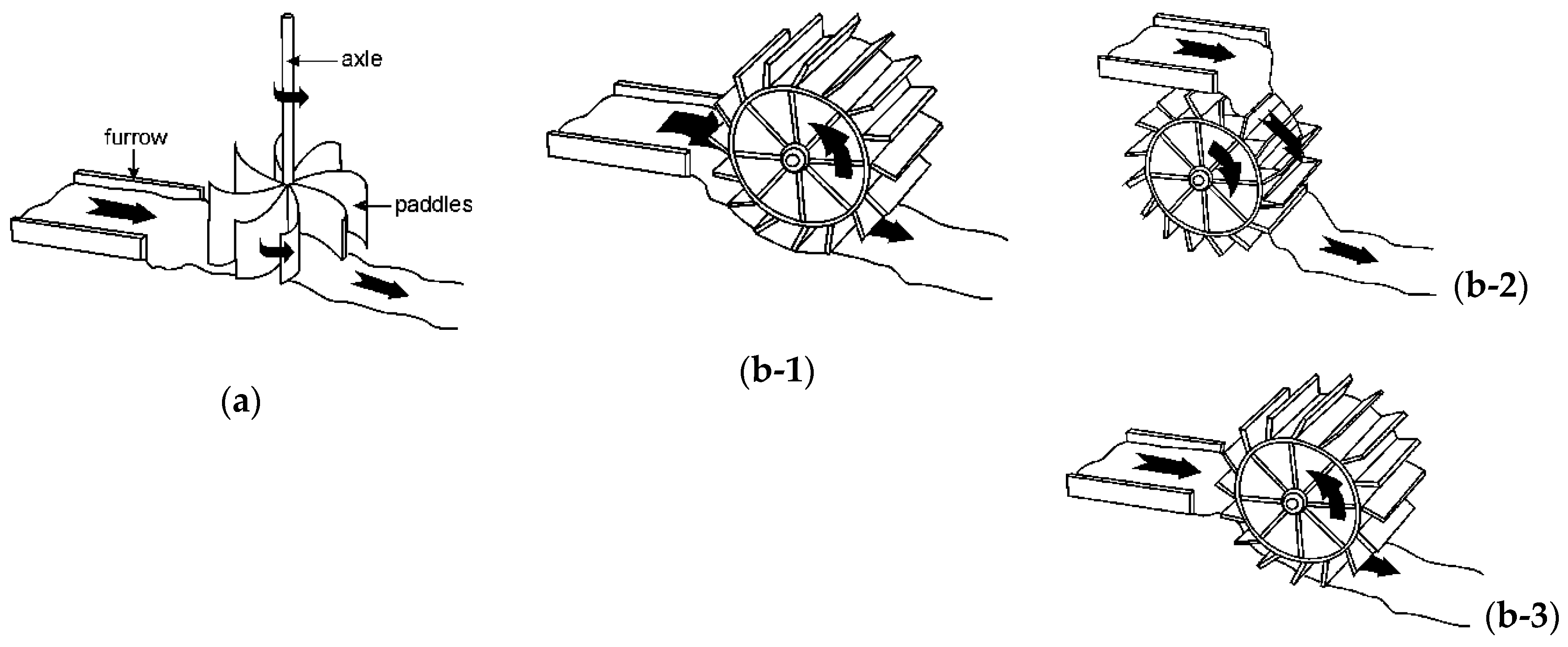
1.3. Hydropower
1.4. Archimedes Screws
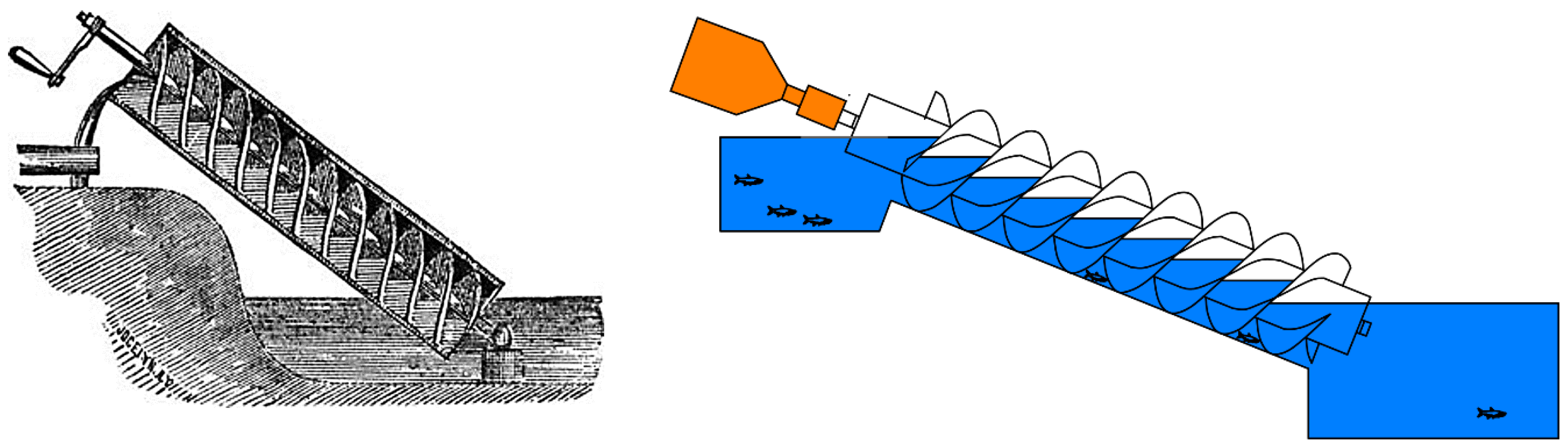
1.4.1. Archimedes Screw Pump
1.4.2. Archimedes Screw Turbine
2. Advantages of Archimedes Screw Generators
2.1. Technical Advantages
2.2. Economic Aspects of ASTs
2.2.1. Capital Costs
2.2.2. Operational and Maintenance Costs
2.3. Environmental and Social Advantages
Wildlife and Social Advantages
3. Disadvantages of Archimedes Screw Generators
3.1. A Relatively New Technology
3.2. Insufficient General Design Guideline
3.3. Technical Limitations
4. ASTs: A Conceptual Approach
4.1. Site Considerations
- -
- Allowing hydroelectricity generation in regions where construction of large dams is not reasonable or feasible. For example, in relatively smooth plains where suitable conditions do not exist to support the construction of large dams.
- -
- Maximizing the hydroelectricity generation even in regions where a large dam exists by extracting energy alongside the river downstream.
- -
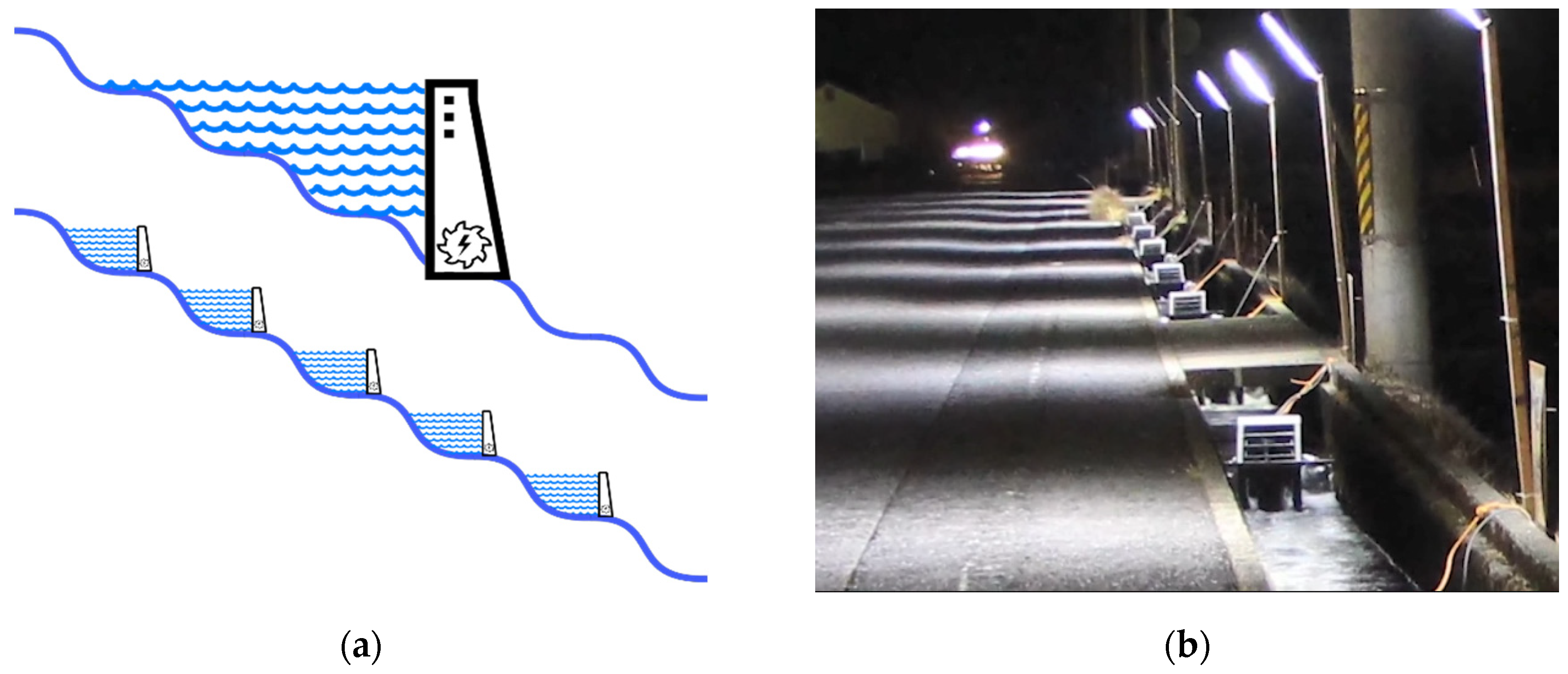
- Reducing the electricity power loss alongside the distribution network by generating power near where it is required and consumed, which could reduce the length and cost of the distribution network (such as illustrated in Figure 7b).
- -
- Generating baseload power with small hydropower plants. Currently, in many locations, the majority of electricity baseload is mainly generated by fossil fuel and nuclear powerplants and hydropower is used to meet peak demands. However, the proposed theoretical chain of ROR powerplants could generate baseload since most of the ROR plants do not store water.
4.2. Reducing Erosion and Disturbance of Natural Sedimentation Processes
4.3. Power Generation from Unconventional Water Resources
4.4. Conservation and Improvement of Resources
4.5. AST Plant Configurations
4.6. Future Sustainability
5. Design Archimedes Screw Hydro Powerplants Principles
5.1. Archimedes Screw Hydro Powerplants Design Assessments
- -
- Estimate the required power as well as predict the possible future changes in demand.
- -
- Determine whether the powerplant will be connected to the grid or will be off-grid.
- -
- If the AST powerplant is designed to be off-grid, it would be important to:
- -
- Consider the comparison of the value of reliable baseload power versus maximizing the annual production of the powerplant in making decisions for the design.
- -
- Define and consider the needed voltages and/or currents.
- -
- Permitting requirements, restrictions on access or water use should be determined.
- -
- The flow duration curve of the river should be used to determine the baseload and other options for the operation of the powerplant. This information also helps to make decisions in the plant design step.
- -
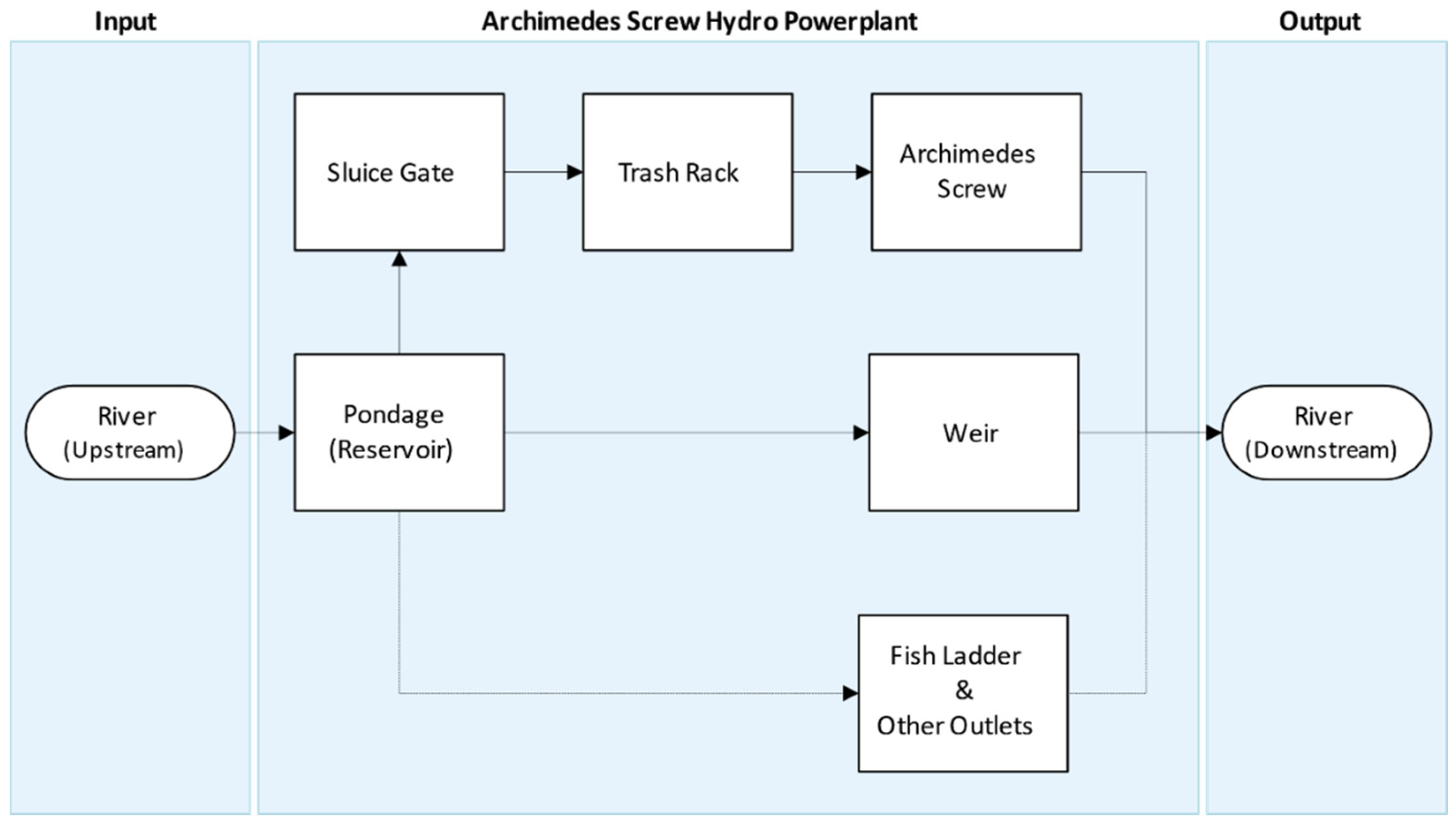
- Ecological assessments should be done, and the water needs of other users or ecological functions should be determined. For example, the required flow for fish passage or installing a fish ladder should be determined.
- -
- The potential plant location should be selected based on the following considerations:
- -
- Accessibility for construction, operation, and maintenance. This is important for civil works and installation of the screw, especially for larger powerplants that have big and bulky screw(s) that need cranes for installation
- -
- Geotechnical concerns, particularly stability and suitability for plant foundations
- -
- Supply channel and outlet channel routing
- -
- Conflicts with other site use considerations.
- -
- For steady flow, a single-speed plant could be considered as a simpler and more efficient option. On average, the cost per watt of these systems is less than the variable-speed ones. Even if the available flow is not sufficient to fill the screw at its operating speed, fixed speed screws can still generate power in a partially full condition [30].
- -
- For large surplus flow, variable-speed screws could be recommended to generate partial power at low flow times. It would be particularly important if the powerplant will be off-grid, or other power sources (like diesel generators) are not available or are expensive. Generally, variable-speed screws are recommended when there is an excess flow that could be used to generate more power from an available flow of when the flow varies. The main reason is that although operating ASTs at the full capacity may be the most mechanically efficient operating condition, it will not definitely lead to the highest overall energy generation. Therefore, it may not be the most economically efficient operating condition [30].
- -
- A sluice gate to control flow to the plant, and trash racks to prevent large debris from entering the plant, must be planned upstream of the screw. Ease of trash rack cleaning is important.
- -
- Provision to dry out the top and bottom of the screw for bearing inspection, maintenance should be included in the plant design. The sluice gate should be able to shut off all flow. At the outlet, build vertical grooves to hold stop logs to allow drying out of the screw outlet.
- -
- Be sure to plan for flooding water levels, and be sure to protect electrical components from water damage. This could be done by elevating the generator, sealing the powerhouse, and/or putting control equipment on the bank at a higher level.
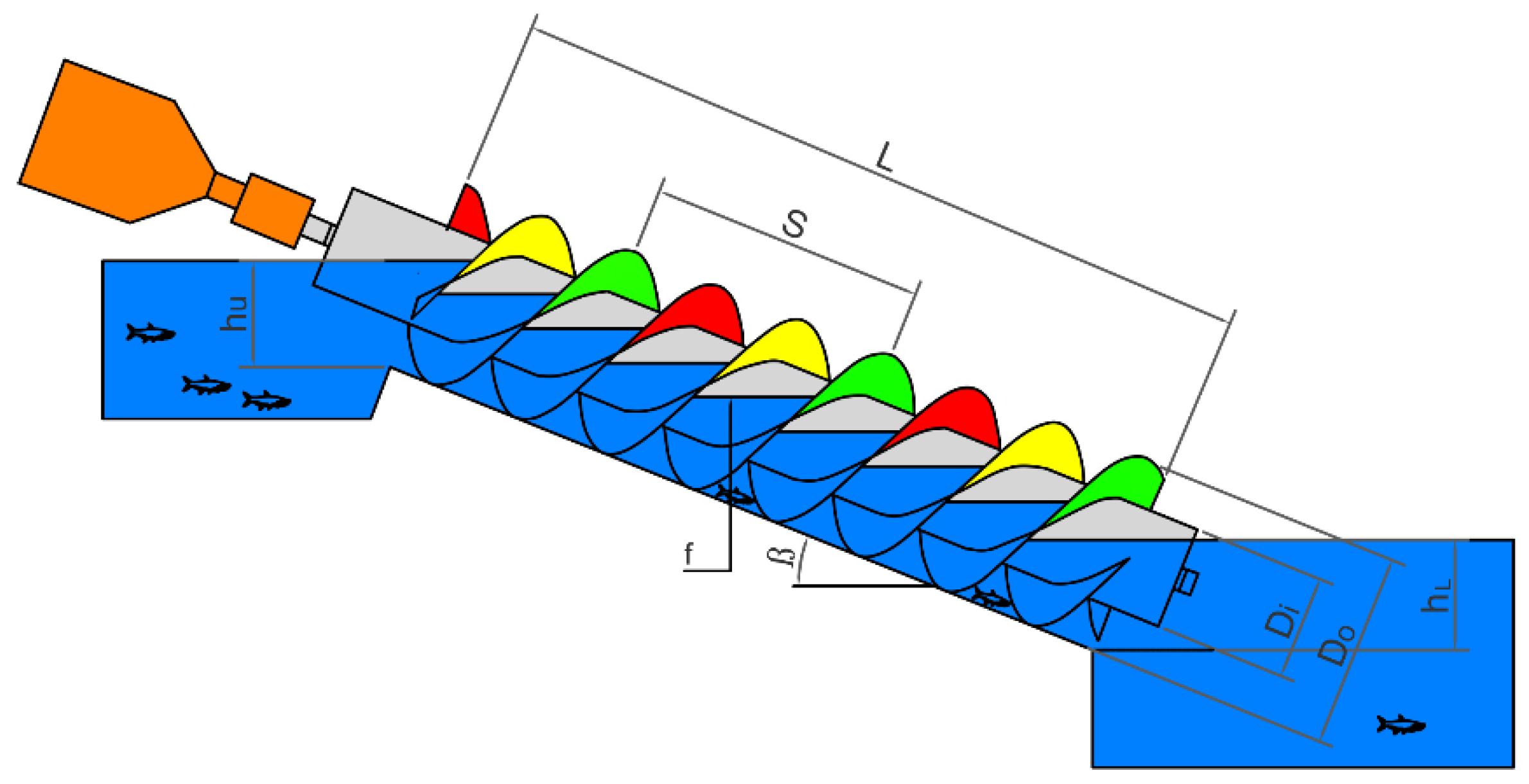
5.2. Design of Archimedes Screws
- Di: Inner diameter
- DO: Outer diameter
- L: Total length of the screw
- β: Inclination Angle of the Screw
- N: Number of helical planed surfaces
- S: Screw pitch (Distance along the screw axis for one complete helical plane turn)
- f: Fill Height of the bucket [30]
- Gw: The gap between the trough and screw
- hu: Upper (inlet) water level
- hL: Lower (outlet) water level
5.3. Estimating the Generated Power of the Archimedes Screws
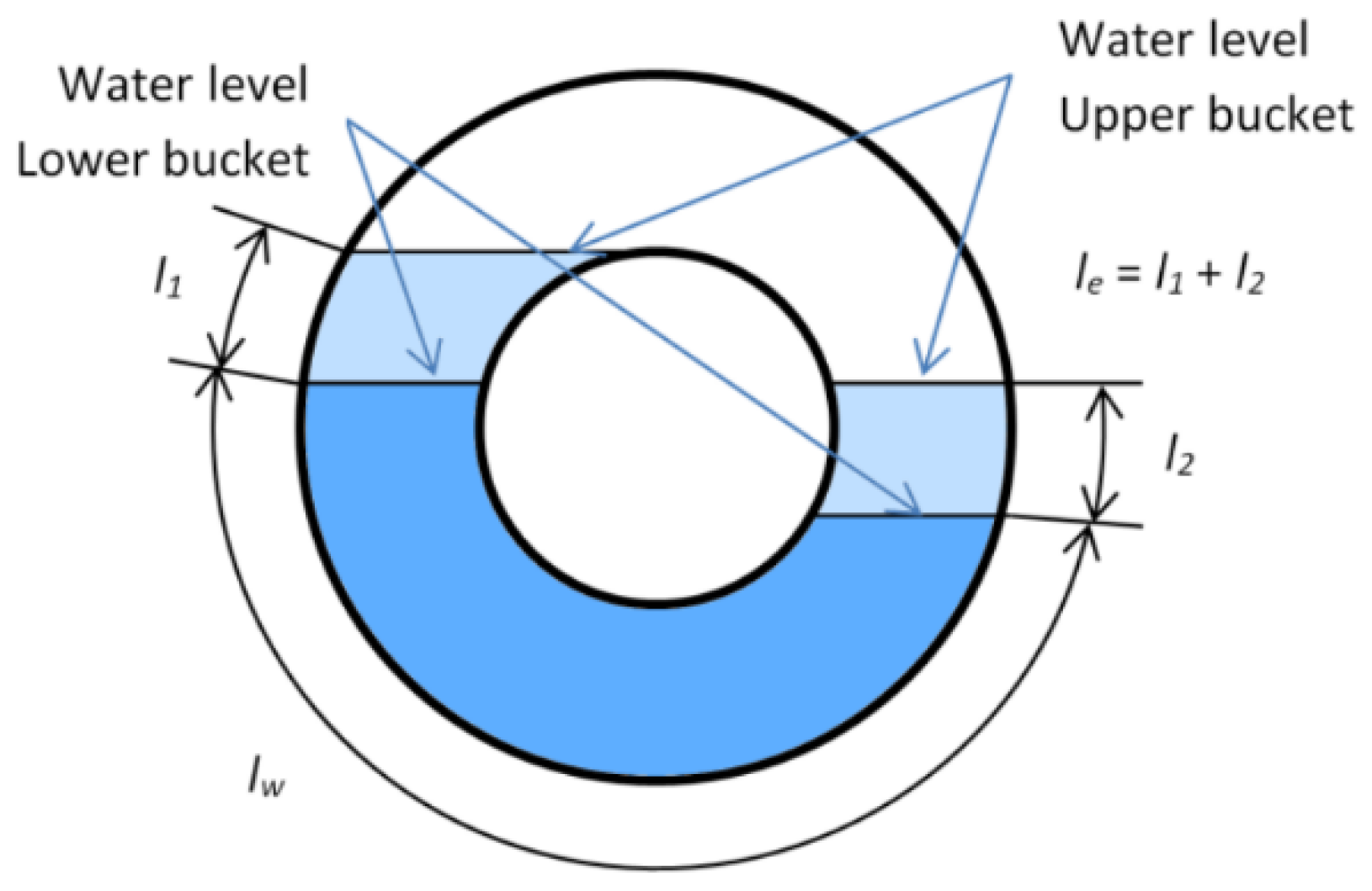
5.3.1. Bucket Volume Theory
5.3.2. Flow Rate and Leakage Models
5.3.3. Torque and Power Models
5.4. Archimedes Screw Power Loss Models
- -
- Inlet losses due to head loss through the screw entrance
- -
- Internal hydraulic friction between water and moving screw surfaces
- -
- Outlet losses due to exit effects, geometric head losses, and additional drag torque
- -
- Friction of bearings
- -
- Additional mechanical and electrical losses in gearboxes, generators, and electrical controls
6. Conclusions
- To increase the number of suitable sites for power generation even in sites with very low flow rates and/or water head. ASTs can be designed to operate in a wide range of flow rates (currently from 0.01–10 m3/s) and water heads (currently from 0.1–10 m), including at sites where other types of turbines may not be feasible. This increases the number of potentially suitable sites for hydropower.
- To maximize hydropower generation even in rivers with high flow rate fluctuations. ASTs can handle flow rates even of up to 20% more than optimal filling without a significant loss in efficiency [63]. Even when the conditions are not perfect for a single screw, installing more than one screw, and utilizing variable-speed ASTs, allows developers to fully utilize available flow at a wider range of sites, including those with high seasonal variability.
- To retrofit old dams or upgrade current dams or mills to make them economically (power generation) and environmentally (renewable energy) reasonable. Using ASTs as an upgrade for retrofitting old dams or upgrading operational dams makes it possible to add electrical generation with extremely low incremental environmental impact, at reasonable costs and with good potential for low social impacts while providing an incentive to maintain aging dams and infrastructure. ASTs utilized in this manner could help to reduce fossil fuel usage and greenhouse gas emissions by displacing electricity generated by more polluting methods.
- To reduce the hydroelectricity major operational and/or maintenance costs: In addition to retrofit/upgrade current dams advantages, at appropriate sites, the capital costs of AST hydropower can be less than other hydropower technologies. The overall maintenance demands and costs of ASTs are often lower than other turbines. Major maintenance is required after the 20 to 30 years.
- To reduce the disturbance of natural erosion and sedimentation processes which could lead to soil and land conservation.
- To make hydropower generation safer for aquatic wildlife, especially for fish.
- To generate electricity for small communities or regions that are hard to access or connect to the power grid, especially because of the low operation and maintenance demands and costs of ASTs. These characteristics make ASTs a potential candidate for providing electrical power in undeveloped, remote regions, and small communities that currently lack energy infrastructure.
- To improve the welfare of the developing countries and regions with limited access to the power grid or other infrastructures. Despite many other technologies, ASTs do not require high manufacturing capabilities and hi-tech technologies to design, implement, operate, or maintain. Simplicity, low operational demands, and moderate costs make ASTs a practical environment-friendly and sustainable solution for supplying energy, especially in developing countries. At remote locations with a low head water supply, ASTs may provide a possible means of providing electricity that would otherwise be impractical in developing communities. Improving the economy and welfare of such communities is a win-win futuristic sustainable development approach that could be facilitated by using AST hydroelectric plants.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Effective cross-sectional water area at the screw’s inlet | (m2) | |
| Maximum cross-sectional water area at the screw’s inlet | (m2) | |
| Coefficient of dimensionless flow rate | (-) | |
| Coefficient of dimensionless area constant | (-) | |
| Coefficient of dimensionless rotation speed constant | (-) | |
| The inner diameter of the Archimedes screw | (m) | |
| The outer diameter of the Archimedes screw | (m) | |
| Fill height of water in a bucket of screw | (-) | |
| Gravitational constant | (9.81 m/s2) | |
| Upper (inlet) water level of the screw | (m) | |
| Lower (outlet) water level of the screw | (m) | |
| Gap width (The gap between the trough and screw) | (m) | |
| Overflow head | (m) | |
| The total length of the screw | (m) | |
| The wetted gap length along with a single turn of one flight that is submerged on one side and exposed to air on the other | (m) | |
| The wetted gap length along with a single turn of one flight that is submerged on both sides | (m) | |
| Number of helical planed surfaces | (-) | |
| The hydrostatic pressure at any point on the plane surfaces at a depth z below the water level | (Pa) | |
| Output power/shaft power of screw | (W) | |
| Total flow rate passing through the screw | (m3/s) | |
| Friction-leakage | (m3/s) | |
| Gap leakage flow | (m3/s) | |
| The main flow that is contained with the buckets and causes torque generation | (m3/s) | |
| The maximum flow rate that could pass through a screw when and | (m3/s) | |
| Overfilling flow leakage | (m3/s) | |
| No guiding plate leakage | (m3/s) | |
| r | Radial position | (m) |
| Pitch of the screw (Distance along the screw axis for one complete helical plane turn) | (m) | |
| The torque of a single bucket | (Nm) | |
| V | The overall volume of a bucket | (m3) |
| Axial transport velocity | (m/s) | |
| Total torque of the entire screw | (Nm) | |
| The location along screw centerline | (m) | |
| z | Vertical location | (m) |
| Minimum bucket water depth of the screw | (m) | |
| Maximum bucket depth of screw without overflowing | (m) | |
| The actual water depth within the bucket | (m) | |
| , , | Wetted angles around the gap | (rad) |
| The inclination angle of the screw | (rad) | |
| The head difference | (m) | |
| θ | Angular position | (rad) |
| Coefficient of the loss | ||
| Contraction discharge coefficient | ||
| Density of water | (1000 kg/m3) | |
| ω | The rotation speed of the screw | (rad/s) |
| The maximum rotation speed of the screw (Muysken limit) | (rad/s) | |
| Subscripts | ||
| inner | ||
| minimum | ||
| Maximum | ||
| O | Outer | |
| Total | ||
| Water surface level | ||
| Surface 1 (downstream side of bucket) | ||
| Surface 2 (upstream side of bucket) | ||
References
- Mensah, J.; Ricart Casadevall, S. Sustainable development: Meaning, history, principles, pillars, and implications for human action: Literature review. Cogent Soc. Sci. 2019, 5, 1653531. [Google Scholar] [CrossRef]
- UN. Our Common Future: Report of the World Commission on Environment and Development; United Nations: New York, NY, USA, 1987; p. 37. [Google Scholar]
- UNICEF; FN-SAMBANDENT. What Is Sustainable Development? 2017. Available online: https://www.youtube.com/watch?v=7V8oFI4GYMY&t (accessed on 29 January 2020).
- Passet, R. The Economic and the living (L’Économique et Le Vivant); FeniXX Réédition Numérique, ECONOMICA: Paris, France, 1996. [Google Scholar]
- United Nations. Prototype Global Sustainable Development Report; Online Unedited; United Nations Department of Economic and Social Affairs, Division for Sustainable Development: New York, NY, USA, 2014. [Google Scholar]
- James, P.; Magee, L.; Scerri, A.; Steger, M.B. Urban Sustainability in Theory and Practice: Circles of Sustainability; Routledge: London, UK, 2015. [Google Scholar]
- Shaker, R.R. The spatial distribution of development in Europe and its underlying sustainability correlations. Appl. Geogr. 2015, 63, 304–314. [Google Scholar] [CrossRef]
- Dréo, J. Sustainable Development.svg; Wikipedia: Washington, DC, USA, 2007; Available online: https://en.wikipedia.org/wiki/File:Sustainable_development.svg (accessed on 3 December 2018).
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Appavou, F.; Brown, A.; Epp, B.; Gibb, D.; Kondev, B.; McCrone, A.; Murdock, H.E.; Musolino, E.; Ranalder, L.; Sawin, J.L.; et al. Renewables 2019 Global Status Report; REN21 Secretariat: Paris, France, 2019. [Google Scholar]
- McNally, A.; Magee, D.; Wolf, A.T. Hydropower and sustainability: Resilience and vulnerability in China’s powersheds. J. Environ. Manag. 2009, 90, S286–S293. [Google Scholar] [CrossRef]
- Williamson, S.J.J.; Stark, B.H.H.; Booker, J.D.D. Low head pico hydro turbine selection using a multi-criteria analysis. RENE 2014, 61, 43–50. [Google Scholar] [CrossRef]
- Date, A.; Akbarzadeh, A. Design and cost analysis of low head simple reaction hydro turbine for remote area power supply. Renew. Energy 2009, 34, 409–415. [Google Scholar] [CrossRef]
- Lafitte, R. Survey of Energy Resources; World Energy Council: London, UK, 2001. [Google Scholar]
- Cleveland, C.J.; Morris, C.G. Handbook of Energy: Chronologies, Top Ten Lists, and Word Clouds; Elsevier: Waltham, MA, USA; Amesterdam, The Netherlands; Oxford, UK, 2013; Volume 2. [Google Scholar]
- Icold. Role of Dams. International Commission on Large Dams, 2014. Available online: http://www.icold-cigb.org/GB/Dams/role_of_dams.asp (accessed on 7 July 2020).
- Born, S.; Field, K.; Lander, D.; Bendewald, M. Water Resources: Why Do We Build Dams? Teach Engineering. 2007. Available online: https://www.teachengineering.org/lessons/view/cub_dams_lesson01 (accessed on 3 May 2020).
- Casini, M. Harvesting energy from in-pipe hydro systems at urban and building scale. Int. J. Smart Grid Clean Energy 2015, 4, 316–327. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Techlogies: Cost Analysis Series, Hydropower; Volume 1, no. 3/5; IRENA Innovation and Technology Centrer: Bonn, Germany, 2012. [Google Scholar]
- Suh, S.H.; Kim, K.Y.; Kim, B.H.; Kim, Y.T.; Kim, T.G.; Roh, H.W.; Yoo, Y.I.; Park, N.H.; Park, J.M.; Shin, C.S.; et al. Theory and Applications of Hydraulic Turbines, 1st ed.; Dong Myeong Publishers: Paju, Gyeonggi-do, Korea, 2014. [Google Scholar]
- Muller, G.; Senior, J. Simplified theory of Archimedean screws Théorie simplifiée de la vis d’Archimède. J. Hydraul. Res. 2009, 47, 666–669. [Google Scholar] [CrossRef]
- Simmons, S.; Lubitz, W. Archimedes screw generators for sustainable energy development. In Proceedings of the 2017 IEEE Canada International Humanitarian Technology Conference (IHTC), Toronto, ON, Canada, 21–22 July 2017; pp. 144–148. [Google Scholar] [CrossRef]
- Koetsier, T.; Blauwendraat, H. The Archimedean Screw-Pump: A Note on Its Invention and the Development of the Theory. In International Symposium on History of Machines and Mechanisms; Springer: Dordrecht, The Netherlands, 2004; pp. 181–194. [Google Scholar]
- Dalley, S.; Oleson, J.P. Sennacherib, Archimedes, and the Water Screw: The Context of Invention in the Ancient The Context of Invention in the Ancient World. Technol. Cult. 2003, 44, 1–26. [Google Scholar] [CrossRef]
- Brada, K. Wasserkraftschnecke ermöglicht Stromerzeugung über Kleinkraftwerke [Hydraulic screw generates electricity from micro hydropower stations]. Masch. Würzbg 1999, 105, 52–56. [Google Scholar]
- Rorres, C. The Turn of the Screw: Optimal Design of an Archimedes Screw. J. Hydraul. Eng. 2000, 126, 72–80. [Google Scholar] [CrossRef]
- Kozyn, A. Power Loss Model for Archimedes Screw Turbines. Master’s Thesis, University of Guelph, Guelph, ON, Canada, 2016. [Google Scholar]
- Lashofer, A.; Hawle, W.; Pelikan, B. State of technology and design guidelines for the Archimedes screw turbine. In Proceedings of the Hydro 2012—Innovative Approaches to Global Challenges, Bilbao, Spain, 29–31 October 2012. [Google Scholar]
- Kibel, P. Fish Monitoring and Live Fish Trials. In Archimedes Screw Turbine, River Dart, No. Phase 1 Report: Live Fish Trials, Smolts, Leading Edge Assessment, Disorientation Study, Outflow Monitoring; Moretonhampstead Fishtek Consult. Ltd.: Moretonhampstead, Devon, UK, 2007; Volume September, pp. 1–40. [Google Scholar]
- Lubitz, W.D.; Lyons, M.; Simmons, S. Performance Model of Archimedes Screw Hydro Turbines with Variable Fill Level. J. Hydraul. Eng. 2014, 140, 04014050. [Google Scholar] [CrossRef]
- Lynch, A.J.; Rowland, C.A. The History of Grinding; Society for Mining, Metallurgy, and Exploration: Littleton, CO, USA, 2005. [Google Scholar]
- Siyavula. Water-Wheels. Openstax CNX. 10 September 2009. Available online: https://cnx.org/contents/IRxiIGmY@1/Water-wheels (accessed on 13 May 2020).
- Werner, H.; Alois, L.; Bernhard, P. Lab Testing of the Archimedean Screw. In Proceedings of the Hidroenergia Conference, Wroclaw, Poland, 23–26 May 2012. [Google Scholar]
- Rorres, C. Archimedes in the 21st Century: Proceedings of a World Conference at the Courant Institute of Mathematical Sciences; Springer Basel AG: Cham, Switzerland, 2017. [Google Scholar]
- Schwizer, J. Map of Hydro Turbines. WikiMedi. 16 February 2018. Available online: https://commons.wikimedia.org/wiki/File:Kennfeld_Wasserturbinen.svg (accessed on 23 August 2020).
- Voith-Siemens. Plan View of a Pelton Turbine Installation. Voith Siemens Hydro Power Generation, 16 December 2005. Available online: https://en.wikipedia.org/wiki/File:S_vs_pelton_schnitt_1_zoom.png (accessed on 23 August 2020).
- Breeze, P.A. Power Generation Technologies, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Bermiego. Turgo Turbine. WikiPedia. 29 April 2005. Available online: https://en.wikipedia.org/wiki/File:Turgo_turbine.png (accessed on 23 August 2020).
- Subramanya, K. Hydraulic Machines; McGraw Hill Education (India) Private: New Delhi, India, 2013. [Google Scholar]
- Elbatran, A.H.; Yaakob, O.B.; Ahmed, Y.M.; Shabara, H.M. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Voith-Siemens. Sectional Drawing of a Francis Turbine for the Xingu Power Plant, Brazil. WikiMedia. 16 December 2005. Available online: https://commons.wikimedia.org/wiki/File:M_vs_francis_schnitt_1_zoom.jpg (accessed on 23 August 2020).
- Schweiss, M. Sectional Drawing of a Kaplan Turbine with a Diameter of 9.5 m for Yacyretá, Argentina. WikiMedia. 31 December 2005. Available online: https://commons.wikimedia.org/wiki/File:S_vs_kaplan_schnitt_1_zoom.jpg (accessed on 23 August 2020).
- Durgaiah, D.R. Fluid Mechanics and Machinery; New Age International: New Delhi, India, 2007. [Google Scholar]
- Quaranta, E.; Revelli, R. Gravity water wheels as a micro hydropower energy source: A review based on historic data, design methods, efficiencies and modern optimizations. Renew. Sustain. Energy Rev. 2018, 97, 414–427. [Google Scholar] [CrossRef]
- UNIDO. Renewable Energy: Micro Hydraulic Power Unit (Spiral Type Pico-Hydro Unit ‘PicoPica10′, ‘PicoPica500′); United Nations Industrial Development Organization: Tokyo, Japan, 2020; Available online: http://www.unido.or.jp/en/technology_db/5276/ (accessed on 7 July 2020).
- Landustrie. Linton Lock. Landustrie Sneek BV, 2017. Available online: https://www.landustrie.nl/en/products/hydropower/projects/linton-lock.html (accessed on 29 July 2020).
- ANDRITZ (Formerly Ritz-Atro). Hydrodynamic Screws: Energy Extraction-Efficient and Fish-Friendly; ANDRITZ (Formerly Ritz-Atro): Nurnberg, Germany, 2006. [Google Scholar]
- Senior, J.A. Hydrostatic Pressure Converters for the Exploitation of Very Low Head Hydropower Potential. Ph.D. Thesis, University of Southampton, Southampton, UK, 2009. [Google Scholar]
- Adlard, J. Archimedes Screw: Copley Hydropower Generator; Future Energy Yorkshire: Leeds, UK, 2011. [Google Scholar]
- Bennion, D. Maintaining Archimedes Screw Pumps. ECS Engineering Services, 2013. Available online: http://www.ecsengineeringservices.com/maintaining-archimedes-screw-pumps/ (accessed on 26 June 2018).
- ECS. Archimedes Screw Pumps. ECS Engineering Services, 2018. Available online: http://www.ecsengineeringservices.com/archimedes-screw-pumps/ (accessed on 26 June 2018).
- SBH. Archimedean Screw Turbine; Spaans Babcock B.V., Spaans Babcock Hydro Power: Balk, The Netherlands, 2012. [Google Scholar]
- Dada, O.M.; Daniyan, I.A.; Adaramola, O. Optimal Design of Micro Hydro Turbine (Archimedes Screw Turbine) in Arinta Waterfall in Ekiti State, Nigeria. Res. J. Eng. Appl. Sci. 2014, 4, 34–38. [Google Scholar]
- Pringle, C.M.; Freeman, M.C.; Freeman, B.J. Regional Effects of Hydrologic Alterations on Riverine Macrobiota in the New World: Tropical-Temperate ComparisonsThe massive scope of large dams and other hydrologic modifications in the temperate New World has resulted in distinct regional trends of biotic impoverishment. While neotropical rivers have fewer dams and limited data upon which to make regional generalizations, they are ecologically vulnerable to increasing hydropower development and biotic patterns are emerging. Bioscience 2000, 50, 807–823. [Google Scholar] [CrossRef]
- Neves, R.J.; Bogan, A.E.; Williams, J.D.; Ahlstedt, S.A.; Hartfield, P.W. Status of Aquatic Mollusks in the Southeastern United States: A Downward Spiral of Diversity. In Aquatic Fauna in Peril: The Southeastern Perspective; Lenz Design and Communications: Decatur, GA, USA, 1997; pp. 43–86. [Google Scholar]
- Boys, C.A.; Pflugrath, B.D.; Mueller, M.; Pander, J.; Deng, Z.D.; Geist, J. Physical and hydraulic forces experienced by fish passing through three different low-head hydropower turbines. Mar. Freshw. Res. 2018, 69, 1934–1944. [Google Scholar] [CrossRef]
- McNabb, C.D.; Liston, C.R.; Borthwick, S.M. Passage of Juvenile Chinook Salmon and other Fish Species through Archimedes Lifts and a Hidrostal Pump at Red Bluff, California. Trans. Am. Fish. Soc. 2003, 132, 326–334. [Google Scholar] [CrossRef]
- Kibel, P.; Pike, R.; Coe, T. Archimedes Screw Turbine Fisheries Assessment. Phase II: Eels and Kelts; Fishtek Consulting Ltd.: Moretonhampstead, UK, 2008. [Google Scholar]
- Kibel, P.; Pike, R.; Coe, T. The Archimedes Screw Turbine: Assessment of Three Leading Edge Profiles; Fishtek Consulting Ltd.: Moretonhampstead, UK, 2009. [Google Scholar]
- United Kingdom Environment Agency. Hydropower Good Practice Guidelines Screening requirements. J. Hydraul. Res. 2012, 4, 1–16. [Google Scholar]
- Piper, A.T.; Rosewarne, P.J.; Wright, R.M.; Kemp, P.S. The impact of an Archimedes screw hydropower turbine on fish migration in a lowland river. Ecol. Eng. 2018, 118, 31–42. [Google Scholar] [CrossRef]
- Nuernbergk, D.M.; Rorres, C. Analytical Model for Water Inflow of an Archimedes Screw Used in Hydropower Generation. J. Hydraul. Eng. 2013, 139, 213–220. [Google Scholar] [CrossRef]
- Brada, K.; Radlik, K.-A. Wasserkraftschnecke: Eigenschaften und Verwendung. In Heat Exchange and Renewable Energy Sources; International Symposium: Szczecin, Poland, 1996; pp. 43–52. [Google Scholar]
- Aigner, D. Current Research in Hydraulic Engineering 1993–2008; Institut für Wasserbau und Technisch Hydromechanik der TU Association: Dresden, Germany, 2008. [Google Scholar]
- Schmalz, W. Studies on fish migration and control of possible fish loss caused by the hydrodynamic screw and hydropower plant. In Fischo—Kologische und Limnol. Untersuchungsstelle Sudthurign, Rep.; Thüringer Landesanstalt für Umwelt und Geol: Jena, Germany, 2010. [Google Scholar]
- Lashofer, A.; Kaltenberger, F.; Pelikan, B. Does the archimedean screw turbine stand the test? (Wie gut bewährt sich die Wasserkraftschnecke in der Praxis?). Wasserwirtschaft 2011, 101, 76–81. [Google Scholar] [CrossRef]
- Nuernbergk, D.M. Wasserkraftschnecken—Berechnung und Optimaler Entwurf von Archimedischen Schnecken als Wasserkraftmaschine (Hydro-Power Screws—Calculation and Design of Archimedes Screws), 2nd ed.; Verlag Moritz Schäfer: Detmold, Germany, 2020. [Google Scholar]
- Fraenkel, P.; Paish, O.; Harvey, A.; Brown, A.; Edwards, R.; Bokalders, V. Micro-Hydro Power: A Guide for Development Workers; Intermediate Technology Publications: London, UK, 1999. [Google Scholar]
- NationalTrust. Hydropower Returns to Cragside|National Trust. 2020. Available online: https://www.nationaltrust.org.uk/features/hydropower-returns-to-cragside (accessed on 1 July 2020).
- Sumino, M. Ultra-Small Water Power Generator. 14 May 2019. Available online: https://youtu.be/XjEgFlngZ04 (accessed on 23 June 2020).
- Rosser. The Cragside Estate Archimedes Screw Water Turbine and Generator. Rothbury, England. Wikimedia Commons. 14 October 2016. Available online: https://commons.wikimedia.org/wiki/File:The_Cragside_Estate_Archimedes_screw_water_turbine_and_generator,_Rothbury,_England.jpg (accessed on 5 July 2020).
- Down, C. Cragside Archimedes’ Screw from Bottom. Wikimedia Commons. 17 May 2017. Available online: https://commons.wikimedia.org/wiki/File:Cragside_Archimedes%27_screw_from_bottom.jpg (accessed on 5 July 2020).
- Spaans Babcock Ltd. Hydro Power Using Waste Water at Esholt WwTW. Spaans Babcock Ltd., 2009. Available online: https://cms.esi.info/Media/documents/54053_1316689157666.pdf (accessed on 29 July 2020).
- Padhy, M.K.; Saini, R.P. A review on silt erosion in hydro turbines. Renew. Sustain. Energy Rev. 2008, 12, 1974–1987. [Google Scholar] [CrossRef]
- Awasthi, A.K. Design for Small hydro-An Innovative Approach. In Proceedings of the 2nd International Conference on Silting Problems in Hydropower Plants, Bangkok, Thailand, 26–28 September 2001; pp. 83–89. [Google Scholar]
- Kang, M.W.; Park, N.; Suh, S.H. Numerical Study on Sediment Erosion of Francis Turbine with Different Operating Conditions and Sediment Inflow Rates. Procedia Eng. 2016, 157, 457–464. [Google Scholar] [CrossRef]
- Rinaldi, M.; Gurnell, A.M.; Belletti, B.; Berga Cano, M.I.; Bizzi, S.; Bussettini, M.; del Tánago, M.; Grabowski, R.; Habersack, H.; Klösch, M.; et al. Final Report on Methods, Models, Tools to Assess the Hydromorphology of Rivers. 2015. Available online: https://reformrivers.eu/ (accessed on 7 September 2020).
- Durrani, A.M.; Uzair, M. Micro Hydro Power Plant using Sewage Water of Hayatabad Peshawar. In Proceedings of the 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2–3 December 2019. [Google Scholar]
- IWPDC. A Quiet Revolution. International Water Power & Dam Construction. 29 November 2010. Available online: https://www.waterpowermagazine.com/features/featurea-quiet-revolution/ (accessed on 6 July 2020).
- Yorkshire Water. Words Of Water: UK’s First Energy Self-Sufficient Large Sewage Works. Yorkshire Water, 2014. Available online: http://wordsofwater.blogspot.com/2012/01/uks-first-energy-self-sufficient-large.html (accessed on 29 July 2020).
- Born, S.M.; Genskow, K.D.; Filbert, T.L.; Hernandez-Mora, N.; Keeper, M.L.; White, K.A. Socioeconomic and institutional dimensions of dam removals: The Wisconsin experience. Environ. Manag. 1998, 22, 359–370. [Google Scholar] [CrossRef] [PubMed]
- Babbit, B. What Goes Up, May Come Down. New Sci. 2002, 52, 656–658. [Google Scholar] [CrossRef]
- Lejon, A.G.C. Ecosystem Response to Dam Removal; Department of Ecology and Environmental Science, Umeå University: Umeå, Sweden, 2012. [Google Scholar]
- Tahmiscioğlu, M.S.; Durmuş, N. Positive and negative impacts of dams on the environment. In Proceedings of the International Congress On River Basin Management, Ankara, Turkey, 8 March 2007; pp. 759–769. [Google Scholar]
- D’Antonio, C.; Meyerson, L.A. Exotic plant species as problems and solutions in ecological restoration: A synthesis. Restor. Ecol. 2002, 10, 703–713. [Google Scholar] [CrossRef]
- Shafroth, P.B.; Friedman, J.M.; Auble, G.T.; Scott, M.L.; Braatne, J.H. Potential Responses of Riparian Vegetation to Dam Removal. Bioscience 2002, 52, 703–712. [Google Scholar] [CrossRef]
- Orr, C.H.; Stanley, E.H. Vegetation development and restoration potential of drained reservoirs following dam removal in Wisconsin. River Res. Appl. 2006, 22, 281–295. [Google Scholar] [CrossRef]
- Grant, G. Dam removal: Panacea or Pandora for rivers? Hydrol. Process. 2001, 15, 1531–1532. [Google Scholar] [CrossRef]
- Ashley, J.T.F.; Bushaw-Newton, K.; Matt, W.; Boettner, A.; Drames, G.; Velinsky, D.J. The Effects of Small Dam Removal on the Distribution of Sedimentary Contaminants. Environ. Monit. Assess. 2006, 114, 287–312. [Google Scholar] [CrossRef]
- Hetling, L.; Horn, E.; Tofflemire, J. Summary of Hudson River PCB Study Results; NYS Department of Environmental Conservation: New York, NY, USA, 1978.
- Waters, S.; Aggidis, G.A. Over 2000 years in review: Revival of the Archimedes Screw from Pump to Turbine. Renew. Sustain. Energy Rev. 2015, 51, 497–505. [Google Scholar] [CrossRef]
- Keyes, J.; Pastinak, O. MNR’s Role in Public Safety Around Dams—An Overview. Ministry of Natural Resources, Biodiversity Branch Policy Division. Presentation to Ontario Waterpower Association. 11 April 2011. Available online: https://slideplayer.com/slide/6376193/ (accessed on 9 May 2020).
- Demal, L. Dam Safety in Ontario New Dam Safety Technical Guidelines—What do they mean for Ontario? Ministry of Natural Resources. In Proceedings of the Ontario Waterpower Association—Annual Power of Water Conference, Niagara-on-the Lake, ON, Canada, 23 October 2012. [Google Scholar]
- ASDSO. The Cost of Rehabilitating Our Nation’s Dams: A Methodology, Estimate & Proposed Funding Mechanisms; Association of State Dam Safety Officials: Lexington, KY, USA, 2016.
- Ontario Energy Board. Ontario’s System-Wide Electricity Supply Mix: 2013 Data; Ontario Energy Board: Toronto, ON, Canada, 2014. [Google Scholar]
- Ontario Ministry of Energy. Ontario’s Long-Term Energy Plan; Queen’s Printer for Ontario: Toronto, ON, Canada, 2010.
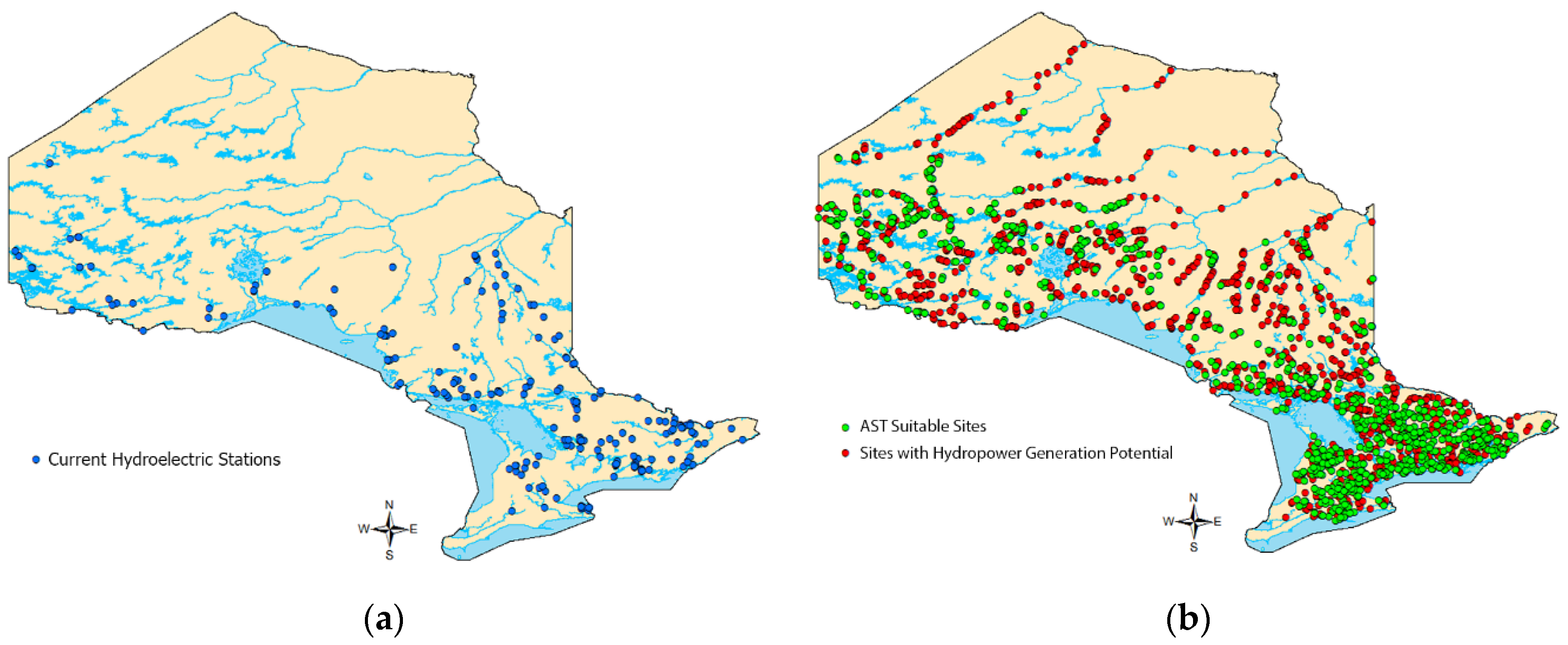
- Hatch Acres. Evaluation and Assessment of Ontario’s Waterpower Potential Ministry of Natural Resources Final Report; Hatch Acres: Peterborough, ON, Canada, 2005. [Google Scholar]
- Ontario Ministry of Natural Resources. Potential Waterpower Generation Sites (WPPOTSTE). Ontario Ministry of Natural Resources, 2004. Available online: https://www.ontario.ca/data/potential-waterpower-generation-sites-wppotste (accessed on 10 January 2015).
- Kozyn, A.; Ash, S.; Lubitz, W.D. Assessment of Archimedes Screw Power Generation Potential in Ontario. In Proceedings of the 4th Climate Change Technology Conference, Montreal, QC, Canada, 25–27 May 2015; no. 1570095585. pp. 1–11. [Google Scholar]
- Muysken, J. Calculation of the Effectiveness of the Auger. De Ingenieur 1932, 21, 77–91. [Google Scholar]
- Lashofer, A. Project Hydropower Screw Location—Ingenieurbüro Lashofer! Lashofer Ingenieurbüro für Wasserwirtschaft. Available online: https://www.lashofer.at/deutsch/wasserkraftschnecke/projekt-wasserkraftschnecken-verortung/ (accessed on 4 July 2020).
- AberdareOnline. Weir—D What Ronald Kear Knows about Archimedes, the Royal Family and a Successful Fish Pass|AberdareOnline. AberdareOnline, 23 September 2009. Available online: https://web.archive.org/web/20110416143406/http://www.aberdareonline.co.uk/content/weir-–-d-what-ronald-kear-knows-about-archimedes-royal-family-and-successful-fish-pass (accessed on 5 July 2020).
- Jones, R. Monmouth New Hydro Scheme. Wikimedia Commons. 20 March 2009. Available online: https://commons.wikimedia.org/wiki/File:Monmouth_New_Hydro_Scheme_-_geograph.org.uk_-_1538784.jpg (accessed on 5 July 2020).
- RenewablesFirst. Radyr Weir Hydro Turbines. Renewables First, 28 October 2015. Available online: https://www.renewablesfirst.co.uk/project-blog/radyr-weir-hydro-scheme/ (accessed on 5 July 2020).
- Rose, R. Linton Falls and Low Wood Hydropower Schemes. In River Coast; No. UK Water Projects 2011: Manchester, UK, 2011; pp. 197–202. [Google Scholar]
- James, G. Radyr Weir Hydro Scheme. Geograph.org.uk. 11 September 2016. Available online: https://commons.wikimedia.org/wiki/File:Radyr_weir_hydro_scheme_(geograph_5112329).jpg (accessed on 5 July 2020).
- James, P. Linton Falls Hydroelectric Power Station. Wikimedia Commons. 7 July 2018. Available online: https://commons.wikimedia.org/wiki/File:Linton_Falls_Hydroelectric_Power_Station.jpg (accessed on 5 July 2020).
- SinFin. Solvay Industrial Plant. SinFin Energy, 2019. Available online: http://www.sinfinenergy.com/en/projects/solvay/ (accessed on 8 July 2020).
- Fergnani, N. Hydroelectric plants Energy efficiency. Hydrosmart Srl. 2020. Available online: https://www.hydrosmart.it/energia-rinnovabile (accessed on 2 August 2020).
- Sto98. Marengo Hydropower Plant-Goito [Centrale Idroelettrica Marengo—Goito]. YouTube. 19 February 2015. Available online: https://youtu.be/19px1EKa--4 (accessed on 19 July 2020).
- Hart, C.; Saling, S. To Cut Poverty in Asia and the Pacific. ‘Energy Plus’ Package a Must, Says UN Report|UNDP. United Nations Development Programme, 19 January 2012. Available online: https://www.undp.org/content/undp/en/home/presscenter/pressreleases/2012/01/19/to-cut-poverty-in-asia-and-the-pacific-energy-plus-package-a-must-says-un-report.html (accessed on 29 July 2020).
- Khan, M.J.; Iqbal, M.T.; Quaicoe, J.E. River current energy conversion systems: Progress, prospects and challenges. Renew. Sustain. Energy Rev. 2008, 12, 2177–2193. [Google Scholar] [CrossRef]
- Muhammad, U. Rural solar electrification in Nigeria: Renewable energy potentials and distribution for rural development. In Proceedings of the World Renewable Energy Forum, WREF 2012, Including World Renewable Energy Congress XII and Colorado Renewable Energy Society (CRES) Annual Conference, Denver, CO, USA, 13–17 May 2020; Volume 4, pp. 2674–2681. [Google Scholar]
- Eberhard, A.; Rosnes, O.; Shkaratan, M.; Vennemo, H. Africa’s Power Infrastructure Investment, Integration, Efficiency Infrastructure; World Bank Publications: Washington, DC, USA, 2011. [Google Scholar]
- Nuramal, A.; Daratha, N.; Setiawan, A. The Effect of the Ratio of the Hub Diameter (d) to the Diameter of the Screw (D) to the Performance of the Archimides Screw. IOP Conf. Ser. Mater. Sci. Eng. 2020, 874, 1–8. [Google Scholar] [CrossRef]
- Siswantara, A.I.; Gumelar, M.H.S.; Budiarso; Harmadi, R.; Warjito; Adanta, D. Analysis of the Effects of Overflow Leakage Phenomenon on Archimedes Turbine Efficiency. In Proceedings of the 2018 4th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 August 2018; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Erinofiardi; Nuramal, A.; Bismantolo, P.; Date, A.; Akbarzadeh, A.; Mainil, A.K.; Suryono, A.F. Experimental Study of Screw Turbine Performance based on Different Angle of Inclination. Energy Procedia 2017, 110, 8–13. [Google Scholar] [CrossRef]
- Syam, I.; Maulana, M.I.; Syuhada, A. Design and Performance of Archimedes Single Screw Turbine as Micro Hydro Power Plant with Flow Rate Debit Variations (Case Study in Air Dingin, Samadua—South Aceh). J. Inotera 2019, 4, 13. [Google Scholar] [CrossRef]
- Kakuno Seisakusho Co. Ltd. Small Hydro. Suminoseisakusho. Available online: http://suminoseisakusho.jp/saisei.html (accessed on 21 July 2020).
- Kakuno Manufacturing Co. The Ecological Arita River Town in the Sankei Shimbun; Kakuno Manufacturing Co., Ltd.: Ena, Gifu, Japan, 2017; Available online: https://www.fb.com/YouXianHuiSheJiaoYeZhiZuoSuo/posts/1900744169952506 (accessed on 21 July 2020).
- SuminoSeisakusho. Multi-AST Two Pico Pika Units Running Since 2012 in ibi-Cho, Gifu; Kakuno Manufacturing Co., Ltd.: ibi-Cho, Gifu, Japan, 2018; Available online: https://www.fb.com/YouXianHuiSheJiaoYeZhiZuoSuo/posts/2201719083188345 (accessed on 5 August 2020).
- Kakuno Manufacturing Co. Reniks Project in Suginami Tree Park in Nikko City, Tochigi, Japan. 2016. Available online: https://www.fb.com/YouXianHuiSheJiaoYeZhiZuoSuo/posts/1535798529780407 (accessed on 21 July 2020).
- UNIDO. Technologies from Japan. In Sustainable Technology Promotion Platform (STePP); UNIDO: Vienna, Austria, 2019; Volume 1, p. 18. [Google Scholar]
- Nagel, G.; Radlik, K.A. Wasserförderschnecken: Planung, Bau und Betrieb von Wasserhebeanlagen [Water Lifting Screws: Planning, Construction and Operation of Water Lifting Systems]; Pfriemer: Berlin, Germany, 1988. [Google Scholar]
- YoosefDoost, A.; Lubitz, W.D. Development of an Equation for the Volume of Flow Passing through an Archimedes Screw Turbine. In Proceedings of the Sustaining Tomorrow Symposium 2020, Windsor, ON, Canada, 18–19 June 2012. [Google Scholar]
- Nagel, G. Archimedian Screw Pump Handbook: Fundamental Aspects of the Design and Operation of Water Pumping Installations Using Archimedian Screw Pumps; RITZ-Pumpenfabrik OHG: Schwäbisch Gmünd, Germany, 1968. [Google Scholar]
- Lubitz, W.D. Gap Flow in Archimedes Screws. In Proceedings of the Canadian Society for Mechanical Engineering International Congress 2014 CSME International Congress 2014, Toronto, ON, Canada, 1–4 June 2014; pp. 1–6. [Google Scholar]
- Tullis, B.P.; Robinson, S.C. Quantifying Culvert Exit Loss. J. Irrig. Drain. Eng. 2008, 134, 263–266. [Google Scholar] [CrossRef]
- Passamonti, A. Investigation of Energy Losses in Laboratory and Full-Scale Archimedes Screw Generators. Master’s Thesis, Politecnico Di Milano, Milan, Italy, 2017. [Google Scholar]
- Kozyn, A.; Lubitz, W.D. A power loss model for Archimedes screw generators. Renew. Energy 2017, 108, 260–273. [Google Scholar] [CrossRef]
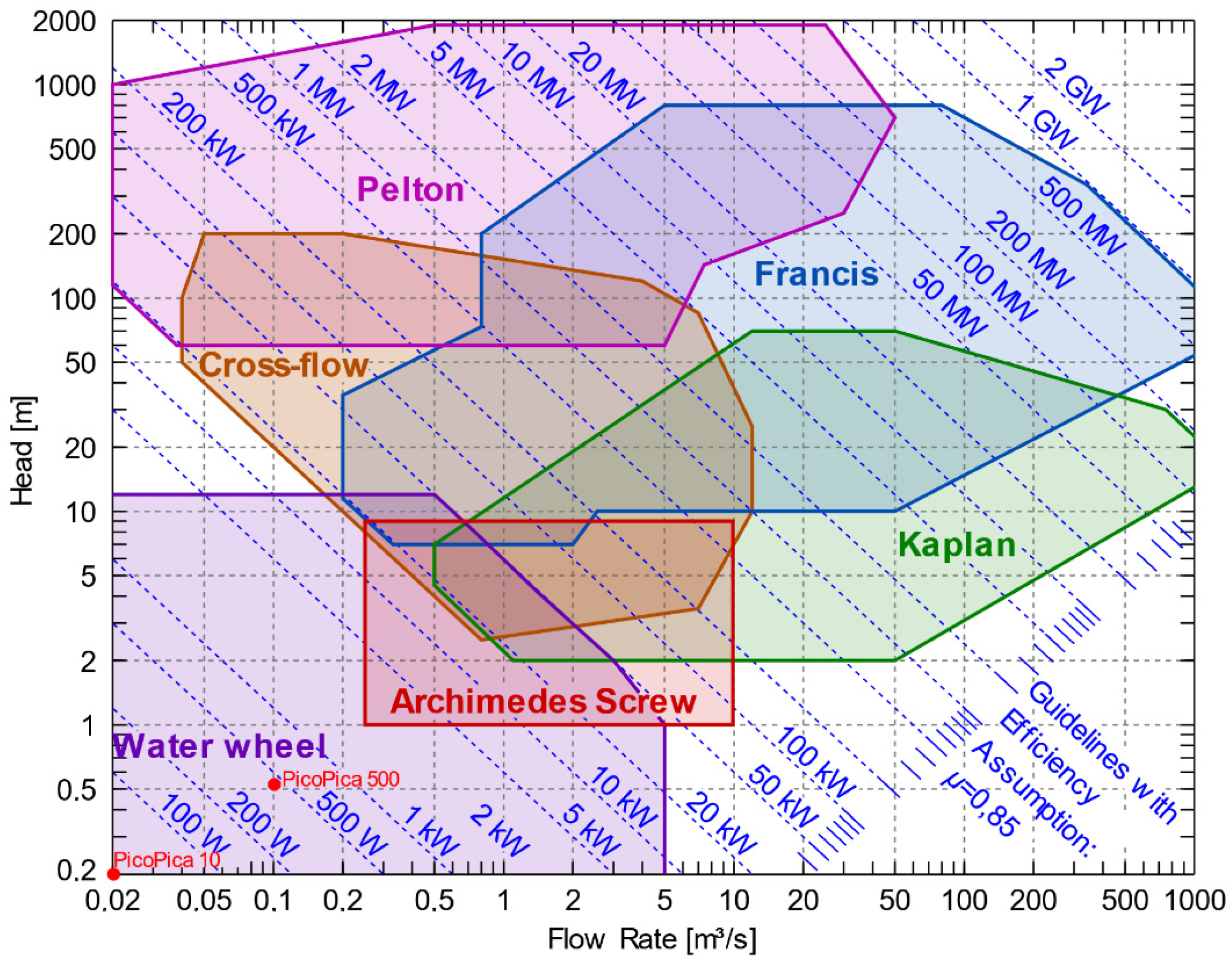









| Type | Turbine | Head (m) | Flow Rate (m3/s) | Notes |
|---|---|---|---|---|
| Impulse | Pelton [36] | 50 *–1000 [12] | <50 [35] | A high-pressure jet of water is directed at bucket-shaped blades and nearly all of the flow energy to be converted to rotational mechanical energy [37]. |
Turgo [38] | 50 **–250 [39] | <10 [40] | A modification of a Pelton that incoming water jet is directed at an angle of 20 degrees to the buckets. A larger jet stream of water relative to the turbine diameter for the same flow and head produces more power or can be constructed smaller [39]. | |
| Reaction | Francis [41] | 40–600 [39] | 0.2–1000 [35] (Specific Flow) | Flow enters the turbine radially then is redirected in a direction along the axial length of the turbine. The pressure difference across the blades is accomplished by changing flow direction and can be 90% to 95% efficient [37]. Efficiency reduces dramatically in flow rates below 75% of the design flow [37] |
Kaplan [42] | <50 [43] | 0.5–1000 [35] | Flowing water pushing past the propeller blades creates a pressure difference [37]. Best suited for headsless than impulse and Francis turbines for the same flow, and for flow rates higher than Francis and Pelton turbines for the same head. The propeller angle can vary to optimize energy extraction. | |
| Quasi-static Pressure | Water wheel [32]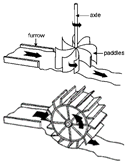 | <10 | <5 | Vertical axis Water Wheels rotate due to the force exerted to the paddles by the momentum of the flow. Horizontal axis Water Wheels rotate because of the momentum of the water, as well as the weight of water on the small water buckets formed between the paddles. So, they are a bit more efficient than conventional horizontal ones [31]. The efficiency of well-constructed WWs is 50%–70% [31]. The hydraulic efficiency of Vertical Water Wheels is reported up to 85% [44]. |
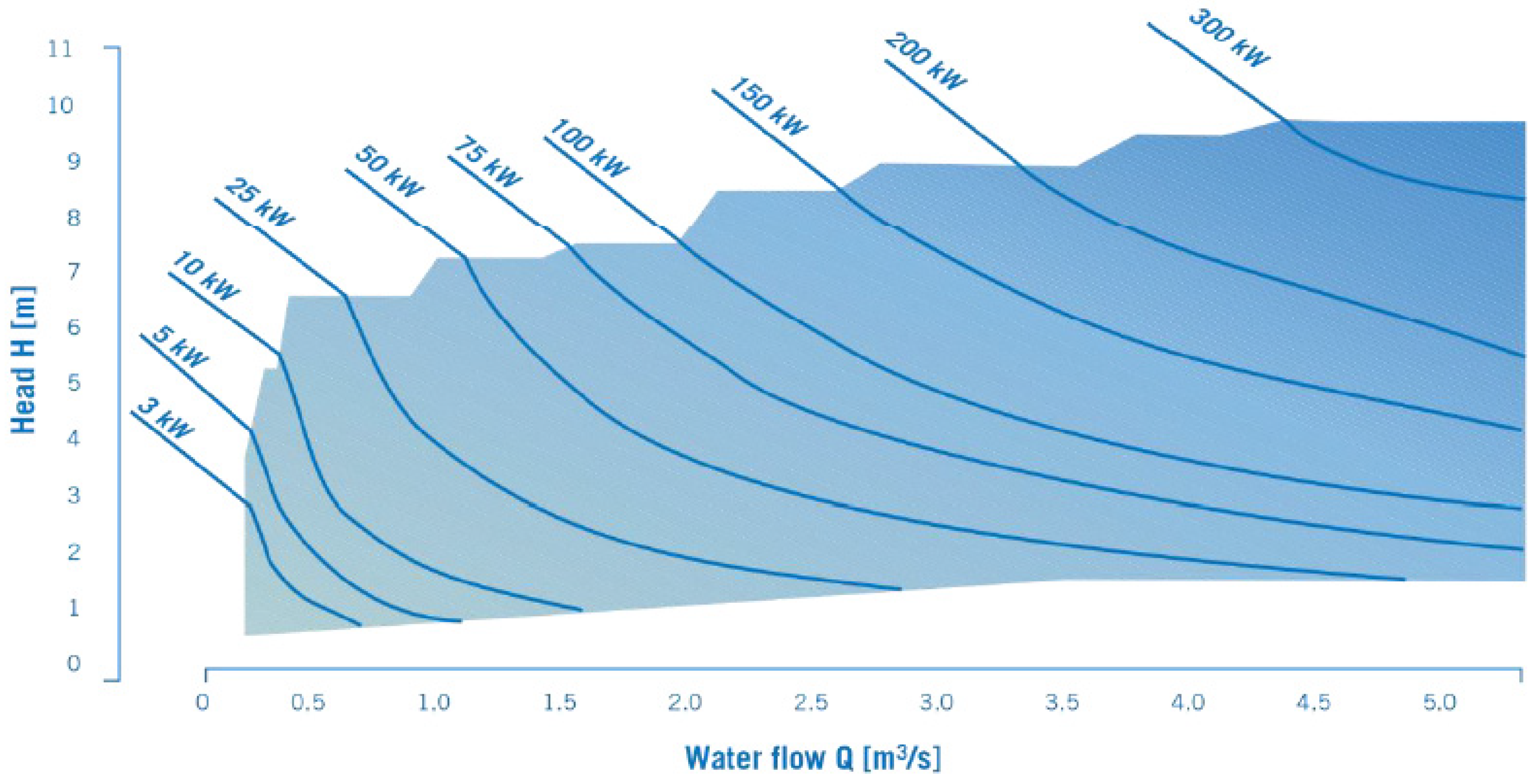
Archimedes Screw | <10 [33,40] | <10 [33,45] | Efficiency range between 60% and 80% and remains high even as available head approaches zero. Produce up to 355 kW [46] of power [28]. Practical even in combined low head and low flow |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability 2020, 12, 7352. https://doi.org/10.3390/su12187352
YoosefDoost A, Lubitz WD. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability. 2020; 12(18):7352. https://doi.org/10.3390/su12187352
Chicago/Turabian StyleYoosefDoost, Arash, and William David Lubitz. 2020. "Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures" Sustainability 12, no. 18: 7352. https://doi.org/10.3390/su12187352
APA StyleYoosefDoost, A., & Lubitz, W. D. (2020). Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability, 12(18), 7352. https://doi.org/10.3390/su12187352