Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core
Abstract
1. Introduction
2. Analysis Methodology
2.1. Theoretical Bases
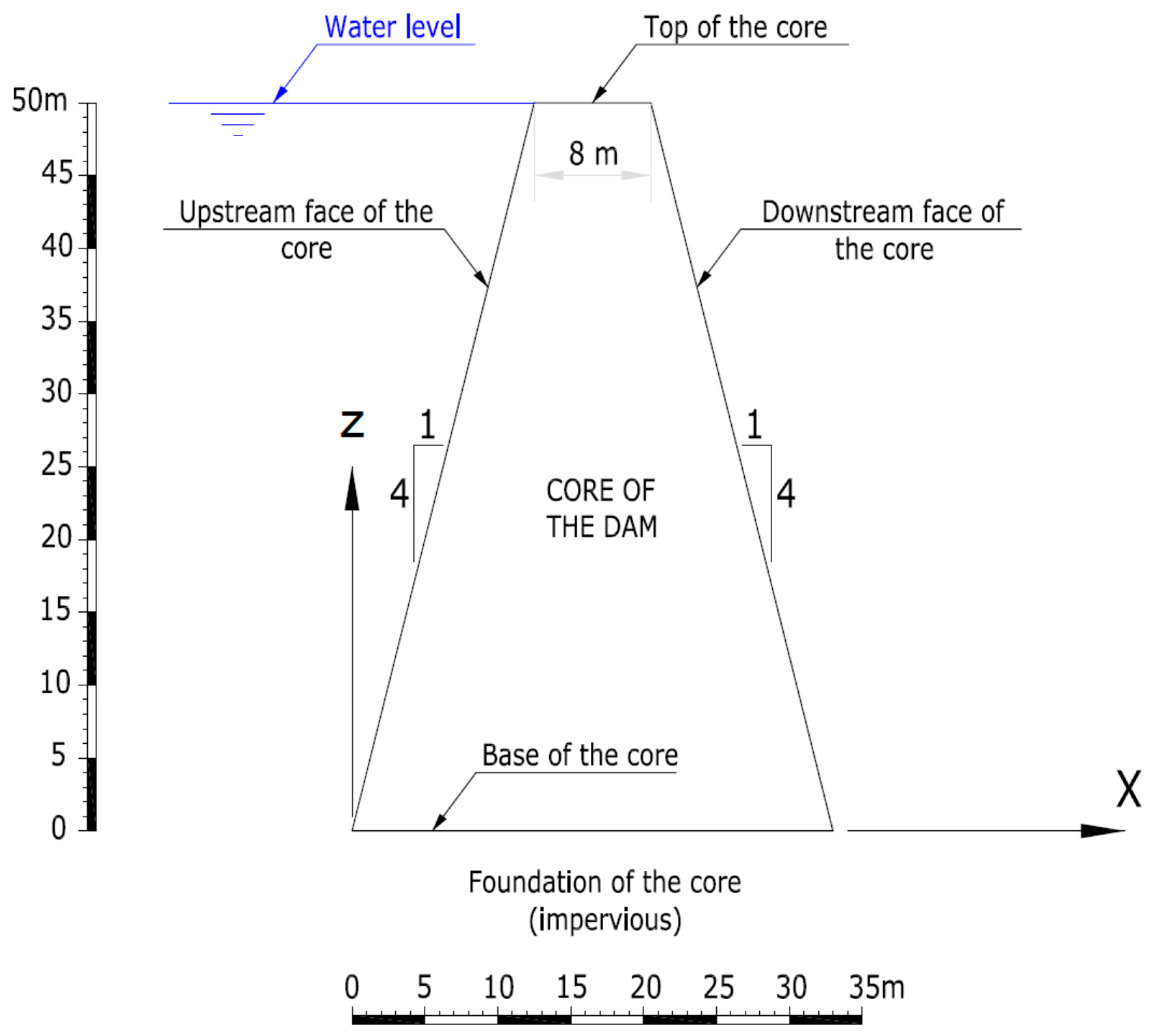
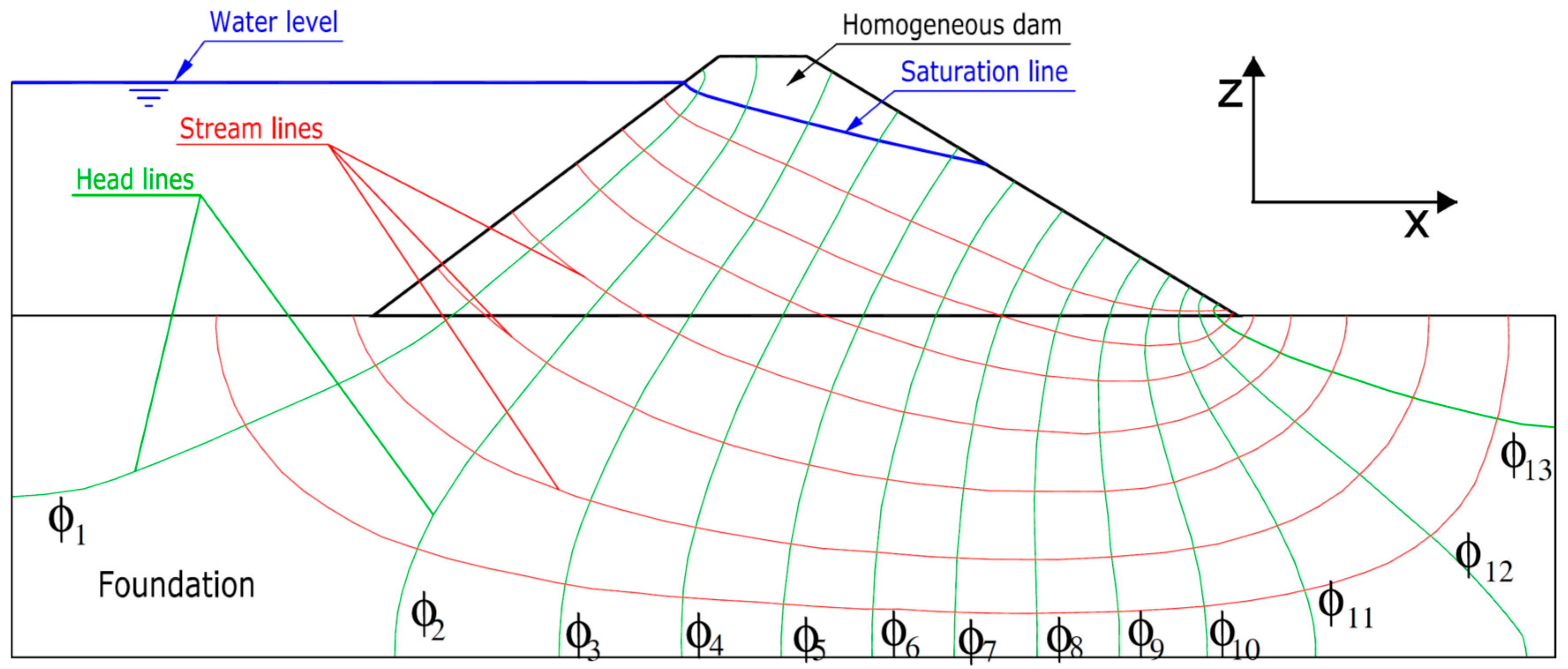
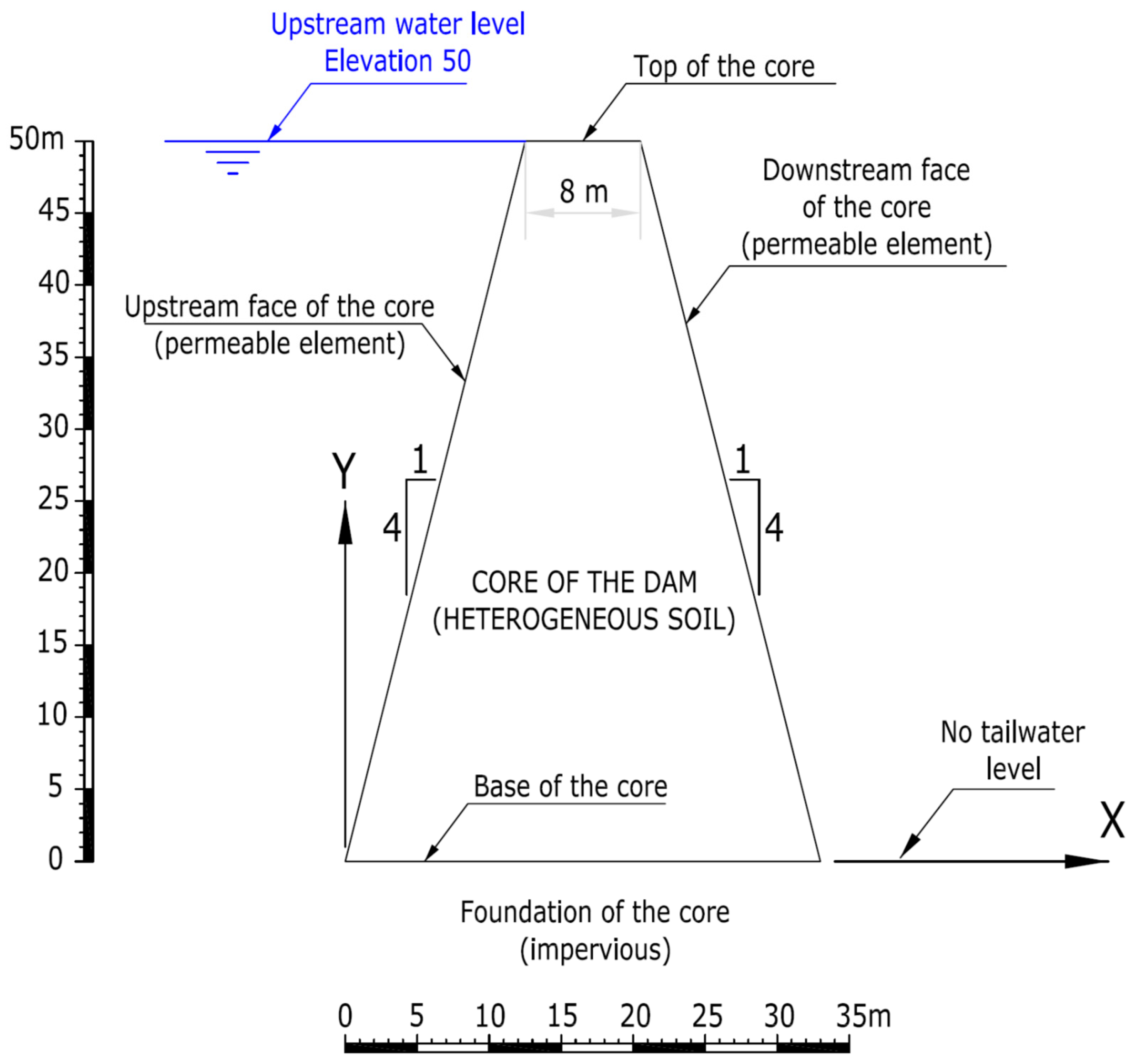
- Plain deformation. The two-dimensional problem with water flow in the directions defined within the dam cross section was considered (Figure 1). Therefore, the seepage flow per linear meter of the dam was studied and the total flow defined by the total length of the dam constructed in the dam site. In Figure 1, the water level is represented at the top of the dam core, without freeboard. As indicated later in Section 3.2, different calculations were made to account for different situations of the reservoir and to be able to see the sensitivity of the filtration flow results with the increase in water heights.
- The filtration calculation was considered decoupled with the stress-strain analysis. Therefore, its compactness did not vary throughout the filtration process.
- Darcy’s law was considered valid [23] and, therefore, the speed of the water flow in each point of the soil was proportional to the permeability of the soil and to the variation of the hydraulic potential with respect to its trajectory. It should be pointed out that due to the dam’s own construction process, which was carried out by compacted layers of 20 to 40 cm thick. The permeability was considered not be isotropic.
2.2. Finite Difference Method
2.2.1. Basis
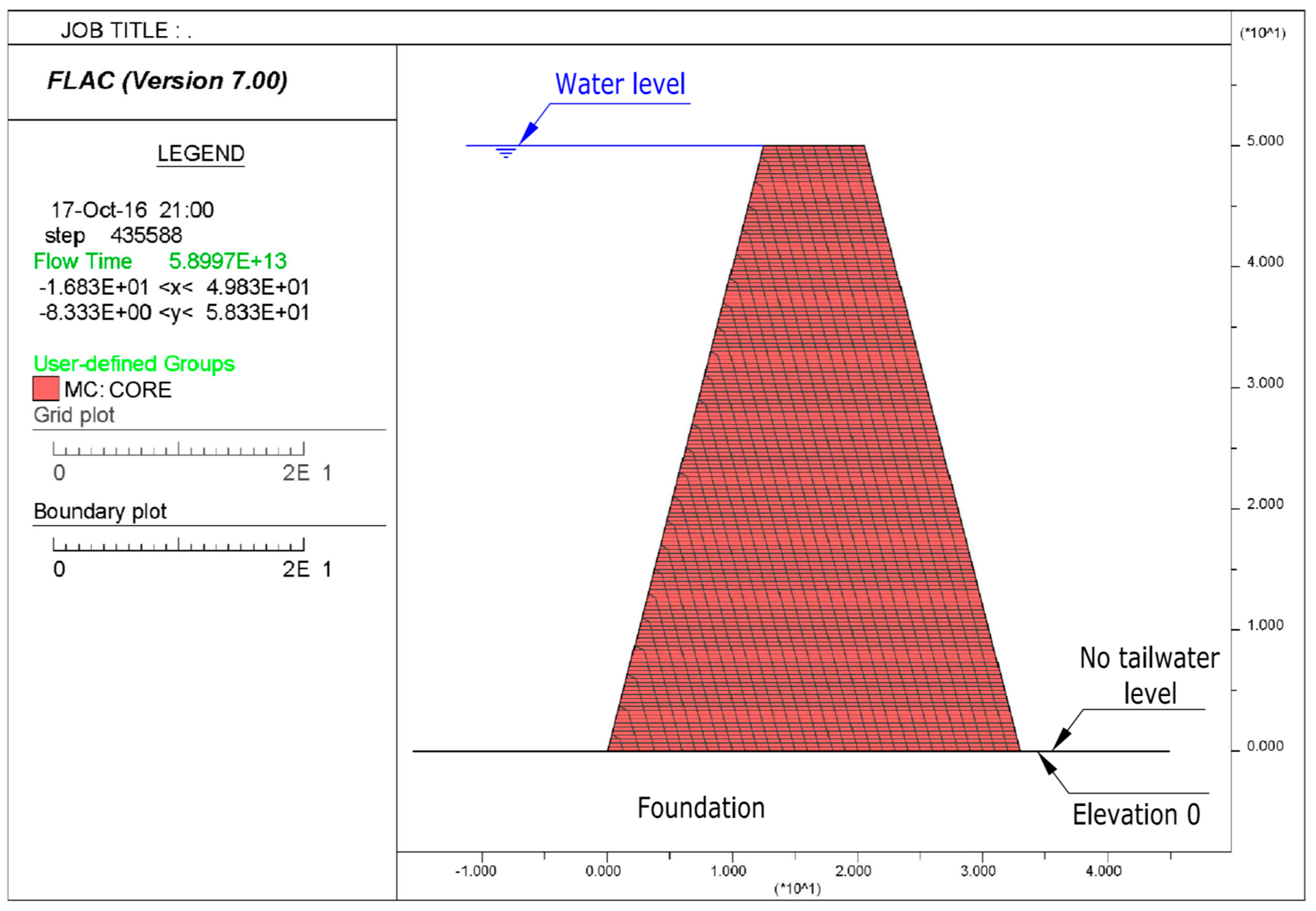
2.2.2. Finite Difference Model
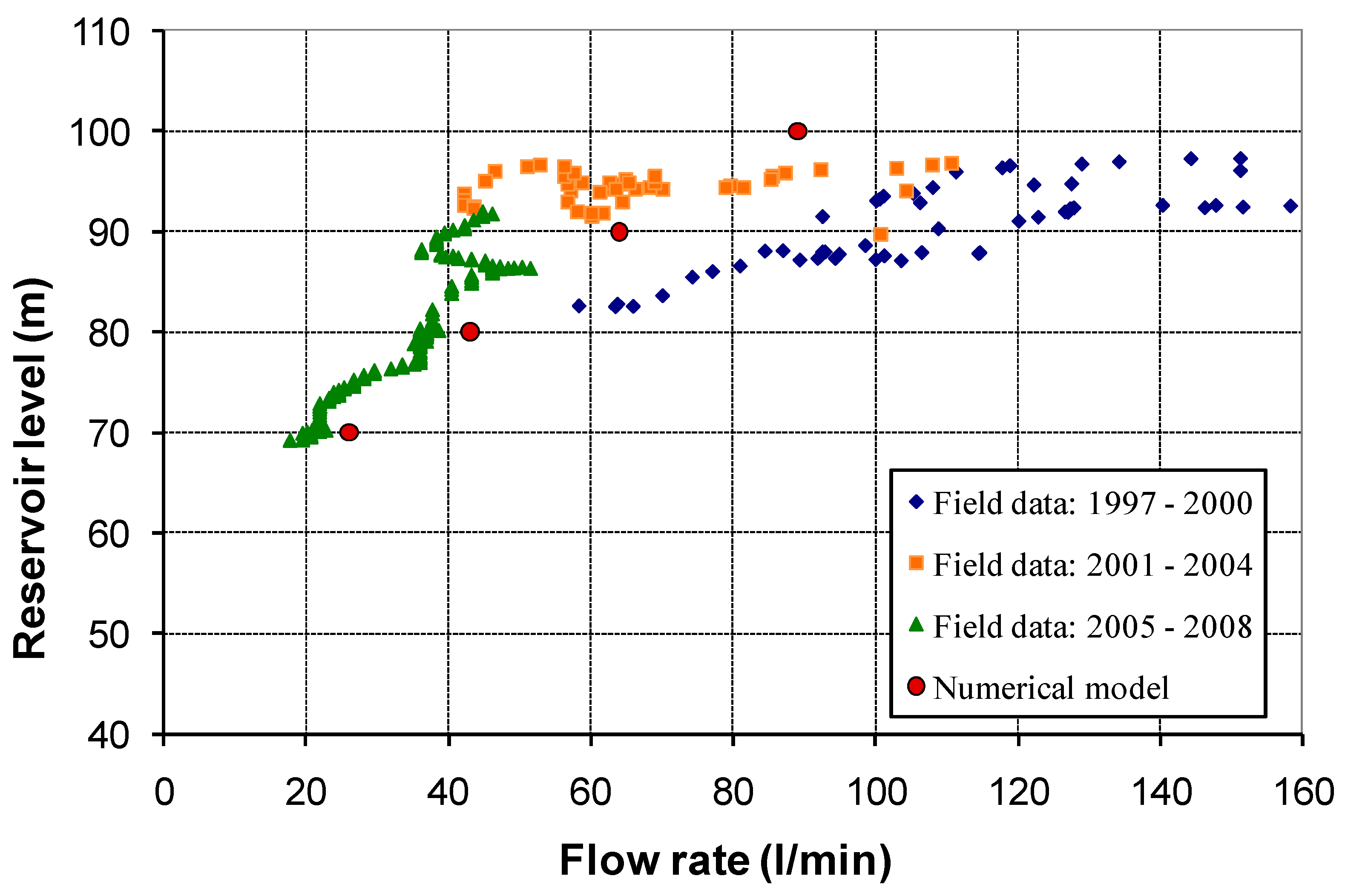
2.2.3. Model Validation
3. Core Zoning Study
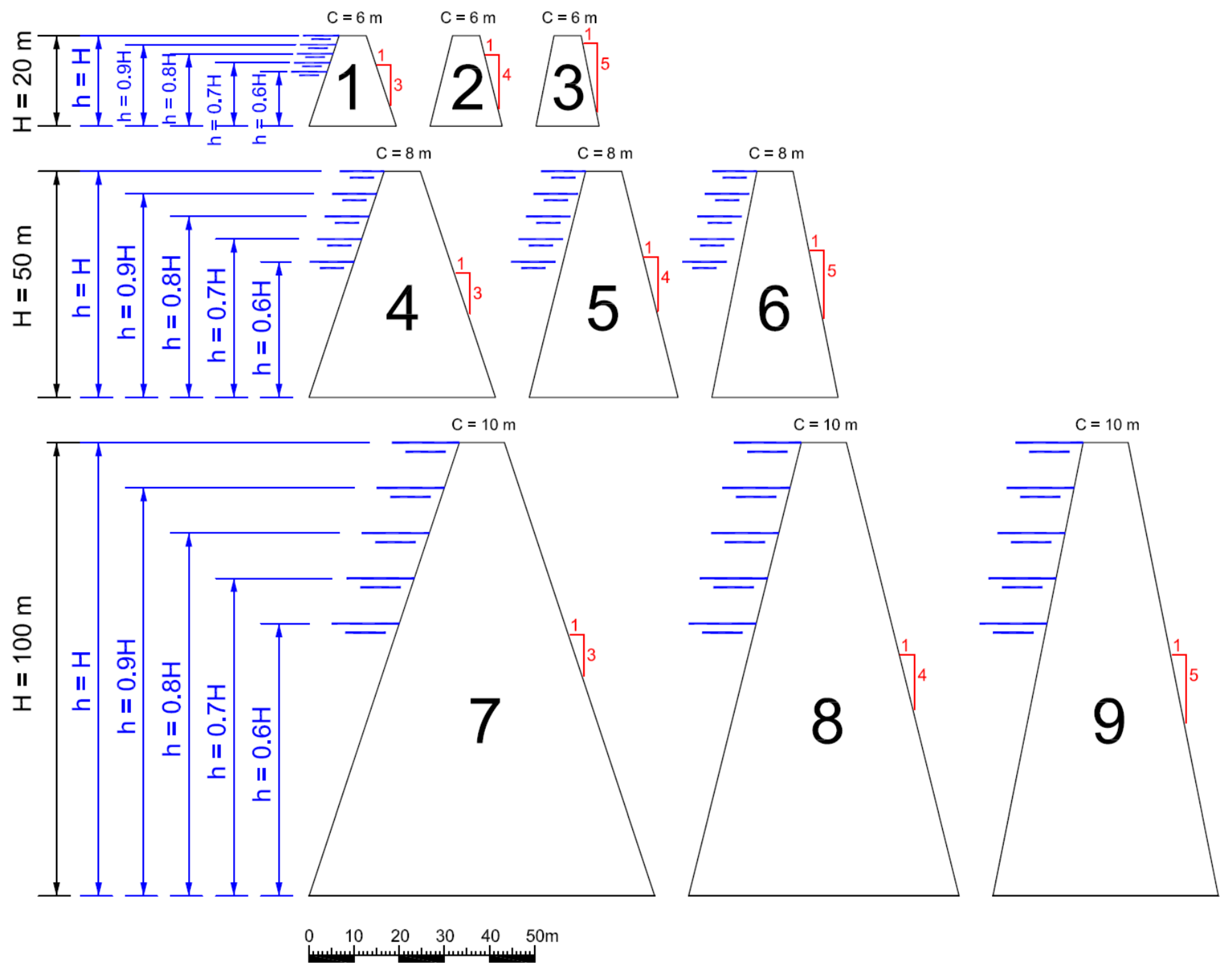
3.1. Core Geometry
3.2. Water Height
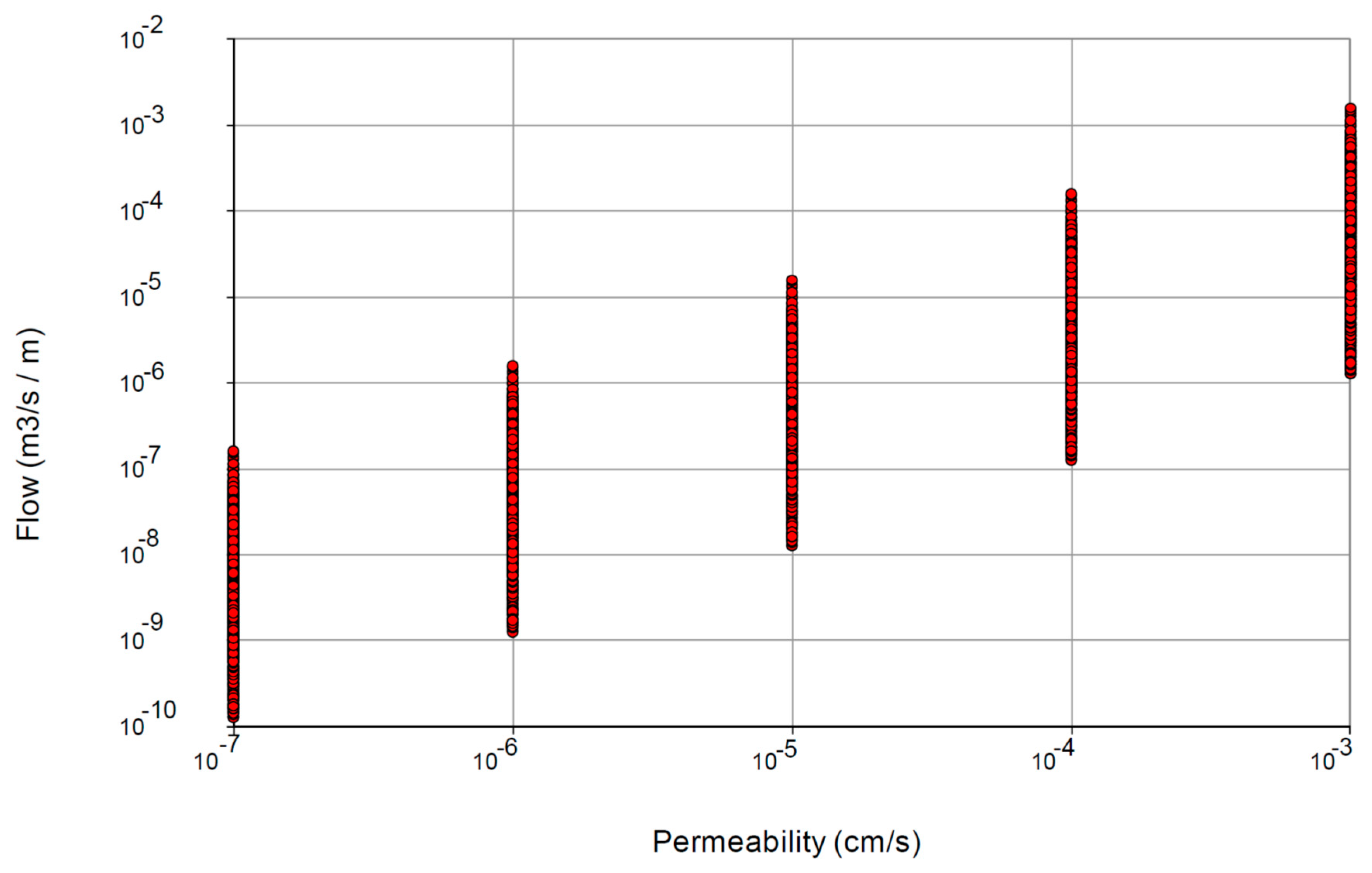
3.3. Material Permeability
3.4. Materials Zoning
- Case 0 corresponded to a homogeneous core, without zoning, made up of a single material with horizontal permeability k = k1.
- Case I showed a core dividing the height in half, i.e., 2 zones. Two sub-cases (I-A and I-B) were analyzed depending on whether the greater horizontal permeability and k1, was considered in the upper half or in the lower half.
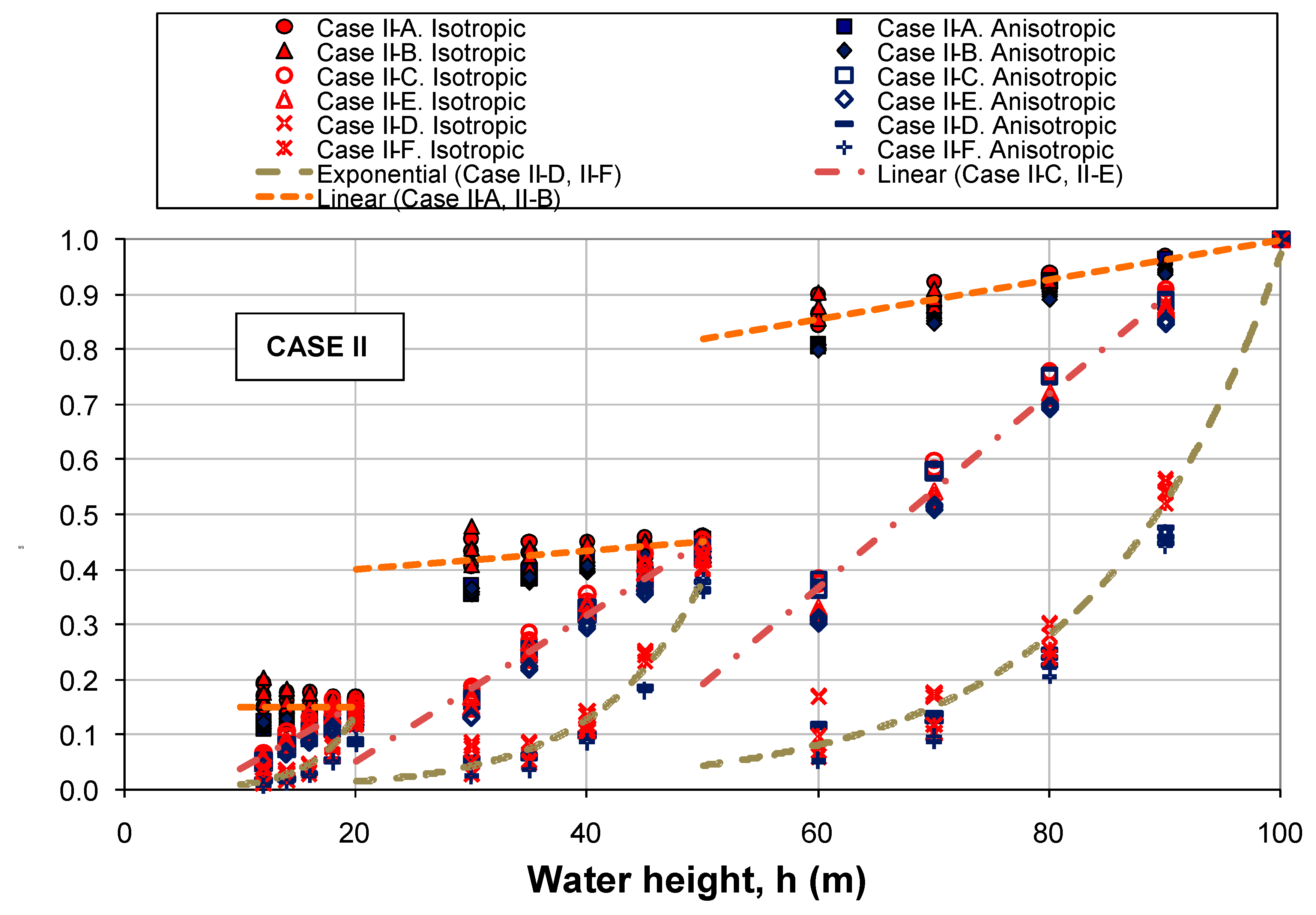
- Case II was similar to the previous one, but dividing the core height into three zones of identical sub-heights. Six subcases (II-A to II-F) were studied based on the distribution of horizontal permeabilities k1, k2 and k3.
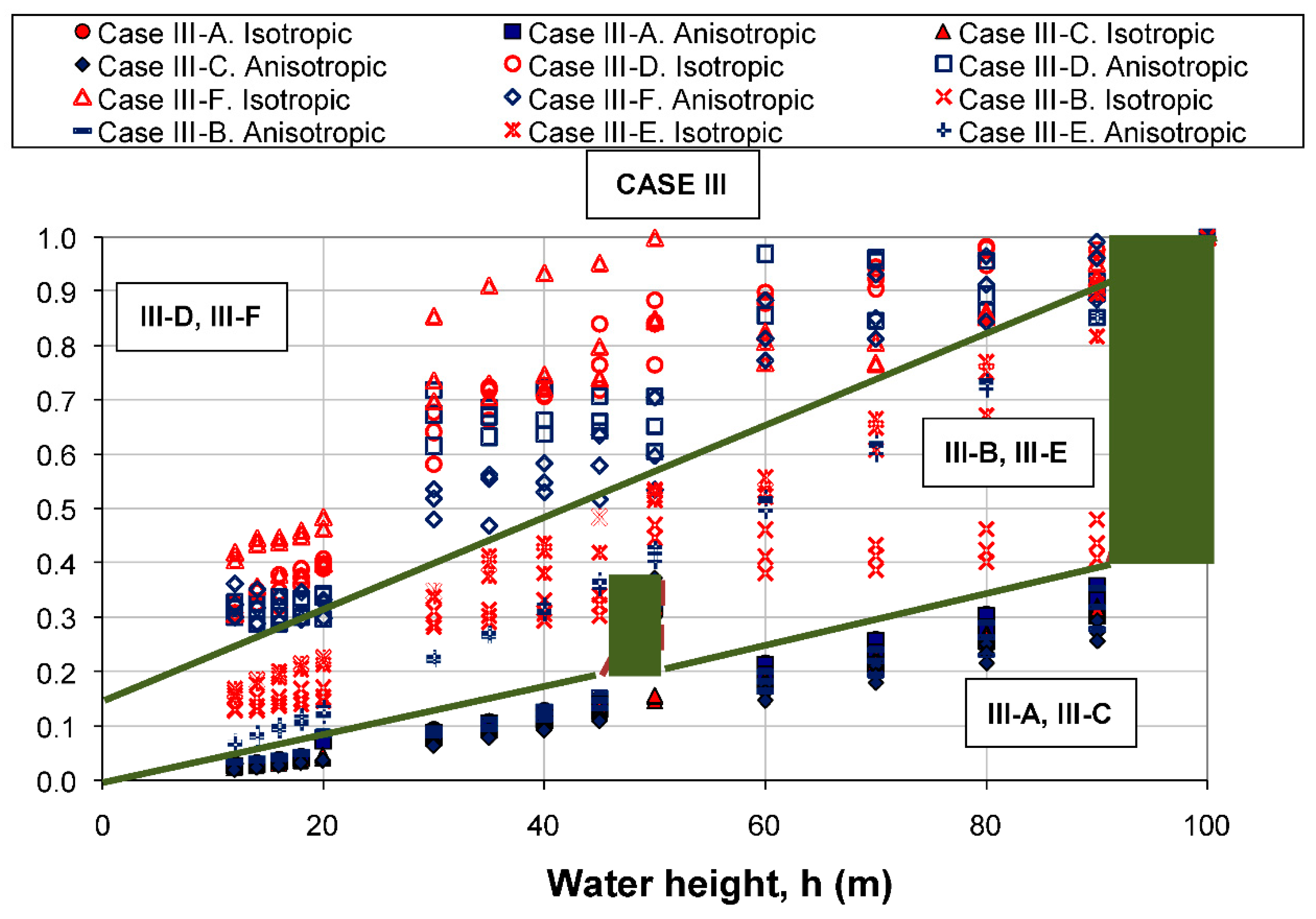
- Case III showed the zoning of the core in three parts, all of equal height. To carry out this zoning, a width of 1 m was taken in the central area of the top of the core and the central region was delimited with inclinations that were doubly inclined regarding the inclinations of the upstream and downstream faces of the core, as previously defined and indicated in Figure 7. In the same way as for case II, six subcases (III-A to III-F) were analyzed based on the distribution of horizontal permeabilities k1, k2 and k3.
3.5. Results
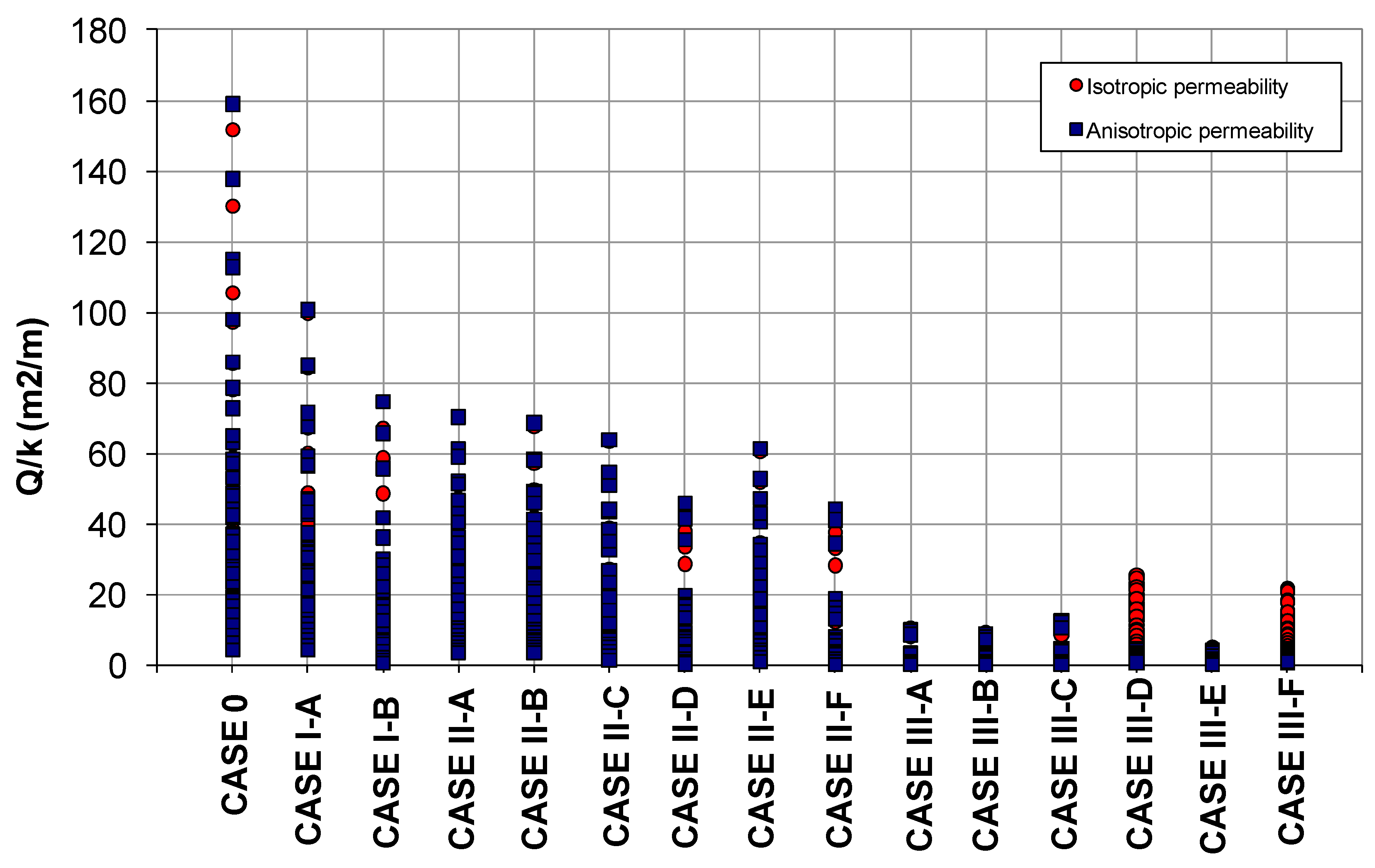
- The highest seepage flows were obtained when no zoning of the core was carried out (case 0). Then, the highest seepage flow were obtained for case I-A (lower half of the core with the highest permeability, k1, and upper half of the core with the lowest permeability, k2 = k1/10) and case I-B (distribution of permeabilities at contrary to those adopted for case I-A), in that order.
- Case II obtained lower seepage flows than those obtained for cases 0 and I, resulting in the lowest seepage flows in cases II-D and II-F. Case studies in which the upper third of the core had the highest permeability coefficient, k1, were assigned, and lower permeabilities were assigned to the lower two thirds, k2 = k1/10 and k3 = k1/100.
- Finally, the lowest seepage flow was obtained for calculation cases III and, more specifically, in cases III-A, III-B, III-C y III-E; the lowest permeability soil was not located in the downstream zone of the core.
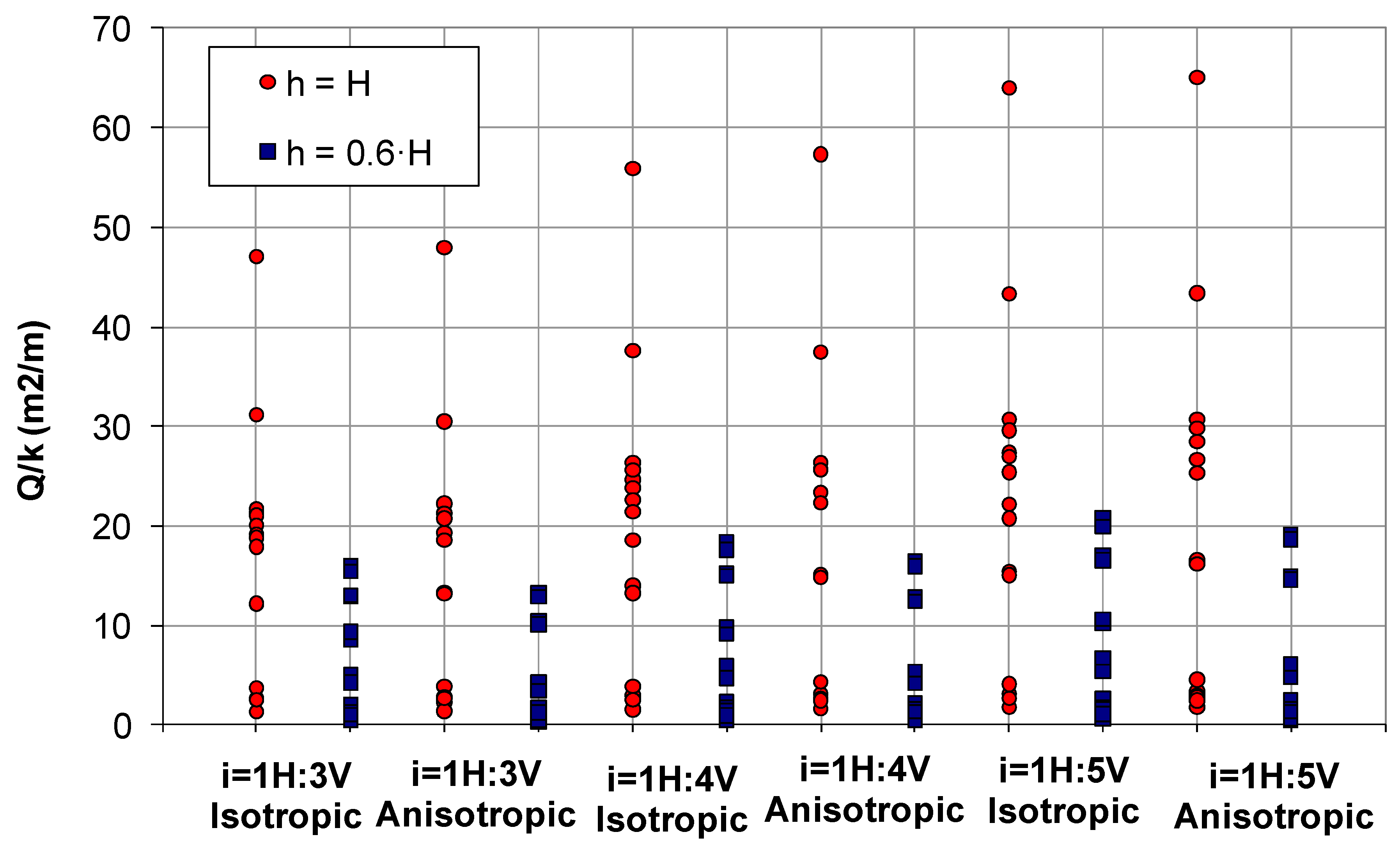
- In general, similar flow rates were observed practically in all cases studied, regardless of whether an isotropic or anisotropic permeability distribution was considered. In Figure 10, the variation of the flow seepage is represented for the particular case of a 50 m height dam core verifying the little influence of the anisotropy in the variation range. Greater differences were only obtained in the calculation cases III-D and III-F, i.e., those in which the lowest permeability material was placed in the downstream face of the core (more detail given in the next section).
- Variations in the registered seepage flows were also observed depending on the geometry of the core. The seepage flow rates were higher for greater inclinations of the upstream and downstream core faces. Figure 10 shows the seepage flow variation as a function of the inclination of the upstream and downstream faces of the core for the particular case of H = 50 m dam core.
- The height of the water was also a factor taken into account for the resulting flow rates, logically obtaining higher seepage flow rates through the core for higher water heights. The influence for a maximum water height and a 0.60H water height is shown in Figure 10.
3.6. Discussion of Results
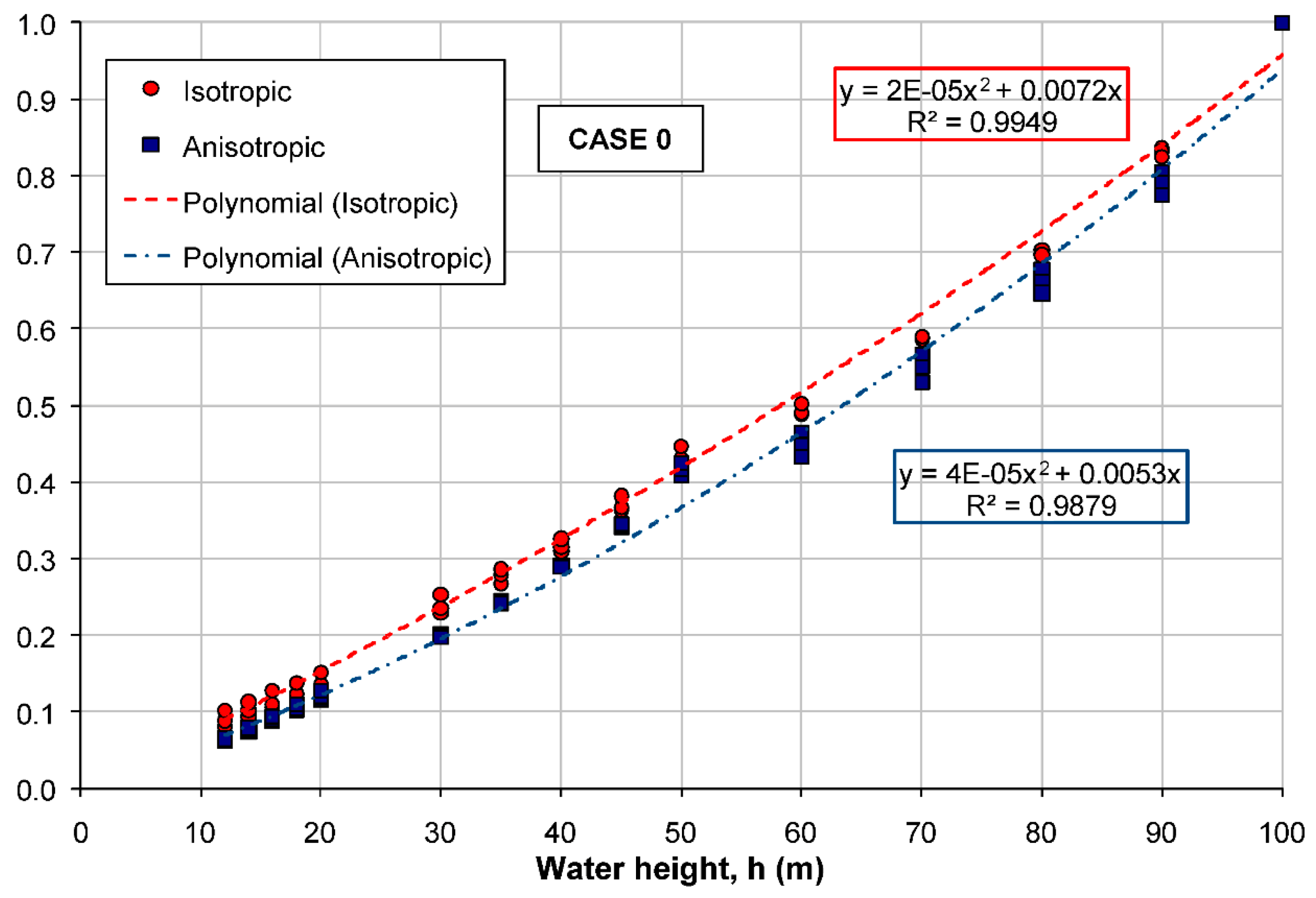
3.6.1. Case 0: Only One Material
- The anisotropy of the permeability hardly exerts an influence because the flow is preferably horizontal, with the value of the horizontal permeability the one that controls the seepage. It can be seen that the adjustment curves are very close to each other and have a high correlation, regardless of the anisotropy.
- The higher the water level in the reservoir, the more seepage flow is filtered, obtaining in the normalized representation of Figure 11 a practically linear trend.
- All the results of the normalized representation are approximately aligned in a single curve regardless of the height of the dam core, the inclination of the upstream and downstream faces of the core, the anisotropy and the permeability value.
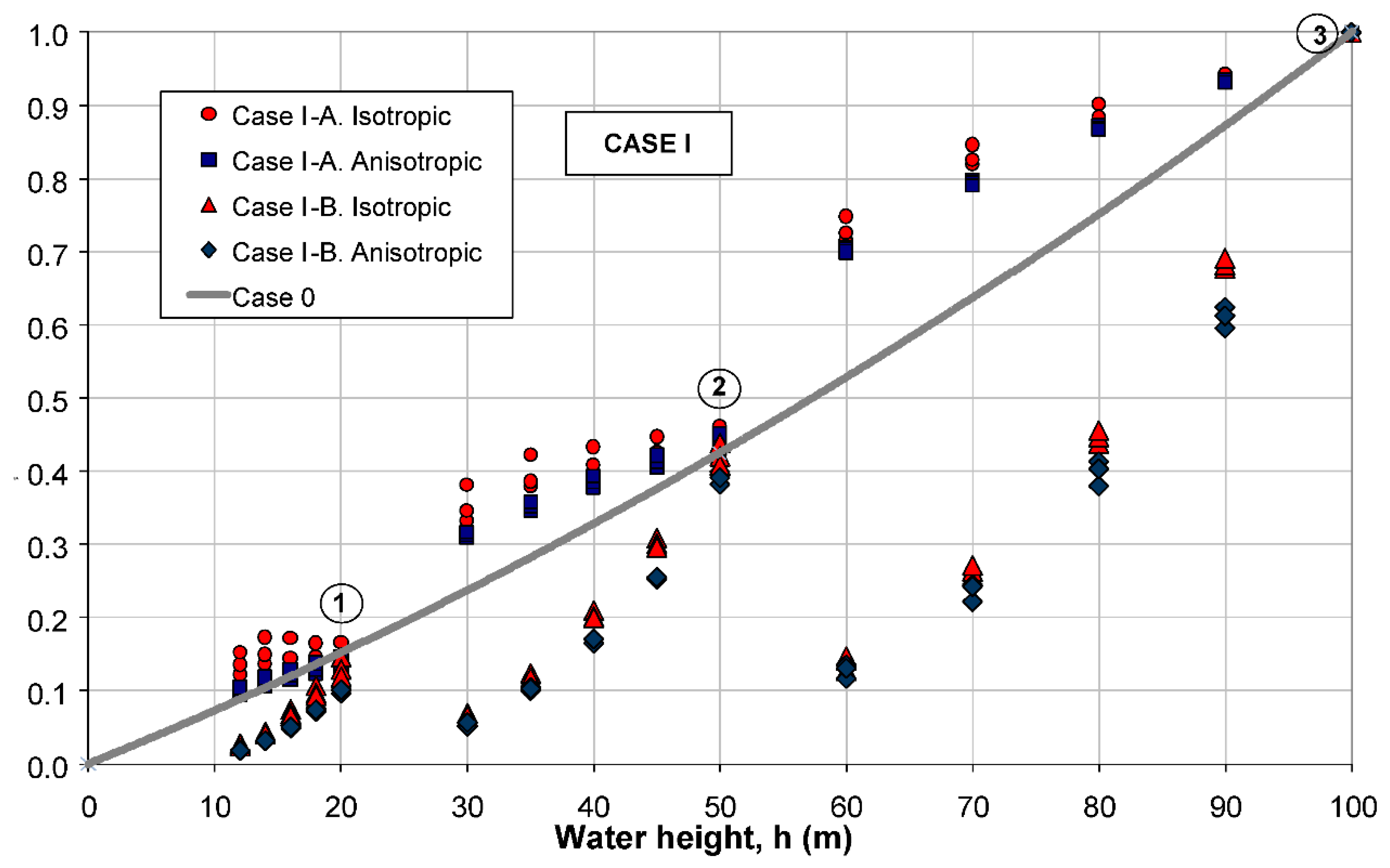
3.6.2. Case I: Two Materials Set Horizontally
- The anisotropy of the permeability hardly has any influence because the flow is preferably horizontal.
- The higher the water height, the more seepage flow is produced, thus obtaining a practically linear trend in the normalized representation of Figure 13.
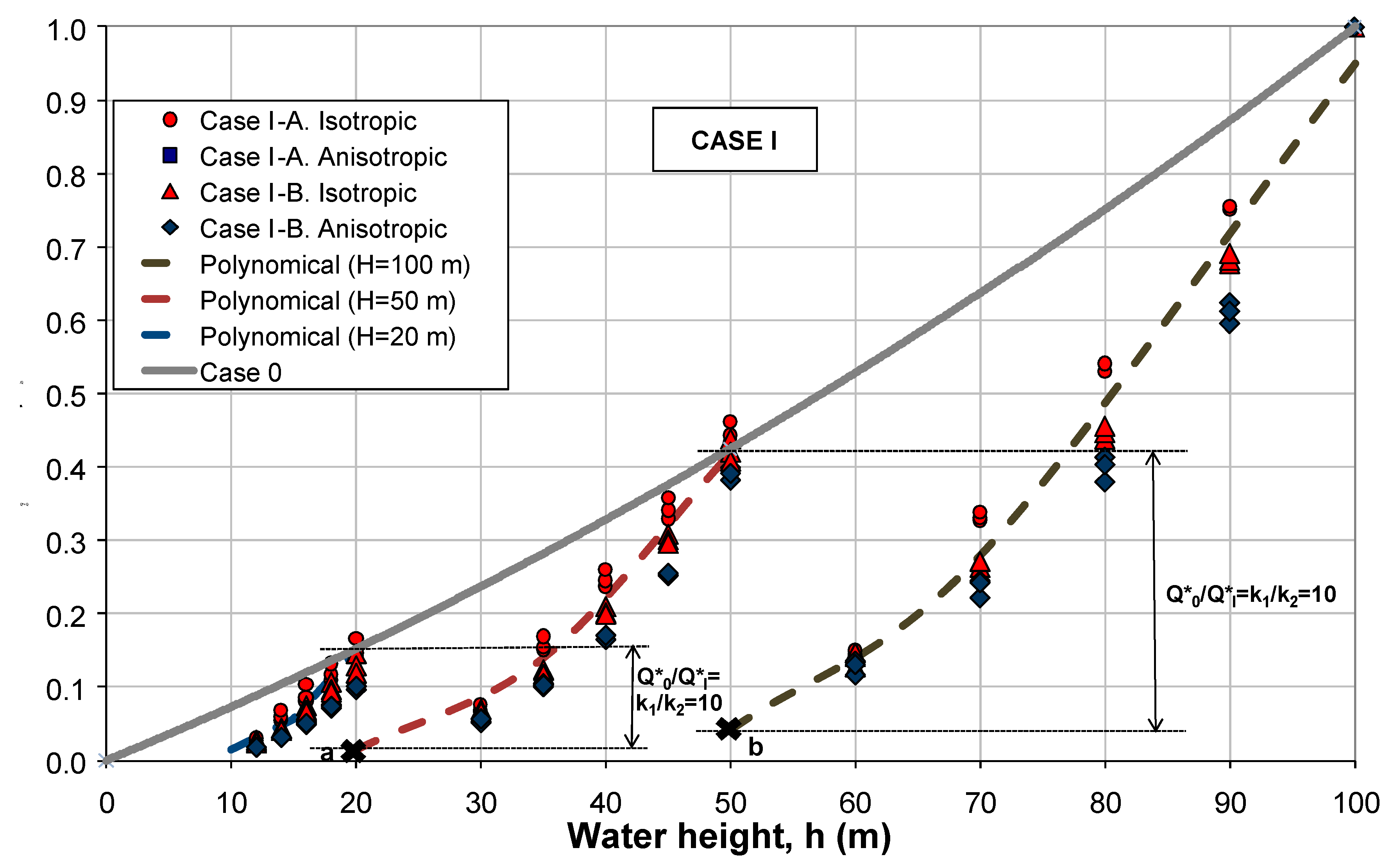
- The incorporation of the coefficient α allows the subcases I-A and I-B to be aligned in the same 3 curves, corresponding to the dam core heights of 20 m, 50 m, and 100 m.
- Following the evolution of the curves in case I, points “a” and “b” can be extrapolated to correspond to a water height h = 20 m for the dam core of H = 50 m, and to a water height of h = 50 m for the H = 100 m dam core, respectively. In these cases, it can be observed that the evolution of the curves moves away from the normalized general seepage flow predicted in the homogeneous case as the height of the water in the dam decreases. Specifically, points “a” and “b” correspond to all the material that is homogeneously more impermeable (k2) and, therefore, regarding case 0 (of normalized general seepage flow Q0*), where the soil has homogeneous permeability k1, a seepage flow (Q1*) in the ratio k2/k1 = 0.1, as can easily be observed in Figure 13.
- The zoning corresponding to subcase I-B is more efficient, as it reduces the seepage flow, although it requires about twice as much low permeability material as in subcase I-A.
- The values represented in Figure 12 and Figure 13 correspond to normalized seepage flows. To make an analysis of absolute seepage flows, it is necessary to refer the values to maximum flows. In case I, the maximum seepage flow is Qmax = 1 L/s for subcase I-A and Qmax = 0.75 L/s for subcase I-B, and they correspond to h = H = 100 m, i = 1:5 and anisotropic permeability.
3.6.3. Case II: Three Materials Set Horizontally
- The anisotropy of the permeability hardly has any influence because the seepage flow tends to be horizontal.
- The higher water height is than the more seepage flow is produced, resulting in the normalized representation of Figure 14. Thus, there is a practically linear trend in subcases II-A, II-B, II-C, and II-E, as well as an exponential trend in the II-D and II-F subcases.
- The permeable layer of soil controls the seepage paths, so that if this more permeable soil is below, the order of the two materials above hardly have any influence. Thus, in subcases II-A and II-B, similar results were obtained.
- When the flow stream lines are controlled by the lower soil because it is the most permeable, as in case I, a factor α can be applied to transfer these subcases (II-A and II-B) to that corresponding to a lower impermeable soil, where the upper seepage paths are controlled by the intermediate soil when it is more permeable than the upper soil (corresponding to sub-cases II-C and II-E). In case II, the factor can be defined by αII for the case of three materials, so that in general:
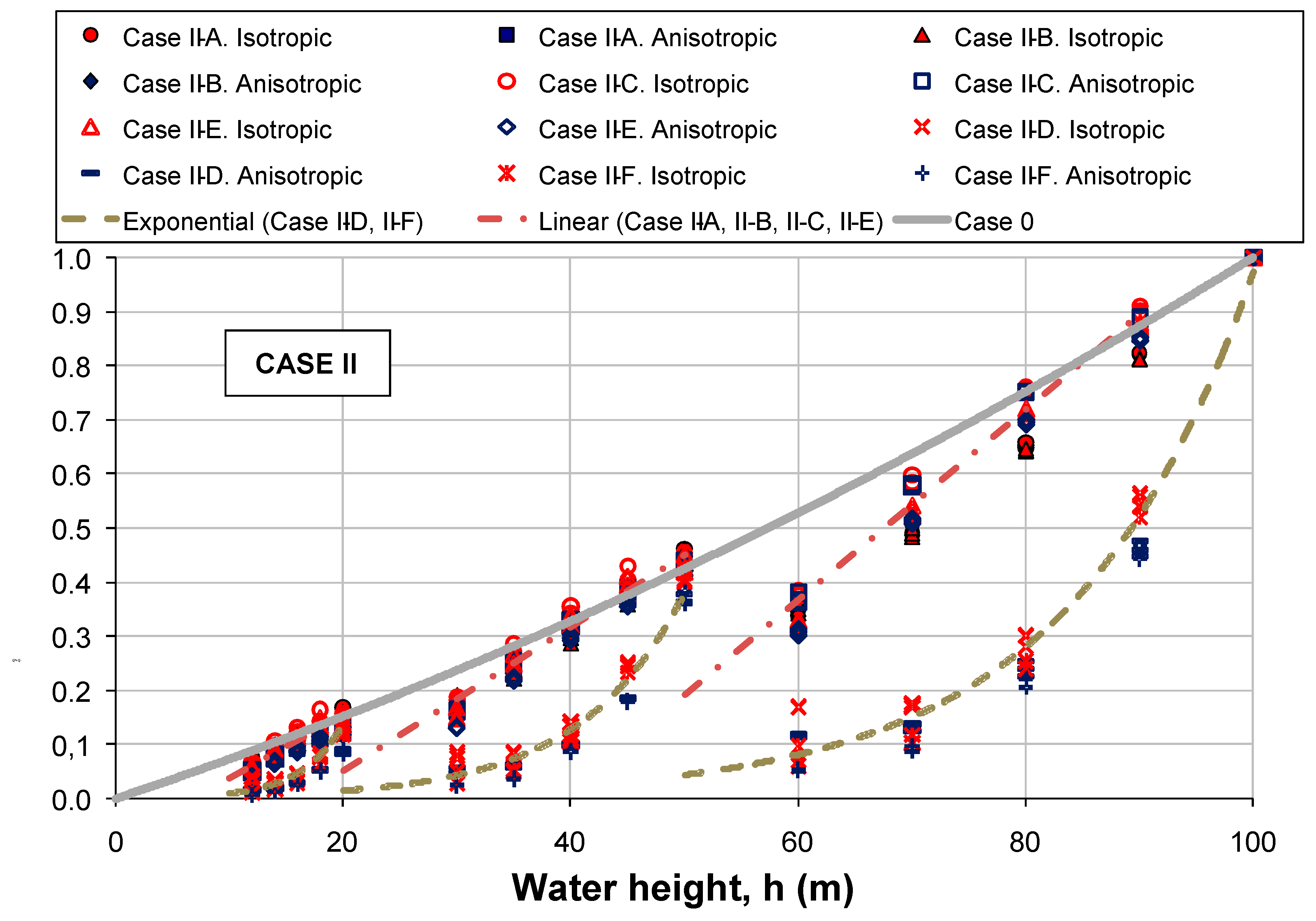
- The seepage flow corresponding to the parametric study of case 0 is represented in Figure 15, which clearly shows that it corresponds to an upper envelope of all the results of case II.
- Once again, attention is drawn to the fact that the values represented in Figure 14 and Figure 15 correspond to normalized seepage flows. To make an analysis of absolute seepage flows it is necessary to refer to the values of maximum seepage flows. In case II, the maximum seepage flow is Qmax = 0.7L/s for subcase II-A, Qmax = 0.69L/s for subcase II-B, Qmax = 0.64 L/s for subcase II-C, Qmax = 0.46 L/s for subcase II-D, Qmax = 0.62 L/s for subcase II-E, and Qmax = 0.44 L/s for subcase II-F. All of them correspond to h = H = 100 m, i = 1: 5, and anisotropic permeability.
3.6.4. Case III: Three Materials Set Vertically
- The effect of anisotropy is clearly appreciated in cases where the intermediate permeability material (k2) is in the last position, since flows with a greater vertical component are generated in the transitions between materials.
- The efficiency of the core zoning is directly related to the permeability of the last vertical layer since, in case III, the entire seepage flow passes through all the materials, but the greatest loss of water head always corresponds to the last layer that cancels the hydraulic potential. Therefore, the more effective the flow in this last stratum than the lower the seepage flow rate. The most favorable situation corresponds, as mentioned, to subcases III-A and III-C, with the most impervious material at the end. However, this situation changes abruptly for maximum water height, where the seepage flows exceed those corresponding to intermediate subcases III-B and III-E with the intermediate permeability soil (k2) positioned at the end. In the event that the soil with the highest permeability (k1) is located in the last position, it corresponds to the situation of maximum seepage flow (subcases III-D and III-F), as is shown in Figure 16.
- The values represented in Figure 16 correspond to normalized seepage flows. To make an analysis of absolute seepage flows it is necessary to refer to the values of maximum seepage flows. In case III, the maximum flow is Qmax = 0.1 L/s for subcase III-A, Qmax = 0.09 L/s for subcase III-B, and Qmax = 0.05 L/s for subcase III-E. All of them correspond to h = H = 100 m, i = 1:5, and isotropic permeability; Qmax = 0.13 L/s for sub-case III-C of h = H = 100 m, i = 1:5, and anisotropic permeability. Qmax = 0.25 L/s for subcase III-D and Qmax = 0.22 L/s for subcase III-F corresponds to h = H = 100 m and i = 1:4 and isotropic permeability, respectively.
- The maximum seepage flow rates are progressively smaller from case 0, case I, case II, and case III. In case III, minimum values were obtained with Qmax ∈ (0.05 L/s, 0.25 L/s); in case II the values were Qmax ∈ (0.44 L/s, 0.70 L/s); in case I the values were Qmax ∈ (0.75 L/s, 1 L/s); and finally, the highest values of maximum seepage flow corresponded to case 0 with values that reach 159 L/s.
- Attention should be drawn to the fact that the volume of all materials in case III were approximately the same, thus minimizing the environmental and economic impact. Whereas in case II and case I, a higher proportion of the more impervious material was always needed to optimize the seepage flow.
- For case III, with water heights under 90% of the dam core height, the most effective zoning was obtained for subcases III-A and III-C. However, for maximum water height, the seepage flow increased exponentially in these two subcases, and the zoning that presents cases III-B and III-E was more effective for the maximum water height situation.
4. Study of Heterogeneous Material for the Dam Core
4.1. Dam Core Geometry
4.2. Water Height
4.3. Permeability of the Material
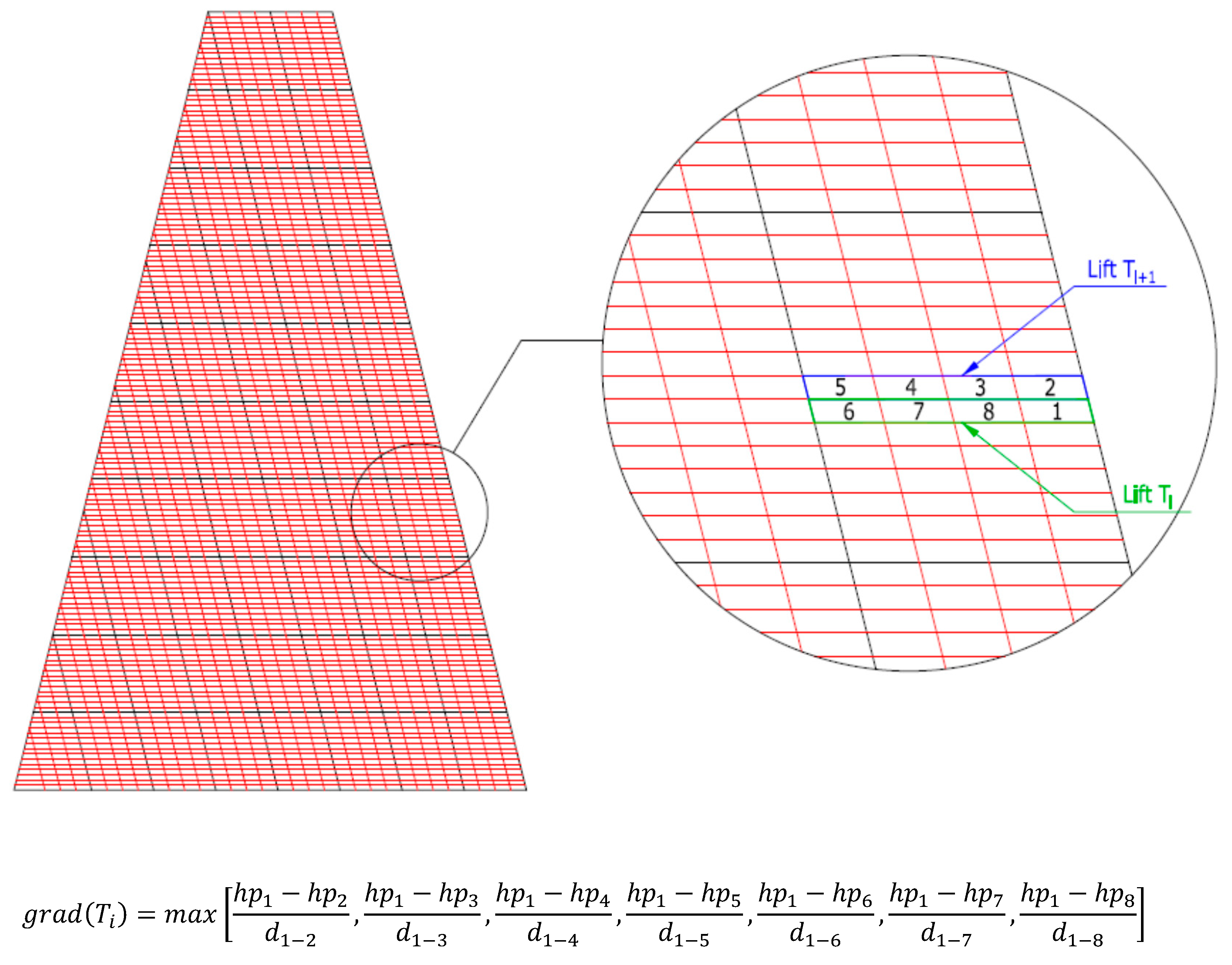
4.4. Seepage Path and Streamlines
4.5. Results and Discussion
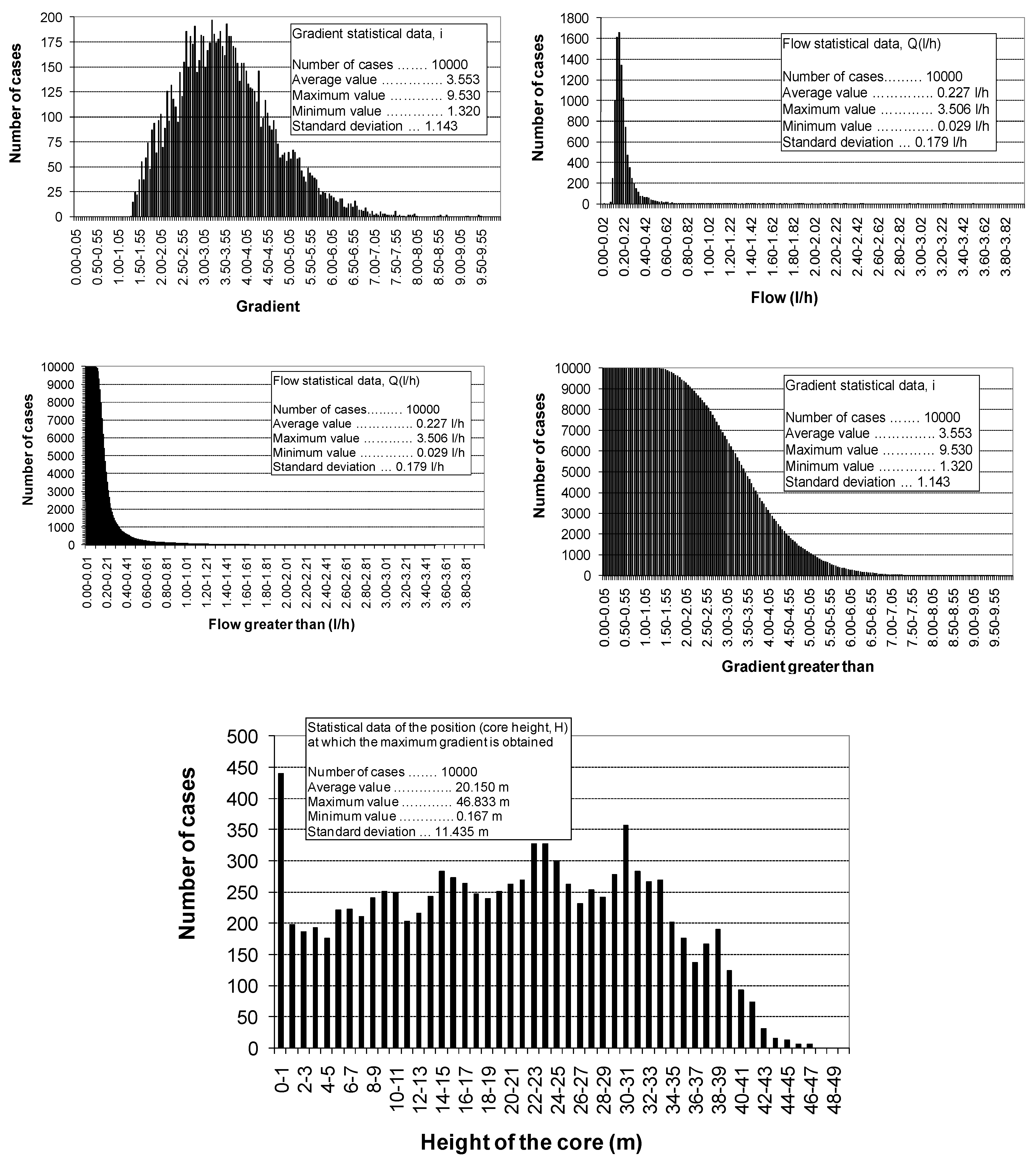
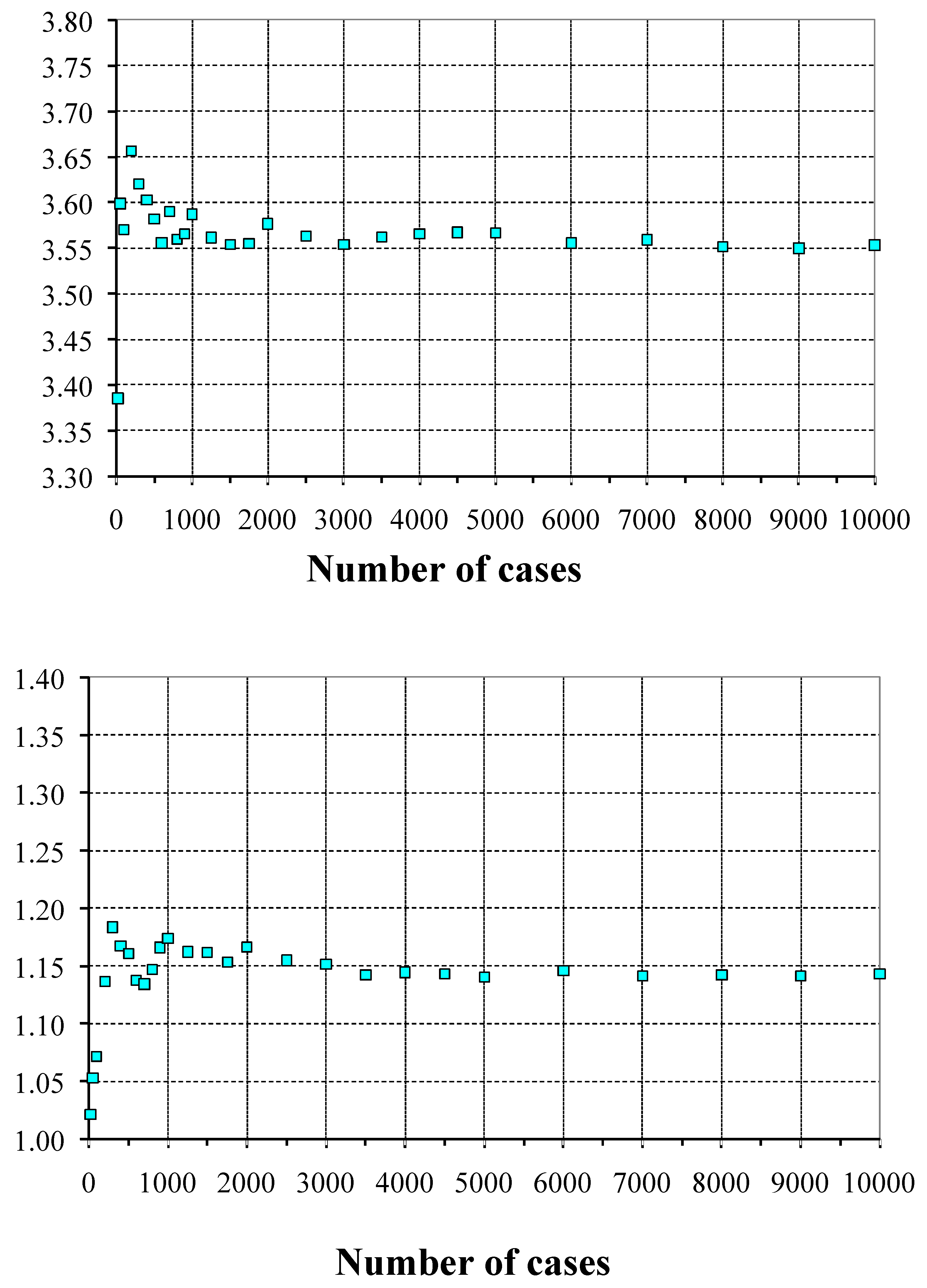
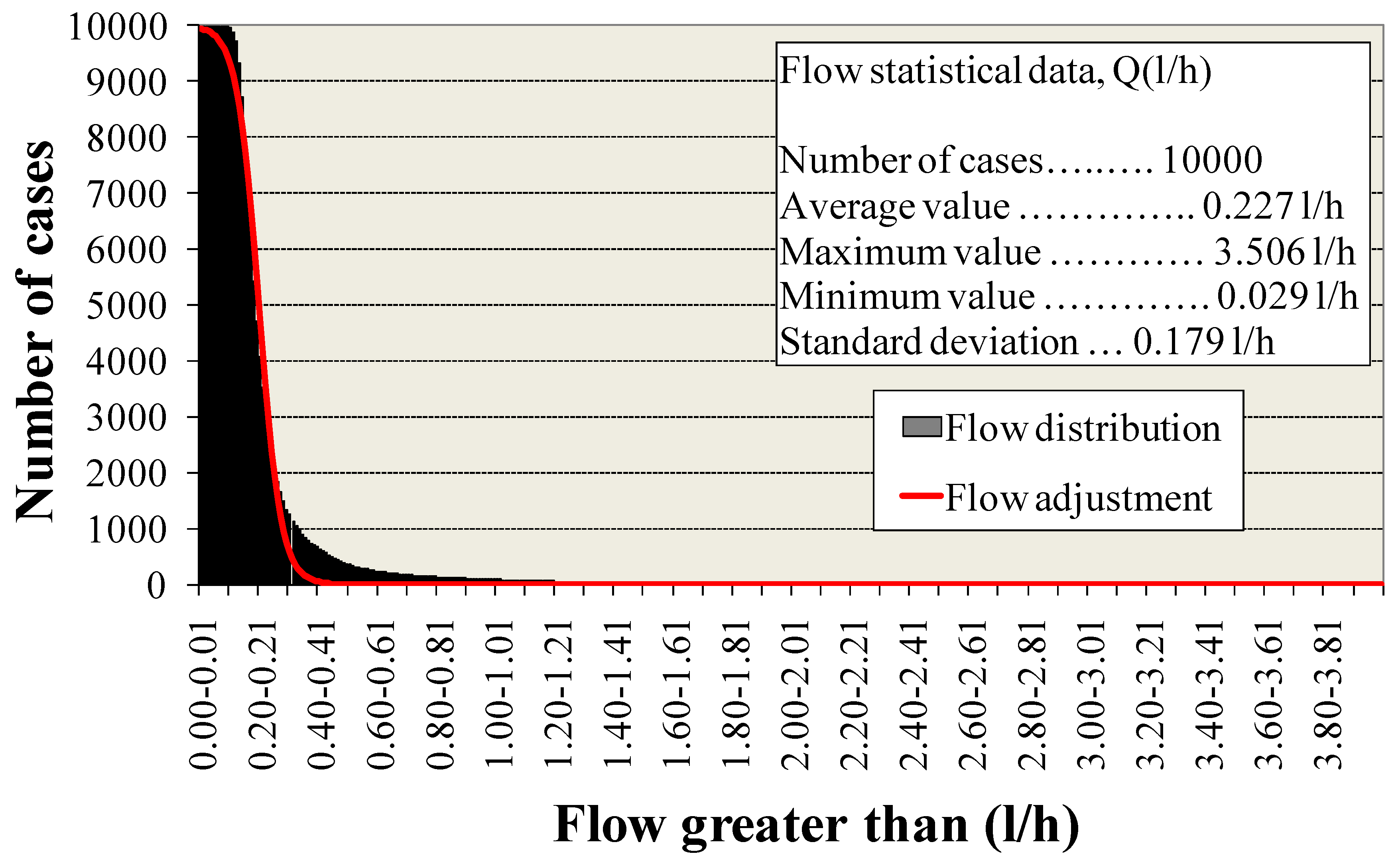
- The seepage flow rates are limited to sufficiently low values when the average value of the permeability is 10−6, despite the great dispersion of the material. In this regard, it can be compared with the seepage flow rates obtained for the analysis with homogeneous materials indicated in Section 3. In this case, permeabilities between 10−3 and 10−7 were used. If we compare the result for the homogeneous material with permeability k = 10−6, a value of 2.06 L/h was obtained, which was much higher than the average value of 0.23 L/h. This resulted in the case of heterogeneous material. It should be noted that the maximum value for the 10,000 Montecarlo calculation cases was 3.51 L/h, resulting in a low probability (19/10,000 = 0.19%) of obtaining values higher than the homogeneous calculation value of 2.06 L/h.
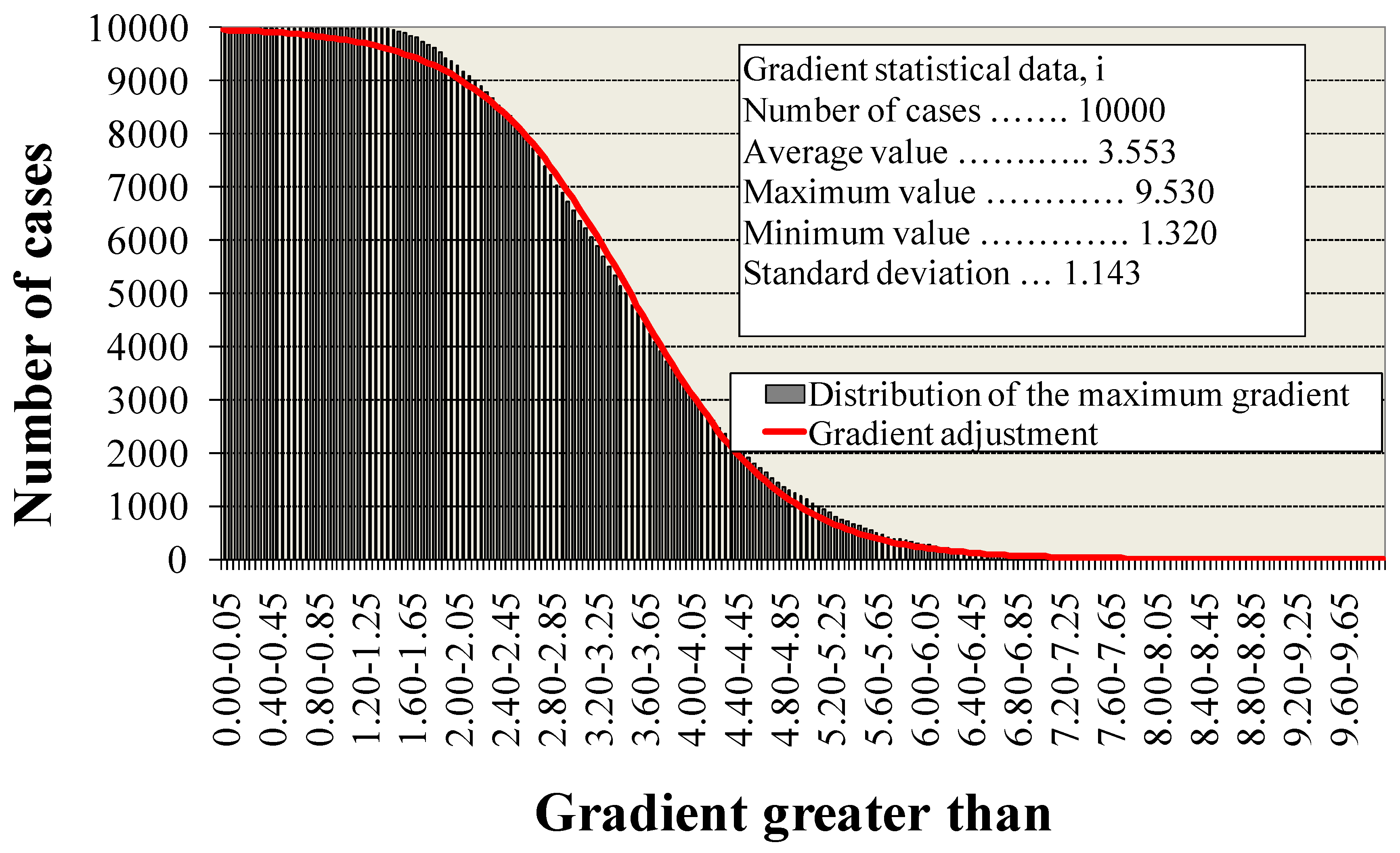
- In addition, since there is a great dispersion, there is the possibility of finding great variability of permeability between lifts, thus being able to raise the gradient and cause internal erosion problems. In this case, the average value stood at 3.55, which is below the risk limits. It should be noted that maximum values close to 10 were reached with an occurrence probability of (1134/10,000 = 11.34%) of values greater than 5. Therefore, there is a moderately low risk that the core potentially has internal erosion problems. Moreover, the situation did not degrade the construction of core dams with homogeneous material, where in any case the transition to the shoulders must be made using filters that cancel any risk of erosion.
5. Conclusions
- The maximum seepage flow rates are progressively smaller from case 0 (a single material with horizontal permeability k1), case I (two materials set horizontally with horizontal permeability k1 and k2), case II (three materials set horizontally with horizontal permeability k1, k2, and k3), and case III (three materials set vertically with horizontal permeability k1, k2, and k3), with this last zoning being the most effective in decreasing the seepage flow, where for all cases: k1 > k2> k3.
- Attention should also be drawn to the fact that the volume of all the materials in case III is approximately the same, thus minimizing the environmental and the economic impact. Whereas in case II and case I, a higher proportion of the more impermeable material is needed to optimize the seepage flow.
- For each case, different sub-cases were also studied by varying the materials in the dam core. In the most effective case, case III, with water heights under 90% of the height of the dam core, the most optimized zoning (minimal seepage flow rates) was obtained for subcases III-A and III-C corresponding to the most impermeable soil situated downstream. However, for the maximum water height, the seepage flow increased exponentially in these two subcases, and zoning III-B and III-E for maximum water height was more optimized, which corresponds to the intermediate permeability material located downstream.
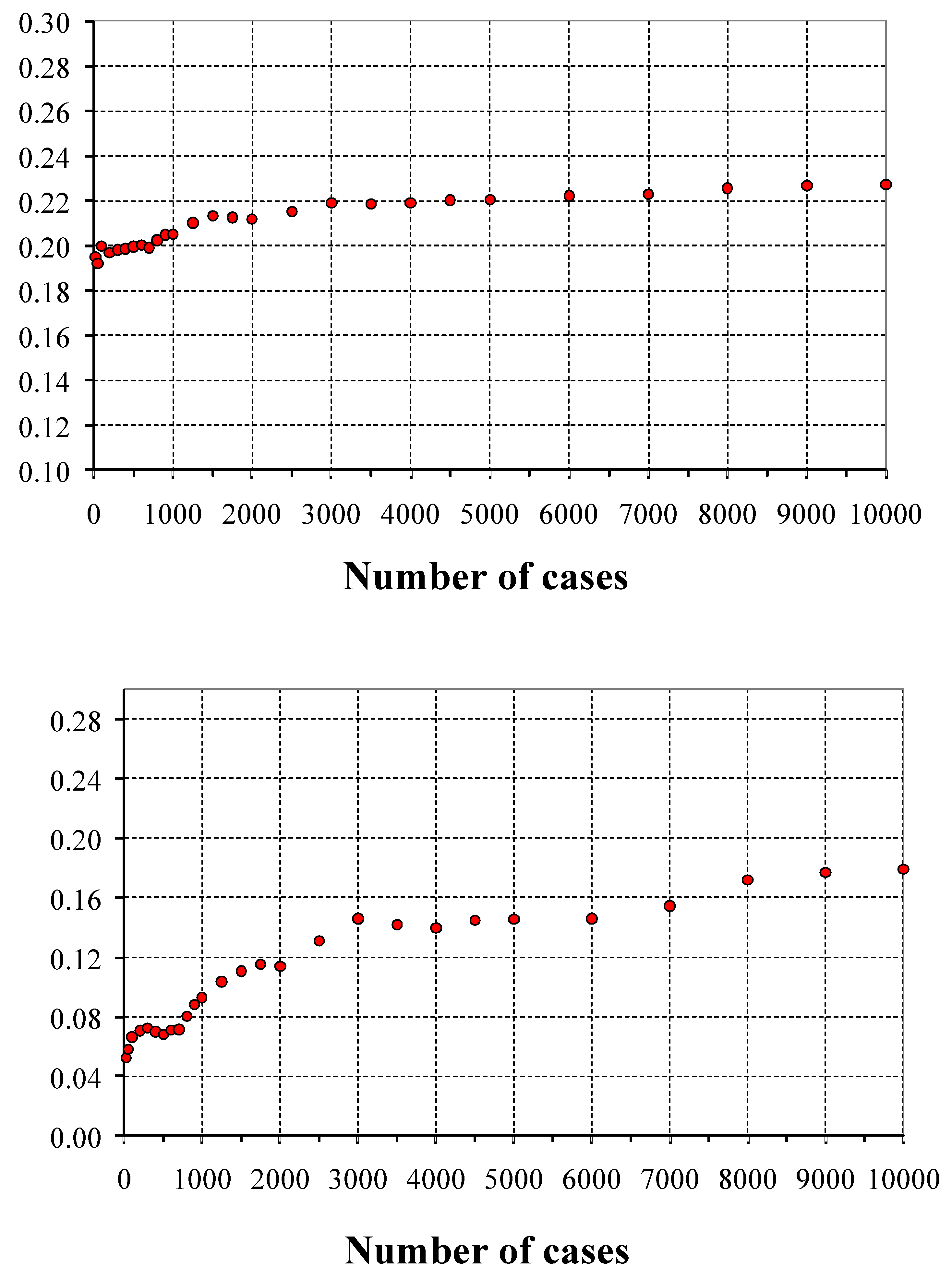
- Both mean values of the seepage flows and mean values of the maximum hydraulics gradients had a tendency to stabilize, as the number of results of the available calculations increased.
- The seepage flow rates were limited to sufficiently low values when the average value of the permeability was 10−6, despite the large dispersion of the permeability of the material. Comparing the result for the homogeneous material with permeability k = 10−6, a value of 2.06 L/h was obtained, which was much higher than the average value of 0.23 L/h in the case of heterogeneous material.
- It was possible to verify how the values of the highest maximum hydraulic gradients were not necessarily associated with the values of the highest seepage flow rates. High gradients were obtained for situations in which the seepage flow rates were moderate and low.
- The highest maximum gradients were observed in the lowest lifts of the dam core (near the foundation, height below 1–2 m). In other words, the probability of obtaining the maximum gradient increased when the core height was low.
- Given the wide dispersion, there was the possibility of finding great variability of permeability between lifts, thus being able to raise the gradient and cause internal erosion problems. In the calculations, the average value of the maximum hydraulic gradient was around 3.55, obtaining values below the risk limits and the situation does not worsen for dams with core of homogeneous material, where in any case must be made filters that minimize any risk of erosion.
- The probabilistic calculation can be extended with an adequate distribution law of adjustment of the results. For these purposes, and for possible safety and reliability studies, an adjustment was made to the distribution functions of the maximum flows and gradients obtained in the 10,000 calculations.
Author Contributions
Funding
Conflicts of Interest
References
- Alonso, M.; Yague, J. Earth materials for cores and homogeneous earth fill dams; singularities. In Proceedings of the 19th International Congress on Large Dams, Florence, Italy, 19–31 May 1997; pp. 381–401. [Google Scholar]
- Aladelokun, A.O. The Sustainability of Dam Construction through Environmental Management. IOSR J. Environ. Sci. Toxicol. Food Technol. 2012, 1, 1–5. [Google Scholar] [CrossRef]
- ICOLD. Dam Failures Statistical Analysis; Bulletin 99; International Commission on Large Dams: Paris, France, 1995. [Google Scholar]
- Chahar, B. Determination of Length of a Horizontal Drain in Homogeneous Earth Dams. J. Irrig. Drain. Eng. 2004, 130, 530–536. [Google Scholar] [CrossRef]
- Fell, R.; Wan, C.F.; Cyganiewicz, J.; Foster, M. Time for Development of Internal Erosion and Piping in Embankment Dams. J. Geotech. Geoenvironmental Eng. 2003, 129, 307–314. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S. Study of Seepage through Earth-Fill Dam Using Physical and Numerical Models. Master’s Thesis, University Putra Malaysia, Seri Kembangan, Malaysia, July 2013. [Google Scholar]
- Delgado-Ramos, F.; Escudero-Merino, D.; Olalla, C. The importance of permeability in granular filter design and control. Scour Erosion 2016, 979–985. [Google Scholar]
- Malekpour, A.; Farsadizadeh, D.; Hosseinzadeh Dalir, A.; Sadrekarimi, J. Effect of horizontal drain size on the stability of an embankment dam in steady and transient seepage conditions. Turk. J. Eng. Environ. Sci. 2012, 36, 139–152. [Google Scholar]
- Chahar, B.; Graillot, D.; Gaur, S. Storm-Water Management through Infiltration Trenches. J. Irrig. Drain. Eng. 2012, 138, 274–281. [Google Scholar] [CrossRef]
- Jamel, A.A.J.; Ali, M.I. Influence of Cavity Under Hydraulic Structures on Seepage Characteristics. Int. J. Eng. Technol. 2018, 7, 461–471. [Google Scholar] [CrossRef]
- Ullah, A.; Kassim, A.; Alam, I.; Junaid, M.; Ahmad, I.S. Efficiency analysis of seepage of Baz Ali small dam, Kurram Agency using clay blanket and cut-off wall with sand filter. Bull. Geol. Soc. Malays. 2019, 67, 113–118. [Google Scholar] [CrossRef]
- Kanchana, H.; Prasanna, H. Adequacy of Seepage Analysis in Core Section of the Earthen Dam with Different Mix Proportions. Aquat. Procedia 2015, 4, 868–875. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S.; Ghazali, A.H.; Ghazaw, Y.M.; Afan, H.A.; Al-Ansari, N.; Yaseen, Z.M. Experimental and Numerical Analysis for Earth-Fill Dam Seepage. Sustainability 2020, 12, 2490. [Google Scholar] [CrossRef]
- Khassaf, S.I. Effect of impervious core on seepage through earth dam (case study: Khassa chai dam). Int. J. Sci. Eng. Res. 2017, 8, 1053–1064. [Google Scholar]
- Zahedi, P.; Aghajani, H.F. The effect of clay core specifications on the seepage behaviour of an earthfill dam. In Proceedings of the 5th International Symposium on Dam Safety and Exhibition, Istanbul, Turkey, 27–31 October 2018. [Google Scholar]
- Majeed, Q.G. Flow and Deformation Analysis of Zoned Earth Dam by the Finite Element Method. Diyala J. Eng. Sci. 2015, 8, 38–62. [Google Scholar] [CrossRef]
- Hassan Al, J. 2D-Flow Analysis Through Zoned Earth Dam Using Finite Element Approach. Eng. Technol. J. 2000, 28, 6316–6324. [Google Scholar]
- Choi, B.-I.; Shin, N.-H.; Kim, K.-Y.; Kang, C.-K. Evaluation of seepage quantity of fill dam using 3D FEM analysis. Jpn. Geotech. Soc. Spéc. Publ. 2016, 2, 1703–1707. [Google Scholar] [CrossRef]
- Jamel, A.A.J. Investigation and Estimation of Seepage Discharge Through Homogenous Earth Dam with Core by Using SEEP/W Model and Artificial Neural Network. Diyala J. Eng. Sci. 2018, 11, 54–61. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Al-Labban, S.; Salman, F.A. Seepage Analysis of a Zoned Earth Dam by Finite Elements. Int. J. Civ. Eng. Technol. 2014, 5, 128–139. [Google Scholar]
- Hellström, J.G.; Ljung, A.; Lundström, T.S. Forces on grains located in model geometry with application to internal erosion in embankment dams. In Proceedings of the International Symposium on Modern Technology of Dams: The 4th EADC Symposium, Chengdu, China, 30 September 2007. [Google Scholar]
- Sherard, J.L.; Woodward, R.J.; Gizienski, S.J. Earth and Earth Rock Dams: Engineering Problems of Design and Construction; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1963. [Google Scholar]
- Hofmann, J.R.; Hofmann, P.A. Darcy’ s Law and Structural Explanation in Hydrology. In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association; Hull, D., Forbes, M., Okruhlik, K., Eds.; The University of Chicago Press: Chicago, IL, USA, 1992; Volume 1, pp. 23–35. [Google Scholar]
- Wilkins, M.L. Fundamental Methods in Hydrodynamics. Methods Comput. Phys. 1964, 3, 211–263. [Google Scholar]
- FLAC. Manuals, Complete Set; Itasca: Minneapolis, MN, USA, 2011. [Google Scholar]
- Ministry for the Ecological Transition and the Demographic Challenge, Government of Spain. Available online: https://www.miteco.gob.es/es/agua/temas/seguridad-de-presas-y-embalses/inventario-presas-y-embalses/ (accessed on 18 August 2020).
- Hatanaka, M.; Uchida, A.; Takehara, N. Permeability Characteristics of High-Quality Undisturbed Sands Measured in A Triaxial Cell. Soils Found. 1997, 37, 129–135. [Google Scholar] [CrossRef]
- Murray, E.J. Procedure for the Determination of the Permeability of Clayey Soils in a Triaxial Cell Using the Accelerated Permeability Test; Technical Report P1-398/TR; Environment Agency: Bristol, UK, 2003.
- Brown, E. Reducing risks in the investigation, design and construction of large concrete dams. J. Rock Mech. Geotech. Eng. 2017, 9, 197–209. [Google Scholar] [CrossRef]
- Radchenko, V.; Belkova, I.; Rumyantsev, O. The Russian practice of earth dam seepage strength. In Proceedings of the ICSE-6 (6th International Conference on Scour and Erosion), Paris, France, 27–31 August 2012; pp. 577–584. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Martín, J.; Galindo, R.; Arévalo, C.; Menéndez-Pidal, I.; Kazanskaya, L.; Smirnova, O. Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core. Sustainability 2020, 12, 6667. https://doi.org/10.3390/su12166667
Sánchez-Martín J, Galindo R, Arévalo C, Menéndez-Pidal I, Kazanskaya L, Smirnova O. Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core. Sustainability. 2020; 12(16):6667. https://doi.org/10.3390/su12166667
Chicago/Turabian StyleSánchez-Martín, José, Rubén Galindo, Carlos Arévalo, Ignacio Menéndez-Pidal, Liliya Kazanskaya, and Olga Smirnova. 2020. "Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core" Sustainability 12, no. 16: 6667. https://doi.org/10.3390/su12166667
APA StyleSánchez-Martín, J., Galindo, R., Arévalo, C., Menéndez-Pidal, I., Kazanskaya, L., & Smirnova, O. (2020). Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core. Sustainability, 12(16), 6667. https://doi.org/10.3390/su12166667





