Abstract
The convenient design of a maximum power point tracking (MPPT) controller is key to the success of photovoltaic (PV) system performance in order to maximize the extracted power, which is affected significantly by weather fluctuations, particularly partial shading condition (PSC). This paper proposes a novel hybrid MPPT approach based on a modified Perturb and Observe (P&O) assisted by the Extremum Seeking Control (ESC) strategy, combining the benefits of these simple algorithms and, meanwhile, eliminating their drawbacks. The proposed algorithm is able to track the maximum possible power under any level of weather fluctuation, with comprehensive enhancement on all aspects of high performance, boosting the PV array efficiency to 100%, reducing the convergence time to less than 100 ms, completely eradicating the oscillations around the achieved power, and maintaining the simplicity levels of both involved strategies. More importantly, this algorithm is applicable for any PV array configuration, which enhances the robustness and novelty of the algorithm. The performance is verified using MATLAB/Simulink. A boost converter is used for controlling DC to DC (direct current to direct current) power. The proposed algorithm’s performance is compared with the conventional P&O and incremental conductance (IC) algorithms under four different cases of weather conditions. The shortcomings of these algorithms are illustrated and the analysis confirms the effectiveness of the proposed algorithm accordingly.
1. Introduction
Increased demands of electrical power threaten traditional power sources, which are no longer sufficient. Therefore, renewable energy sources have gained significant importance for electrical power generation throughout the world. In addition to the permanence of renewable energy sources, they also have very beneficial advantages, such that they do not cause any kind of environmental pollution, are inexpensive and clean, require little maintenance, and emit no noise. Solar photovoltaic (PV) array is the most popular renewable energy source due to solar illumination availability being normal and continual. PV panel performance is highly sensitive to weather variations and environmental parameters, such as the irradiation level and temperature. Therefore, efficient control schemes are desired in order to extract the maximum available power under full sun illumination and also under the presence of any atmospheric fluctuations. Therefore, using a maximum power point tracking (MPPT) controller is the proper approach to derive the PV array at the maximum power point (MPP). Unique MPP occurs in the power - voltage (P‒V) curve of the PV array under uniform weather condition, while under partial shading condition (PSC) numerous power peaks exist, which are known as the local maximum power points (LMPPs), except for the one with the highest power, which is called the global maximum power point (GMPP), which expands the challenge for the MPPT system to locate the right global power peak point [1]. The common target is to maximize the efficiency of the PV system by keeping the PV module at its maximum power operation [2].
Many MPPT techniques have been proposed by researchers during the last decades, and these techniques can be classified based on the implementation methods into two categories—conventional MPPT algorithms and intelligence computing algorithms. The conventional algorithms, such as Perturb and Observe (P&O) [3] and incremental conductance (IC) [4,5,6] are considered economical and easy to implement but with non-steady efficiency [7]. On the other hand, the intelligence computing algorithms, for example fuzzy logic control [8], artificial neural networks [9], particle swarm optimization [10], genetic algorithms [11], hybrid BAT-Fuzzy [12], and Cuckoo Search (CS) [13] are complicated methods and have long computational time and weak convergence speed but with high efficiency [14]. In the case of uniform irradiation, the previous research works have confirmed that conventional MPPT methods can track the MPP efficiently, while under PSC these techniques fail to guarantee effective and accurate tracking of the GMPP [15]. Therefore, the challenges in implementing MPPT can be summarized by the algorithm complexity, cost, tracking time, power loss due to oscillation occurrence, and failure while operating under shading conditions [7]. During the past years, the researchers’ attention has been concentrated on the accurate tracking of the global power peak under PSC. Each proposed tracking algorithm attempted to overcome the aforementioned performance challenges [16], but the achievements were different from one algorithm to the other.
Two main categories were followed for the previous MPPT algorithms’ propositions under PSC; the first one was based on creating particular modifications to the existing conventional tracking algorithms, and the second category was established based on intelligence computing methods. Among the conventional techniques, P&O is the most extensively used due to its simplicity, low cost, and faster response compared to other conventional approaches [17]. Nevertheless, the high oscillation occurrence around the MPP, which aids to considerable energy loss, and its inability to extract the correct maximum power from the partially shaded PV array are considered as the two main drawbacks of this algorithm. Therefore, many researchers have made some modifications to P&O to overcome these drawbacks.
A newly formulated P&O method for MPPT was proposed in [18], and this algorithm aims to minimize the steady-state oscillation occurrence around the extracted MPP during the tracking process. In addition, this algorithm considers the irradiation level as an additional input beside the output voltage of the module for controlling the duty cycle of the boost converter. Two sensors are employed for this procedure; one is for measuring the output voltage, and another sensor is for measuring the irradiation level instead of the current sensor in the conventional method. The simulation results illustrate that the proposed method outperforms the conventional P&O method in tracking the MPP in the case of the unique maximum power peak, but the work does not provide any guarantee that the proposed newly formulated P&O method is able to track the GMPP with the presence of more than one power peak. Another enhanced P&O algorithm with variable step size was proposed in [19], which employs a fuzzy logic control to supply variable step-size convergence in order to boost the efficiency of the PV system. The MPPT process in [20] was introduced in order to solve the problem of the drift caused in the case of a rapid increase in radiation. The suggested solution was by integrating the information of the change in current, voltage, and power in the decision procedure, and the authors implied that in the case of high insolation, the simple P&O algorithm may experience the drift issue due to the inaccurate decision-making ability of the algorithm. [19] and [20] are costly, complex, and need previous knowledge to be handled. An improved P&O algorithm was presented by [21], in which the improvement can be summarized by considering the variation in the PV current as a third test in its flowcharts, and this is the difference between this algorithm and the conventional one. Moreover, the authors investigated eight cases of the operating point perturbation as follows; four of them were the same as the original algorithm with fixed irradiation, and the others were applied to provide an indication about the states of the fast changing of the irradiation level, either increasing or decreasing, based on comparing the changes of voltage signs with the current and accordingly changing the converter duty cycle. The results confirm that the proposed controller is able to track MPPs effectively with a minimized ability of diverging from the correct tracking path under uniform conditions. However, for effective performance under PSC, this algorithm has to be modified majorly. In addition, another novel adapted variable step-size P&O MPPT strategy of a PV system was introduced by [1]. The proposed adaption is based on a famous geometric theorem idea, known as Pythagorean theorem, which assists in perfectly overcoming the weaknesses and restrictions of the conventional P&O MPPT, such as the oscillations around the detected MPP with a maintained high speed convergence. However, the performance is still not efficient under PSC. Another intelligent modification on a variable step-size P&O procedure was proposed by [22] in order to boost the performance ability to work under PSC. The modification is based on deliberate comparison sequences, which are able to lead the process to track the GMPP efficiently, with enhanced tracking speed. The study in [23] proposed an improved cuckoo search (ICS) MPPT method in order to track the GMPP efficiently under PSC, and the improvement can be outlined by removing the random step from the original CS algorithm and further introducing the ideation of low-power, high-power, ordinary, and marked zones with adaptive step adjustment based on the diverse stages of the nest place. This algorithm was able to precisely track the actual maximum power under PSC with higher efficiency than the original CS algorithm. Another MPPT approach based on soft computing algorithms was proposed by [24]: a hybrid MPPT controller, which combines fuzzy logic control and the P&O method in order to track the MPP of the PV under PSC. The proposed approach provides a clear enhancement of the steady and dynamic performance under PSC. On the other hand, the algorithms proposed by [23,24] suffer from the same major drawbacks, such as the high cost, low convergence speed, and the difficulty of implementing a stable, efficient controller. Besides, with the evolution of MPPT techniques, several researchers have given their attention to the Extremum Seeking Control (ESC) technique, which is performed to seek the maximum or the minimum of a non-linear map [25]. Sinusoidal ESC was proposed in [25] which is efficiently able to track the MPP of PV systems. This technique employs a sinusoidal perturbation to estimate the gradient of the P‒V curve. Using this gradient function, ESC leads the PV system to the MPP. The main advantages of the ESC method are simplicity, the high convergence speed, and the independence of PV array characteristics, which can significantly benefit the system performance [26].
Based on the proposed MPPT algorithms from the literature papers, we can observe that one of the performance aspects is improved at the expense of the other, and these aspects can be classified as an algorithm’s complexity, tracking speed, the required computation time, stability, oscillations around the maximum extracted power, array dependency, and steady-state accuracy under uniform illumination or under any level of partial shading conditions. In this paper we propose a novel approach for maximum power extraction from PV array under any shading condition, in which the proposed algorithm combines the benefits of the ESC and P&O algorithms aiming to offer considerable enhancement to all the aforementioned performance aspects. In other words, the proposed algorithm should be able to track the global MPP accurately with high convergence speed during less than 100ms, with guaranteed stability over a wide range of weather fluctuations, having nil oscillations around the actual extracted power and also without any extra cost and complexity compared to the conventional algorithms.
2. Modelling of Solar PV under Uniform Irradiation and PSC
The electrical characteristics of PV cells can be modeled precisely using a single diode of PV cell [27], which is considered as the basic unit for converting the sunlight energy into electrical energy by the PV effect, hence, acting as a DC current source. The schematic of an ideal PV cell is shown in Figure 1. The magnitude of the output current I is affected by the level of the temperature and the intensity of the experienced irradiation [28]. By applying Kirchhoff’s current law, the output equation of the PV cell current is given by Equation (1).
where I output current, V output voltage, Ipv cell current produced by actual solar arrays, RS series resistance, RP parallel resistance, IO reverse saturation current, VT thermal voltage of PV module, T temperature of the p‒n junction, NS series number of cells, K Boltzmann constant =1.38073 × 10−23 J K, NP parallel number of cells, q electron charge = 1.6022 × 10−19 C, and α diode ideality factor.
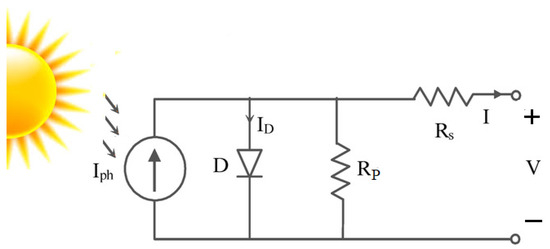
Figure 1.
Explanatory scheme of the photovoltaic (PV) cell in the single diode model.
The PV model used in this study had thirty-six solar cells in a series of connections to form a string, which acted as a module. The open circuit voltage (Voc) of each cell was 22.1V, and the short circuit current (Isc) was 4.8 A. The solar array was formed by combination of such modules. Under the full irradiation of 1000, the maximum power was 80 W at a voltage and current of 17.6 V and 4.55 A, respectively.
3. Partial Shading Effect on Solar PV
Under steady weather conditions, when the series of connected modules are experiencing equal irradiation levels, the P‒V curve presents only single power peak. While multiple peaks exist under uneven levels of irradiation, which can occur due to building and tree shadows; items moving in the sky, such as a bird falling and a plane in motion [29]; and anything that can hurdle the received irradiation and cause shading conditions. Consequently, the shaded PV panels suffer from hotspots, which cause considerable power dissipation [30]. Bypass diodes are applied to prevent hotspot effects [31], and blocking diodes are connected in series to each PV string in order to protect the entire PV array from the reverse flow of current [32]. In order to demonstrate the PSC effect, a PV array connected in six series (6S) configuration was considered in this study and simulated for both uniform and shading conditions. Several PV patterns are shown in Figure 2. However, during shading occurrence, the bypass diodes were activated by the generated reverse voltage across the shaded PV module, which resulted in the appearance of multiple power peaks in the P‒V curves, as shown in Figure 3.
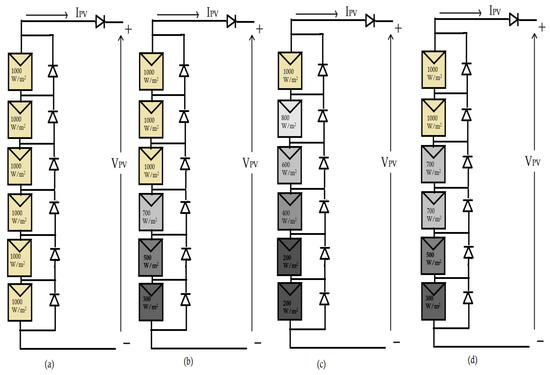
Figure 2.
PV patterns used for simulation: (a) first pattern, (b) second pattern, (c) third pattern, and (d) fourth pattern.
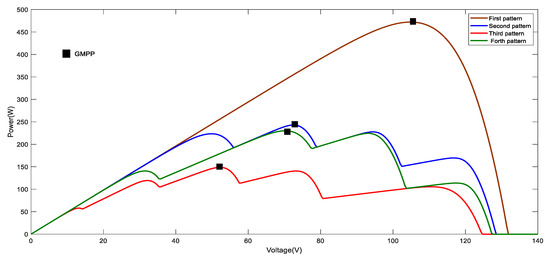
Figure 3.
P‒V curve characteristics under uniform irradiation and partial shading conditions PSCs.
4. Boost Converter
A power conversion unit is employed between the PV module and the load in a MPPT system in order to improve the performance of the output of the PV system. In this study, a boost converter was used to control the MPPT system operation to track the accurate GMPP, and the output of the boost converter was adapted according to the duty cycle of the pulse width Modulation (PWM) signal. For efficient controlling, the boost converter has to be designed carefully based on the system specifications and objectives. Output voltage (Vo), input voltage (Vin), inductor (L), output capacitance (Cout), and the operational frequency were determined using Equations (3) to (5), as considered in [33,34,35]. The converter design parameters are presented in Table 1.
where is duty cycle, is switching frequency, is expected output current, and is the maximum allowable voltage ripple.

Table 1.
Boost converter component values.
5. The Proposed MPPT Technique
Among all the MPPT algorithms, P&O is considered the most popular and preferable due to its significant features, such as simplicity and ease of implementation [7]. Moreover, the basic benchmark to evaluate the effectiveness of any newly published modified MPPT method is set at the level of P&O regarding the main performance aspects, such as simplicity, implementation, cost effectiveness, and popularity [16]. Figure 4 clarifies the operation principle of the P&O algorithm, which is based on periodically perturbing the terminal voltage of the PV module in order to decide the correct direction toward the MPP. The operating voltage of the PV module is perturbed and the new corresponding power is calculated and compared with that of the previous perturbation cycle, and if the current power is found to be greater than that of the previous perturbation cycle, the control system will keep the perturbation in the same direction, otherwise it will be reversed until reaching the MPP. However, the P&O algorithm suffers from two main issues. First, the produced oscillations around the achieved MPP can impact the tracking speed, and second, this algorithm in its original form is not efficient in extracting the actual maximum power under PSC, in which it is not able to recognize the global maximum among the local maximums. This work proposes a novel, simpler, and efficient approach based on smart cooperation between the ESC strategy and P&O algorithm in an organized procedure. The proposed algorithm can accommodate all the aforementioned limitations, taking into account a balanced achievement between the desired high-performance features under any atmospheric condition.
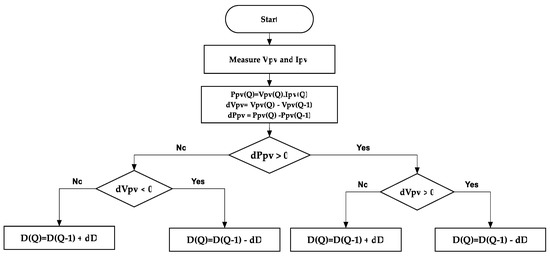
Figure 4.
Flowchart of conventional Perturb and Observe (P&O) algorithm.
MPPT using the ESC method is an optimal control strategy, which aims to track an extremum value on P-V characteristics with reduced oscillations around the maximum point [25], and hence, boosts the PV system efficiency [36]. For this work, the extremum seeking scheme was utilized to provide robustness and accuracy to a modified P&O algorithm for tracking the actual MPP efficiently under any weather fluctuation. The ESC that was used has been applied in much of the literature, but is seen in particular in [37,38,39]. The ESC method consists basically of the power from P-V characteristics, a gradient detector, and a small sinusoidal perturbation signal with a and ω as its amplitude and frequency. The gradient estimator is the key factor of successful peak point seeking, and a combination of a low-pass filter (LPF) and a high-pass filter (HPF) is usually used to accomplish the gradient estimator [39].
The PV power acted as the input to the gradient detector, the DC component of power was removed by the HPF, and in order to obtain the gradient function, the remaining component was multiplied by the perturbation signal to decide if the current is less than or greater than the optimum value based on if it is in phase or out of phase of the perturbation signal. Then, the low-pass filter eliminated unnecessary components and the resulting signal represented the estimated gradient [38]. The frequencies of the low-pass filter, ωl, high-pass filter, ωh, and small sinusoidal perturbation, ω had to be designed in such a manner that ωh ≤ ωl << ω in order to be able to respond quickly to the control input perturbations as illustrated in [40]. We can conclude that the gradient function was used for guiding the operating power point to converge to the maximum point at the optimized current value, and this process worked efficiently to track MPP under uniform irradiations, while under PSC, the performance was degraded with the presence of multiple MPPs. Therefore, we developed a robust technique, which was able to track the GMPP under PSC with high efficiency and convergence speed and avoid power loss and oscillations during the extracting process. It was composed of a modified P&O algorithm cooperating with a simple ESC strategy, which provided the gradient and reference current (Iref) that were employed in the algorithm procedure to perform accurate and fast global MPP tracking, as shown in Figure 5. This combination promised to get better PV system utilization efficiency under continuous variations in solar irradiation. The gradient detection procedure led the proposed tracking process until reaching the global MPP in the presence of multiple maximums. The produced gradient was introduced as an additional input for the proposed modified P&O algorithm and the reference current initiated the algorithm, which made considerable enhancement in the tracking speed. The PV voltage acted as the input voltage for the boost converter, as observed in the Figure 5. The obtained duty cycle from the MPPT controller was limited initially from 0.08 until 0.9 to ensure the effectiveness of the converter.
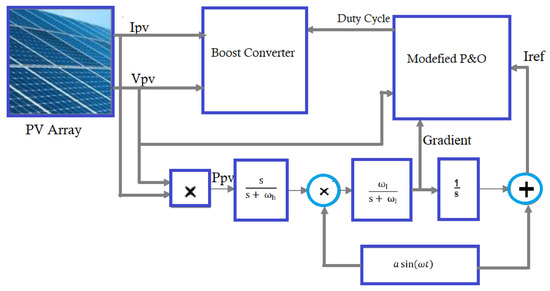
Figure 5.
Block diagram of the proposed technique in the system.
Accordingly, the process was based on gradient considerations. Basically, at all the stationary points in the P‒V curve, the gradient was equal to zero, at a maximum point or a minimum point. For maximum points, the gradient was positive just before the maximum; it is zero at the maximum and it is negative just after the maximum; and for minimum points, the gradient is negative, zero, then positive. Figure 6 illustrates the gradient variations and the stationary points in the P‒V curve for partial shading scenarios which are (Ppv1, V1), (Ppv2, V2), (Ppv4, V4), (Ppv5, V5), and (Ppv7, V7).
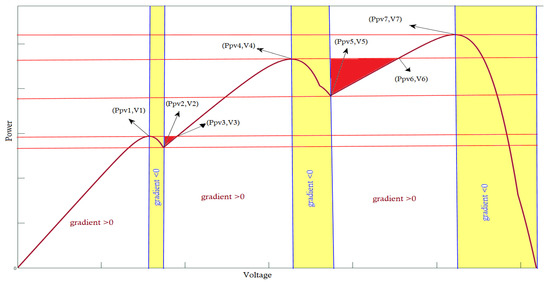
Figure 6.
P-V characteristics of the PV array under PSC with gradient variations.
The main idea of the proposed algorithm is illustrated by the flow chart in Figure 7: it was to update the optimal voltage value during the period of positive gradient for searching for the maximum peak (LMPP). When the gradient became zero at the LMPP, the optimal voltage value was updated and then remained as it is during the negative gradient period until it became positive again and the maximum power increased another time, except for the region when the last maximum point was still greater than the operating PV power, even that with positive gradient, as clarified by the red regions in Figure 6. The red regions indicate that the gradient was positive, meanwhile, the operating power was less than the previous maximum point, hence, the optimal voltage value should not be updated as in the negative gradient regions (yellow regions). The global MPP tracking approach is elucidated in Figure 8. This process aids the achievement of the global MPP for any applied PV array configuration accurately with considerable time provisioning and power loss reduction in addition to many features that are not available in other MPPT techniques under same conditions.
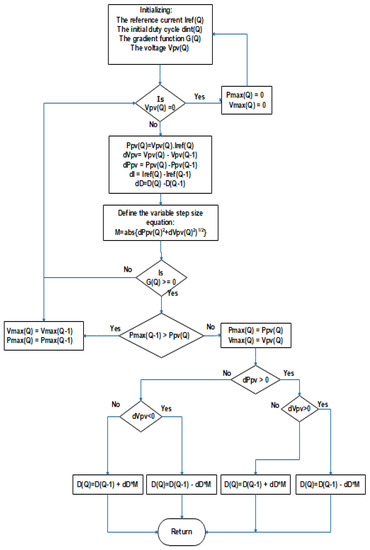
Figure 7.
The proposed modified P&O algorithm.
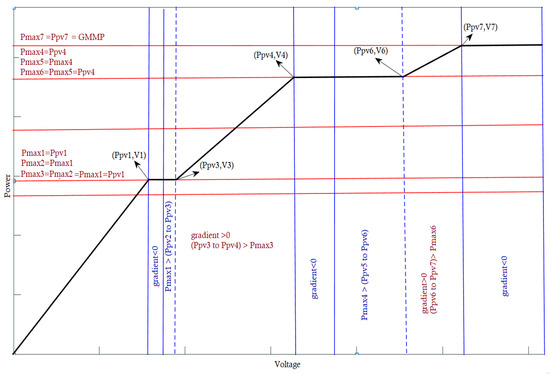
Figure 8.
Maximum power point variation versus voltage.
6. Simulation Results and Discussion
To validate the performance of the proposed algorithm under PSC and under uniform weather conditions, the four patterns (a)–(d) shown in Figure 2 in Section 2 were considered. These shading cases were selected for the comprehensive formulation of the partial shading issues. The performance of the proposed algorithm was compared with the conventional P&O and IC algorithms. Simulations were performed in MATLAB Simulink and the results with respect to its power, voltage, and current are presented in detail. Furthermore, detailed discussions relating to the power oscillation and tracking speed are briefly analyzed. The quantitative analysis for simulation results is presented in Table 2. Furthermore, three more comprehensive PV array configurations are considered and studied in Appendix A in order to confirm the validity of the proposed algorithm to extract the actual MPP for any utilized PV array configuration and under any complex PSC, with the same high effectiveness.

Table 2.
Detailed quantitative analysis for performance of the proposed algorithm.
6.1. Performance under Uniform Solar Irradiation
In this case, all PV modules received equal full-sun irradiation, (1000 W/m2) at 250C. Single peak existed in the P-V characteristics, as shown in Figure 9. Figure 10 illustrates the simulation results for this case with performance comparison between the proposed algorithm and the conventional P&O and IC algorithms in power, voltage, and current. It was observed that the proposed algorithm converges exactly to the MPP of 472 W at 224.5 V and 2.1 A, within very short tracking time (less than 100 ms) and with very reduced oscillations and 100% efficiency. Part (d) shows the obtained gradient from the ESC scheme, which indicated the stability and idealistic execution under uniform conditions. The other two algorithms were able to extract the MPP with an average power of 470.6 W, with 99.7% efficiency, but with the presence of oscillations at the same voltage and current as the proposed algorithm. The quantitative analysis of Figure 10 is shown in Table 2.
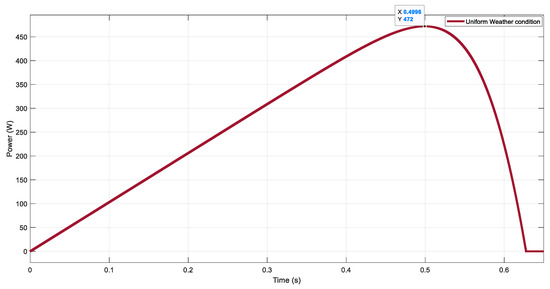
Figure 9.
Scenario of the first pattern (uniform weather conditions).
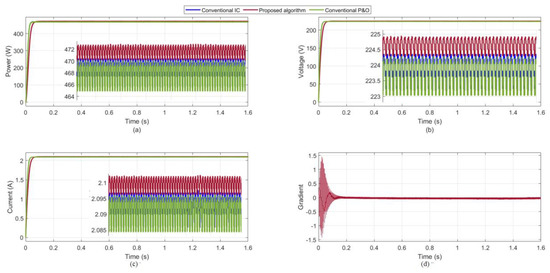
Figure 10.
The simulation results of the proposed algorithm and the conventional P&O and IC algorithms for the first pattern: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter; and (d) the gradient behavior for the proposed algorithm.
6.2. Performance under Partial Shading Conditions
In order to confirm the high performance of the proposed algorithm under PSC, three different patterns of partial shading are considered in this section. Figure 11 presents the maximum power peaks for the three scenarios of shading, indicating the GMPP for each case as 242.9 W for the first shading pattern, 148.7 W for the second pattern, and 230 W for the third pattern. The comparisons of simulation results under the first PSC pattern are illustrated in Figure 12. The achieved power and tracking time at the maximum voltage and current of 160.8 V and 1.603 A for the proposed algorithm were 242.9 W in 77 ms with efficiency of 100%, while for the conventional P&O and IC algorithms, the average of extracted powers were 224.8 W and 222.4 W, respectively, and both at the maximum voltage and current, around 154.9 V and 1.45 A, which is around the first LMPP. This indicates the failure of both algorithms to track GMPP. The obtained gradient is shown in part (d) which indicates the behavior under this case of PSC. The proposed algorithm validated the same effectiveness under the second pattern of PSC with five power peaks in its characteristic, as shown in Figure 11, and the GMPP of 148.7 W was tracked at the maximum voltage and current of 125.8 V and 1.18 A by the proposed algorithm with 100% efficiency in just 83 ms, as shown in Figure 13. However, the average extracted powers by the conventional IC and P&O algorithms at the maximum voltage and current, about 113 V and 1.055 A, were 119.1 W. Therefore, this shows the same failure in tracking the actual MPP. The best efficiency of 100% was confirmed by the proposed algorithm as well as under any level of partial shading conditions. The behavior of the obtained gradient under this strong level of shading is shown Figure 13d. The third PSC pattern was tested to give more confirmation of the proposed algorithm’s validity to work efficiently under any case of weather fluctuation. As shown in Figure 14, the GMPP of 230 W was achieved accurately by the proposed algorithm at 156.8 V and 1.468 A with nil oscillations within less than 100 ms, as approved in all studied patterns in this works, which means this algorithm is more beneficial than all other MPPT techniques in literature. Meanwhile, the conventional P&O and IC algorithms could track the correct MPP under PSC. It is clear in Figure 14 that the average power of 139 W was extracted by these algorithms at 122 V and 1.141 A. Moreover, the stability of the gradient extraction was clear in all cases, which can improve the stability and accuracy of the proposed algorithm. Table 2 presents the detailed performance for the studied scenarios.
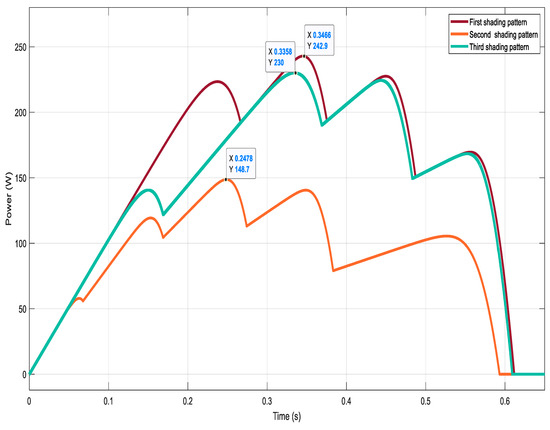
Figure 11.
Scenarios of the shading patterns (PSC).
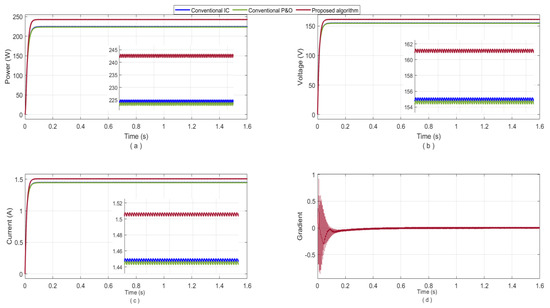
Figure 12.
The simulation results of the proposed algorithm and the conventional P&O and IC algorithms for the first shading pattern: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter; and (d) the gradient behavior for the proposed algorithm.
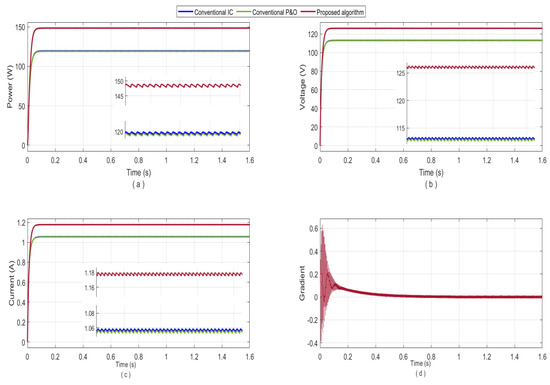
Figure 13.
The simulation results of the proposed algorithm and the conventional P&O and IC algorithms for the second shading pattern: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter; (d) the gradient behavior for the proposed algorithm.
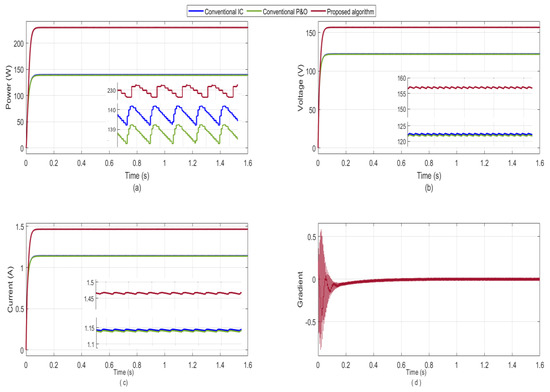
Figure 14.
The simulation results of the proposed algorithm and the conventional P&O and IC algorithms for the third shading pattern: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the Boost converter; and (d) the gradient behavior for the proposed algorithm.
6.3. Performance of the Proposed Algorithm under Rapid Change in Irradiation Conditions
The performance of the suggested enhanced P&O technique was further evaluated for different cases in order to confirm the effectiveness of the algorithm under variations of the weather conditions. The algorithm was tested under four diverse levels of experienced irradiation. Figure 15 presents the performance of the proposed algorithm under transitions between uniform shadowing and the three patterns of shadowing. The sequences of weather condition changes were from the pattern of uniform to the first shading pattern, then to the second and the third. This arrangement constitutes a comprehensive sample of the worst cases of weather fluctuations. The robustness and realization of the proposed algorithm is obviously illustrated in Figure 15, in terms of the tracked power, the maximum voltage and current, and also the gradient variations under this change in irradiation conditions. The first pattern was carried out for 0.3 s, then the shadowing event occurred in the second pattern for another 0.3 s. Then the shading level was increased significantly under the third pattern. Then the sun illumination was enhanced to less shading intensity during the fourth pattern after 0.9 s. The maximum available power was extracted from the PV array under each of the existing shadowing patterns, conserving its performance aspects, such as convergence time to be less than 100 ms, tracking accuracy and efficiency of 100%, and the output stability with absent oscillations. The quantitative analysis for these simulation results is presented in Table 3.
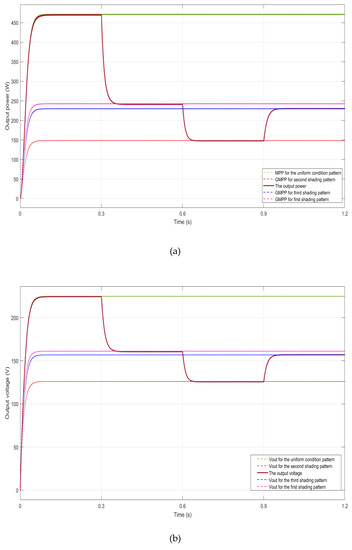
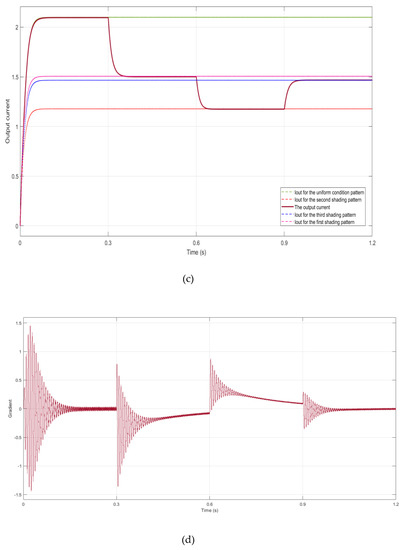
Figure 15.
Performance under the sequence of the combined uniform and three shading patterns with (a) the output power, (b) the output voltage, (c) the output current, and (d) the gradient behavior.

Table 3.
Performance analysis of the proposed algorithm under the sequence of the uniform and three shading patterns.
7. Conclusions
This paper proposes a novel hybrid MPPT algorithm based on a modified P&O assisted by the ESC strategy for gradient searching, which is employed to lead the suggested tracking procedure. The proposed algorithm is able to track the maximum achievable power under any level of weather fluctuations. The algorithm’s performance was tested under four different patterns—the first was a uniform weather condition and the other three were comprehensive shadowing patterns, and these were all compared with the conventional P&O and IC algorithms. Simulation results guarantee the performance superiority of energy extraction and prove the ability of the proposed scheme to enhance the tracking efficiency of the conventional algorithms to 100%, reduce the convergence time to less than 100 ms, eliminate the oscillations around the tracked power, and keep the simplicity level for both involved strategies. Moreover, this algorithm is applicable for any PV array configuration as approved in Appendix A. All of these features qualify this algorithm to be a novel, robust, simple, fast, and accurate MPPT algorithm.
Author Contributions
Conceptualization, A.N.M.M., M.A.M.R., N.A., and S.S.; investigation, A.N.M.M., M.A.M.R., N.A., S.S. and M.A.A.M.Z.; methodology, A.N.M.M.; resources, S.S. and M.A.A.M.Z.; software, A.N.M.M.; supervision, M.A.M.R. and N.A.; validation, M.A.M.R.; visualization, M.A.A.M.Z.; writing—original draft, A.N.M.M.; writing—review and editing, M.A.M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Grant Scheme (FRGS), Ministry of Higher Education, Grant number: FRGS/1/2019/TK07/UPM/02/2.
Acknowledgments
The authors are grateful to the Ministry of Higher Education and Universiti Putra Malaysia for supporting this manuscript especially regarding research funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In order to further approve the effectiveness of the proposed algorithm tracking mechanism for any PV array configuration and under complex partial shading, we proposed an additional three comprehensive configurations to test the algorithm tracking ability. The first configuration was for complex partial shading study. This type of shading happens when a large number of PV modules are connected in series under PSC. Therefore, the array with eight series (8S) of PV models was considered for the first array configuration, as shown in Figure A1 for two cases of complex PSCs, and also for uniform weather condition. The resulted two shading scenarios were complicated due to the multiple closely associated peaks, which have a unique maximum as presented in Figure A2. The simulation results of the proposed algorithm performance under the uniform and the two complex PSC patterns are illustrated in Figure A3. The GMPP for the uniform of 630.6 W was extracted accurately at the maximum voltage and current of 263.4 V and 2.394 A. While under the second pattern of complex PSC, the maximum peak among all of the existed MPPs was 380.5 W. The proposed algorithm showed the ability of accurate GMPP tracking at 204.6V and 1.86 A. The same effectiveness was confirmed under the third pattern of more complex PSC, and the GMPP of 259.6 W was tracked at 169 V and 1.536 A within less than 100 ms in all cases, which is the most important characteristic of this algorithm, as well as its efficiency of 100% with ignored oscillations. All of these features confirm the proposed approach validity and reality for efficient maximum power extraction under any weather condition fluctuation, even the worst PSC cases.
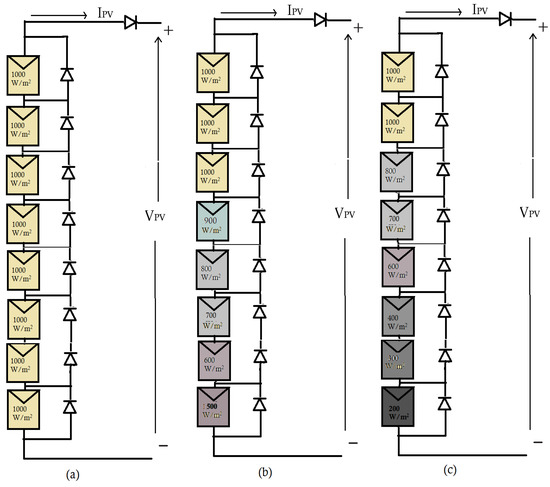
Figure A1.
PV patterns used for simulation: (a) first pattern, (b) second pattern, and (c) third pattern.
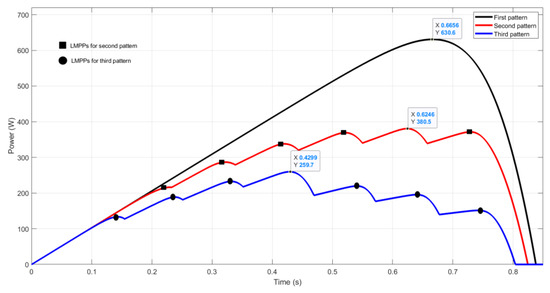
Figure A2.
The scenarios of the three patterns.
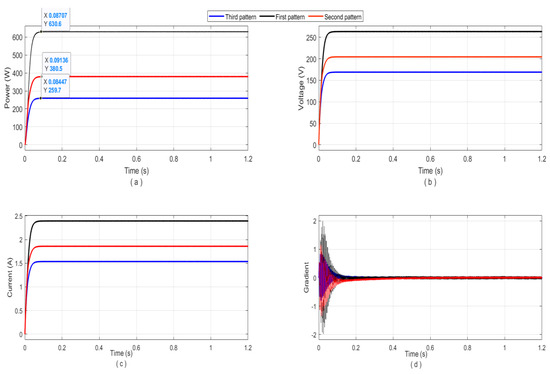
Figure A3.
The simulation results of the proposed algorithm for the three patterns: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter, and (d) the gradient behaviors.
Another two PV array configurations are presented in Figure A4a,b—two parallel of four series (4S2P) and two parallel of three series (3S2P), respectively. The PSC scenarios, three for each configuration, are illustrated in Figure A5a,b, and the simulation results of the proposed algorithm under all PSC cases for both configurations are expressed in Figure A6 and Figure A7. All of the aforementioned benefits and performance features were confirmed at the same superb level. The detailed performance analysis for these two configurations is presented in Table A1 and Table A2.
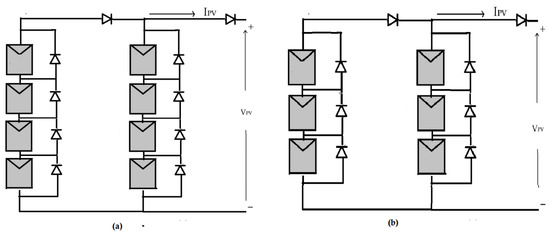
Figure A4.
PV array configurations used for simulation: (a) first array of 4S2P and (b) second array of 3S2P.
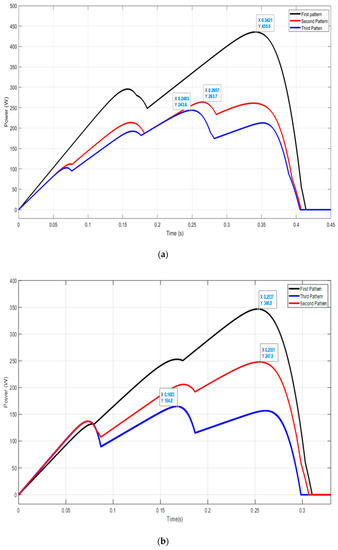
Figure A5.
The PSC scenarios for both configurations: (a) PSC scenarios for the first array of 4S2Pand (b) PSC scenarios for the first array of 3S2P.
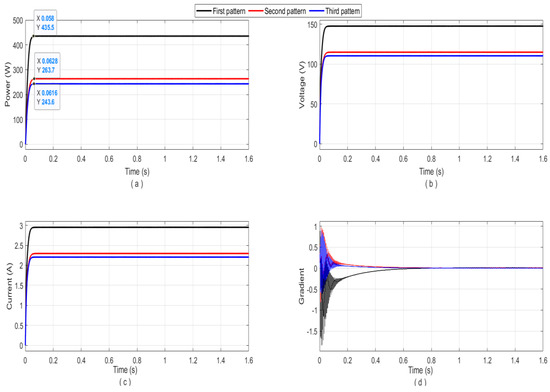
Figure A6.
The simulation results of the proposed algorithm for the three PSC patterns of 4S2P array: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter, and (d) the gradient behaviors.
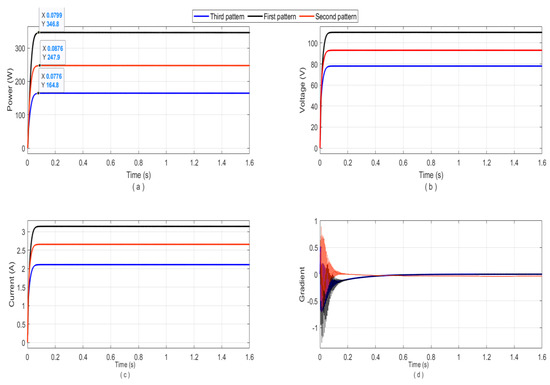
Figure A7.
The simulation results of the proposed algorithm for the three PSC patterns of 3S2P array: (a) the tracked output power; (b) the output voltage of the boost converter; (c) the output current of the boost converter, and (d) the gradient behaviors.

Table A1.
Detailed quantitative analysis for performance of the proposed algorithm.
Table A1.
Detailed quantitative analysis for performance of the proposed algorithm.
| Pattern | Irradiation of the Parallel First and Second 4 Series Modules | Ideal Power at GMMP (A) | Tracked Power at GMMP (B) | Efficiency | Tracking Speed |
|---|---|---|---|---|---|
| First (partial shading) | [1000,1000,800,800] [1000,1000,500,500] | 435.5 W | 435.5 W | 100% | 0.0633 s |
| Second (partial shading) | [1000,1000,600,400] [600,400,400,400] | 263.7 W | 263.7 W | 100% | 0.0638 s |
| Third (partial shading) | [1000,800,600,400] [600,400,400,200] | 243.6 W | 243.6 W | 100% | 0.0581 s |

Table A2.
Detailed quantitative analysis for performance of the proposed algorithm.
Table A2.
Detailed quantitative analysis for performance of the proposed algorithm.
| Pattern | Irradiation of the Parallel First and Second 3 Series Modules | Ideal Power at GMMP (A) | Tracked Power at GMMP (B) | Efficiency | Tracking Speed |
|---|---|---|---|---|---|
| First (partial shading) | [1000,1000,800] [800,600,600] | 346.8 W | 346.8 W | 100% | 0.0799 s |
| Second (partial shading) | [1000,500,300] [1000,700,700] | 247.9 W | 247.9 W | 100% | 0.0876 s |
| Third (partial shading) | [1000,500,300] [1000,500,300] | 164.8 W | 164.8 W | 100% | 0.0776 s |
References
- Loukriz, A.; Messalti, S.; Harrag, A.; Harrag, A. Design, simulation, and hardware implementation of novel optimum operating point tracker of PV system using adaptive step size. Int. J. Adv. Manuf. Technol. 2019, 101, 1671–1680. [Google Scholar] [CrossRef]
- Stitou, M.; Fadili, A.E.; Chaoui, F.Z.; Giri, F. Output feedback control of sensorless photovoltaic systems, with maximum power point tracking. CONPRA Control Eng. Pract. 2019, 84, 1–12. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, S.; Wang, M.; Zou, Z.; Wang, B.; Chen, Q. An improved perturbation and observation maximum power point tracking algorithm based on a PV module four-parameter model for higher efficiency. APEN Appl. Energy 2017, 195, 523–537. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size Incremental Conductance MPPT algorithm for PV systems. ISATRA ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Radjai, T.; Rahmani, L.; Mekhilef, S.; Gaubert, J.P. Implementation of a modified incremental conductance MPPT algorithm with direct control based on a fuzzy duty cycle change estimator using dSPACE. SE Sol. Energy 2014, 110, 325–337. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using cuk converter. IEEE Trans. Ind. Electron. 2011, 58, 1154–1161. [Google Scholar] [CrossRef]
- Subudhi, B.; Pradhan, R. A comparative study on maximum power point tracking techniques for photovoltaic power systems. IEEE Trans. Sustain. Energy 2013, 4, 89–98. [Google Scholar] [CrossRef]
- Kwan, T.H.; Wu, X. Maximum power point tracking using a variable antecedent fuzzy logic controller. SE Sol. Energy 2016, 137, 189–200. [Google Scholar] [CrossRef]
- Bouselham, L.; Hajji, M.; Hajji, B.; Bouali, H. A New MPPT-based ANN for Photovoltaic System under Partial Shading Conditions. Energy Procedia 2017, 111, 924–933. [Google Scholar] [CrossRef]
- de Oliveira, F.M.; Oliveira da Silva, S.A.; Durand, F.R.; Sampaio, L.P.; Bacon, V.D.; Campanhol, L.B. Grid-tied photovoltaic system based on PSO MPPT technique with active power line conditioning. IET Power Electron. 2016, 9, 1180–1191. [Google Scholar] [CrossRef]
- Larbes, C.; Aït Cheikh, S.M.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar] [CrossRef]
- Ge, X.; Ahmed, F.W.; Rezvani, A.; Aljojo, N.; Samad, S.; Foong, L.K. Implementation of a novel hybrid BAT-Fuzzy controller based MPPT for grid-connected PV-battery system. CONPRA Control Eng. Pract. 2020, 98, 104380. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. APEN Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- A Novel Ten Check Maximum Power Point Tracking Algorithm for a Standalone Solar Photovoltaic System. Electronics 2018, 7, 327. [CrossRef]
- Ram, J.P.; Babu, T.S.; Rajasekar, N. A comprehensive review on solar PV maximum power point tracking techniques. Renew. Sustain. Energy Rev. 2017, 67, 826–847. [Google Scholar] [CrossRef]
- Ahmad, R.; Murtaza, A.F.; Sher, H.A. Power tracking techniques for efficient operation of photovoltaic array in solar applications—A review. Renew. Sustain. Energy Rev. 2019, 101, 82–102. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Lauss, G. The performance of perturb and observe and incremental conductance maximum power point tracking method under dynamic weather conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; El-Mohandes, M.T.; El-Ghazaly, M. An Efficient Tracking of MPP in PV Systems Using a Newly-Formulated P&O-MPPT Method Under Varying Irradiation Levels. J. Electr. Eng. Technol. 2019, 15, 501–513. [Google Scholar]
- Aashoor, F.A.O.; Robinson, F.V.P. A variable step size perturb and observe algorithm for photovoltaic maximum power point tracking. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012. [Google Scholar]
- Killi, M.; Samanta, S. Modified Perturb and Observe MPPT Algorithm for Drift Avoidance in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- Belkaid, A.; Colak, I.; Kayisli, K. Implementation of a modified P&O-MPPT algorithm adapted for varying solar radiation conditions. Electr. Eng.-Berl. 2017, 99, 839–846. [Google Scholar]
- Mahmod Mohammad, A.N.; Mohd Radzi, M.A.; Azis, N.; Shafie, S.; Atiqi Mohd Zainuri, M.A. An Enhanced Adaptive Perturb and Observe Technique for Efficient Maximum Power Point Tracking Under Partial Shading Conditions. Appl. Sci. 2020, 10, 3912. [Google Scholar] [CrossRef]
- Shi, J.-Y.; Xue, F.; Qin, Z.-J.; Zhang, W.; Ling, L.-T.; Yang, T. Improved Global Maximum Power Point Tracking for Photovoltaic System via Cuckoo Search under Partial Shaded Conditions. J. Power Electron. 2016, 16, 287–296. [Google Scholar] [CrossRef]
- Bataineh, K.; Eid, N. A hybrid maximum power point tracking method for photovoltaic systems for dynamic weather conditions. Resources 2018, 7, 68. [Google Scholar] [CrossRef]
- Leyva, R.; Alonso, C.; Queinnec, I.; Cid-Pastor, A.; Lagrange, D.; Martinez-Salamero, L. MPPT of Photovoltaic Systems using Extremum—Seeking Control. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 249. [Google Scholar] [CrossRef]
- Malek, H.; Dadras, S.; Chen, Y. Performance analysis of fractional order extremum seeking control. ISA Trans. 2016, 63, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Muhammadsharif, F.F.; Hashim, S.; Hameed, S.S.; Ghoshal, S.K.; Abdullah, I.K.; Macdonald, J.E.; Yahya, M.Y. Brents algorithm based new computational approach for accurate determination of single-diode model parameters to simulate solar cells and modules. Sol. Energy 2019, 193, 782–798. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. An improved P&O algorithm integrated with artificial bee colony for photovoltaic systems under partial shading conditions. Sol. Energy 2019, 178, 37–47. [Google Scholar]
- Pillai, D.S.; Rajasekar, N.; Ram, J.P.; Chinnaiyan, V.K. Design and testing of two phase array reconfiguration procedure for maximizing power in solar PV systems under partial shade conditions (PSC). ECM Energy Convers. Manag. 2018, 178, 92–110. [Google Scholar] [CrossRef]
- Li, X.; Peng, J.; Li, N.; Wu, Y.; Fang, Y.; Li, T.; Wang, M.; Wang, C. Optimal design of photovoltaic shading systems for multi-story buildings. J. Clean. Prod. 2019, 220, 1024–1038. [Google Scholar] [CrossRef]
- Wen, Z.; Chen, J.; Cheng, X.; Niu, H.; Luo, X. A new and simple split series strings approach for adding bypass diodes in shingled cells modules to reduce shading loss. Sol. Energy 2019, 184, 497–507. [Google Scholar] [CrossRef]
- Kolsi, S.; Samet, H.; Amar, M.B. Design Analysis of DC-DC Converters Connected to a Photovoltaic Generator and Controlled by MPPT for Optimal Energy Transfer throughout a Clear Day. JPEE J. Power Energy Eng. 2014, 2, 27–34. [Google Scholar] [CrossRef]
- Bennett, T.; Zilouchian, A.; Messenger, R. A proposed maximum power point tracking algorithm based on a new testing standard. SE Sol. Energy 2013, 89, 23–41. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A comprehensive MATLAB Simulink PV system simulator with partial shading capability based on two-diode model. Sol. Energy 2011, 85, 2217–2227. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K. A Novel Adaptive P&O MPPT Algorithm Considering Sudden Changes in the Irradiance. IEEE Trans. Energy Convers. EC 2014, 29, 602–610. [Google Scholar]
- Ghaffari, A.; Seshagiri, S.; Krstic, M. Power optimization for photovoltaic micro-converters using multivariable gradient-based extremum-seeking. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3383–3388. [Google Scholar]
- Ariyur, K.B.; Krstic, M. Real Time Optimization by Extremum Seeking Control; Wiley Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kebir, A.; Woodward, L.; Akhrif, O. Extremum-Seeking Control with Adaptive Excitation: Application to a Photovoltaic System. IEEE Trans. Ind. Electron. 2018, 65, 2507–2517. [Google Scholar] [CrossRef]
- Tan, Y.; Moase, W.H.; Manzie, C.; Nesic, D.; Mareels, I.M.Y. Extremum seeking from 1922 to 2010. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 14–26. [Google Scholar]
- Ghaffari, A.; Seshagiri, S.; Krstic, M. Multivariable maximum power point tracking for photovoltaic micro-converters using extremum seeking. Control Eng. Pract. 2015, 35, 83–91. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).