Weight Approximation for Spatial Outcomes
Abstract
1. Introduction
2. Literature Review
3. Methods
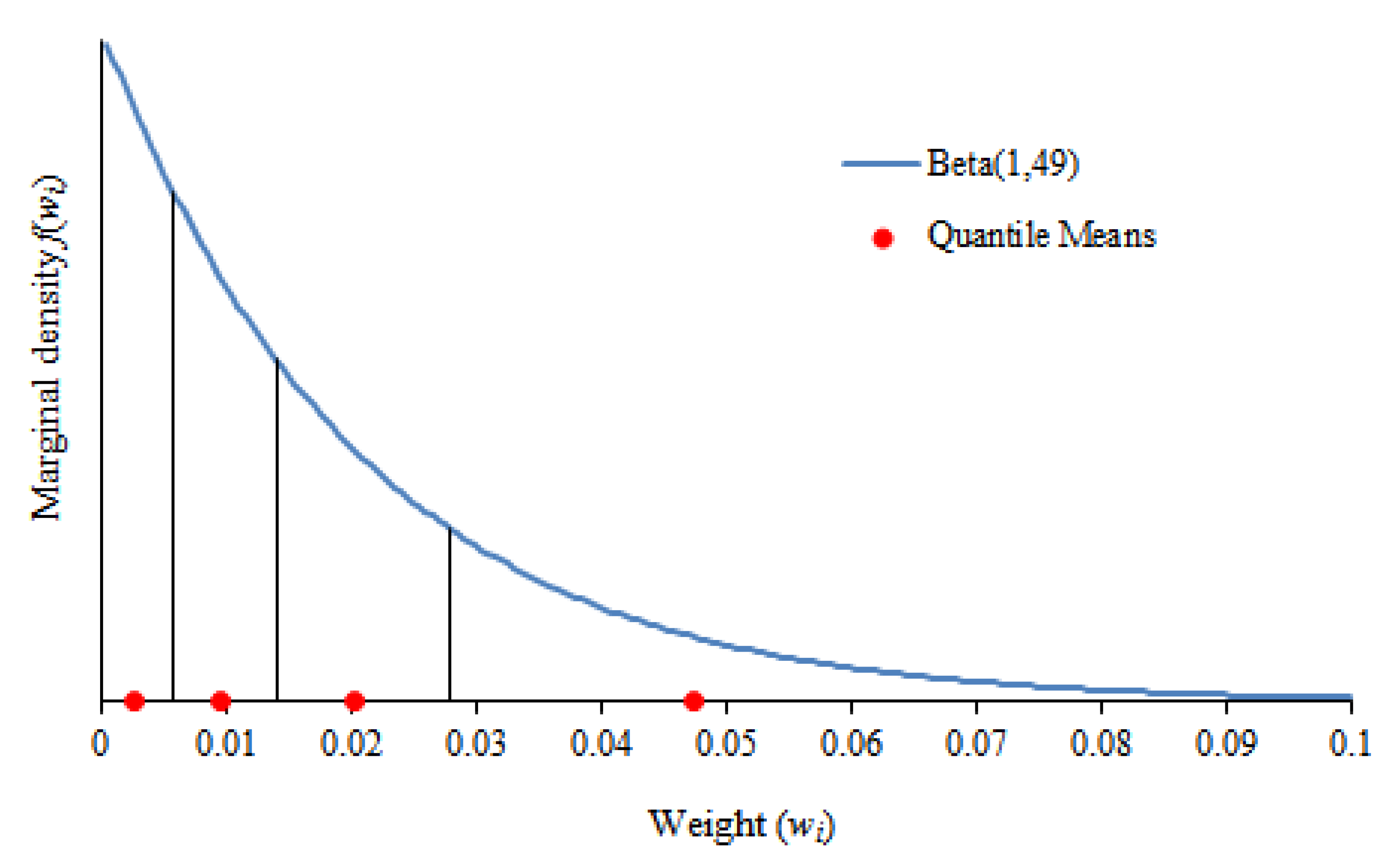
3.1. Simulation Approach
3.2. Approximation Methods
4. Results
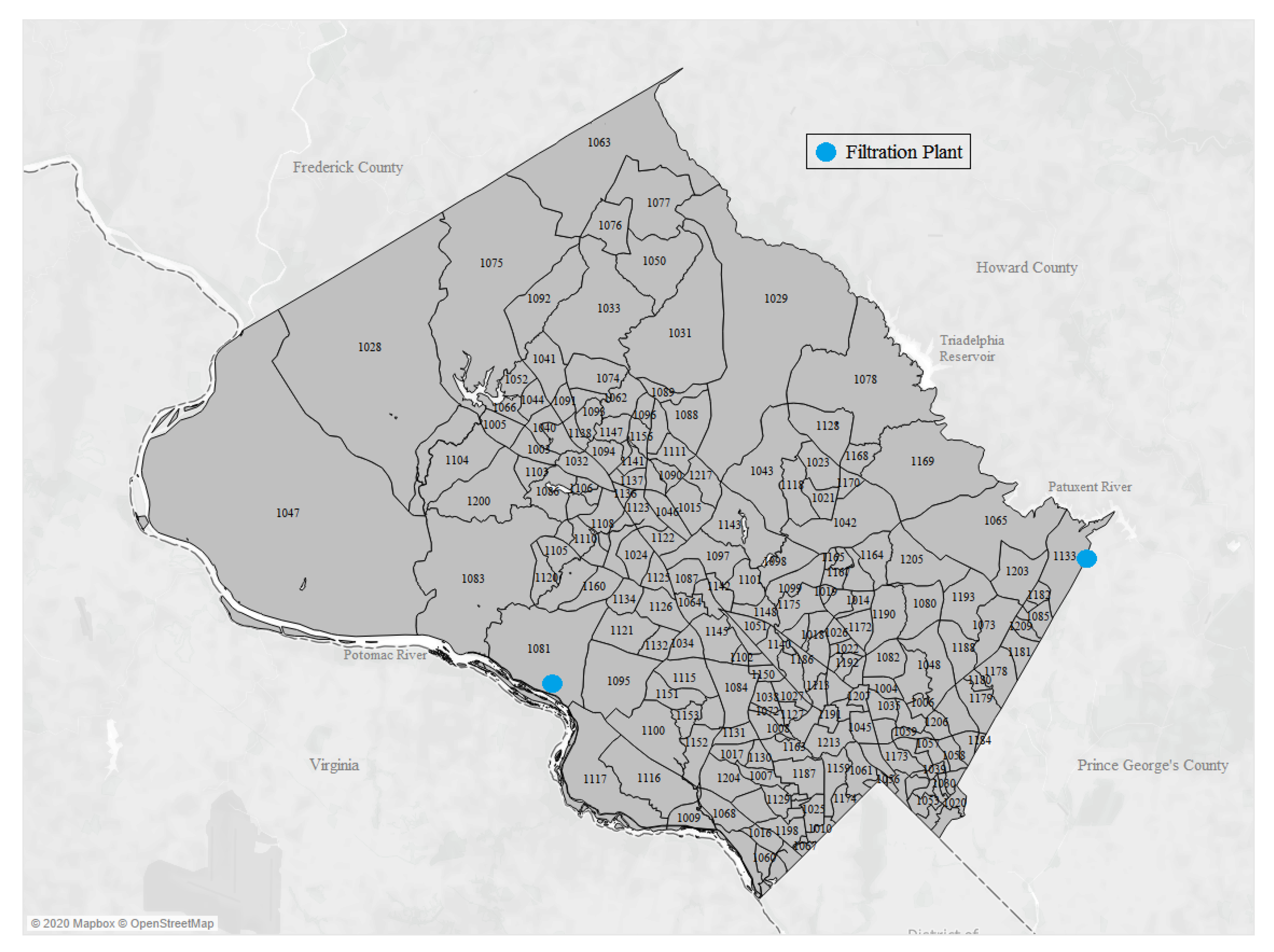
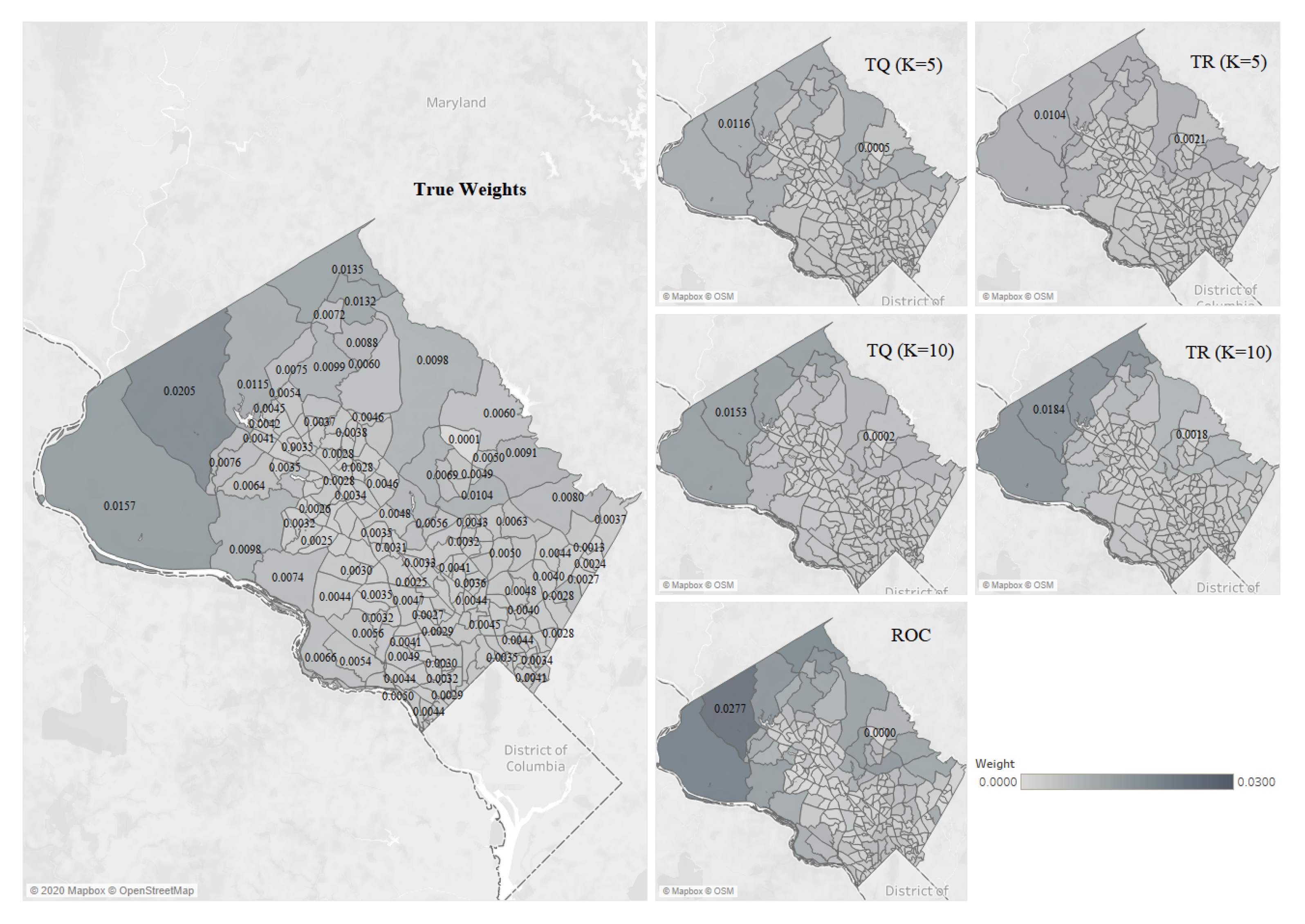
5. Example
6. Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Apartment Attributes Experiment
- Size of the apartment;
- Number of bedrooms;
- Number of bathrooms;
- Monthly rent amount;
- Pet policies and restrictions;
- Parking availability;
- Condition of the apartment;
- Appearance of the building;
- Laundry machine availability;
- Shared facilities (gym, pool, etc.);
- Rating of nearby public schools;
- Neighborhood crime rate;
- Proximity to stores;
- Proximity to parks/nature;
- Proximity to public transportation;
- View from apartment;
- Level of furnishing;
- Surrounding noise level;
- Damage deposit and policies;
- Security policies (gate, IDs, etc.).
- Enter a number from 1–3 for each of the 20 characteristics below according to how much influence it would have on your choice of apartment, where 1 means “little-to-no influence,” 2 means “some influence,” and 3 means “a large influence”.
- Enter a number from 1–7 for each of the 20 characteristics below according to how much influence it would have on your choice of apartment, where 1 means: “would have little-to-no influence on my choice” and 7 means: “would greatly influence my choice”.
- Enter a ranking from 1–20 for each of the 20 characteristics below according to how much they would influence your choice of apartment, where 1 is the most important characteristic and 20 is the least important.
Appendix B. Montgomery County Example: Weights and Approximations
| Block Number | True Weight | EW | RS | RR | ROC | TS (K = 5) | TS (K = 10) | TR (K = 5) | TR (K = 10) | TQ (K = 5) | TQ (K = 10) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1003 | 0.0035 | 0.0047 | 0.0024 | 0.0010 | 0.0014 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1004 | 0.0041 | 0.0047 | 0.0045 | 0.0015 | 0.0031 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1005 | 0.0041 | 0.0047 | 0.0041 | 0.0014 | 0.0027 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1006 | 0.0040 | 0.0047 | 0.0039 | 0.0013 | 0.0025 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1007 | 0.0034 | 0.0047 | 0.0018 | 0.0010 | 0.0010 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1008 | 0.0045 | 0.0047 | 0.0059 | 0.0021 | 0.0046 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1009 | 0.0050 | 0.0047 | 0.0072 | 0.0035 | 0.0070 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1010 | 0.0048 | 0.0047 | 0.0067 | 0.0028 | 0.0060 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1011 | 0.0046 | 0.0047 | 0.0062 | 0.0023 | 0.0051 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1012 | 0.0038 | 0.0047 | 0.0032 | 0.0012 | 0.0020 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1013 | 0.0047 | 0.0047 | 0.0064 | 0.0025 | 0.0055 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1014 | 0.0047 | 0.0047 | 0.0063 | 0.0024 | 0.0053 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1015 | 0.0046 | 0.0047 | 0.0060 | 0.0022 | 0.0049 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1016 | 0.0038 | 0.0047 | 0.0031 | 0.0012 | 0.0019 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1017 | 0.0041 | 0.0047 | 0.0042 | 0.0014 | 0.0028 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1018 | 0.0041 | 0.0047 | 0.0044 | 0.0015 | 0.0030 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1019 | 0.0032 | 0.0047 | 0.0014 | 0.0009 | 0.0008 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1020 | 0.0042 | 0.0047 | 0.0047 | 0.0016 | 0.0033 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1021 | 0.0055 | 0.0047 | 0.0078 | 0.0049 | 0.0087 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1022 | 0.0043 | 0.0047 | 0.0052 | 0.0018 | 0.0038 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1023 | 0.0056 | 0.0047 | 0.0080 | 0.0054 | 0.0091 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1024 | 0.0036 | 0.0047 | 0.0026 | 0.0011 | 0.0015 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1025 | 0.0050 | 0.0047 | 0.0074 | 0.0037 | 0.0073 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1026 | 0.0042 | 0.0047 | 0.0049 | 0.0016 | 0.0035 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1027 | 0.0045 | 0.0047 | 0.0059 | 0.0022 | 0.0048 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1028 | 0.0205 | 0.0047 | 0.0093 | 0.1681 | 0.0277 | 0.0066 | 0.0071 | 0.0104 | 0.0184 | 0.0116 | 0.0153 |
| 1029 | 0.0098 | 0.0047 | 0.0089 | 0.0168 | 0.0145 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1030 | 0.0034 | 0.0047 | 0.0016 | 0.0009 | 0.0009 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1031 | 0.0060 | 0.0047 | 0.0081 | 0.0060 | 0.0096 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1032 | 0.0050 | 0.0047 | 0.0073 | 0.0037 | 0.0072 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1033 | 0.0099 | 0.0047 | 0.0090 | 0.0210 | 0.0156 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1034 | 0.0034 | 0.0047 | 0.0020 | 0.0010 | 0.0011 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1035 | 0.0041 | 0.0047 | 0.0041 | 0.0014 | 0.0027 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1036 | 0.0037 | 0.0047 | 0.0029 | 0.0011 | 0.0017 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1037 | 0.0041 | 0.0047 | 0.0043 | 0.0015 | 0.0029 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1038 | 0.0034 | 0.0047 | 0.0017 | 0.0010 | 0.0010 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1039 | 0.0034 | 0.0047 | 0.0020 | 0.0010 | 0.0011 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1040 | 0.0037 | 0.0047 | 0.0030 | 0.0011 | 0.0018 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1041 | 0.0054 | 0.0047 | 0.0077 | 0.0044 | 0.0081 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1042 | 0.0104 | 0.0047 | 0.0090 | 0.0280 | 0.0171 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1043 | 0.0100 | 0.0047 | 0.0090 | 0.0240 | 0.0163 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1044 | 0.0042 | 0.0047 | 0.0048 | 0.0016 | 0.0034 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1045 | 0.0045 | 0.0047 | 0.0058 | 0.0020 | 0.0045 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1046 | 0.0047 | 0.0047 | 0.0065 | 0.0025 | 0.0055 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1047 | 0.0157 | 0.0047 | 0.0092 | 0.0840 | 0.0230 | 0.0066 | 0.0071 | 0.0104 | 0.0184 | 0.0116 | 0.0153 |
| 1048 | 0.0056 | 0.0047 | 0.0079 | 0.0053 | 0.0089 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1049 | 0.0048 | 0.0047 | 0.0068 | 0.0029 | 0.0061 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1050 | 0.0088 | 0.0047 | 0.0088 | 0.0140 | 0.0136 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1051 | 0.0033 | 0.0047 | 0.0016 | 0.0009 | 0.0009 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1052 | 0.0045 | 0.0047 | 0.0059 | 0.0021 | 0.0047 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1053 | 0.0043 | 0.0047 | 0.0050 | 0.0017 | 0.0036 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1054 | 0.0039 | 0.0047 | 0.0034 | 0.0012 | 0.0021 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1055 | 0.0044 | 0.0047 | 0.0054 | 0.0019 | 0.0041 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1056 | 0.0035 | 0.0047 | 0.0022 | 0.0010 | 0.0013 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1057 | 0.0041 | 0.0047 | 0.0044 | 0.0015 | 0.0030 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1058 | 0.0037 | 0.0047 | 0.0028 | 0.0011 | 0.0017 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1059 | 0.0049 | 0.0047 | 0.0070 | 0.0031 | 0.0065 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1060 | 0.0044 | 0.0047 | 0.0056 | 0.0019 | 0.0042 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1061 | 0.0050 | 0.0047 | 0.0072 | 0.0034 | 0.0069 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1062 | 0.0049 | 0.0047 | 0.0071 | 0.0032 | 0.0067 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1063 | 0.0135 | 0.0047 | 0.0092 | 0.0560 | 0.0207 | 0.0066 | 0.0071 | 0.0104 | 0.0184 | 0.0116 | 0.0153 |
| 1064 | 0.0034 | 0.0047 | 0.0018 | 0.0010 | 0.0010 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1065 | 0.0080 | 0.0047 | 0.0087 | 0.0120 | 0.0129 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1066 | 0.0042 | 0.0047 | 0.0047 | 0.0016 | 0.0033 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1067 | 0.0033 | 0.0047 | 0.0015 | 0.0009 | 0.0008 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1068 | 0.0044 | 0.0047 | 0.0053 | 0.0018 | 0.0040 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1069 | 0.0041 | 0.0047 | 0.0043 | 0.0014 | 0.0029 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1070 | 0.0038 | 0.0047 | 0.0033 | 0.0012 | 0.0021 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1071 | 0.0036 | 0.0047 | 0.0027 | 0.0011 | 0.0016 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1072 | 0.0027 | 0.0047 | 0.0005 | 0.0008 | 0.0002 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1073 | 0.0039 | 0.0047 | 0.0037 | 0.0013 | 0.0023 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1074 | 0.0061 | 0.0047 | 0.0082 | 0.0065 | 0.0099 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1075 | 0.0115 | 0.0047 | 0.0091 | 0.0336 | 0.0180 | 0.0066 | 0.0071 | 0.0104 | 0.0184 | 0.0116 | 0.0153 |
| 1076 | 0.0072 | 0.0047 | 0.0085 | 0.0088 | 0.0114 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1077 | 0.0132 | 0.0047 | 0.0091 | 0.0420 | 0.0191 | 0.0066 | 0.0071 | 0.0104 | 0.0184 | 0.0116 | 0.0153 |
| 1078 | 0.0060 | 0.0047 | 0.0081 | 0.0062 | 0.0097 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1079 | 0.0035 | 0.0047 | 0.0023 | 0.0010 | 0.0013 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1080 | 0.0055 | 0.0047 | 0.0078 | 0.0048 | 0.0085 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1081 | 0.0074 | 0.0047 | 0.0085 | 0.0093 | 0.0117 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1082 | 0.0051 | 0.0047 | 0.0075 | 0.0039 | 0.0076 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1083 | 0.0098 | 0.0047 | 0.0089 | 0.0187 | 0.0150 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1084 | 0.0047 | 0.0047 | 0.0062 | 0.0023 | 0.0051 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1085 | 0.0024 | 0.0047 | 0.0002 | 0.0008 | 0.0001 | 0.0026 | 0.0029 | 0.0026 | 0.0026 | 0.0016 | 0.0020 |
| 1086 | 0.0067 | 0.0047 | 0.0084 | 0.0080 | 0.0109 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1087 | 0.0035 | 0.0047 | 0.0025 | 0.0011 | 0.0015 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1088 | 0.0055 | 0.0047 | 0.0079 | 0.0051 | 0.0088 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1089 | 0.0046 | 0.0047 | 0.0061 | 0.0023 | 0.0050 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1090 | 0.0038 | 0.0047 | 0.0031 | 0.0012 | 0.0019 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1091 | 0.0049 | 0.0047 | 0.0068 | 0.0029 | 0.0062 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1092 | 0.0075 | 0.0047 | 0.0086 | 0.0099 | 0.0120 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1093 | 0.0044 | 0.0047 | 0.0055 | 0.0019 | 0.0041 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1094 | 0.0042 | 0.0047 | 0.0048 | 0.0016 | 0.0034 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1095 | 0.0044 | 0.0047 | 0.0055 | 0.0019 | 0.0042 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1096 | 0.0038 | 0.0047 | 0.0034 | 0.0012 | 0.0021 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1097 | 0.0048 | 0.0047 | 0.0068 | 0.0028 | 0.0061 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1098 | 0.0056 | 0.0047 | 0.0080 | 0.0056 | 0.0092 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1099 | 0.0049 | 0.0047 | 0.0069 | 0.0030 | 0.0063 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1100 | 0.0056 | 0.0047 | 0.0081 | 0.0058 | 0.0094 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1101 | 0.0066 | 0.0047 | 0.0083 | 0.0073 | 0.0105 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1102 | 0.0025 | 0.0047 | 0.0003 | 0.0008 | 0.0002 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1103 | 0.0035 | 0.0047 | 0.0023 | 0.0010 | 0.0013 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1104 | 0.0076 | 0.0047 | 0.0086 | 0.0105 | 0.0122 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1105 | 0.0032 | 0.0047 | 0.0012 | 0.0009 | 0.0006 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1106 | 0.0030 | 0.0047 | 0.0009 | 0.0009 | 0.0005 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1107 | 0.0033 | 0.0047 | 0.0016 | 0.0009 | 0.0009 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1108 | 0.0048 | 0.0047 | 0.0067 | 0.0028 | 0.0059 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1109 | 0.0034 | 0.0047 | 0.0017 | 0.0009 | 0.0009 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1110 | 0.0026 | 0.0047 | 0.0003 | 0.0008 | 0.0002 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1111 | 0.0037 | 0.0047 | 0.0030 | 0.0012 | 0.0018 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1112 | 0.0040 | 0.0047 | 0.0040 | 0.0014 | 0.0026 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1113 | 0.0044 | 0.0047 | 0.0056 | 0.0020 | 0.0043 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1114 | 0.0043 | 0.0047 | 0.0049 | 0.0016 | 0.0035 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1115 | 0.0035 | 0.0047 | 0.0022 | 0.0010 | 0.0013 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1116 | 0.0054 | 0.0047 | 0.0076 | 0.0043 | 0.0080 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1117 | 0.0066 | 0.0047 | 0.0084 | 0.0076 | 0.0107 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1118 | 0.0069 | 0.0047 | 0.0084 | 0.0084 | 0.0112 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1119 | 0.0027 | 0.0047 | 0.0004 | 0.0008 | 0.0002 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1120 | 0.0036 | 0.0047 | 0.0026 | 0.0011 | 0.0015 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1121 | 0.0044 | 0.0047 | 0.0057 | 0.0020 | 0.0044 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1122 | 0.0036 | 0.0047 | 0.0028 | 0.0011 | 0.0016 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1123 | 0.0034 | 0.0047 | 0.0019 | 0.0010 | 0.0010 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1124 | 0.0028 | 0.0047 | 0.0006 | 0.0008 | 0.0003 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1125 | 0.0036 | 0.0047 | 0.0027 | 0.0011 | 0.0016 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1126 | 0.0035 | 0.0047 | 0.0025 | 0.0011 | 0.0015 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1127 | 0.0039 | 0.0047 | 0.0036 | 0.0013 | 0.0023 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1128 | 0.0001 | 0.0047 | 0.0000 | 0.0008 | 0.0000 | 0.0013 | 0.0007 | 0.0021 | 0.0018 | 0.0005 | 0.0002 |
| 1129 | 0.0041 | 0.0047 | 0.0042 | 0.0014 | 0.0028 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1130 | 0.0035 | 0.0047 | 0.0025 | 0.0011 | 0.0014 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1131 | 0.0036 | 0.0047 | 0.0028 | 0.0011 | 0.0017 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1132 | 0.0030 | 0.0047 | 0.0009 | 0.0009 | 0.0005 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1133 | 0.0037 | 0.0047 | 0.0029 | 0.0011 | 0.0018 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1134 | 0.0029 | 0.0047 | 0.0009 | 0.0009 | 0.0005 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1135 | 0.0030 | 0.0047 | 0.0011 | 0.0009 | 0.0006 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1136 | 0.0028 | 0.0047 | 0.0006 | 0.0008 | 0.0003 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1137 | 0.0038 | 0.0047 | 0.0033 | 0.0012 | 0.0020 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1138 | 0.0039 | 0.0047 | 0.0037 | 0.0013 | 0.0024 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1139 | 0.0028 | 0.0047 | 0.0007 | 0.0008 | 0.0004 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1140 | 0.0046 | 0.0047 | 0.0060 | 0.0022 | 0.0048 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1141 | 0.0032 | 0.0047 | 0.0013 | 0.0009 | 0.0007 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1142 | 0.0034 | 0.0047 | 0.0019 | 0.0010 | 0.0011 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1143 | 0.0087 | 0.0047 | 0.0087 | 0.0129 | 0.0132 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1144 | 0.0031 | 0.0047 | 0.0011 | 0.0009 | 0.0006 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1145 | 0.0043 | 0.0047 | 0.0050 | 0.0017 | 0.0035 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1146 | 0.0028 | 0.0047 | 0.0007 | 0.0008 | 0.0004 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1147 | 0.0039 | 0.0047 | 0.0037 | 0.0013 | 0.0024 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1148 | 0.0039 | 0.0047 | 0.0036 | 0.0013 | 0.0023 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1149 | 0.0030 | 0.0047 | 0.0010 | 0.0009 | 0.0005 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1150 | 0.0032 | 0.0047 | 0.0014 | 0.0009 | 0.0007 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1151 | 0.0033 | 0.0047 | 0.0015 | 0.0009 | 0.0008 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1152 | 0.0049 | 0.0047 | 0.0069 | 0.0031 | 0.0064 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1153 | 0.0032 | 0.0047 | 0.0012 | 0.0009 | 0.0007 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1154 | 0.0034 | 0.0047 | 0.0021 | 0.0010 | 0.0012 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1155 | 0.0044 | 0.0047 | 0.0053 | 0.0018 | 0.0039 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1156 | 0.0039 | 0.0047 | 0.0035 | 0.0013 | 0.0022 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1157 | 0.0035 | 0.0047 | 0.0024 | 0.0011 | 0.0014 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1158 | 0.0040 | 0.0047 | 0.0038 | 0.0013 | 0.0025 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1159 | 0.0051 | 0.0047 | 0.0075 | 0.0040 | 0.0077 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1160 | 0.0025 | 0.0047 | 0.0003 | 0.0008 | 0.0001 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1161 | 0.0039 | 0.0047 | 0.0034 | 0.0012 | 0.0022 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1162 | 0.0042 | 0.0047 | 0.0047 | 0.0016 | 0.0032 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1163 | 0.0042 | 0.0047 | 0.0046 | 0.0015 | 0.0032 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1164 | 0.0052 | 0.0047 | 0.0075 | 0.0041 | 0.0078 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1165 | 0.0044 | 0.0047 | 0.0056 | 0.0020 | 0.0044 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1166 | 0.0043 | 0.0047 | 0.0050 | 0.0017 | 0.0036 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1167 | 0.0046 | 0.0047 | 0.0061 | 0.0022 | 0.0049 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1168 | 0.0050 | 0.0047 | 0.0071 | 0.0034 | 0.0068 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1169 | 0.0091 | 0.0047 | 0.0088 | 0.0153 | 0.0141 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1170 | 0.0049 | 0.0047 | 0.0071 | 0.0033 | 0.0067 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1171 | 0.0043 | 0.0047 | 0.0052 | 0.0018 | 0.0038 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1172 | 0.0055 | 0.0047 | 0.0077 | 0.0045 | 0.0083 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1173 | 0.0048 | 0.0047 | 0.0066 | 0.0027 | 0.0058 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1174 | 0.0051 | 0.0047 | 0.0074 | 0.0038 | 0.0074 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1175 | 0.0044 | 0.0047 | 0.0057 | 0.0020 | 0.0045 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1176 | 0.0044 | 0.0047 | 0.0054 | 0.0018 | 0.0040 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1177 | 0.0034 | 0.0047 | 0.0019 | 0.0010 | 0.0011 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1178 | 0.0077 | 0.0047 | 0.0087 | 0.0112 | 0.0126 | 0.0066 | 0.0064 | 0.0104 | 0.0092 | 0.0116 | 0.0089 |
| 1179 | 0.0041 | 0.0047 | 0.0040 | 0.0014 | 0.0027 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1180 | 0.0028 | 0.0047 | 0.0006 | 0.0008 | 0.0003 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1181 | 0.0027 | 0.0047 | 0.0004 | 0.0008 | 0.0002 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1182 | 0.0017 | 0.0047 | 0.0001 | 0.0008 | 0.0001 | 0.0026 | 0.0029 | 0.0026 | 0.0026 | 0.0016 | 0.0020 |
| 1183 | 0.0035 | 0.0047 | 0.0022 | 0.0010 | 0.0012 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1184 | 0.0028 | 0.0047 | 0.0005 | 0.0008 | 0.0003 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1185 | 0.0039 | 0.0047 | 0.0035 | 0.0012 | 0.0022 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1186 | 0.0038 | 0.0047 | 0.0032 | 0.0012 | 0.0020 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1187 | 0.0055 | 0.0047 | 0.0078 | 0.0047 | 0.0084 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1188 | 0.0040 | 0.0047 | 0.0038 | 0.0013 | 0.0024 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1189 | 0.0041 | 0.0047 | 0.0043 | 0.0014 | 0.0029 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1190 | 0.0050 | 0.0047 | 0.0073 | 0.0036 | 0.0071 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1191 | 0.0047 | 0.0047 | 0.0065 | 0.0026 | 0.0057 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1192 | 0.0041 | 0.0047 | 0.0045 | 0.0015 | 0.0031 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1193 | 0.0044 | 0.0047 | 0.0053 | 0.0018 | 0.0039 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1194 | 0.0047 | 0.0047 | 0.0063 | 0.0024 | 0.0053 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1195 | 0.0030 | 0.0047 | 0.0010 | 0.0009 | 0.0005 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1196 | 0.0034 | 0.0047 | 0.0021 | 0.0010 | 0.0012 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1197 | 0.0032 | 0.0047 | 0.0013 | 0.0009 | 0.0007 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1198 | 0.0047 | 0.0047 | 0.0062 | 0.0024 | 0.0052 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1199 | 0.0029 | 0.0047 | 0.0008 | 0.0008 | 0.0004 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1200 | 0.0064 | 0.0047 | 0.0083 | 0.0070 | 0.0103 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1201 | 0.0037 | 0.0047 | 0.0031 | 0.0012 | 0.0019 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1202 | 0.0042 | 0.0047 | 0.0046 | 0.0015 | 0.0031 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1203 | 0.0047 | 0.0047 | 0.0065 | 0.0026 | 0.0056 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1204 | 0.0049 | 0.0047 | 0.0070 | 0.0032 | 0.0066 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1205 | 0.0063 | 0.0047 | 0.0082 | 0.0067 | 0.0101 | 0.0053 | 0.0057 | 0.0052 | 0.0061 | 0.0055 | 0.0065 |
| 1206 | 0.0043 | 0.0047 | 0.0051 | 0.0017 | 0.0037 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1207 | 0.0047 | 0.0047 | 0.0064 | 0.0025 | 0.0054 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1208 | 0.0043 | 0.0047 | 0.0051 | 0.0017 | 0.0037 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1209 | 0.0024 | 0.0047 | 0.0002 | 0.0008 | 0.0001 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1210 | 0.0032 | 0.0047 | 0.0012 | 0.0009 | 0.0006 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1211 | 0.0029 | 0.0047 | 0.0008 | 0.0009 | 0.0004 | 0.0040 | 0.0036 | 0.0035 | 0.0031 | 0.0031 | 0.0028 |
| 1212 | 0.0013 | 0.0047 | 0.0001 | 0.0008 | 0.0000 | 0.0026 | 0.0021 | 0.0026 | 0.0023 | 0.0016 | 0.0013 |
| 1213 | 0.0053 | 0.0047 | 0.0076 | 0.0042 | 0.0079 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1214 | 0.0045 | 0.0047 | 0.0058 | 0.0021 | 0.0046 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1215 | 0.0040 | 0.0047 | 0.0039 | 0.0013 | 0.0026 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
| 1216 | 0.0048 | 0.0047 | 0.0066 | 0.0027 | 0.0058 | 0.0053 | 0.0050 | 0.0052 | 0.0046 | 0.0055 | 0.0049 |
| 1217 | 0.0040 | 0.0047 | 0.0040 | 0.0014 | 0.0026 | 0.0040 | 0.0043 | 0.0035 | 0.0037 | 0.0031 | 0.0037 |
References
- Malczewski, J.; Jankowski, P. Emerging trends and research frontiers in spatial multicriteria analysis. Int. J. Geogr. Inf. Sci. 2020, 34, 1257–1282. [Google Scholar] [CrossRef]
- Simon, J.; Kirkwood, C.W.; Keller, L.R. Decision Analysis with Geographically Varying Outcomes: Preference Models and Illustrative Applications. Oper. Res. 2014, 62, 182–194. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Tradeoffs; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Eisenfuhr, F.; Weber, M.; Langer, T. Rational Decision Making; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Edwards, W. How to use multiattribute utility measurement for social decisionmaking. IEEE Trans. Syst. Man Cybern. 1977, 7, 326–340. [Google Scholar] [CrossRef]
- Von Winterfeldt, D.; Edwards, W. Decision Analysis and Behavioral Research; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Dawes, R.M.; Corrigan, B. Linear models in decision making. Psychol. Bull. 1974, 81, 95–106. [Google Scholar] [CrossRef]
- Barron, F.H. Selecting a best multiattribute alternative with partial information about attribute weights. Acta Psychol. 1992, 80, 91–103. [Google Scholar] [CrossRef]
- Debreu, G. Topological Methods in Cardinal Utility Theory. In Mathematical Methods in the Social Sciences; Arrow, K.J., Karlin, P.S., Eds.; Stanford University Press: Stanford, CA, USA, 1960; pp. 16–26. [Google Scholar]
- Fishburn, P.C. Independence in Utility Theory with Whole Product Sets. Oper. Res. 1965, 13, 28–45. [Google Scholar] [CrossRef]
- Diamond, J.T.; Wright, J.R. Design of an integrated spatial information system for multiobjective land-use planning. Environ. Plan. Plan. Des. 1988, 15, 205–214. [Google Scholar] [CrossRef]
- Antoine, J.; Fischer, G.; Makowski, M. Multiple criteria land use analysis. Appl. Math. Comput. 1997, 83, 195–215. [Google Scholar] [CrossRef]
- Agrell, P.J.; Stam, A.; Fischer, G.W. Interactive multiobjective agro-ecological land use planning: The Bungoma region in Kenya. Eur. J. Oper. Res. 2004, 158, 194–217. [Google Scholar] [CrossRef]
- Pereira, A.G.; Munda, G.; Paruccini, M. Generating alternatives for siting retail and service facilities using genetic algorithms and multiple criteria decision techniques. J. Retail. Consum. Serv. 1994, 1, 40–47. [Google Scholar] [CrossRef]
- MacDonald, M.L. A multi-attribute spatial decision support system for solid waste planning. Comput. Environ. Urban Syst. 1996, 20, 1–17. [Google Scholar] [CrossRef]
- Leao, S.; Bishop, I.; Evans, D. Spatial–temporal model for demand and allocation of waste landfills in growing urban regions. Comput. Environ. Urban Syst. 2004, 28, 353–385. [Google Scholar] [CrossRef]
- De Araújo, C.C.; Macedo, A.B. Multicriteria geologic data analysis for mineral favorability mapping: Application to a metal sulphide mineralized area, Ribeira Valley Metallogenic Province, Brazil. Nat. Resour. Res. 2002, 11, 29–43. [Google Scholar] [CrossRef]
- Kangas, J.; Store, R.; Leskinen, P.; MehtaÈtalo, L. Improving the quality of landscape ecological forest planning by utilising advanced decision-support tools. For. Ecol. Manag. 2000, 132, 157–171. [Google Scholar] [CrossRef]
- Schlaepfer, R.; Iorgulescu, I.; Glenz, C. Management of forested landscapes in mountain areas: An ecosystem-based approach. For. Policy Econ. 2002, 4, 89–99. [Google Scholar] [CrossRef]
- Sironen, S.; Mononen, L. Spatially Referenced Decision Analysis of Long-Term Forest Management Scenarios in Southwestern Finland. J. Environ. Assess. Policy Manag. 2018, 20, 1850009. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Schoemaker, P.J.; Waid, C.C. An experimental comparison of different approaches to determining weights in additive utility models. Manag. Sci. 1982, 28, 182–196. [Google Scholar] [CrossRef]
- Borcherding, K.; Eppel, T.; Von Winterfeldt, D. Comparison of weighting judgments in multiattribute utility measurement. Manag. Sci. 1991, 37, 1603–1619. [Google Scholar] [CrossRef]
- Pöyhönen, M.; Hämäläinen, R.P. On the convergence of multiattribute weighting methods. Eur. J. Oper. Res. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Hobbs, B.F. A comparison of weighting methods in power plant siting. DEcision Sci. 1980, 11, 725–737. [Google Scholar] [CrossRef]
- Keller, L.R.; Simon, J. Preference Functions for Spatial Risk Analysis. Risk Anal. 2019, 39, 244–256. [Google Scholar] [CrossRef] [PubMed]
- Harju, M.; Liesiö, J.; Virtanen, K. Spatial multi-attribute decision analysis: Axiomatic foundations and incomplete preference information. Eur. J. Oper. Res. 2019, 275, 167–181. [Google Scholar] [CrossRef]
- Ferretti, V.; Montibeller, G. Key challenges and meta-choices in designing and applying multi-criteria spatial decision support systems. Decis. Support Syst. 2016, 84, 41–52. [Google Scholar] [CrossRef]
- Ferretti, V.; Montibeller, G. An integrated framework for environmental multi-impact spatial risk analysis. Risk Anal. 2019, 39, 257–273. [Google Scholar] [CrossRef] [PubMed]
- Stillwell, W.G.; Seaver, D.A.; Edwards, W. A comparison of weight approximation techniques in multiattribute utility decision making. Organ. Behav. Hum. Perform. 1981, 28, 62–77. [Google Scholar] [CrossRef]
- Barron, F.H.; Barrett, B.E. Decision quality using ranked attribute weights. Manag. Sci. 1996, 42, 1515–1523. [Google Scholar] [CrossRef]
- Ahn, B.S.; Park, K.S. Comparing methods for multiattribute decision making with ordinal weights. Comput. Oper. Res. 2008, 35, 1660–1670. [Google Scholar] [CrossRef]
- Danielson, M.; Ekenberg, L.; He, Y. Augmenting ordinal methods of attribute weight approximation. Decis. Anal. 2014, 11, 21–26. [Google Scholar] [CrossRef]
- Chung, E.S.; Won, K.; Kim, Y.; Lee, H. Water resource vulnerability characteristics by district’s population size in a changing climate using subjective and objective weights. Sustainability 2014, 6, 6141–6157. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, G.; Fang, L.; Nie, Y. GIS-based integration of subjective and objective weighting methods for regional landslides susceptibility mapping. Sustainability 2016, 8, 334. [Google Scholar] [CrossRef]
- Niu, Q.; Yu, L.; Jie, Q.; Li, X. An urban eco-environmental sensitive areas assessment method based on variable weights combination. Environ. Dev. Sustain. 2018. [Google Scholar] [CrossRef]
- Sokal, R.R.; Oden, N.L. Spatial autocorrelation in biology: 1. Methodology. Biol. J. Linn. Soc. 1978, 10, 199–228. [Google Scholar] [CrossRef]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Koenig, W.D. Spatial autocorrelation of ecological phenomena. Trends Ecol. Evol. 1999, 14, 22–26. [Google Scholar] [CrossRef]
- Malczewski, J. Local weighted linear combination. Trans. GIS 2011, 15, 439–455. [Google Scholar] [CrossRef]
- Şalap-Ayça, S.; Jankowski, P. Analysis of the influence of parameter and scale uncertainties on a local multi-criteria land use evaluation model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2699–2719. [Google Scholar] [CrossRef]
- Rao, J.; Sobel, M. Incomplete Dirichlet integrals with applications to ordered uniform spacings. J. Multivar. Anal. 1980, 10, 603–610. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Generating random vectors uniformly distributed inside and on the surface of different regions. Eur. J. Oper. Res. 1982, 10, 205–209. [Google Scholar] [CrossRef]
- Danielson, M.; Ekenberg, L. Rank ordering methods for multi-criteria decisions. In Proceedings of the International Conference on Group Decision and Negotiation, Toulouse, France, 10–13 June 2014. [Google Scholar]
- Akl, S.G. Parallel Sorting Algorithms; Academic Press: Cambridge, MA, USA, 2014; Volume 12. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81. [Google Scholar] [CrossRef]
- Ewing, P.L., Jr.; Tarantino, W.; Parnell, G.S. Use of decision analysis in the army base realignment and closure (BRAC) 2005 military value analysis. Decis. Anal. 2006, 3, 33–49. [Google Scholar] [CrossRef]
| Method | ||||||
|---|---|---|---|---|---|---|
| Rank-Sum | 33.3% | 33.3% | 33.3% | 33.2% | 33.3% | |
| Rank-Reciprocal | 36.5% | 87.7% | 144.6% | 203.4% | 261.3% | |
| Rank-Order Centroid | 9.4% | 6.1% | 4.7% | 3.8% | 3.3% | |
| Tier-Sum: | 48.7% | 50.8% | 51.6% | 51.9% | 52.2% | |
| 42.6% | 45.0% | 45.7% | 46.0% | 46.3% | ||
| 39.1% | 41.5% | 42.3% | 42.7% | 43.0% | ||
| 36.9% | 39.4% | 40.2% | 40.6% | 40.9% | ||
| 35.4% | 37.9% | 38.7% | 39.1% | 39.4% | ||
| 34.3% | 36.8% | 37.6% | 38.0% | 38.3% | ||
| 33.5% | 36.0% | 36.8% | 37.2% | 37.5% | ||
| 32.8% | 35.4% | 36.2% | 36.6% | 36.9% | ||
| Tier-Reciprocal: | 42.3% | 44.5% | 45.3% | 45.6% | 45.9% | |
| 30.7% | 33.1% | 33.9% | 34.2% | 34.6% | ||
| 23.3% | 25.5% | 26.4% | 26.7% | 27.0% | ||
| 18.3% | 20.3% | 21.2% | 21.5% | 21.8% | ||
| 14.9% | 16.8% | 17.6% | 18.0% | 18.2% | ||
| 12.8% | 14.5% | 15.2% | 15.5% | 15.8% | ||
| 11.6% | 13.0% | 13.7% | 14.0% | 14.2% | ||
| 10.9% | 12.2% | 12.8% | 13.1% | 13.3% | ||
| Tier-Quantile: | 29.1% | 32.0% | 33.1% | 33.5% | 33.9% | |
| 20.8% | 23.6% | 24.5% | 24.9% | 25.3% | ||
| 16.0% | 18.4% | 19.4% | 19.7% | 20.2% | ||
| 12.8% | 15.0% | 15.9% | 16.4% | 16.7% | ||
| 10.6% | 12.7% | 13.6% | 14.0% | 14.3% | ||
| 9.0% | 11.0% | 11.8% | 12.1% | 12.5% | ||
| 7.8% | 9.6% | 10.4% | 10.7% | 11.0% | ||
| 6.9% | 8.6% | 9.3% | 9.6% | 9.9% | ||
| Equal Weights (Baseline) | 2.26 | 5.94 | 2.69 | 1.52 | 9.79 | |
| Method | ||||||
|---|---|---|---|---|---|---|
| Rank-Sum | 84.5% | 84.1% | 83.1% | 83.9% | 83.3% | |
| Rank-Reciprocal | 80.8% | 78.8% | 79.4% | 76.9% | 75.8% | |
| Rank-Order Centroid | 92.0% | 92.9% | 94.1% | 95.0% | 95.0% | |
| Tier-Sum: | 79.9% | 79.2% | 79.0% | 79.6% | 78.5% | |
| 81.1% | 80.8% | 81.0% | 80.6% | 80.5% | ||
| 82.5% | 82.5% | 81.8% | 81.4% | 81.2% | ||
| 83.4% | 82.6% | 82.2% | 82.4% | 81.7% | ||
| 83.8% | 83.7% | 82.3% | 82.9% | 82.0% | ||
| 83.7% | 83.0% | 82.5% | 83.1% | 82.6% | ||
| 84.1% | 83.2% | 83.3% | 83.2% | 82.9% | ||
| 84.5% | 83.7% | 83.3% | 83.5% | 82.7% | ||
| Tier-Reciprocal: | 82.0% | 80.7% | 80.1% | 80.7% | 79.7% | |
| 85.3% | 83.6% | 83.3% | 83.4% | 82.3% | ||
| 86.6% | 86.1% | 85.9% | 85.3% | 84.5% | ||
| 88.1% | 86.8% | 87.0% | 86.3% | 85.8% | ||
| 88.3% | 87.8% | 87.5% | 87.6% | 87.1% | ||
| 88.3% | 88.5% | 87.7% | 87.5% | 87.5% | ||
| 88.7% | 88.6% | 88.1% | 88.6% | 87.7% | ||
| 89.3% | 88.6% | 89.3% | 88.5% | 88.2% | ||
| Tier-Quantile: | 82.3% | 80.6% | 80.1% | 80.7% | 79.6% | |
| 85.3% | 83.5% | 83.4% | 83.2% | 82.6% | ||
| 87.0% | 86.6% | 85.8% | 85.4% | 84.7% | ||
| 88.4% | 87.7% | 86.6% | 86.5% | 86.2% | ||
| 89.7% | 88.6% | 88.0% | 88.0% | 87.5% | ||
| 90.0% | 89.6% | 88.4% | 88.8% | 88.3% | ||
| 91.2% | 90.0% | 89.4% | 89.9% | 88.9% | ||
| 92.5% | 90.4% | 90.4% | 90.0% | 89.8% | ||
| Method | ||||||
|---|---|---|---|---|---|---|
| Rank-Sum | 0.706% | 0.442% | 0.412% | 0.353% | 0.296% | |
| Rank-Reciprocal | 0.710% | 0.704% | 0.604% | 0.644% | 0.611% | |
| Rank-Order Centroid | 0.169% | 0.100% | 0.052% | 0.036% | 0.030% | |
| Tier-Sum: | 1.009% | 0.729% | 0.665% | 0.554% | 0.531% | |
| 0.851% | 0.610% | 0.559% | 0.471% | 0.408% | ||
| 0.772% | 0.527% | 0.488% | 0.400% | 0.363% | ||
| 0.723% | 0.518% | 0.484% | 0.414% | 0.346% | ||
| 0.681% | 0.493% | 0.443% | 0.372% | 0.330% | ||
| 0.677% | 0.446% | 0.434% | 0.357% | 0.329% | ||
| 0.645% | 0.454% | 0.430% | 0.374% | 0.320% | ||
| 0.634% | 0.441% | 0.405% | 0.369% | 0.302% | ||
| Tier-Reciprocal: | 0.856% | 0.635% | 0.570% | 0.464% | 0.484% | |
| 0.605% | 0.442% | 0.421% | 0.337% | 0.312% | ||
| 0.467% | 0.356% | 0.323% | 0.294% | 0.241% | ||
| 0.411% | 0.308% | 0.288% | 0.239% | 0.206% | ||
| 0.365% | 0.279% | 0.258% | 0.210% | 0.186% | ||
| 0.323% | 0.240% | 0.223% | 0.194% | 0.183% | ||
| 0.298% | 0.228% | 0.224% | 0.194% | 0.168% | ||
| 0.283% | 0.218% | 0.216% | 0.195% | 0.164% | ||
| Tier-Quantile: | 0.857% | 0.632% | 0.557% | 0.466% | 0.484% | |
| 0.601% | 0.427% | 0.407% | 0.332% | 0.301% | ||
| 0.466% | 0.359% | 0.320% | 0.277% | 0.233% | ||
| 0.375% | 0.301% | 0.271% | 0.218% | 0.192% | ||
| 0.321% | 0.243% | 0.216% | 0.180% | 0.156% | ||
| 0.260% | 0.205% | 0.176% | 0.164% | 0.144% | ||
| 0.232% | 0.195% | 0.169% | 0.148% | 0.126% | ||
| 0.188% | 0.172% | 0.148% | 0.129% | 0.119% | ||
| Equal Weights | 4.985% | 3.717% | 2.844% | 2.549% | 2.285% | |
| Method | MSE () |
|---|---|
| EW | 0.050 |
| RS | 0.032 |
| RR | 1.462 |
| ROC | 0.065 |
| TS: | 0.026 |
| TS: | 0.024 |
| TR: | 0.012 |
| TR: | 0.007 |
| TQ: | 0.014 |
| TQ: | 0.004 |
| Method | Elicitation Difficulty | Overall Accuracy | Variability of Weights |
|---|---|---|---|
| Equal Weights | Easy | Very Low | None |
| Rank-Sum | Difficult | Moderate | Low |
| Rank-Reciprocal | Difficult | Low | Very High |
| Rank-Order Centroid | Difficult | Very High | High |
| Tier-Sum | Moderate | Moderate | Low |
| Tier-Reciprocal | Moderate | High | Moderate |
| Tier-Quantile | Moderate | High | Moderate |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, J. Weight Approximation for Spatial Outcomes. Sustainability 2020, 12, 5588. https://doi.org/10.3390/su12145588
Simon J. Weight Approximation for Spatial Outcomes. Sustainability. 2020; 12(14):5588. https://doi.org/10.3390/su12145588
Chicago/Turabian StyleSimon, Jay. 2020. "Weight Approximation for Spatial Outcomes" Sustainability 12, no. 14: 5588. https://doi.org/10.3390/su12145588
APA StyleSimon, J. (2020). Weight Approximation for Spatial Outcomes. Sustainability, 12(14), 5588. https://doi.org/10.3390/su12145588




