Sound-Absorption Properties of Materials Made of Esparto Grass Fibers
Abstract
1. Introduction
Empirical Model for Fibrous Sound-Absorbing Materials
2. Materials and Methods
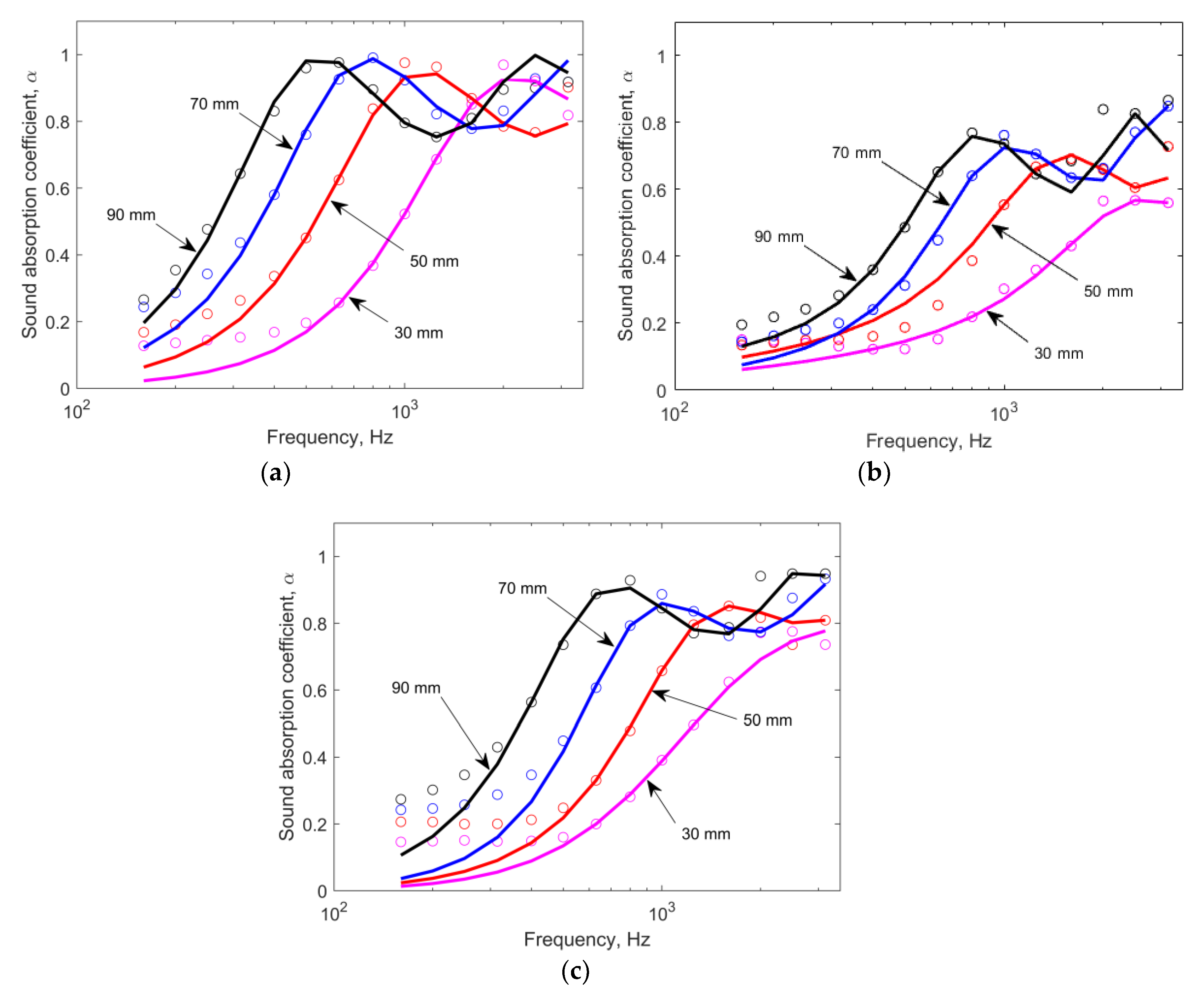
3. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crocker, M.J.; Arenas, J.P. Use of sound-absorbing materials. In Handbook of Noise and Vibrations; Crocker, M.J., Ed.; John Wiley and Sons: New York, NY, USA, 2007; pp. 696–713. [Google Scholar]
- Arenas, J.P.; Crocker, M.J. Recent trend in porous sound-absorbing materials. Sound Vib. 2010, 44, 12–17. [Google Scholar]
- Arenas, J.P.; Asdrubali, F. Eco-materials with noise reduction properties. In Handbook of Ecomaterials; Martinez, L.M.T., Kharissova, O.V., Kharisov, B.I., Eds.; Springer: Cham, Switzerland, 2019; pp. 3031–3056. [Google Scholar]
- Arenas, J.P. Applications of Acoustic Textiles in Automotive/Transportation. In Acoustic Textiles; Padhye, R., Nayak, R., Eds.; Springer: Singapore, 2016; pp. 143–161. [Google Scholar]
- Faruk, O.; Bledzki, A.K.; Fink, H.P.; Sain, M. Biocomposites reinforced with natural fibers: 2000–2010. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Asdrubali, F.; Schiavoni, S.; Horshenkov, K. A review of sustainable materials for acoustic applications. Build. Acoust. 2012, 19, 283–312. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Acoustic characterization of natural fibers for sound absorption applications. Build. Environ. 2015, 94, 840–852. [Google Scholar] [CrossRef]
- Koruk, H.; Genc, G. Investigation of the acoustic properties of bio luffa fiber and composite materials. Mater. Lett. 2015, 157, 166–168. [Google Scholar] [CrossRef]
- Ersoy, S.; Küçük, H. Investigation of industrial tea-leaf-fibre waste material for its sound absorption properties. Appl. Acoust. 2009, 70, 215–220. [Google Scholar] [CrossRef]
- Fouladi, M.H.; Nor, M.J.M.; Ayub, M.; Leman, Z.A. Utilization of coir fiber in multilayer acoustic absorption panel. Appl. Acoust. 2010, 71, 241–249. [Google Scholar] [CrossRef]
- Fouladi, M.H.; Ayub, M.; Nor, M.J.M. Analysis of coir fiber acoustical characteristics. Appl. Acoust. 2011, 72, 35–42. [Google Scholar] [CrossRef]
- Ramis, J.; del Rey, R.; Alba, J.; Godinho, L.; Carbajo, J. A model for acoustic absorbent materials derived from coconut fiber. Mater. Constr. 2014, 64, e008. [Google Scholar] [CrossRef]
- Rahman, L.A.; Raja, R.I.; Rahman, R.A. Experimental study on natural fibers for green acoustic absorption materials. Am. J. Appl. Sci. 2013, 10, 1307–1314. [Google Scholar]
- Oldham, D.J.; Egan, C.A.; Cookson, R.D. Sustainable acoustic absorbers from the biomass. Appl. Acoust. 2011, 72, 350–363. [Google Scholar] [CrossRef]
- Yang, W.D.; Li, Y. Sound absorption performance of natural fibers and their composites. Sci. China Technol. Sci. 2012, 55, 2278–2283. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, X.; Zhang, H.; Zhuang, X.; Yan, X. Corn husk for noise reduction: Robust acoustic absorption and reduced thickness. Appl. Acoust. 2018, 134, 60–68. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G.; Di Gabriele, M. The acoustic characterization of broom fibers. J. Nat. Fibers 2017, 14, 858–863. [Google Scholar] [CrossRef]
- Lima, Z.Y.; Putra, A.; Nor, M.J.M.; Yaakob, M.Y. Sound absorption performance of natural kenaf fibres. Appl. Acoust. 2018, 130, 107–114. [Google Scholar] [CrossRef]
- Koizumi, T.; Tsujiuchi, N.; Adachi, A. The development of sound absorbing materials using natural bamboo fibers. High performance structures and composites. WIT Trans. Built Environ. 2002, 59, 157–166. [Google Scholar]
- Malawade, U.A.; Jadhav, M.G. Investigation of the acoustic performance of bagasse. J. Mater. Res. Technol. 2020, 9, 882–889. [Google Scholar] [CrossRef]
- Gomez, T.S.; Navacerrada, M.A.; Diaz, C.; Fernandez-Morales, P. Fique fibres as a sustainable material for thermoacoustic conditioning. Appl. Acoust. 2020, 164, 107240. [Google Scholar] [CrossRef]
- Othmani, C.; Taktak, M.; Zein, A.; Hentati, T.; Elnady, T.; Fakhfakh, T.; Haddar, M. Experimental and theoretical investigation of the acoustic performance of sugarcane wastes-based material. Appl. Acoust. 2016, 109, 90–96. [Google Scholar] [CrossRef]
- Or, K.H.; Putra, A.; Selamat, M.Z. Oil palm empty fruit bunch fibres as sustainable acoustic absorber. Appl. Acoust. 2017, 119, 9–16. [Google Scholar] [CrossRef]
- Taban, E.; Khavanin, A.; Faridan, M.; Samaei, S.E.; Samimi, K.; Rashidi, R. Comparison of acoustic absorption characteristics of coir and date palm fibers: Experimental and analytical study of green composites. Int. J. Environ. Sci. Technol. 2020, 17, 39–48. [Google Scholar] [CrossRef]
- Putra, A.; Or, K.H.; Selamat, M.Z.; Nor, M.J.M.; Hassan, M.H.; Prasetiyo, I. Sound absorption of extracted pineapple-leaf fibres. Appl. Acoust. 2018, 136, 9–15. [Google Scholar] [CrossRef]
- Yun, B.Y.; Cho, H.M.; Kim, Y.U.; Lee, S.C.; Berardi, U.; Kim, S. Circular reutilization of coffee waste for sound absorbing panels: A perspective on material recycling. Environ. Res. 2020, 184, 109281. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, Y.; Jiang, B.; Li, Y. Sound Absorption Characterization of Natural Materials and Sandwich Structure Composites. Aerospace 2018, 5, 75. [Google Scholar] [CrossRef]
- Kusno, A.; Sakagami, K.; Okuzono, T.; Toyoda, M.; Otsuru, T.; Mulyadi, R.; Kamil, K. A pilot study on the sound absorption characteristics of chicken feathers as an alternative sustainable acoustical material. Sustainability 2019, 11, 1476. [Google Scholar] [CrossRef]
- Allard, J.F.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, 3rd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Delany, M.; Bazley, E. Acoustical properties of fibrous absorbent materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Predicting the sound absorption of natural materials: Best-fit inverse laws for the acoustic impedance and the propagation constant. Appl. Acoust. 2017, 115, 131–138. [Google Scholar] [CrossRef]
- Mechel, F. Eine Modelltheorie zum Faserabsorber Teil I: Regulare Faserordnung. Acustica 1976, 36, 53–64. [Google Scholar]
- Miki, Y. Acoustical properties of porous materials—Modifications of Delany-Bazley models. J. Acoust. Soc. Jpn. E 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Attenborough, K. Acoustical characteristics of porous materials. Phys. Rep. 1982, 82, 179–227. [Google Scholar] [CrossRef]
- Dunn, I.P.; Davern, W.A. Calculation of acoustic impedance of multi-layer absorbers. Appl. Acoust. 1986, 19, 321–334. [Google Scholar] [CrossRef]
- Garai, M.; Pompoli, F. A simple empirical model of polyester fibre materials for acoustical applications. Appl. Acoust. 2005, 66, 1383–1398. [Google Scholar] [CrossRef]
- del Rey, R.; Alba, J.; Arenas, J.P.; Sanchis, V. An empirical modelling of porous sound absorbing materials made of recycled foam. Appl. Acoust. 2012, 73, 604–609. [Google Scholar]
- Arenas, J.P.; Rebolledo, J.; del Rey, R.; Alba, J. Sound absorption properties of unbleached cellulose loose-fill insulation material. Bioresources 2014, 9, 6227–6240. [Google Scholar] [CrossRef]
- da Silva, C.C.B.; Terashima, F.J.H.; Barbieri, N.; de Lima, K.F. Sound absorption coefficient assessment of sisal, coconut husk and sugar cane fibers for low frequencies based on three different methods. Appl. Acoust. 2019, 156, 92–100. [Google Scholar] [CrossRef]
- Sair, S.; Mansouri, S.; Tanane, O.; Abboud, Y.; El Bouari, A. Alfa fiber-polyurethane composite as a thermal and acoustic insulation material for building applications. SN Appl. Sci. 2019, 1, 667. [Google Scholar] [CrossRef]
- Bousshine, S.; Boubel, A.; Garoum, M.; Ammar, A. Sound absorption measurements of bio-sourced esparto-fibres: Effect of the compression. Int. J. Innov. Technol. Explor. Eng. 2019, 9, 1827–1832. [Google Scholar]
- Maghchiche, A.; Haouam, A.; Immirzi, B. Extraction and characterization of Algerian alfa grass short fibers (Stipa Tenacissima). Chem. Chem. Technol. 2013, 7, 339–344. [Google Scholar] [CrossRef]
- Nadji, H.; Diouf, P.N.; Benaboura, A.; Bedard, Y.; Riedl, B.; Stevanovic, T. Comparative study of lignins isolated from Alfa grass (Stipa tenacissima L.). Biores Technol. 2009, 100, 3585–3592. [Google Scholar] [CrossRef]
- Belkhir, S.; Koubaa, A.; Khadhri, A.; Ksontini, M.; Smiti, S. Variations in the morphological characteristics of Stipa tenacissima fiber: The case of Tunisia. Ind. Crops Prod. 2012, 37, 200–206. [Google Scholar] [CrossRef]
- ISO 10534-2. Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method; International Organization for Standardization: Geneve, Switzerland, 1998. [Google Scholar]
- Ingard, K.U.; Dear, T.A. Measurement of acoustic flow resistance. J. Sound Vib. 1985, 403, 567–572. [Google Scholar] [CrossRef]
- ISO 9053. Acoustics—Determination of Airflow Resistance—Part 1: Static Airflow Method; International Organization for Standardization: Geneve, Switzerland, 2018. [Google Scholar]
- del Rey, R.; Alba, J.; Arenas, J.P.; Ramis, J. Evaluation of two alternative procedures for measuring airflow resistance of sound absorbing materials. Arch. Acoust. 2013, 38, 547–554. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comp. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optimiz. 1998, 9, 112–147. [Google Scholar] [CrossRef]


| Esparto | Thickness (mm) | Density (kg/m3) | Airflow Resistivity (kPa s/m2) |
|---|---|---|---|
| Type 1 | 30.0 ± 0.3 | 167.6 ± 2.7 | 5.40 ± 0.64 |
| 50.0 ± 0.3 | 173.0 ± 2.7 | ||
| 71.0 ± 0.3 | 159.1 ± 2.5 | ||
| 90.0 ± 0.3 | 156.4 ± 2.5 | ||
| Type 2 | 30.7 ± 0.5 | 121.8 ± 2.1 | 1.49 ± 0.28 |
| 50.7 ± 1.2 | 126.4 ± 2.7 | ||
| 70.5 ± 1.5 | 125.2 ± 3.7 | ||
| 90.2 ± 0.8 | 124.9 ± 1.5 | ||
| Type 3 | 29.8 ± 0.4 | 101.2 ± 1.6 | 2.98 ± 0.34 |
| 48.8 ± 0.9 | 103.5 ± 2.3 | ||
| 69.8 ± 0.4 | 101.9 ± 1.3 | ||
| 89.8 ± 1.0 | 101.6 ± 1.7 |
| Esparto | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ε |
|---|---|---|---|---|---|---|---|---|---|
| Type 1 | 0.1585 | 1.2083 | 0.0190 | 0.6871 | 0.1504 | 0.5079 | 0.0918 | 1.0001 | 0.0395 |
| Type 2 | 0.3443 | 0.6185 | 0.0781 | 0.7815 | 0.1320 | 0.6378 | 0.6378 | 0.1322 | 0.0300 |
| Type 3 | 0.1725 | 1.2473 | 0.0217 | 0.8553 | 0.1535 | 0.4185 | 0.0930 | 1.0452 | 0.0383 |
| Delany and Bazley | 0.0571 | 0.7540 | 0.0870 | 0.7320 | 0.1890 | 0.5950 | 0.0978 | 0.7000 | --- |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arenas, J.P.; del Rey, R.; Alba, J.; Oltra, R. Sound-Absorption Properties of Materials Made of Esparto Grass Fibers. Sustainability 2020, 12, 5533. https://doi.org/10.3390/su12145533
Arenas JP, del Rey R, Alba J, Oltra R. Sound-Absorption Properties of Materials Made of Esparto Grass Fibers. Sustainability. 2020; 12(14):5533. https://doi.org/10.3390/su12145533
Chicago/Turabian StyleArenas, Jorge P., Romina del Rey, Jesús Alba, and Roberto Oltra. 2020. "Sound-Absorption Properties of Materials Made of Esparto Grass Fibers" Sustainability 12, no. 14: 5533. https://doi.org/10.3390/su12145533
APA StyleArenas, J. P., del Rey, R., Alba, J., & Oltra, R. (2020). Sound-Absorption Properties of Materials Made of Esparto Grass Fibers. Sustainability, 12(14), 5533. https://doi.org/10.3390/su12145533






