1. Introduction
Optimal Power Flow (OPF) is one of the significant tools used over decades to date in energy management systems for reliable operation and proper planning of modern power systems. This problem is a non-linear, non-convex, and multi-dimensional optimization problem with control variables such as voltage magnitude and real power generation as continuous variables, and transformer tap ratios and shunt capacitor as discrete variables [
1,
2,
3,
4]. These variables are adjusted to operate the system efficiently and economically for continuous change in the load demand. Thus, the aim of OPF is to optimize the certain selective objectives of the system such as fuel cost, real and reactive power loss, voltage stability enhancement, and environmental emissions, ensuring the equality and inequality constraints [
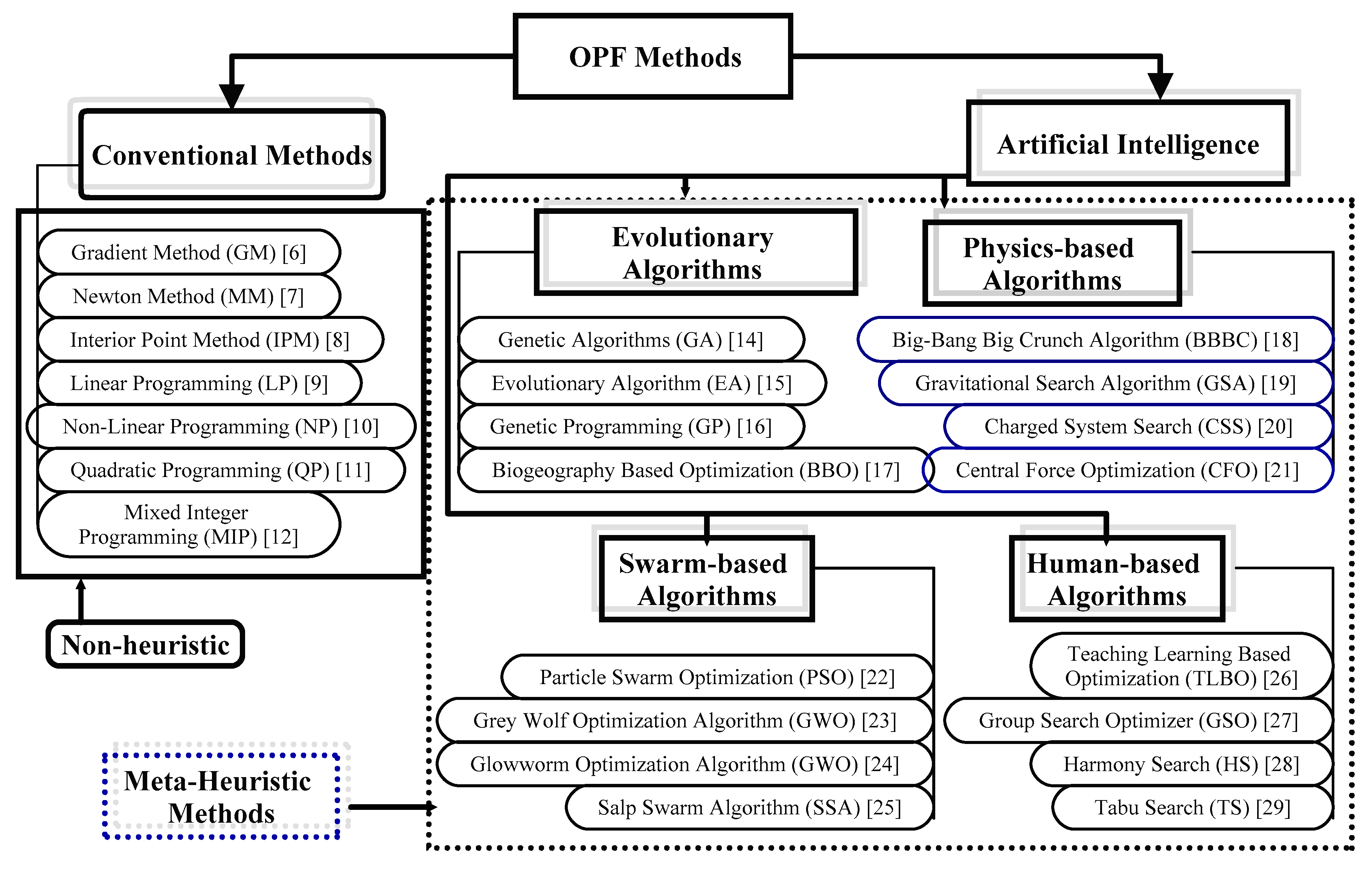
5]. Numerous classical and intelligence-based methods were used to solve the OPF problem and are portrayed in
Figure 1. Through rigorous analysis, it is observed that the conventional mathematical methods such as the gradient-based approach, the Newton method, the interior point method, and linear, non-linear, quadratic, and mixed integer programming have been successfully used to solve OPF problem [
6,
7,
8,
9,
10,
11,
12]. These methods give the optimal results but fail at local minima, if the initial point is not assumed close to the solution. In addition, the quality of solutions highly degrades as the number of control variables increases. Further, the complexity of the problem is very high because of the number of non-linear constraints of the system [
5,
13]. To cater this problem, researchers for the last few decades use non-gradient, non-deterministic, and highly flexible meta-heuristic-based techniques to obtain the solution for OPF without trapping into local minima due to the advancement in computer technologies [
1].
To date, the various meta-heuristic methods that have been used to solve OPF are portrayed in [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29]. Generally, the meta-heuristic approaches are categorized into four major classes:
Evolutionary, swarm intelligence, physics and human-based algorithms [
30]: The evolutionary algorithms (EA) are based on evolutionary principles that exist in nature such as selection, cross-over and mutation. The most well-known methods are the Genetic Algorithm (GA), evolution strategy, Differential Evolution (DE) and biogeography-based optimizations. All of these techniques are heuristic and initiated with random solutions, and the solution is updated by evaluating the fitness functions. On the other hand, the Swarm Intelligence (SI) techniques mimic creatures in nature and are very popular meta-heuristic optimization methods. SI-based methods include particle swarm, artificial bee colony [
31], firefly algorithm [
32], chaotic krill heard [
33], backtracking search algorithm [
34], efficient evolutionary algorithm [
35], faster evolutionary algorithm [
36], group search algorithm [
37], differential evolution algorithm [
38], multi-hive bee foraging algorithm [
39], etc. Moreover, the affine arithmetic method [
40], the knowledge-based framework human learning method [
41], and linear compression methods [
42] were used to solve optimal power flow problems. These methods are self-organizing systems that can operate based on mathematical equations developed using a set of rules depicting the behavior of a swarm to give the stable solution after convergence. On the flipside, the physics-based intelligence approaches imitate the physical laws that govern the evolution of the universe—the law of gravity, the electromagnetism law, the force of attraction, and so on. The various algorithms based on physics include the Gravitational Search Algorithm (GSA), Central Force Optimization (CFO), Big Bang-Big Crunch, galaxy-based, and magnetic optimization, etc.; these techniques are reviewed and presented in [
43]. The human-based optimization techniques are developed based on human traits and their invention; some of these methods are teaching learning, group search, harmony, and tabu search used to minimize real world complex problems. The aforementioned various intelligence-based methods are applied to many engineering problems and give effective solutions to some problems, but fail for other kinds of problems.
Regardless of the different methods, the common features that exist are the exploration and exploitation characteristics. In the former phase, the algorithm should utilize its randomized parameters as much as possible and find the feature space through its local search ability in the search regions. In the later phase of exploitation, the algorithm tries to find a global optimal solution by intensifying the search process in a local region instead of an entire region of search space. A well-optimized technique should posses the following characteristics for avoiding the possibility of convergence to local optima [
22,
44,
45]. In relation to the previously published work, it is inferred that most of the study focused on single objective optimization, and in particular, the minimization of either power loss or generating cost. However, recently the increase in the environmental pollutant gases such as
emissions during power generation and its serious impact on the environment has gained more attention. The US clean air act amendments of1990 directed utility companies to produce energy in keeping the pollution at the minimum level in association with other power system constraints [
45]. In view of this, different methods such as the hybrid dragonfly and particle swarm optimization algorithm, penalty function methods and the improved strength pare to evolutionary algorithm have been implemented to curtail this harmful emission, like implementing Carbon Capture and Sequestration (CCS) technology [
15,
46,
47].
Furthermore, real world design and optimization problems always involve more than one conflicting objectives. Thus, Multi-Objective (MO) optimization has earned huge attention among researchers [
26]. To handle such opponent objectives simultaneously, AI techniques have transferred into multi-objective optimization by modifying it with the aid of various classical methods. To solve this MO function, numerous methods have been presented in [
48,
49,
50], such as the penalty function method, weighted sum method, ϵ-constant method, non-dominated sorting genetic algorithm-based approach, strength Pareto evolutionary algorithm, etc. Despite of having a variety of intelligence algorithms, none of these methods can assure the consistency of an optimal solution for solving all of the objectives. This incentivizes the researcher to develop many new nature-inspired algorithms day by day, which possess the traits of exploration and exploitation that can solve all the real-time optimization problems without reaching divergence or local convergence [
15,
51]. In this paper, a maiden attempt has been made to apply a Harris Hawks-based Optimization (HHO) approach for OPF. HHO is a nature-inspired optimization technique proposed by Heidari [
49] that competes with other optimization methods portrayed in the literature with its cooperative behaviors to attack the hunting prey. Moreover, the hunting and escaping strategies are analyzed through mathematical calculations to reach a global solution with effective computational time. The main contributions of this work areas follows:
To optimize the fuel cost, power loss, and emission cost of the system by solving single- and multi-objective OPFs using the HHO algorithm;
To handle the equality and inequality constraints such as voltage magnitude, transformer tap ratio, and real and reactive power constraints of the generator while optimizing the various objectives;
To optimally place the Distributed Generation (DG) based on a real power sensitivity index for minimizing the loss and emission;
To statistically compare the results obtained with other well-known nature-inspired methods such as SSA, WOA, MF, and GWO.
The remainder of the paper is organized as follows:
Section 2 deals with the OPF problem formulation, which contains single and multi-objective problem formations mathematically, including equality and inequality constraints.
Section 3 presents an extended introduction of the proposed intelligence-based HHO algorithms with numerical presentation and with a dynamic levy flight strategy. The comparison of numerical results and discussion among well-known other nature-inspired methods of optimization and proposed approaches are portrayed in
Section 4.
Section 5 describes the comparative analysis of the proposed method with the literature work. Finally,
Section 6 presents the conclusion and the future scope of the work.
3. Application of HHO to the OPF Problem
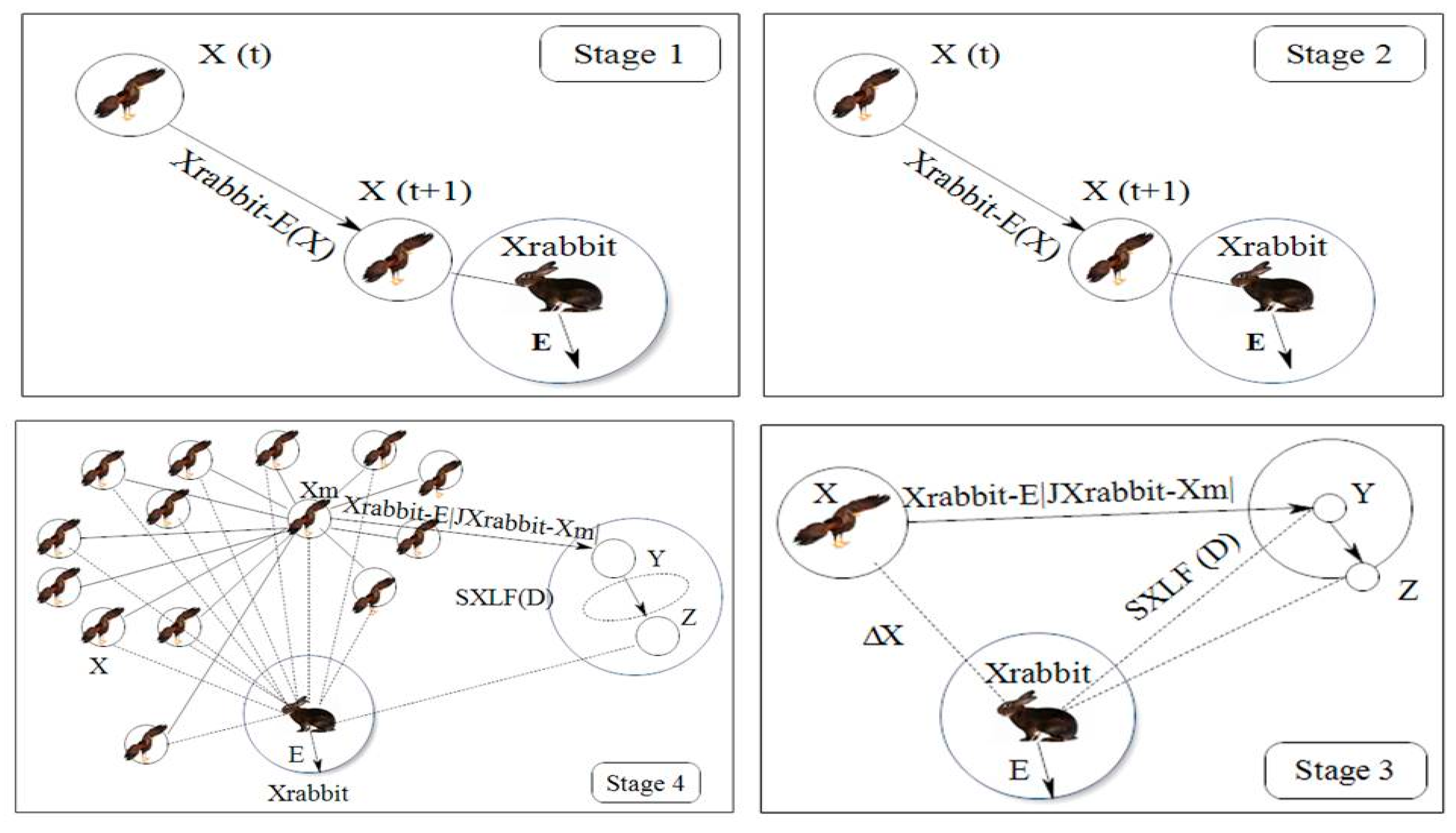
The Harris hawk is one of the most intelligent and distinguished predator birds in nature that demonstrates distinctive collective chasing capabilities in tracing, encircling, flushing out, and capturing the potential animal (rabbit) in a group for its food. Here, the initial population is assumed as a group of hawks that try to chase the targeted rabbit (solution of the optimization problem) from different directions by using seven killing strategies or a surprise pounce. Initially, the leader hawk tries to attack the prey; if it fails to grab the animal because of the dynamic nature and escaping behavior of the prey, the switching tactics are followed, so that the other party members (hawks in the group) will hit the escaped prey until seized. The main advantage of this collaborative tactic is that the birds can pursue the pointed rabbit by means of puzzling and exhaustion of the escaping prey. In HHO, the candidate solutions are the Harris Hawks and the optimal/global solution is the intended prey. Thus, HHO exhibits the exploratory and exploitative phases and are explained in
Figure 2 and below [
49].
Step1—Exploration phase: Harris hawks perch randomly and wait in some locations, observe and monitor to attack the prey. The leader hawks perch based on position of family members and prey. This is described in the form of a mathematical equation for changing in distance (q) between the hawks and prey as follows:
where X(t+1) is the updating vector of the Hawk’s position atthei+1 iteration, X
r(t) is the position of the prey, X(t)is the position vector of the hawks at the ith iteration, r
1, r
2, r
3, r
4, and q are random numbers in the range of (0,1), UB and LB are the Upper and Lower Bounds of variables, and X
rand (t) and X
m(t)are the initial population assumed randomly.
The average position of each hawk is defined as:
where X
i(t) is the current position of hawks, X
i+1(t) is the updating position vector, and the total number of hawks is represented by N.
Step2: During the exploration phase, the hawks try to find and hit the prey. Due to this there is considerable change in the energy (E) of the prey and it is given by:
where T is the maximum iteration count, t is the current iteration, and the initial energy (
randomly changes between (−1 to 1) at every iteration. E ≥ 1 indicates the leaping behavior of the prey and the hawks search for prey in other location, E < 1 indicates that the prey becomes exhausted and the hawk intensifies its attack by a surprise pounce that makes the solution to the exploitation phase.
Step3—Exploitation phase: At this stage, the switching tactics follow to attack the prey. The prey always tends to escape from hawks, and the chance of escaping of the prey is illustrated as r. When r < 0.5 the prey is successfully escaping, and on the flipside when r ≥ 0.5 the chance of escaping is unsuccessful. At any rate, the hawks will attack the prey and will be either successful or not through a soft or hard siege. If the prey escaped when (r ≥ 0.5) and |E| < 0.5 then a hard siege takes place. On the other hand, if (r ≥ 0.5) and |E| ≥ 0.5, then a soft siege occurs. Here, r is the chance of the prey escaping. This can be modeled in mathematical form as follows.
Step4—Soft siege: Here, the rabbit possesses energy and tries to escape by jumping and the hawks surround it softly, which is modeled as
The random jump of the rabbit is given by J = 2(1 − r5),where ∆X(t) is the difference between the position vectors of consecutive iteration and r5 is the random number that lies in the range of (0,1).
Step5—Hard siege: In this case, the prey is fully exhausted and the hawks encircle it hardly and perform the surprise pounce. The positions are updated using (28) as given by
Step6—Soft siege with continuous rapid dives:
The rabbit still possesses the energy and tries to escape, and this is represented as |E| ≥ 0.5 and r < 0.5, and a further soft siege is required before the surprise pounce by the hawks. This step is more intelligent than the previous case. Here the Levy flight (LF) concept was introduced for progressive rapid dives of hawks to perform a soft siege and the next move of the prey is evaluated by the hawks using the following equation:
Despite several attempts, the hawks compare each of their movements with the previous dive, to determine if it was a good dive or not. If the dive is not reasonable, it performs an irregular, abrupt and rapid dive for approaching the prey animal. We assume that the hawks dive based on LF-based patterns using the rule given as follows:
where D is the dimension of the problem, S is the random vector of size 1×D, and the LF function is defined as:
LF = the levy flight function which can be demonstrated as follows:
Where Y and Z are defined as
where u and v are accidental values lying in the range (0,1) and β is an assumed constant equal to 1.5.
Hence, the final updating rule of the hawk’s position in the soft siege phase is:
where Y and Z are calculated using (32) and (33).
Step7—Hard siege with continuous rapid dives:
In this case, |E| <0.5 and r < 0.5, the prey animal loses its energy and becomes exhausted. A hard siege is next used by the hawks and it decreases the distance of their location from the prey for killing the prey. The updating rule for this case is given by:
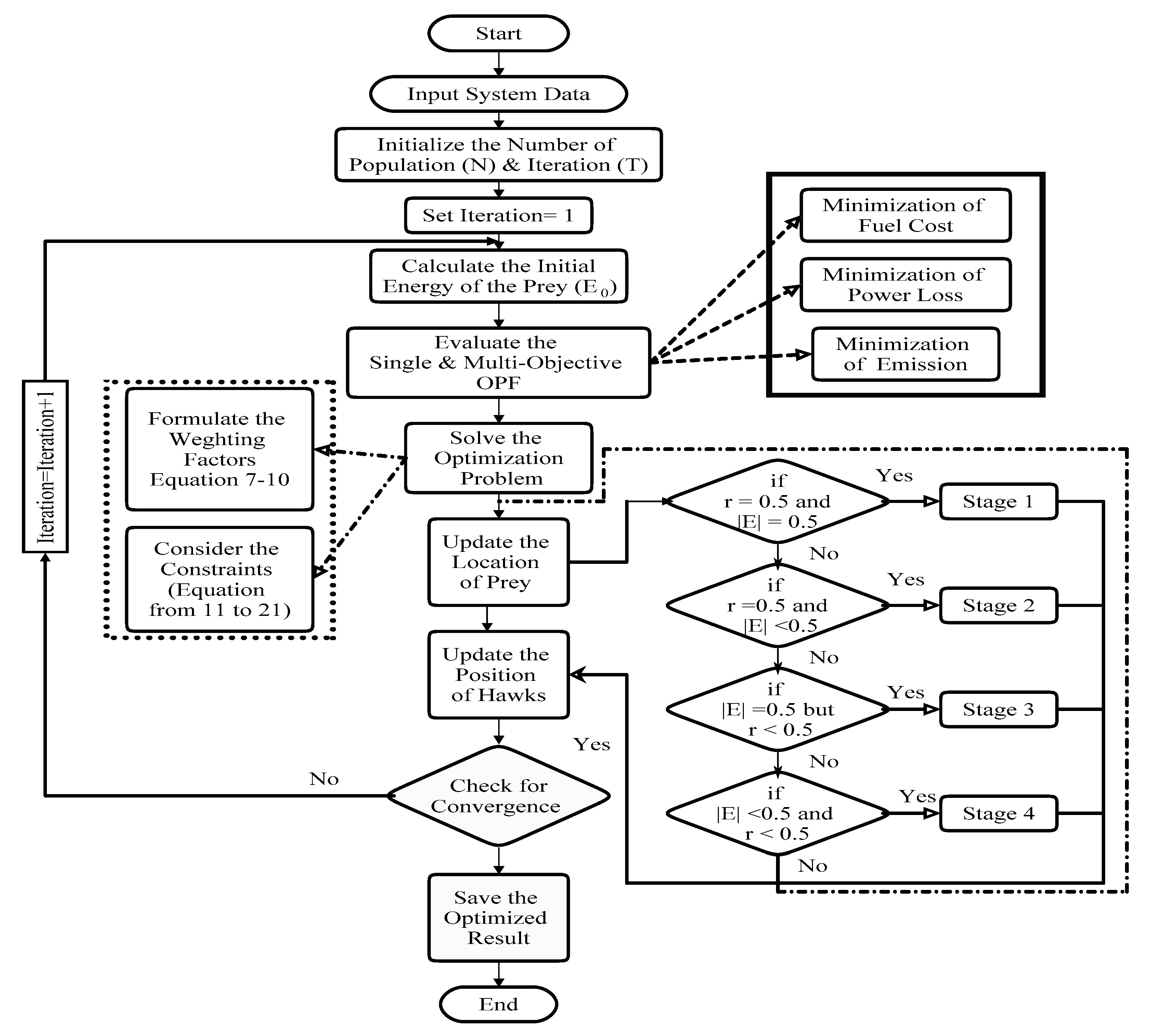
The Y or Z in (38) and (39) are the next locations for the new iteration until the prey is killed, i.e., obtaining the optimal solution. The proposed method is presented in the form of pseudo-code for simplicity and explained as a flowchart, detailing the application of HHO in
Figure 3.
Pseudo-code of the proposed HHO method
Initialize the number of hawks (N) and
iteration (T) randomly
Xi (i = 1, 2, . . . , N)
while (stopping condition is reached) do
Evaluate the fitness value of hawks
Now, set Xrabbit as the best location of rabbit
for (several hawk (Xi)) do
update Energy(E) and its jumping strength (J)
Initial Energy (E0) = 2rand() − 1, J = 2(1 − rand())
Update E using (10)
if (|E| ≥ 1) then
Exploration phase
if (|E| < 1) then
if (r ≥ 0.5 and |E| ≥ 0.5) then
Exploitation phase
Soft siege
else if (r ≥ 0.5 and |E| < 0.5) then
Hard siege
else if (r < 0.5 and |E| ≥ 0.5) then
Soft siege
else if (r < 0.5 and |E| < 0.5) then
Hard siege
Return best location of Xrabbit (global optimal solution)
Scope of limitation of Proposed Method
The proposed work aims to solve the single and multi-objective optimal power flow to minimize the following objective functions such as fuel cost, loss, and emissions. Finally, a comprehensive analysis was made by the placement of DG into the system to study its effect on the aforementioned optimizing parameters for sustainable power generation.
4. Results and Discussion
In order to validate the feasibility and effectiveness of the proposed method, the algorithm was tested on an IEEE 30-bus system. The power system model consists of six generator buses at buses 1, 2, 3, 8, 11, and 13, four transformers in lines 6–9, 6–10, 4–12, and 28–27, and nine shunt compensations at buses 10, 12, 15, 17, 20, 21, 23, 24, and 29. The total real and reactive power demand are2.834 and 1.262 p.u, respectively, at the base MVA of 100. The data for the simulations are given in [
54]. In addition, the data for the emission coefficients of each generator are represented in
Table 1. The intended method was coded using MATLAB software in aPC with the following characteristics: Intel core i5, CPU 2.60 GHz, RAM 4GB, anda64-bit operating system. The feasibility of the method was validated for selective multi-objective of the system to minimize the fuel cost, power losses and environmental emissions by adjusting the control variables of the system. The proposed and other various nature-inspired algorithms were run for a maximum of 200 iterations and the comparative analysis was carried out for each case of selected objectives as detailed in the forthcoming subsections. The optimal settings of the controlling parameters for the proposed method have also been detailed in
Table 2.
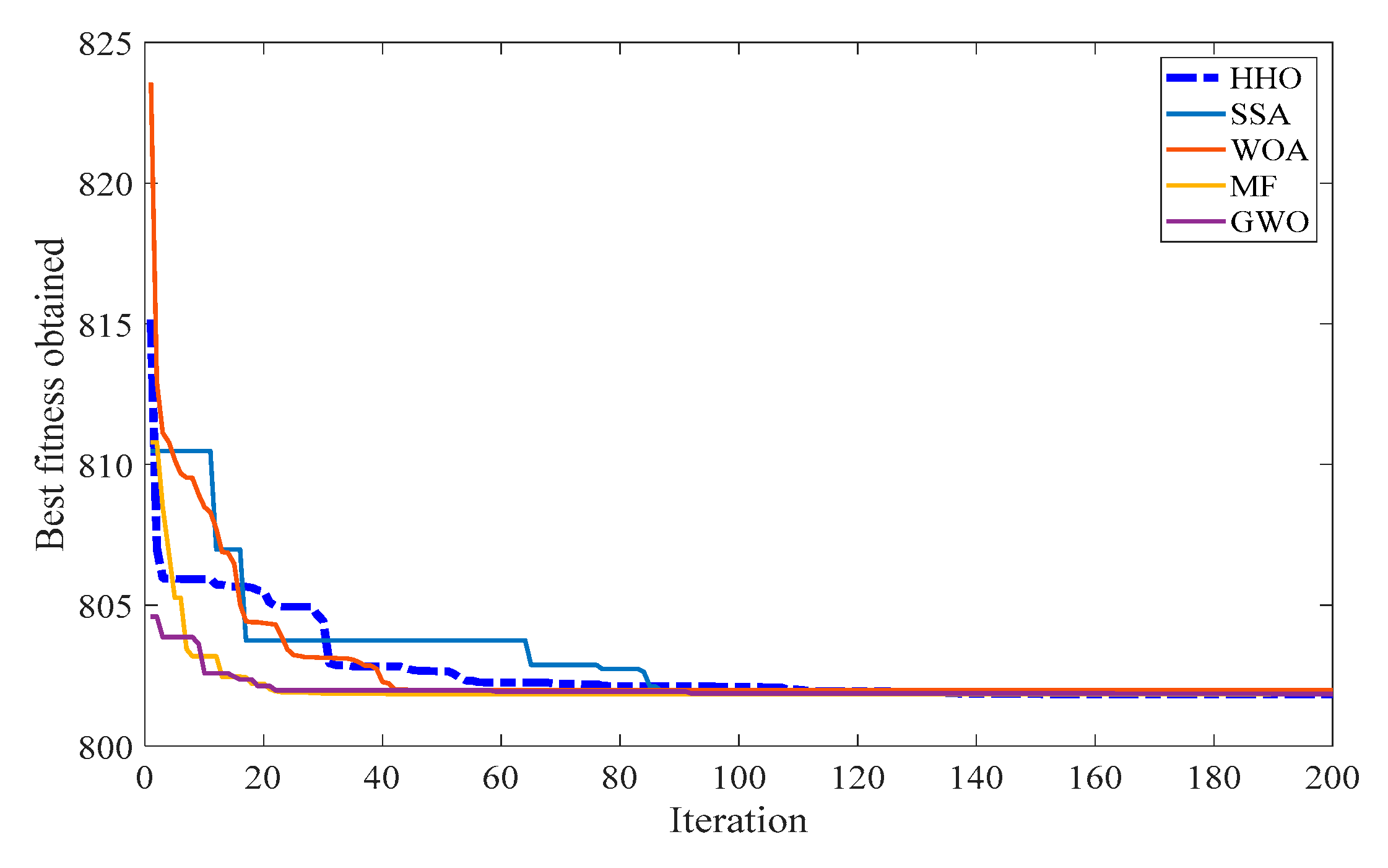
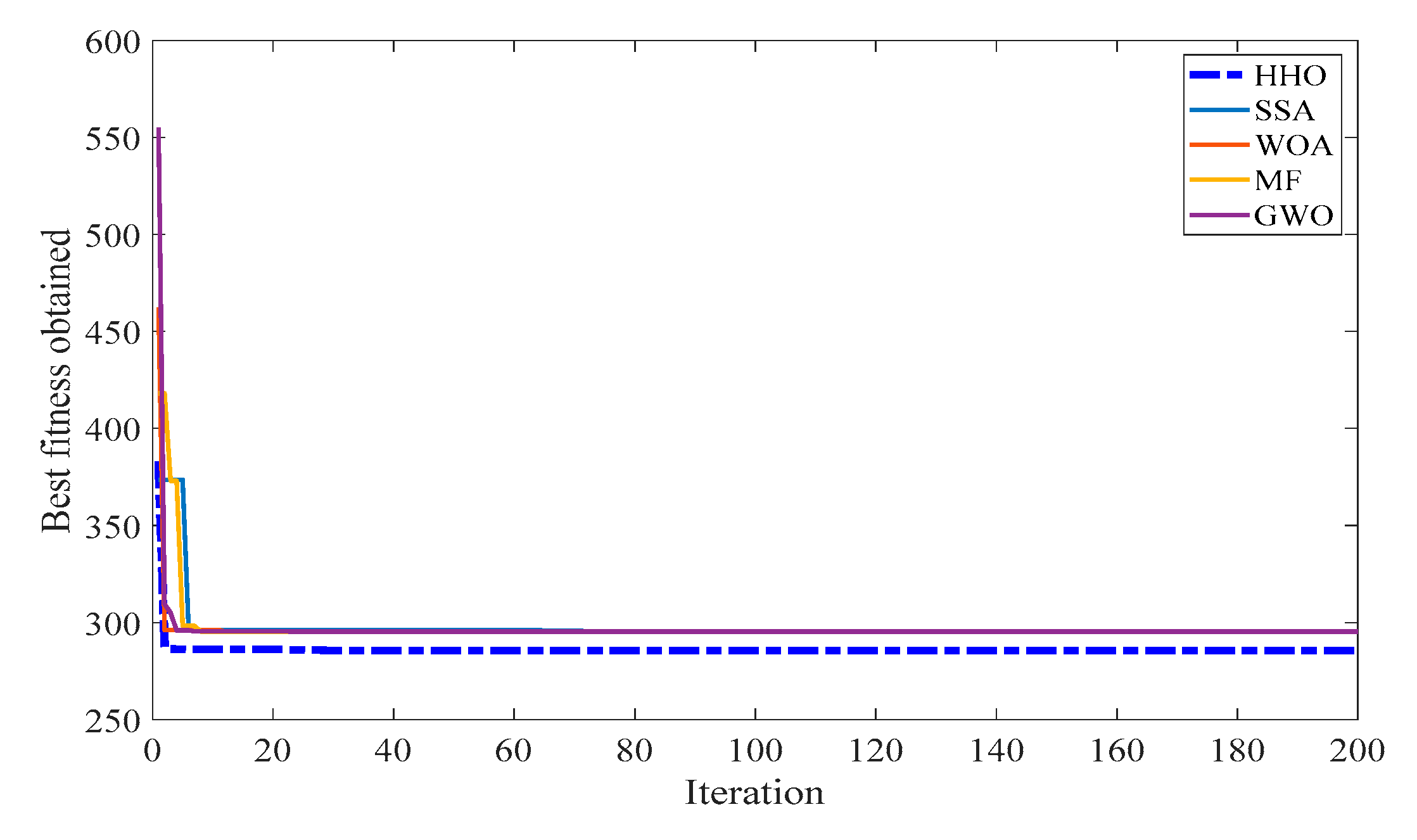
Case 1—Quadratic Total Fuel Cost Minimization
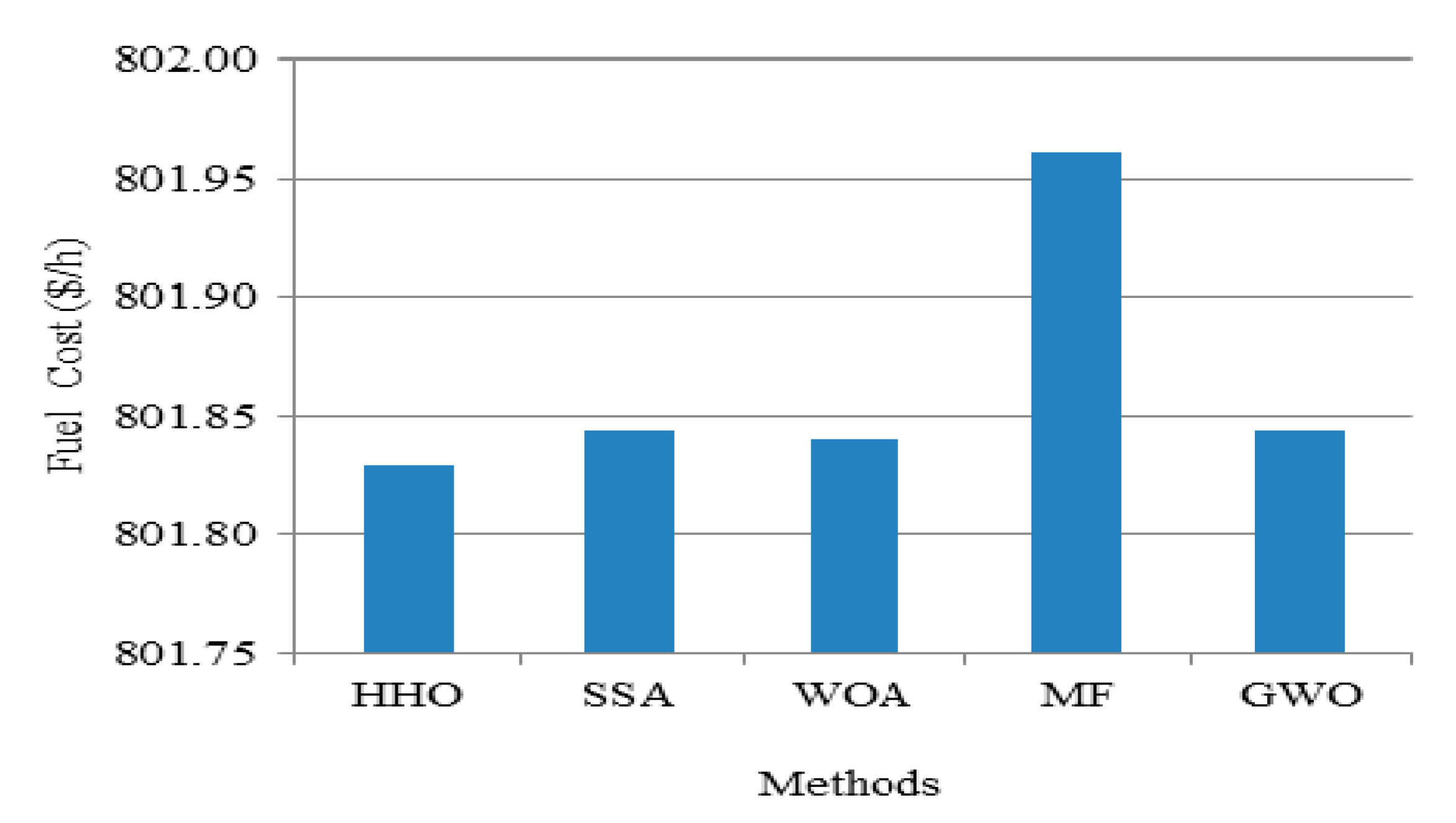
The quadratic fuel cost characteristics of a generator were chosen as the single-objective function to be minimized by the proposed HHO algorithm as defined in (1). The obtained optimal value of control variables by optimizing the total fuel cost (TFC) of the system is illustrated in
Table 3. To achieve this, the proposed method undergoes several stages of exploration and exploitation by dividing the search region in the space. Initially, the generators are initialized randomly by exploring the search regions and they give the various local solutions of TFC as
$/h 842.131,
$/h 835.204,
$/h 828.532,
$/h 814.891, and so on for different iterations. Then, the hawks undergo the soft and hard siege stages to find their global best by exploiting the solution in the search region to reach the global minima value of 801.829 as TFC. Hence, the obtained global solution is recorded as the best minimal value of TFC after 50 individual runs by the proposed method and compared with other nature-inspired methods. It is seen that the TFC is decreased to 801.829
$/h by the proffered method and its comparison with other intelligence algorithms is illustrated in
Table 3. Thus, the HHO method optimized to give superior results for the selected single objective. In addition to the control parameters and TFC, the other computational parameters, such as real power loss, environmental emissions, iteration, and convergence time, are promising but stuck at a certain time and reported in
Table 3. Additionally, the obtained fuel cost for various methods with its convergence characteristics is portrayed in
Figure 4 and
Figure 5.
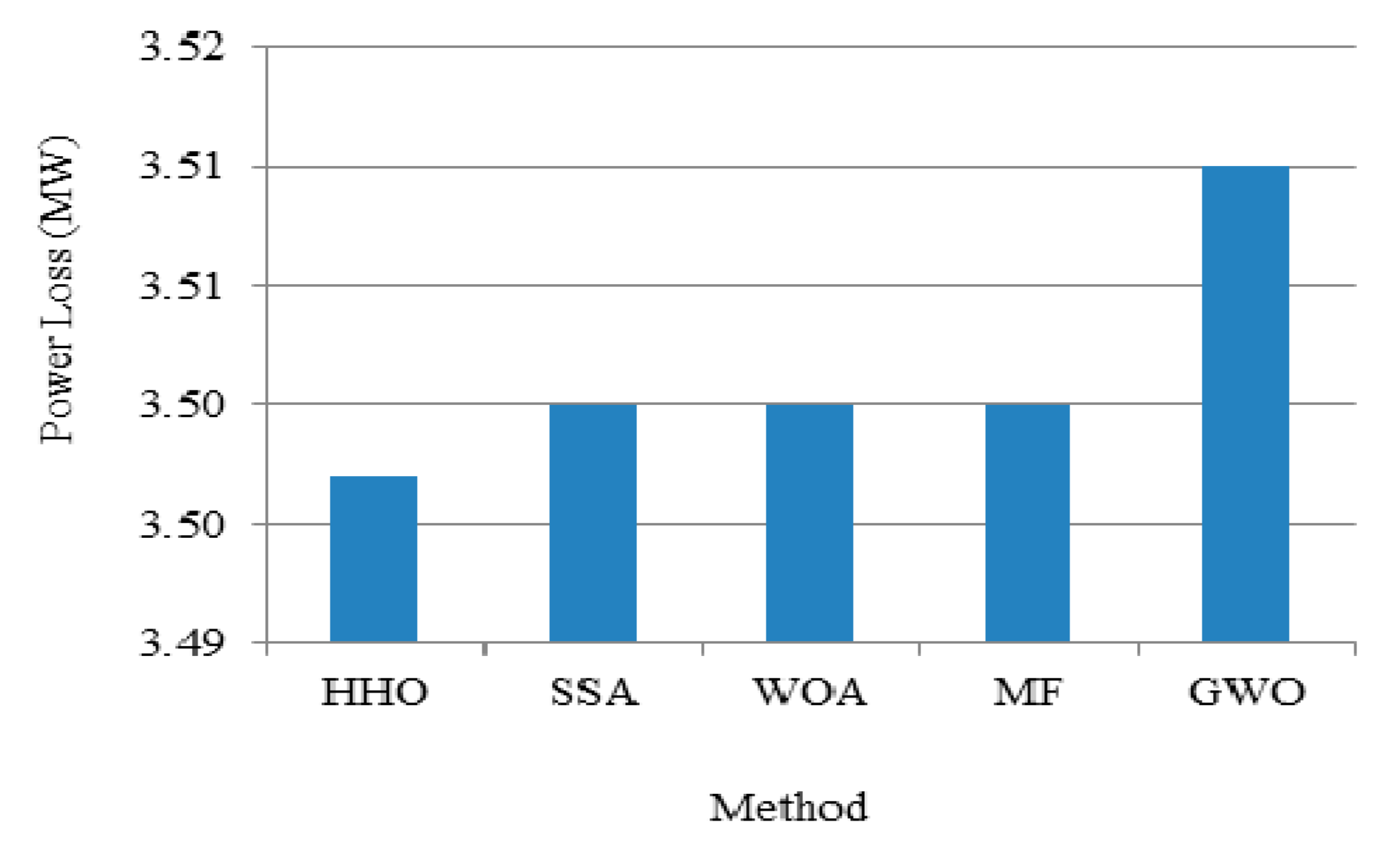
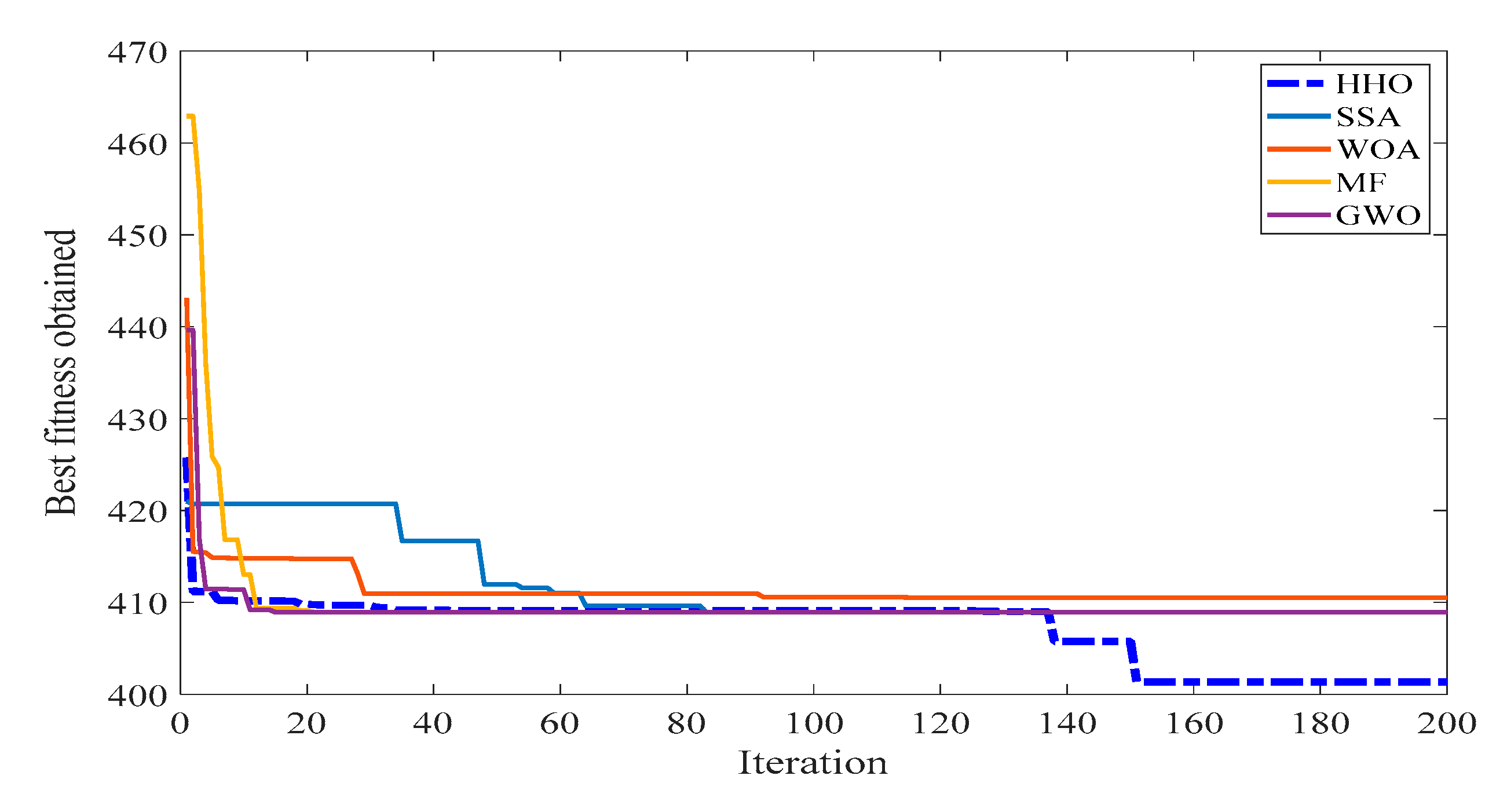
Case 2—Active Power Loss Minimization
To validate the effectiveness of the proposed method of OPF, the active power loss (APL) is regarded as a second single-objective function to be minimized and its formulation is represented in (2). The losses of the system can be minimized by optimally satisfying the load demand and the constraints of the system. The simulation results under this case are compared with other recent evolutionary meta-heuristic methods and are given in
Table 4. It can be seen that the APL in the IEEE 30-bus test system has declined to 3.49 MW and the performance of the proposed method is infinitesimally improved in comparison to other recent literatures such as the SSA, WOA, MF, and GWO presented above. In addition, the proffered method outperforms relative to the other methods to give a minimum TFC of 966.12
$/h. However, the performance is found similar to literature works for other computational parameters like emissions and number of iterations. In addition, the presented method takes a smaller amount of time for convergence.
Figure 6 and
Figure 7 portray the comparison of power loss minimization by various methods and its fitness curve, respectively. The results demonstrate that the proposed method attains the optimal solution with a minimum number of iterations and requires a shorter computation time because of its local and global search ability.
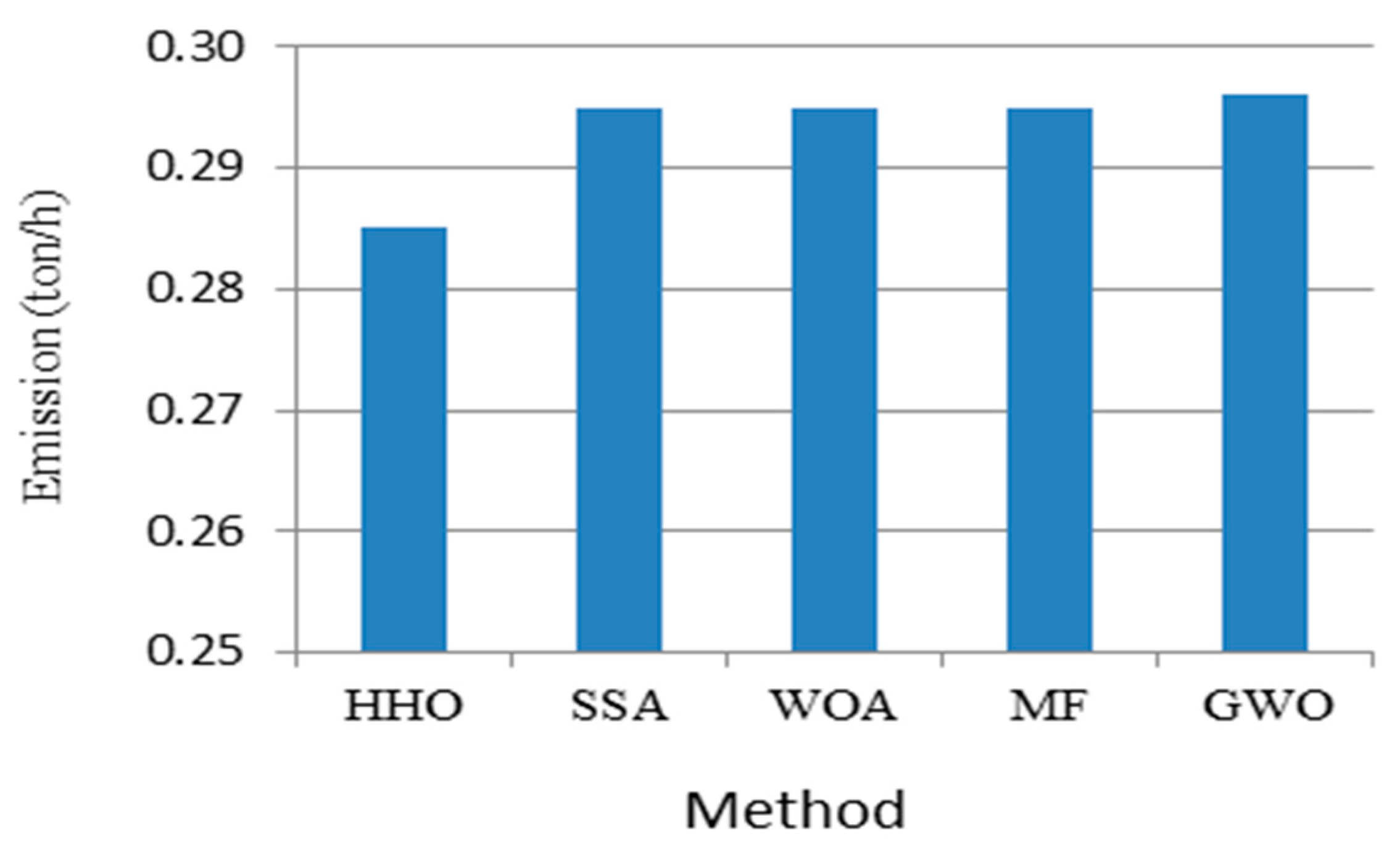
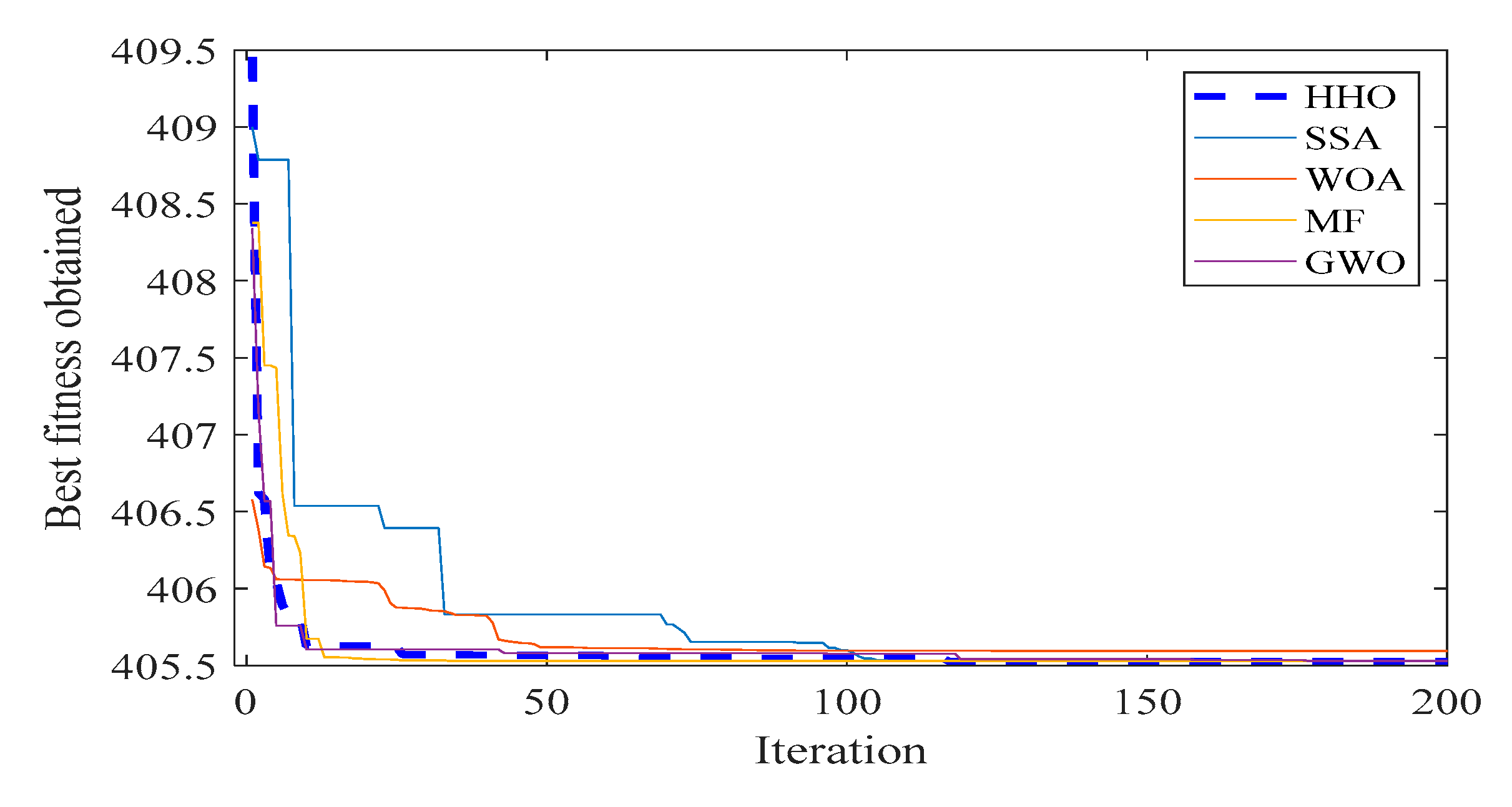
Case 3—Total Emission Cost Minimization
In this case, the total emission cost (TEC) is regarded as the third single-objective function to be minimized and its formulation is given in (3). The attained optimal values of control variables for minimization of TEC by the propounded method and the other techniques are illustrated in
Table 5. The result based on the least emissions reveals that the proposed method outperforms compared to other presented literature work to give significant improvements and the TEC is reduced to 0.285 (ton/h).
Moreover, the computational parameters, such as losses and convergence time, are more enhanced than other evolutionary methods. The fuel cost is found to be similar to other techniques, but the proposed method takes a minimum number of iterations for the convergence of a solution. This inference is presented as
Figure 8 and
Figure 9 for better understanding, showing that the performance in reaching a global optimal solution by the hawks optimizer is better than other nature-inspired techniques.
Selection of Weightsfor Solving Multi-ObjectiveOPF Functions
In general, the multi-objective optimization can be solved with or without the preferences of specific objectives. However, the proposed work chooses the no preference weighted sum method. In this approach, the optimization problem aims to optimize all of the objectives with equal importance without giving prime importance to any of the objectives to be minimized. However, in order to study the assumed effects on weight based on the priority given to specific objectives, this work solves the two objectives (cost and loss) and three objective (cost, loss, and emission) using the proposed HHO method and its corresponding results are represented in
Table 6 and
Table 7. It is inferred that the solution obtained has no significant compromising results for different combinations of weight values assumed, and therefore an equal weight is considered for all of the objective functions. Additionally, in present days owing to the growth of renewable energy sources, the economy to improve the assets of generation, transmission, and distribution systems considering the environmental factors leads this research to choose the equal preference. On the flipside, solving three objective functions as multi-objective, the change in environmental conditions due to pollution is considered of prime importance with weight values of 0.34 than cost and losses for sustainable energy development.
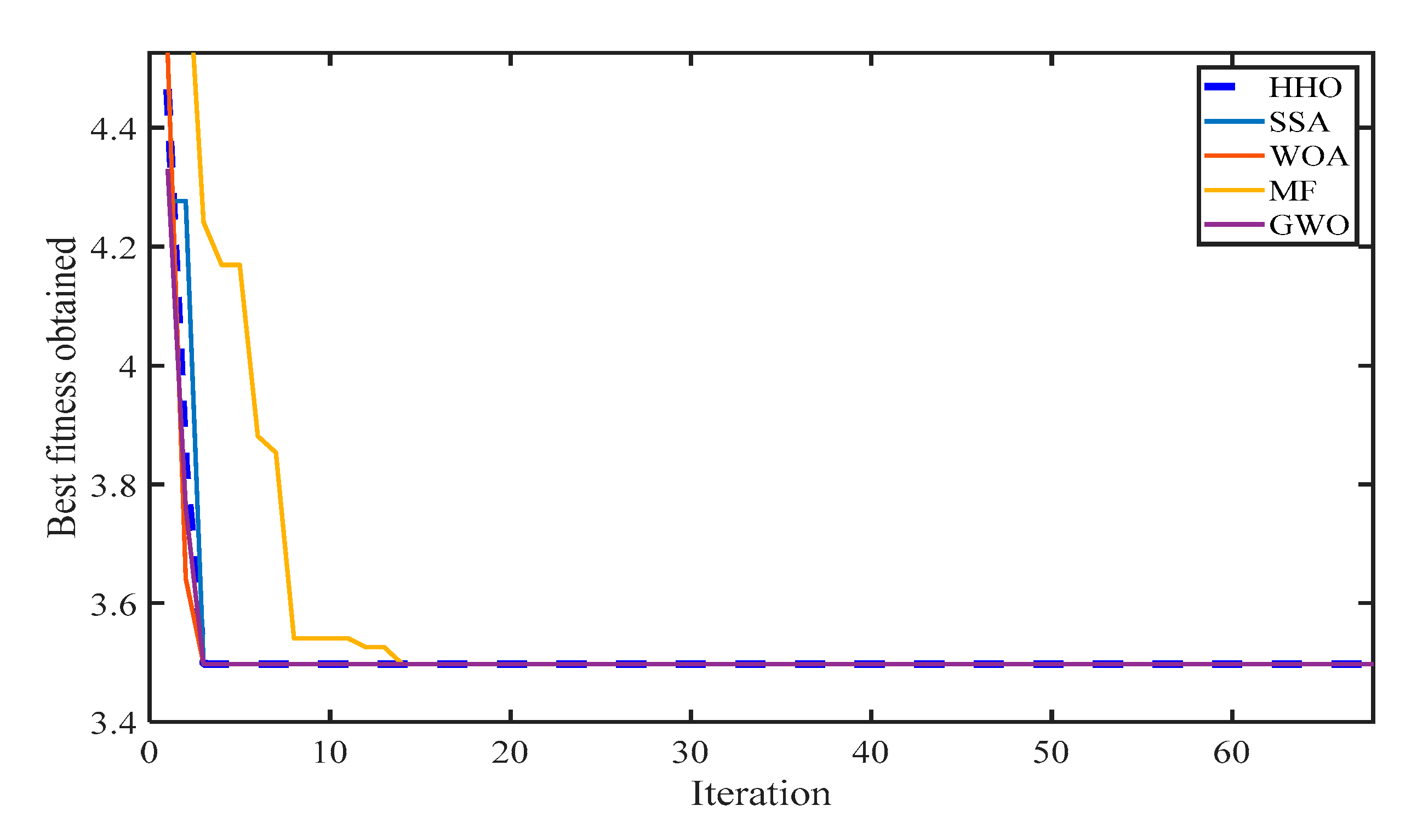
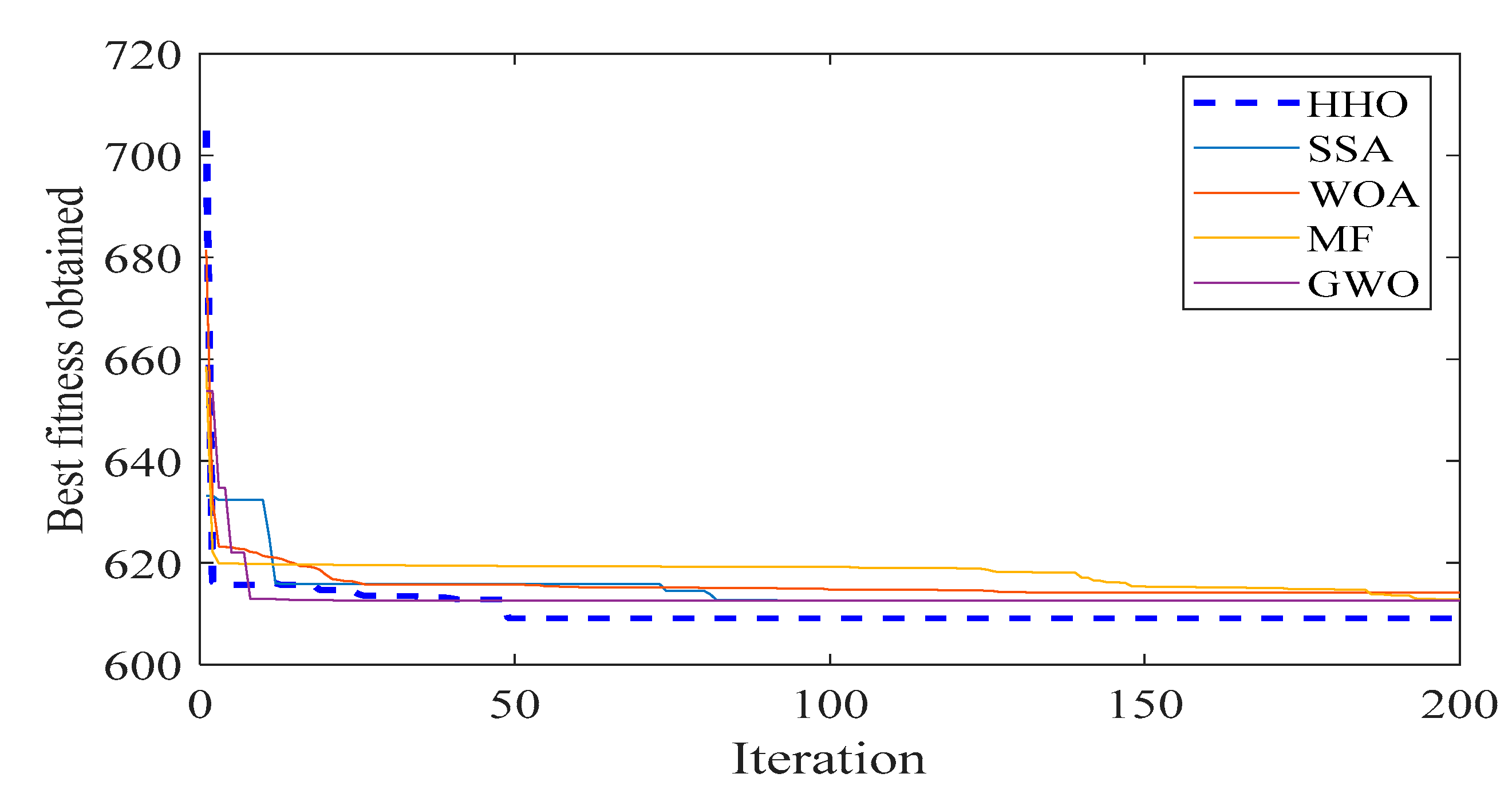
Case 4—TFC and APL minimization
In this case, two prime contradictory objectives such as fuel cost and power loss were optimized simultaneously using the weighted sum method by the proposed HHO algorithm in Equation (7). The no preference weighted method has been chosen by assuming the sum of the weight values to be one (i.e., w1 = w2 = 0.5).
Table 8 shows the best optimal values of the control variables obtained by minimizing the TFC and APL. Additionally, the obtained results by the proffered method are compared with the literature work, such as SSA, WOA, MF, and GWO. It is seen that the HHO outperforms these to give superior results with a TFC of 802.01 (S/h) and an APL of 9.04 (MW). However, the value of TFC is minimum using WOA, but the APL is not reduced as compared to HHO. On the other hand, MF and GWO give similar results to optimize the selective fitness function but the emission cost increases relative to other techniques.
Figure 10 demonstrates the convergence characteristics finding the optimal value of TFC and APL by HHO and various optimization methods. Overall, the performance of HHO for solving multi-objective OPF problem is decent compared to other presented techniques. Additionally, the obtained results of other computational parameters during optimization are promising.
Case 5—TFC and TEC Minimization
In this study, the fitness function to be optimized simultaneously in Equation (8) is fuel cost and environmental emissions; by adapting the control variables the objective function can be minimized by optimally satisfying the equality and inequality constraints. The obtained results for the IEEE30-bus system with the control variables and its variation for the proposed and other intelligence methods are depicted in
Table 9.
Table 9 represents the compromising solutions for the selected objective function such as TFC and TEC, and their values are recorded as 903.22
$/h and 0.315 ton/h, respectively. In addition, the TFC and TEC variations as a function of control variables for various iterations and their comparison with other intelligence methods are also illustrated in
Figure 11. It is clearly inferred that the multi-objective function minimized by the proposed method and achieves promising results compared to other techniques.
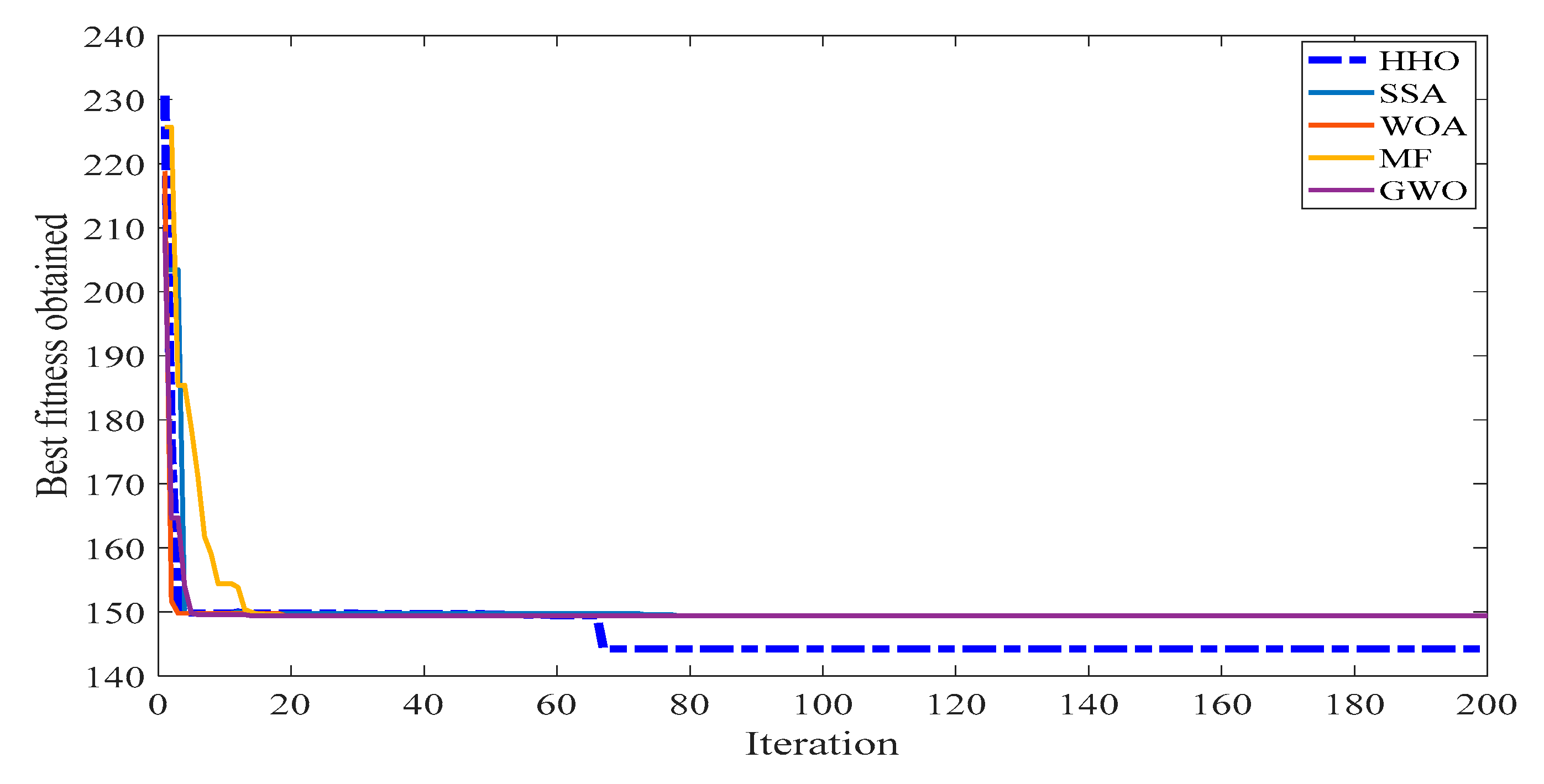
Case 6—APL and TEC Minimization
In this phase, APL and TEC were considered as an objective function to be optimized in Equation (9). In general, the emission dispatching is directly concerned with the generating units. Thus, the fitness function is minimized by adjusting the control variables, and its variations for the proposed and other intelligence methods are depicted in
Table 10.
Table 10 shows the compromising solution for both power loss and emission by fulfilling the constraints. It is found that the proposed HHO gives the best optimal solution for APL and TEC minimization of 3.538 MW and 0.298 ton/h, respectively.
Figure 12 demonstrates the convergence property of the selected fitness function consisting of all compared methods. It is found from
Table 10 that the intelligence methods like GWO give the best value for fuel cost (960.49
$/h), but the method gives pessimistic results for the actual objective function. Overall, it is observed that the HHO method gives optimistic results for the multi-objective function by controlling all the computational parameters of the OPF problem. The convergence performance is recorded at the lowest in terms of time and iteration by the proposed technique.
Case 7—TFC, APL, and TEC Minimization
In this case, three competing objective functions are optimized by the proposed HHO algorithm simultaneously using the weighted sum method with the weights of various functions like TFC, APL, and TEC as w
1 = 0.33, w
2 = 0.33, and w
3 = 0.34, respectively. Equation (10) represents the objective function to be minimized by optimally dispatching the generating units and satisfying the power flow constraints.
Table 11 shows the result obtained by the proposed and other intelligence methods. The best optimal values are recorded for APL of 4.21 MW and TEC of 0.29 ton/h by the HHO method and its performance is reasonable for a TFC of 906.52
$/h. On the flipside, the TFC is well optimized by the SSA and MF methods, but it seems to give pessimistic results for other objectives such as APL and TEC. Finally, it is clear that the obtained results of TFC, APL, and TEC cannot be further improved without degrading the performance of other parameters by all the intelligence methods presented. However, from inspection of the convergence curve portrayed in
Figure 13, it can be inferred that the proposed HHO algorithm outperforms the other intelligence techniques to give a minimum value of fitness function.
Case 7a—Minimization of TFC, APL, and TEC with presence of 5 MW DG
This case is similar to case 7 with the presence of DG for reducing the losses and emission costs of the system. The optimal location of DG is done using a real power sensitivity analysis based on the procedure detailed in [
53].
Table 12 depicts the ranking for placement of DG based on estimated sensitivity index. It is observed that bus 30 is the critical candidate bus with a maximum magnitude of index value of 0.1359 compared to all other load buses in the IEEE30-bus system. Thus, the placement of 5 MW DG in the 30-bus system results in the generation dispatch of PG1, PG2, PG5, PG8, PG11, and PG13 as 71.66 MW, 79.53 MW, 38.54 MW, 35 MW, 30 MW, and 32.88 MW, respectively. The result shows that the TFC, APL, and TEC of the system have been reduced from
$/h 906.52 to
$/h 905.19, 4.21 MW to 4.02 MW, and 0.297 ton/h to 0.219 ton/h, respectively, compared to the normal case as depicted in
Table 13. It is inferred that the change is not very significant for all the three parameters considered. However, the type of DG considered is of a smaller size and the optimal sizing of the DG needs to be done for remarkable changes in the parameters. However, the scope of this study is limited to analyze the effect of DG placement on system losses and emissions. The result also reveals that the losses and emissions of the system are reduced to 9.8355% and 26.2%, respectively, which enhances the sustainable power generation.
5. Comparative Analysis
In this section, the performance of HHO-based OPF to minimize the TFC is only considered for comparison with the literature work because of its prime importance in the electric sector compared to any other OPF objectives.
Table 14 illustrates the various optimization methods for minimizing the fuel cost whilst optimizing the control parameters such as real power generation of generators. It is seen from the results that the Stochastic Search algorithm (SS) shows the worst optimized TFC of 804.1072
$/h by uneconomical dispatches of the generators PG1 (193 MW) and PG8 (11.62 MW). On the flipside, Tabu search (TS), Evolutionary Programming(EP), Differential Evolution(DE), Modified Differential Evolution (MDE), the Enhanced Genetic Algorithm (EGA), and Ant Colony Optimization(ACO) exhibit TFC in the range of 802
$/h to 802.7
$/h. Additionally, the Modified Honey Bee Mating Optimization (MHBMO), Teaching Learning-Based Optimization (TLBO), and Modified TLBO showed that the TFC is optimized in the range between 801.8925
$/h and 801.985
$/h. However, the proposed HHO technique outperforms these to give the TFC of 801.829
$/h, indicating the best optimal solution among the various methods presented. Additionally, the % improvement of the proposed HHO method has been evaluated by choosing the PSO technique as a benchmark method. The result claims that the proffered method can significantly outperform by 0.023% more than the PSO compared to other optimization techniques. Additionally, the performance of TS, EP, IEP, DE, MDE, SS, EGA, ACO, and HBMO is not superior to that of the PSO method, which shows the solutions obtained from these optimization methods are not feasible. Among all the techniques the SS method underperforms by an amount of 0.26% compared to the PSO method. However, the proposed HHO method demonstrates its better performance through the exploration and exploitation characteristics of Hawks to tune the parameters of the generator output power. This claim makes the HHO better to optimize the generator parameters for a different combination of objective functions considered.