Calculation of Potential Radiation Doses Associated with Predisposal Management of Dismantled Steam Generators from Nuclear Power Plants
Abstract
:1. Introduction
2. Methodology
2.1. Target Large Component and Its Characteristics
2.2. Scenarios for Predisposal Management of Dismantled Steam Generators
2.3. Basic Equations to Calculate Radiation Dose
2.4. Calculation Tools
3. Results and Discussions
3.1. General Assessment for the Predisposal Management of Dismantled Steam Generators
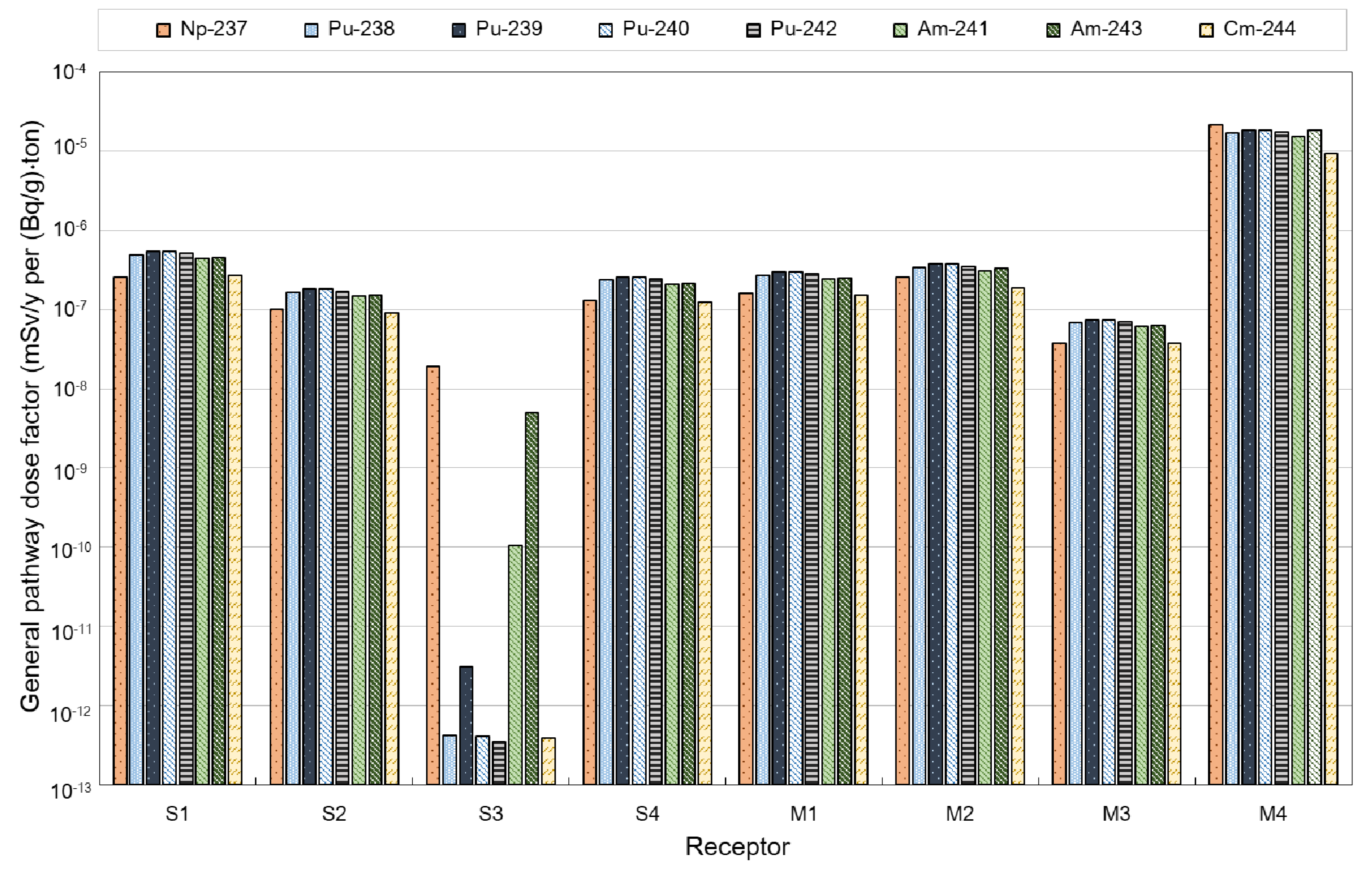
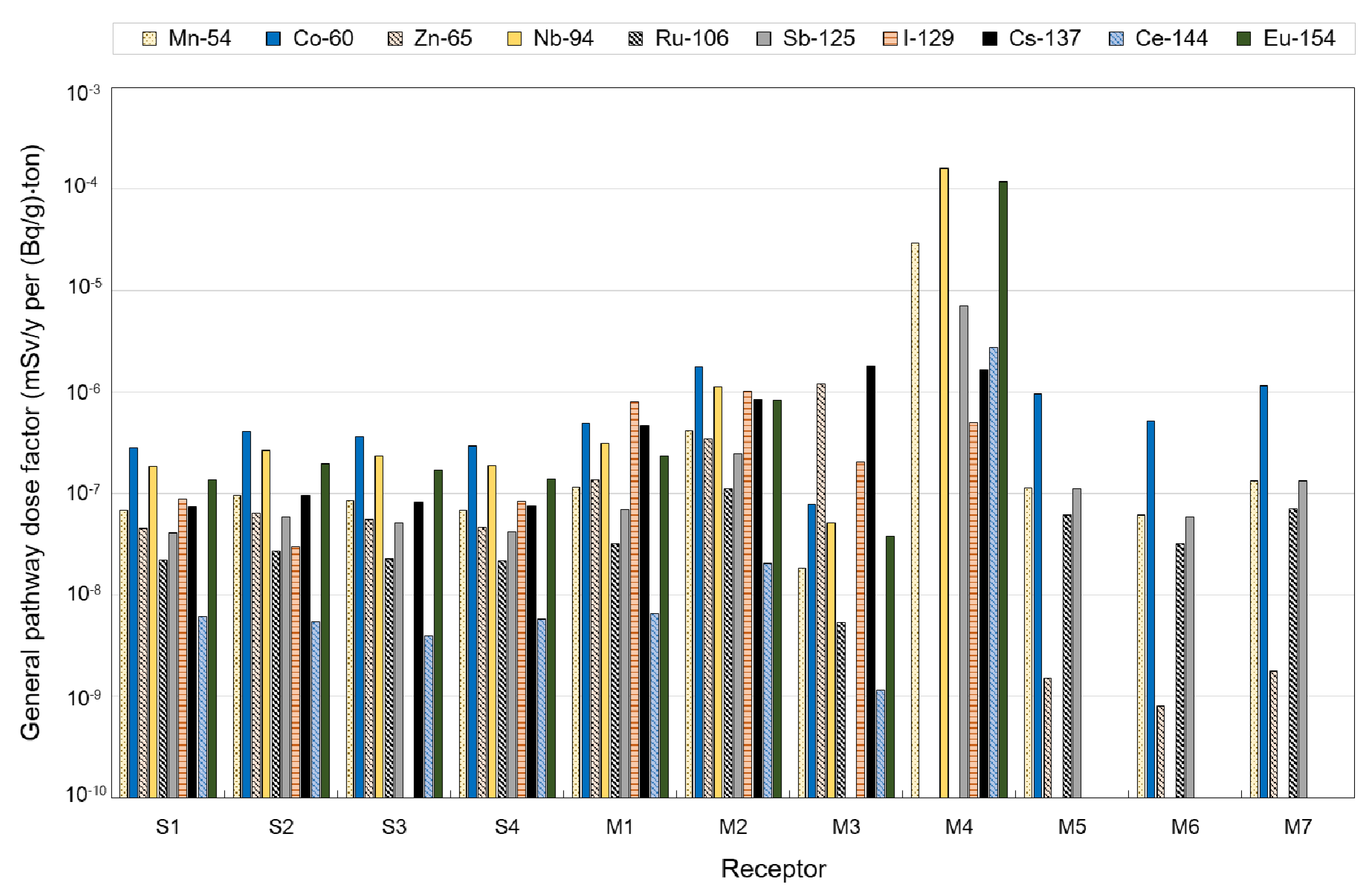
3.1.1. General Pathway Dose Factors for Processing of Dismantled Steam Generators
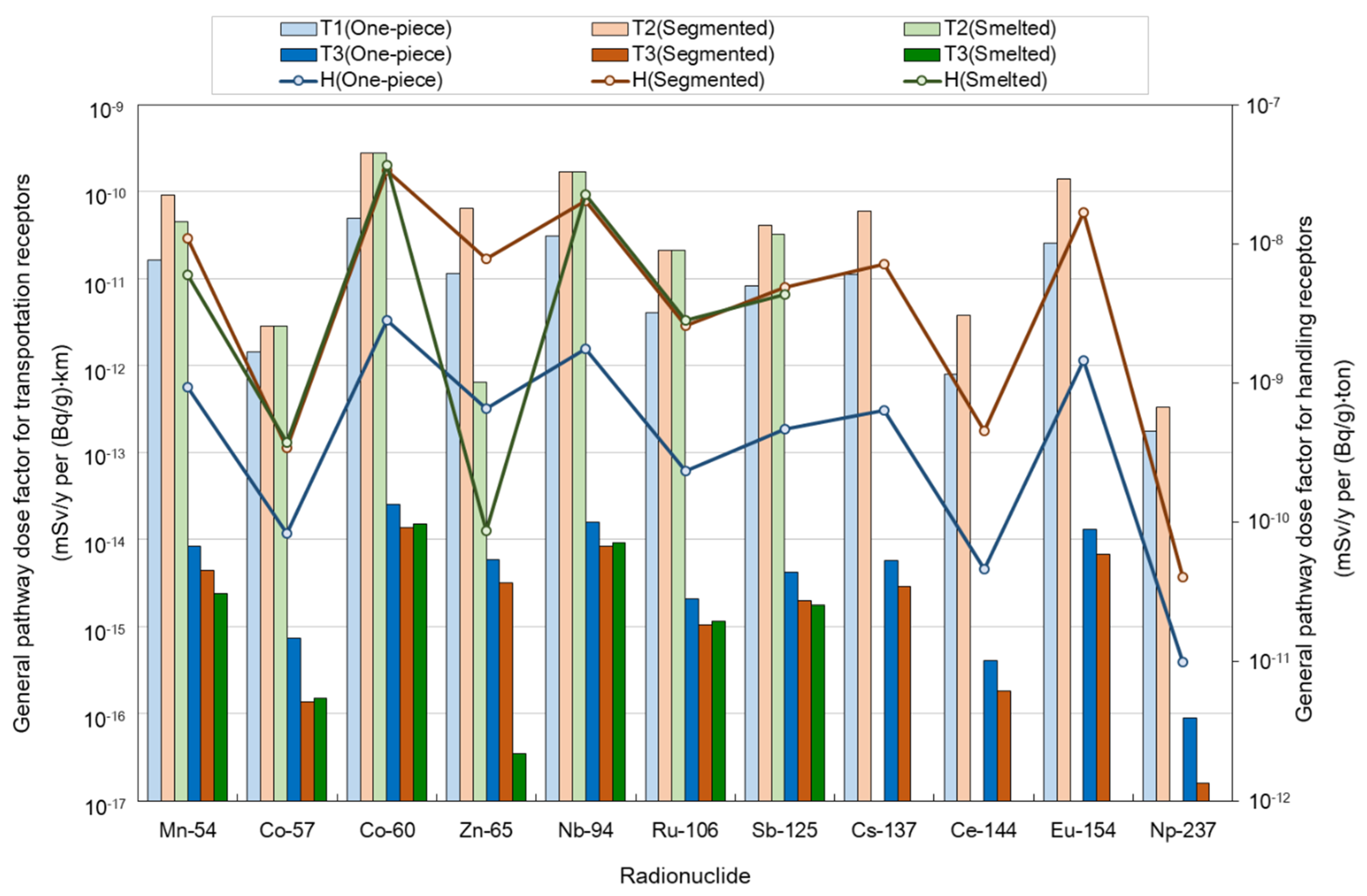
3.1.2. General Pathway Dose Factors for Transportation and Handling of Dismantled Steam Generators
3.2. Specific Assessment for Predisposal Management of Dismantled Steam Generators
3.2.1. Characteristics and Source Terms of Dismantled Steam Generators
3.2.2. Specific Scenarios for Predisposal Management of Dismantled Steam Generators
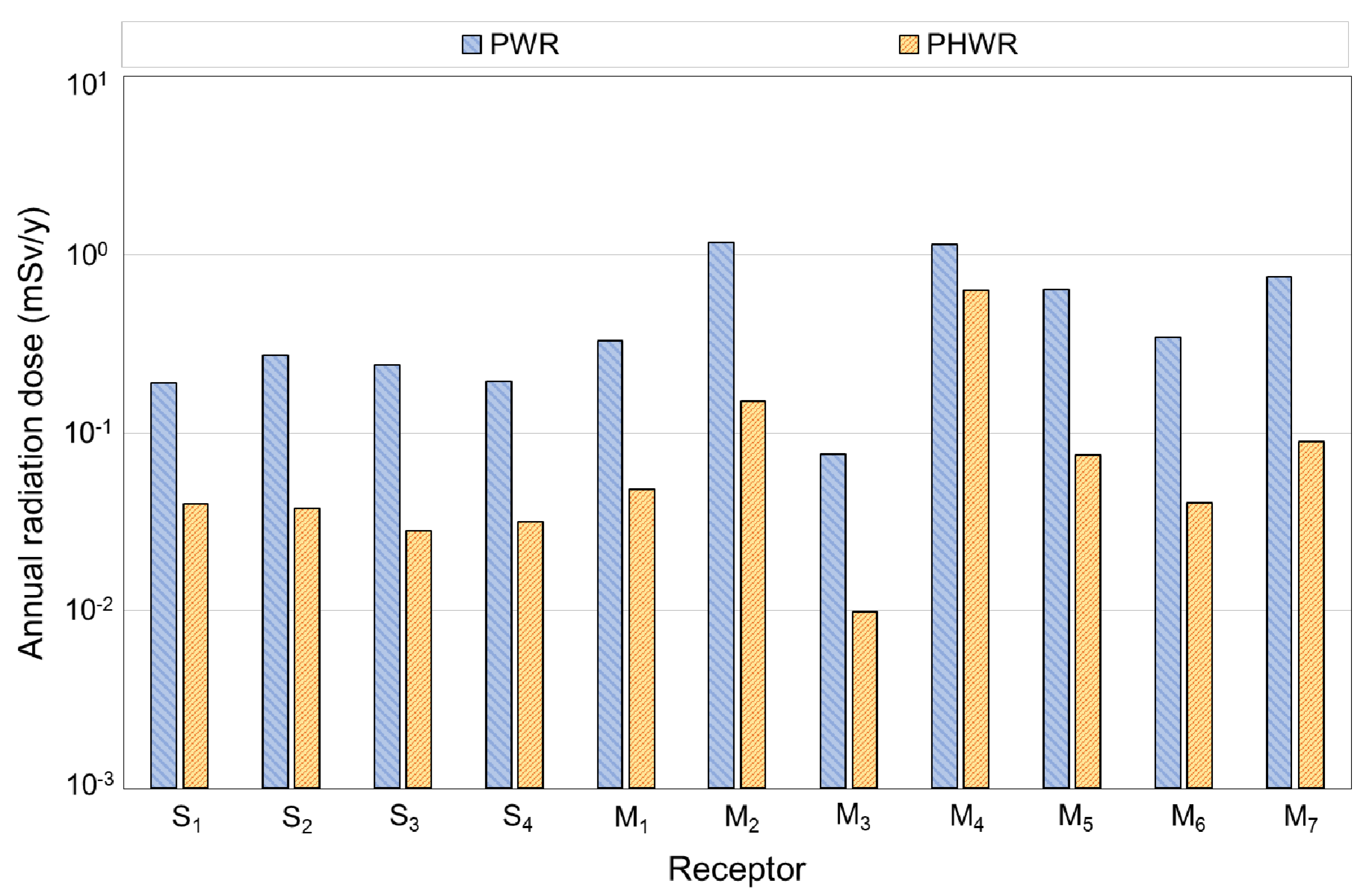
3.2.3. Calculation of Radiation Dose from Processing of Dismantled Steam Generators
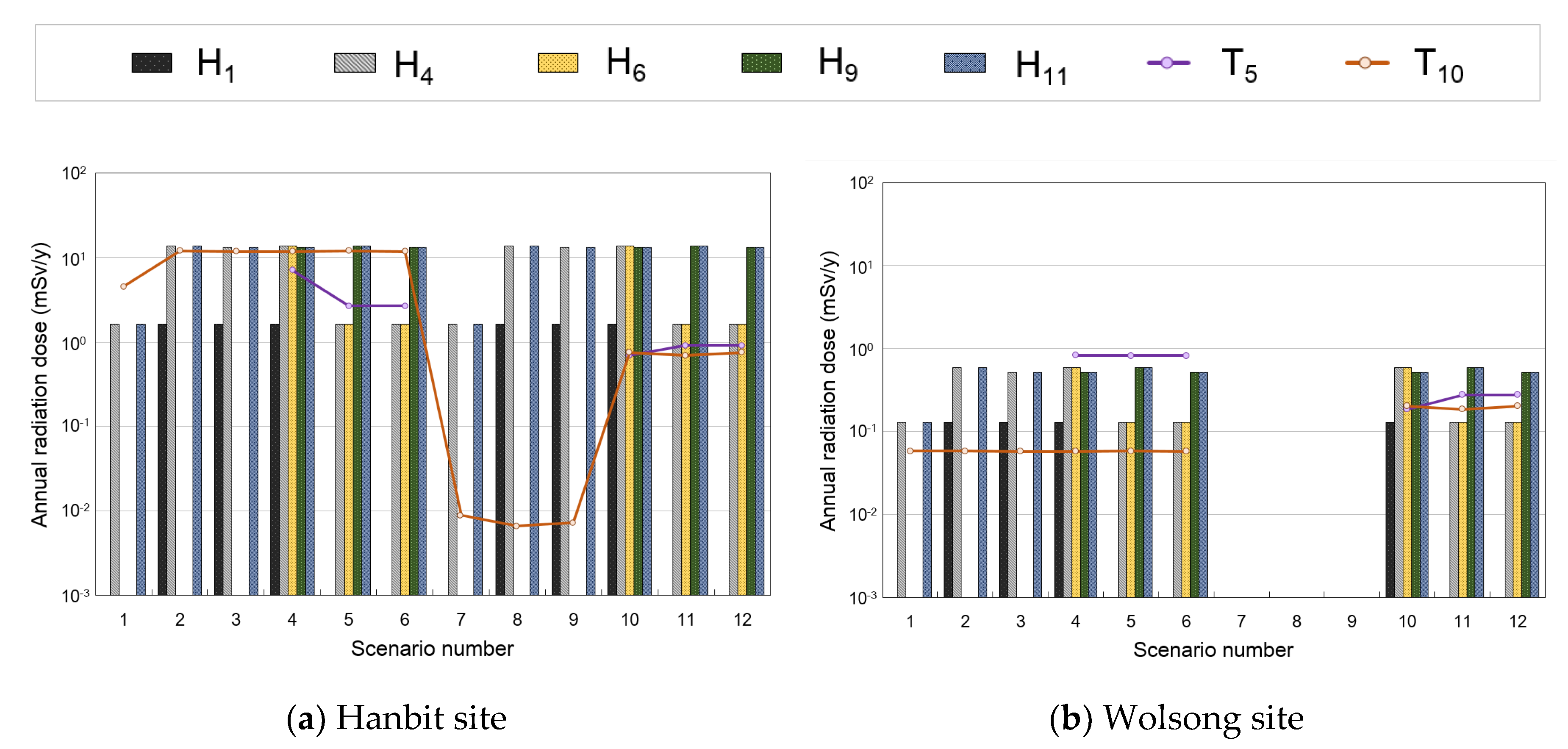
3.2.4. Calculation of Radiation Dose from Transportation and Handling of Dismantled Steam Generators
3.3. Comparison with Actual Experiences in and Studies on Predisposal Management of Steam Generators
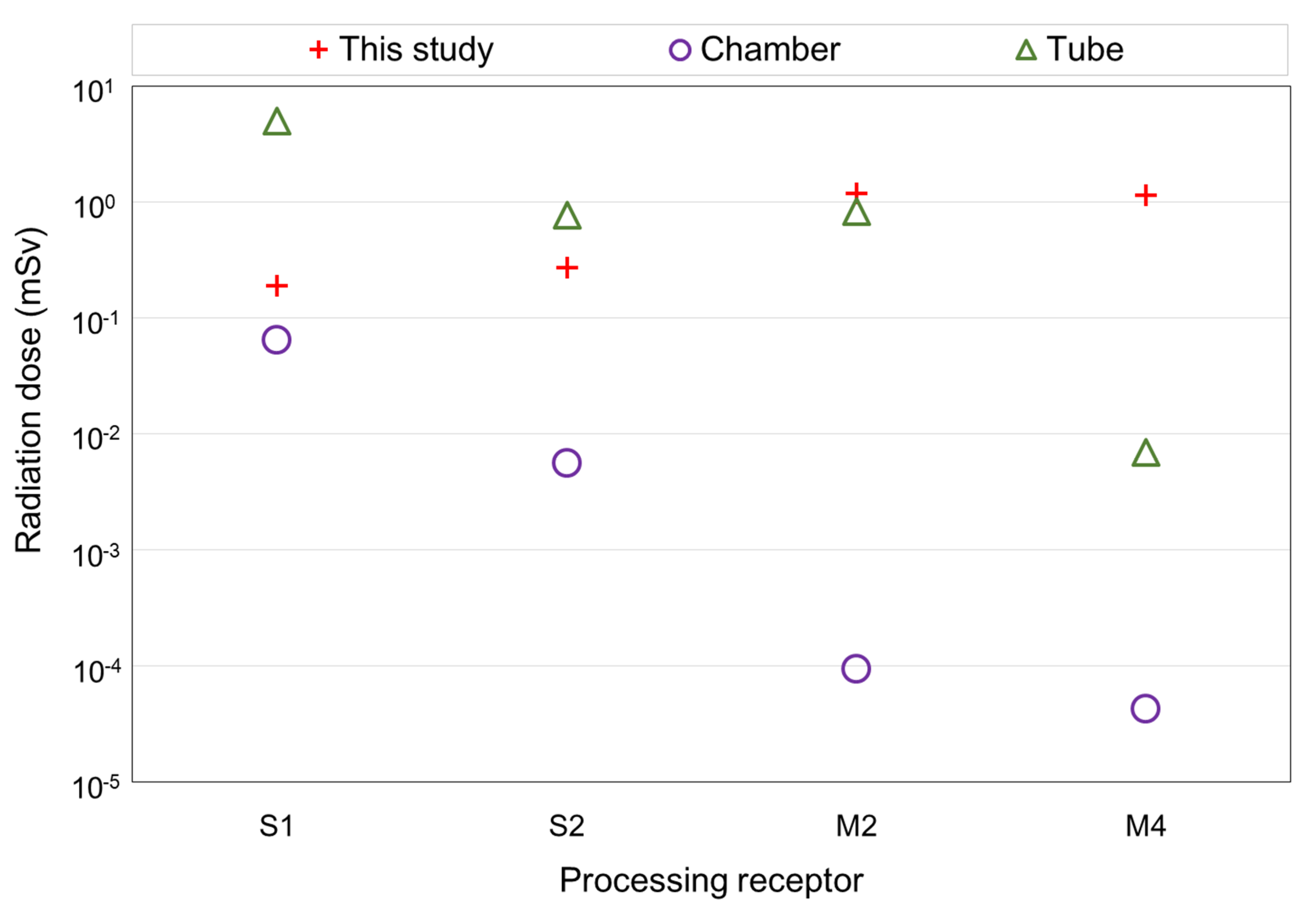
3.3.1. Comparative Studies for Processing of Steam Generators
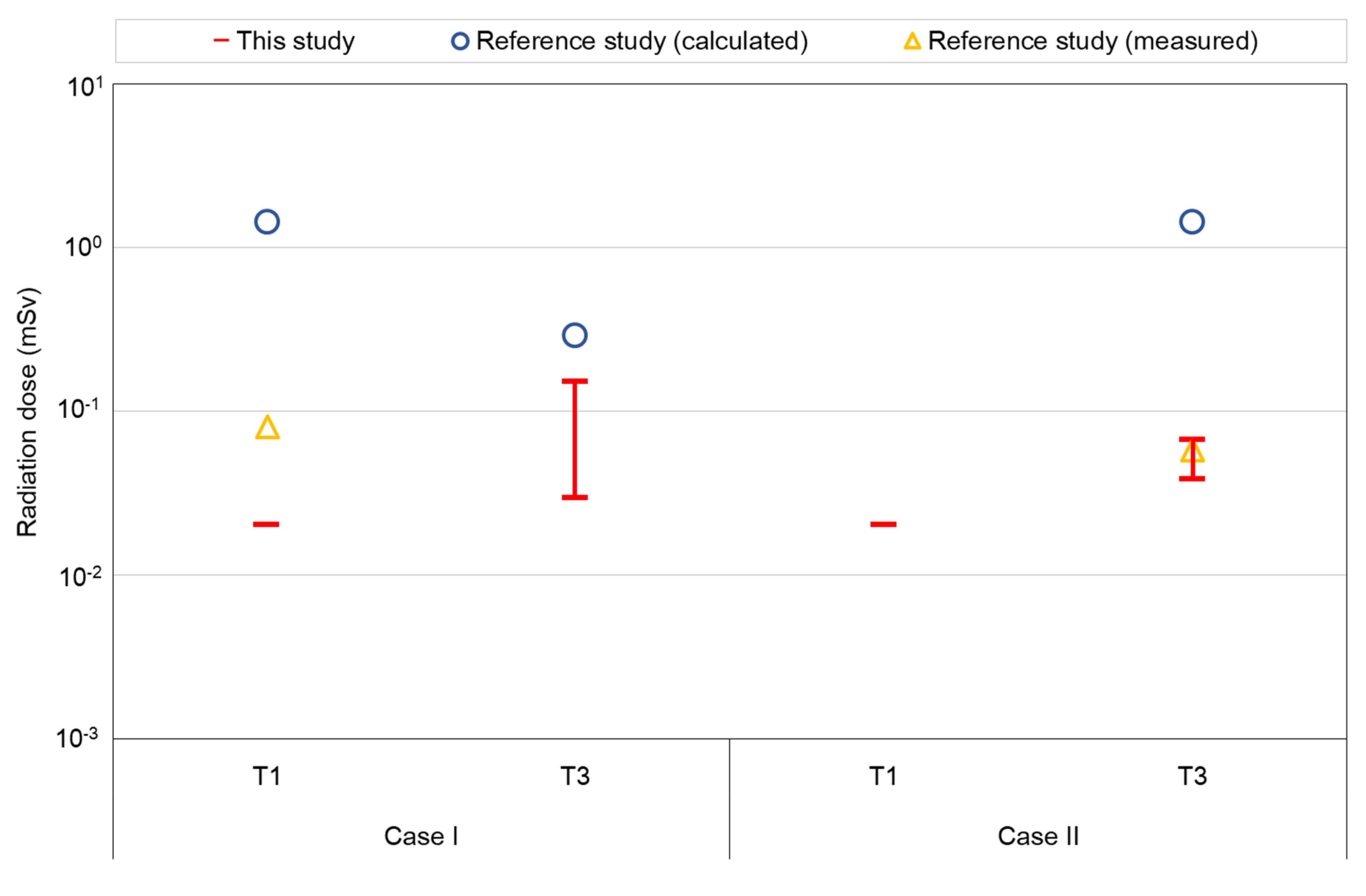
3.3.2. Comparative Studies for Transportation of Steam Generators
3.4. Application of Regulations to Transport of One-Piece Steam Generators
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nuclear Energy Agency (NEA). The Economics of Long-term Operation of Nuclear Power Plants; NEA No.7054; NEA: Paris, France, 2012. [Google Scholar]
- International Atomic Energy Agency (IAEA). Heavy Component Replacement in Nuclear Power Plants: Experience and Guidelines; Nuclear Energy Series No.NP-T-3.2; IAEA: Vienna, Austria, 2008. [Google Scholar]
- International Atomic Energy Agency (IAEA). Power Reactor Information System (PRIS). Available online: https://pris.iaea.org/PRIS/WorldStatistics/OperationalByAge.aspx (accessed on 17 April 2020).
- Nuclear Energy Agency (NEA). The Management of Large Components from Decommissioning to Storage and Disposal; NEA/RWM/R(2012)8; NEA: Paris, France, 2012. [Google Scholar]
- International Atomic Energy Agency (IAEA). Decommissioning of Facilities; Safety Standards Series No. GSR Part 6; IAEA: Vienna, Austria, 2014. [Google Scholar]
- International Atomic Energy Agency (IAEA). Predisposal of Management of Radioactive Waste; Safety Standards Series No. GSR Part 5; IAEA: Vienna, Austria, 2009. [Google Scholar]
- Korea Hydro & Nuclear Power Co., Ltd. Replacement of Large Components for Operation Nuclear Power Plants. Available online: https://npp.khnp.co.kr/index.khnp?menuCd=DOM_000000105002002000 (accessed on 15 June 2020).
- Nuclear Regulatory Agency (NRA). Radiation Management Report on Nuclear Facilities in 2017; NRA: Tokyo, Japan, 2018. [Google Scholar]
- Maheras, S.J.; Best, R.E.; Ross, S.B.; Buxton, K.A.; England, J.L.; McConnell, P.E.; Massaro, L.M.; Jensen, P.J. Preliminary Evaluation of Removing Used Nuclear Fuel from Shutdown Sites; PNNL-22676 Rev. 10; PNNL: Richland, WA, USA, 2017. [Google Scholar]
- McGrath, R.; Reid, R. Waste Management for Decommissioning of Nuclear Power Plants: An EPRI Decommissioning Program Report. In Proceedings of the Symposium on Recycling Metals Arising from Operation and Decommissioning of Nuclear Facilities, Nyköping, Sweden, 8–10 April 2014; EPRI: California, CA, USA, 2014. [Google Scholar]
- Westinghouse Electric Company. PWR Reactor Vessel and Reactor Internals Segmentation and Packaging; DDR-0004; Westinghouse: New York city, NY, USA, 2018. [Google Scholar]
- Ken, S. Safe and Secure Transport and Storage of Radioactive Materials, 1st ed.; Woodhead Publishing: Cambridge, UK, 2015; p. 277. [Google Scholar]
- Nitsche, F.O.; Fasten, C. Transport of large components in Germany-some experiences and regulatory aspects. RAMTRANS 2010, 22, 54–58. [Google Scholar] [CrossRef]
- Son, Y.J.; Park, S.J.; Byon, J.; Ahn, S. The assessment and Reduction Plan of Radiation Exposure during Decommissioning of the Steam Generator in Kori Unit 1. JNFCWT 2018, 16, 377–387. [Google Scholar] [CrossRef]
- Hornáček, M.; Nečas, V. The analysis of management of radioactive waste arisen from steam generator’s dismantling from radiological and economical point of view. Prog. Nucl. Energy 2017, 100, 406–418. [Google Scholar] [CrossRef]
- Riznic, J. Steam Generators for Nuclear Power Plants; Woodhead: Duxford, UK, 2017; p. 53. [Google Scholar]
- Park, J.H.; Cheong, J.H. Potential Management Options of Radioactive Large Metallic Components from NPPs in Operation and Decommissioning. In Proceedings of the Korean Radioactive Waste Society Spring 2018, Busan, Korea, 30 May–1 June 2018. [Google Scholar]
- International Atomic Energy Agency (IAEA). Application of Exemption Principles to the Recycle and Reuse of Materials from Nuclear Facilities; Safety Series No.111-p-1.1; IAEA: Vienna, Austria, 1992. [Google Scholar]
- Cheng, J.J.; Kassas, B.; Yu, C.; Lepoire, D.; Arnish, J.; Dovel, E.S.; Chen, S.Y.; Williams, W.A.; Wallo, A.; Peterson, H. RESRAD-RECYCLE: A Computer Model For Analyzing the Radiological Doses and Risks Resulting from the Recycling of Radioactive Scrap Metal and the Reuse of Surface-Contaminated Material and Equipment; ANL/EAD-3; Argonne National Laboratory: Illinois, IL, USA, 2000.
- United States Nuclear Regulatory Commission (US NRC). Radiological Assessment for Clearance of Materials from Nuclear Facilities; NUREG-1640; US NRC: Washington, DC, USA, 2003.
- Cheng, J.J.; Yu, C.; Williams, W.A.; Murphie, W. Validation of the RESRAD-RECYCLE computer code. In Proceedings of the WM’02 Conference, Tucson, AZ, USA, 24–28 February 2002. [Google Scholar]
- Song, J.S.; Kim, D.M.; Lee, S.H. A Study on the Application of Standards for Clearance of Metal Waste Generated During the Decommissioning of NPP by Using the RESRAD-RECYCLE. JNFCWT 2016, 14, 305–320. [Google Scholar] [CrossRef]
- Weiner, R.F.; Hinojosa, D.; Heames, T.J.; Farnum, C.O.; Kalinina, E.A. RADTRAN 6/RadCat 6 User Guide; SAND2013-8095; Sandia National Laboratories: Albuquerque, NM, USA, 2013. [Google Scholar]
- Obsborn, D.M.; Weiner, R.F.; Mills, G.S.; Hamp, S.C. Verification and Validation of RADTRAN 5.5; SAND2005-12741274; Sandia National Laboratories: Albuquerque, NM, USA, 2005. [Google Scholar]
- Yoon, J.; Kim, W.; Park, K.T.; Kang, W.M.; Kang, B.S. Development of Temporary Lifting Device for Steam Generator in Containment Vessel at Nuclear Power Plant, Transaction of the Korean Society of Mechanical Engineers. 2020. Available online: https://doi.org/10.3795/KSME-A.2020.44.4.291 (accessed on 23 June 2020).
- Korea Institute of Nuclear Safety (KINS). Technical Review Report on Hanul Nuclear Power Plant Units 3 and 4 Operation Change Permit (Steam Generator Replacement); 12-060, U-AM-57(12); KINS: Daejeon, Korea, 2013. [Google Scholar]
- Ontario Power Generation (OPG), Inc. Reference Low and Intermediate Level Waste Inventory for the Deep Geological Repository; 00216-REP-03902-00003-R003; OPG, Inc.: Ontario, ON, Canada, 2010. [Google Scholar]
- U.S. Environmental Protection Agency (EPA). Limiting Values of Radionuclide Intake and Air Concentration and Dose Conversion Factors for Inhalation, Submersion, and Ingestion; Federal Guidance Report No. 11; U.S. EPA: Washington, DC, USA, 1988.
- International Commission on Radiological Protection (ICRP). ICRP Publication 119: Compendium of Dose Coefficients Based on ICRP Publication 60; Annals of the ICRP; ICRP: Stockholm, Sweden, 2013; Volume 42, pp. 1–130. [Google Scholar]
- International Commission on Radiological Protection (ICRP). ICRP Publication 60: 1990 Recommendations of the International Commission on Radiological Protection; Ann. ICRP 21 (1-3); ICRP: Stockholm, Sweden, 1991. [Google Scholar]
- U.S. Environmental Protection Agency (EPA). Potential Recycling of Scrap Metal from Nuclear Facilities, Part I: Radiological Assessment of Exposed Individuals Volume 1; U.S. EPA: Washington, DC, USA, 2001.
- Alexander, W.R.; McKinley, L.E. Deep Geological Disposal of Radioactive Waste; Elsevier Radioactivity in the Environment Volume 9; Elsevier: Amsterdam, The Netherlands, 2011; p. 30. [Google Scholar]
- Weiner, R.F.; Neuhauser, K.S.; Heames, T.J.; O’Donell, B.M.; Dennis, M.L. RADTRAN 6 Technical Manual; SAND2014-0780; Sandia National Laboratories: Albuquerque, NM, USA, 2014.
- United States Nuclear Regulatory Commission (US NRC). Calculation of Annual Doses to Man from Routine Releases of Reactor Effluents for the Purpose of Evaluating Compliance with 10 CFR 50, Appendix I; Regulatory Guide 1.109, Revision 1; US NRC: Washington, DC, USA, 1977.
- United States Nuclear Regulatory Commission (US NRC). Standards for Protection against Radiation; Code of Federal Regulations Title 10, Part 20, Appendix B—Annual Limits on Intake (ALIs) and Derived Air Concentrations (DACs) of Radionuclides for Occupational Exposure; Effluent Concentrations; Concentrations for Release to Sewerage; US NRC: Washington, DC, USA, 2015.
- Grove Software, Inc. MicroShield® User’s Manual; Grove Software Inc.: Lynchburg, USA, 2011. [Google Scholar]
- Michael, F.L. Handbook of Radioactivity Analysis (Third Edition); Academic Press: Oxford, UK, 2012; pp. 1051–1052. [Google Scholar]
- Canadian Nuclear Safety Commission (CNSC). Special Form Certificates; CDN/5255/X-96 (Rev. 0); CNSC: Ottawa, ON, Canada, 2010.
- Seo, M.H.; Hong, S.W.; Park, J.B. Radiological Impact Assessment for the Domestic On-road Transportation of Radioactive Isotopes Wastes. JNFCWT 2016, 14, 279–287. [Google Scholar] [CrossRef]
- Swedish Nuclear Fuel and Waste Management (SKB). Available online: https://web.archive.org/web/20120506092817/http://www.skb.se/Templates/Standard____15149.aspx (accessed on 11 May 2020).
- Walberg, M.; Viermann, J.; Beverungen, M.; Kemp, L.; Lindström, A. Disposal of Steam Generators from Decommissioning of PWR Nuclear Power Plants. In Proceedings of the International Youth Nuclear Congress, Interlaken, Switzerland, 20–26 September 2008. [Google Scholar]
- Korea Electric Power Corporation (KEPCO). Kori Unit 1 Steam Generator Replacing Experience Report; ‘99-0328- DAN-38; KEPCO: Naju, Korea, 1999. [Google Scholar]
- Bruce Power. Bruce A Refurbishment for Life Extension and Continued Operation Project; Bruce Power: Ontario, ON, Canada, 2004. [Google Scholar]
- Shin, S.W.; Son, J.K.; Cho, C.H.; Song, M.J. Analysis of Dose Rates from Steam Generators to be Replaced from Kori Unit 1. JRPR 1998, 23, 175–184. [Google Scholar]
- SEARATES. Available online: https://www.searates.com/services/distances-time/ (accessed on 11 May 2020).
- Google Map. Available online: https://goo.gl/maps/jMEeWeMBeKjYwR6i8 (accessed on 13 May 2020).
- Kim, J.K.; Jin, H.H.; Lee, Y.C. A Legal Study on the Transportation of the Radioactive Waste by Sea under Act on the Arrival, Departure, etc. of Ships. Marit. Law Rev. 2017, 29, 201–228. [Google Scholar]
- Google Map. Available online: https://goo.gl/maps/KYBDENWaqc3W8asn7 (accessed on 13 May 2020).
- Google Map. Available online: https://goo.gl/maps/XnLYcbSJ1ZJFTeWj6 (accessed on 13 May 2020).
- Google Map. Available online: https://goo.gl/maps/ah4FA1nWxu7j2vTTA (accessed on 11 May 2020).
- International Atomic Energy Agency (IAEA). Regulations for the Safe Transport of Radioactive Materials; Safety Standards Series No. SSR-6 (Rev.1); IAEA: Vienna, Austria, 2018. [Google Scholar]
- International Atomic Energy Agency (IAEA). Advisory Material for the IAEA Regulations for the Safe Transport of Radioactive Material (2012 Edition); Safety Standards Series No. SSG-26; IAEA: Vienna, Austria, 2014. [Google Scholar]
- United States Nuclear Regulatory Commission (US NRC). Interim Guidance on Transportation of Steam Generators (Generic Letter 96-07); US NRC: Washington, DC, USA, 1996.
- James, L.W.; Rick, W.B. Large Component Regulatory Relief in the United States. In Proceedings of the 14th International Symposium on the Packaging and Transportation of Radioactive Materials (PATRAM (2004)), Berlin, Germany, 20–24 September 2004. [Google Scholar]
- Shirai, K.; Ozaki, S. Evaluation of transport experience for large-scale radioactive wastes produced from decommissioning of nuclear plant and re-use of metallic radioactive wastes to the transport container. Denryoku Chuo Kenkyusho Hokoku 2003, 12, 1–4. [Google Scholar]
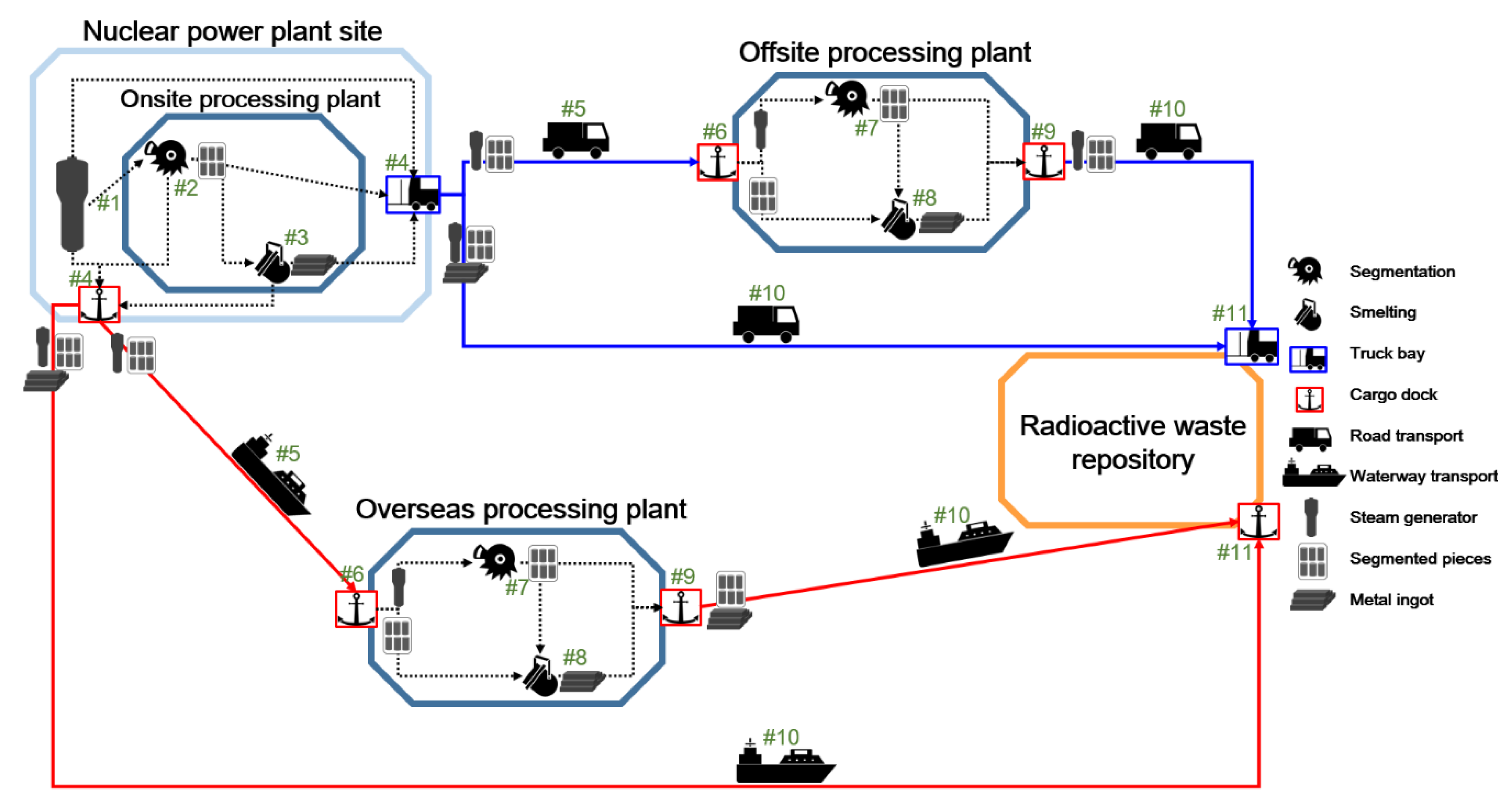
| Scenario No. | Stage of Predisposal Management | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nuclear Power Plant Site | On/Offsite Processing Plant | Repository | |||||||||
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | |
| 1 | - | - | - | H4 | - | - | - | - | - | T110 | H11 |
| 2 | H1 | Sj | - | H4 | - | - | - | - | - | T210 | H11 |
| 3 | H1 | Sj | Mk | H4 | - | - | - | - | - | T210 | H11 |
| 4 | H1 | Sj | - | H4 | T25 | H6 | - | Mk | H9 | T210 | H11 |
| 5 | - | - | - | H4 | T15 | H6 | Sj | - | H9 | T210 | H11 |
| 6 | - | - | - | H4 | T15 | H6 | Sj | Mk | H9 | T210 | H11 |
| 7 | - | - | - | H4 | - | - | - | - | - | T310 | H11 |
| 8 | H1 | Sj | - | H4 | - | - | - | - | - | T310 | H11 |
| 9 | H1 | Sj | Mk | H4 | - | - | - | - | - | T310 | H11 |
| 10 | H1 | Sj | - | H4 | T35 | H6 | - | Mk | H9 | T310 | H11 |
| 11 | - | - | - | H4 | T35 | H6 | Sj | - | H9 | T310 | H11 |
| 12 | - | - | - | H4 | T35 | H6 | Sj | Mk | H9 | T310 | H11 |
| Nuclide | Element Partitioning Factor (%) | Nuclide | Element Partitioning Factor (%) | ||||
|---|---|---|---|---|---|---|---|
| Ingot | Slag | Dust | Ingot | Slag | Dust | ||
| 3H 1 | 10 | 0 | 0 | 125Sb | 80 | 20 | 0 |
| 14C 1 | 63.5 | 0 | 0 | 129I 1 | 0 | 25 | 25 |
| 54Mn | 49 | 50 | 1 | 137Cs | 0 | 3 | 97 |
| 55Fe | 97 | 2 | 1 | 144Ce | 0 | 99 | 1 |
| 57Co | 99 | 0 | 1 | 154Eu | 0 | 99 | 1 |
| 60Co | 99 | 0 | 1 | 237Np | 0 | 99 | 1 |
| 59Ni | 99 | 0 | 1 | 238Pu | 0 | 99 | 1 |
| 63Ni | 99 | 0 | 1 | 239Pu | 0 | 99 | 1 |
| 65Zn | 1 | 0 | 99 | 240Pu | 0 | 99 | 1 |
| 90Sr | 0 | 99 | 1 | 242Pu | 0 | 99 | 1 |
| 94Nb | 99 | 0 | 1 | 241Am | 0 | 99 | 1 |
| 99Tc | 99 | 0 | 1 | 243Am | 0 | 99 | 1 |
| 106Ru | 99 | 0 | 1 | 244Cm | 0 | 99 | 1 |
| Radionuclide | ||||
|---|---|---|---|---|
| 3H | 1.31 10−10 | 3.70 103 | 3.55 10−14 | 2.81 1013 |
| 14C | 5.33 10−9 | 1.11 102 | 4.80 10−11 | 2.08 1010 |
| 129I | 7.30 10−9 | 1.48 100 | 4.93 10−9 | 2.03 108 |
| Radionuclide | Dose Rate (mSv/h per Bq/g) | ||
|---|---|---|---|
| One Piece | Segmented | Smelted | |
| 54Mn | 1.34 10−4 | 8.96 10−5 | 4.88 10−5 |
| 57Co | 1.18 10−5 | 2.78 10−6 | 3.06 10−6 |
| 60Co | 4.04 10−4 | 2.75 10−4 | 3.02 10−4 |
| 65Zn | 9.38 10−5 | 6.35 10−5 | 7.06 10−7 |
| 94Nb | 2.53 10−4 | 1.68 10−4 | 1.84 10−4 |
| 106Ru | 3.33 10−5 | 2.10 10−5 | 2.31 10−5 |
| 125Sb | 6.66 10−5 | 4.00 10−5 | 3.56 10−5 |
| 137Cs | 9.06 10−5 | 5.84 10−5 | 0 |
| 144Ce | 6.54 10−6 | 3.70 10−6 | 0 |
| 154Eu | 2.07 10−4 | 1.37 10−7 | 0 |
| 237Np | 1.42 10−6 | 3.27 10−7 | 0 |
| Transport Means | Processing Methods | Speed (km/h) [38,39,40] | Vehicle | |||
|---|---|---|---|---|---|---|
| Road | One piece | 20 | Trailer | 540 | 100 | 1 |
| Segmented | 60 | Truck | 20 | 100 | 27 | |
| Smelted | 60 | Truck | 20 | 100 | 24.3 | |
| Waterway [41] | One piece | 22 | Ship [42] | 540 | 100 | 1 |
| Segmented | 22 | Ship | 540 | 100 | 1 | |
| Smelted | 22 | Ship | 486 | 100 | 1 |
| PWR Steam Generator from Kori Unit 1 [44] | PHWR Steam Generator from Bruce A Unit 1 [38] | ||||
|---|---|---|---|---|---|
| Radionuclide | Half-Life (year) | Total Activity (MBq) | Radionuclide | Half-Life (year) | Total Activity (MBq) |
| 51Cr | 7.59 10−2 | 1.71 105 | 3H | 1.20 101 | 2.15 104 |
| 54Mn | 8.57 10−1 | 3.50 104 | 14C | 5.70 103 | 1.50 103 |
| 59Fe | 1.22 10−1 | 2.59 104 | 55Fe | 2.70 100 | 2.43 104 |
| 57Co | 7.42 10−1 | 3.06 103 | 60Co | 5.27 100 | 8.47 104 |
| 58Co | 1.94 10−1 | 1.13 106 | 59Ni | 7.50 104 | 5.20 102 |
| 60Co | 5.27 100 | 6.36 105 | 63Ni | 9.60 101 | 6.69 104 |
| 65Zn | 6.70 10−1 | 1.97 104 | 90Sr | 2.90 101 | 4.71 104 |
| 85Sr | 1.78 10−1 | 1.51 105 | 94Nb | 2.00 104 | 1.50 101 |
| 95Zr | 10−1 | 6.40 104 | 125Sb | 2.80 100 | 4.11 101 |
| 95Nb | 9.61 10−2 | 1.25 105 | 99Tc | 2.10 105 | 9.00 10−2 |
| 103Ru | 1.08 10−1 | 1.93 105 | 129I | 1.60 107 | 3.90 10−4 |
| 106Ru | 1.01 100 | 1.85 105 | 137Cs | 3.00 101 | 8.21 102 |
| 113Sn | 3.15 10−1 | 5.67 103 | 181Hf | 1.16 10−1 | 6.74 102 |
| 136Cs | 3.62 10−2 | 5.13 105 | 154Eu | 8.80 100 | 2.91 102 |
| 141Ce | 8.90 10−2 | 3.91 104 | 237Np | 2.10 106 | 7.50 10−1 |
| 144Ce | 7.79 10−1 | 3.84 104 | 238Pu | 8.80 101 | 4.80 103 |
| 239Pu | 2.40 104 | 4.90 103 | |||
| 240Pu | 6.50 103 | 6.99 103 | |||
| 242Pu | 3.80 105 | 7.10 100 | |||
| 241Am | 4.30 102 | 1.61 104 | |||
| 243Am | 7.40 103 | 1.60 101 | |||
| 244Cm | 7.80 102 | 8.24 103 | |||
| Total activity | 3.3 106 | Total activity | 2.89 105 | ||
| Origin | Distance to Destination (km) | |||
|---|---|---|---|---|
| Wolsong LILW Disposal Center | Processing Plant | |||
| Road [46] | Waterway [47] | Road | Waterway [45] | |
| Kori | 80 | 96 | 100 | 21,500 |
| Hanul | 170 | 207 | 100 | 21,500 |
| Parameter | This Study | Reference Study [14] |
|---|---|---|
| Component and weight | Kori Unit 1 SG (300 ton) | |
| Parts | Assumed to be in one piece | Separated into tubes and chambers |
| Radionuclide | 54Mn, 60Co, 65Zn, 106Ru, and 144Ce | |
| Activity concentration | Homogeneous (see PWR SG in Table 6) | Chamber: 15.9 and 0.03 Bq/g for 60Co and 106Ru, respectively Tube: 0.53, 4309, 0.04, 8.47, and 0.28 Bq/g for 54Mn, 60Co, 65Zn, 106Ru, and 144Ce, respectively |
| Radioactive decay | Decay prior to processing not considered | Decay for 28 years prior to processing |
| Shielding | Not considered | Considered |
| Decontamination | Not considered | Considered |
| Mass partitioning | 90% for ingot, 10% for slag, and 1% for dust (see Section 3.1) | 98.35% for ingot, 1.64% for slag, and 0.01% for dust |
| Exposure duration | See footnote 1 | S1: 40 h (chamber), 100 h (tube) S2: 43 h (chamber), 15 h (tube) M2: 73 h (chamber), 60 h (tube) M4: 3 h (chamber), 2.5 h (tube) |
| Parameter | Case I | Case II | ||
|---|---|---|---|---|
| This Study | Reference Study [13] | This Study | Reference Study [13] | |
| Component | Two SGs (16.5 m height, 3.6 m outer diameter, and 177 ton weight) | Four SGs (16.5 m height, 3.5 m outer diameter, and 160 ton weight) | ||
| Route | From Obrigheim NPP to Lubmin interim storage | From Stade NPP to Studsvik in Sweden | ||
| Transport measure and distance | Road: 1 km [48] Waterway: 1399 km | Road (onsite) and waterway 1400 km total | Road: 1 km [49] Waterway: 920 km [50] | Road (onsite) and waterway Distances not given |
| Transport time 1 | Road: 1 h Waterway: 63.6 h or 15 days | 15 days | Road: 1 h Waterway: 50 h or 4 days | 4 days |
| Dose rate from SG | 0.1 mSv/h 2 m from surface [51] | Not given | 0.1 mSv/h 2 m from surface [51] | Not given |
| Quantitative Criterion | Qualitative Criterion | |
|---|---|---|
| (a) | Conveyance activity limit 10A2 for inland waterway or 100A2 for other modes [51] |
|
| (b) | External radiation level 3 m from unshielded component 10 mSv/h | |
| (c) | Maximum radiation level on outside shell of and at plane formed by opening/penetration on the component < 2 mSv/h | |
| (d) | Accidental intake of radionuclide by a person ~10−6A2 or corresponding inhalation dose of 50 mSv | |
| (e) | Non-fixed contamination of the component’s accessible surface Limiting value for surface contaminated objects (SCOs) [51] 1 | |
| Country | Applied Standards | Type of Object and Package |
|---|---|---|
| United States [53,54] |
| SCO Type IP-2 |
| Germany [13] |
| SCO-II Type IP-2 |
| Canada [38] |
| SCO-I Type IP-1 |
| Japan [55] |
| SCO-I Type IP-1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chun, G.H.; Park, J.-h.; Cheong, J.H. Calculation of Potential Radiation Doses Associated with Predisposal Management of Dismantled Steam Generators from Nuclear Power Plants. Sustainability 2020, 12, 5149. https://doi.org/10.3390/su12125149
Chun GH, Park J-h, Cheong JH. Calculation of Potential Radiation Doses Associated with Predisposal Management of Dismantled Steam Generators from Nuclear Power Plants. Sustainability. 2020; 12(12):5149. https://doi.org/10.3390/su12125149
Chicago/Turabian StyleChun, Ga Hyun, Jin-ho Park, and Jae Hak Cheong. 2020. "Calculation of Potential Radiation Doses Associated with Predisposal Management of Dismantled Steam Generators from Nuclear Power Plants" Sustainability 12, no. 12: 5149. https://doi.org/10.3390/su12125149
APA StyleChun, G. H., Park, J.-h., & Cheong, J. H. (2020). Calculation of Potential Radiation Doses Associated with Predisposal Management of Dismantled Steam Generators from Nuclear Power Plants. Sustainability, 12(12), 5149. https://doi.org/10.3390/su12125149





