Revised SEDD (RSEDD) Model for Sediment Delivery Processes at the Basin Scale

Abstract

Sediment transport to river channels in a basin is of great significance for a variety of reasons ranging from soil preservation to siltation prevention of reservoirs. Among the commonly used models of sediment transport, the SEdiment Delivery Distributed model (SEDD) uses an exponential function to model the likelihood of eroded soils reaching the rivers and denotes the probability as the Sediment Delivery Ratio of morphological unit i (SDR_i). The use of probability to model SDR_i in SEDD led us to examine the model and check for its statistical validity. As a result, we found that the SEDD model had several false assertions and needs to be revised to correct for the discrepancies with the statistical properties of the exponential distributions. The results of our study are presented here. We propose an alternative model, the Revised SEDD (RSEDD) model, to better estimate SDR_i. We also show how to calibrate the model parameters and examine an example watershed to see if the travel time of sediments follows an exponential distribution. Finally, we reviewed studies citing the SEDD model to explore if they would be impacted by switching to the proposed RSEDD model.

1. Introduction

Surface soil erosion is a major threat to food production and the environment, and the problem has been compounded by climate change in recent years. As the weather becomes more unpredictable and extreme, soil erosion is expected to increase more rapidly and therefore to become more damaging in the future. Furthermore, when the eroded soils or sediments are carried away by overland flow to navigable rivers, they also create significant problems for the safe navigation and the proper use of waterways. In the case of non-navigable rivers (such as those leading to reservoirs), the situation is worse. The accumulation of sediments can be a major origin of non-point source pollution, critically affecting water supply and demand in the region. Because of the damaging consequences of soil erosion, establishing a model to assess the creation and transport of sediments is vitally important at the basin scale, and it has been a topic of research for the last quarter-century.

1.1. SEDD Model

Sediment Delivery Ratio (SDR) is the ratio between the sediment yield at the basin outlet and the gross erosion of the basin. There are several basin-scale sediment delivery models, such as the SEdiment Delivery Distributed (SEDD), the Unit Stream Power Based Erosion Deposition (USPED), and the WaTEM/SEDEM models. The WaTEM/SEDEM is a soil erosion and deposition model developed and extended by KU Leuven [1,2,3]. This model considers the transport capacity of sediments and the flow routing according to topological changes to determine whether the dominant process for each grid cell is deposition or erosion. Similar to WaTEM/SEDEM, the USPED model assumes that the soil erosion rate and flow accumulation are transport capacity limited [4,5,6,7]. The LS factor of the Universal Soil Loss Equation (USLE) model is modified with the upslope contributing area to determine the transport capacity function (T). In the USPED model, the divergence of the transport capacity index (∆T) for each grid cell determines whether deposition or erosion is the dominant process. Finally, the SEDD model was proposed by Ferro and Porto [8], although its formulation can be traced back to Ferro and Minacapilli [9]. Based on probability, the authors of SEDD hypothesized that “the Sediment Delivery Ratio, SDR_i, of each morphological area is a measurement of the probability that the eroded particles arrive from the considered area into the nearest stream reach” [9]. Furthermore, the authors defined the travel time as “the time that particles eroded from the source area and transported through the hillslope conveyance system take to arrive at the channel network” [9]. Assuming that F_i is the cumulative distribution function (CDF) of the travel time t_p,i, the authors assert that the relationship between lnF_i and t_p,i is linear. Then, they support the assertion with data from seven Sicilian basins. As a result, the following exponential function was used to describe the relationship between the SDR_i and the travel time:

$$SD{R}_i=e^{-\beta t_{p,i}}$$

(1)

where SDR_i is the SDR of morphological unit i, β is a constant for a given basin (1/m), and t_p,i is the travel time of morphological unit i (m) and defined as:

$$t_{p,i}=\frac{l_{p,i}}{\sqrt{s_{p,i}}}={\displaystyle \sum }_{j=1}^{N_p}\frac{{\lambda }_{i,j}}{\sqrt{s_{i,j}}}$$

(2)

where $s_{p,i}$ = the slope of the hydraulic path (m/m), $l_{p,i}$ = the length of the hydraulic path (m). Combining Equations (1) and (2), SDR_i can be represented as:

$$SD{R}_i=e^{-\beta t_{p,i}}=e^{-\beta \frac{l_{p,i}}{\sqrt{s_{p,i}}}}=e^{-\beta {{\displaystyle \sum }}_{j=1}^{N_p}\frac{{\lambda }_{i,j}}{\sqrt{s_{i,j}}}}$$

(3)

where N_p = the number of morphological units localized along the hydraulic path j, and λ_i,j and s_i,j = the length (m) and slope (m/m) of each morphological unit i localized along the hydraulic path j.

Many studies have used Equations (1)–(3) and the subsequent SDR_w (SDR for the entire basin) to estimate the movement of sediments and their impact on particular watersheds [10,11,12,13,14]. However, our examination of the SEDD model led us to believe that the model might have been inadequately formulated to represent the probability concept declared. We will show why we think so and present our revised version of the model in the following sections.

1.2. Incorrect Assertions of SEDD

There are several improper assumptions and false assertions of SEDD:

(a)

“the Sediment Delivery Ratio, SDR_i, of each morphological area is a measurement of the probability that the eroded particles arrive from the considered area into the nearest stream reach” [9];

(b)

the SDR_i equation is an exponential distribution (exponential probability distribution);

(c)

“the relationship between lnF_i and −t_p,i is linear” [9];

(d)

“the probability that the eroded particles arrive from the morphological unit into the nearest stream reach is assumed proportional to the probability of non-exceedance of the travel time, t_p,i ” [9];

(e)

the β coefficient can be lumped together with “the effects due to roughness and runoff along the hydraulic path” [8];

(f)

the F_i is a CDF of the travel time represented by Equation (2).

It was further asserted by Ferro and Minacapilli [9] that:

$${\beta }_i=\frac{-ln{F}_i}{t_{p,i}}$$

(4)

These incorrect assertions will be discussed in Section 2.2.

2. Analysis

We will start by describing the statistical properties of exponential functions and distributions, outline the potential issues of the SEDD model, and explain how to formulate a Revised SEDD (RSEDD) model.

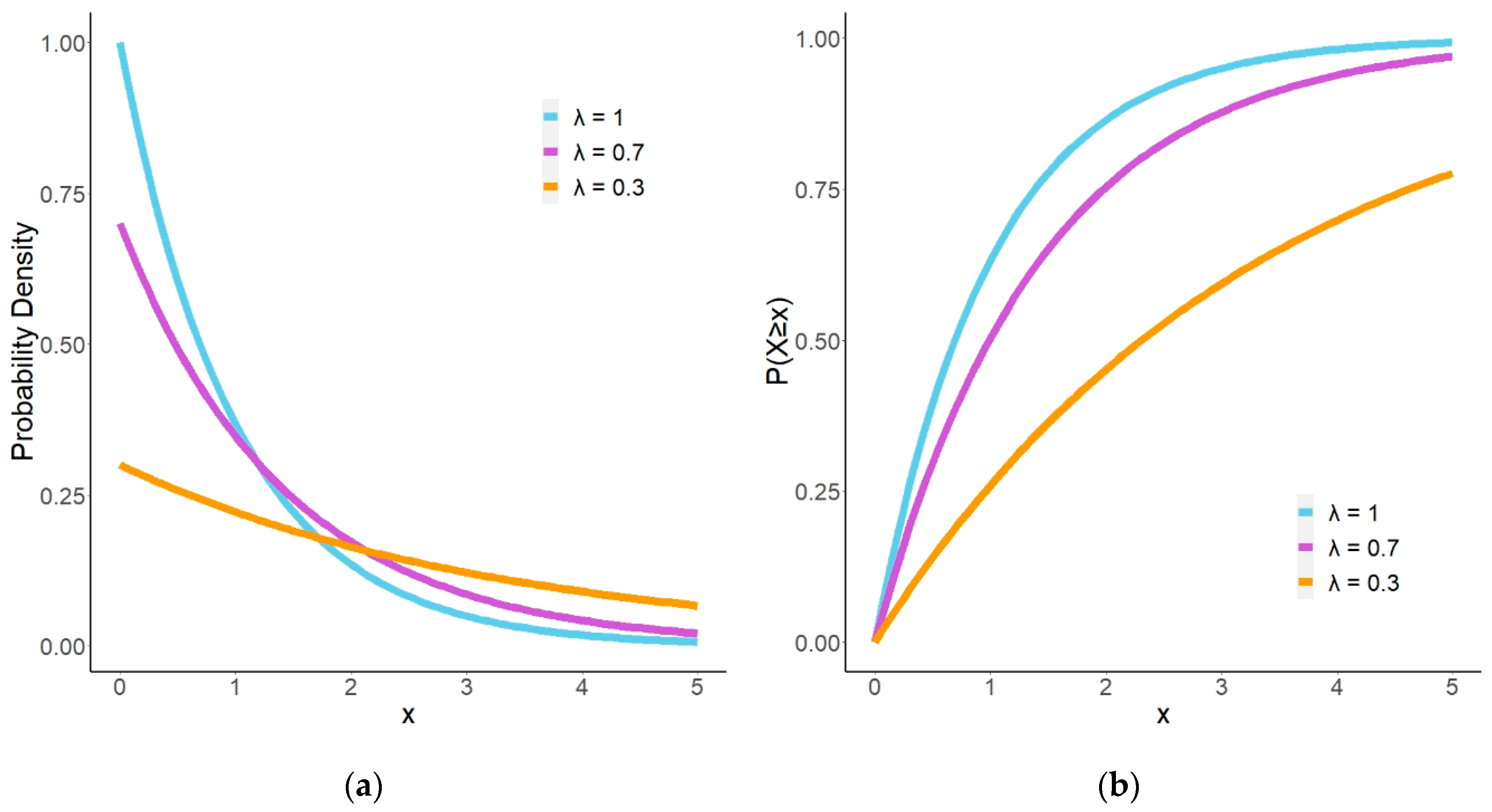
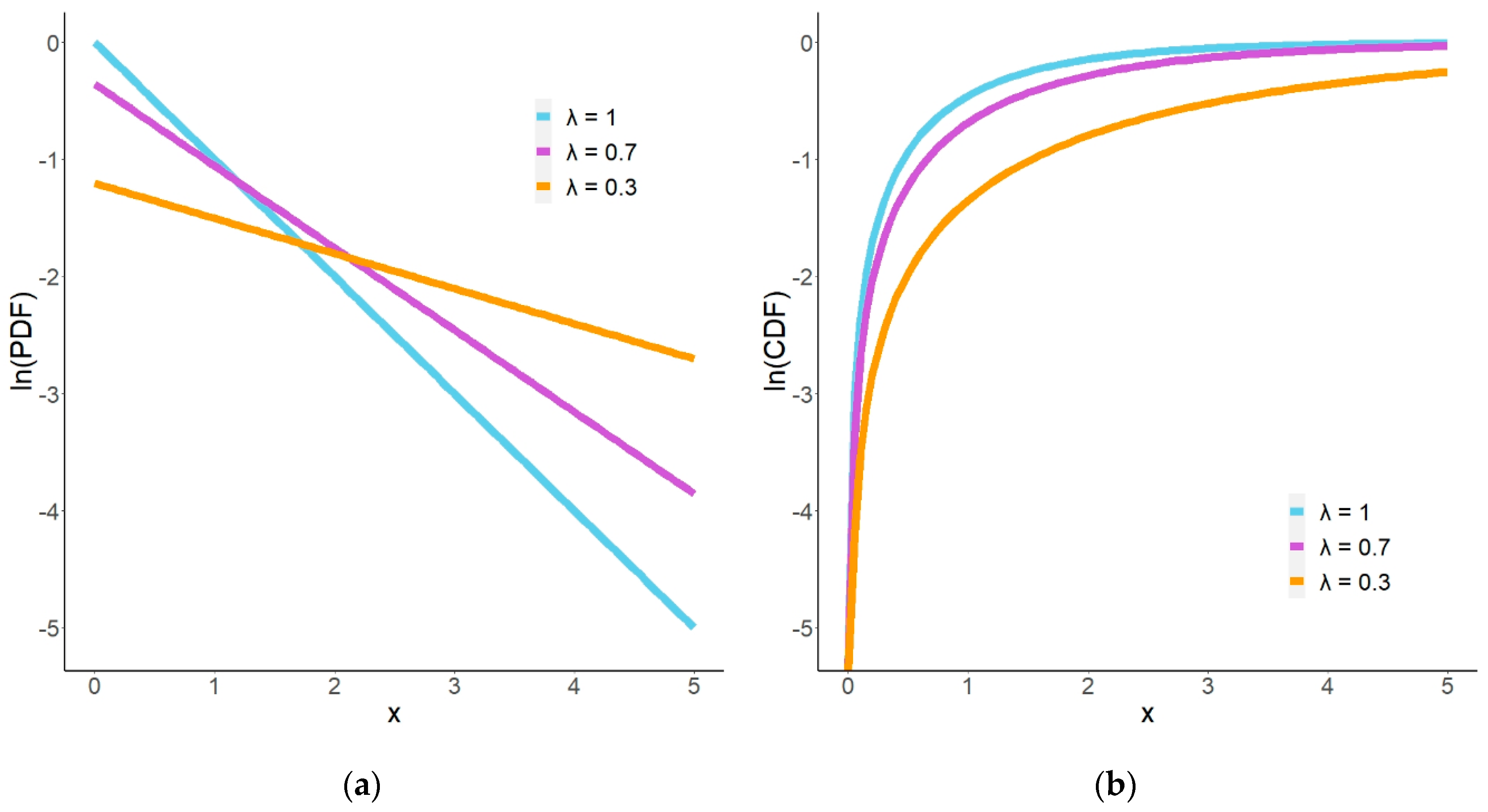
2.1. Properties of Exponential Distributions

The exponential function has a nice property concerning its differentiation and integration:

$$\frac{d}{dx}\left(e^x\right)=e^x$$

(5)

$${{\displaystyle \int }}^{}{e}^{x}dx=e^x+C$$

(6)

where e^x is the exponential function and C is a constant.

In other words, the differentiation and integration of an exponential function is still an exponential function. Exponential functions play a crucial role in statistical analysis. For example, if a probability distribution takes the form of an exponential function, its probability distribution function (or probability density function, PDF) will be an exponential distribution. The exponential distribution is generally written as:

$$f\left(x\right)=\lambda e^{-\lambda x} x\ge 0\mathrm{and}\lambda >0$$

(7)

where f(x) denotes a PDF, the curve of a continuous probability distribution. Equation (7) is also called the exponential PDF. Note the difference between exponential functions and exponential distributions. It is also worth noting that the value f(x) is known as the probability density at x, not the probability at x. For discrete random variables, however, relative frequency is the probability density. Unfortunately, for continuous random variables, “it is not meaningful to associate a probability value with each possible outcome on a continuum. Instead, for continuous random variables we associate probability values with intervals on the continuum” [15]. For a continuous random variable, the probability at x is zero. It is the area under the curve of a PDF that represents the probability of a variable falling in the corresponding interval.

The exponential distribution is a one-parameter probability distribution, which is $\lambda$. The mean of the exponential distribution is $1/\lambda$, and the standard deviation of the exponential distribution is also $1/\lambda$. The exponential distribution has been applied to various fields of study, such as vehicle headway distribution [16], the failure rates of air conditioning system in airplanes [17], the catchment-scale water residence time [18], and the relative species abundance [19]. The cumulative distribution function (CDF) of the exponential distribution is:

$$F\left(x\right)={{\displaystyle \int }}_{-\infty }^{x}f\left(u\right)du={{\displaystyle \int }}_0^x\lambda e^{-\lambda u}du=1-e^{-\lambda x} x\ge 0\mathrm{and}\lambda >0$$

(8)

where F(x) denotes a CDF (the F_i in SEDD). The PDF and CDF of the exponential distribution of typical values of $\lambda$ are shown in Figure 1a,b, respectively.

2.2. Examination of SEDD Assertions

The SEDD model was described in Section 1.1, and the incorrect assertions were listed in Section 1.2. We will devote this section to discussing the issues of SEDD. We will identify the potential problems that call for a revised SEDD (RSEDD) model to better suit the underlying statistical requirements for modeling SDR_i.

As mentioned earlier, using morphological units, Ferro and Minacapilli [9] considered SDR_i as the probability that the eroded particles arrive from the source area into the nearest river channel. This seems to imply that they consider SDR_i to be the PDF of travel time, t_p,i. On the other hand, they also wrote that the probability as mentioned above is “proportional to the probability of non-exceedance of the travel time”. This statement seems to suggest that they consider SDR_i to be the CDF of travel time instead. Although the statements might be contradictory to each other, it would not matter because neither is correct. To formulate the relationship between SDR_i and t_p,i, the authors of SEDD decided to use an exponential function as shown in Equation (1) and repeated here as Equation (9):

$$SD{R}_i=e^{-\beta t_{p,i}}$$

(9)

This is probably because of the nice properties of the exponential function (Equations (5) and (6)) and the fact that they needed a linear relationship (Equation (4)) between lnF_i and t_p,i to explain the observed linear data from the seven Sicilian basins. However, there are a few critical problems. First, the total area under a PDF has to be equal to one:

$${{\displaystyle \int }}_{-\infty }^{\infty }f\left(x\right)dx=1$$

(10)

$$f\left(x\right)\ge 0\mathrm{for}\mathrm{all}\mathrm{x}$$

(11)

Second, the CDF should be a non-decreasing function of x and satisfy the following equation:

$$\underset{x\to +\infty }{lim}F\left(x\right)=1$$

(12)

The integration of Equation (9) is:

$${{\displaystyle \int }}_{-\infty }^{x}SD{R}_i={{\displaystyle \int }}_{-\infty }^{x}f\left(u\right)du={{\displaystyle \int }}_0^x{e}^{-\lambda u}du=\frac{1}{\lambda }\left(1-e^{-\lambda x}\right)=\frac{1}{\beta }\left(1-e^{-\beta t_{p,i}}\right)$$

(13)

Obviously, the total area under Equation (9) is not equal to one, and Equation (13) does not approach one when x approaches infinity. Hence, Equation (9) is not a PDF. Moreover, since Equation (9) is not a non-decreasing function, Equation (9) is not a CDF, either. As a result, we can conclude that assertions (a), (b), (d), and (f) are incorrect.

In addition, it can be seen that the logarithm of the CDF of Equation (9) is not linear because Equation (13) is not a linear function. It can also be observed from Equation (13) that the integration (i.e., CDF) of Equation (9) is not an exponential function. Therefore, a linear relationship between lnF_i and t_p,i such as that in Equation (4) does not exist. The only condition that Equation (4) is valid occurs when Equation (9) is a CDF. Since we have already shown that Equation (9) is not a CDF, we can conclude that assertion (c) and Equation (4) are incorrect.

Finally, the SEDD model assumes that t_p,i of each morphological unit increases with the increase of the length of the hydraulic path ($l_{p,i}$) and with the decrease of the square root of the slope of the hydraulic path ($s_{p,i}$):

$$t_{p,i}\propto l_{p,i}$$

(14)

$$t_{p,i}\propto \frac{1}{\sqrt{s_{p,i}}}$$

(15)

Therefore, there exists a constant between t_p,i and the product of $l_{p,i}$ and $1/\sqrt{s_{p,i}}$. The SEDD model lumps together the constant and the β coefficient, which changes the coefficient β from its original meaning. Therefore, we think assertion (e) is not appropriate. We will correct these problems by presenting the Revised SEDD (RSEDD) model in the next section.

2.3. RSEDD Model

To distinguish from the SEDD model, we will call the following model the Revised SEDD model (RSEDD). To comply with the statistical requirements of a probability distribution function, Equation (1) is re-written as follows:

$$SD{R}_i=\beta e^{-\beta t_{p,i}} t_{p,i}\ge 0$$

(16)

Note that β is always positive and t_p,i is an exponential random variable. The CDF of Equation (16) is the integration of Equation (16):

$$F_i=F\left(t_{p,i}\right)={{\displaystyle \int }}_0^{t_{p,i}}\beta e^{-\beta u}du=1-e^{-\beta t_{p,i}} t_{p,i}\ge 0$$

(17)

We plot the natural logarithm of Y-axis values in Figure 2. The PDF and CDF of the exponential distribution of typical values of $\lambda$ are shown in Figure 2a,b, respectively. Note that the logarithm of Equation (17) is not a linear function (Figure 2b). Therefore, the relationship between lnF_i and t_p,i is not linear as was suggested by the SEDD model. On the contrary, Figure 2a reveals that the natural logarithm of the exponential PDF is linear. We will use this linear property to solve for the model parameters of RSEDD later.

Recall that the original SEDD model assumes that t_p,i of each morphological unit increases with the increase of the ratio of the length of the hydraulic path ($l_{p,i}$) to the square root of the slope of the hydraulic path ($s_{p,i}$). Therefore,

$$SD{R}_i=e^{-\beta t_{p,i}}=e^{-\beta \frac{l_{p,i}}{\sqrt{s_{p,i}}}} t_{p,i}\ge 0$$

(18)

Equation (18) holds because the SEDD model lumps together the constant between t_p,i and $l_{p,i}/\sqrt{s_{p,i}}$ (representing “the effects due to roughness and runoff along the hydraulic path”) and the β coefficient. However, this would change the coefficient β from its original meaning. We will introduce a new constant k (dimensionless) and re-write Equation (2) as follows:

$$t_{p,i}=k\frac{l_{p,i}}{\sqrt{s_{p,i}}}=k{d}_{p,i}$$

(19)

$$d_{p,i}=\frac{l_{p,i}}{\sqrt{s_{p,i}}}$$

(20)

where d_p,i is the pseudo travel time (m). Therefore,

$$SD{R}_i=\beta e^{-\beta t_{p,i}}=\beta e^{-\beta k\frac{l_{p,i}}{\sqrt{s_{p,i}}}}=\beta e^{-\beta k{d}_{p,i}} d_{p,i}\ge 0$$

(21)

The rest is the same as the SEDD model. The exponent term has to be summed along the path traveled by the sediments from the morphological unit i to the nearest river. This summation is illustrated in Figure 3 and Equation (22):

$$\frac{l_{p,i}}{\sqrt{s_{p,i}}}={\displaystyle \sum }_{j=1}^{N_p}\frac{{\lambda }_{i,j}}{\sqrt{s_{i,j}}}$$

(22)

where N_p = the number of morphological units localized along the hydraulic path j, and λ_i,j and s_i,j = the length (m) and slope (m/m) of each morphological unit i localized along the hydraulic path j.

There are two parameters (β and k) of the RSEDD model as shown in Equation (21). As previously shown in Figure 2, the logarithm of CDF is not linear, but the logarithm of PDF is. Therefore, to determine the model parameters, the PDF of a basin (instead of the CDF) should be used. This modification will guarantee that the new RSEDD model is a proper depiction of the exponential distribution of travel time and that SDR_i is the “probability density” of the eroded particles arriving from the considered area into the nearest stream reach. To solve for model parameters β and k, take the natural logarithm of Equation (21):

$$ln(SD{R}_i)=ln(\beta e^{-\beta k{d}_{p, i}})=ln\beta -\beta k{d}_{p,i}$$

(23)

Equation (23) is a linear function. By plotting ln(SDR_i) against d_p,i, we can determine β from the intercept and k from the slope of the linear plot (similar to Figure 2a). In other words, given SDR_i and pseudo travel time d_p,i, we can determine β and k and use RSEDD to model sediment delivery at the basin scale.

3. Example Watershed

To test if the travel time follows an exponential distribution, we use a watershed from literature as an example [20]. Conceptually, the basin can be divided into morphological units with uniform gradients (and properties) as shown in Figure 4. Assuming that all units have the same gradient of 0.3 and that their hydraulic paths (arrows) are shown in Figure 5, we can calculate the slope lengths and travel times using Figure 5 and

Table 1. Pseudo travel time of each morphological area.

Morphological Unit	Hydraulic Path	${\mathit{\lambda }}_{\mathit{i},\mathit{j}}$	${\mathit{s}}_{\mathit{i},\mathit{j}}$	$\frac{{\mathit{\lambda }}_{\mathit{i},\mathit{j}}}{\sqrt{{\mathit{s}}_{\mathit{i},\mathit{j}}}}$	dp,i
1	1	1.0	0.3	1.83	1.83
2	2	2.7	0.3	4.93	4.93
3	3	2.6	0.3	4.75	4.75
4	4	1.6	0.3	2.92	2.92
5	5	3.9	0.3	7.12	7.12
6	6–7	1.6	0.3	2.92	6.02
7	7	1.7	0.3	3.10	3.10
8	8–9	0.9	0.3	1.64	2.92
9	9	0.7	0.3	1.28	1.28
10	10	2.6	0.3	4.75	4.75
11	11	2.1	0.3	3.83	3.83
12	12	1.3	0.3	2.37	2.37

. Note that ordinary GIS software calculates the flow lengths to the outlet of the basin, but RSEDD (SEDD) calculates the flow lengths only to the river channels. Here are the null hypothesis and alternative hypothesis:

H₀: the travel times follow an exponential distribution

(24)

H_a: the travel times do not follow an exponential distribution

(25)

We used the Kolmogorov-Smirnov test in our statistical hypothesis testing. Reordering the d_p,i in Table 1 from the smallest to the largest, we can calculate the cumulative distribution of our sample watershed and the corresponding cumulative distribution of the exponential distribution as shown in

Table 2. Results of the Kolmogorov-Smirnov test.

	x	Frequency	Cumulative	Cumulative (%)	Corresponding Exponential CDF (%)	Difference
	1.28	1	1	0.083	0.284	0.201
	1.83	1	2	0.167	0.380	0.213
	2.37	1	3	0.250	0.463	0.213
	2.92	1	4	0.333	0.535	0.201
	2.92	1	5	0.417	0.535	0.118
	3.10	1	6	0.500	0.556	0.056
	3.83	1	7	0.583	0.634	0.050
	4.75	1	8	0.667	0.711	0.045
	4.75	1	9	0.750	0.711	0.039
	4.93	1	10	0.833	0.725	0.108
	6.02	1	11	0.917	0.794	0.123
	7.12	1	12	1.000	0.845	0.155
Total	12
Mean	3.82				Dn	0.213
λ	0.262				D12,0.05	0.375

. For a confidence coefficient (1–α) of 0.95, we obtained the sample statistic of 0.213 (D_n). Since D_n is not greater than the critical value of 0.375 (D_12,0.05), we cannot reject the null hypothesis (H₀) that these data come from an exponential distribution. However, we cannot accept the null hypothesis (H₀) either because we only know a Type I error (probability equal to α = 0.05) and do not know the probability of making a Type II error [21]. The hypothesis testing on this example watershed is not conclusive.

4. Discussion

The original studies of the SEDD model preceded several studies evaluating SDR, and its impact on geomorphology and other related issues was far-reaching. Therefore, a revision to the model would have an impact on the conclusions of some (but not all) of the publications which cited the original model. There are two different categories of impacts we have ascertained from our literature review: (a) foundation research that established and confirmed the SEDD model and validated the use of the model, and (b) studies which merely mention the SEDD model without implementation. The first category is strongly impacted by the revision of SEDD, while the revision has no impact on the second category.

The first collection of studies are studies that established, tested, and calibrated the SEDD model parameters (or its offsets, such as MOSEDD) and those studies in which SEDD plays a significant role in the procedure of the research. The first type of studies established that although there were many different gross erosion estimation models (RUSLE, USLE, USLE-M, USLE-MM, etc.), the SDR of the SEDD model was conceptually practical for estimating the sediment yield. Therefore, the specific gross erosion model considered was not particularly influential. The conclusions of these studies would require recalibration as the base model would be changed. However, the separation of the physical concept of sediment delivery and the SEDD from the gross erosion estimation concept remains intact. Alternatively, the second type of study used the SEDD model as a significant component. The conclusions and results would need to be re-evaluated to see the extent of the impact due to the use of a new model. These studies and their contributions are as follows: the relationship between channel network parameters and the sediment transport efficiency [22], the testing and calibration of the SEDD model [8,23,24,25,26,27,28], the assessment of sediment connectivity in dendritic and parallel Calanchi systems [29,30], sediment load impact on a reservoir [14], the estimation of the response to land use/cover change in a catchment [31], sediment yield in monocrop plantation areas, such as reafforested eucalyptus and olive orchards [13,32], the assessment of sediment delivery/soil erosion processes using Caesium-137 [23,33,34,35,36,37], testing of the correction of the topographic factors of the RUSLE [38,39,40,41,42], soil erosion and sediment yield estimation [10,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58], agricultural non-point pollution [59], clay content relationship with sediment delivery [60], the assessment of the temporal variation of sediment yield [61], chemical transport in sediment delivery processes [62,63], agricultural methods impact on soil erosion and sediment yield [11,12], impact of bushfire or wildfire on soil erosion [64], comparison of multiple SDR models/gross erosion models [65,66], soil texture prediction [67], relating geomorphic features to soil erosion [68], landscape management and water resources management [69], and land use and impact of check dams on sediment yield [70,71,72].

Many studies have cited the conclusions or observations made by Ferro and Minacapilli [9] and the SEDD model within their literature review. However, they have not explicitly employed the SEDD model or the SDR equation. These represent the second collection of studies related to the SEDD model. Common citations are for the following reasons: (1) as an example of research which uses RUSLE, (2) travel time as a basis for the regionalization of SDR, (3) defining SDR, (4) sediment transport and its relationship with storage time and the sediment delivery ratio, (5) lumped sediment delivery ratio, (6) linkage between different scales using the SDR equation, (7) empirical models to evaluate sediment yield and soil erosion, (8) sediment yield being proportional to the sediment delivery processes, (9) topographic factors and their relationship with SDR, (10) spatially distributed empirical erosion models, and (11) calibration of measured and calculated sediment yields [2,68,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129].

The preceding literature review includes all accessible papers to the authors of this study (using the Scopus database). It confirms that between 1995, the year the SEDD model was published, to 2019, there has been no revision of the SEDD model similar to what is proposed in this study. Note that there might be additional studies that have not been included in the literature review of this study because these papers utilized the SEDD model but did not reference the original study of the SEDD model [9]. For example, Diwediga et al. [130] utilized the SEDD model to study soil erosion response to sustainable land management in the Mo River Basin, Togo, Africa, but referenced the Di Stefano et al. [36] equation instead. Finally, the great influence the original paper on sediment delivery research over the past 25 years gives rise to an innumerable number of references. These references might exist in less accessible databases, conference materials, and in national/state/municipal level public research that are beyond our ability to review.

5. Summary and Conclusions

Using exponential distributions to model naturally occurring phenomena is quite common in natural science and engineering analysis. The use of exponential distribution to model the probability of sediments entering river channels is an essential contribution of SEDD, and the model has been widely used to study different basins in the world. However, there are several false assertions by the SEDD model, which do not seem to have been noticed in the literature. We reviewed this often used model and proposed to revise it to better suit the underlying statistical requirements. As a result, the RSEDD model was introduced with two model parameters, β and k. The calibration of these parameters can be done using the logarithm of PDF. We also reviewed literature citing the SEDD model to see the impact of the revision on these studies. The first collection of studies are studies that calibrated the SEDD model parameters or used the SEDD model as a significant component of the studies. These studies need to be re-evaluated to see the extent of the impact. The second collection of studies used the SEDD model as an example or merely mentioned the model without implementation. The revision does not affect these studies. However, it remains to be seen whether the new RSEDD model can reliably predict SDR_i and sediment yield in future watershed research.