Sensitivity Analysis in Probabilistic Structural Design: A Comparison of Selected Techniques

Abstract

Although more and more reliability-oriented sensitivity analysis (ROSA) techniques are now available, review and comparison articles of ROSA are absent. In civil engineering, many of the latest indices have never been used to analyse structural reliability for very small failure probability. This article aims to analyse and compare different sensitivity analysis (SA) techniques and discusses their strengths and weaknesses. For this purpose, eight selected sensitivity indices are first described and then applied in two different test cases. Four ROSA type indices are directly oriented on the failure probability or reliability index beta, and four other indices (of a different type) are oriented on the output of the limit state function. The case study and results correspond to cases under common engineering assumptions, where only two independent input variables with Gaussian distribution of the load action and the resistance are applied in the ultimate limit state. The last section of the article is dedicated to the analysis of the different results. Large differences between first-order sensitivity indices and very strong interaction effects obtained from ROSA are observed for very low values of failure probability. The obtained numerical results show that ROSA methods lack a common platform that clearly interprets the relationship of indices to their information value. This paper can help orientate in the selection of which sensitivity measure to use.

1. Introduction

Evaluating the reliability of building structures is a problem whose final goal remains a decision-making process [1]. In a probabilistic framework, the basic characteristic of engineering reliability is the probability of failure P_f, which represents the key quantity of interest in decision-making processes [2]. It is recommended by the best practices that such a report is supplemented with sensitivity analysis (SA), which describes the effect of changes in model inputs on the measure of reliability [3].

A classical measure of change in P_f is the derivative ∂P_f/∂μ_xi with respect to the mean value μ of input variable X_i [4,5,6,7]. A drawback of the derivative-based SA is that it cannot detect interactions between input variables. Since only one μ_xi is varied at a time while others are fixed, it can be labelled as the One-At-a-Time (OAT) method or local SA (at point μ_xi). The aforementioned drawback can partially be overcome by using the factorial experiment, where SA is computed using two-level changes of μ_xi for all X_i in combinations, which permit the computation of interaction effects [8]. However, only absolute change of the distribution parameter μ_xi on P_f is investigated, not the relative influence of the random variability of X_i on P_f. For structural reliability, it is better to prefer such SA types that can compute the effects of the random variabilities of input variables and their interactions on P_f and not just changes in distribution parameters.

Compared with the local SA, global SA [9] can measure the effect of input variables on the model output in their entire distribution ranges and provide the interaction effect among different input variables. In the literature, many global SA techniques, such as the non-parametric techniques [10], screening approaches [11], Sobol’s variance-based (ANOVA) methods [12,13] and moment-independent methods [14,15], can be found, among which the variance-based method has gained the most attention. Variance is an important component of reliability analysis, but is insufficient on its own for the analysis of structural reliability; see, for e.g., [16]. A more general approach, which generalized Sobol’s sensitivity indices, was introduced by Fort et al. [17]. These indices are generally applicable (goal-oriented) because they can analyze various key quantities of interest, including P_f.

The selection of SA methods that focus on P_f or design quantiles is usually based on a stochastic model with binary output failure/nonfailure, 1/0 [18], but it is not a necessity. In first-order reliability method (FORM), P_f can be replaced by reliability index β [19], which is computed using the first two moments of resistance, and load action and can be applied as an alternative measure of reliability; see Figure 1. However, global SA of β has not yet been developed.

From a computational point of view, probabilistic sensitivity measures have been comprehensively studied; however, from a decision-analytic point of view, they remain much less understood [20]. Their relationship to information value has not yet been particularly established. Linking the information value, SA, and forecasting with scoring rules remains a subject of research [20]. For a particular reliability task, it is necessary to look for means to select the most appropriate sensitivity measure with common rationale for this selection.

In civil and construction engineering, the scientific community uses SA in structural mechanics [21,22], geotechnics [23,24], landscape water management [25], building performance analysis [26], multi-criteria decision making (MCDM) [27], sustainable development of the building sector [28] or sensitivity audits to assess sustainability [29], but with a lower publication frequency than in basic sciences, such as chemistry, economics or mathematics [30]. In structural reliability, research deals with limit states [31] or the verification of partial safety factors of Eurocode standards [32] using various types of global SA based, for example, on the variance of model outputs [33,34].

The term “sensitivity analysis” can be understood differently in civil engineering than in basic sciences, where local and global SA types with random inputs are well established. For example, very specific (non-stochastic) SA methods based on advanced non-linear models are sometimes used for structures susceptible to buckling when the subject of interest is the stability (or potential energy) of structures [35,36] or imperfection sensitivity [37,38], whereby the main objective of these methods is to increase the stability limits of the structures through the variation of suitable design variables. In stochastic systems, stability often means insensitivity or low sensitivity of the output characteristics to the shapes of some input distributions [39]. In construction engineering, it is necessary to focus more on cooperation and integration of SA development [3] with reliability analysis tools [31,40] and decision-making processes [41,42].

This paper compares several existing sensitivity measures in the context of structural reliability in civil engineering. For this purpose, eight selected sensitivity indices are first described and then applied in two different test cases.

Four indices are oriented on the probability of failure or reliability index β, another four on the distribution or some moments of the output from the ultimate limit state function Equation (2). The reason for the inclusion of the second group of indices is their common use in the analysis of limit states, despite being only sensitive to reliability; see, for e.g., [43,44]. Correlations present a typical example; however, sensitivity techniques based on fuzzy probability analysis of constructions [45,46] are no exception. These alternative types of SA are not directly focused on the probability of failure, but they provide basic insight into the behaviour of computational models, their structures and their reactions to changes in model inputs.

The presented article deals with four ROSA type SA and four other SA, which are empathetic to reliability in civil engineering. Special attention is paid to small failure probabilities, which are relevant for assessing the engineering reliability of structures using design reliability conditions.

2. Design Reliability Conditions

In limit state design, the resistance of a structure R must be greater than the load action F with a predetermined probability [19]. Structural reliability can also be assessed by comparing the lower quantile of R with the upper quantile of F [19], where the quantiles represent alternative key quantities of interest. The decision-maker who develops or implements stochastic models is expected to provide a forecast of structural reliability, which can be performed by estimating the failure probability, quantiles or other computational statistics related to limit states of structure.

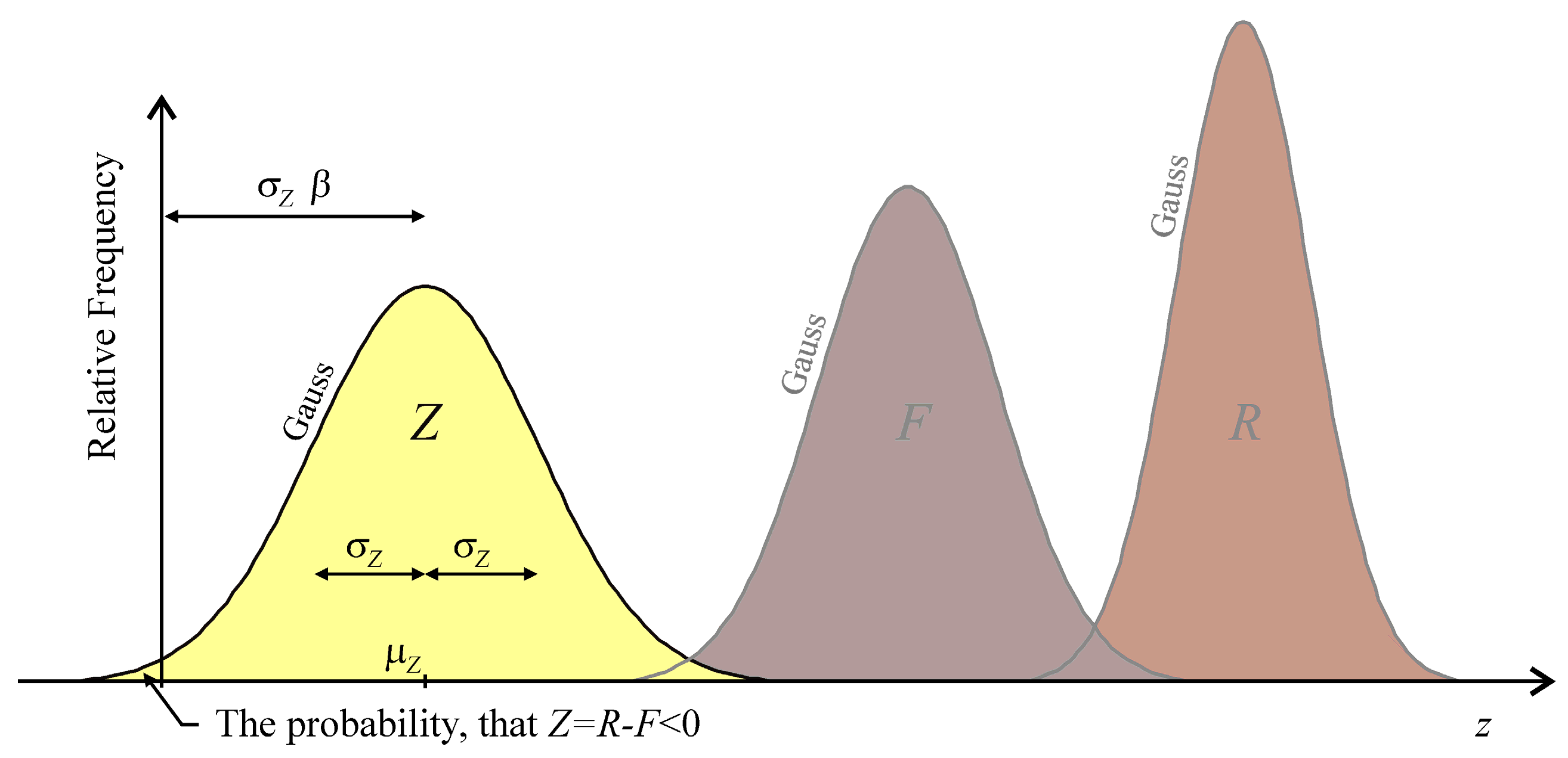
Let the reliability of building structures be a one-dimensional random variable Z, which is a function of random variables.

$$Z=g\left(X\right)=g\left(X_1,\hspace{0.17em}{X}_2,\hspace{0.17em}\dots ,X_M\right).$$

(1)

The reliability assessment of load-bearing structures is based on a semi-probabilistic approach of standard [19], which falls into the category of FORM methods [47]. Structural reliability is often expressed as a limit state function of random resistance R and random load action F:

$$Z=R-F\ge 0,$$

(2)

where R and F are statistically independent variables for which Gauss probability density functions (pdfs) are assumed with mean values μ_R, μ_F and standard deviations σ_R, σ_F. If R and F have Gauss pdfs, then Z has a Gauss pdf with mean value μ_Z and standard deviation σ_Z:

$${\mu }_{\mathrm{Z}}={\mu }_{\mathrm{R}}-{\mu }_{\mathrm{F}},$$

(3)

$${\sigma }_{\mathrm{Z}}=\sqrt{{\sigma }_{\mathrm{R}}^2+{\sigma }_{\mathrm{F}}^2}.$$

(4)

The transformation of Z into a normalized Gaussian pdf of U with mean value μ_U = 0, and standard deviation σ_U = 1 is written as

$$U=\frac{Z-{\mu }_{\mathrm{Z}}}{{\sigma }_{\mathrm{Z}}}.$$

(5)

The probability of failure (key quantity of interest) can be expressed as

$$P_{\mathrm{f}}=P\left(Z<0\right)=P\left(U<-\frac{{\mu }_{\mathrm{Z}}}{{\sigma }_{\mathrm{Z}}}\right)=P\left(U<-\beta \right)={\mathsf{\Phi }}_U\left(-\beta \right),$$

(6)

where Φ_U(•) is the cumulative distribution function of normalized Gaussian pdf and μ_Z/σ_Z is the so-called reliability index β; see Equation (7) and Figure 1.

It is assumed that β > 0. Standard [19] verifies reliability by comparing the obtained reliability index β with the target reliability index β_d.

$$\beta =\frac{{\mu }_{\mathrm{Z}}}{{\sigma }_Z}\ge {\beta }_{\mathrm{d}},$$

(7)

For instance, the reliability index has a target value of β_d = 3.8 (P_fd = 7.2·10⁻⁵), provided that we consider the ultimate limit state for common design situations within the reference period of 50 years; see Table C2 in [19] or [48]. Equation (8) can be written to obtain σ_Z as

$${\sigma }_Z=\hspace{0.17em}\sqrt{{\sigma }_R^2+{\sigma }_F^2}=\frac{{\sigma }_R^2+{\sigma }_F^2}{\sqrt{{\sigma }_R^2+{\sigma }_F^2}\hspace{0.17em}}=\frac{{\sigma }_R}{\sqrt{{\sigma }_R^2+{\sigma }_F^2}\hspace{0.17em}}{\sigma }_R+\frac{{\sigma }_F}{\sqrt{{\sigma }_R^2+{\sigma }_F^2}\hspace{0.17em}}{\sigma }_F={\alpha }_{\mathrm{R}}{\sigma }_R+{\alpha }_F{\sigma }_F,$$

(8)

where α_F, α_R are values of sensitivity coefficients (weight factors) according to the FORM method, which [19] introduces with constant values α_F = 0.7, α_R = 0.8. Substituting Equations (3) and (8) into Equation (7), we can write

$$\beta =\frac{{\mu }_R-{\mu }_F}{{\alpha }_R{\sigma }_R+{\alpha }_F{\sigma }_F}\ge {\beta }_d.$$

(9)

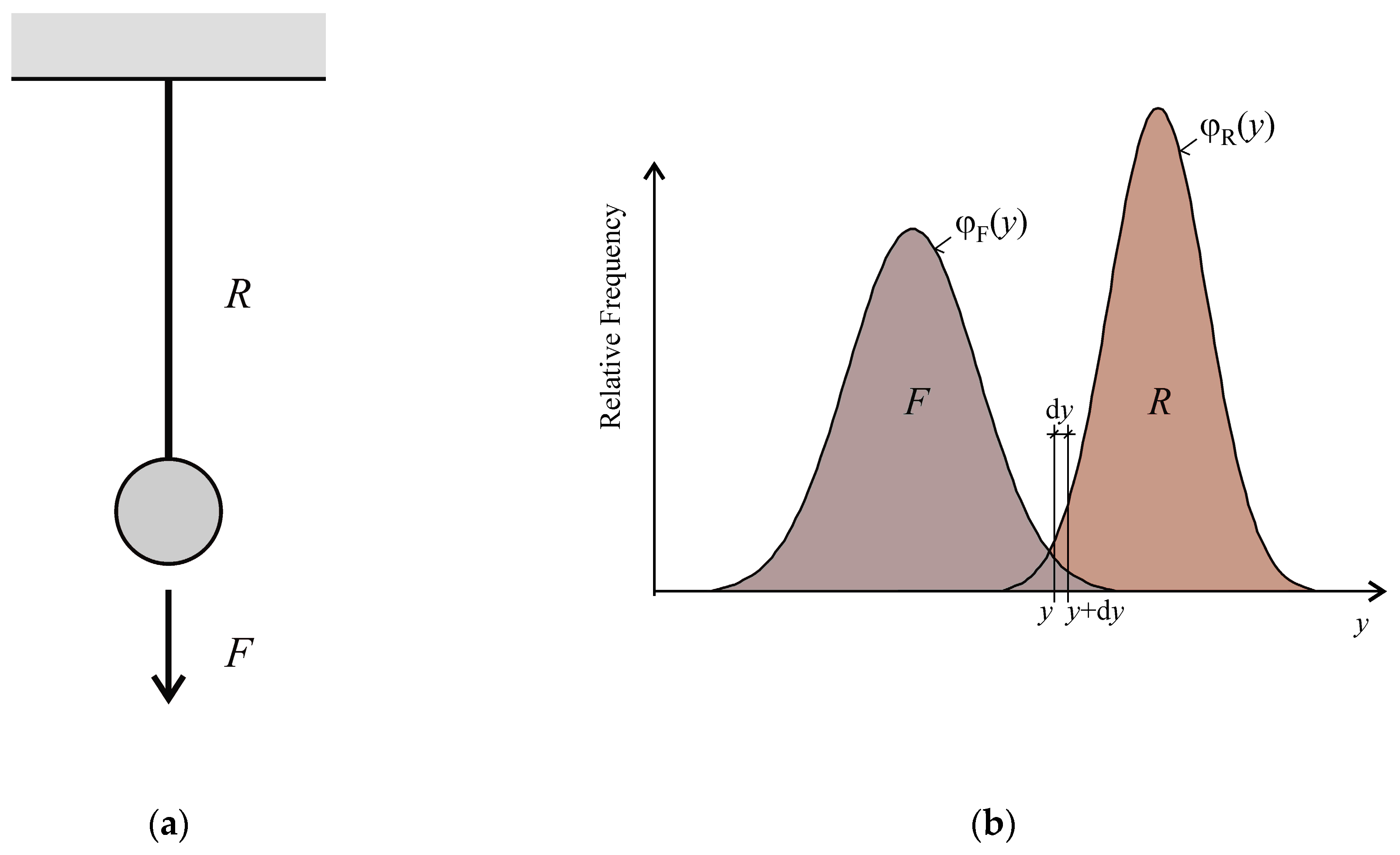
Equation (9) is the design reliability condition with formally separated random variables that can be expressed as

$${\mu }_F+{\alpha }_F{\beta }_d{\sigma }_F\le {\mu }_R-{\alpha }_R{\beta }_d{\sigma }_R.$$

(10)

where the left-hand side represents the design load F_d and the right-hand side the design resistance R_d; see Figure 2. The basic reliability targets for design values in the ultimate limit state recommended in [19] are based on the semi-probabilistic approach in Figure 2, with the target value of reliability index β_d = 3.80 for a 50 years reference period [48,49]. For β_d = 3.8, R_d can be approximately computed as 0.1 percentile [40]. Standard [19] enables the determination of design values F_d, R_d not only from a Gauss pdf but also from a two- or three-parameter lognormal (for resistance) or Gumbel or Gama (for load) pdfs. The probability of failure for non-Gaussian R and F can be estimated using Monte Carlo (or quasi-Monte Carlo) methods.

3. Selected Types of Sensitivity Analysis Methods

In reliability engineering, SA methods quantify the effects of input variables on the failure probability, reliability index β or design quantiles. However, other statistical model-based inferences sensitive to reliability are often used. In this chapter, we present selected formulae of selected types of sensitivity measures in forms that are adapted to structural reliability analysis.

Cramér–von Mises indices [50]. Input random variables in Equation (1) are assumed to be statistically independent. Let Φ_Z be the distribution function of Z:

$${\mathsf{\Phi }}_Z\left(t\right)=P\left(Z\le t\right)=E\left(1_{Z\le t}\right) \mathrm{for} t\in R,$$

(11)

and ${\mathsf{\Phi }}_Z^i$ is the conditional distribution function of Z conditionally on X_i:

$${\mathsf{\Phi }}_Z^i\left(t\right)=P\left(Z\le t|X_i\right)=E\left(1_{Z\le t}|X_i\right) \mathrm{for} t\in R.$$

(12)

The first-order Cramér–von Mises index G_i is based on measuring the distance between probability Φ_Z(t) and conditional probability ${\mathsf{\Phi }}_Z^i$(t) when an input is fixed [50].

$$G_i={\displaystyle \underset{R}{\int }\frac{E\left[{\left({\mathsf{\Phi }}_Z\left(t\right)-{\mathsf{\Phi }}_Z^i\left(t\right)\right)}^2\right]}{{\mathsf{\Phi }}_Z\left(t\right)\left(1-{\mathsf{\Phi }}_Z\left(t\right)\right)}}\mathrm{d}{\mathsf{\Phi }}_Z\left(t\right).$$

(13)

The second-order Cramér–von Mises index G_i can be expressed, on the basis of [50], as

$$G_{ij}={\displaystyle \underset{R}{\int }\frac{E\left[{\left({\mathsf{\Phi }}_Z\left(t\right)-{\mathsf{\Phi }}_Z^{ij}\left(t\right)\right)}^2\right]}{{\mathsf{\Phi }}_Z\left(t\right)\left(1-{\mathsf{\Phi }}_Z\left(t\right)\right)}}\mathrm{d}{\mathsf{\Phi }}_Z\left(t\right)-G_i-G_j,$$

(14)

where ${\mathsf{\Phi }}_Z^{ij}$ is the conditional distribution function of Z conditionally on X_i, X_j, for i < j:

$${\mathsf{\Phi }}_Z^{ij}\left(t\right)=P\left(Z\le t|X_i,X_j\right)=E\left(1_{Z\le t}|X_i,X_j\right) \mathrm{for} t\in R.$$

(15)

Integration Equation (13) and Equation (14) respect t. Equation (13) is not oriented to one failure probability value P_f, but, depending on t, integrates the averages of squared values from the differences of all probabilities Equations (11) and (12) normalized by F(t)(1 − F(t)). The same applies to other higher-order indices [50]. Indices G_i, G_ij, etc., are based on Hoeffding decomposition; therefore, the sum of all indices is equal to 1 [50]. It can be noted that Cramér–von Mises indices can be formulated in copula theory framework [51].

Sensitivity indices subordinated to contrasts associated with probability [17] (in short, Contrast P_f indices). These indices measure the distance between probability P_f and the conditional probability P_f|X_i using the contrast function in Equation (16). The input random variables in Equation (1) are assumed to be statistically independent.

$$\mathsf{\psi }\left(\theta \right)=E\left(\psi \left(Z,\theta \right)\right)=E{\left(1_{Z<0}-\theta \right)}^2.$$

(16)

The first-order probability contrast index C_i is defined as Equation (17), where the contrast $\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)$ is computed for probability estimator θ* = Argmin ψ(θ) = P_f.

$$C_i=\frac{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)-E\left(\underset{\theta }{\min E} \left(\psi \left(Z,\theta \right)|X_i\right)\right)}{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)}.$$

(17)

The second term in the numerator in Equation (17) is computed as the average value of the conditional contrast functions whose probability estimator is P_f|X_i. The second-order probability contrast index C_ij can be expressed as

$$C_{ij}=\frac{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)-E\left(\underset{\theta }{\min E} \left(\psi \left(Z,\theta \right)|X_i{X}_j\right)\right)}{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)}-C_i-C_j,$$

(18)

where i < j. Indices of the third and higher orders are computed similarly [17]. Sensitivity indices subordinated to contrasts are based on decomposition; therefore, the sum of all indices must be equal to one. Examples of the computation of indices using the Latin Hypercube Sampling method (LHS) [52,53] in engineering applications are in [54,55].

Sensitivity indices subordinated to contrasts associated with α-quantile [17]. The contrast function ψ associated with α-quantile can be written with parameter θ as [17]:

$$\mathsf{\psi }\left(\theta \right)=E\left(\psi \left(Z,\theta \right)\right)=E\left(\left(Y-\theta \right)\left(\alpha -1_{Y<\theta }\right)\right),$$

(19)

where the input random variables in Equation (1) are assumed to be statistically independent. The first-order quantile contrast index Q_i is defined as

$$Q_i=\frac{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)-E\left(\underset{\theta }{\min E} \left(\psi \left(Y,\theta \right)|X_i\right)\right)}{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)},$$

(20)

where $\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)$ is the contrast computed for the estimator of α-quantile θ* = Argmin ψ(θ).

$$Q_{ij}=\frac{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)-E\left(\underset{\theta }{\min E} \left(\psi \left(Y,\theta \right)|X_i\right)\right)}{\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)}-Q_i-Q_j.$$

(21)

The second-order quantile contrast index Q_ij is defined as Equation (21), where i < j. Indices of the third and higher orders are computed in a similar manner [17]. Sensitivity indices subordinated to contrasts are based on decomposition; therefore, the sum of all indices must be equal to one. In engineering applications, the random variable Y is, for example, the load action F or resistance R [56]; see Figure 1.

Borgonovo moment independent importance measure [14] (in short, Borgonovo indices). The sensitivity indices described in [14] are defined by introducing a moment-independent uncertainty indicator that looks at the entire input/output distribution and whose definition is well-posed also in the presence of correlations among the input parameters.

$$B_i=\frac{1}{2}E{\displaystyle \int \left|{\varphi }_Z\left(z\right)-{\varphi }_{Z|X_i}\left(z\right)\right|dz},$$

(22)

where ϕ_Z(z) is the pdf of Z and ϕ_Z│Xi(z) is the conditional pdf of Z given that one of the parameters, X_i, assumes a fixed value [14]. Fixing pairs X_i, X_j, leads to the second-order index B_ij, where i < j. Fixing triplets X_i, X_j, X_k leads to the third-order index B_ijk, where i < j < k, etc. The sum of all indices is not equal to one. As a general rule, 0 $\le$ B_i $\le$ B_ij$\le$..$\le$ B_1,2,…,M $\le$ 1 [14].

Reliability sensitivity index defined by Xiao et al. [57] (in short, Xiao indices). All the input variables are independent of each other. The first-order index S_i measures the individual effect of X_i on P_f.

$$K_i=\frac{1}{2P_f}E\left(\left|P_f-P_f|X_i\right|\right),$$

(23)

where |P_f – P_f|X_i| measures the absolute difference between the unconditional failure probability P_f and the conditional failure probability P_f|X_i. The second-order interaction indices K_ij, where $i\ne j$, are asymmetrical:

$$K_{ij}=\frac{1}{2}E\left(\left|\frac{P_f|X_i}{P_f}-\frac{P_f|X_i,X_j}{P_f|X_j}\right|\right).$$

(24)

K_ij may or may not be equal to K_ji. Third-order and higher-order indices are not defined in [57].

Reliability sensitivity index defined by Ling et al. [58] (in short, Ling indices). The first-order index is the same as in Equation (23) L_i = K_i. Fixing pairs X_i, X_j, leads to the second-order index L_ij, where i < j:

$$L_{ij}=\frac{1}{2P_f}E\left(\left|P_f-P_f|X_i,X_j\right|\right).$$

(25)

Fixing triplets X_i, X_j, X_k leads to the third-order index L_ijk, where i < j < k, etc. The sum of all indices defined by Ling et al. [58] is not equal to one. As a general rule [58], 0 $\le$ L_i $\le$ L_ij$\le$...$\le$ L_1,2,…,M $\le$ 1.

Sobol’s sensitivity indices [12,13] (in short, Sobol’s indices). Sobol’s first-order sensitivity indices can be written in the form:

$$S_i=\frac{V\left(Z\right)-E\left(V\left(Z|X_i\right)\right)}{V\left(Z\right)}=\frac{V\left(E\left(Z|X_i\right)\right)}{V\left(Z\right)}=cor{r}^2\left(Z,E\left(Z|X_i\right)\right),$$

(26)

where corr is Pearson correlation coefficient. Fixing pairs X_i, X_j, leads to the second-order index S_ij, where i < j. Fixing triplets X_i, X_j, X_k leads to the third-order index S_ijk, where i < j < k, etc.; see, for example [9]. The sum of all indices is equal to one. It can be noted that Sobol’s indices present a special case of sensitivity indices subordinated to contrasts in which the contrast function is associated with variance ψ(θ) = E(Z − θ)² [17].

Omission sensitivity factor [59] (in short, Madsen’s factor). The omission sensitivity factor O_i is defined as the ratio between the conditional reliability index β|X_i = μ_xi and the reliability index β (7).

$$O_i=\frac{\beta |\left(X_i={\mu }_{X_i}\right)}{\beta }.$$

(27)

Random variable X_i is fixed at its mean value μ_xi in the numerator in Equation (27), but the possibility of fixing at the characteristic value [60] or median [3] is also indicated.

The indices described above can be divided into two groups. The first group (Sobol, Borgonovo and Cramér–von Mises) focuses on the distribution or some moments of the output function Z, while the second group (Xiao, Ling, Contrast, Madsen’s) considers P_f, β or quantiles as the quantity of interest and thus can be referred to as reliability analysis indices. The first group can be classified as global SA, while the second group can be classified as reliability-oriented sensitivity analysis (ROSA) [3], of which Xiao, Ling and Contrast indices can terminologically [54,57,58] be classified as global ROSA. It can be noted that Xiao, Ling and Contrast ROSA indices are typical examples of ambiguous “local–global” indices [3]. On one hand, they can be considered as global since they are based on changes of P_f with regard to the variability of the inputs over their entire distribution ranges and they provide the interaction effect between different input variables. On the other hand, they can be considered as local in the sense of regional SA since they are based on the frequency of failures from the random realization in “region” of pairs of large load actions and small resistances.

Correlations. The last SA methods used are the analysis of the correlation between the input X_i and output Z according to Pearson, Spearman and Kendal Tau.

4. Case Studies

Many new sensitivity indices have been developed, but their ability in applications has not yet been reliably demonstrated. In this article, the properties of the selected sensitivity indices mentioned in Chapter 3 are examined in a case study of the probabilistic analysis of the reliability of a steel bar under axial tension; see Figure 3. A static time-independent study is considered.

In general, the random load action F and resistance R are usually described using appropriate types of distribution functions Φ_F(y), Φ_R(y) and corresponding pdfs ϕ_F(y), ϕ_R(y), where y denotes a general point of the observed variable (force with the unit of Newton), through which both variables F and R are expressed; see right part of Figure 3. It is assumed that F and R are statistically independent of each other with mean values μ_F, μ_R and standard deviations σ_F, σ_R.

The probability of failure $P_f=P\left(Z<0\right)=P\left(R<F\right)$ can be computed as the integral:

$$P_f={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\mathsf{\Phi }}_R\left(y\right){\varphi }_F\left(y\right)\mathrm{d}y}.$$

(28)

In the case studies, integration in Equation (28) is performed numerically by Simpson’s rule, using more than ten thousand integration steps over the interval [μ_Z − 10σ_Z, μ_Z + 10σ_Z].

Reliability can be assessed by comparing the computed P_f in Equation (6) with the target value of P_f, where target values for design cases are listed in standard EN1990 [19]. Target values of P_f in

Table 1. Recommended minimum values of β and related P_f.

Reliability Class	β	Pf
RC3	4.3	8.5·10−6
RC2	3.8	7.2·10−5
RC1	3.3	4.8·10−4

are taken from Table B2 in [19]. Table 1 lists the minimum values of P_f (the reliability index β) for ultimate limit state and 50 years reference period. The description of subsequent classes RC1, RC2, and RC3 with examples of building and civil engineering works are in [19,48].

The aim of the presented study is the SA of the influence of input factors R, F on the output P_f using different types of sensitivity indices and the subsequent comparison of obtained results. Resistance R is the input random variable X₁, and load action F is the input random variable X₂.

4.1. Computation of Sensitivity Indices

This section includes a description of numerical methods for computing the size of sensitivity indices based on numerical integration methods in combination with sampling-based methods or analytical computation. Sensitivity indices were computed for eight SA types.

Contrast P_f indices [17] (ROSA). The contrast function Equation (16) is minimum if θ* = P_f. By substituting P_f into Equation (16), we can write first-order index in Equation (17) using $\underset{\theta }{\min } \mathsf{\psi }\left(\theta \right)$ = P_f (1 − P_f), and similarly for P_f|X_i, we can write $\underset{\theta }{\min E} \left(\psi \left(Z,\theta \right)|X_i\right)$ = (P_f |X_i)(1 − (P_f |X_i)).

$$C_i=\frac{P_f\left(1-P_f\right)-E\left(\left(P_f|X_i\right)\left(1-P_f|X_i\right)\right)}{P_f\left(1-P_f\right)}.$$

(29)

By substituting P_f (1 − P_f) and (P_f|X_i)(1 − (P_f|X_i)) into Equation (17), we can derive Equation (29) for practical use. C_i measures, on average, the effect of fixing X_i on P_f. The estimate of P_f is computed as the integral Equation (28). In the first loop, the estimate of P_f|X_i = P((Z|X_i) < 0) is computed by numerical integration across z∈[μ_Z − 10σ_Z, μ_Z + 10σ_Z]. In the second loop, E[•] is computed by numerical integration of the pdf of X_i with a small step Δx_i taken over [μ_Xi − 10σ_Xi, μ_Xi + 10σ_Xi]. Since the second term in the numerator in Equation (18) is always equal to zero (P_f|X₁,X₂ is always equal to zero or one), C₁₂ = 1 − C₁ − C₂.

Xiao indices [57] (ROSA). Indices K₁, K₂ are estimated from Equation (23) using double-nested-loop computation. In the outer loop, E[•] is computed by numerical integration of the pdf of X_i with a small step Δx_i taken over [μ_Xi − 10σ_Xi, μ_Xi + 10σ_Xi]. Note: the estimate E[•] obtained using the LHS method would be inaccurate because it requires an extremely high number of runs for small values of P_f. In the nested loop, estimates of P_f and P_f|X_i are computed by integrating according to Equation (28). Indices K₁₂ and K₂₁ defined in Equation (24) are computed in a similar manner.

Ling indices [58] (ROSA). By definition, L₁ = K₁, L₂ = K₂. The computation of L₁₂ includes an estimate of E[•], which is based on double numerical integration. In the outer loop, the pdf of X₂ is numerically integrated with a small step Δx₂ taken over [μ_X2 − 10σ_X2, μ_X2 + 10σ_X2]. In the inner loop, the pdf of X₁ is numerically integrated with a small step Δx₁ taken over [μ_X1 − 10σ_X1, μ_X1 + 10σ_X1]. During integration, the term P_f|X₁,X₂ can only have a value of 0 or 1.

Madsen factor [59] (ROSA). Indices O₁, O₂ are computed using one million LHS runs.

Cramér–von Mises indices [50]. Indices G₁ and G₂ are computed using Equation (13). Three nested loops are applied. In the first (outer) loop, numerical integration is computed with a small step Δt = t_l+1 − t_l, where t = (t_l+1 + t_l)/2, t∈[μ_Z − 10σ_Z, μ_Z + 10σ_Z], l = 1, 2,..., 10000. To each Δt belongs dΦ(t)≈P(t_l $\le$ Z $\le$ t_l+1) and Φ(t)≈P(Z $\le$ (t_l+1 + t_l)/2). In the second loop, E[•] in the numerator in Equation (13) is computed by numerical integration of the pdf of X_i with a small step Δx_i taken over [μ_Xi−10σ_Xi, μ_Xi+10σ_Xi]. Note: The LHS estimation of E[•] would be numerically very challenging but is possible. In the third (deep) loop, Φⁱ(t)≈P(Z $\le$ (t_l+1 + t_l)/2|X_i = ξ_i) is computed by numerical integration for fixed ξ_i, where ξ_i is the middle of interval Δx_i from the second loop. The index G₁₂ is computed on the basis of Equation (14) in a similar manner.

Borgonovo indices [14]. Indices B₁, B₂ are estimated from Equation (13) using double-nested-loop computation. In the outer loop, 0.5·E[•] is computed using one million runs of the LHS method. In the nested loop, numerical integration |ϕ_Z(z) – ϕ_Z|Xi(z)| is taken over [μ_Z − 10σ_Z, μ_Z + 10σ_Z] using ten thousand runs. B₁₂ = 1 in all case studies.

Sobol’s indices [12,13]. Sobol’s sensitivity indices are included only for comparison; these indices analyse the influence of the variance of R or F on the variance of Z, but not the influence on P_f. Sobol’s indices are computed analytically as S₁ = ${\sigma }_R^2$/(${\sigma }_R^2+{\sigma }_F^2$), S₂ = ${\sigma }_F^2$/(${\sigma }_R^2+{\sigma }_F^2$), S₁₂ = 0. It can be noted that Sobol’s first-order indices are equal to the squares of the sensitivity coefficients (weight factors) in Equation (8): S₁ = ${\alpha }_R^2$, S₂ = ${\alpha }_F^2$.

Correlations. Correlation corr(X₁, Z) and corr(X₂, Z) are evaluated even though direct sensitivity to P_f is not measured by correlation. Pearson, Spearman and Kendal Tau correlation coefficients between input X_i and output Z are computed using one hundred thousand runs of the LHS method.

All E[•] are computed by numerical integration with the exception of Borgonovo indices and correlation. It can be noted that E[•] in the formulae in chapter 3 can also be numerically computed using Monte Carlo- (or quasi-Monte Carlo-) type simulation methods; however, the repeated computation of small values of P_f requires extremely high numbers of simulation runs and is numerically challenging.

4.2. Case Study 1

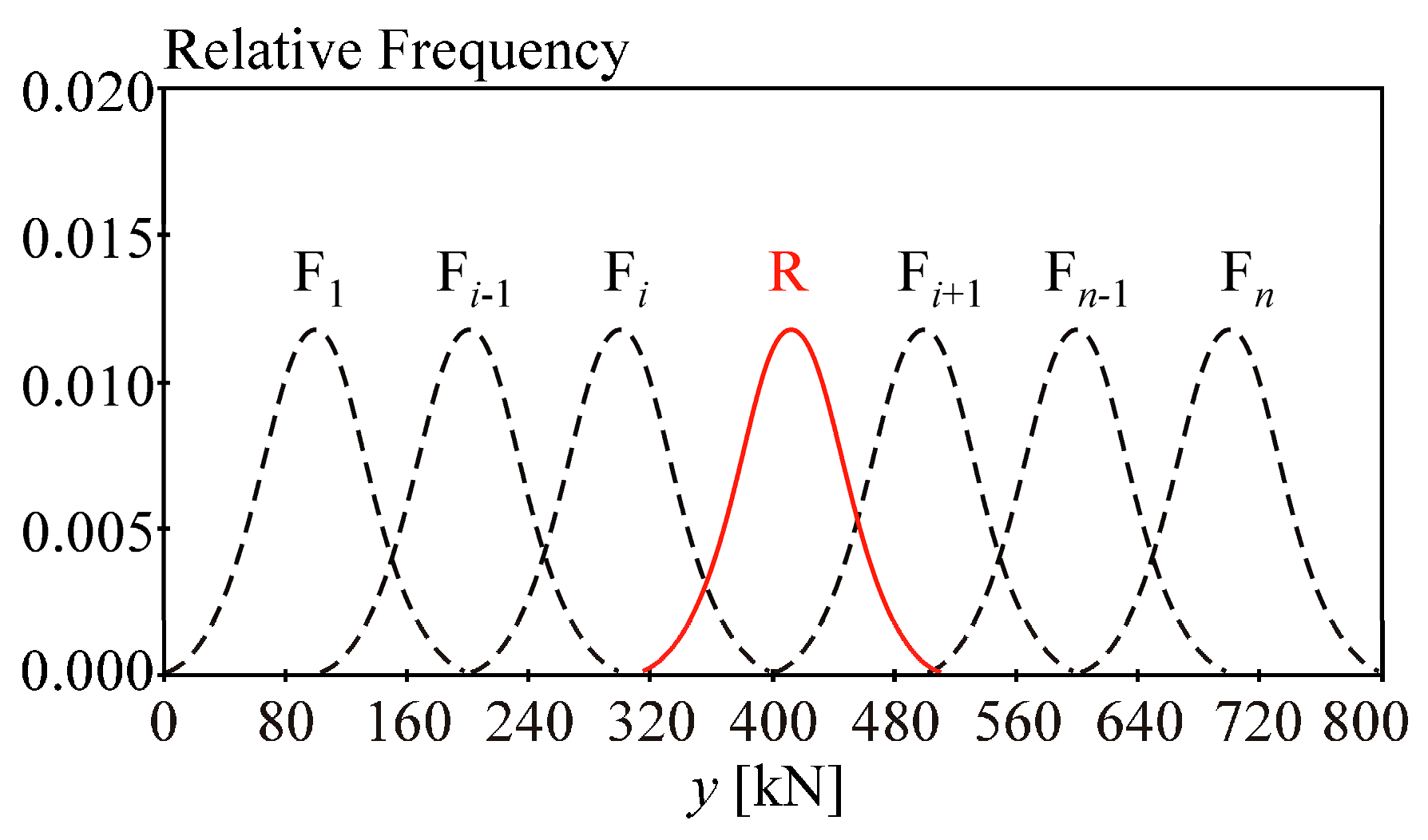
The aim of SA is to assess the influence of R and F on P_f. Let R (resistance) and F (load action) be statistically independent variables X₁, X₂ with Gauss pdfs, where μ_R = 412.54 kN, σ_R = 34.132 kN, σ_F = 34.132 kN, and mean value μ_F is the parameter; see Figure 4. Let parameter μ_F change with the step Δμ_F = 10 kN and gradually attain the values 92.54 kN, 102.54 kN,..., 722.54 kN. The sensitivity indices are plotted in dependence on P_f, where P_f = Φ_U(−(412.54 − μ_F)/(2^0.5·34.132)) is a function only of parameter μ_F. If μ_F decreases, then P_f decreases.

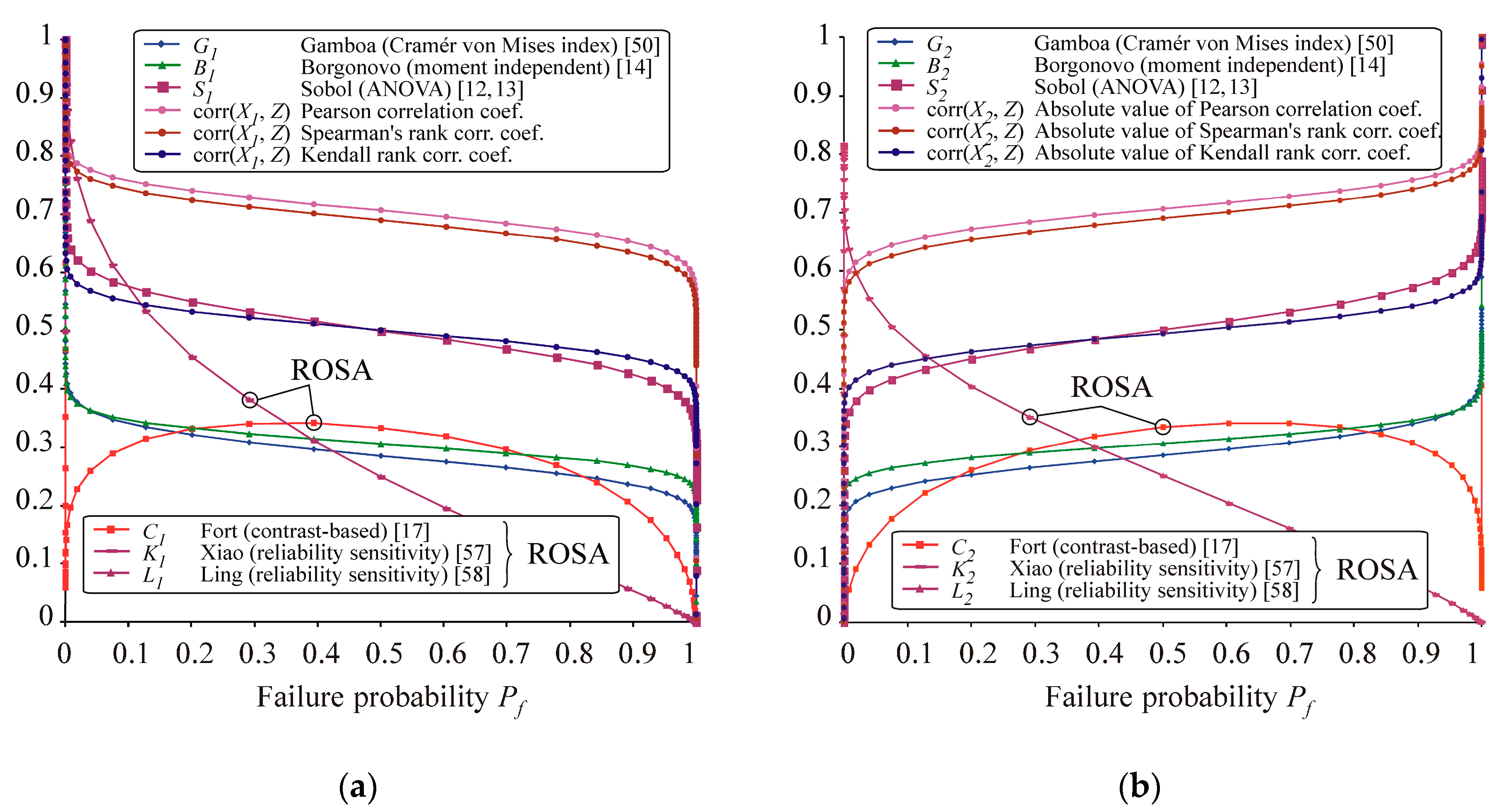
First-order indices are depicted in Figure 5 and the second-order indices are depicted on the left part of Figure 6. Correlation coefficients corr(X₁, Z) and corr(X₂, Z) are added to Figure 5. Only indices within the interval [0, 1] are depicted. Madsen’s factors are not plotted because they have a constant value O₁ = O₂ = 1.415 for all P_f (μ_F).

Changing P_f (μ_F) influences only indices C₁, C₂, C₁₂, indices K₁, K₂, K₁₂, K₂₁ and indices L₁, L₂, L₁₂; see Figure 5 and the left part of Figure 6. For the other five types of SA, it was observed that two variables that have a different influence on the output have the same indices. This demonstrates properties of sensitivity indices that will prove useful in the interpretation of the result.

Ling and Xiao indices are the only indices with asymmetric plots and decrease with increasing P_f. Xiao asymmetrical interaction indices are identical: K₁₂ = K₂₁. Contrast-based sensitivity indices have values of C₁ = C₂ = C₁₂ = 0.33 for P_f = 0.5, but, otherwise, decrease with absolute distance from P_f = 0.5. Approaching P_f → 0 or P_f → 1 leads to C₁ = C₂ → 0 and C₁₂ → 1. Change in mean value μ_F has no influence on the values of Sobol’s indices, which are functions of only the variance and therefore remain constant S₁ = S₂ = 0.5, S₁₂ = 0. Kendall’s tau coefficient is approximately equal to 0.5 for all P_f (μ_F). Spearman’s and Pearson coefficients confirm the dependence between the inputs R, F and the output Z. Borgonovo and Cramér–von Mises first-order indices have approximately the same value B₁ = 0.306, G₁ = 0.286, while the second-order indices are B₁₂ = 1.0 and G₁₂ = 1.0 − G₁ − G₂ = 0.428.

For common design situations, building constructions are considered reliable if P_f < 7.2·10⁻⁵ (RC2 in Table 1). For this case study, it occurs approximately for μ_F < 0.55·μ_R. Detail of the plots of sensitivity indices for P_f < 1·10⁻⁴ are depicted on the right part of Figure 6.

4.3. Case Study 2

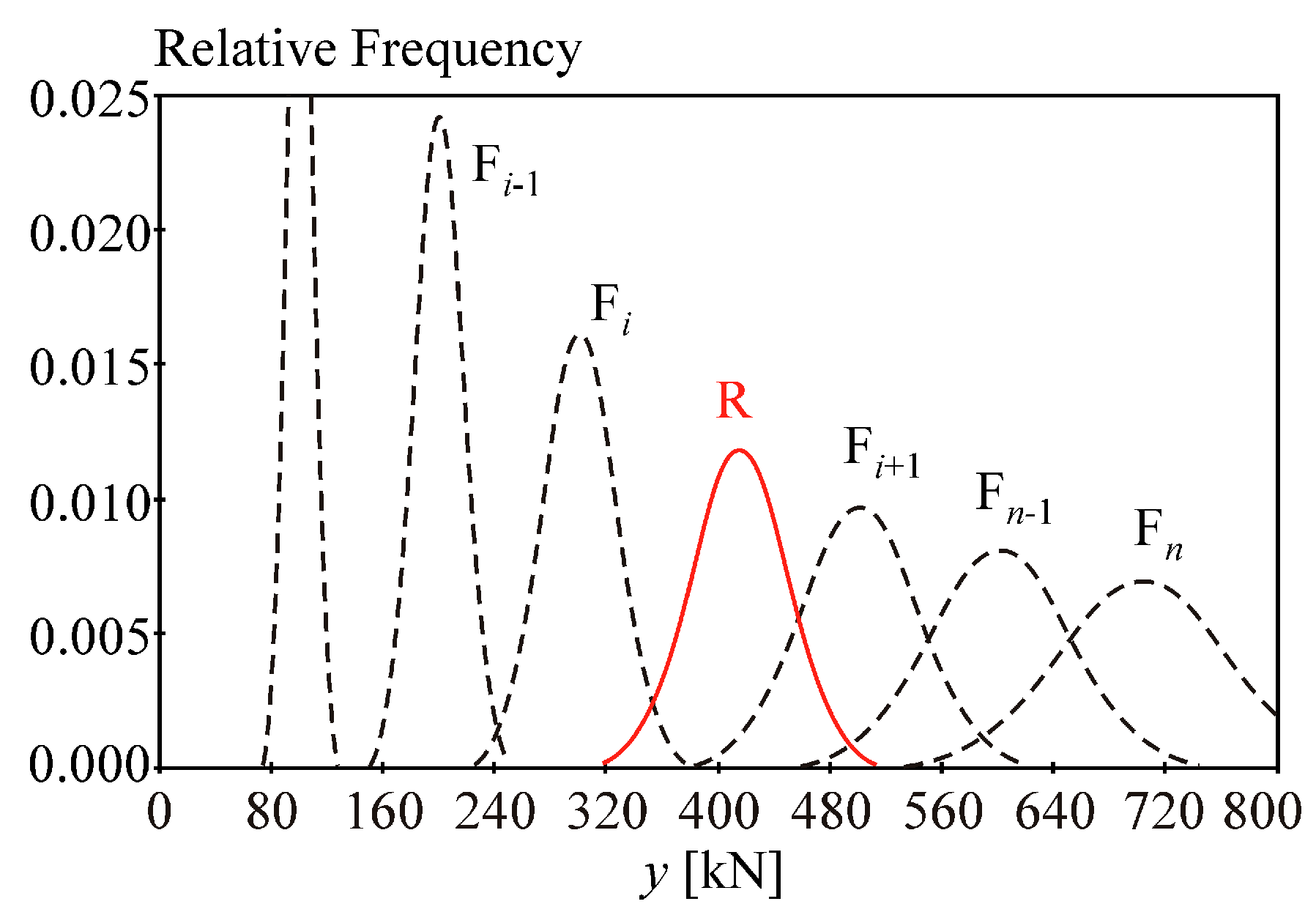
Let R (resistance) and F (load action) be statistically independent variables X₁, X₂ with Gauss pdfs, where μ_R = 412.54 kN, σ_R = 34.132 kN and mean value μ_F is the parameter, while variation coefficient of F is constant v_F = v_R = 34.132/412.54 = 0.0827 and thus σ_F = v_F·μ_F; see Figure 7. Let parameter μ_F change with the step Δμ_F = 12.89 kN and gradually attain values of 0.06 kN, 12.95 kN,..., 902.36 kN.

The sensitivity indices are plotted in dependence on P_f, where P_f = Φ_U(−(412.54 − μ_F)/(34.132² + (μ_F·34.132/412.54)²)^0.5) in Equation (6) is a function of only parameter μ_F, where P_f decreases if μ_F decreases.

The first-order indices are depicted in Figure 8 and the second-order indices are depicted on the left part of Figure 9. Correlation coefficients corr(X₁, Z) and corr(X₂, Z) are added to Figure 8. Only indices within the interval [0, 1] are depicted. Omission sensitivity indices are not plotted because they have a value greater than one. The curves meet the expectation that small P_f (due to small μ_F and small σ_F) are less sensitive to F and more sensitive to R.

The parametric change of P_f (μ_F) influences the values of all indices. All first-order indices of variable X₁ (R) are axially symmetrical to indices X₂ (F) along the vertical axis P_f = 0.5 with the exception of Ling and Xiao indices. Xiao asymmetrical interaction indices are K₁₂ ≠ K₂₁ with the exception of P_f = 0.5 where K₁₂ = K₂₁. The plots of Borgonovo and Cramér–von Mises first-order indices are similar; the second-order indices are B₁₂ = 1.0 and G₁₂ = 1.0 − G₁ − G₁₂. The plots of Kendall’s tau coefficient and plots of Sobol’s indices are similar. The plots of Spearman’s and Pearson coefficients are also similar. On the left side of the graphs, contrast P_f indices reach their extreme at point P_f = 3.216·10⁻¹⁰, C₁ = 0.06, C₁₂ = 0.94, but no extreme on C₂. On the right side of the graphs, the extreme is at point P_f = 1 − 3.216·10⁻¹⁰, C₂ = 0.06, C₁₂ = 0.94, but no extreme on C₁. Ling and Xiao indices have an extreme at P_f = 3.216·10⁻¹⁰, K₂ = L₂ = 0.82, K₁₂ = 0.94; other extremes of Ling and Xiao indices are difficult to identify numerically (compared to other indices) because they quickly attain relatively small or large values for large or small P_f.

For standard design case P_f = 7.2·10⁻⁵ we obtain K₁ = L₁ = 0.97, K₂ = L₂ = 0.76, K₁₂ = 0.91, K₁₂ = 0.994, L₁₂ = 0.99993. A detail of the plot of sensitivity indices for P_f < 1·10⁻⁴ is depicted on the right part of Figure 9. For instance, for P_f = 7.2·10⁻⁵, we obtain O₁ = 1.88, O₂ = 1.18, or for P_f = 8.5·10⁻⁶, we obtain O₁ = 1.99, O₂ = 1.16.

5. Observation, Discussion and Questions

Reliability-oriented sensitivity indices (Xiao, Ling, Contrast and Madsen’s) are computed together with the global indices (Sobol, Borgonovo and Cramér–von Mises). The effects of R and F on structural reliability are first analysed separately for each of the eight selected sensitivity indices.

Contrast P_f indices have relatively small values of first-order indices and high values of second-order indices for small P_f. The numerical results of reliability engineering tasks [54,55] with five input random variables have shown that the smaller P_f is, the smaller the values of first-order indices and the higher the values of higher-order indices. Change in the mean value or standard deviation of the dominant variables had a clear effect on P_f, confirming the rationality of the contrast indices applied in [54]. The sum of all indices is equal to one, which makes it easier to compare SA results for different P_f associated with different reliabilities, for e.g., different design conditions, different stages of the structural life or different loading conditions. For very small values of P_f, Equation (29) can be written approximately as:

$$C_i\approx \frac{P_f-E\left(\left(P_f|X_i\right)\right)}{P_f},$$

(30)

and similarly

$$C_{ij}\approx \frac{P_f-E\left(\left(P_f|X_i,X_j\right)\right)}{P_f}-C_i-C_j.$$

(31)

The clear addressability to P_f is evident from Equation (30) and Equation (31). If the binary random variable 1_Z<0 is considered, Equation (30) can then be written as:

$$C_i\approx \frac{E\left(1_{Z<0}\right)-E\left(E\left(1_{Z<0}|X_i\right)\right)}{E\left(1_{Z<0}\right)}=cor{r}^2\left(1_{Z<0},E\left(1_{Z<0}|X_i\right)\right),$$

(32)

where corr is Pearson correlation coefficient. SA based on contrast functions yields the same (symmetrical) results for unreliability (P_f) and reliability (1 − P_f) because C_i in Equation (29) is computed from the values of the contrast functions P_f (1 − P_f) and (P_f|X_i)(1 − (P_f|X_i)). If 1_Z<0 is rare, the evaluation of Equation (32) using Monte Carlo type methods requires an extreme number of samples.

The sum of all Ling or Xiao indices is not equal to one. For small P_f, the values of the first-order indices are relatively high; moreover, the second-order index is always greater than the first-order index, which complicates the comparison of the influence on P_f. The advantage of computing Ling indices is that the computation of the higher-order indices does not depend on the computation (accuracy) of lower-order indices; therefore, their computation may be performed parallelly on multiple processor cores.

Cramér–von Mises indices have the sum of all indices equal to one. However, there is no addressability of indices to the P_f level because Equations (13) and (14) are integrated over all dΦ_Z(t), i.e., over all t (which means over all P_f). This is also the reason that, at intervals relevant to reliability, index values are not extremely high or low. The advantage is that a zero value of the Cramér-von Mises index clearly means that the input is not important. Triple-nested-loop computation makes these indices very numerically challenging. Nevertheless, numerous effective approaches to reduce this computational complexity already exist; see, for e.g., [61].

Borgonovo first-order indices yield reasonable values in intervals relevant to reliability, similar to Cramér–von Mises indices. The advantage of these indices is the transparency and the clear interpretation of the influence of input uncertainty on the entire output distribution regardless of the specific moment of the output (moment independence). Moreover, the indices can be computed even in the presence of correlation between input variables. The computational complexity of indices is not high. The disadvantage is that the sum of all indices is not equal to one and the indices are not directly addressable to P_f.

Sobol’s indices are functions of only the variance, which, although important, is not enough for SA of reliability. The computation of Sobol’s indices is based on the double-nested-loop computation and can be numerically very challenging for engineering tasks. However, if we consider the binary random variable 1_Z<0 as the quantity of interest, Sobol’s indices can be an interesting reliability-oriented sensitivity technique [62].

Madsen’s factor can be applied as a computationally undemanding (simple) SA in engineering tasks, but with a number of limitations. Madsen’s factor can only be applied for P_f < 0.5. The disadvantage of Madsen’s factor is that factor O_i can have values significantly greater than 1. For example, in Case study 2, for P_f = 6.14·10⁻³² we obtain O₁ = 32. A model with one random variable would theoretically lead to O₁ = ∞. A significant computational problem can occur in non-linear problems when fixing to the mean value X_i leads to the limit case of a given physical phenomenon. For example, the amplitude of the axial curvature of a slender bar subjected to buckling has a mean value equal to zero, which means a perfectly straight bar [63]. The resistance of such a perfectly straight (unrealistic) bar is always higher than the resistance of a bar with any non-zero imperfection [64], and thus the mean value of zero is not suitable for fixing in reliability analysis or SA. The modification of Equation (27) to the form E(β|X_i)/β can be discussed, but with the proviso that fixing X_i must not lead to negative values of β. So far there is no global SA based on β, and it is questionable whether the first two statistical moments are sufficient to describe the influence on reliability.

The correlation coefficients are not directly addressable to P_f but can be used as sensitivity indicators if the output (Z) is monotonically dependent on the input variables R and F. Correlation points to dependence, but the opposite is not true. The advantage of correlation coefficients is their availability in computer software and they are relatively computationally inexpensive in simulation approaches.

ROSA-type indices have a different explanatory power than those of other types. Similar results cannot be expected from these two types (ROSA vs. non-ROSA) of indices as an input variable could be influential on P_f but not on the distribution of Z and conversely. Nevertheless, there is relatively good agreement between contrast Cramér–von Mises indices, Borgonovo indices and P_f indices in the interval of approximately P_f $ϵ$ (0.1, 0.9). However, common building structures are designed with a reliability of P_f < 4.8·10⁻⁴; see Table 1. For such small P_f, only Cramér–von Mises indices and Borgonovo indices have similar values. The values of the other sensitivity indices are considerably different.

It can be concluded from all the obtained numerical results that if σ_F < σ_R (σ_F > σ_R), the sensitivity of P_f to R is higher (lower) than the sensitivity of P_f to F. It was confirmed that only ROSA-type indices are suitable for probability-based reliability assessment. The results of Case study 1 showed that change in μ_F together with σ_F = const. changes only the values of contrast P_f indices and Ling and Xiao indices, the other indices remain unchanged. Furthermore, change in σ_F together with μ_F = const. changes the values of all indices, except of course B₁₂ = 1 and S₁₂ = 0. The results of Case study 2 showed that changes in σ_F and μ_F with the condition v_F = σ_F/μ_F = const. causes changes in the values of all indices; therefore, none of these indices is a pure indicator of the influence of v_F on P_f.

It can be noted that resistance is generally a random variable that is a product of random variables such as yield strength (material characteristic), cross-sectional area (geometric characteristic), etc. Material and geometric characteristics usually do not have perfect Gauss pdf due to small skewness and kurtosis observed in histograms from real experiments [65,66]. The dead load can be roughly approximated using Gauss pdf, but other load types (wind, snow, traffic, long-term load action) have pdfs significantly different from Gauss pdf. For more complex structures, numerous load conditions and tens to hundreds of random variables with different pdfs can be expected. Furthermore, input random variables may have mutual correlations, which are implemented in beams [67] in more detail than in systems where each beam is represented by a smaller number of random variables independent of another beam; see for e.g., [68].

The question is, to what extent can different types of sensitivity indices oriented to P_f be influenced by the skewness and kurtosis values of the input variables or by correlations between them, and what is its importance for the analysis of reliability? For instance, the values of Sobol’s indices change when the kurtosis changes, but not when the skewness changes [34]. Of the SA types presented here, only Borgonovo indices [14] have the ability to have correlations between input variables. This ability must also be sought in other indices suitable for structural reliability analysis.

A generally accepted measure of reliability is P_f; therefore, P_f should be the overall objective of SA. However, the concept of Eurocodes [19] assesses reliability according to the limit states using the so-called semi-probabilistic method, which compares the design values (quantiles) of resistance and load. Because probabilistic reliability analysis would be too expensive in common engineering practice, design values are usually computed deterministically according to design standards. These design values can be verified using the lower quantity of resistance (for e.g., 0.1 percentile) and upper quantity of load, where resistance and load are functions of other random variables; see Figure 2. Another useful property of SA could be that sensitivity indices oriented to P_f and design quantiles form pairs based on the same theoretical basis. For example, global SA subordinated to contrasts can be associated with both P_f and quantities R_d and F_d; see Figure 2. However, the question is whether there is a link between indices Equations (17), (18) and (20), (21) when the contrast functions Equations (16) and (19) are different. Preliminary studies show that partial similarity can be expected between the total indices.

6. Conclusions

The presented case studies have shown that the numerical results of reliability-oriented sensitivity analysis (ROSA) are inconsistent. ROSA was evaluated using Contrast, Xiao, Ling and Madsen’s indices. For structural reliability, the key quantity of interest is failure probability P_f, which is lower than 4.8·10⁻⁴.

Contrast P_f indices have relatively small values of first-order indices and high values of second-order indices for small P_f. Ling or Xiao indices have relatively high values of first-order indices, but also high values of second-order indices for small P_f. For instance, in the first case study, if P_f → 0 then C₁ = 0, C₂ = 0, C₁₂ = 1 and L₁ = 1, L₂ = 1, L₁₂ = 1. In civil engineering, P_f is generally very small, and extreme values of sensitivity indices estimated by ROSA can be expected. The advantage of contrast P_f indices is that the sum of all indices is equal to one. The sum of all Ling or Xiao indices is not equal to one. The Madsen factor values were significantly greater than 1 and therefore cannot be compared in size with Contrast, Xiao and Ling indices. Madsen’s factor does not reflect change in the mean value of input variables, although this change causes a change in P_f.

In contrast, Xiao, Ling and Madsen’s indices have correctly identified the order of importance of input random variables to P_f; however, this observation only applies to the presented case studies and cannot be generalized. In the case studies, it is not possible to determine, even approximately, the percentage by which the dominant variable is more influential than the others, so this conclusion is true for each type of SA. Structural reliability lacks a common platform of SA that provides a clear interpretation of the size of sensitivity indices and defines their information value.

The other indices (Sobol, Borgonovo and Cramér–von Mises) and correlation coefficients are not directly addressable to P_f and therefore are not generally suitable for the analysis of reliability. As expected, these (out of ROSA type) sensitivity indices do not reflect the change in mean value of input variables, although this change causes a change in P_f. This means that the two variables that have a different influence on the reliability may have the same indices. In relation to the reliability of structures, the information value of these indices is not unambiguous. In the case of ROSA, Xiao and Ling indices, no two different P_f values exist for which the same sets of sensitivity indices exist, but contrast P_f indices have the same or similar values for unreliability (P_f) and reliability (1 − P_f).

There are many engineering reliability assessments in which non-ROSA indices are applied, although the connection with reliability is mentioned. The reason for these applications may be the simplicity of evaluating indices as well as the experience that known indices have at least partial sensitivity for reliability, which, along with other experience, is sufficient for basic decision-making. With the development of ROSA, a gradual transition to new types of reliability-oriented indices can be expected.

In connection with sustainable reliability, it is possible to discuss which type of ROSA should be applied and which key quantities of interest ROSA should be oriented to in particular. The Eurocode standards for structural design assess reliability using a so-called semi-probabilistic approach, which is based on design quantiles. The question remains whether P_f can be adequately replaced by design quantities, reliability index β or other model-based inferences so that the information value of SA results in relation to reliability is approximately maintained. Design quantiles are an important part of reliability analysis, and SA of the design quantiles may be required to provide results consistent with P_f.

In general, ROSA directly addressable to P_f may be preferred rather than focusing on the reliability index β or quantiles. Indices with the sum of one and a clear addressability to P_f present one SA, an advantage that facilitates the comparison of the results of different probability models. Contrast functions are a more general tool for estimating various parameters associated with probability distributions, and thus the partial consistency of requirements could perhaps be sought on the basis of contrasts. These and other tasks need to be addressed in order to make SA of structural reliability a useful and practical tool.