Spatial Simulation Modeling of Settlement Distribution Driven by Random Forest: Consideration of Landscape Visibility
Abstract
1. Introduction
2. Literature Review
2.1. Landscape Visibility Analysis
2.2. Random Forest Algorithm
2.3. Hyperparameter Analysis
3. Materials and Methods
3.1. Study Area
3.2. Materials
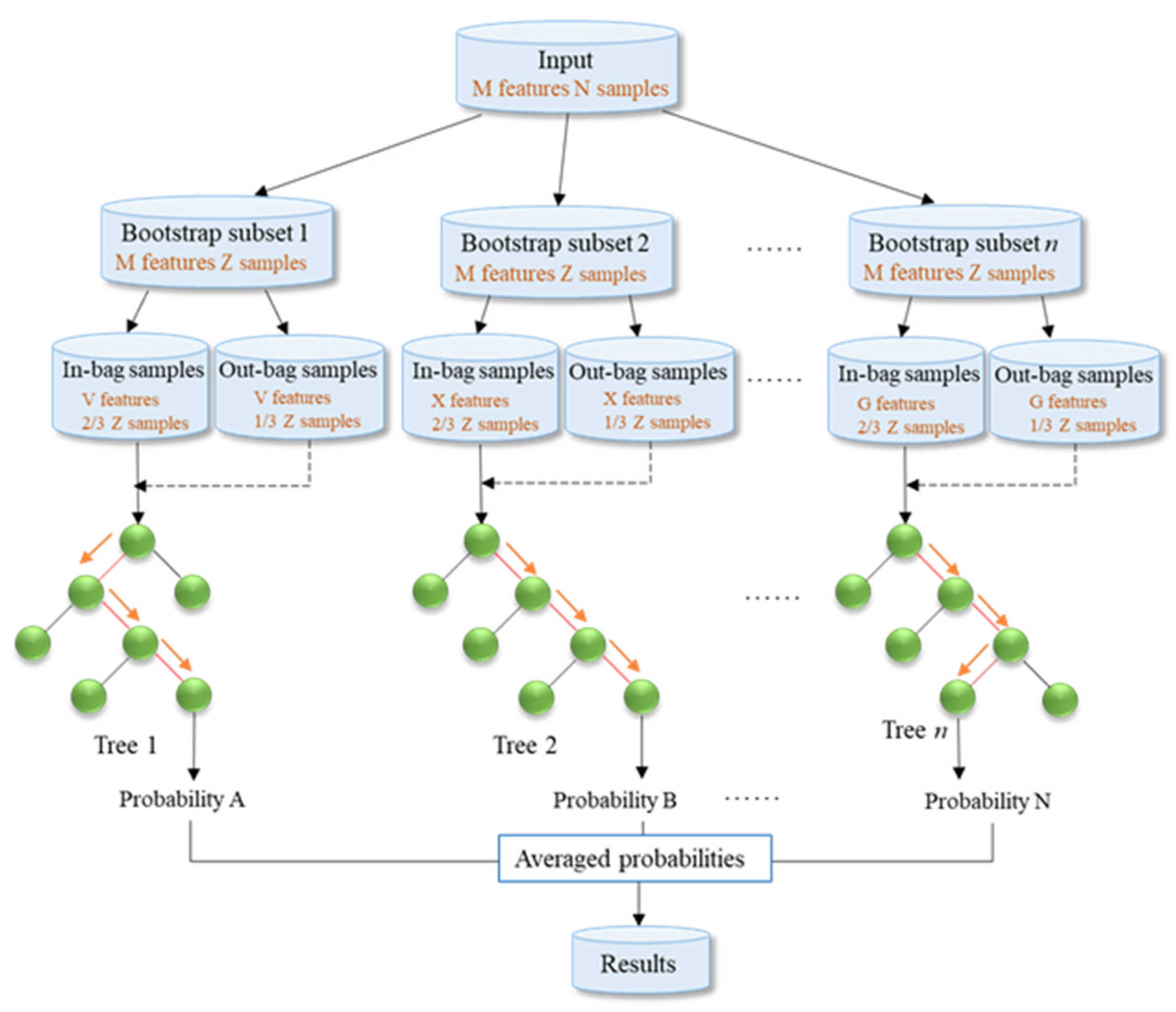
3.3. Methods
3.4. Implementation
4. Results
4.1. Experimental Design
4.2. Results of Hyperparameter Analysis
4.3. Evaluating the Goodness-of-Fit of the Random Forest Algorithm
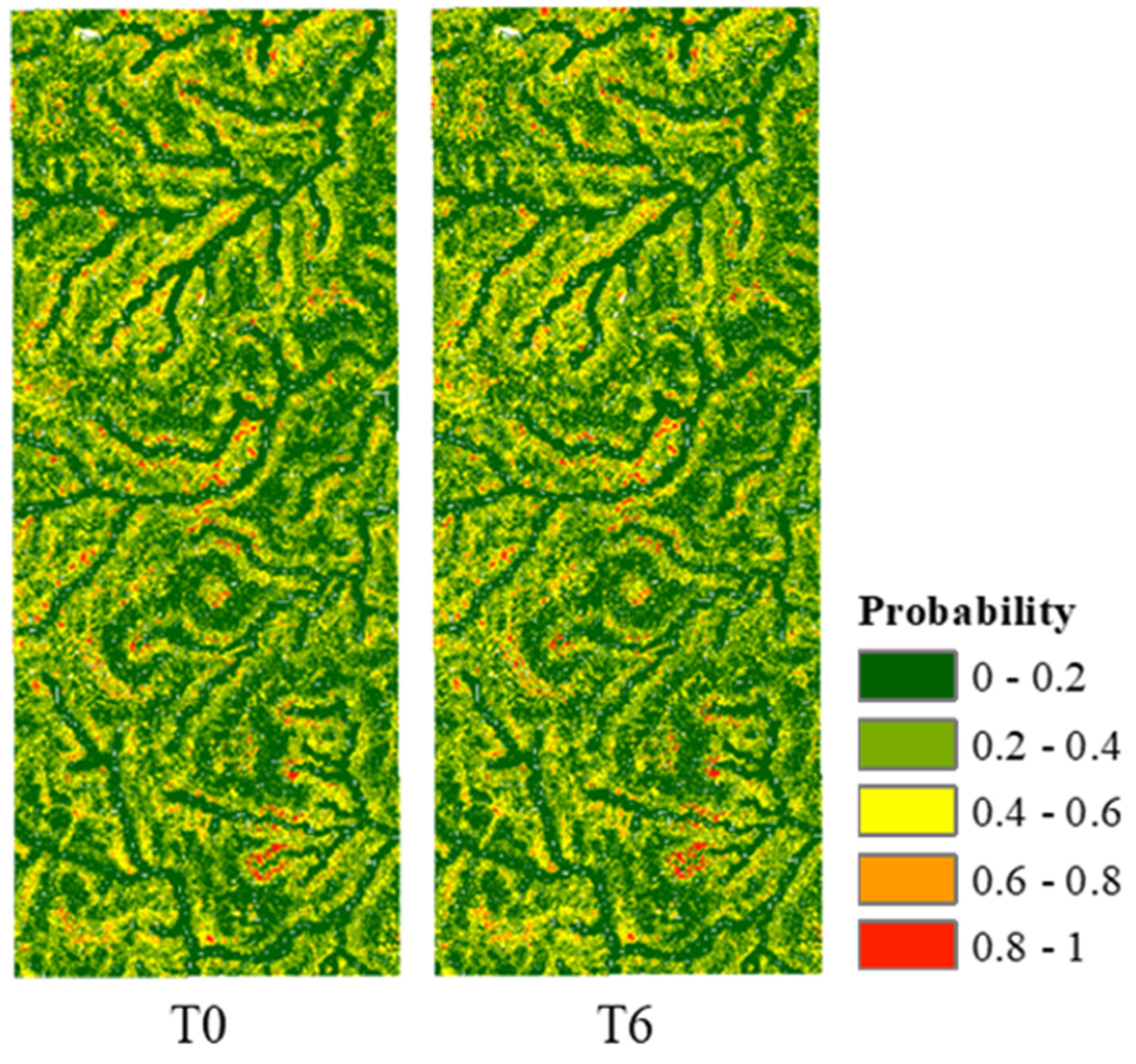
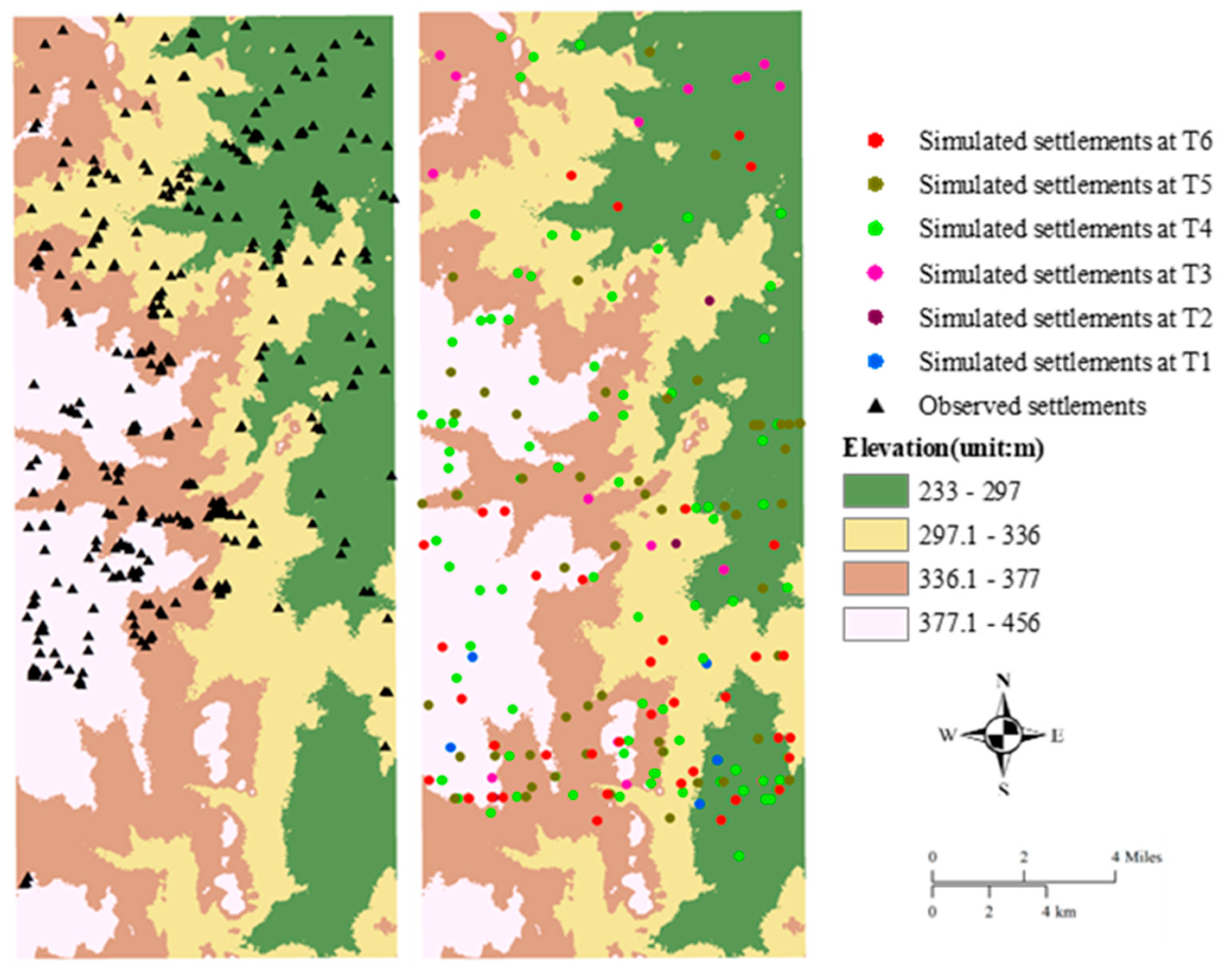
4.4. Results of Simulated Settlements
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veldkamp, A.; Fresco, L. CLUE-CR: An integrated multi-scale model to simulate land use change scenarios in Costa Rica. Ecol. Model. 1996, 91, 231–248. [Google Scholar] [CrossRef]
- Turner, B.L.; Moss, R.H.; Skole, D.L. Relating Land Use and Global Land-Cover Change; International Geosphere-Biosphere Programme (IGBP) Secretariat, Royal Swedish Academy of Sciences: Stockholm, Sweden, 1993. [Google Scholar]
- Swihart, R.K.; Moore, J.E. Conserving Biodiversity in Agricultural Landscapes: Model-Based Planning Tools; Purdue University Press: West Lafayette, IN, USA, 2004. [Google Scholar]
- Hiebeler, D. The Swarm Simulation System and Individual-Based Modeling; Santa Fe Institute: Santa Fe, NM, USA, 1994. [Google Scholar]
- Kohler, T.A.; Carr, E. Swarm-based modeling of prehistoric settlement systems in southwestern North America. In Proceedings of the Colloquium II, UISPP, XIIIth Congress, Forli, Italy, September 1996. [Google Scholar]
- Tang, W.; Malanson, G.P.; Entwisle, B. Simulated village locations in Thailand: A multi-scale model including a neural network approach. Landsc. Ecol. 2009, 24, 557–575. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, L.; Judge, W.J. Predicting the past: Correlation, explanation, and the use of archaeological models. In Quantifying the Present and Predicting the Past: Theory, Method and Application of Archaeological Predictive Modeling; U.S. Department of the Interior, Bureau of Land Management: Washington, DC, USA, 1988; pp. 1–18. [Google Scholar]
- Wescott, K.L.; Brandon, R.J. Practical Applications of GIS for Archaeologists: A Predictive Modelling Toolkit; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Romanowska, I. So you think you can model? A guide to building and evaluating archaeological simulation models of dispersals. Hum. Biol. 2015, 87, 169–193. [Google Scholar] [CrossRef] [PubMed]
- Kohler, T.A.; Parker, S.C. Predictive models for archaeological resource location. In Advances in Archaeological Method and Theory; Elsevier: Amsterdam, The Netherlands, 1986; pp. 397–452. [Google Scholar]
- Brandt, R.; Groenewoudt, B.J.; Kvamme, K.L. An experiment in archaeological site location: Modeling in the Netherlands using GIS techniques. World Archaeol. 1992, 24, 268–282. [Google Scholar] [CrossRef]
- Kohler, T.A.; Kresl, J.; Van West, C.; Carr, E.; Wilshusen, R.H. Be there then: A modeling approach to settlement determinants and spatial efficiency among late ancestral Pueblo populations of the Mesa Verde region, US Southwest. In Dynmics in Human Primate Societies: Agent-Based Modeling of Social and Spatial Processes; Oxford University Press: Oxford, UK, 2000; pp. 145–178. [Google Scholar]
- Bi, S.; Ji, H.; Liang, J.; Qiao, W.; Li, X. Spatial distribution of prehistoric settlement sites in Zhengzhou-Luoyang region based on index model. Prog. Geogr. 2013, 32, 1454–1462. [Google Scholar]
- Wheatley, D. Cumulative viewshed analysis: A GIS-based method for investigating intervisibility, and its archaeological application. In Archaeology and GIS: A European Perspective; Routledge: London, UK, 1995; pp. 171–186. [Google Scholar]
- Gaffney, V.; Van Leusen, P. Extending GIS methods for regional archaeology: The Wroxeter Hinterland Project. In Interfacing the Past: Computer Applications and Quantitative Methods in Archaeology CAA95: Analecta Praehistorica Leidensia 28; Institute of Prehistory: Leiden, The Netherlands, 1996; Volume 2, pp. 297–306. [Google Scholar]
- Sevenant, M.; Antrop, M. Settlement models, land use and visibility in rural landscapes: Two case studies in Greece. Landsc. Urban Plan. 2007, 80, 362–374. [Google Scholar] [CrossRef]
- Gillings, M. Landscape phenomenology, GIS and the role of affordance. J. Archaeol. Method Theory 2012, 19, 601–611. [Google Scholar] [CrossRef]
- Eve, S.J.; Crema, E.R. A house with a view? Multi-model inference, visibility fields, and point process analysis of a Bronze Age settlement on Leskernick Hill (Cornwall, UK). J. Archaeol. Sci. 2014, 43, 267–277. [Google Scholar] [CrossRef]
- Brughmans, T.; Brandes, U.J.F.i.D.H. Visibility network patterns and methods for studying visual relational phenomena in archeology. Front. Digit. Humanit. 2017, 4, 17–37. [Google Scholar] [CrossRef]
- Van Leusen, P. Line-of-site and cost surface analysis. In Computer Applications and Quantitative Methods in Archaeology; BAR International: Oxford, UK, 1998; pp. 1–8. [Google Scholar]
- Ducke, B. Archaeological predictive modelling in intelligent network structures. In The Digital Heritage of Archaeology. Computer Applications and Quantitative Methods in Archaeology; Hellenic Ministry of Culture, Archive of Monuments and Publications: Heraklion, Greece, 2003. [Google Scholar]
- Barceló, J.A. Computational intelligence in archaeology. State of the art. In Proceedings of the Making History Interactive. Computer Applications and Quantitative Methods in Archaeology (CAA), Barcelona, Spain, March 1998; pp. 11–21. [Google Scholar]
- Venditti, C.P.; Mele, P. Digital Transformation and Archaeology: Innovating Using the Cloud and Artificial Intelligence. In Developing Effective Communication Skills in Archaeology; IGI Global: Hershey, PA, USA, 2020; pp. 224–244. [Google Scholar]
- Oonk, S.; Spijker, J. A supervised machine-learning approach towards geochemical predictive modelling in archaeology. J. Archaeol. Sci. 2015, 59, 80–88. [Google Scholar] [CrossRef]
- Verhagen, P.; Whitley, T.G. Integrating archaeological theory and predictive modeling: A live report from the scene. J. Archaeol. Method Theory 2012, 19, 49–100. [Google Scholar] [CrossRef]
- Czibula, G.; Ionescu, V.-S.; Miholca, D.-L.; Mircea, I.-G. Machine learning-based approaches for predicting stature from archaeological skeletal remains using long bone lengths. J. Archaeol. Sci. 2016, 69, 85–99. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl.-Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Zheng, M.; Tang, W.; Zhao, X. Hyperparameter optimization of neural network-driven spatial models accelerated using cyber-enabled high-performance computing. Int. J. Geogr. Inf. Sci. 2019, 33, 314–345. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual land-cover classification: Incorporating spatial dependence in land-cover classification models using random forests and the Getis statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef]
- Gong, Z.; Tang, W.; Thill, J.-C. Parallelization of ensemble neural networks for spatial land-use modeling. In Proceedings of the 5th ACM SIGSPATIAL International Workshop on Location-Based Social Networks, Redondo Beach, CA, USA, November 2012; pp. 48–54. [Google Scholar]
- Steele, B.M. Combining multiple classifiers: An application using spatial and remotely sensed information for land cover type mapping. Remote Sens. Environ. 2000, 74, 545–556. [Google Scholar] [CrossRef]
- Llobera, M. Modeling visibility through vegetation. Int. J. Geogr. Inf. Sci. 2007, 21, 799–810. [Google Scholar] [CrossRef]
- Fry, G.L.; Skar, B.; Jerpåsen, G.; Bakkestuen, V.; Erikstad, L.J.L.; Planning, U. Locating archaeological sites in the landscape: A hierarchical approach based on landscape indicators. Landsc. Urban Plan. 2004, 67, 97–107. [Google Scholar] [CrossRef]
- Higuchi, T. The Visual and Spatial Structure of Landscapes; Mit Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Antrop, M. Invisible connectivity in rural landscapes. In Proceedings of the 2nd International Seminar of IALE, Connectivity in Landscape Ecology, Munster, Germany, September 1988; pp. 57–62. [Google Scholar]
- Nutsford, D.; Reitsma, F.; Pearson, A.L.; Kingham, S.J.A.G. Personalising the viewshed: Visibility analysis from the human perspective. Appl. Geogr. 2015, 62, 1–7. [Google Scholar] [CrossRef]
- Wheatley, D.; Gillings, M. Vision, perception and GIS: Developing enriched approaches to the study of archaeological visibility. In Beyond the Map: Archaeology and Spatial Technologies; IPO Press: Amsterdam, The Netherlands, 2000; Volume 321, pp. 1–27. [Google Scholar]
- Rua, H.; Gonçalves, A.B.; Figueiredo, R. Assessment of the Lines of Torres Vedras defensive system with visibility analysis. J. Archaeol. Sci. 2013, 40, 2113–2123. [Google Scholar] [CrossRef]
- Heyns, A.; Van Vuuren, J. Terrain visibility-dependent facility location through fast dynamic step-distance viewshed estimation within a raster environment. In Proceedings of the 2013 Annual Conference of the Operations Research Society of South Africa, Stellenbosch, South Africa, 15–18 September 2013; pp. 112–121. [Google Scholar]
- Brughmans, T.; van Garderen, M.; Gillings, M. Introducing visual neighbourhood configurations for total viewsheds. J. Archaeol. Sci. 2018, 96, 14–25. [Google Scholar] [CrossRef]
- Llobera, M. Extending GIS-based visual analysis: The concept of visualscapes. Int. J. Geogr. Inf. Sci. 2003, 17, 25–48. [Google Scholar] [CrossRef]
- Gillings, M. Mapping liminality: Critical frameworks for the GIS-based modelling of visibility. J. Archaeol. Sci. 2017, 84, 121–128. [Google Scholar] [CrossRef]
- Lake, M.; Ortega, D. Compute-Intensive GIS Visibility Analysis of the Settings of Prehistoric Stone Circles. Comput. Approach. Archaeol. Spaces 2013, 60, 213. [Google Scholar]
- Lake, M.W. Explaining the past with ABM: On modelling philosophy. In Agent-Based Modeling and Simulation in Archaeology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–35. [Google Scholar]
- Jones, E.E. Using viewshed analysis to explore settlement choice: A case study of the Onondaga Iroquois. Am. Antiq. 2006, 71, 523–538. [Google Scholar] [CrossRef]
- Gonçalves, C.; Cascalheira, J.; Bicho, N. Shellmiddens as landmarks: Visibility studies on the Mesolithic of the Muge valley (Central Portugal). J. Anthropol. Archaeol. 2014, 36, 130–139. [Google Scholar] [CrossRef]
- Benedikt, M.L. To take hold of space: Isovists and isovist fields. Environ. Plan. B Plan. Des. 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Turner, A.; Doxa, M.; O’sullivan, D.; Penn, A. From isovists to visibility graphs: A methodology for the analysis of architectural space. Environ. Plan. B Plan. Des. 2001, 28, 103–121. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Turner, A. Visibility graphs and landscape visibility analysis. Int. J. Geogr. Inf. Sci. 2001, 15, 221–237. [Google Scholar] [CrossRef]
- McGarigal, K. Landscape pattern metrics. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Page, M.; Parisel, C.; Pumain, D.; Sanders, L. Knowledge-based simulation of settlement systems. Comput. Environ. Urban Syst. 2001, 25, 167–193. [Google Scholar] [CrossRef]
- Malanson, G.P.; Zeng, Y.; Walsh, S.J. Complexity at advancing ecotones and frontiers. Environ. Plan. A 2006, 38, 619–632. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 307–323. [Google Scholar]
- Lebedev, A.; Westman, E.; Van Westen, G.; Kramberger, M.; Lundervold, A.; Aarsland, D.; Soininen, H.; Kłoszewska, I.; Mecocci, P.; Tsolaki, M. Random Forest ensembles for detection and prediction of Alzheimer’s disease with a good between-cohort robustness. NeuroImage Clin. 2014, 6, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Yue, D.; Peng, C.; Du, D.; Zhang, T.; Zheng, M.; Han, Q. Intelligent Computing, Networked Control, and Their Engineering Applications, In Proceedings of the International Conference on Life System Modeling and Simulation, LSMS 2017 and International Conference on Intelligent Computing for Sustainable Energy and Environment, ICSEE 2017, Nanjing, China, 22–24 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; Volume 762. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the ICML’13: the 30th International Conference on International Conference on Machine Learning, Atalanta, GA, USA, June 2013; Volume 28, pp. I-115–I-123. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. arXiv 2016, arXiv:1603.06560. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Agbaje-Williams, B. A Contribution to the Archaeology of Old Oyo; University of Ibadan: Ibadan, Nigeria, 1983. [Google Scholar]
- Ogundiran, A. Material life and domestic economy in a frontier of the Oyo Empire during the Mid-Atlantic Age. Int. J. Afr. Hist. Stud. 2009, 42, 351. [Google Scholar]
- Agbaje-Williams, B. Field Report: Oyo Ruins of NW Yorubaland, Nigeria. J. Field Archaeol. 1990, 17, 367–378. [Google Scholar] [CrossRef]
- Adetoro, A.O. People’s Perceptions of the Old Oyo National Park, Nigeria: Germane Issues in Park Management. Environ. Res. J. 2008, 2, 182–186. [Google Scholar]
- Ogundiran, A. The Oyo Empire Archaeological Research Project, 2019 (Third Season): Interim Report of the Fieldwork in Bara, Nigeria, January 11–February 15, 2019. Natl. Comm. Mus. Monum. 2019. Submitted. [Google Scholar]
- Doran, J. Systems theory, computer simulations and archaeology. World Archaeol. 1970, 1, 289–298. [Google Scholar] [CrossRef]
- Kohler, T.A. Putting social sciences together again: An introduction to the volume. In Dynamics in Human and Primate Societies: Agent-Based Modelling of Social and Spatial Processes; Oxford University Press: Oxford, UK, 2000; pp. 1–44. [Google Scholar]
- Banks, J. Handbook of Simulation: Principles, Methodology, Advances, Applications, and Practice; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- McGarigal, K.; Marks, B.J. Fragstats: Spatial Pattern Analysis Program for Quantifying Landscape Structure. Reference Manual; Forest Science Department, Oregon State University: Corvallis, OR, USA, 1994; Volume 62. [Google Scholar]
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical and Continuous Maps; Computer Software Program; Version 4; University of Massachusetts: Amherst, MA, USA, 2012. [Google Scholar]
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Zheng, M.T.; Wen, w.; Ogundiran, A.; Chen, T.; Yang, J. Parallel landscape visibility analysis: A case study in archaeology. High Perform. Comput. Geospatial Appl. 2020, in press. [Google Scholar]
- Hajian-Tilaki, K. Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation. Casp. J. Intern. Med. 2013, 4, 627. [Google Scholar]
- Pumain, D. Settlement systems in the evolution. Geogr. Ann. Ser. B Hum. Geogr. 2000, 82, 73–87. [Google Scholar] [CrossRef]




| Datasets | Unit | Description | Source |
|---|---|---|---|
| DEM | Meter | elevation | SRTM |
| Slope | slope | Derived from DEM | |
| Aspect | Decimal degree | aspect | Derived from DEM |
| Stream | Meter | distance to the nearest stream | Derived from DEM |
| Stream (order > 2) | Meter | distance to the nearest stream with higher order (order > 2) | Derived from DEM |
| Viewshed | number of visible settlements | Derived from DEM | |
| Settlements (including different types, such as towns, villages, and hamlets) | 1 = settlement, 0 = non-settlement | whether the place is a settlement | Digitized from Google Earth |
| Treatment ID | Driving Factors |
|---|---|
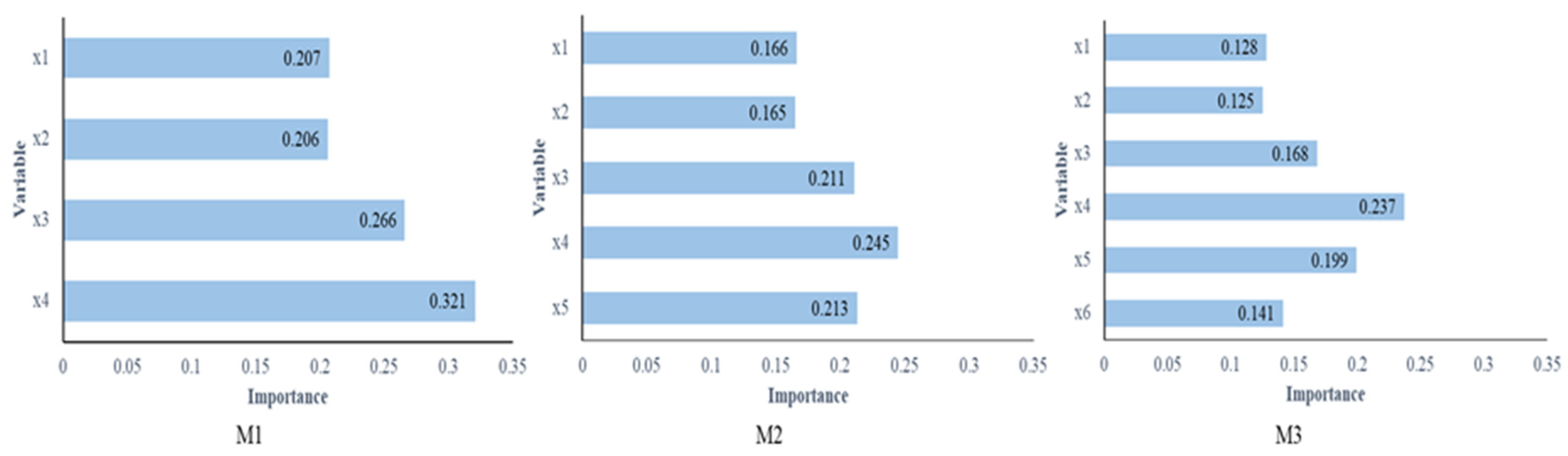
| M1 | Slope, aspect, distance to the nearest stream, distance to the nearest stream with higher order (order > 2) |
| M2 | Slope, aspect, distance to the nearest stream, distance to the nearest stream with higher order (order > 2), viewsheds |
| M3 | Slope, aspect, distance to the nearest stream, distance to the nearest stream with higher order (order > 2), viewsheds, landscape metrics |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Tang, W.; Ogundiran, A.; Yang, J. Spatial Simulation Modeling of Settlement Distribution Driven by Random Forest: Consideration of Landscape Visibility. Sustainability 2020, 12, 4748. https://doi.org/10.3390/su12114748
Zheng M, Tang W, Ogundiran A, Yang J. Spatial Simulation Modeling of Settlement Distribution Driven by Random Forest: Consideration of Landscape Visibility. Sustainability. 2020; 12(11):4748. https://doi.org/10.3390/su12114748
Chicago/Turabian StyleZheng, Minrui, Wenwu Tang, Akinwumi Ogundiran, and Jianxin Yang. 2020. "Spatial Simulation Modeling of Settlement Distribution Driven by Random Forest: Consideration of Landscape Visibility" Sustainability 12, no. 11: 4748. https://doi.org/10.3390/su12114748
APA StyleZheng, M., Tang, W., Ogundiran, A., & Yang, J. (2020). Spatial Simulation Modeling of Settlement Distribution Driven by Random Forest: Consideration of Landscape Visibility. Sustainability, 12(11), 4748. https://doi.org/10.3390/su12114748






