5.1. Data Generation
In this study, the size of test instances is measured by the planning horizon
, the number of satellites
and the number of customers in each satellite’s distribution area
. Under the basic scale, the planning horizon
is selected between 6 and 15, the number of satellites
R is selected between 5 and 12 and the number of customers in each satellite’s area is chosen from
. These numbers are chosen in accordance with the settings in Qiu et al. [
41]. The specific scale of some analyses, which will be explained in detail in the corresponding sections, will be adjusted accordingly.
The exponential deterioration rate, inventory cost, customer demand and other parameter settings are similar to those applied in Dolgui et al. [
43]. The generation of coordinates of the depot, satellite and customer nodes is referred to by Liu et al. [
31], whose research content is the two-echelon capacitated VRP with grouping constraints. Besides, we note that in order to facilitate the calculation, the lead time
is set to 1 for subsequent experiments. The generation of coordinates and parameters are described as follows.
(1) Deterioration rate
According to the expression of deterioration rate of perishable products in Dolgui et al. [
43], the deterioration rate formula is
where
A is the deterioration rate when products are initially produced and B is the time cost for deterioration rate to reach
e times of the initial deterioration rate (can be understood as shelf life).
The deterioration rate of products produced in period
can be denoted as
(2) Inventory cost
In this study, the inventory cost increases linearly as follows:
where
is the increment of inventory cost and
is the basic inventory cost in the depot and satellites. The basic inventory cost in the satellites is 20% more than that in the depot.
(3) Coordinate of each point, cost of replenishment, and distribution
Referring to the coordinate generation method in Liu et al. [
31], all coordinates are in a
square, and the coordinate of the depot is (50,50). In this study, the number of satellites is increased based on the references, and the corresponding coordinates of satellites are given in
Table 7.
The customers are distributed around the satellite responsible for them, and their horizontal and vertical coordinates differ within from those of the corresponding satellite. The distance between each node is measured by the linear distance of coordinates. Considering that the satellites are far from the depot and truck-load transportation is used for replenishment, the replenishment cost of the first echelon is designed as 5 times the distance between the satellites and the depot. Moreover, considering that each satellite is relatively close to its customer nodes, the transportation cost on each arc in the second echelon is designed as 0.5 times the distance between two nodes.
(4) Customer demand
The average demand of each customer node at each period is
The total customer demand in each satellite’s distribution area is .
When the demand changes periodically, we take one week as a cycle for simulation. Note that the customer demand is smaller in the first four days, and will increase in the last three days because of weekends. Specifically, the demand of each customer in the first four days is uniformly distributed in the interval , and the demand in the subsequent three days is uniformly distributed in .
For a stable demand, the customer demand changes without periodic fluctuations. Specifically, the demand of each customer in each period is uniformly distributed in .
5.5. Impact of Parameters Related to Deterioration Rate on Different Inventory Strategies
For the conventional PRP, the main factors that affect the performance of inventory strategy combinations are the deterioration rate and the increase in inventory cost. Accordingly, in this section, the performance of different inventory strategy combinations (OF–OF, OF–FF, FF–OF and FF–FF) are compared when the four types of combinations change. The parameters related to deterioration rate are A and B, and the parameters related to the inventory cost are and .
When analyzing the influence of each parameter on the performance of inventory strategy combinations, the evaluated parameter is changed with the remaining parameters fixed. For example, when evaluating the influence of parameter A, parameters B, and will be fixed.
The performance of each inventory strategy is measured by the costs and customer satisfaction. Specifically, under different inventory strategy combinations, the growth ratios (% increase) of total costs, fixed production costs, variable production costs, inventory costs and replenishment costs are observed. The ratios are calculated by
, where
represents the result of the corresponding strategy combination and
represents the result of the optimal–optimal combination. Additionally, customer satisfaction is used to test the product freshness, and the fresher the product, the higher the customer satisfaction. The freshness of products in this study is measured by the weighted average storage time (
), and its calculation method is given by Formula (
64). The shorter the weighted average storage time, the higher the freshness of products and customer satisfaction. To facilitate comparison, the drop ratio (% decrease) of
is used for observation. The ratio is calculated by
, where
represents the result of the corresponding strategy combination and
represents the result of the optimal–optimal combination.
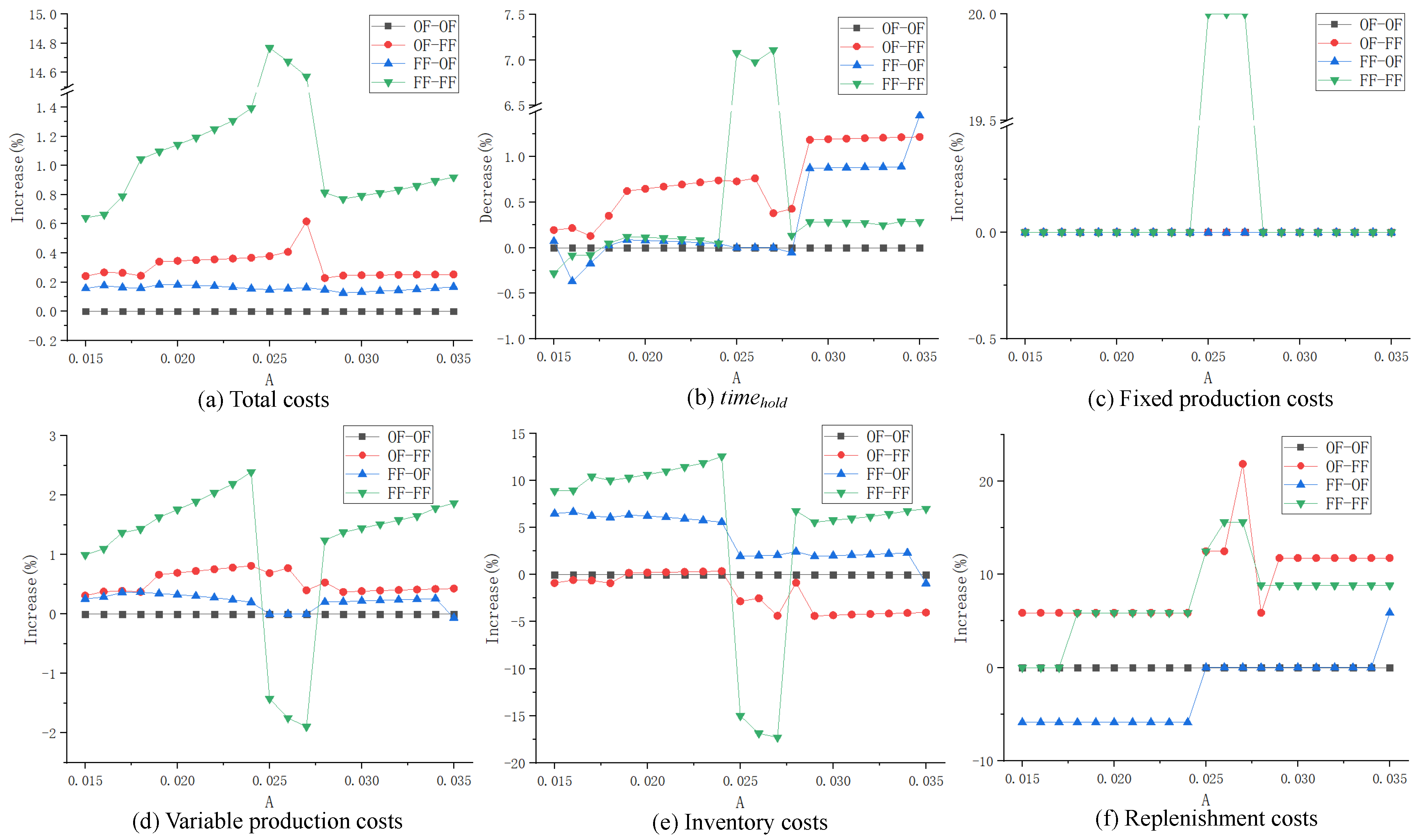
(1) Impact of parameter A on different inventory strategy combinations
When parameter
A ranges from 0.015 to 0.035 (increased by 0.001 at each time), the ratio of costs (% increase) and ratio of
(% decrease) under different inventory strategy combinations are shown in
Figure 2.
From the perspective of costs, the OF–OF strategy combination has a smaller gap compared to the OP, followed by the FF–OF strategy combination; the total costs of these two combinations are almost unaffected when parameter A changes. The gap of the total cost between the OF–FF strategy combination and the OP is also small, which is within 0.8% all the time, and the fluctuation is relatively small in general. The FF–FF strategy combination has the biggest gap, and in the process where parameter A increases, a sudden increase occurs in the interval (from to ), with the gap reaching more than 14%. Apart from that interval, the gap between the FF–FF strategy combination and the OP increases with the increase in parameter A.
Based on the analysis, the cost of the OF–OF strategy combination is almost unaffected. For the FF–OF strategy combination, the fixed production cost is not affected, the variable production cost is barely affected, the inventory cost decreases in a downward trend as parameter A increases, and the replenishment cost increases in an upward trend with the increase in parameter A. The reason for the change in the inventory cost and replenishment cost is that when parameter A increases, the deterioration of products will be accelerated. To lessen the deterioration, some products will be produced later; thus, the inventory duration of these products will be reduced but the replenishment frequency will be increased accordingly. For the OF–FF strategy combination, the fixed production cost is not affected, while the variable production cost is higher than that of the OP, with a small fluctuation (1%) when parameter A increases. However, when A increases to , its inventory cost begins to decrease, and after that, the gap stays relatively stable at −5%. Additionally, the replenishment cost fluctuates violently when A is increased to ; this is caused by the shorter inventory time and the increased replenishment frequency due to the later production of some products. For the FF–FF strategy combination, within the interval where the total cost surges, the gap of fixed production cost rushes to 20%, the gap of variable production cost decreases abruptly to approximately −2%, the gap of inventory cost plunges to approximately −17% and the gap of replenishment cost increases to approximately 17%. It can be observed that the sudden increase in the FF–FF total cost is mainly caused by the fixed production cost; this is because the product deteriorates faster as A increases. The FF–FF strategy, which prioritizes the use of new products in the replenishment and distribution phases, is the combination that results in the highest amount of product deterioration. Therefore, when the product deteriorates to a certain value (A = 0.025), the product deteriorates considerably. To satisfy the customer demand in time, a higher production frequency is adopted. As A continues to increase to , the OP also needs to increase the production frequency to meet the demand. At this time, the gap between the FF–FF and OP is restored to a lower level.
From the perspective of of distributed products, as A increases, the product freshness of OF–FF is the highest in most cases, and the gap between it and the OP tends to increase as A increases. The gap of product freshness between the OF–FF strategy combination and the OP starts to increase when , but it is still lower than that of the OF–FF strategy combination. The product freshness of the OF–OF and FF–FF strategy combinations is the lowest in most cases, in which the product freshness of the FF–FF strategy combination also shows a sudden increase in the interval where the total cost surges.
To summarize, with different values of parameter A, the strategy combination OF–FF is optimal, because it can obtain the same or higher product freshness at a lower cost increment; therefore, it can obtain higher customer satisfaction within the acceptable range of cost increase. The strategy combinations OF–OF and FF–OF are the second most optimal. They could hardly increase the cost nor the customer satisfaction. Only when A is large enough can the FF–OF strategy combination achieve a similar performance to that of the OF–FF strategy combination. The FF–FF strategy combination is the worst, because in most cases, it results in large cost increases and an improvement in customer satisfaction is not achieved. Only in the interval where the total cost surges did FF–FF obtain high customer satisfaction. At the same time, the costs increase sharply; therefore, its utilization is not recommended.
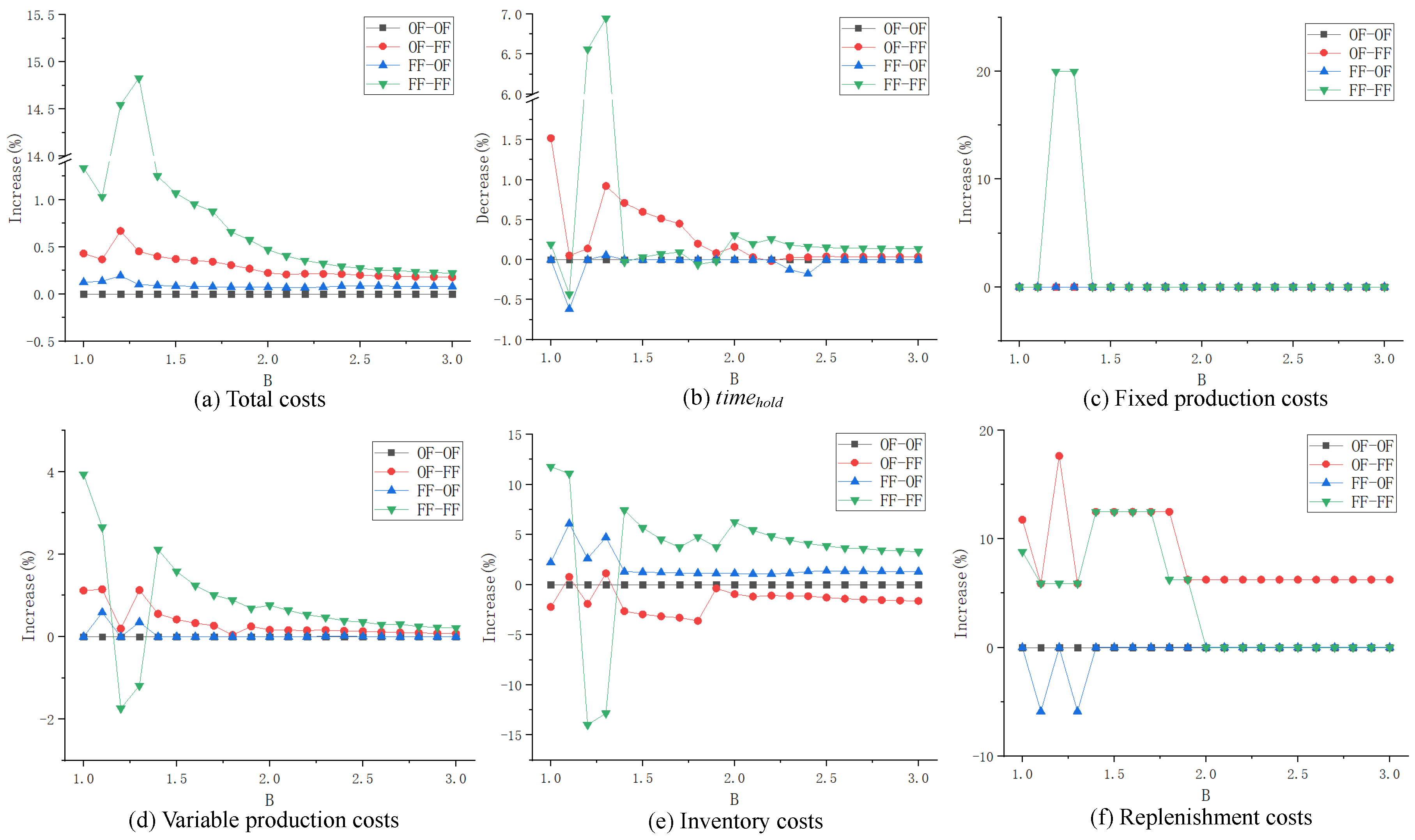
(2) Influence of parameter B on different inventory strategy combinations
When parameter
B ranges from 1 to 2 (increased by 0.001 at each time), the ratio of costs (% increase) and the ratio of
(% decrease) under different inventory strategy combinations are shown in
Figure 3.
From the perspective of cost, the OF–OF strategy combination is the optimal, followed by the FF–OF and OF–FF strategy combinations. When B changes, the costs of these three combinations hardly increase compared to that of the OP, while the FF–FF strategy combination performs the worst. With the increase in parameter B, the OF–OF strategy combination is not affected, but the gap of the total cost between the FF–OF/OF–FF strategy combinations and the OP has a general decreasing trend; only when is there a slight increase. As B increases, the FF–FF strategy combination increases sharply in the interval , and then decreases sharply when , showing a decreasing trend before and after that interval.
Integrating all types of costs, the gap between the FF–OF strategy combination and the OP results mainly from the inventory cost. Because the unit inventory cost is smaller in the depot, more products would be stored in the depot, and when fresher products are preferred in the replenishment echelon, the inventory cost at the depot will increase, resulting in an increase in the total inventory cost. The gap between the FF–OF strategy combination and the OP mainly comes from the replenishment cost. It is obvious that when new products are given priority in the distribution echelon, in order to minimize deterioration, some products will be produced later and the replenishment frequency will increase. It is noted that the sharp increase in the total cost of FF–FF is mainly caused by the fixed production cost, because the product will deteriorate more slowly due to the increase in B. When it slows down to a certain extent, other strategy combinations including the OP will reduce the production frequency without affecting the satisfaction of demand, while the FF–FF strategy combination causes the most deterioration and cannot reduce the production frequency, resulting in a sharp increase in cost changes. However, as B continues to increase, FF–FF can maintain the same production frequency similar to other strategies; thus, the cost recovered.
From the respective of , when , the product freshness is the highest under the OF–FF strategy combination, while other strategy combinations cannot improve the product freshness in most cases. Furthermore, only the FF–FF strategy combination has a sharp increase within the range where the total cost surges. When , the product freshness is the highest under the FF–FF strategy combination. Other strategy combinations cannot improve the product freshness.
In general, as B changes, when B is relatively small, the OF–FF strategy combination is optimal, and it can achieve higher customer satisfaction with a lower increase in costs. When B is relatively large, the FF–FF strategy combination is optimal, and it can obtain higher customer satisfaction easily. When parameter B is not decided, it is recommended to use the OF–FF strategy combination, because its overall performance is relatively stable, which would not cause a sharp increase in costs and can effectively improve customer satisfaction in most cases.
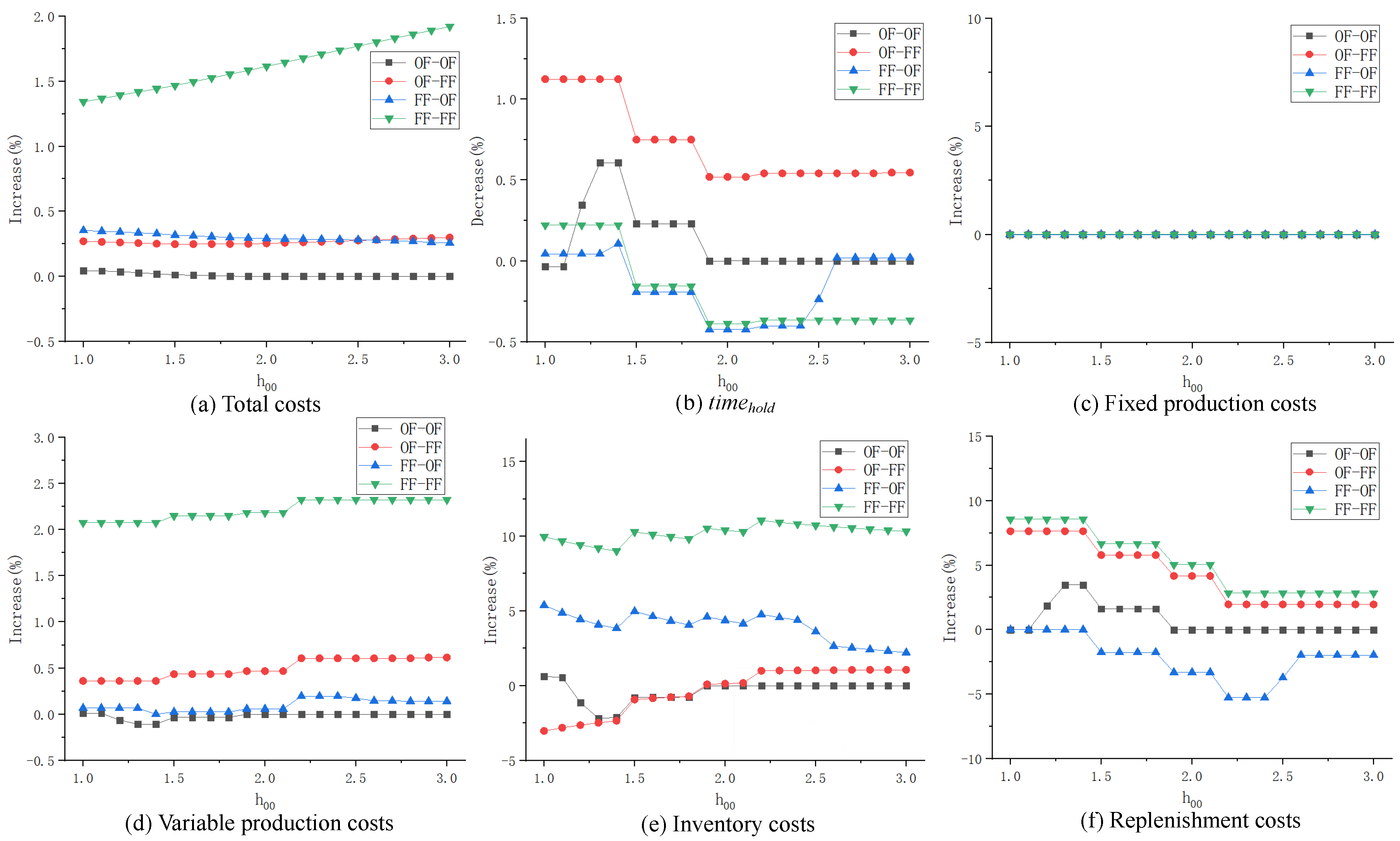
(3) Influence of parameter on different inventory strategy combinations
When parameter
ranges from 1 to 3 (increased by 0.2 at each time), the ratio of costs (% increase) and ratio of
(% decrease) under different inventory strategy combinations are shown in
Figure 4.
From the perspective of the total costs, OF–OF is the optimal one, followed by the OF–FF and FF–OF strategy combinations. The total costs of these three combinations are relatively stable, while the gap between the FF–FF strategy combination and OP is the largest and increases with increasing .
Combined with all types of costs, the total cost under the FF–FF strategy combination changes synchronously with the variable production cost, inventory cost and replenishment cost. This is because new products are preferred to be used in the two echelons, resulting in more product deterioration and increasing total output. Moreover, an increased inventory cost of old products and an increased inventory of new products will both cause an increase in inventory cost. In the second echelon, the replenishment cost of the OF–FF and FF–FF strategy combinations that give priority to using new products is higher than that of other strategy combinations. This is because there is more deterioration of old products left in the satellites; thus, a higher replenishment frequency is required.
From the perspective of , the product freshness of the OF–FF strategy combination is the highest and is always higher than that of the OP, while that of the FF–OF strategy combination is better than that of the OP when ; however, it also gradually declines to a lower level afterward. The product freshness of OF–OF fluctuates and is higher than that of the OP when . The product freshness of FF–FF gradually decreases as changes, and is lower than that of the OP in most cases.
In summary, has little impact on the gap of the total cost between the OF–FF/FF–OF/OF–OF strategy combinations and the OP, but it has a great impact under the FF–FF strategy combination. Among the strategy combinations, OF–FF is optimal, because its product freshness increases the most with less cost increase. Besides, when is small, the FF–FF and FF–OF strategy combinations are adoptable. Note that the FF–FF strategy combination has no improvement in customer satisfaction but increases costs the most; thus, it is the worst one and is not recommended.
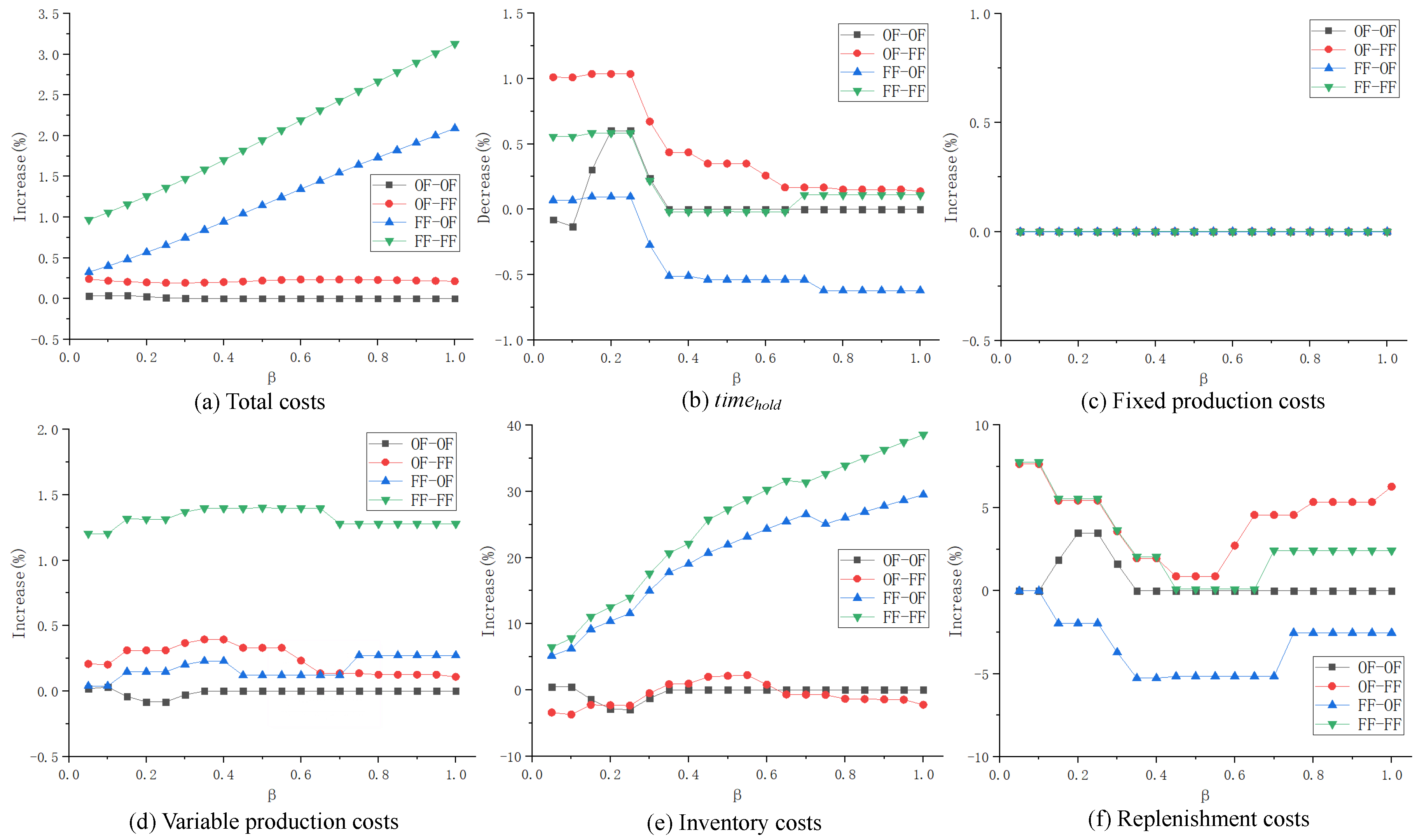
(4) Influence of parameter on different inventory strategy combinations
When the parameter
ranges from 0.05 to 1 (increased by 0.05 at each time), the ratio of costs (% increase) and the ratio of
(% decrease) under different inventory strategy combinations are shown in
Figure 5.
For the total costs, the strategy combinations with the smallest gaps are OF–OF and OF–FF, which change little with the increase in parameter . The gap between FF–OF/FF–FF and the OP has an apparent upward trend as increases, among which the gap between FF–OF and the OP is always the largest.
Combined with all types of costs, it can be observed that the gaps of the cost between FF–OF/FF–FF and the OP are mainly caused by the variable production cost and inventory cost, among which the gap of inventory cost increases with increasing . Moreover, there is no obvious variation trend of the variable production cost, indicating that the upward trend of the gap is mainly caused by the inventory cost. However, the gap of the inventory cost between FF–OF/FF–FF and the OP has no obvious increasing trend; it is either stable or fluctuating in a small range. Apparently, the inventory cost in the depot is lower; therefore, more products are stored in the depot. If new products are preferred in the replenishment (FF–OF and FF–FF), the inventory cost brought by the old product will be relatively large and will be larger with increasing ; this is why the strategy combinations show such a trend.
From the perspective of , it is the OF–FF strategy combination that can maximize the product freshness, while there is no significant difference of for other strategies as changes. When is small (), there are significant differences between the OF–FF strategy combination and others.
In general, as changes, the OF–FF strategy combination is optimal and should be given priority, as it can improve the product freshness when the cost increment is relatively small. The OF–OF strategy combination does not increase the total cost, but it does not improve customer satisfaction in most cases. The FF–OF and FF–FF strategy combinations offer poor improvement to customer satisfaction, and FF–OF may even decrease it. In addition, the cost increases with these two strategies are relatively high; these two are not recommended for utilization.