Production, Replenishment and Inventory Policies for Perishable Products in a Two-Echelon Distribution Network

Abstract

The research on production, delivery and inventory strategies for perishable products in a two-echelon distribution network integrates the production routing problem (PRP) and two-echelon vehicle routing problem (2E-VRP), which mainly considers the inventory and delivery sustainability of perishable products. The problem investigated in this study is an extension of the basic problems, and it simultaneously optimizes production, replenishment, inventory, and routing decisions for perishable products that will deteriorate over the planning horizon. Additionally, the lead time has been considered in the replenishment echelon, and the unit inventory cost varying with the inventory time is considered in the inventory management. Based on a newly designed model, different inventory strategies are discussed in this study: old first (OF) and fresh first (FF) strategies both for the first echelon and second echelon, for which four propositions to model them are proposed. Then, four valid inequalities, including logical inequalities, a $(\ell ,S,WW)$ inequality, and a replenishment-related inequality, are proposed to construct a branch-and-cut algorithm. The computational experiments are conducted to test the efficiency of valid inequalities, branch-and-cut, and policies. Experimental results show that the valid inequalities can effectively increase the relaxed lower bound by 4.80% on average and the branch-and-cut algorithm can significantly reduce the computational time by 58.18% on average when compared to CPLEX in small and medium-sized cases. For the selection of strategy combinations, OF–FF is suggested to be used in priority.

1. Introduction

This study focuses on the problem of production, delivery, inventory and route planning for perishable products in a two-echelon production routing problem (2E-PRP), which is an integration and extension of the conventional production routing problem (PRP) and the two-echelon vehicle routing problem (2E-VRP) for perishable products.

The PRP is integrated with two classic problems: the lot-sizing problem (LSP) and vehicle routing problem (VRP). The benefits of studying PRP were first discussed by Chandra [1] and Chandra and Fisher [2], who indicated that utilizing PRP can save approximately 3–20% of the total cost, compared with solving by a single problem (LSP and VRP) separately. Moreover, due to the complexity of PRP, few studies have focused on exact algorithms or lower bound calculation methods.

The 2E-VRP is an extension of the conventional VRP. In general, the conventional VRP only considers vehicle route planning for a single-echelon transportation networks, but for real supply chain systems, the two-echelon network is more practical. The two-echelon and single-echelon vehicle route planning differ in several aspects, including the effects of customer number and store location on the total distribution cost [3], and the impact of other factors, i.e., fixed cost, operating cost and sustainable cost, on the optimal strategy [4]. It was confirmed that the delivery strategy of the two-echelon vehicle route planning outperforms that of the single-echelon vehicle route planning strategy.

The PRP is widely used in the manufacturing industry in an attempt to optimize production, inventory, distribution and routing decisions. The 2E-VRP aims at planning routes in a two-echelon distribution network in which the deliveries from the depot to customers are indirect, i.e., through intermediate capacitated depots. In the study, we conduct an integration of PRP and 2E-VRP, which to the best of our knowledge has rarely been studied. However, such an integrated problem is actually common in the supply chain and can better reduce operating costs, which means that this research has theoretical significance for supply chain management. Additionally, the perishability of products is considered in this study. As the scale of the cold-chain market expands and the total amount of cold-chain logistics increases in order to achieve higher service levels, the management of sustainability for perishable products possesses increasing importance. In fact, the development of the perishable product logistics is inseparable from path planning, optimization of distribution methods, and improvement of distribution efficiency, manifesting that considering the combination of perishable products and 2E-PRP has significant research value.

For the 2E-PRP with perishable products, we develop the optimization procedure from the four aspects of production, replenishment, inventory and route planning so as to construct sustainability for the entire system. In practice, perishable products are initially produced and stored in the depot; then, they are transported to stores (often called satellites) and delivered to customers. In the process, “depot to satellite”, i.e., the replenishment, is the first stage, and “satellite to customer”, i.e., the distribution, is the second stage. Actually, a lead time for replenishment often exists because of the long distance between depots and satellites. Additionally, satellites are always far away from each other and possess their own distribution areas.

Specifically, this paper mainly investigates the production, replenishment, inventory, and route planning for perishable products with replenishment lead time in a two-echelon distribution network. To better examine the cost structure and performance of product sustainability more effectively, different inventory strategies are derived and analyzed. Compared with the conventional PRP, the perishable products considered in this study will deteriorate with the increase in inventory time, and the inventory cost of such unsustainable products is synchronized with inventory time. As far as we know, it is also the first time that the lead time has been considered.

A mixed-integer programming (MIP) model is first formulated for our problem, in which the subordinate relation between satellites and customers is taken into consideration to ensure that the service area of each satellite does not overlap. Then four theorems are presented to construct the inventory strategies for two echelons: the old first (OF) strategy and fresh first (FF) strategy for both the replenishment echelon and distribution echelon. Furthermore, several valid inequalities are used to build the branch-and-cut algorithm, which can effectively solve the problem and significantly reduce the computational time by 58.18% on average when compared to CPLEX at different scales. To provide managerial insights, some necessary work has been performed: (1) a weighted average storage time is introduced to measure the sustainability of products, (2) different strategies are analyzed based on costs and customer satisfaction, (3) the cost sensitivity to parameter changes is tested under the optimal strategy, and (4) a comparison among different strategy combinations under the condition of stable and fluctuating customer demands is conducted.

The remainder of this paper is organized as follows: the literature review is presented in Section 2, the construction of formulations are described in Section 3, the branch-and-cut algorithm is detailed in Section 4, the numerical experiments conducted are discussed in Section 5, and the conclusions drawn are presented in Section 6.

2. Literature Review

Considering that the problem studied combines three parts, the literature review is thus categorized into three streams in order to provide a detailed overview for this topic. The first stream encompasses the development of formulations and algorithms for PRP, which contains 16 papers and contributes to the construction of the first echelon in 2E-PRP. The second stream entails the application and exploration of perishable products in the field of PRP, which encloses 10 papers and mainly focuses on the policies and strategies for sustainability. Then, the third stream comprises 11 papers and focuses on the variants of 2E-VRP and corresponding solution approaches. Note that perishable products have not been considered for 2E-VRP in the current literature. With the combination of related PRP and 2E-VRP problems, this study can explore the production, replenishment and inventory policies and a branch-and-cut algorithm for perishable products in 2E-PRP in a comprehensive way.

2.1. Production Routing Problem

The PRP has been widely studied in various forms by practitioners and researchers over the past few decades since the seminar papers presented by Chandra [1] and Chandra and Fisher [2]. Readers who are not familiar with the development of PRP can refer to the comprehensive reviews by Amorim et al. [5], Díaz-Madroñero et al. [6] and Adulyasak et al. [7].

Various formulations have been developed for different scenarios, such as the programming model for integrating production and procurement transport decisions (Díaz-Madroñero et al. [8]), the mixed integer model for closed-loop production routing problems with reverse logistics and remanufacturing (Qiu et al. [9]), and the stochastic reverse logistics production routing formulation with emissions control policy selection (Shuang et al. [10]). Additionally, the solution approaches, including exact algorithms and heuristics, were designed to solve this problem. For exact algorithms, most researchers were inclined to adopt the branch-and-cut algorithms. Archetti et al. [11] considered a production–distribution system, where a facility produces one commodity, which is distributed to a set of retailers by a fleet of vehicles, and presented a branch-and-cut algorithm for a problem with one vehicle. For a similar problem, Coelho and Laporte [12] proposed a branch-and-cut algorithm for the solution with multiple products and multiple vehicles and considered the inclusion of consistency features that are meaningful in a multi-product environment. Subsequently, Adulyasak et al. [13] extended the research of Archetti et al. [11] to multi-vehicle scenarios, in which they proposed a branch-and-cut algorithm, used different modeling methods and compared the efficiency difference.

For large-scale problems, such branch-and-cut algorithms suffer from the defect of computational time especially for sophisticated industry-oriented problems; hence, some researchers developed heuristics as an alternative. Lei et al. [14] proposed a two-phase algorithm and verified the correctness and effectiveness through its application in a practical network. Boudia et al. [15] developed metaheuristics that simultaneously tackle production and routing decisions, including a greedy randomized adaptive search procedure and two improved versions using either a reactive mechanism or a path-relinking process. Boudia et al. [16] developed two greedy heuristics and two local search procedures: the first set computes, in a classical way, a production plan and then a distribution plan, and the second one determines the two plans simultaneously. Boudia and Prins [17] proposed a metaheuristic called a memetic algorithm with population management by which the production and distribution decisions can be simultaneously tackled.

2.2. Production Inventory and Routing Problem of Perishable Products

In addition to the conventional PRP, the problem aimed at perishable products has received extensive attention in recent years. In the fields of production and inventory management for perishable products, there are mainly two types of research approaches. One is to set a fixed shelf life for perishable items; once the shelf life is exceeded, the product cannot be used anymore. The other is to regard the deterioration of perishable products as a process of gradual consumption; the total amount of products will be continuously reduced and failure to use them in time will lead to waste.

Federgruen et al. [18] presented an allocation model for a perishable product that is distributed from a regional center to a given set of locations with random demands. Hsu et al. [19] presented an economic lot size model for perishable products where the costs of holding inventory stocks (having backorders) in each period depend on the age of inventories (backorders). Le et al. [20] studied the production inventory and routing problem for a certain type of fresh product based on the assumption that the product has a fixed shelf life. Column generation is applied in solving the linear relaxation problem of the model. Ali et al. [21] proposed a logistic-based approach to a class of inventory problems with shortages and time decay functions, and used an extended approach of Wagner–Whitin to determine lot sizes, replenishment cycles, and schedules. Duong et al. [22] studied a multi-criteria inventory management system for perishable and substitutable products.

In recent years, for developing sustainable policies, Yang et al. [23] investigated a joint decision of pricing strategy, shelf space allocation, and replenishment policy in a single-item food supply chain setting, where the goal is to maximize the retailer’s total expected profit subject to a stochastic retail demand. Tekin and Erol [24] developed a new pricing policy for product stocks, whose shelf lives are about to expire and generally become waste, to increase salability with reference to fresher stocks of these products. Duong et al. [25] used the analytic hierarchy process to weight the importance of consumer demand, product lifetime and substitution ratio on perishable inventory management. Jiang et al. [26] focused on an integrated perishable agricultural product scheduling problem, which combines harvest and distribution simultaneously, with the purpose of reducing processing time and quality decay. He et al. [27] focused on optimizing the replenishment policy for a channel with a stock-dependent demand considering item deterioration and order backlogging under two financial schemes of progressive trade credit periods.

2.3. Two-Echelon Vehicle Routing Problem

The delivery of products from origin to destination is often managed through one or more intermediate facilities, where storing and consolidation activities are performed. This type of distribution system is commonly called a multi-echelon distribution network, one of which is the two-echelon network [28]. The 2E-VRP is proposed based on this, and the delivery from the depot to customers is indirect and managed through an intermediate capacitated depot (often referred to as the satellite) [29]. In a 2E-VRP, the first echelon is composed of the vehicle depots and satellites, and the second echelon contains satellites and customers. Over the past few years, the 2E-VRP, which is the basic framework of 2E-PRP, has been conducted on this type of problem in two directions: the variant of the basic problem and the solution approach.

For the first direction, Crainic et al. [30] incorporated the strict coordination and time synchronization, and studied the 2E-VRP by integrating short-term operation scheduling and resource management. Liu et al. [31] added grouping constraints and developed several valid inequalities to enhance the 2E-VRP with grouping constraints. Zhou et al. [32] studied a problem where customers could choose multi-warehouses with different deliveries in the second echelon. Wang et al. [33] discussed a 2E-VRP by considering environmental factors, and constructed a new arc-and-route-based mathematical model.

For the second direction, Baldacci et al. [34] integrated a bounded method into exact algorithm to decompose the problem into a set of limited multi-warehouse VRPs with side constraints. Perboli et al. [35] introduced some valid inequalities and presented two math heuristics based on the 2E-VRP models. Santos et al. [36] introduced a branch-and-cut-and-price algorithm, which overcomes symmetry issues observed in a formulation and is strengthened with several classes of valid inequalities. Breunig et al. [37] proposed a hybrid metaheuristic, which combines enumerative local searches with destroy-and-repair principles, as well as some tailored operators to optimize the selections of intermediate facilities. He and Li [38] presented an optimum solution with a heuristic in which the dynamic satellite is transferred as the static case for a two-echelon multi-trip VRP with a dynamic satellite.

3. Formulation

3.1. Problem Description and Assumptions

The two-echelon distribution network comprises three types of nodes: the depot, satellites and customers. The depot and satellites form the first echelon, and the satellites and customers form the second echelon. The relationship between the different echelons is shown in Figure 1, where T represents the set of time periods. The first echelon is responsible for the replenishment, and each satellite can only be replenished once at each period. Initially, the depot produces items under its capacity. Then the completed products can be stored in the depot or transported to satellites in the transportation mode of Full-Truck-Load. It is worth mentioning that the transportation cost of replenishment remains the same for each satellite in each period, and there is a lead time for replenishment.

In the second echelon, the satellites deliver products to each customer with a certain demand in different cycles. Each satellite is only responsible for its own distribution area, which contains the stable customer group; that is, customers are assigned to different areas in advance and the relationship remains unchanged over the planning horizon. Besides, only the routes in the same distribution area are accessible with distance-related transportation cost. Products can be stored in either of the depot or satellites, but the inventory cost in the depot is higher. Furthermore, certain inventory capacity limits, which cannot be exceeded, exist in the depot and satellites. Vehicles in both the replenishment and distribution echelon cannot be overloaded. Lastly, perishable products will deteriorate with the increase in inventory time, and the deterioration rate and unit inventory cost will also be increased.

To formulate the problem more effectively, the following assumptions are considered in the decision-making:

• The inventory fluctuation caused by the deterioration of perishable products is represented by the deterioration rate, and the deterioration rate and unit inventory cost increase with inventory time.
• The depot and satellites cannot exceed their inventory capacity limits.
• Truck-load transportation with fixed cost is applied in the first replenishment echelon from the depot to satellites. The types of capacitated vehicles are different in the two echelons, with no quantity limitations.
• Inventory is recorded at the end of the period, i.e., the depot records after production and replenishment, and satellites record after receiving and delivering goods. The lead time of replenishment from the depot to satellites is fixed as 1, and the delivery from satellites to customers is instantaneous.
• Stock-out is not allowed, and customers cannot be repeatedly accessed during the same period.
• Each satellite has non-overlapping distribution areas, and only customers in the same distribution area can be reached from each other.

3.2. Notations

The sets and parameters used in the model are defined in

Table 1. Definition of sets.

Set	Definition
G	Set of directed graphs, $G=(V,A)$
V	Set of vertices, $V=V_0\cup V_r\cup V_c$
$V_0$	Set of depots, $V_0=0$
$V_r$	Set of satellites, $V_r=\{1,2,\cdots ,R\}$
$V_c$	Set of customers, $V_c=V_{c_1}\cup V_{c_2}\cup \cdots \cup V_{c_i}\cup \cdots \cup V_{c_R}$
$V_{c_i}$	Set of customers in the distribution area of satellite $i(i\in V_r)$
A	Set of arcs, $A=\left\{(i,j)\right|i,j\in V_r\cup V_c,i\ne j\}\setminus \left\{(i,j)\right|i,j\in V_r,i\ne j\}$
T	Set of planning periods, $T=\{1,2,\cdots ,|T\left|\right\}$
$T_0$	Set of periods, $T_0=\{0,1,2,\cdots ,|T\left|\right\}$

and

Table 2. Definition of parameters.

Parameter	Definition
$\theta$	Lead time for replenishment
C	Capacity of depot
f	Fixed cost of production
u	Unit production cost
$h_{i\tau t}$	Unit inventory cost at node i at the end of period t for products produced in period $\tau (\tau \in T_0)$
${\alpha }_{\tau t}$	Deterioration rate of products at period $t(t\in T)$ for products produced in period $\tau (\tau \in T_0)$
$L_i$	Upper limit of inventory capacity at location $i(i\in V_0\cup V_r)$
$Q_1$	Capacity of replenishment vehicles at the first echelon (from the depot to satellites)
$Q_2$	Capacity of distribution vehicles at the second echelon (from satellites to customers)
$f_{e{e}_i}$	Transportation cost of replenishment from the depot to satellites $i(i\in V_r)$
$c_{ij}$	Transportation cost on arc $(i,j)\in A$
$o_{ij}$	1, if customer $j(j\in V_c)$ stays in the distribution area of satellite $i(i\in V_r)$; 0 otherwise
$d_{it}$	Demand of location $i(i\in V_r\cup V_c)$ at period $t(t\in T),(d_{it}=0,i\in V_r,t\in T)$
$in{v}_i$	Beginning inventory of satellite $i(i\in V_r)$
M	A sufficiently large positive value
$\epsilon$	A sufficiently small positive value

, and the decision variables are defined in

Table 3. Decision variables.

Decision Variable	Definition
$x_{it}$	1, if replenishment occurs in satellite $i(i\in V_r)$ at period $t(t\in T)$; 0 otherwise
$v_{i\tau t}$	Number of products produced at period $\tau (\tau \in T)$ and replenished to satellite $i(i\in V_r)$ at the end of period $t(t\in T)$
$s_{ij\tau t}$	Number of products distributed from satellite $i(i\in V_r)$ to customer $j(j\in V_c)$ at the end of period $t(t\in T)$, and the products produced at period $\tau (\tau \in T_0)$
$y_{ijt}$	1, if arc $(i,j)\in A$ is assigned to a vehicle at period $t(t\in T)$; 0 otherwise
$l_{ijt}$	Load of vehicle passing by arc $(i,j)\in A$ at period $t(t\in T)$
$z_t$	1, if the depot produces at period $t(t\in T)$; 0 otherwise
$q_t$	Output of the depot at period $t(t\in T)$
$I_{i\tau t}$	Inventory of products at node $i(i\in V_r\cup V_c)$ at the end of period $t(t\in T)$ for products produced in period $\tau (\tau \in T_0)$

.

3.3. MIP Formulation

An MIP model is proposed with the objective of minimizing the total cost, including the fixed production cost and variable production cost of the depot, the inventory cost in the depot and stores, the transportation cost of the replenishment from the depot to satellites, and the transportation cost of the distribution from satellites to customers. The formulation is described as follows:

In the formulation, the objective function (1) is to minimize the total cost. Constraints (2) and (3) ensure the balance of production, inventory and delivery at the depot. Constraints (4) and (5) guarantee the balance of inventory, delivery and consumption at the satellites. Constraint (6) means that satellites can only serve the customers within their own distribution area. Constraints (7) and (8) state that the demand of each customer should be met. Constraint (9) defines the 0–1 relationship between $q_t$ and $z_t$. Constraints (10) and (11) ensure that the vehicle and inventory capacity limits are met, respectively. Constraints (12) and (13) ensure that the balance of vehicle flow and the relationship at each customer point cannot be repeatedly visited. Constraint (14) restrains that only customer points within the same distribution area can be reached from each other. Constraints (15) and (16) realize the vehicle load feasibility and capacity limits on each arc in the second distribution echelon. Constraints (17) and (18) are MTZ-type constraints of vehicle load for the second echelon and ensure the relationship between the load of vehicles and demands. Note that the MTZ formulations introduced by Miller et al. [39] for TSP problems are recognized as a relaxation of subtour elimination constraints. Constraints (19) to (21) mean that stock-out is not allowed. Constraint (24) restricts the lead time of replenishment, i.e., there are no current products in the satellites. Finally, the range of all variables is defined by constraints (25) to (33).

$$\begin{array}{c}\mathbf{min}{\sum }_{t\in T}(f{z}_t+u{q}_t+{\sum }_{i\in V_0\cup V_r}\sum _{\tau =0}^t{h}_{i\tau t}{I}_{i\tau t}+{\sum }_{i\in V_r}fe{e}_i{x}_{it}+{\sum }_{(i,j)\in A}{c}_{ij}{y}_{ijt})\end{array}$$

(1)

$$\begin{array}{c}\mathbf{s}.\mathbf{t}.q_t={\sum }_{i\in V_r}{v}_{it,t+\theta -1}+I_{0tt},\forall t\in T\end{array}$$

(2)

$$\begin{array}{c}(1-{\alpha }_{\tau ,t-\theta })I_{0\tau ,t-\theta }={\sum }_{i\in V_r}{v}_{i\tau t}+I_{0\tau ,t-\theta +1},\forall t\in T,\tau \in T,t>\theta ,\tau \le t-\theta \end{array}$$

(3)

$$\begin{array}{c}(1-{\alpha }_{0,t-1})I_{i0,t-1}={\sum }_{j\in V_{c_i}}{s}_{ij0t}+I_{i0t},\forall i\in V_r,t\in T\end{array}$$

(4)

$$\begin{array}{c}(1-{\alpha }_{\tau ,t-1})(I_{i\tau ,t-1}+v_{i\tau ,t-1})={\sum }_{j\in V_{c_i}}{s}_{ij\tau t}+I_{i\tau t},\forall i\in V_r,t\in T,\tau \in T,t>\theta ,\tau \le t-\theta \end{array}$$

(5)

$$\begin{array}{c}{\sum }_{t\in T}{s}_{ij0t}+\sum _{t=\theta +1}^{\left|T\right|}\sum _{\tau =1}^{t-\theta }{s}_{ij\tau t}\le M{o}_{ij},\forall i\in V_r,j\in V_c\end{array}$$

(6)

$$\begin{array}{c}{\sum }_{i\in V_r}{s}_{ij0t}=d_{jt},\forall j\in V_c,t\in T,t\le \theta \end{array}$$

(7)

$$\begin{array}{c}{\sum }_{i\in V_r}\sum _{\tau =1}^{t-\theta }{s}_{ij\tau t}=d_{jt},\forall j\in V_c,t\in T,t>\theta \end{array}$$

(8)

$$\begin{array}{c}{q}_t\le C{z}_t,\forall t\in T\end{array}$$

(9)

$$\begin{array}{c}\sum _{\tau =1}^{t-\theta +1}{v}_{i\tau t}\le Q_1{x}_{it},\forall i\in V_r,t\in T\end{array}$$

(10)

$$\begin{array}{c}\sum _{\tau =0}^t{I}_{i\tau t}\le L_i,\forall i\in V_0\cup V_r,t\in T\end{array}$$

(11)

$$\begin{array}{c}{\sum }_{(i,j)\in A}{y}_{ijt}={\sum }_{(j,i)\in A}{y}_{jit},\forall i\in V_r\cup V_c,t\in T\end{array}$$

(12)

$$\begin{array}{c}{\sum }_{(j,i)\in A}{y}_{jit}\le 1,\forall i\in V_c,t\in T\end{array}$$

(13)

$$\begin{array}{c}{y}_{ijt}\le {\sum }_{k\in V_r}{o}_{ki}{o}_{kj},\forall (i,j)\in A,t\in T\end{array}$$

(14)

$$\begin{array}{c}{l}_{ijt}\ge d_{jt}{y}_{ijt},\forall (i,j)\in A,t\in T\end{array}$$

(15)

$$\begin{array}{c}{l}_{ijt}\le (Q_2-d_{it})y_{ijt},\forall (i,j)\in A,t\in T\end{array}$$

(16)

$$\begin{array}{c}{\sum }_{(j,i)\in A}{l}_{jit}=\sum _{(i,j)\in A}{l}_{ijt}+d_{it},\forall i\in V_c,t\in T\end{array}$$

(17)

$$\begin{array}{c}{\sum }_{(i,j)\in A}{l}_{ijt}={\sum }_{j\in V_{c_i}}{d}_{jt},\forall i\in V_r,t\in T\end{array}$$

(18)

$$\begin{array}{c}{v}_{i\tau t}=0,\forall i\in V_r,t\in T,\tau \in T,\tau >t\end{array}$$

(19)

$$\begin{array}{c}{s}_{ij\tau t}=0,\forall i\in V_r,j\in V_c,t\in T,\tau \in T,\tau \ge t\end{array}$$

(20)

$$\begin{array}{c}{I}_{i\tau t}=0,\forall i\in V_0\cup V_r,t\in T,\tau \in T,\tau >t\end{array}$$

(21)

$$\begin{array}{c}{I}_{00t}=0,t\in T_0\end{array}$$

(22)

$$\begin{array}{c}{I}_{i00}=in{v}_i,i\in V_r\end{array}$$

(23)

$$\begin{array}{c}{I}_{itt}=0,\forall i\in V_r,t\in T\end{array}$$

(24)

$$\begin{array}{c}{I}_{i\tau t}\ge 0,\forall i\in V_0\cup V_r,T\in T_0,\tau \in T_0\end{array}$$

(25)

$$\begin{array}{c}{q}_t\ge 0,\forall t\in T\end{array}$$

(26)

$$\begin{array}{c}{v}_{i\tau t}\ge 0,\forall i\in V_r,\forall t\in T,\tau \in T,t\ge \tau +\theta -1\end{array}$$

(27)

$$\begin{array}{c}{l}_{ijt}\ge 0,\forall (i,j)\in A,\forall t\in T\end{array}$$

(28)

$$\begin{array}{c}{s}_{ij0t}\ge 0,\forall i\in V_r,j\in V_c,t\in T\end{array}$$

(29)

$$\begin{array}{c}{s}_{ij\tau t}\ge 0,\forall i\in V_r,j\in V_c,\tau \in T,t\in T,t>\theta \end{array}$$

(30)

$$\begin{array}{c}{y}_{ijt}\in \{0,1\},\forall (i,j)\in A,\forall t\in T\end{array}$$

(31)

$$\begin{array}{c}{x}_{it}\in \{0,1\},\forall i\in V_r,t\in T\end{array}$$

(32)

$$\begin{array}{c}{z}_t\in \{0,1\},\forall i\in T\end{array}$$

(33)

3.4. Modeling the Inventory Management/Delivery Policy

The model formulated in Section 3.3 under the optimal policy (OP) considers no special inventory strategy, and all products in the inventory are sold with the sole purpose of minimizing the total cost. However, to make inventory management more practicable and realize different sales modes, manufacturers often use different inventory strategies. Similar to those in [40,41], the following inventory strategies are discussed.

In addition to the OP, there are two other inventory strategies in the first echelon (replenishment). One strategy is OF, which ensures that the earlier-produced products, i.e., the older ones, would be used for replenishment in priority, which can be understood as the “first in, first out” principle. The other strategy is FF, in which the later-produced products, i.e., fresher products, would be first used, similar to the “last in, first out” principle.

Similarly, in the second echelon (distribution), there are also two other adoptable inventory strategies in addition to the OP. One is the OF strategy, which ensures that the earlier-produced products would be distributed in priority; the other is the FF strategy, in which the later-produced products would be first distributed. Accordingly, considering the inventory strategies in the two-echelon distribution network, there are nine inventory strategy combinations.

Then, some new decision variables, which are listed in

Table 4. Newly added decision variables.

Decision Variable	Definition
$p_{\tau t}$	1, if products produced in period $\tau (\tau \in T)$ are used for replenishment at period $t(t\in T)$; 0 otherwise
$w_{i\tau t}$	1, if products produced in period $\tau (\tau \in T_0)$ are used for distribution by satellite $i(i\in V_r)$ at period $t(t\in T)$; 0 otherwise

, need to be introduced.

In the first echelon (replenishment), when the satellites replenish products from the depot, the earlier-produced products are required to be handled in priority under the OF strategy. Accordingly, if a product produced in a certain period is used for replenishment, it is required that the products produced before it are out of stock and unable to fulfill the replenishment.

Proposition 1.

The OF strategy in the replenishment echelon is expressed by the following formula:

$$\begin{array}{c}\sum _{\tau =1}^{\eta }{I}_{0\tau t}\le L_0(1-\lceil \frac{{\sum }_{i\in V_r}{v}_{i,\eta +1,t}}{M}\rceil ),\forall t\in T,\eta \in T,t>\theta ,\eta \le t-\theta \end{array}$$

(34)

Proof of Proposition 1.

If ${\sum }_{i\in V_r}{v}_{i,\eta +1,t}=0$, considering the inventory capacity constraint of the depot (11), apparently Formula (34) is true; if ${\sum }_{i\in V_r}{v}_{i,\eta +1,t}>0$, Formula (34) ensures that if products produced in period $\eta +1$ are used for replenishment at period t, then the inventory of products produced before period $\eta +1$ must be equal to 0 at period t. □

Contrary to the OF strategy, the FF strategy means that the fresher products need to be handled first. That is, when the products produced in a certain period are adopted, it is required that the product with a later production date be insufficient to fulfill the replenishment.

Proposition 2.

The FF strategy in the replenishment echelon is expressed by the following formula:

$$\begin{array}{c}\sum _{\tau =\eta +1}^{t-\theta +1}{I}_{0\tau t}\le L_0(1-\lceil \frac{{\sum }_{i\in V_r}{v}_{i\eta t}}{M}\rceil ),\forall t\in T,\eta \in T,t>\theta ,\eta \le t-\theta \end{array}$$

(35)

Proof of Proposition 2.

If ${\sum }_{i\in V_r}{v}_{i\eta t}=0$, considering the inventory capacity constraint of the depot (11), apparently Formula (35) is true; if ${\sum }_{i\in V_r}{v}_{i\eta t}>0$, Formula (35) ensures that if products produced in period $\eta$ are used for replenishment at period t, then the inventory of products produced before period $\eta$ must be equal to 0 at period t. □

In the second echelon (distribution), when each satellite distributes products to customers within their own distribution area, the products with an earlier production date are required to be handled in priority under the OF strategy. Accordingly, if the product produced in a certain period is adopted, it is required that the products produced before it are insufficient to fulfill the replenishment.

Proposition 3.

The OF strategy in the distribution echelon is expressed by the following formula:

$$\begin{array}{c}\sum _{\tau =0}^{\eta }{I}_{i\tau t}\le L_i(1-\lceil \frac{{\sum }_{j\in V_{c_i}}{s}_{ij,\eta +1,t}}{M}\rceil ),\forall i\in V_r,t\in T,\eta \in T_0,t>\theta ,\eta \le t-\theta -1\end{array}$$

(36)

Proof of Proposition 3.

If ${\sum }_{j\in V_{c_i}}{s}_{ij,\eta +1,t}=0$, considering the inventory capacity constraint of satellites (11), apparently Formula (36) is true; if ${\sum }_{j\in V_{c_i}}{s}_{ij,\eta +1,t}>0$, Formula (36) ensures that if products produced in period $\eta +1$ are used for replenishment at period t, then the inventory of products produced before period $\eta +1$ must be equal to 0 at period t. □

Contrary to the OF strategy, the products with later production dates need to be handled first under the FF strategy. Thus, when the product produced in a certain period is adopted, it is required that the products with later production dates are insufficient in inventory to fulfill the replenishment.

Proposition 4.

The FF strategy in the distribution echelon is expressed by the following formula:

$$\begin{array}{c}\sum _{\tau =\eta +1}^{t-\theta }{I}_{i\tau t}\le L_i(1-\lceil \frac{{\sum }_{j\in V_{c_i}}{s}_{ij\eta t}}{M}\rceil ),\forall i\in V_r,t\in T,\eta \in T_0,t>\theta ,\eta \le t-\theta -1\end{array}$$

(37)

Proof 

(Proof of Proposition 4). If ${\sum }_{j\in V_{c_i}}{s}_{ij\eta t}=0$, considering the inventory capacity constraint of satellites (11), apparently Formula (37) is true; if ${\sum }_{j\in V_{c_i}}{s}_{ij\eta t}>0$, Formula (37) ensures that if products produced in period $\eta$ are used for replenishment at period t, then the inventory of products produced before period $\eta$ must be equal to 0 at period t. □

3.5. Linearization

To linearize constraints (34) to (37) constructed in Propositions 1 to 4, the following constraints are introduced.

$$\begin{array}{c}{p}_{\tau t}\ge \frac{{\sum }_{i\in V_r}{v}_{i\tau t}}{M}-\epsilon ,\forall \tau \in T,t\in T\end{array}$$

(38)

$$\begin{array}{c}{p}_{\tau t}\le \frac{{\sum }_{i\in V_r}{v}_{i\tau t}}{M}+1-\epsilon ,\forall \tau \in T,t\in T\end{array}$$

(39)

$$\begin{array}{c}{w}_{i\tau t}\ge \frac{{\sum }_{j\in V_{c_i}}{s}_{ij\tau t}}{M}-\epsilon ,\forall i\in V_r,\tau \in T_0,t\in T\end{array}$$

(40)

$$\begin{array}{c}{w}_{i\tau t}\le \frac{{\sum }_{j\in V_{c_i}}{s}_{ij\tau t}}{M}+1-\epsilon ,\forall i\in V_r,\tau \in T_0,t\in T\end{array}$$

(41)

$$\begin{array}{c}{p}_{\tau t}=\{0,1\},\forall i\in V_r,\tau \in T,t\in T\end{array}$$

(42)

$$\begin{array}{c}{w}_{i\tau t}=\{0,1\},\forall i\in V_r,\tau \in T_0,t\in T\end{array}$$

(43)

Constraints (38) and (39) ensure that if the products produced in the depot at period $\tau$ are used for replenishment at period t, then the corresponding 0–1 variable is equal to 1. Constraints (40) and (41) guarantee that if the products produced in period $\tau$ are used for distribution at period t, then the corresponding 0–1 variable is equal to 1. Moreover, constraints (42) to (43) confine the range of variables.

With the added constraints, constraints (34) to (37) can be linearized to constraints (44) to (47):

• The OF strategy in the replenishment echelon

  $$\begin{array}{c}\sum _{\tau =1}^{\eta }{I}_{0\tau t}\le L_0(1-p_{\eta +1,t}),\forall t\in T,\eta \in T,t>\theta ,\eta \le t-\theta \end{array}$$

  (44)
• The FF strategy in the replenishment echelon

  $$\begin{array}{c}\sum _{\tau =\eta +1}^{t-\theta +1}{I}_{0\tau t}\le L_0(1-p_{\eta t}),\forall t\in T,\eta \in T,t>\theta ,\eta \le t-\theta \end{array}$$

  (45)
• The OF strategy in the distribution echelon

  $$\begin{array}{c}\sum _{\tau =0}^{\eta }{I}_{i\tau t}\le L_i(1-w_{i,\eta +1,t}),\forall i\in V_r,t\in T,\eta \in T_0,t>\theta ,\eta \le t-\theta -1\end{array}$$

  (46)
• The FF strategy in the distribution echelon

  $$\begin{array}{c}\sum _{\tau =\eta +1}^{t-\theta }{I}_{i\tau t}\le L_i(1-w_{i\eta t}),\forall i\in V_r,t\in T,\eta \in T_0,t>\theta ,\eta \le t-\theta -1\end{array}$$

  (47)

Accordingly, the aforementioned nine strategy combinations can be realized by adding different constraint combinations into the original model. The modeling method of each strategy combination is presented in

Table 5. Description of modeling methods under different strategy combinations. OF: old first; FF: fresh first.

Strategy Combination	Model (Described by Formula)
OF–OF	(1)−(33), (38)− (43), (44), (46)
OF–FF	(1)−(33), (38)− (43), (44), (47)
OF–Optimal	(1)−(33), (38)−(39), (42), (44)
FF–OF	(1)−(33), (38)−(43), (45), (46)
FF–FF	(1)−(33), (38)− (43), (45), (47)
FF–Optimal	(1)−(33), (38)−(39), (42), (45)
Optimal-OF	(1)−(33), (40)−(41), (43), (46)
Optimal-FF	(1)−(33), (40)−(41), (43), (47)
OP	(1)−(33)

.

4. Branch-and-Cut Algorithm

4.1. Valid Inequalities

Some logical inequalities are introduced first.

In VRPs, one of the commonly used logical inequalities is the limit of the minimum number of vehicles. In this study, this logical inequality is extended and improved to the limit of minimum number of vehicles per satellite at each period.

$$\begin{array}{c}{\sum }_{j\in V_{c_i}}{y}_{ijt}\ge \lceil \frac{{\sum }_{j\in V_{c_i}}{d}_{jt}}{Q_2}\rceil ,\forall i\in V_r,t\in T\end{array}$$

(48)

In inequality (48), the left side represents the number of vehicles from each satellite per period, and the right side rounds up the ratio between the total customer demand within the satellite’s own distribution area and the capacity of the second-echelon distribution vehicles. Therefore, inequality (48) can restrict the number of vehicles from each satellite per period.

There is also a logical relationship between distribution decisions and access decisions.

$$\begin{array}{c}{\sum }_{j\in V_r\cup V_c}{y}_{jit}\le {\sum }_{j\in V_r}\sum _{\tau =0}^{t-\theta }{s}_{ji\tau t},\forall i\in V_c,t\in T\end{array}$$

(49)

Inequality (49) indicates that if no product is delivered to a customer at a certain period, then no arc will reach that node at that period, i.e., the node cannot be visited at that period.

In addition to the above logical inequalities, there are also valid inequalities for production decisions and replenishment decisions.

The first is the $(\ell ,S,WW)$ inequality for production decision making, expressed as (50) and (51).

$$\begin{array}{c}{\sum }_{i\in V_0\cup V_r}(1-{\alpha }_{00})I_{i00}+\sum _{\delta =1}^{\eta -1}\sum _{\tau =\delta +1}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau }{z}_{\delta }\ge \sum _{\tau =1}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau },\forall \eta \in T,1<\eta \le \left|T\right|\end{array}$$

(50)

$$\begin{array}{c}{\sum }_{i\in V_0\cup V_r}\sum _{\tau =0}^{t-\theta }(1-{\alpha }_{\tau ,t-1})I_{i\tau ,t-1}+{\sum }_{i\in V_r}\sum _{\tau =1}^{t-\theta }(1-{\alpha }_{\tau ,t-1})v_{i\tau ,t-1}+\sum _{\delta =t}^{\eta -1}\sum _{\tau =\delta +1}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau }{z}_{\delta }\\ \ge \sum _{\tau =t}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau },\forall t\in T,\eta \in T,1<t<\eta \le \left|T\right|\end{array}$$

(51)

The $(\ell ,S,WW)$ inequality expressed as Formula (52) is proposed in [42], and it is applicable to LSP with Wagner–Whitin costs.

$$\begin{array}{c}{s}_{t-1}\ge \sum _{\tau =t}^{\eta }{d}_{\tau }(1-y_t-y_{t+1}-\cdots -y_{\tau }),\forall t\in T,\eta \in T,t<\eta <\left|T\right|\end{array}$$

(52)

$s_{t-1}$ represents the inventory level at period $t-1$, $d_{\tau }$ represents the demand of period $\tau$ and $y_t$ is the 0–1 variable of whether to produce the product at period t.

In [42], LSP with Wagner–Whitin costs are defined as follows:

If an LSP satisfies constraint (53) for all periods, then the problem is an LSP with Wagner–Whitin costs. ($p_t$ represents the production cost at period t and $h_t$ represents the unit inventory cost at period t).

$$\begin{array}{c}{p}_t+h_t\ge p_{t+1}\end{array}$$

(53)

The characteristics of LSPs with Wagner–Whitin costs are described in [42], in which it is optimal to produce as late as possible. Constraint (52) means that only when there is no production during periods $[k,\cdots ,j]$ can the inventory level of period $k-1$ satisfy the demand of periods $[k,\cdots ,j]$.

In this study, because the unit production cost u is constant and the unit inventory cost increases with the inventory time, inequality (53) naturally holds.

Considering the lead time of replenishment and the deterioration of perishable products, the corresponding variation of inequality $(\ell ,S,WW)$ is considered. Then, inequality (52) is transformed into (54) to (55).

$$\begin{array}{c}{\sum }_{i\in V_0\cup V_r}(1-{\alpha }_{00})I_{i00}\ge {\sum }_{i\in V_c}{d}_{i1}+\sum _{\tau =2}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau }(1-z_1-z_2-\cdots -z_{\tau -1}),\forall \eta \in T,1<\eta <\left|T\right|\end{array}$$

(54)

$$\begin{array}{c}{\sum }_{i\in V_0\cup V_r}\sum _{\tau =0}^{t-\theta }(1-{\alpha }_{\tau ,t-1})I_{i\tau ,t-1}+{\sum }_{i\in V_r}\sum _{\tau =1}^{t-\theta }(1-{\alpha }_{\tau ,t-1})v_{i\tau ,t-1}\\ \ge {\sum }_{i\in V_c}{d}_{it}+\sum _{\tau =t+1}^{\eta }{\sum }_{i\in V_c}{d}_{i\tau }(1-z_t-z_{t+1}-\cdots -z_{\tau -1}),\forall t\in T,\eta \in T,1<t<\eta \le \left|T\right|\end{array}$$

(55)

Obviously, inequalities (50) to (51) can be obtained after adjusting (54) to (55).

Then, there are also corresponding inequalities for the replenishment decision of each satellite, which are expressed as (56) to (57).

$$\begin{array}{c}(1-{\alpha }_{00})I_{i00}+\sum _{\delta =1}^{\eta -1}\sum _{\tau =\delta +1}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau }{x}_{i\delta }\ge \sum _{\tau =1}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau },\forall i\in V_r,\eta \in T,1<\eta <\left|T\right|\end{array}$$

(56)

$$\begin{array}{c}\sum _{\tau =0}^{t-\theta }(1-{\alpha }_{\tau ,t-1})I_{i\tau ,t-1}+\sum _{\tau =1}^{t-\theta }(1-{\alpha }_{\tau ,t-1})v_{i\tau ,t-1}+\sum _{\delta =t}^{\eta -1}\sum _{\tau =\delta +1}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau }{x}_{i\delta }\\ \ge \sum _{\tau =t}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau },\forall i\in V_r,t\in T,\eta \in T,1<t<\eta \le \left|T\right|\end{array}$$

(57)

For all periods of t, the unit inventory cost in the depot is lower than that in each satellite. That is, if the products are not used immediately after replenishment, the total inventory cost will be reduced if the products are stored in the depot. Therefore, we can get the valid inequalities (56) to (57), which means that only when there is no replenishment during the periods $[k-1,\cdots ,j-1]$ can the inventory level of period $k-1$ satisfy the demand of periods $[k,\cdots ,j]$.

Similarly, considering the lead time of replenishment and deterioration of perishable products, the inequalities are given as (58) to (59).

$$\begin{array}{c}(1-{\alpha }_{00})I_{i00}\ge {\sum }_{j\in V_{c_i}}{d}_{j1}+\sum _{\tau =2}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau }(1-x_{i1}-x_{i2}-\cdots -x_{i,\tau -1}),\forall i\in V_r,\eta \in T,1<\eta <\left|T\right|\end{array}$$

(58)

$$\begin{array}{c}\sum _{\tau =0}^{t-\theta }(1-{\alpha }_{\tau ,t-1})I_{i\tau ,t-1}+\sum _{\tau =1}^{t-\theta }(1-{\alpha }_{\tau ,t-1})v_{i\tau ,t-1}\ge {\sum }_{j\in V_{c_i}}{d}_{jt}\\ +\sum _{\tau =t+1}^{\eta }{\sum }_{j\in V_{c_i}}{d}_{j\tau }(1-x_{i,t+1}-x_{i,t+2}-\cdots -x_{i,\tau -1}),\forall i\in V_r,t\in T,\eta \in T,1<t<\eta <\left|T\right|\end{array}$$

(59)

After adjusting inequalities (58) to (59), inequalities (56) to (57) can be obtained.

4.2. Algorithm Framework

In this study, four types of valid inequalities as presented in the previous section are obtained, and they can be applied to the branch-and-cut algorithm. The specific framework is given in

Table 6. Algorithm framework.

Algorithm 1: Branch-and-cut algorithm.

1 Initialization: Set the current optimal value (the current upper bound) to infinity, $z^{*}\leftarrow +\infty$; add the root node to the set of initial active nodes (nodes to be processed),    $N\leftarrow \left\{N_0\right\}$.

2 Generate and add valid inequalities: Generate inequalities (56) to (57) related to replenishment and add them to the root node; generate the logical inequalities (48) to    (49) and $(\ell ,S,WW)$ inequalities (50) to (51) and add them to the cutting plane pool.

3 Determine if termination conditions are met: If the set of active points $N=\varnothing$ or the time requirement is reached, the calculation terminates and output the calculation    results according to the current situation:

Situation 1    if the current optimal value has no corresponding optimal solution that conforms to integer conditions, then output “no feasible solution.”

Situation 2    if the current optimal value has corresponding optimal solution that conforms to integer conditions, then output the solution;

otherwise, go to step 4.

4 Select the node: According to the best-bound search strategy, select and delete an active node from the current active node set. Solve and record the relaxation solution of    the node, and then judge and process the node according to the situation:

Situation 1    if no feasible solution is available at the active node, cut the branch and return to step 3.

Situation 2    if a feasible solution is available at the active node, record the optimal value as z. If $z\ge z^{*}$, cut the branch and return to step 3. If $z\le z^{*}$, conduct further judgment and processing according to the following situation:    Situation a if the optimal solution of the active node satisfies the integer condition, the current optimal value is updated $z^{*}\leftarrow z$; then cut the branch and return to step 3.    Situation b if the optimal solution of the active node does not satisfy the integer condition, add the valid inequalities in the cutting plane pool to the node and solve the node again. If the solution conforms to other conditions in step 4, the corresponding operation should be performed; otherwise, go to step 5.

5 Branch: Select a non-integer variable to branch, set the variable as 0 on the left node and 1 on the right node, and add the two nodes to the set of active nodes; then return to step 3.

.

Overall, the algorithm is performed as follows: firstly, constraints (31) to (33) are relaxed, with 0–1 variables $y_{ijt}$, $x_{it}$ and $z_t$ relaxed to continuous variables (from 0 to 1); then the problem is branched and cut. The relaxation solution of each node is the lower bound of this node, and it is also the benchmark to compare with the current optimal value. If the three variables $y_{ijt}$, $x_{it}$ and $z_t$ in the relaxation solution of this node are all integers, then the optimal solution of this node satisfies the integer condition. For each node solving, if the current node does not perform a cutting operation, and the optimal solution of this node does not satisfy the integer condition, then the cutting plane in the cutting plane pool should be added to this node for further solving and subsequent operations.

5. Computational Results

5.1. Data Generation

In this study, the size of test instances is measured by the planning horizon $\left|T\right|$, the number of satellites $|V_R|$ and the number of customers in each satellite’s distribution area $|V_C|/|V_R|$. Under the basic scale, the planning horizon $\left|T\right|$ is selected between 6 and 15, the number of satellites R is selected between 5 and 12 and the number of customers in each satellite’s area is chosen from $\{15,20,25,30\}$. These numbers are chosen in accordance with the settings in Qiu et al. [41]. The specific scale of some analyses, which will be explained in detail in the corresponding sections, will be adjusted accordingly.

The exponential deterioration rate, inventory cost, customer demand and other parameter settings are similar to those applied in Dolgui et al. [43]. The generation of coordinates of the depot, satellite and customer nodes is referred to by Liu et al. [31], whose research content is the two-echelon capacitated VRP with grouping constraints. Besides, we note that in order to facilitate the calculation, the lead time $\theta$ is set to 1 for subsequent experiments. The generation of coordinates and parameters are described as follows.

(1) Deterioration rate

According to the expression of deterioration rate of perishable products in Dolgui et al. [43], the deterioration rate formula is

$$\begin{array}{c}Det\left(t\right)=A{e}^{t/B}\end{array}$$

(60)

where A is the deterioration rate when products are initially produced and B is the time cost for deterioration rate to reach e times of the initial deterioration rate (can be understood as shelf life).

The deterioration rate of products produced in period $\tau$ can be denoted as

$$\begin{array}{c}{\alpha }_{\tau t}={\int }_{t-\tau }^{t-\tau +1}Det\left(t\right)d_t.\end{array}$$

(61)

(2) Inventory cost

In this study, the inventory cost increases linearly as follows:

$$\begin{array}{c}{h}_{i\tau t}=h_{i0}+\beta (t-\tau ),\forall i\in V_0\cup V_r,\tau \in T_0,t\in T\end{array}$$

(62)

where $\beta$ is the increment of inventory cost and $h_{i0}$ is the basic inventory cost in the depot and satellites. The basic inventory cost in the satellites is 20% more than that in the depot.

(3) Coordinate of each point, cost of replenishment, and distribution

Referring to the coordinate generation method in Liu et al. [31], all coordinates are in a $[0,100]\times [0,100]$ square, and the coordinate of the depot is (50,50). In this study, the number of satellites is increased based on the references, and the corresponding coordinates of satellites are given in

Table 7. Coordinates of satellites.

Satellite	Coordinate	Satellite	Coordinate
1	(25,25)	7	(62.5,62.5)
2	(25,75)	8	(37.5, 62.5)
3	(75,75)	9	(50, 25)
4	(75,25)	10	(75,50)
5	(37.5,37.5)	11	(50,75)
6	(62.5,37.5)	12	(25,50)

.

The customers are distributed around the satellite responsible for them, and their horizontal and vertical coordinates differ within $\pm 10$ from those of the corresponding satellite. The distance between each node is measured by the linear distance of coordinates. Considering that the satellites are far from the depot and truck-load transportation is used for replenishment, the replenishment cost of the first echelon is designed as 5 times the distance between the satellites and the depot. Moreover, considering that each satellite is relatively close to its customer nodes, the transportation cost on each arc in the second echelon is designed as 0.5 times the distance between two nodes.

(4) Customer demand

The average demand of each customer node at each period is

$$\begin{array}{c}{d}_{avg}=20\end{array}$$

(63)

The total customer demand in each satellite’s distribution area is $\left(\right|V_c|/|V_r\left|\right)d_{avg}$.

When the demand changes periodically, we take one week as a cycle for simulation. Note that the customer demand is smaller in the first four days, and will increase in the last three days because of weekends. Specifically, the demand of each customer in the first four days is uniformly distributed in the interval $[0,20]$, and the demand in the subsequent three days is uniformly distributed in $[20,47]$.

For a stable demand, the customer demand changes without periodic fluctuations. Specifically, the demand of each customer in each period is uniformly distributed in $[0,40]$.

(5) Other parameters (

Table 8. Setting of other parameters.

Type of Data	Setting
Depot data	$C=\lceil 1.3d_{avg}|V_C|\rceil ,f=8C,u=2,L_0=3C$
Satellite data	$L_i=3d_{avg}|V_c|/|V_r|,I_{i00}=\lceil 1.2d_{avg}|V_c|/|V_r|\rceil$
Vehicle data	$Q_1=2.5d_{avg}|V_c|/|V_r|,Q_2=d_{avg}|V_c|/|V_r|$

)

5.2. Effect of Valid Inequalities

In this study, the impact of valid inequalities on the model is first verified. By generating different instances at different scales, the relaxed lower bounds obtained by adding each valid inequality and by adding CPLEX default inequalities at the root node are calculated and compared with the relaxed lower bound obtained by CPLEX without adding any default inequalities. As presented in

Table 9. Coordinates of satellites.

$\left|\mathit{T}\right|$	$|{\mathit{V}}_{\mathit{R}}|$	$\frac{|{\mathit{V}}_{\mathit{C}}|}{|{\mathit{V}}_{\mathit{R}}|}$	LP	(48) (%)	(49) (%)	(50) and (51) (%)	(56) and (57) (%)	ALL (%)	CPLEX (%)
6	5	15	38,614.34	0.08	0	1.62	2.60	3.71	0
6	5	20	52,006.04	0.06	0	2.14	2.32	4.15	0
6	6	15	47,227.11	0.08	0	1.55	2.25	3.47	0
6	6	20	62,675.74	0.06	0	1.83	2.03	3.62	0
6	7	15	54,308.19	0.08	0	1.51	2.22	3.41	0
6	7	20	71,229.65	0.06	0	1.65	1.95	3.34	0
6	8	15	64,887.73	0.10	0	1.04	1.82	2.76	0
6	8	20	80,385.99	0.05	0	2.11	2.11	3.90	0
9	5	15	67,257.21	0.07	0	3.03	2.89	5.16	0
9	5	20	92,821.88	0.05	0	3.02	2.18	4.77	0
9	6	15	80,242.79	0.07	0	3.03	2.77	5.13	0
12	5	15	89,948.75	0.06	0	3.50	3.58	5.95	0
12	5	20	117,146.52	0.05	0	4.13	2.92	6.23	0
12	6	15	105,567.58	0.08	0	3.67	3.41	6.04	0
12	6	20	143,067.64	0.06	0	3.81	2.59	5.74	0
12	7	15	122,362.95	0.10	0	3.98	3.22	6.28	0
12	7	20	164,453.37	0.04	0	3.94	2.56	5.90	0
12	8	15	137,910.56	0.08	0	4.04	3.24	6.34	0
12	8	20	184,663.49	0.05	0	4.11	2.53	6.05	0
		Average		0.07	0	2.85	2.50	4.80	0

, columns $\left|T\right|$, $|V_R|$ and $|V_C|/|V_R|$ are the scale measurement parameters of the instances; column LP is the root relaxation lower bound obtained without adding any valid inequalities or CPLEX default inequalities; column (48) is the growth ratio $(\%)$ of the relaxed lower bound obtained by adding only valid inequality (48) compared to that of LP, and the next four columns have similar definitions; column ALL represents the growth ratio (%) of the upper bound obtained by adding all valid inequalities ((48) to (51), (56) and (57)), compared to LP; column CPLEX is the growth ratio (%) of the upper bound obtained by adding only CPLEX default inequalities, compared to LP.

In this study, when verifying the impact of valid inequalities on the model, five sets of different instances are generated for each scale to take the average value. From Table 9, it is obvious that the default inequalities in CPLEX cannot improve the relaxed lower bounds, but three types of valid inequalities designed in this study can make improvements, and adding all four types of valid inequalities to the root node can improve the relaxed lower bounds most (4.8%). Specifically, the growth ratio of valid inequalities (50) to (51) is the largest (2.85%), and that of the valid inequalities (56) to (57) is the second largest (2.5%). We observe that the relaxed lower bounds are not increased by the valid inequality (49). This is because this constraint is aimed at making ${\sum }_{j\in V_r\cup V_c}{y}_{jit}$ as small as possible, and it will not increase the total cost. However, because this inequality can logically reduce the solution space, we do not delete it directly. In the subsequent branch-and-cut algorithm, we will consider two cases of adding and not adding inequality (49), respectively, and verify the influence of this constraint according to the data analysis.

5.3. Effect of Branch-and-Cut Algorithm

To verify the validity of the algorithm, 27 groups of small and medium-sized test instances were generated, in which $\left|T\right|$ was selected from $\{6,9,12\}$, $|V_R|$ was selected from $\{8,10,12\}$ and $|V_C|/|V_R|$ was selected from $\{15,20,25\}$. Meanwhile, large-sized instances with $\left|T\right|=13,14$ and 15 were generated. By comparing the computational time of CPLEX and branch-and-cut, the performance of branch-and-cut in different scales was verified. As presented in

Table 10. Validity of algorithm effectiveness. B&C: branch-and-cut.

$\left|\mathit{T}\right|$	$|{\mathit{V}}_{\mathit{R}}|$	$\frac{|{\mathit{V}}_{\mathit{C}}|}{|{\mathit{V}}_{\mathit{R}}|}$	CPLEX (s)	B&C_1 (s)	decrease_1 (%)	B&C_2 (s)	decrease_2 (%)
6	8	15	54.48	27.56	49.41	28.23	48.18
6	8	20	108.89	54.96	49.53	55.63	48.91
6	8	25	200.79	119.03	40.72	119.35	40.56
6	10	15	67.88	35.88	47.14	38.50	43.28
6	10	20	148.33	80.25	45.90	107.39	27.60
6	10	25	357.77	214.56	40.03	214.99	39.91
6	12	15	95.65	41.36	56.76	43.82	54.19
6	12	20	208.12	95.25	54.23	97.68	53.07
6	12	25	401.33	293.30	26.92	307.80	23.31
9	8	15	104.60	40.67	61.12	44.09	57.85
9	8	20	329.97	120.63	63.44	121.13	63.29
9	8	25	811.14	351.97	56.61	503.81	37.89
9	10	15	192.18	58.84	69.38	67.97	64.63
9	10	20	427.14	147.27	65.52	220.72	48.32
9	10	25	839.58	247.51	70.52	511.28	39.10
9	12	15	209.66	73.95	64.73	75.05	64.21
9	12	20	445.23	192.67	56.73	255.41	42.63
9	12	25	1434.50	585.62	59.18	551.66	61.54
12	8	15	204.98	87.76	57.19	104.22	49.15
12	8	20	468.66	179.10	61.78	184.00	60.74
12	8	25	1085.12	240.07	77.88	227.00	79.08
12	10	15	288.00	79.68	72.33	84.43	70.69
12	10	20	715.11	284.14	60.27	326.72	54.31
12	10	25	1485.73	420.70	71.68	473.97	68.10
12	12	15	304.14	117.23	61.46	128.75	57.67
12	12	20	689.31	217.17	68.49	458.41	33.50
12	12	25	2269.94	865.28	61.88	930.47	59.01
	Average		516.60	195.27	58.18	232.68	51.51
13	12	30	3600	2065.34	-	3600	-
13	12	30	3600	1356.41	-	1986.32	-
13	12	30	3015.94	1283.91	-	1219.61	-
14	12	25	2968.19	927.99	-	1320.17	-
14	12	25	3600	1282.89	-	2336.25	-
14	12	25	3202.05	1064.8	-	1798.87	-
14	12	30	3023.58	1399.3	-	1527.29	-
14	12	30	3600	1010.84	-	1454.74	-
14	12	30	3600	1368.18	-	1364.12	-
15	12	25	3600	1052.47	-	1391.98	-
15	12	25	3600	1089.1	-	1019.86	-
15	12	25	3600	941.26	-	2431.72	-

, columns $\left|T\right|$, $|V_R|$ and $|V_C|/|V_R|$ are the parameters to measure the scale of test instances, where the column CPLEX is the computational time (s) of CPLEX, column B&C_1 is the computational time (s) of the branch-and-cut algorithm using all valid inequalities, column B&C_2 is the computational time (s) of the branch-and-cut algorithm using all valid inequalities except (50), and the two columns decrease_1 (%) and decrease_2 (%) represent the proportions of time saved by the two branch-and-cut algorithms compared to CPLEX.

For small- and medium-sized scales, three instances were tested to observe their average performance, and the mean value was recorded. For the large scale, the maximum computational time was set as 3600 s and the computational gap was set as 0.5%. Similarly, the three instances were tested to observe their average performance. It can be observed from Table 10 that the branch-and-cut algorithm proposed in this study can effectively reduce the computational time in small and medium scales, and can reduce more computational time when the scale increases. As observed from the mean value, the time saving ratio of algorithm_1 (adding all valid inequalities) is 58.18%, while the time saving ratio of algorithm_2 (removing valid inequality (50)) is 51.51%, which is approximately 7% lower than the performance when adding all inequalities; therefore, inequality (49) is effective in the algorithm. In the large scale, CPLEX cannot solve the problem effectively, but the designed branch-and-cut algorithm can still find feasible solutions, and algorithm_1 with all valid inequalities has a better effect in most cases. For large-scale instances, we found that the magnitude of time periods and number of customers per satellite have greater influences on the solution quality. When they both increase greatly, it is difficult for CPLEX to find feasible solutions and it would be easy for it to run out of memory. Compared to CPLEX, the branch-and-cut algorithm can find feasible solutions more quickly. Hence, the branch-and-cut algorithm can be used in practice to solve the problem effectively.

5.4. Comparison of Computational Time for Different Inventory Strategies

In Section 5.3, the branch-and-cut algorithms were compared to CPLEX based on the inventory strategy of optimal–optimal combination. In this section, we observe the average computational time solved by the branch-and-cut algorithm (adding all valid inequalities) and CPLEX for four practical and commonly used inventory strategy combinations OF–OF, OF–FF, FF–OF and FF–FF at small- and medium-sized scales. It is worth mentioning that the optimal strategies are difficult to be used in real production and transportation in both echelons, and thus only the manually operable strategy combinations, i.e., OF–OF, OF–FF, FF–OF and FF–FF strategy combinations, are analyzed here. As presented in

Table 11. Comparison of computational time by CPLEX for different inventory strategies.

Small- and Medium-Sized Scales	CPLEX (s)				Decrease (%)
	OF–OF	OF–FF	FF–OF	FF–FF	OF–OF	OF–FF	FF–OF	FF–FF
Average	509.23	507.47	505.97	502.04	1.71	1.77	2.06	2.82

and

Table 12. Comparison of computational time by B&C for different inventory strategies.

Small- and Medium-Sized Scales	B&C (s)				Decrease (%)
	OF–OF	OF–FF	FF–OF	FF–FF	OF–OF	OF–FF	FF–OF	FF–FF
Average	191.28	190.14	187.94	185.09	2.39	2.63	3.75	5.21

, the columns that belong to B&C and CPLEX are the computational time of aforementioned inventory strategy combinations, and the decrease (%) represents the proportions of time saved by the three inventory strategies compared to OP–OP. From the results, it is apparent that the time savings of B&C are more significant compared to those of CPLEX; the three inventory strategy combinations can all save computational time compared to OP–OP; and FF–FF performs best in computational time both by B&C and CPLEX. As a result, the FF–FF strategy combination is recommended when the computational time is of more concern.

5.5. Impact of Parameters Related to Deterioration Rate on Different Inventory Strategies

For the conventional PRP, the main factors that affect the performance of inventory strategy combinations are the deterioration rate and the increase in inventory cost. Accordingly, in this section, the performance of different inventory strategy combinations (OF–OF, OF–FF, FF–OF and FF–FF) are compared when the four types of combinations change. The parameters related to deterioration rate are A and B, and the parameters related to the inventory cost are $h_{00}$ and $\beta$.

When analyzing the influence of each parameter on the performance of inventory strategy combinations, the evaluated parameter is changed with the remaining parameters fixed. For example, when evaluating the influence of parameter A, parameters B, $h_{00}$ and $\beta$ will be fixed.

The performance of each inventory strategy is measured by the costs and customer satisfaction. Specifically, under different inventory strategy combinations, the growth ratios (% increase) of total costs, fixed production costs, variable production costs, inventory costs and replenishment costs are observed. The ratios are calculated by $\frac{Cos{t}_{*}-Cos{t}_{OO}}{Cos{t}_{OO}}$, where $Cos{t}_{*}$ represents the result of the corresponding strategy combination and $Cos{t}_{OO}$ represents the result of the optimal–optimal combination. Additionally, customer satisfaction is used to test the product freshness, and the fresher the product, the higher the customer satisfaction. The freshness of products in this study is measured by the weighted average storage time ($tim{e}_{hold}$), and its calculation method is given by Formula (64). The shorter the weighted average storage time, the higher the freshness of products and customer satisfaction. To facilitate comparison, the drop ratio (% decrease) of $tim{e}_{hold}$ is used for observation. The ratio is calculated by $\frac{tim{e}_{hold}^{*}-tim{e}_{hold}^{OO}}{tim{e}_{hold}^{OO}}$, where $tim{e}_{hold}^{*}$ represents the result of the corresponding strategy combination and $tim{e}_{hold}^{OO}$ represents the result of the optimal–optimal combination.

$$\begin{array}{c}tim{e}_{hold}=\sum _{t=1}^T\sum _{\tau =0}^{t-1}{\sum }_{i\in V_r}{\sum }_{j\in V_{c_i}}\frac{s_{ij\tau t}}{{\sum }_{t=1}^T{\sum }_{j\in V_c}{d}_{jt}}(t-\tau )\end{array}$$

(64)

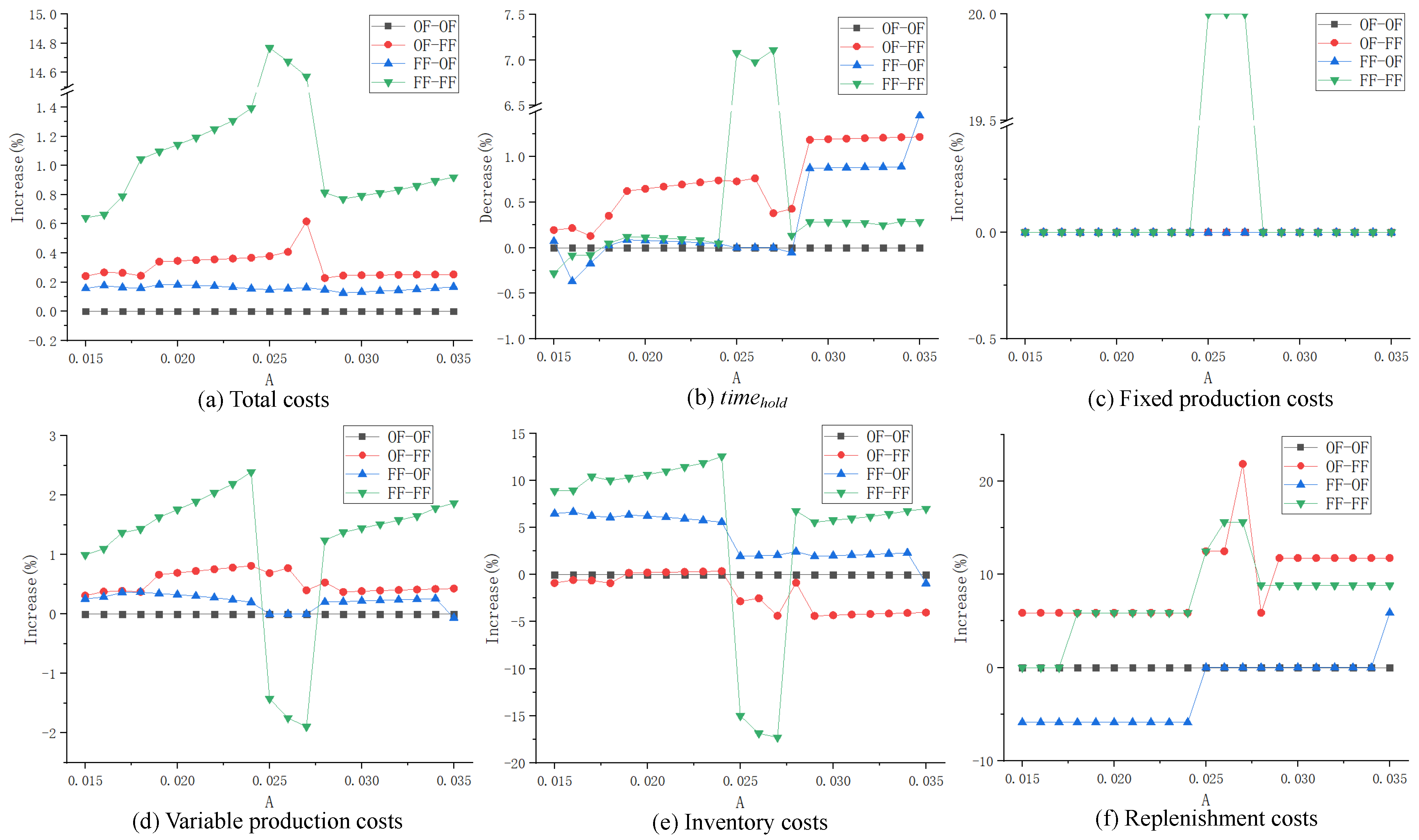
(1) Impact of parameter A on different inventory strategy combinations

When parameter A ranges from 0.015 to 0.035 (increased by 0.001 at each time), the ratio of costs (% increase) and ratio of $tim{e}_{hold}$ (% decrease) under different inventory strategy combinations are shown in Figure 2.

From the perspective of costs, the OF–OF strategy combination has a smaller gap compared to the OP, followed by the FF–OF strategy combination; the total costs of these two combinations are almost unaffected when parameter A changes. The gap of the total cost between the OF–FF strategy combination and the OP is also small, which is within 0.8% all the time, and the fluctuation is relatively small in general. The FF–FF strategy combination has the biggest gap, and in the process where parameter A increases, a sudden increase occurs in the interval (from $0.025$ to $0.027$), with the gap reaching more than 14%. Apart from that interval, the gap between the FF–FF strategy combination and the OP increases with the increase in parameter A.

Based on the analysis, the cost of the OF–OF strategy combination is almost unaffected. For the FF–OF strategy combination, the fixed production cost is not affected, the variable production cost is barely affected, the inventory cost decreases in a downward trend as parameter A increases, and the replenishment cost increases in an upward trend with the increase in parameter A. The reason for the change in the inventory cost and replenishment cost is that when parameter A increases, the deterioration of products will be accelerated. To lessen the deterioration, some products will be produced later; thus, the inventory duration of these products will be reduced but the replenishment frequency will be increased accordingly. For the OF–FF strategy combination, the fixed production cost is not affected, while the variable production cost is higher than that of the OP, with a small fluctuation (1%) when parameter A increases. However, when A increases to $0.25$, its inventory cost begins to decrease, and after that, the gap stays relatively stable at −5%. Additionally, the replenishment cost fluctuates violently when A is increased to $0.25$; this is caused by the shorter inventory time and the increased replenishment frequency due to the later production of some products. For the FF–FF strategy combination, within the interval where the total cost surges, the gap of fixed production cost rushes to 20%, the gap of variable production cost decreases abruptly to approximately −2%, the gap of inventory cost plunges to approximately −17% and the gap of replenishment cost increases to approximately 17%. It can be observed that the sudden increase in the FF–FF total cost is mainly caused by the fixed production cost; this is because the product deteriorates faster as A increases. The FF–FF strategy, which prioritizes the use of new products in the replenishment and distribution phases, is the combination that results in the highest amount of product deterioration. Therefore, when the product deteriorates to a certain value (A = 0.025), the product deteriorates considerably. To satisfy the customer demand in time, a higher production frequency is adopted. As A continues to increase to $A=0.028$, the OP also needs to increase the production frequency to meet the demand. At this time, the gap between the FF–FF and OP is restored to a lower level.

From the perspective of $tim{e}_{hold}$ of distributed products, as A increases, the product freshness of OF–FF is the highest in most cases, and the gap between it and the OP tends to increase as A increases. The gap of product freshness between the OF–FF strategy combination and the OP starts to increase when $A=0.028$, but it is still lower than that of the OF–FF strategy combination. The product freshness of the OF–OF and FF–FF strategy combinations is the lowest in most cases, in which the product freshness of the FF–FF strategy combination also shows a sudden increase in the interval where the total cost surges.

To summarize, with different values of parameter A, the strategy combination OF–FF is optimal, because it can obtain the same or higher product freshness at a lower cost increment; therefore, it can obtain higher customer satisfaction within the acceptable range of cost increase. The strategy combinations OF–OF and FF–OF are the second most optimal. They could hardly increase the cost nor the customer satisfaction. Only when A is large enough can the FF–OF strategy combination achieve a similar performance to that of the OF–FF strategy combination. The FF–FF strategy combination is the worst, because in most cases, it results in large cost increases and an improvement in customer satisfaction is not achieved. Only in the interval where the total cost surges did FF–FF obtain high customer satisfaction. At the same time, the costs increase sharply; therefore, its utilization is not recommended.

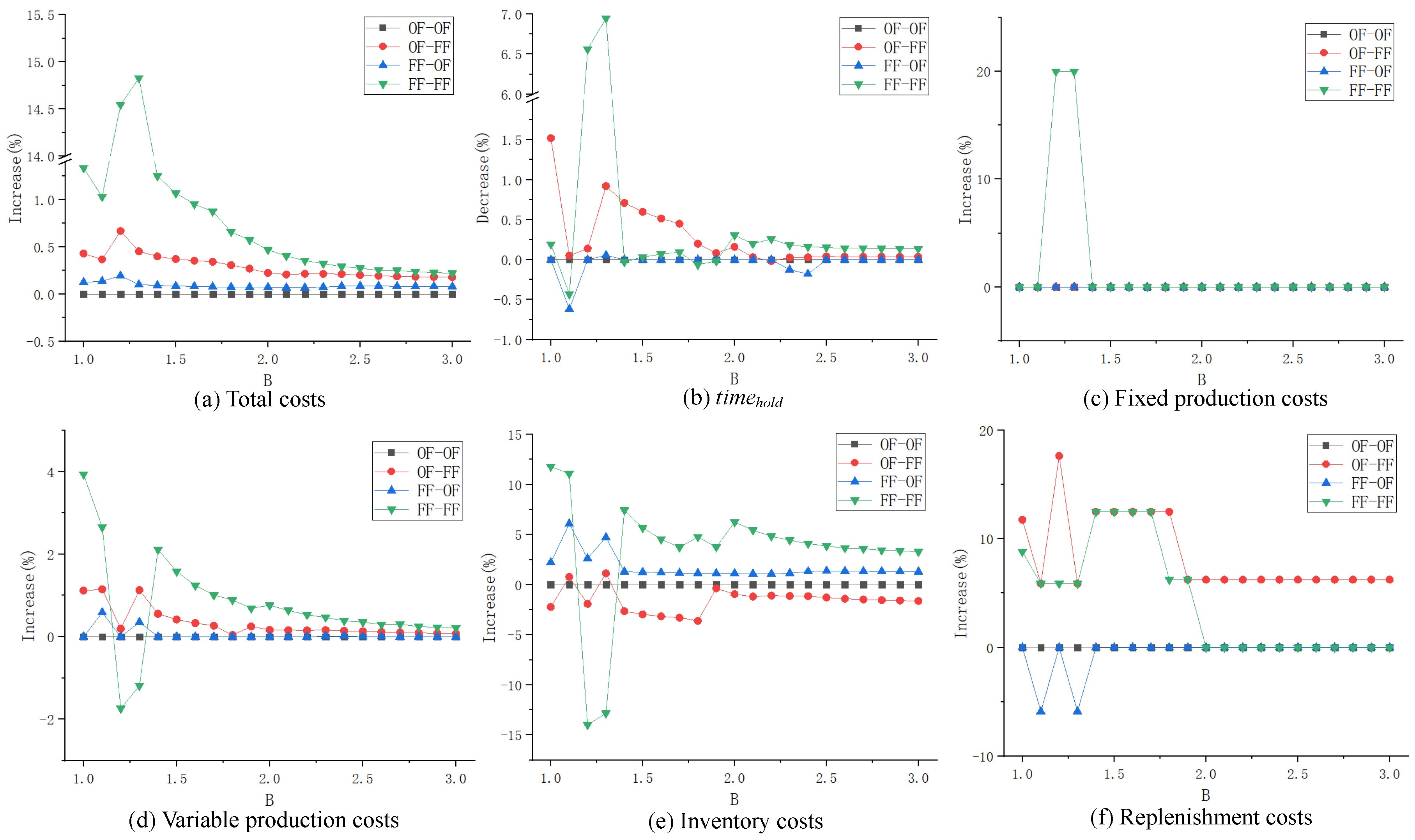
(2) Influence of parameter B on different inventory strategy combinations

When parameter B ranges from 1 to 2 (increased by 0.001 at each time), the ratio of costs (% increase) and the ratio of $tim{e}_{hold}$ (% decrease) under different inventory strategy combinations are shown in Figure 3.

From the perspective of cost, the OF–OF strategy combination is the optimal, followed by the FF–OF and OF–FF strategy combinations. When B changes, the costs of these three combinations hardly increase compared to that of the OP, while the FF–FF strategy combination performs the worst. With the increase in parameter B, the OF–OF strategy combination is not affected, but the gap of the total cost between the FF–OF/OF–FF strategy combinations and the OP has a general decreasing trend; only when $B=1.2$ is there a slight increase. As B increases, the FF–FF strategy combination increases sharply in the interval $[1.2,1.3]$, and then decreases sharply when $B=1.4$, showing a decreasing trend before and after that interval.

Integrating all types of costs, the gap between the FF–OF strategy combination and the OP results mainly from the inventory cost. Because the unit inventory cost is smaller in the depot, more products would be stored in the depot, and when fresher products are preferred in the replenishment echelon, the inventory cost at the depot will increase, resulting in an increase in the total inventory cost. The gap between the FF–OF strategy combination and the OP mainly comes from the replenishment cost. It is obvious that when new products are given priority in the distribution echelon, in order to minimize deterioration, some products will be produced later and the replenishment frequency will increase. It is noted that the sharp increase in the total cost of FF–FF is mainly caused by the fixed production cost, because the product will deteriorate more slowly due to the increase in B. When it slows down to a certain extent, other strategy combinations including the OP will reduce the production frequency without affecting the satisfaction of demand, while the FF–FF strategy combination causes the most deterioration and cannot reduce the production frequency, resulting in a sharp increase in cost changes. However, as B continues to increase, FF–FF can maintain the same production frequency similar to other strategies; thus, the cost recovered.

From the respective of $tim{e}_{hold}$, when $B<2$, the product freshness is the highest under the OF–FF strategy combination, while other strategy combinations cannot improve the product freshness in most cases. Furthermore, only the FF–FF strategy combination has a sharp increase within the range where the total cost surges. When $B\ge 2$, the product freshness is the highest under the FF–FF strategy combination. Other strategy combinations cannot improve the product freshness.

In general, as B changes, when B is relatively small, the OF–FF strategy combination is optimal, and it can achieve higher customer satisfaction with a lower increase in costs. When B is relatively large, the FF–FF strategy combination is optimal, and it can obtain higher customer satisfaction easily. When parameter B is not decided, it is recommended to use the OF–FF strategy combination, because its overall performance is relatively stable, which would not cause a sharp increase in costs and can effectively improve customer satisfaction in most cases.

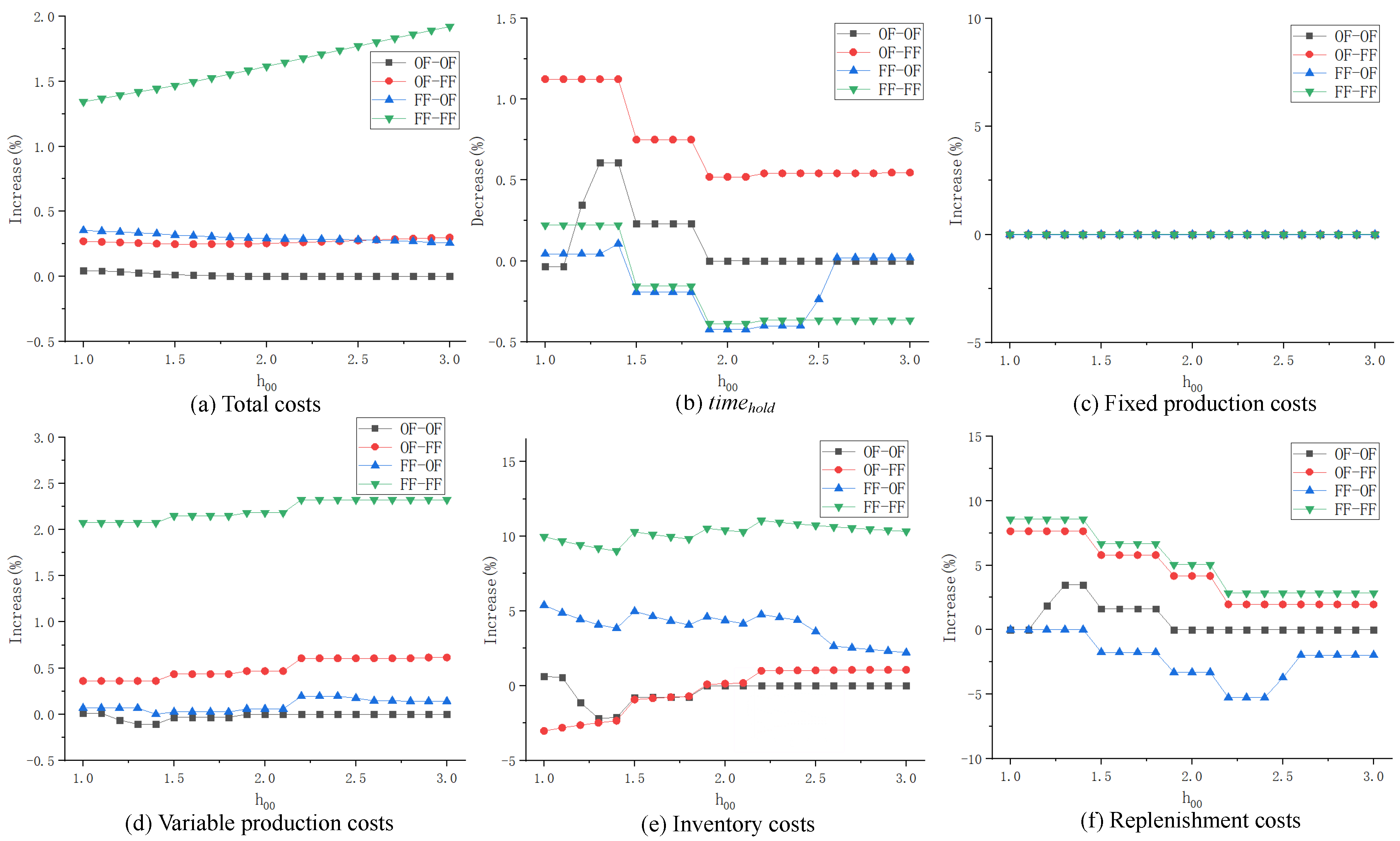
(3) Influence of parameter $h_{00}$ on different inventory strategy combinations

When parameter $h_{00}$ ranges from 1 to 3 (increased by 0.2 at each time), the ratio of costs (% increase) and ratio of $tim{e}_{hold}$ (% decrease) under different inventory strategy combinations are shown in Figure 4.

From the perspective of the total costs, OF–OF is the optimal one, followed by the OF–FF and FF–OF strategy combinations. The total costs of these three combinations are relatively stable, while the gap between the FF–FF strategy combination and OP is the largest and increases with increasing $h_{00}$.

Combined with all types of costs, the total cost under the FF–FF strategy combination changes synchronously with the variable production cost, inventory cost and replenishment cost. This is because new products are preferred to be used in the two echelons, resulting in more product deterioration and increasing total output. Moreover, an increased inventory cost of old products and an increased inventory of new products will both cause an increase in inventory cost. In the second echelon, the replenishment cost of the OF–FF and FF–FF strategy combinations that give priority to using new products is higher than that of other strategy combinations. This is because there is more deterioration of old products left in the satellites; thus, a higher replenishment frequency is required.

From the perspective of $tim{e}_{hold}$, the product freshness of the OF–FF strategy combination is the highest and is always higher than that of the OP, while that of the FF–OF strategy combination is better than that of the OP when $h_{00}\le 1.5$; however, it also gradually declines to a lower level afterward. The product freshness of OF–OF fluctuates and is higher than that of the OP when $h_{00}\le 1.9$. The product freshness of FF–FF gradually decreases as $h_{00}$ changes, and is lower than that of the OP in most cases.

In summary, $h_{00}$ has little impact on the gap of the total cost between the OF–FF/FF–OF/OF–OF strategy combinations and the OP, but it has a great impact under the FF–FF strategy combination. Among the strategy combinations, OF–FF is optimal, because its product freshness increases the most with less cost increase. Besides, when $h_{00}$ is small, the FF–FF and FF–OF strategy combinations are adoptable. Note that the FF–FF strategy combination has no improvement in customer satisfaction but increases costs the most; thus, it is the worst one and is not recommended.

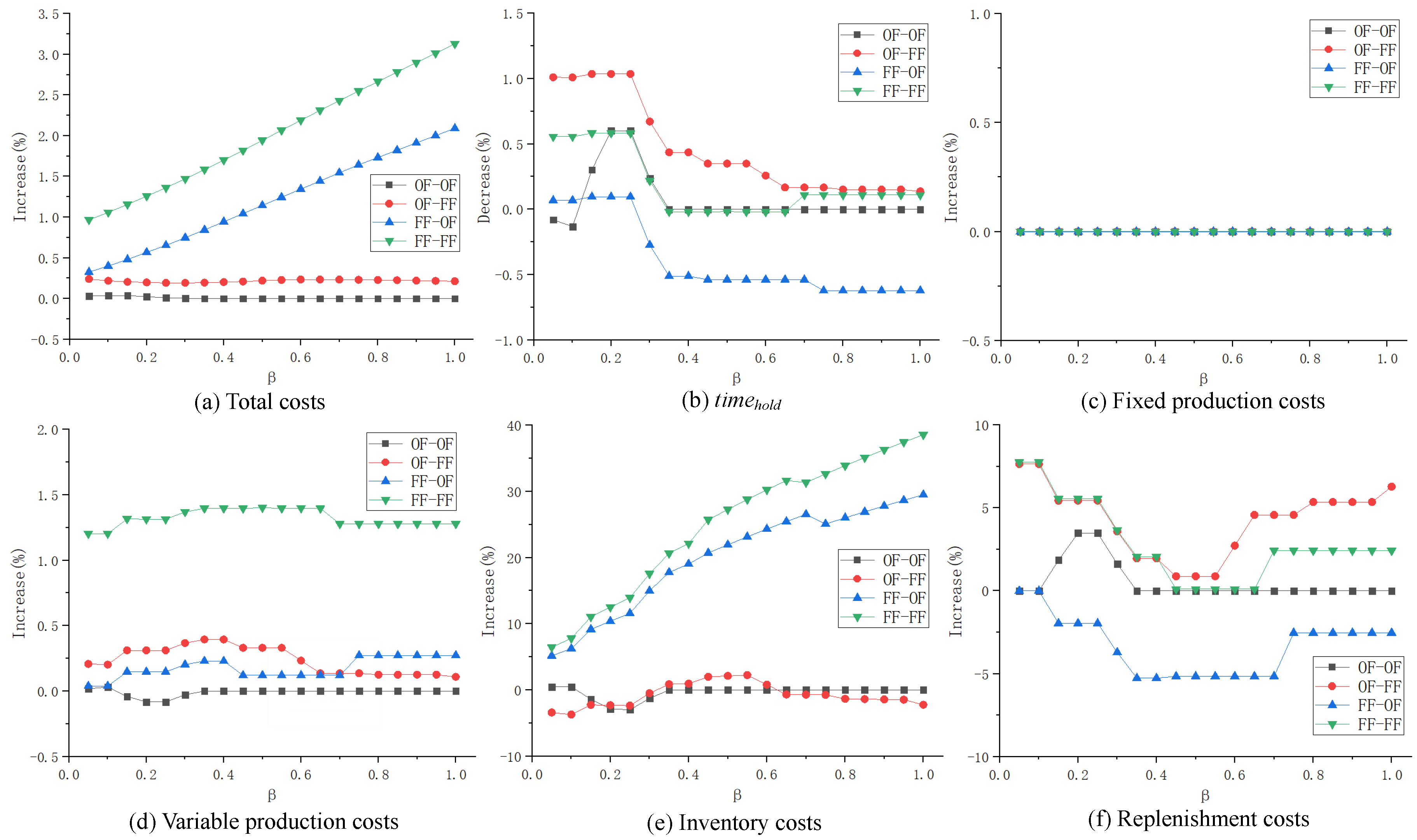
(4) Influence of parameter $\beta$ on different inventory strategy combinations

When the parameter $\beta$ ranges from 0.05 to 1 (increased by 0.05 at each time), the ratio of costs (% increase) and the ratio of $tim{e}_{hold}$ (% decrease) under different inventory strategy combinations are shown in Figure 5.

For the total costs, the strategy combinations with the smallest gaps are OF–OF and OF–FF, which change little with the increase in parameter $\beta$. The gap between FF–OF/FF–FF and the OP has an apparent upward trend as $\beta$ increases, among which the gap between FF–OF and the OP is always the largest.

Combined with all types of costs, it can be observed that the gaps of the cost between FF–OF/FF–FF and the OP are mainly caused by the variable production cost and inventory cost, among which the gap of inventory cost increases with increasing $\beta$. Moreover, there is no obvious variation trend of the variable production cost, indicating that the upward trend of the gap is mainly caused by the inventory cost. However, the gap of the inventory cost between FF–OF/FF–FF and the OP has no obvious increasing trend; it is either stable or fluctuating in a small range. Apparently, the inventory cost in the depot is lower; therefore, more products are stored in the depot. If new products are preferred in the replenishment (FF–OF and FF–FF), the inventory cost brought by the old product will be relatively large and will be larger with increasing $\beta$; this is why the strategy combinations show such a trend.

From the perspective of $tim{e}_{hold}$, it is the OF–FF strategy combination that can maximize the product freshness, while there is no significant difference of $tim{e}_{hold}$ for other strategies as $\beta$ changes. When $\beta$ is small ($\beta \le 0.7$), there are significant differences between the OF–FF strategy combination and others.

In general, as $\beta$ changes, the OF–FF strategy combination is optimal and should be given priority, as it can improve the product freshness when the cost increment is relatively small. The OF–OF strategy combination does not increase the total cost, but it does not improve customer satisfaction in most cases. The FF–OF and FF–FF strategy combinations offer poor improvement to customer satisfaction, and FF–OF may even decrease it. In addition, the cost increases with these two strategies are relatively high; these two are not recommended for utilization.

5.6. Managerial Insights Derived from the Results of Inventory Strategy Combinations

Through the above analysis, it can be observed that the OF–FF strategy combination is optimal in general, regardless of the values of initial deterioration rate A, unit cost of deterioration B, basic inventory cost of depot $h_{00}$ and increment of inventory cost $\beta$. OF–FF is the most reliable combination in most cases, with customer satisfaction improved mostly and no excessive increment in the total cost. Even if it does not maximize customer satisfaction in some cases, it will not increase the total cost considerably. Furthermore, it is only when A is large and $h_{00}$ and $\beta$ are small that the FF–OF strategy combination can be adopted as appropriate. The OF–OF strategy combination is also adoptable, but it can hardly improve customer satisfaction. In addition, it is only when B is significantly large and A, $h_{00}$ and $\beta$ are small that FF–FF can be adopted.

5.7. Comparison of Inventory Strategies with Stable and Periodic Customer Demand

Under the two scenarios of stable and fluctuating customer demands, the gap between each inventory strategy combination and the OP varies. In this section, the gaps of the total cost and $tim{e}_{hold}$ of products under the two scenarios are analyzed based on the population mean, which is summarized in

Table 13. Comparison of inventory strategy combinations under different demand scenarios.

Comparative Item	Demand Scenario	OF–OF	OF–FF	FF–OF	FF–FF
Total cost (%increase)	Stable	0	0.151	0.034	0.185
	Periodic fluctuation	0.001	0.165	0.181	0.454
Weighted average storage time (%decrease)	Stable	0	0.305	0.009	0.336
	Periodic fluctuation	0	0.262	0.06	0.258

.

As can be observed from Table 13, when comparing the gap between the total cost of each inventory strategy combination and that of the OP, the gap is smaller when the demand remains stable, and larger when the demand changes periodically. In particular, the gaps between FF–OF/FF–FF and the OP increase significantly when the demand becomes periodic. Next, comparing the $tim{e}_{hold}$ of each inventory strategy combination and that of the OP, the gap is larger when the demand is stable, and smaller when the demand changes periodically. It indicates that when the demand is stable. This is inclined to adopt other strategy combinations except for the OP. Overall, compared with the periodic demand, all of the strategy combinations can greatly improve the customer satisfaction and lead to less cost increase in stable demands.

6. Conclusions

This study integrated the conventional PRP and 2E-VRP, and further investigated the joint optimization of production, inventory, replenishment and distribution for perishable products. The formulation and branch-and-cut algorithm were constructed to provide some suggestions for inventory management of perishable products and theoretical guidance for the production, replenishment and distribution planning under the new retail mode.

The lead time of replenishment, product deterioration and inventory cost change were considered simultaneously. Based on the newly designed formulation and branch-and-cut algorithm, numerical experiments were conducted, from which it was observed that the valid inequalities can effectively improve the relaxed lower bound of the root node by 4.80% on average, and the branch-and-cut algorithm can notably reduce the computational time by 58.18% on average when compared to CPLEX in small- and medium-sized cases. Furthermore, the inventory strategy combinations were tested by B&C and CPLEX in terms of computational time. Obviously, they can all save computational time compared to OP–OP, and FF–FF performs best in computational time both by B&C (with a gap of 5.21%) and CPLEX (with a gap of 2.82%). Then, both inventory strategies were compared under different deterioration rates and under two scenarios of demand fluctuation and demand stability. From the results, managerial insights on how to choose an inventory strategy in practical applications were given.

In terms of strategy selection, the primary conclusions of this study are given as follows:

(1) The OF–FF strategy combination is suggested to be used in priority. The FF–FF strategy combination has the most stable performance, which has no improvement on customer satisfaction but does not increase the total cost. Additionally, only when the shelf life is long, the initial deterioration rate is low, and the initial value and incremental quantity of unit inventory cost are low enough, can the FF–FF strategy combination be adopted. Critically, the FF–OF strategy combination is recommended under no circumstances. Moreover, the total cost of the optimal strategy increases with the increase in initial deterioration rate, decreases with the increase in shelf life, and increases with the increase in initial value and incremental quantity of unit inventory cost. Among these parameters, the initial deterioration rate has the greatest effect, while the incremental quantity of unit inventory cost has the least influence.

(2) Compared with the situation where the demand fluctuates periodically, it is more reliable to employ other strategy combinations rather than the optimal strategy when the demand is stable. Such strategy combinations can greatly improve customer satisfaction and reduce cost.

Finally, for future research: (1) the production, replenishment and inventory strategy of perishable products under uncertain demand can be considered; (2) backlogging is not allowed in this study; however, the problem with inventory backlogging can be considered; and (3) in the second echelon (distribution), each satellite has an independent service area, which is developed for the situation where satellites are far apart and customers are concentrated in different regions. When satellites are close to each other and customers are distributed evenly, each customer can be served by any satellite.