1. Introduction
Photovoltaic (PV) and thermal panels using solar energy represent one of the most important and frequently used renewable energy production systems today. So far, the greatest advances in the field of solar energy have focused on improving the design and efficiency of solar photovoltaic panels. Several studies have attempted to develop solutions for efficiency improvement in several urban applications. Qiongjie Dai et al. [
1] presented an integrated system to improve the utilization rate of solar energy resources and to develop sustainable urban efficiency. PV panels are generally based on silicon and are used to convert solar radiation into usable electricity. The most popular PV panels are monocrystalline silicon, polycrystalline silicon, and thin-film silicon called amorphous silicon (A-Si).
In relation with the interconnection of photovoltaic panels, as described by Lavado Villa and al. [
2], generally used configurations are Series Parallel (SP), Total Cross Tied (TCT), Honey comb (HC), and Bridge Link (BL).
Various academic institutions and companies have worked on issues related to the maintenance of photovoltaic systems with the objective of reducing the operating costs of those systems and, in particular, their maintenance cost. For example, B. Chebel-Morello et al. [
3] proposed the adoption of e-maintenance for photovoltaic systems located in remote and isolated areas in order to reduce the cost and time of maintenance. They designed a cooperative distributed platform of e-maintenance, integrating data acquisition systems, control, maintenance management, diagnosis support, and management of documentation.
Failures that occur in photovoltaic systems (panels and wiring) automatically lead to a reduction in their efficiency, durability, and reliability. Tsanakas et al. [
4] summarized solar panel failures in three groups: optical degradation, electrical inadequacy, and unclassified faults. Furthermore, one of the causes of the increased degradation rate of a solar panel is the accumulation of dirt and dust that reduces solar radiation on the photovoltaic module. Saidan et al. [
5] studied the impact of dust accumulation on photovoltaic panels. The experimental results show that depending on the exposure period, the accumulation of dust on the surface of the photovoltaic panel induces the reduction of the system efficiency. The recommendation is to perform cleaning operations to minimize the impact on energy production and thus maintain a stable output power.
Dealing with inspection and failure diagnostic of photovoltaic systems, technological progress today allows the existence of nondestructive and even noncontact diagnostic. For instance, a review of the techniques used for thermography-based inspection of photovoltaic systems is provided in [
6]. Other authors such as Jung et al. [
7] proposed a configurable, hierarchical, model-based scheduling of automated utility control devices of photovoltaic generators. Torrent-Fontbona and López [
8] developed a renewable energy generator plan based on the joint determination of how many new solar panels are needed—and what type, location, and size they should be—in order to maximize installation efficiency, minimize system losses, and improve installation performance.
From a Reliability Centered Maintenance perspective, Villarini et al. [
9] adopted a failure mode and effect analysis approach for a photovoltaic system. They analyzed collected failure- and maintenance-related data from a multinational company. The obtained results were used in order to revise the maintenance strategy of the photovoltaic systems and to optimize their efficiency. Jiménez-Fernández et al. [
10] studied two optimization problems related to a standalone hybrid photovoltaic-batteries-hydrogen (PV-hydrogen) system. The first problem consists of finding the optimal number, distribution (two different types of batteries are proposed), and disposition (slope and azimuth) of the PV panels in the facility, for the case of autonomous operation of a telecommunication system during at least two years. The second problem consists of determining an optimal maintenance plan. The authors proved the achievement of an important reduction in the number of PV panels needed for obtaining an unattended work of the system between successive maintenance visits.
In this paper, we consider the question of what preventive maintenance (PM) strategy should be adopted in order to reduce as much as possible the loss of efficiency over the exploitation time span of a photovoltaic system. This is an important issue for investors in this type of renewable energy as well as for its operators. Condition-based maintenance is an option that has been studied in the literature. Silevster et al. [
11] proposed a simulation-based method for automatic supervision, fault detection, and diagnosis of eventual failure sources leading to total or partial loss of productivity in grid-connected photovoltaic systems. The fault detection algorithm is based on the evaluation of the difference between efficiency related results obtained from simulation and from real-time measurements. It allows analyzing the losses as well as the identification of the type of fault. The developed approach has been tested and validated in the Renewable Energy Development Center in Algeria. Wang et al. [
12] introduced a fault diagnosis technique for photovoltaic panels, which uses sampled data related to current–voltage characteristics. Ferrero Bermejo et al. [
13] proposed a sophisticated Cyber-Physical Systems (CPS) approach for condition monitoring of grid-connected photovoltaic systems. They use multiagent system architecture and artificial neural-networks on top of the existing control and data acquisition system.
It is clear that such condition-based maintenance strategies necessitate a great deal of intelligent computation and hardware infrastructure.
Another option regarding preventive maintenance is periodic preventive replacement. To the best of our knowledge, this option that does not require any condition monitoring and has not been explored for photovoltaic systems. A recent survey on preventive maintenance strategies including replacement actions can be found in [
14]. In the present study, we develop a preventive replacement strategy for a solar photovoltaic system composed of solar panels functioning as a series system. This proposed PM strategy suggests systematically replacing
panels every
T time units over a finite operating time span
H. A mathematical model is developed in order to determine the optimal values of
T and
n, which minimize the average total maintenance cost.
The remainder of this paper is organized as follows:
Section 2 presents the definition of the maintenance strategy and the working assumptions. The mathematical model is presented in
Section 3.
Section 4 is dedicated to the presentation of an illustrative numerical example and the discussion of the obtained results. Finally, conclusions and potential future work are provided in
Section 5.
2. Problem Statement and Working Assumptions
We consider a photovoltaic system composed of
N solar panels functioning as a series system. It is considered in a failed state if the efficiency of the system drops below a predefined threshold or any electrical wiring element is damaged. In such a situation of failure, a minimal repair is performed. Referring to the literature related to reliability and maintenance [
15], minimal repair is defined as a corrective maintenance action performed at breakdowns in order to restart the regular activity of the system but without improving its reliability; meaning that after minimal repair, the system is back to operation with the same failure rate it had before failure. It is then considered in a state called ‘as bad as old’. In the case of a photovoltaic system in this study, minimal repair is considered as a palliative action to bring it back to operation by performing an adjustment or quick replacement of some failed elements, like diodes or wires, without improving its reliability (i.e., without decreasing its failure rate). In order to reduce the likelihood of failure and the corresponding loss, a systematic periodic preventive maintenance is proposed. It consists in replacing
n panels every
T time units over the exploitation time span,
H, of the photovoltaic system. During preventive actions, the maintenance agent selects the panels to be replaced after an on-site overall assessment of all panels in order to avoid replacing panels previously replaced during a given replacement cycle of all panels of the system. Contrarily to minimal repairs, PM actions consisting of the replacement of
n panels improves the reliability of the photovoltaic system. The problem consists of simultaneously determining the optimal PM period,
T; the optimal number of solar panels,
n, to be replaced each time; and the expected total maintenance cost is minimized over the operation time horizon
H.
The following assumptions are considered:
All panels are identical.
The costs of PM and minimal repair are known and constant.
The cost of PM is composed of a fixed cost corresponding to the assessment of the state of the panels in order to decide which one(s) need to be replaced, and a variable cost depending on the number of replaced panels.
3. The Mathematical Model
We develop in this section a mathematical model to express the expected total cost of maintenance as a function of the two decision variables
T and
n. The used notation is shown in
Table 1.
We define a cycle as the time during which the
N panels of the photovoltaic system will have been replaced preventively. The length of a cycle is given by the following expression:
The number of panels in the last replacement during each cycle is
The number of periods in each cycle is given by
Since the ratio
(H/T) is not necessarily an integer number, there will be a last period
LP in the last cycle whose index and length are respectively expressed as follows:
3.1. The Expression of the Reliability Function of the Photovoltaic System
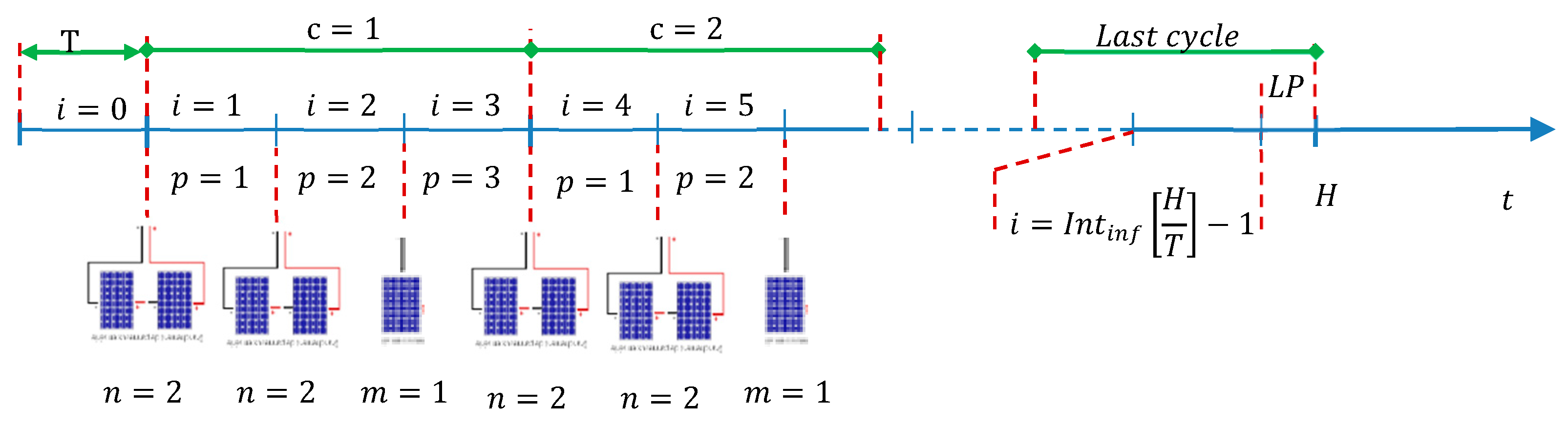
Before developing the general expression of the photovoltaic system reliability function, we consider, for illustration purpose, the case of a photovoltaic system with
N = 5 panels and a PM strategy suggesting
n = 2 different panels to be replaced every
T time units. Hence, every cycle, we have 3 periods (Equation (3)). At the beginning of the two first periods, two panels are replaced; and at the start of the third period, the one remaining panel is replaced (see
Figure 1).
Let us consider as the index of periods with i = 0 corresponding to the first period T.
The photovoltaic system reliability function for each period,
, in each of the first three cycles can be calculated as follows in reference to [
15] (recall that the system is made of 5 panels functioning as a series system):
For
,
: (No panel changed)
In the first cycle :
| , , |
| (2 panels are changed at ) |
| , |
| (2 panels are changed at ) |
|
| (1 panel is changed at ) |
In the first cycle :
| , , |
| (2 panels are changed at ) |
| , |
| (2 panels are changed at ) |
|
| (1 panel is changed at ) |
In the first cycle :
| , , |
| (2 panels are changed at ) |
| , |
| (2 panels are changed at ) |
|
| (1 panel is changed at ) |
Generalizing for all periods over the exploitation time span , the reliability of the photovoltaic system can be expressed as follows:
For
,
For , .
The reliability during all periods except the first and the last periods is expressed by the following equation:
The expression of the
x value is given by
The expression of the
y value is given by
The cycle number
c is obtained as follows:
The value of the period
p used in Equation (8) is obtained by
For .
The reliability during the last period is obtained by the following expression:
3.2. The Expression of the Failure Rate Function of the System for Each Period i
Based on reliability theory, specifically on the well-known expression of the failure rate of a system as a function of its reliability function [
15], the failure rate function of the photovoltaic system is given by the following expressions for every period
i:
For
, the failure rate at the first period is
For
, the expression of the failure rate at all periods except the first and the last ones is
For
the failure rate at the last period is expressed as follows:
3.3. The Expression of the Average Number of Failures (Minimal Repairs) for Every Period i
We recall that the expressions of the photovoltaic system reliability and its failure rate have been developed for each of the intervals over the time span H.
Hence, the average number of failures for every period
i is computed as follows [
15]:
For
, the average number of failures between 0 and
T is given by
For
, the average number of failures between
and
is
The expression of the average number of failures during the last period is
3.4. The Expression of the Expected Total Cost of Maintenance for Every Period i
According to the proposed maintenance strategy, the cost of maintenance is the sum of the costs of minimal repairs and PM actions performed during the exploitation time horizon H of the photovoltaic system. We develop below the expressions of these costs for each period , .
For , .
In the first period, the average cost of maintenance is given by
We recall that for , corresponding to the first period, there are no preventive replacements of panels. Only minimal repairs may be performed.
For , .
The average cost of maintenance in each period
i, except the first and the last ones, is given by
We recall that the value of the cycle number is given by Equation (10) and the average number of minimal repairs is given by Equation (17).
We note that the preventive maintenance cost includes the fixed cost corresponding to the assessment of the state of the panels in order to decide which one(s) need to be replaced; and a variable cost depending on the number of replaced panels.
For .
During the last period over the time horizon
, meaning LP period, since no more preventive replacements are made, we take into account only the average number of failures
(Equation (18)). Consequently, the maintenance cost in this period is given by
3.5. The Expression of the Expected Total Cost of Maintenance Over the Time Horizon H
Finally, by summing the expected costs of maintenance for every period (Equations (19)–(21)), we obtain the expression of the average total maintenance cost over the exploitation time span of the photovoltaic system:
4. Numerical Example
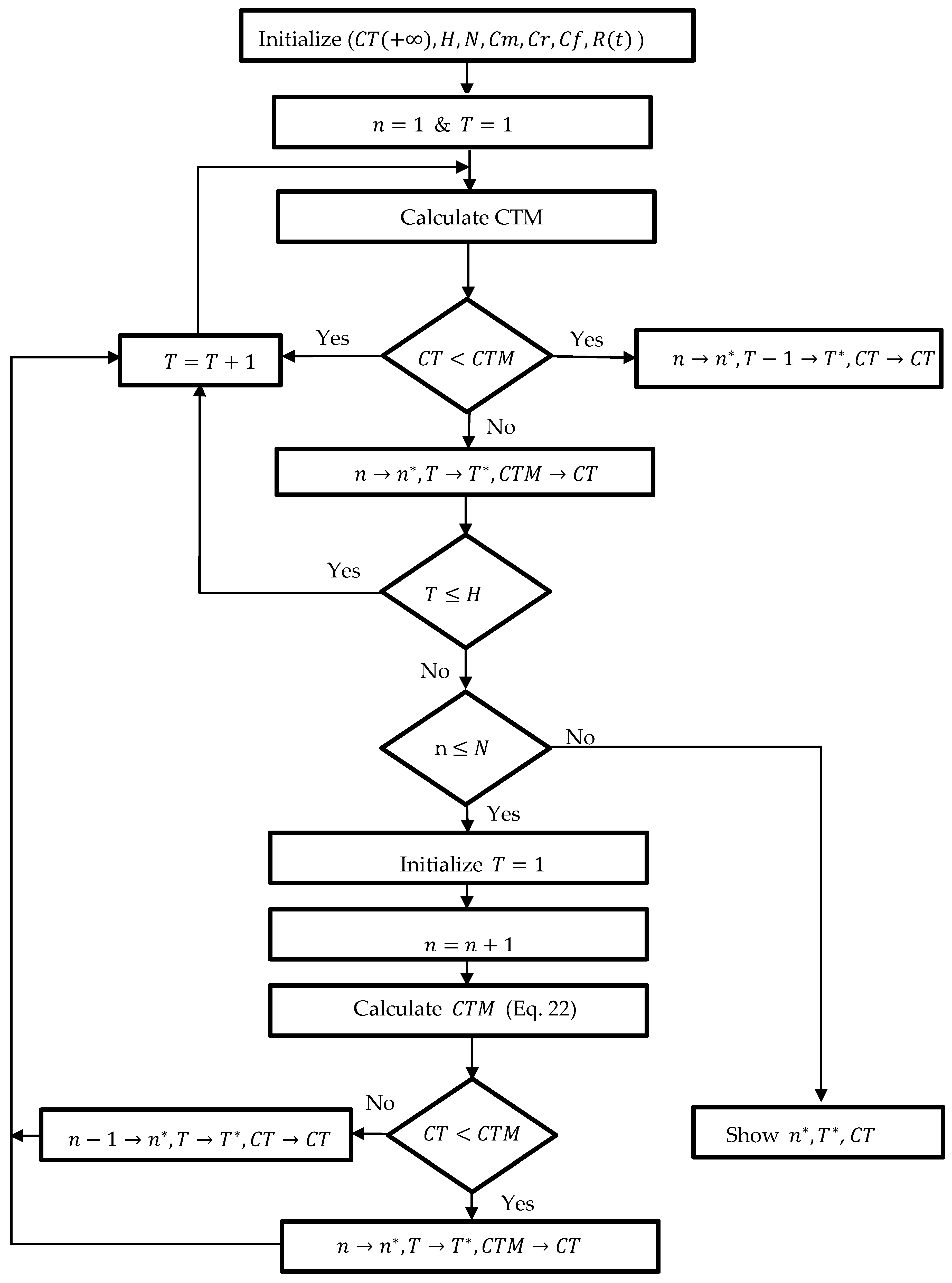
The algorithm we used to carry out the calculation of the values of
T and
n that minimize the expected total cost of maintenance is presented in
Appendix A. We performed a large number of numerical calculations to test the consistency and robustness of our model. In what follows, we present an illustrative numerical example with arbitrary chosen input parameters values with rather realistic settings. MATHEMATICA
® software (V10.2–2015) was used to determine the optimal PM period,
T*, and the optimal number of panels to be replaced,
n*, such that the expected total cost of maintenance (TCM) (Equation (22)) is minimized over the exploitation time span
H.
Table 2 below provides the set of input data corresponding to the example.
The Weibull distribution has been chosen for its known wide range of applications [
15] and also because a previous work [
16] verified the validity of the use a Weibull distribution to model the reliability of photovoltaic panels. The same distribution has also been used in [
17] for photovoltaic panels. We recall that in this study, the degradation of the photovoltaic system is limited to the degradation of the panels including the wiring, diodes, etc. The inverters are not explicitly included in the system because they would constitute additional components in series or parallel–series with the
N panels. This aspect is not covered in this work.
The obtained optimal strategy is summarized in
Table 3 below:
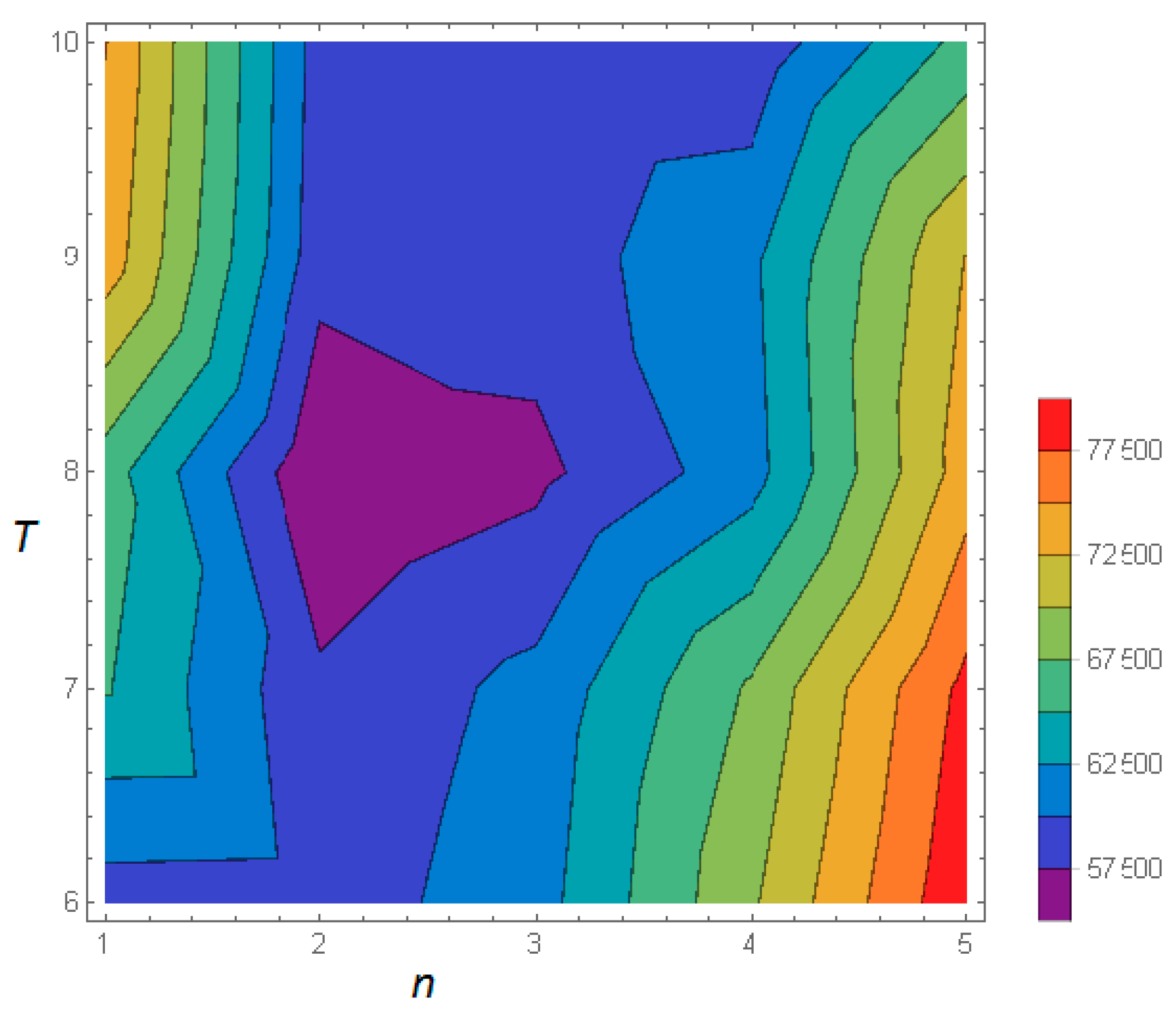
Hence, the optimal maintenance strategy consists in preventively replacing 2 different panels (n* = 2) every (T* = 8 months) over the 10 years exploitation period of the photovoltaic system.
Figure 2 below shows the iso-response curves with the corresponding ranges of the expected total cost of maintenance. One can see that for any given PM period, the expected total cost decreases then increases in terms of the number (
n) of panels to be replaced preventively. On the other hand, for
n = 2 or 3 panels, we have a decrease then an increase of the expected total cost as PM period
increases. For
n = 1, as PM are less frequent (
T increases), the expected total cost increases. However, for values of
n superior to 3, the expected total cost decreases as the PM period gets larger (less frequent preventive replacements).
In order to show the relevance of adopting the proposed PM strategy for the panels, let us compare with the situation without PM, which means performing only minimal repairs at failures without renewing any panel over the exploitation period of the photovoltaic system. To do this comparison, we simply use the same model to compute the expected total cost in the case no PM is performed (forcing the PM period
T be equal to
H, with
n taking any value since there is no preventive replacement).
Table 4 below provides the obtained results.
Hence, the achieved economic gain when adopting the proposed PM strategy is estimated as follows:
In what follows, we look at the effect of the variation of some relevant input data on the optimal solution (T*, n*).
4.1. Effect of the Variation of the Panel Replacement Cost ()
Considering the same input data, we obtained the following results presented in
Table 5 below.
One can notice that increasing the panel replacement cost (Cr) induces a greater PM period (less frequent replacements) while keeping the same number of panels to be replaced—or in the case of Cr = 1050, replacing a smaller number of panels but more frequently. It is also observed that, as expected, the gain compared to the situation without PM will increase as it costs less to replace a panel preventively, and vice versa.
4.2. Effect of the Variation of the Fixed Cost (Cf) Related to Each PM Action
While keeping the same input data, the following results were obtained (
Table 6):
It is interesting to notice that as the fixed cost incurred at each PM increases, there is a simultaneous increase of the number of panels (n*) to replace and the PM period T*. Indeed, as it costs more to perform a PM, the optimal strategy encourages replacing more panels at a time, but as panels have a certain cost (Cr), replacing more panels pushes towards replacing less frequently.
4.3. Effect of the Variation of the Corrective Cost ()
Considering the same input data, the following results have been obtained (
Table 7):
One can observe that—as it should be expected—when it costs more to repair, it is suggested to perform PM more frequently (smaller T*). However, at the same time, more frequent PM may induce the decrease of the number of panels to be replaced each time in order to reduce maintenance costs. It is also worth noticing that below a certain value of the repair cost, it is no longer worth adopting the PM strategy (the gain becomes negative). In such a situation, the best thing to do would be to perform only minimal repairs at failures. For this example, we looked for the break-even value (indifference point) for the repair cost between 600 and 800 and found it equal to 729.
4.4. Effect of the Photovoltaic System Exploitation Time Span () on the optimal solution
The following results were obtained (
Table 8) while keeping the same input data.
It clearly appears that as longer operating periods of the panels are considered, it gets more and more advantageous to adopt the proposed PM strategy (the gain increases).
Furthermore, it is worth pointing out that if we take for example the case of an exploitation period of 15 years, obtained results regarding the number of failures (minimal repairs) show that the expected number of failures per month is 2.11 in the case where no PM is performed; whereas if the proposed PM strategy is adopted (replacing 1 panel every 4 months), the expected number of failures decreases to 0.72 failure per month. This explains in large part the substantial gain achieved (avoiding, on average, a bit more than one failure per month over 15 years).
5. Conclusions
In this paper, we have discussed an optimal preventive maintenance strategy for a photovoltaic system made of solar panels functioning as a series system. Whenever the efficiency of this photovoltaic system drops below a predefined threshold or any electrical component is damaged, it is considered in failed state. In such a situation of failure, a minimal repair is carried out. In order to reduce the probability of failure and the corresponding loss, a set of n panels is preventively replaced every T time units during the whole exploitation period of the photovoltaic system. During a cycle of replacement of all panels, the maintenance agents make sure every time to replace only panels that have not been replaced from the beginning of the cycle.
A mathematical model has been developed allowing expressing the expected total cost of maintenance over the photovoltaic system exploitation time span as a function of the two decision variables T and n. It has then been made possible to determine the optimal values T* and n*, such that the expected total cost of maintenance is minimized for any instance of the problem.
The mathematical model and the numerical solving procedure have been extensively tested with various sets of values of input parameters. A sensitivity study regarding relevant input parameters has been performed. The obtained results showed the consistency and robustness of the model. For each example, it was possible to compute the achieved economic gain when comparing the situations with and without preventive maintenance. It was also possible to numerically determine the cost of repair of the system above which it becomes economically advantageous to adopt the proposed PM strategy. Furthermore, it has been shown through the presented example that the longer the exploitation time of the system, the more advantageous the adoption of the proposed PM policy.
Extensions of this work are under consideration. One of them involves the investigation of more realistic situations in which corrective and preventive maintenance actions are imperfect. Another extension consists of considering other types of operation of the solar panels within the photovoltaic system, such as series–parallel or Bridge link, or other types of configurations. A new condition-based maintenance strategy consisting of directly or indirectly monitoring the efficiency loss of the panels is also an interesting extension of this work currently under consideration. Finally, it would be worth improving the current maintenance strategy making it based not only on economic savings but also on waste management related to the preventive replacement of the photovoltaic panels. This would also make it environmentally profitable.