Short-Term and Medium-Term Drought Forecasting Using Generalized Additive Models
Abstract
1. Introduction
2. Materials and Methods
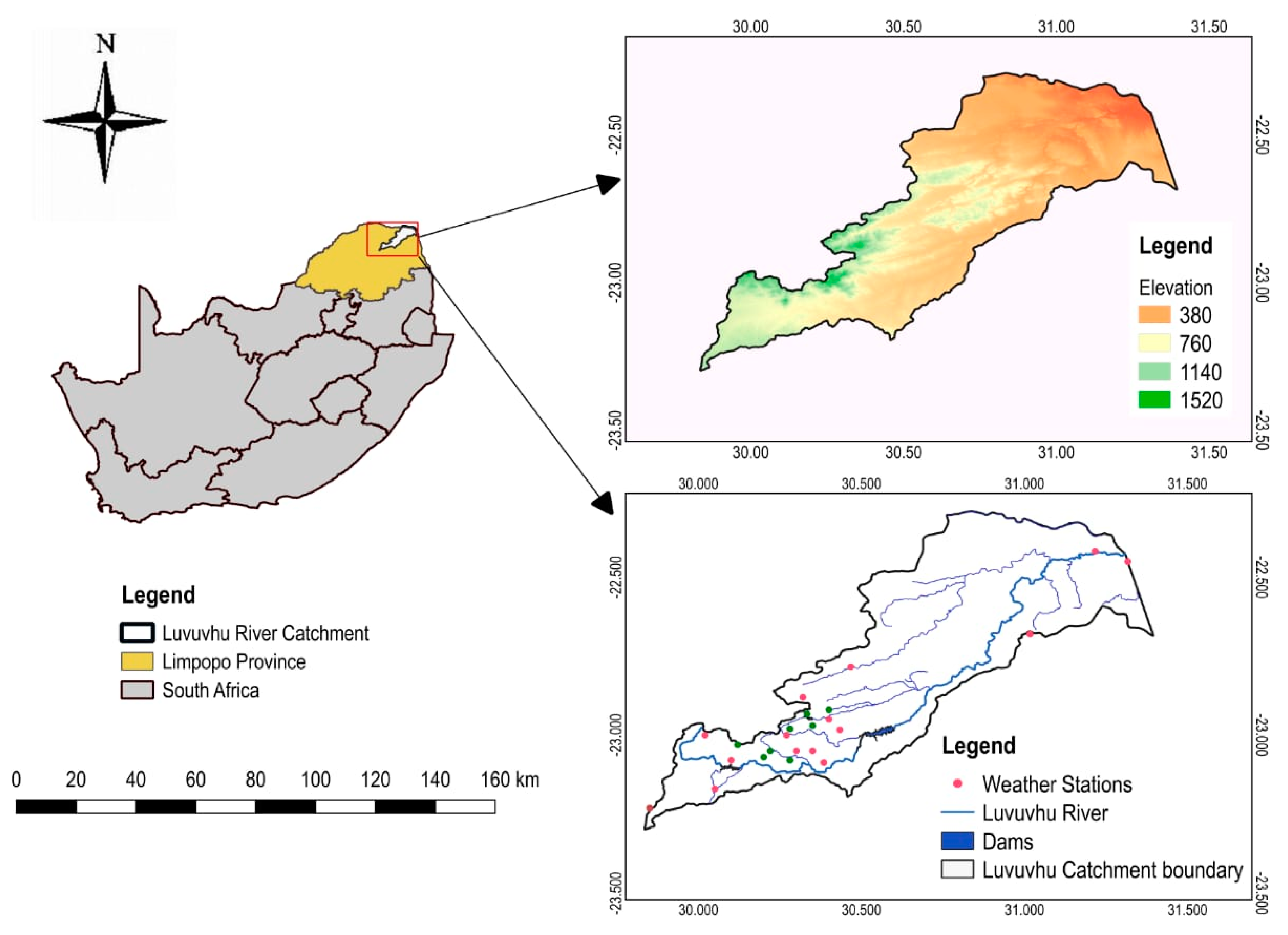
2.1. Case Study Description (LRC) and Datasets
2.2. Formulation of the SPEI for the Study Area
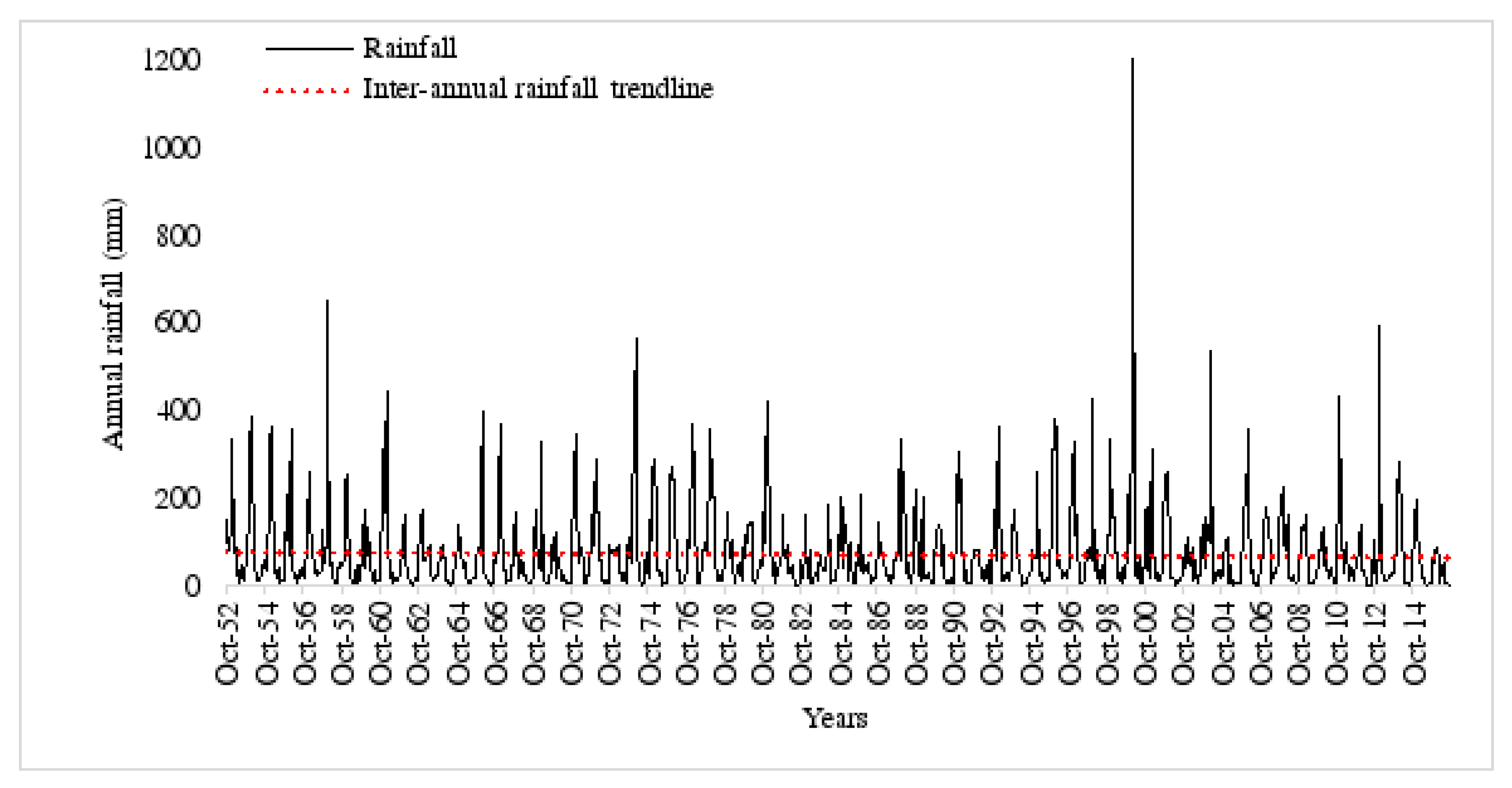
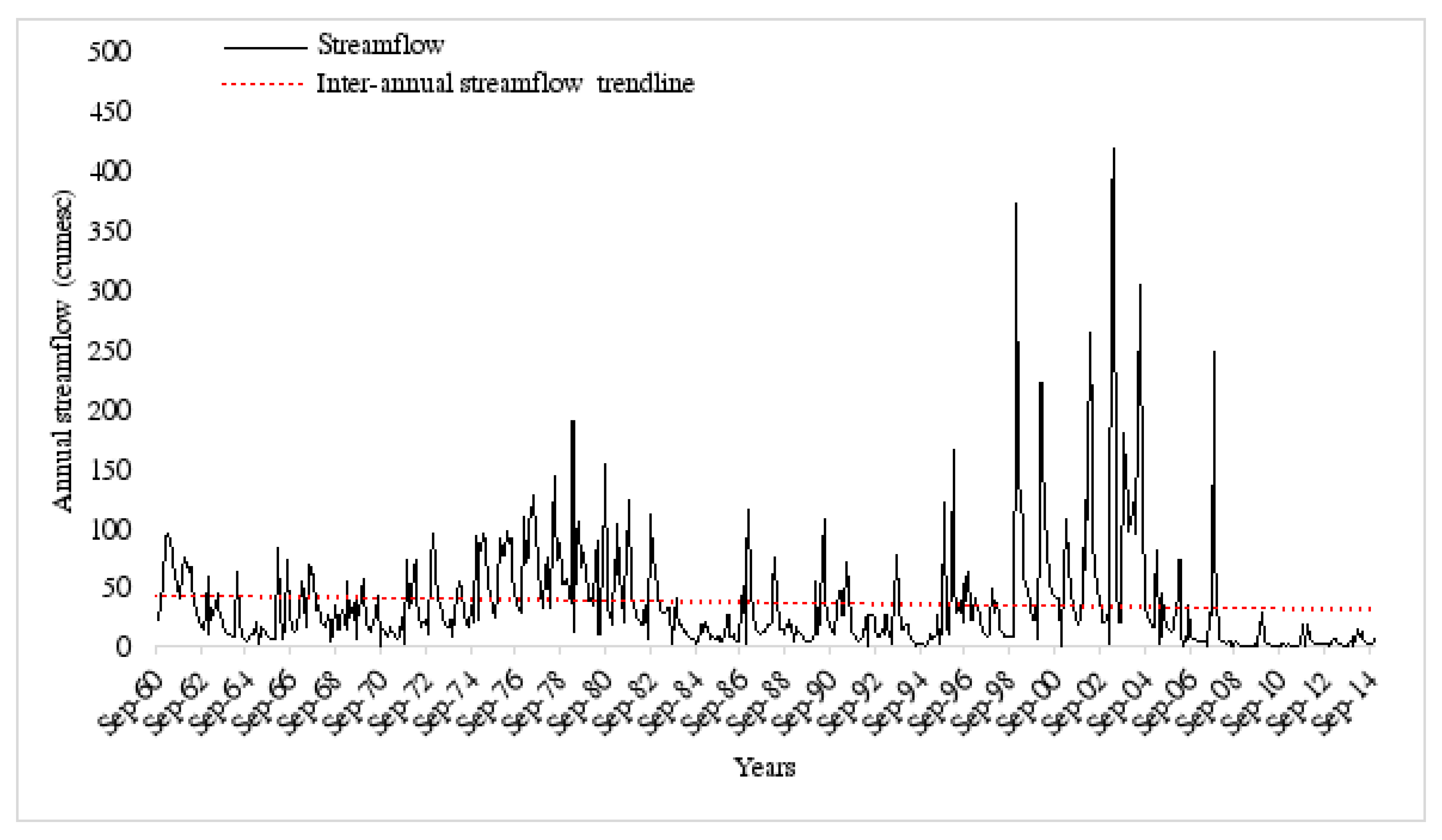
2.3. Drought Trends over North-Eastern South Africa
2.4. SPEI Time Series Forecasting
2.4.1. The Generalized Additive Model without Auto-Correlated Errors
2.4.2. The Generalized Additive Model with Auto-Correlated Errors
3. Results
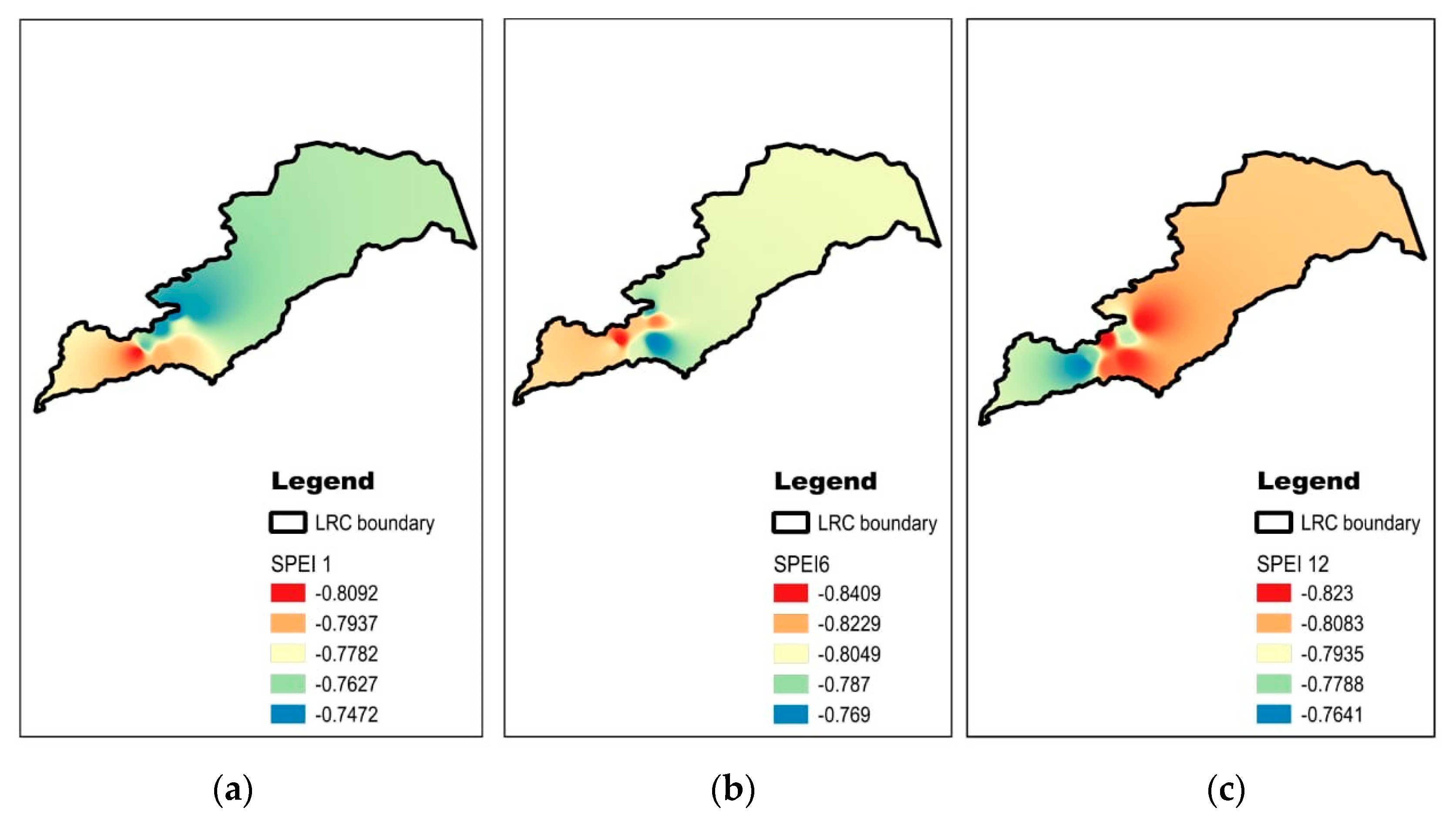
3.1. Spatial Variability of Drought in the Study Area
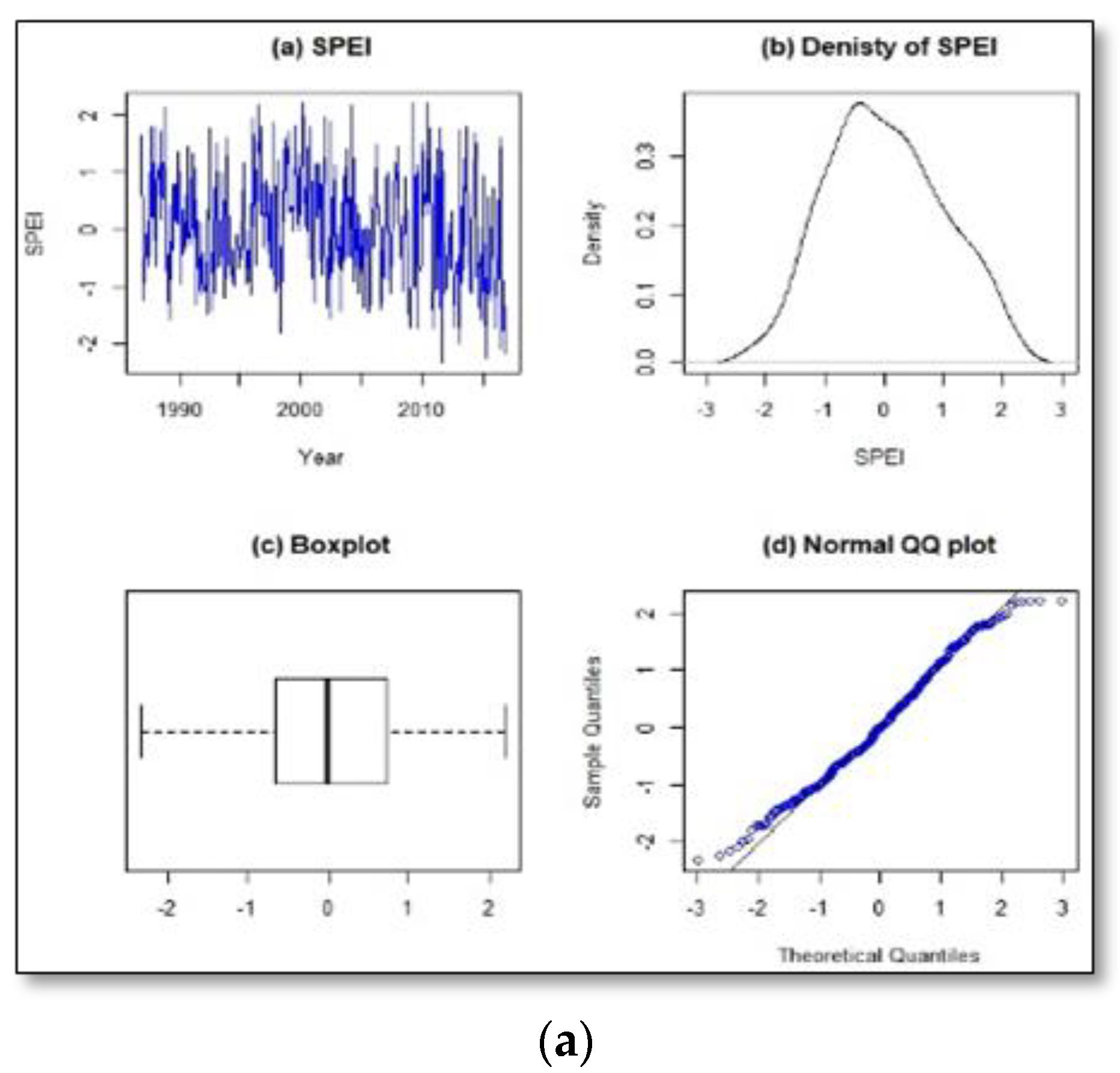
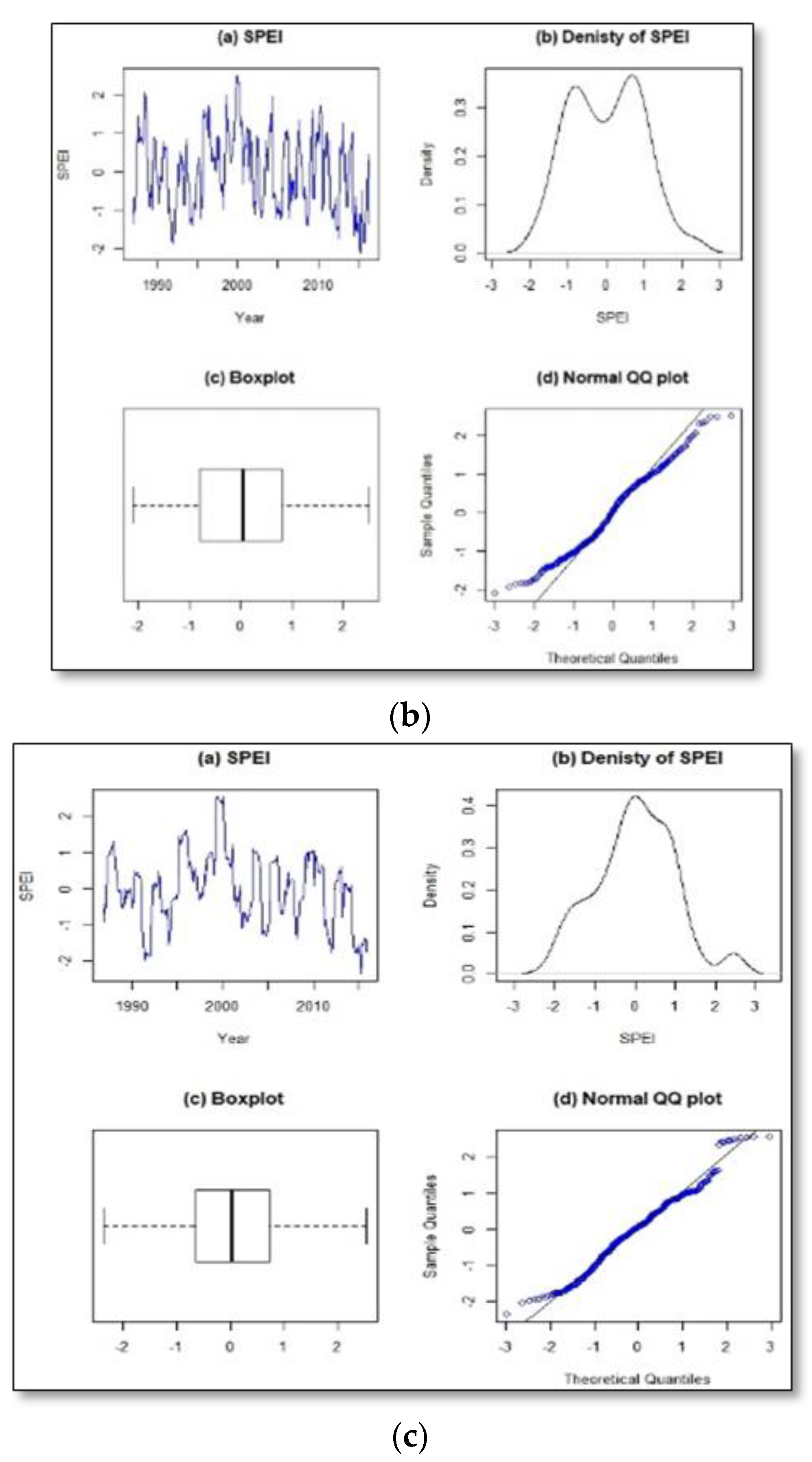
3.2. Exploratory Data Analysis
3.3. Variable Selection
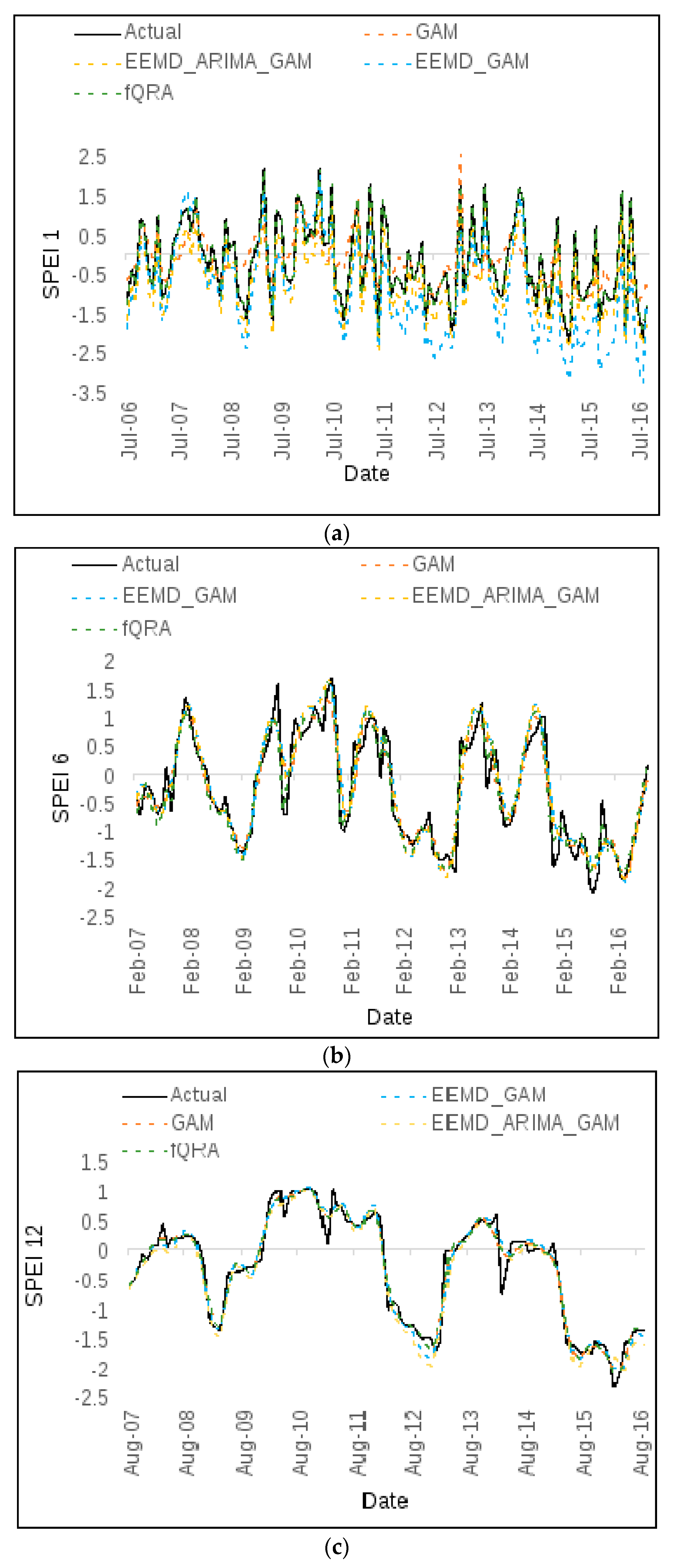
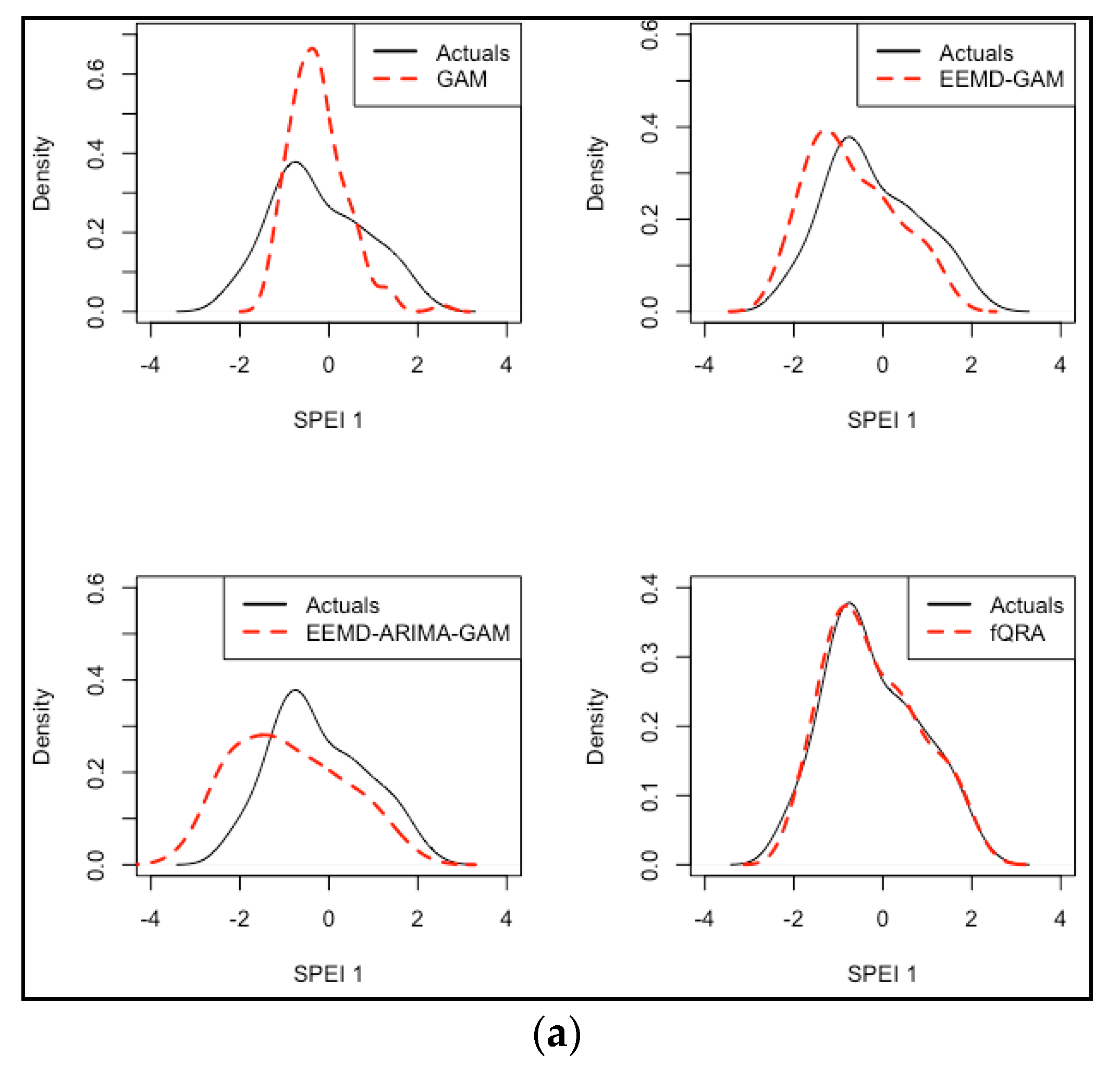
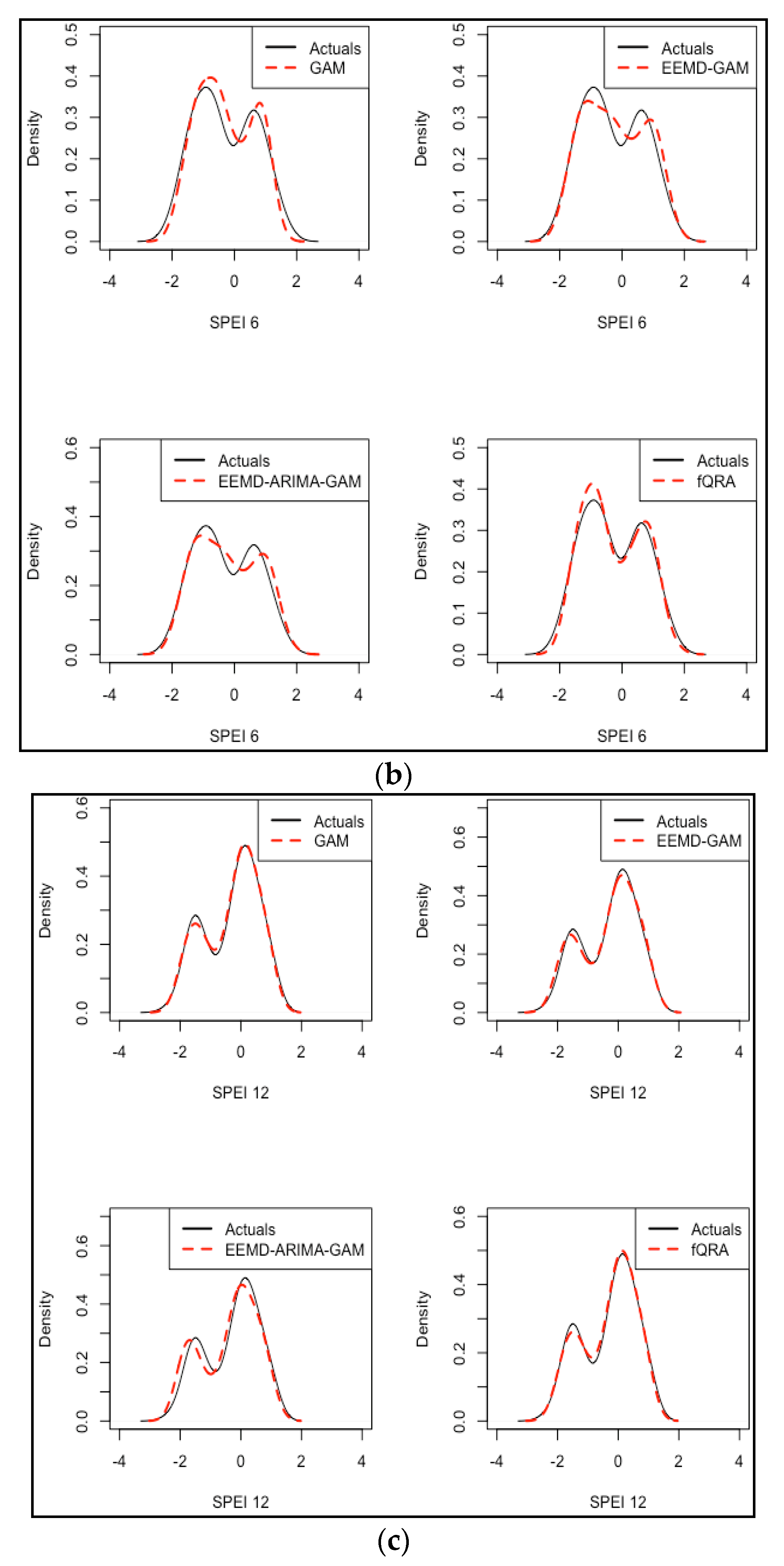
3.4. Short- and Medium-Term Forecasting
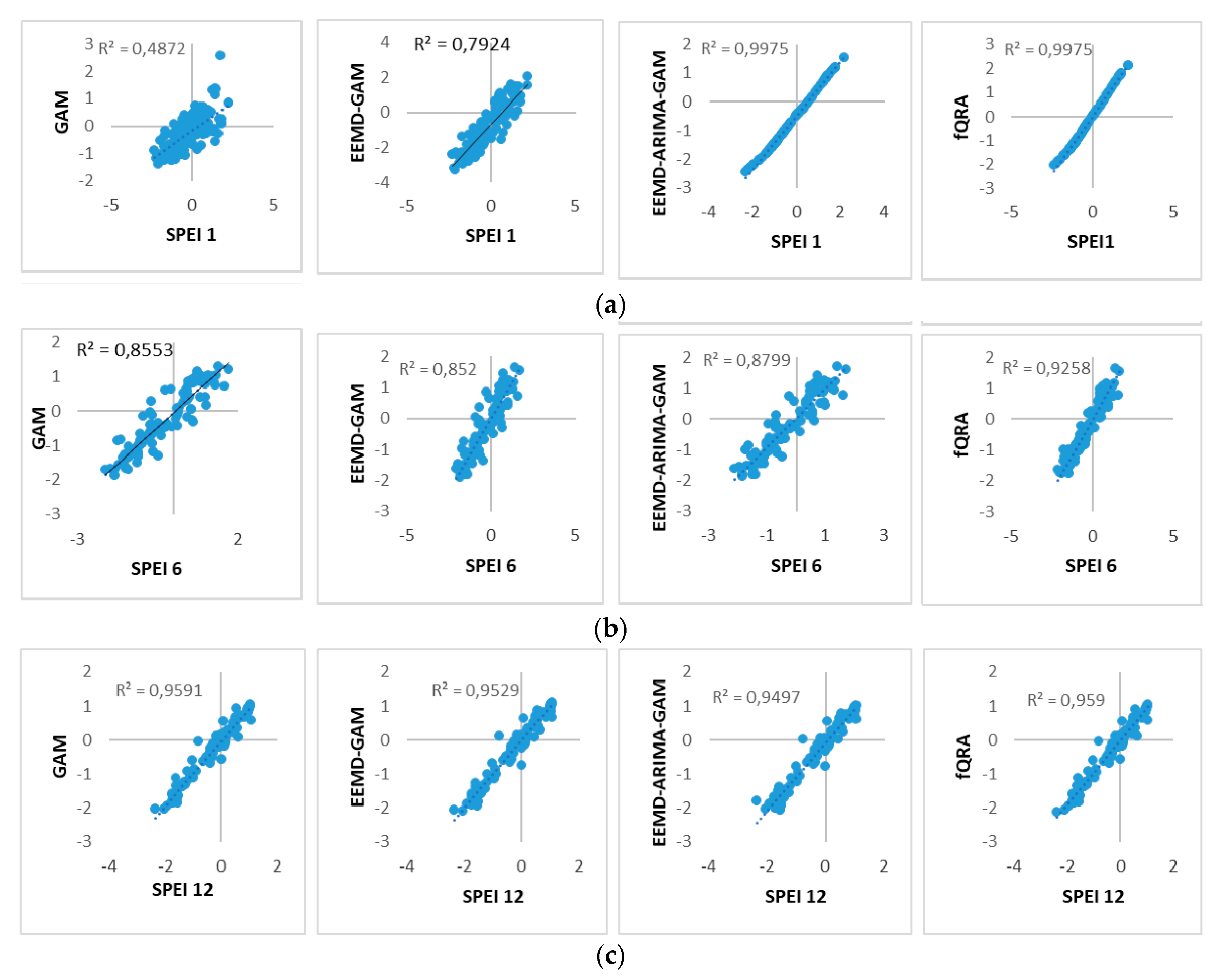
3.5. Model Performance
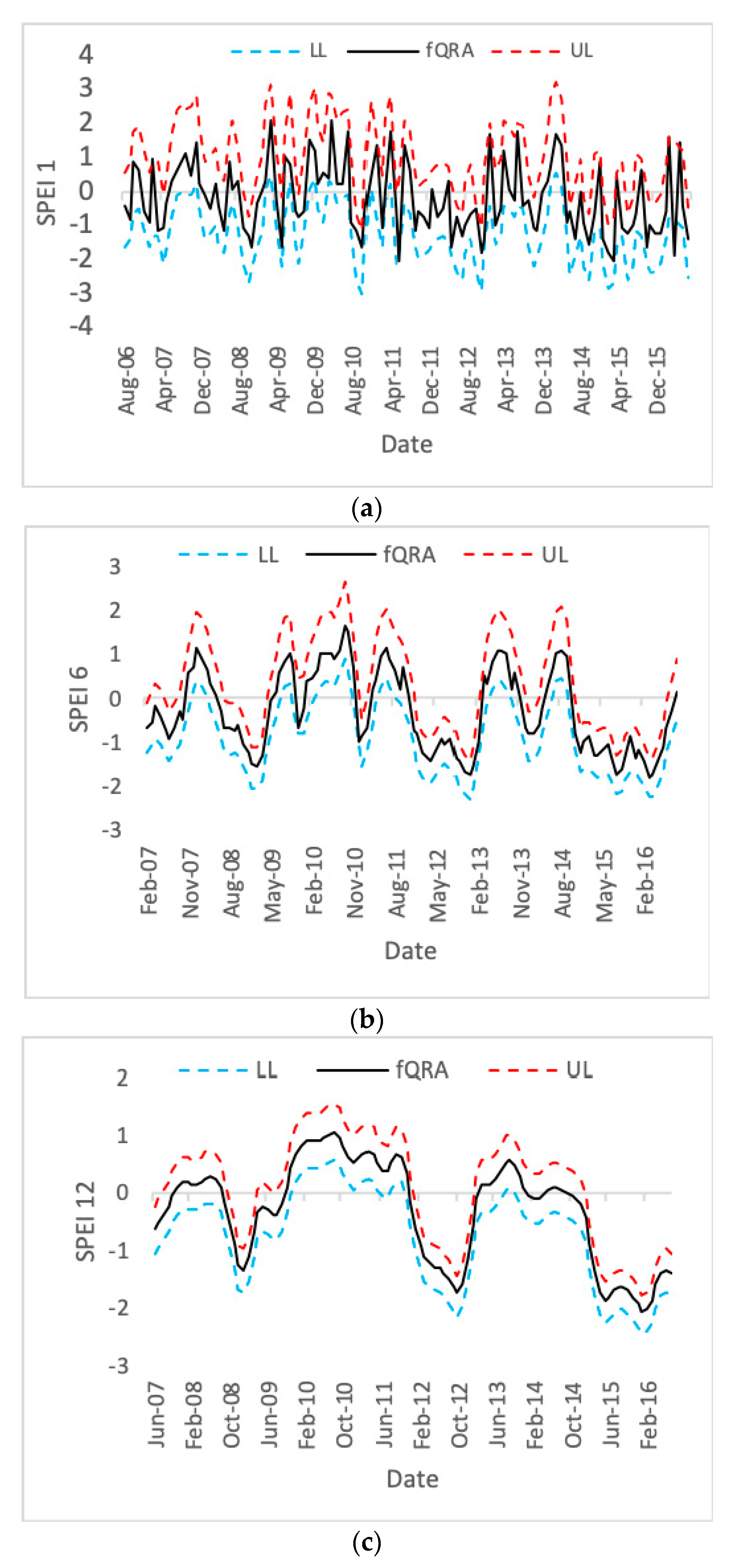
3.6. Evaluation of Model Uncertainity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tyson, P.D. Climatic Change Variability in Southern Africa; Oxford University Press: Cape Town, South Africa, 1986; p. 220. [Google Scholar]
- Nicholson, S.E.; Entekhabi, D. Rainfall variability in equatorial and southern Africa: Relationship with seas surface temperatures along the southwestern coast of Africa. J. Clim. Appl. Meteorol. 1987, 26, 561–578. [Google Scholar] [CrossRef][Green Version]
- Fauchereau, N.; Trzaska1, S.; Rouault, M.; Richard, Y. Rainfall Variability and Changes in Southern Africa during the 20th Century in the Global Warming Context. Nat. Hazards 2003, 29, 139–154. [Google Scholar] [CrossRef]
- Ambrosino, C.; Chandler, R.E.; Tod, M.C. Southern African Monthly Rainfall Variability: An Analysis Based on Generalized Linear Models. J. Clim. 2011, 24, 4600–4617. [Google Scholar] [CrossRef]
- Mason, S.J.; Waylen, P.R.; Mimmack, G.M.; Rajaratnam, B.; Harrison, J.M. Changes in Extreme Rainfall Events in South Africa. Clim. Chang. 1999, 41, 249–257. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate Extremes: Observation, Modeling and Impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. 2006, 111, D14102. [Google Scholar] [CrossRef]
- Kruger, A.C.; Nxumalo, M.P. Historical rainfall trends in South Africa: 1921–2015. Water SA 2017, 43, 285–297. [Google Scholar] [CrossRef]
- Mosase, E.; Ahlablame, L. Rainfall and temperature in Limpopo River Basin, southern Africa: Means, variation and trends from 1979 to 2015. Water 2018, 10, 364. [Google Scholar] [CrossRef]
- Odiyo, J.O.; Makungo, R.; Nkuna, T.R. Long-term changes and variability in rainfall and streamflow in Luvuvhu River Catchment, South Africa. S. Afr. J. Sci. 2015, 111, 1–9. [Google Scholar] [CrossRef][Green Version]
- Gommes, R. Non-parametric crop yeild forecasting. A didactic case study for Zimbabwe. In Proceedings of the ISPRS Archives XXXVI-8/W48 Workshop proceedings: Remote sensing support to crop yield forecast and area estimates, Stresa, Italy, 30 November–1 December 2006; pp. 79–84. [Google Scholar]
- Vicente-Serrano, S.M.; Chura, O.; Lopez-Moreno, J.I.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Aguilar, E.; Moran-Tejeda, E.; Trujillo, F.; Martinez, R.; Nieto, J.J. Spatio-temporal variability of droughts in Bolivia. Int. J. Clim. 2014, 35, 3024–3040. [Google Scholar] [CrossRef]
- Rouault, M.; Richard, Y. Intensity and spatial extent of droughts in southern Africa. Geophys. Res. Lett. 2005, 32, L15702. [Google Scholar] [CrossRef]
- Benson, C.; Clay, E. The Impact of Drought on Sub-Saharan African Economies: A Preliminary Examination; Technical Paper No. 401; World Bank: Washington, DC, USA, 1998. [Google Scholar]
- FAO. Drought Impact Mitigation and Prevention in the Limpopo River Basin: A Situation Analysis; Food and Agricultural Organisation: Rome, Italy, 2004; p. 160. [Google Scholar]
- Odiyo, J.; Mathivha, F.I.; Nkuna, T.R.; Makungo, R. Hydrological hazards in Vhembe district in Limpopo Province, South Africa. Jàmbá J. Disaster Risk Stud. 2019, 11, 698. [Google Scholar] [CrossRef] [PubMed]
- Association for Rural Advancement (AFRA). Drought Relief and Rural Communities; Special Rep. No. 9; AFRA: Pietermaritzburg, South Africa, 1993. [Google Scholar]
- Department of Environmental Affairs (DEA). South Africa’s 2nd Annual Climate Change Report; DEA: Pretoria, South Africa, 2016.
- Levey, K.M.; Jury, M.R. Composite interseasonal oscillation of convection over southern Africa. J. Clim. 1996, 9, 1910–1920. [Google Scholar] [CrossRef][Green Version]
- Cook, C.; Reason, C.; Hewitson, B. Wet and dry spells within particularly wet and dry summers in the South African summer rainfall region. Clim. Res. 2004, 26, 17–31. [Google Scholar]
- Department of Water Affairs and Forestry (DWAF). Luvuvhu/Letaba Water Management Area: Internal Strategic Perspective; DWAF Report No.P WMA 02/000/00/0304; DWAF: Pretoria, South Africa, 2004.
- Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; Hussain, T.; Shad, M.Y.; Shoukry, A.M.; Gani, S.H. Forecasting Drought Using Multilayer Perceptron Artificial Neural Network Model. Adv. Meteorol. 2017, 5681308. [Google Scholar] [CrossRef]
- Barua, S.; Ng, A.W.M.; Perera, B.J.C. Drought assessment and forecasting: A case study on the Yarra River catchment in Victoria, Australia. Aust. J. Water Resour. 2012, 15, 95–108. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Soh, Y.W. Drought forecasting: A review of modelling approaches 2007–2017. J. Water Clim. Chang. 2019, 1–29. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Paulo, A.A.; Pereira, L.S. Stochastic Prediction of drought class transitions. J. Water Resour. Manag. 2008, 22, 1277–1296. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet transforms and machine learning methods. Sustain. Water Resour. Manag. 2016, 2, 87–101. [Google Scholar]
- M’Marete, C.K. Climate and water resources in the Limpopo Province. In Agriculture as the Cornerstone of the Economy in the Limpopo Province; A study commissioned by the Economic Cluster of the Limpopo Provincial Government under the leadership of the Department of Agriculture; Nesamvuni, A.E., Oni, S.A., Odhiambo, J.J.O., Nthakheni, N.D., Eds.; Limpopo Provincial Government: Polokwane, South Africa, 2003; pp. 1–49. [Google Scholar]
- Mzezewa, J.; Misi, T.; van Rensberg, L.D. Characterisation of rainfall at a semi-arid ecotope in the Limpopo Province (South Africa and its implication for sustainable crop production. Water SA 2010, 36, 19–26. [Google Scholar] [CrossRef]
- Zhu, T.; Ringler, C. Climate Change Impacts on Water Availability and Use in the Limpopo River Basin. Water 2012, 4, 64–84. [Google Scholar] [CrossRef]
- Chikoore, H. Drought in Southern Africa: Structure, Characteristics and Impacts. Ph.D. Thesis, University of Zululand, Richards Bay, South Africa, 2016. [Google Scholar]
- Mulenga, H.M.; Rouault, M.; Reason, C.J.C. Dry summers over NE South Africa and associated circulation anomalies. Clim. Res. 2003, 25, 29–41. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. A mechanistic ecohydrological model to investigate complex interactions on cold and warm water-controlled environments: 2. Spatiotemporal analyses. J. Adv. Model. Earth Syst. 2012, 4, 1–22. [Google Scholar] [CrossRef]
- Usman, M.T.; Reason, C.J.C. Dry spell frequency and their variability over southern Africa. Clim. Res. 2004, 26, 199–211. [Google Scholar] [CrossRef]
- Kabanda, T.A. Climatology of Long Term Drought in the Northern Region of the Limpopo Province of South Africa. Ph.D. Thesis, School of Environmental Sciences, University of Venda, Thohoyandou, South Africa, 2004. [Google Scholar]
- Makarau, A. Intra-Seasonal Oscillatory Modes of the Southern Africa Summer Circulation. Ph.D. Thesis, Department of Oceanography, University of Cape Town, Cape Town, South Africa, 1995. [Google Scholar]
- Wehrens, R.; Buydens, L. Self and Super Organizing Maps in R: The kohonen Package. J. Stat. Softw. 2007, 21, 1–19. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Begueria, S.; Lo´pez-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 1998, 23, 1696–1718. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; Food and Agriculture Organisation of the United Nation: Rome, Italy, 1998. [Google Scholar]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. (Ser. B) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with formulas, graphs and mathematical tables; National Bureau of Standards Applied Mathematics Series-55; United States Department of Commerce: Washington, DC, USA, 1965.
- Bezdan, J.; Bezdan, A.; Blagojević, B.; Mesaroš, M.; Pejić, M.; Vranešević, M.; Pavić, D.; Nikolić-Đorić, E. SPEI-Based Approach to Agricultural Drought Monitoring in Vojvodina Region. Water 2019, 11, 1481. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.V. Calculation of the Standardised Precipitation-Evaporation Index, Package ‘SPEI’. Available online: http://sac.csic.es/spei (accessed on 15 January 2017).
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Pal, I.; Al-Tabbaa, A. Trends in seasonal precipitation extremes: An indicator of ‘Climate Change’ in Kerala, India. J. Hydrol. 2009, 367, 62–69. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V. Trend analysis of rainfall and temperature data for India. Curr. Sci. (Bangalore) 2012, 102, 37–49. [Google Scholar]
- Nikhil-Raj, P.P.; Azeez, P.A. Trend analysis of rainfall in Bharathapuzha River basin, Kerala, India. Int. J. Clim. 2012, 32, 533–539. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V.; Saharia, M. Analysis of rainfall and temperature trends in north-east India. Int. J. Clim. 2013, 33, 968–978. [Google Scholar] [CrossRef]
- Pohlert, T. Non-Parametric Trend Tests and Change-Point Detection. Available online: https://cran.rproject.org/web/packages/trend/trend.pdf (accessed on 12 April 2018).
- Wood, S. Generalized Additive Models; Chapman & Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
- Goude, Y.; Nedellec, R.; Kong, N. Local short and middle term electricity load forecasting with semi-parametric additive models. IEEE Trans. Smart Grid 2014, 5, 440–446. [Google Scholar] [CrossRef]
- Wood, S. P-splines with derivative based penalties and tensor product smoothing of unevenly distributed data. Stat. Comput. 2017, 27, 985–989. [Google Scholar] [CrossRef]
- Oztuna, D.; Elhan, A.H.; Tuccar, E. Investigation of four different normality tests in terms of type 1 error rate and power under different distributions. Turk. J. Med Sci. 2006, 36, 171–176. [Google Scholar]
- Field, A. Discovering statistics using SPSS, 3rd ed.; SAGE Publications Ltd.: London, UK, 2009; p. 822. [Google Scholar]
- Haque, M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef]
- Sankaran, M.; Ratnam, J.; Hanan, N. Woody cover in African savannas: The role of resources, fire and herbivory. Glob. Ecol. Biogeogr. 2008, 17, 236–245. [Google Scholar] [CrossRef]
- Benkachcha, S.; Benhra, J.; El-Hassani, H. Seasonal Time Series Forecasting Models based on Artificial Neural Network. Int. J. Comput. Appl. 2015, 116, 0975–8887. [Google Scholar]
- Taşpınar, F. Improving artificial neural network model predictions of daily average PM10 concentrations by applying principle component analysis and implementing seasonal models. J. Air Waste Manag. Assoc. 2015, 65, 800–809. [Google Scholar] [CrossRef] [PubMed]
- Lenton, T.M.; Vasilis Dakos, V.; Bathiany, S.; Scheffer, M. Observed trends in the magnitude and persistence of monthly temperature variability. Sci. Rep. 2017, 7, 5940. [Google Scholar] [CrossRef] [PubMed]
- Ravindra, K.; Rattana, P.; Morb, S.; Aggarwalc, A.N. Generalized additive models: Building evidence of air pollution, climate change and human health. Environ. Int. 2019, 132, 104987. [Google Scholar] [CrossRef]
- Sigauke, C.; Nemukula, M.M.; Daniel Maposa, D. Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models. Energies 2018, 11, 2208. [Google Scholar] [CrossRef]
- UNESCO. Water Resource Systems Planning and Management. Chapter 9: Model Sensitivity and Uncertainty Analysis; UNESCO: Paris, France, 2005; pp. 255–287. [Google Scholar]
- Gore, M.; Abiodun, B.J.; Kucharski, F. Understanding the influence of ENSO patterns on drought over southern Africa using SPEEDY. Clim. Dyn. 2020, 54, 307–327. [Google Scholar] [CrossRef]
- Meng, J.; Fan, J.; Ashkenazy, Y.; Bunde, A.; Havlin, S. Forecasting the magnitude and onset of El Niño based on climate network. New J. Phys. 2018, 20, 043036. [Google Scholar] [CrossRef]
| Station Name | Station Code | Station Number | Data Span | Data Length | |
|---|---|---|---|---|---|
| 1 | Mukumbani | Muk | 0766715 | 1956–2016 | 60 |
| 2 | Klein Australie | KA | 0723363 X | 1959–2016 | 57 |
| 3 | Matiwa | Mat | 0766509 9 | 1959–2016 | 57 |
| 4 | Nooitgedatch | Nooit | 0723334 X | 1959–2016 | 57 |
| 5 | Levubu | Lev | 0723485A | 1964–2016 | 54 |
| 6 | Vondo Bos | VB | 0766596 9 | 1963–2016 | 53 |
| 7 | Shefera | Shef | 0723182 6 | 1948–2016 | 68 |
| 8 | Tshivhase | Tshi | 0766628 W | 1986–2016 | 30 |
| Station | Timescale | Mild (%) | Moderate (%) | Severe (%) | Extreme (%) |
|---|---|---|---|---|---|
| KA | 1 | 68.28 | 23.66 | 5.91 | 0.02 |
| 6 | 63.79 | 27.59 | 8.05 | 0.575 | |
| 12 | 65.68 | 17.16 | 15.98 | 1.18 | |
| Lev | 1 | 65.91 | 22.35 | 2.24 | 0.56 |
| 6 | 66.67 | 16.67 | 16.67 | 0 | |
| 12 | 65.66 | 12.65 | 21.69 | 0 | |
| Mat | 1 | 67.9 | 26.84 | 5.26 | 0 |
| 6 | 65.35 | 25.57 | 8.52 | 0.57 | |
| 12 | 69.14 | 14.2 | 10.49 | 6.14 | |
| Muk | 1 | 68.42 | 23.68 | 7.37 | 0.53 |
| 6 | 65.36 | 25.7 | 6.7 | 2.23 | |
| 12 | 69.33 | 14.11 | 10.42 | 6.14 | |
| Nooit | 1 | 66.86 | 24 | 7.43 | 1.14 |
| 6 | 63.28 | 25.42 | 10.72 | 0.57 | |
| 12 | 61.15 | 23.08 | 14.2 | 1.18 | |
| Shef | 1 | 68.51 | 21.55 | 7.74 | 2.21 |
| 6 | 68.36 | 23.72 | 6.21 | 1.7 | |
| 12 | 70.88 | 21.43 | 6.05 | 1.65 | |
| Tshi | 1 | 70.97 | 23.12 | 4.2 | 1.61 |
| 6 | 68.11 | 21.08 | 10.27 | 0.54 | |
| 12 | 65.06 | 19.88 | 15.06 | 0 | |
| VB | 1 | 71.73 | 19.9 | 6.81 | 1.57 |
| 6 | 71.51 | 18.99 | 6.7 | 2.79 | |
| 12 | 71.88 | 15.63 | 6.65 | 6.65 |
| Variable | 1-Month Timescale | 6-Month Timescale | 12-Month Timescale |
|---|---|---|---|
| SPEI | Rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | Rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | Non-linear trend, SPEIt−1 |
| IMF 1 | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean |
| IMF 2 | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean | SPEI, rain, non-linear trend, SPEIt−1 and SPEIt−2, Tmax, Tmin, Tmean |
| IMF 3 | Non-linear trend | Non-linear trend | Non-linear trend |
| IMF 4 | Non-linear trend | Non-linear trend | Non-linear trend |
| IMF 5 | Non-linear trend | Non-linear trend, SPEIt−1 | Non-linear trend, SPEIt−1 |
| IMF 6 | Non-linear trend, SPEIt−1 | Non-linear trend, SPEIt−1 | Non-linear trend, SPEIt−1 |
| IMF 7 | Non-linear trend, SPEIt−1 and SPEIt−2 | Non-linear trend, SPEIt−1 and SPEIt−2 | Non-linear trend, SPEIt−1 |
| Residual | Non-linear trend, SPEIt−1 and SPEIt−2 | Non-linear trend, SPEIt−1 and SPEIt−2 | Non-linear trend, SPEIt−1 and SPEIt−2, SPEI |
| Timescale | Model | ME | RMSE | MAE | MPE | MAPE |
|---|---|---|---|---|---|---|
| 1 | GAM | 0.0177 | 0.7676 | 0.6127 | −3.8647 | 231.728 |
| EEMD-GAM | 0.6805 | 0.8829 | 0.7410 | −47.4685 | 275.233 | |
| EEMD-ARIMA-GAM | 0.4718 | 0.481 | 0.4718 | −135.946 | 280.609 | |
| fQRA | −0.0116 | 0.0599 | 0.03369 | 11.971 | 17.099 | |
| 6 | GAM | −0.0016 | 0.3644 | 0.2694 | 19.774 | 57.438 |
| EEMD-GAM | −0.0563 | 0.3818 | 0.2833 | 13.330 | 57.293 | |
| EEMD-ARIMA-GAM | −0.0599 | 0.3449 | 0.2595 | 10.227 | 51.763 | |
| fQRA | 0.0030 | 0.2609 | 0.2057 | 8.053 | 37.699 | |
| 12 | GAM | 0.0021 | 0.1809 | 0.1199 | −63.013 | 123.075 |
| EEMD-GAM | 0.0067 | 0.1978 | 0.1373 | −128.169 | 181.563 | |
| EEMD-ARIMA-GAM | 0.0851 | 0.2221 | 0.162 | −77.719 | 183.636 | |
| fQRA | 0.0032 | 0.1811 | 0.1194 | −67.49 | 127.262 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathivha, F.; Sigauke, C.; Chikoore, H.; Odiyo, J. Short-Term and Medium-Term Drought Forecasting Using Generalized Additive Models. Sustainability 2020, 12, 4006. https://doi.org/10.3390/su12104006
Mathivha F, Sigauke C, Chikoore H, Odiyo J. Short-Term and Medium-Term Drought Forecasting Using Generalized Additive Models. Sustainability. 2020; 12(10):4006. https://doi.org/10.3390/su12104006
Chicago/Turabian StyleMathivha, Fhumulani, Caston Sigauke, Hector Chikoore, and John Odiyo. 2020. "Short-Term and Medium-Term Drought Forecasting Using Generalized Additive Models" Sustainability 12, no. 10: 4006. https://doi.org/10.3390/su12104006
APA StyleMathivha, F., Sigauke, C., Chikoore, H., & Odiyo, J. (2020). Short-Term and Medium-Term Drought Forecasting Using Generalized Additive Models. Sustainability, 12(10), 4006. https://doi.org/10.3390/su12104006






