Abstract
Previous studies have introduced different potential pricing strategies for cloud services. However, not much research has been done comparing subscription pricing and pay-per-use pricing, which are commonly used pricing schemes. Also, there are very few studies which analyze a two-part tariff pricing scheme for cloud services, even though this option may increasingly attract service providers as the cloud market becomes more competitive and the profit margin grows narrower. Previous research has focused on firms’ profitability rather than social welfare due to the limitations of free services. This study uses theoretical and numerical analysis to compare the social welfare and profitability of three pricing schemes commonly used by firms: subscription pricing, pay-per-use pricing, and two-part tariff pricing. It shows that the pay-per-use pricing is the best solution from the perspective of social welfare, which contrasts with the conclusion of a previous study stating that social welfare is maximized under a two-part tariff. This paper also shows that the two-part tariff is the most profitable pricing scheme for firms.
1. Introduction
With the development of information technology and Internet services, consumers are benefiting from many digital services free of charge. Many digital content companies provide a large number of free services to consumers in the form of common goods by relying on advertising revenues based on users’ visits and some personal information such as web surfing and purchasing behavior. In particular, cloud computing has changed the traditional computing business environment by enabling customers to access data and use software without the need to install it and providers to offer numerous online services. Cloud services can be regarded as utility computing services, which are delivered in a manner similar to traditional utilities, such as water, electricity, gas, and telecommunications [1]. However, due to the limitations of free services, some companies are paying for digital goods and services to sustain their business models. Therefore, as in other utility services, the implementation of adequate service models and pricing schemes for cloud services is critical. Pricing enables the regulation of the supply and demand of computing services and, along with variations in service models, affects providers’ profits and social welfare [2,3].
Many studies have introduced different potential pricing strategies for cloud services, such as pay-as-you-go pricing, subscription pricing, pay-for-resources pricing, value-based pricing, cost-based pricing, customer-based pricing, competition-based pricing, and other dynamic pricing strategies [4,5]. In reality, the most popular pricing strategies are subscription, pay-as-you-use, and two-part tariff models. Some dynamic pricing strategies have been studied by many researchers [4,6], but a comparative analysis of subscription pricing and pay-per-use pricing has not been done, although these pricing methods are commonly used in cloud service systems. Also, an analytical study is required for the two-part tariff pricing scheme, since the concept of a two-part tariff is nowadays adopted as a cloud services’ pricing strategy and could gain in popularity among service providers as the cloud market becomes more competitive and the profit margin grows narrower. Previous research has focused on firms’ profitability with respect to the limitations of free services. Chun and Choi [7] analyzed the two pricing schemes of subscription and pay-per-use pricing models from a provider’s standpoint and discussed their implications for consumer surplus and social welfare. Chun et al. [8] compared the three pricing schemes of subscription pricing, pay-per-use pricing, and two-part tariff from the perspectives of a provider’s profit, consumer surplus, and social welfare.
This study differentiates itself from previous ones in several aspects. Firstly, I applied two-part tariff pricing to cloud services by considering subscription pricing and pay-per-use pricing and extended the previous two-part tariff to a more generalized customer heterogeneous model, in order to utilize it for a cloud service pricing strategy. Secondly, I clarified the previous two-part tariff model and compared the results from subscription, pay-per-use, and two-part tariff pricing with those obtained from analytical and numerical approaches and recent real-world examples. In particular, I show how two-part tariff pricing can include the other two pricing schemes of subscription and pay-per-use pricing, through theoretical and numerical analysis. Thirdly, I discuss some possible conflicting issues between customers and providers, in terms of consumer and producer surpluses.
This paper shows that the pay-per-use pricing is the best option from the perspective of social welfare when there is no additional metering cost. This conclusion contrasts with that of a previous study [9] stating that social welfare is maximized under a two-part tariff. This paper also shows that the two-part tariff is the most profitable pricing scheme for the firm. This paper is organized as follows: Section 2 discusses service models and pricing models in cloud computing; Section 3 investigates right pricing schemes for cloud services using a theoretical analysis; Section 4 compares the three pricing schemes of subscription pricing, pay-per-use pricing, and two-part tariff from the perspectives of a provider’s profit, consumer surplus, and social welfare, using theoretical and numerical analysis and discusses some implications; Section 5 concludes and discusses future research directions.
2. Research Background: Cloud Service Models and Pricing Models
2.1. Cloud Services and Practical Pricing Cases
Cloud computing is defined as a model for enabling ubiquitous, convenient, on-demand network access to a shared pool of configurable computing resources (e.g., networks, servers, storage, applications, and services) that can be rapidly provisioned and released with minimal management effort or service provider interaction [10]. Cloud service providers offer their services to users through three layers, i.e., software as a service (SaaS), platform as a service (PaaS), and infrastructure as a service (IaaS) [11]. In IaaS, users are provided with processing capability, storage, networks, and other fundamental computing resources and are able to deploy and run arbitrary software, including operating systems and applications [10]. For example, Amazon offers services based on its infrastructure, such as computing services (EC2) or storage services (S3). Amazon S3 provides online storage, data request, and data transfer services. Table 1 shows several Amazon S3 services and price plans. Also, there are other examples of IaaS, such as those offered by AppNexus, Dropbox, EU Reservoir project, FlexiScale, Joyent, and Rackspace. Most IaaS providers offer hourly services, whose costs are based on usage-dependent and component-based rates. They provide users with services at a low price per GB of storage, charge hidden costs for inbound and/or outbound data transfer, and offer basic packages at a fixed price which can be extended according to the user’s needs, similar to a two-part tariff scheme mixing subscription plus pay-per-use pricing. Also, users can pay a fixed price in order to get discounts on usage-dependent prices [5].

Table 1.
Amazon storage services (S3)′ price plans (US East (Ohio), 2019).
PaaS allows users to deploy applications acquired or created using programming languages and tools supported by the provider. A platform as a service provides users with a convenient environment for developing applications [12]. In PaaS, cloud services are provided according to three different pricing schemes: free of charge, as complete packages, and usage-dependent pricing. An example of PaaS is Google App Engine, which is a platform for developing and hosting web applications in data centers. Table 2 shows Google App Engine’s price plans for its services per month or hour. Other examples of PaaS are LongJump, Microsoft Azure, Zoho Creator, and SalesForce.com Lightning Platform.

Table 2.
Google App Engine’s price plans (2019).
In SaaS, users can access providers’ applications running on a cloud infrastructure using various devices through a thin client interface, such as a web browser. The SaaS pricing schemes include free-of-charge services and complete packages at a fixed monthly charge [13]. NetSuite, SalesForce.com, and SAP are examples of companies offering SaaS. For instance, the Sales Cloud of SalesForce.com provides features such a sales representatives service with a complete customer profile and account history for managing marketing campaigns and increasing sales [5]. The pricing plans for Sales Cloud are shown in the Table 3.

Table 3.
Sales Cloud’s price plans.
2.2. Cloud Pricing Models
Recently, some studies have analyzed pricing strategies for cloud computing environments. Two common types of pricing models are static pricing and dynamic pricing [14,15]. In static or fixed pricing, the price charge does not change, and the cloud provider determines the price according to the resource type in advance [16]. A fixed pricing model is more straightforward and easier to understand for users, as compared to dynamic pricing models [2]. Fixed pricing includes pay-per-use, subscription, and list prices or menu pricing [17].
In subscription pricing, users pay on a recurring basis to access software as an online service [2]. The user subscribes to use a preselected combination of service units for a fixed price and a longer time frame, usually monthly or yearly [6]. With subscription-based pricing, a cloud service provider offers fixed recurring pricing on a monthly basis for a service or product, and customers pay upfront, prior to receiving access to the cloud services. A heavy user may choose a longer subscription to get a lower price. However, a subscription-based model can result in customers overpaying for services. Examples of the subscription pricing model can be found in Dropbox, Google, and other cloud storage services, as shown in the Table 4.

Table 4.
Pricing schemes for the subscription pricing model.
In pay-per-use pricing, users only have to pay for what they use and are aware of the cost of doing business and consuming a resource. With a pay-per-use pricing model, a provider charges a price based on the usage and consumption of a service. The major benefit of the pay-per-use pricing model is that there are no wasted resources [18]. In the pay-per-use pricing model, customers are charged on the basis of how much they consume a product or service. Examples are Amazon EC2 and S3 and Google App Engine, shown in the Table 5 [19,20].

Table 5.
Pricing schemes for the pay-per-use pricing model.
For example, as shown in Table 5, Amazon’s pay-per-use price after the first 50 TB is $0.023 per GB/month of storage. This approach is commonly used in PaaS and IaaS. Different providers use different pricing schemes for the provisioning of services to the end user.
In dynamic pricing, the price charges change dynamically, according to supply and demand, for example, by means of auctions. Amazon runs customer’s instances as long as the bid price is higher than the spot price, which is set by Amazon based on their data center utilization [17], whilst dynamic pricing policies could achieve more economically efficient allocations and prices for high-value services [2,6,21]. Other examples of dynamic pricing strategies are a novel financial economic model providing a high level of QoS (Quality of service) to customers [22], a genetic model for pricing in cloud computing [23], a dynamic pricing scheme for federated clouds [24], and a hybrid pricing strategy, mixing fixed-price reserved services with spot-price on-demand services [25]. However, in reality, dynamic pricing is not common, and fixed prices such as subscription pricing and pay-per-use pricing are typical [4,26].
3. The Model
3.1. Model Setting
This paper extends the study of pricing models by Chun et al. [7,8] and investigates subscription pricing, pay-per-use pricing, and two-part tariff pricing from the perspectives of a provider’s profit, consumer surplus, and social welfare. Chun and Choi [7] analyzed the two pricing schemes of subscription and pay-per-use pricing models from a provider’s standpoint and discussed their implications for consumer surplus and social welfare. Chun et al. [8] compared the three pricing schemes of subscription pricing, pay-per-use pricing, and two-part tariff from the perspective of a provider’s profit.
For simplicity, I assume that there is a monopoly provider of cloud services. The cost of providing services depends on both fixed and variable elements and is expressed as , where and are the marginal cost and fixed cost, respectively, and is the quantity of service consumed. I assume that without loss of generality. The provider chooses the pricing scheme, , where is the lump-sum price, and is the unit price. Thus, the pricing scheme can represent subscription pricing when and , pay-per-use pricing when and , and two-part tariff when and . The provider profit can be expressed as
where N is the total number of consumers who are actually participating in the market and buy services, and Q is the total amount of services all consumers purchased.
Let us turn to the demand side. I assume that consumers’ reservation prices are uniformly distributed along [0, U] with unit height, i.e., u∈ [0, U]. Thus, U can also represent the potential market share of the product. Given the provider’s unit price (p), a consumer of type u∈ [0, U] will obtain the following surplus by consuming one unit of the product:
An individual consumer’s demand function is downward sloping and is expressed as , where is the maximum willingness to pay for the services. Thus, a consumer purchases the services when . The consumer has the net utility or surplus when he or she purchases units of services, where is the total value when a consumer buys units of services, and is the payment. Since u is uniformly distributed along [0, U] with unit height, the total number of consumers (or the potential market share of the product) is U. I consider a heterogeneous customer distribution case where each different consumer can purchase a different amount of services according to his or her valuation of the services. For simplicity of analysis, when a representative consumer buys q units of services, I assume that has the specific form of a concave utility function [26,27,28]:
where , , and .
A consumer u has a downward sloping linear demand and maximizes his or her net utility,
and
As explained, u is a representative consumer distributed along the length between 0 and U according to maximum willingness to pay for the services and will buy an amount of services corresponding to Also, a consumer U, who has the maximum willingness to pay, will buy the amount of services Figure 1 shows the amount of services each consumer buys when the price is zero. The y-axis in Figure 1 represents the amount of services a specific consumer will buy. For example, a consumer will buy when a price is zero but a consumer will buy when a price amounts to the positive value .
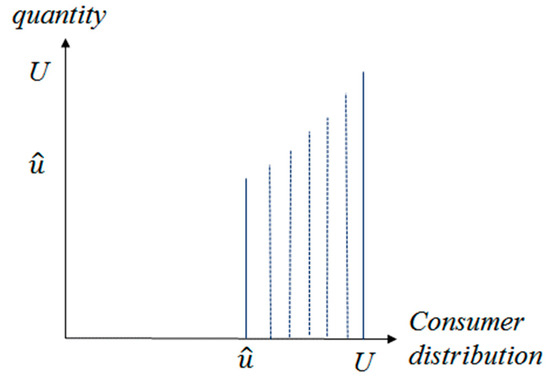
Figure 1.
Consumers’ valuation distribution and amount of purchased services.
Figure 2a depicts the total value or utility of a consumer u, and Figure 2b shows demand function of the consumer u and net utility (shade area) from the amount of services.
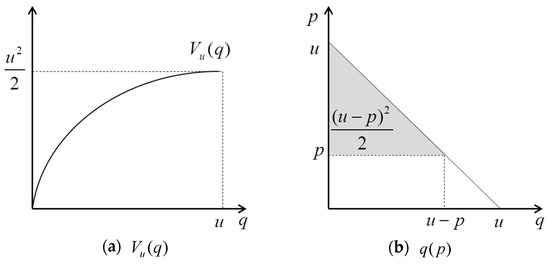
Figure 2.
Total value and demand function of consumer u.
By inserting (1) into the expression of , the net utility for the consumer u is obtained.
The first term on the right-hand side of (2) is the shaded area of Figure 2b.
3.2. Subscription Pricing
Cloud service providers such as Dropbox, Google, and others charge a price based on time (monthly or yearly), irrespective of the amount of consumption. Thus, and . Thus, a consumer’s decision to buy services depends on the lump-sum price of A and his or her valuation of service consumption. The customer compares his or her valuation of a service with the lump-sum price of A and buys the service when his or her net utility is greater than zero. From (1) and (2), the net utility when the customer buys u units of a service is given by
where , and p = 0.
Then, a marginal consumer is defined as follows:
Since u is uniformly distributed along [0, U], the number of consumers (N) who purchase services is
For example, a consumer U, whose willingness to pay is the maximum, would buy the amount of services . A marginal consumer would purchase a zero amount of services when the lump-sum price is A. Therefore, the total amount of services (Q) that are bought can be obtained by summing up all the amounts of services that consumers purchase, as follows:
Then, the profits of the provider are:
The provider finds an optimal price considering the total number of consumers who buy services and the costs of providing the total amount of services requested. The literature about the two-part tariff model assumes that there are one or two types of consumers and the costs depend on the number of consumers. In this model, a provider’s total amount of sales is calculated from the number of consumers who buy services, and the total costs are calculated from the total amount of services all consumers buy. I here extend the two-part tariff model by considering that each consumer buys a different amount of services, according to her/his purchasing decision based on net utility maximization. From the first order condition, the optimal subscription price can be determined as follows:
Note that the superscript S is used to denote ‘subscription pricing’. The marginal consumer who is indifferent to buying or not buying is described by
Using Eqation (3), the number of consumers, the quantity of services used, the profits of the provider, and consumer surplus at the equilibrium can be easily calculated:
The consumer surplus and social welfare can be obtained accordingly:
Equilibrium exists when the maximum willingness to pay is sufficiently larger than the marginal cost of providing services, and the number of consumers is not negative:
Equation (4) assumes the condition of . I assume that Equation (4) holds throughout this paper.
3.3. Pay-Per-Use Pricing
Cloud service providers such as Amazon and Google charge prices based on the usage and consumption of their services offered in EC2, S3, and Google App Engine. When a price is p, a consumer u will buy u − p quantity of services, and his or her surplus will be
Then, the number of consumers purchasing services, the total quantity of services provided, and the profits of the provider can be calculated similarly to the case of subscription pricing:
The first order condition () generates the optimal pay-per-use price:
The superscript P is used to denote ‘pay-per-use pricing’. The marginal consumer who is indifferent to buying or not buying is
Then, the number of consumers purchasing services, the quantity of services consumed, the profits of the provider, the consumer surplus, and social welfare at equilibrium can be obtained as follows:
3.4. Two-Part Tariff Pricing
Many providers use a hybrid pricing mechanism (or two-part tariff pricing) by mixing subscription and pay-per-use pricing, which in fact is not much little different from the original two-part tariff [4]. For example, Google App Engine and Joynet Smart Machine’s prices are assigned on a monthly basis and, if the usage exceeds a set limit, prices are charged as per GB [5].
In this section, I will focus on analyzing two-part tariff pricing, subscription pricing, and pay-per-use pricing, because they are practically used for cloud service pricing. The purpose of a two-part tariff is to extract more of the consumer surplus by using a pricing scheme consisting of a fixed or one-time fee charged to each user and a price per each unit purchased [27,28]. Examples of two-part tariffs are found in the rental of computers and copying machines, country club fees, and the rate structures of some public utilities. A two-part tariff pricing model can be considered as a quantity discounting scheme [26].
I consider the case when a provider charges p on usage and A for a fixed fee, so that , and . Then, it follows that
The condition that a consumer u purchases services is given by
The number of consumers’ purchasing services, the total quantity of services provided, and the profits of the provider are obtained as follows:
By simultaneously solving the first-order conditions (,), optimal two-part tariff prices are obtained,
To denote ‘two-part tariff’, I used the superscript T. The marginal consumer who is indifferent to buying or not buying is
Then, the number of consumers, the quantity of services provided, the profits of the provider, the consumer surplus, and social welfare at equilibrium can be calculated as follows:
4. Results of the Study
Comparisons and Discussion
Table 6 shows equilibrium prices, the number of consumers, the total quantity of services, the consumer surplus, the profits of the provider, and social welfare for each pricing scheme. As expected, optimal prices calculated for the two-part tariff are lower than optimal prices under the subscription and pay-per-use pricing schemes; therefore, and When comparing the price of two-part tariff to the price of subscription, heavy users prefer subscription pricing to pay-per-use pricing, which leads to a higher total number of consumers under the two-part tariff than under pay-per-use pricing () and decreases the price of the two-part tariff (). Also, when comparing the price of two-part tariff to pay-per-use pricing, light users prefer pay-per-use pricing to subscription pricing, which leads to a lower number of consumers under the two-part tariff than under pay-per-use pricing (). However, the total amount of services under the two-part tariff scheme is larger than under pay-per-use pricing (), which decreases the price of the two-part tariff with respect to pay-per-use pricing (). The number of consumers is the highest under pay-per-use pricing, and the total amount of purchased services is the highest under subscription pricing.

Table 6.
Comparison of the results.
Figure 3 shows consumers’ total payments according to each pricing scheme. As shown in Figure 3, light users prefer pay-per-use pricing to subscription pricing, because pay-per-use pricing better reflects their actual amount of consumption. On the other hand, heavy users prefer subscription pricing to pay-per-use pricing, because subscription pricing fixes the consumer’s payment, regardless of the actual amount of consumption. Preference for the two-part tariffs is typical of consumers whose service consumption is intermediate. The consumers’ preference is indicated by the solid line in Figure 3.
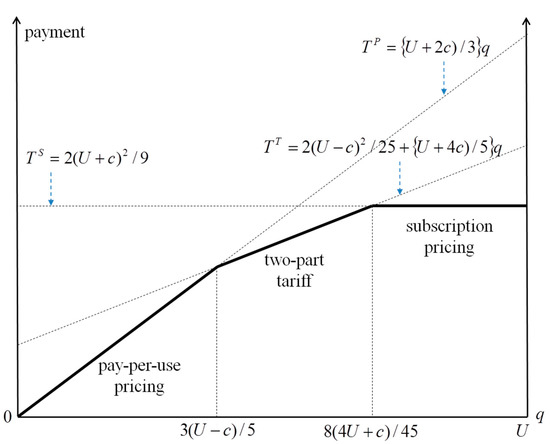
Figure 3.
Comparison of consumers’ payments.
The marginal consumer who is indifferent to buying or not buying under pay-per-use pricing () does not purchase services under a two-part tariff. Similarly, the marginal consumer who is indifferent to buying or not buying under a two-part tariff () does not purchase services under subscription pricing. It follows that and . Under subscription pricing, consumers with a low willingness to pay will not purchase services due to the high initial payment (). Under pay-per-use pricing, the largest number of consumers purchase services at the lowest price, which implies that consumer surplus can be higher than for any other pricing schemes.
Considering the information provided in Table 1 and Figure 3, the following proposition is obtained, by comparing the values of consumer surplus (, i = S, P, T).
Proposition 1.
Consumer surplus is always the highest under the pay-per-use pricing and the lowest under subscription pricing, that is,
when c is not very low:andwhen c is 0:
Proof:
If c is not lower than (or , where is satisfying ), then Also if , □
Proposition 1 implies that the number of consumers in the cloud market is an important factor from the perspective of consumer surplus. Under pay-per-use pricing, low-end consumers can participate in the market with the lowest amount of payment, which leads to a high consumer surplus. Figure 4 shows how consumer surplus changes for each pricing model. For a graphical view, I show the case in which costs change from zero to the maximum value () for U = 20. As shown in Figure 4, pay-per-use pricing is the best from the perspective of consumer surplus. This figure also shows that a two-part tariff generally produces better results for consumer surplus than subscription pricing, although subscription pricing is better than two-part tariff pricing when the costs are very low.
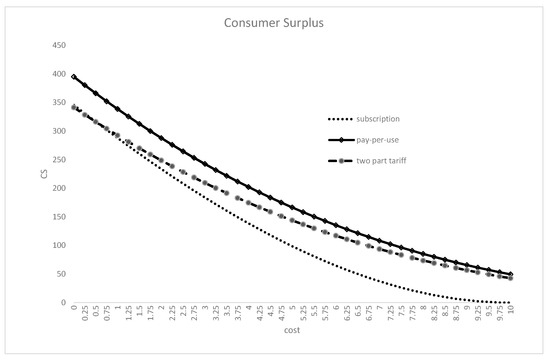
Figure 4.
Consumer surplus variation with service costs.
By comparing the values of (i = S, P, T), the following proposition is obtained:
Proposition 2.
The profits of the monopoly provider are maximized under two-part tariff and minimized under subscription pricing, that is,
This holds only when the marginal cost of providing services is zero.
Proof:
From Eqation (4), and , it holds that when . □
The merit of subscription pricing from the provider’s perspective is to receive revenue from consumers with a lower willingness to pay (or light users). On the contrary, the provider can obtain a large revenue from the consumers with a higher willingness to pay (or heavy users) under pay-per-use pricing. As shown by the fact that when , the provider can make equal revenue from either pricing scheme by optimizing the lump-sum and unit prices. A two-part tariff balances the revenue from high-end and low-end consumers and maximizes the profit of the provider. Considering the examples of Google App Engine and Joynet Smart Machine, two-part tariff pricing is motivated by customer segmentation. Therefore, subscription pricing targets light users, pay-per-use pricing targets heavy users, and two-part tariffs targets users with light-to-heavy service consumption.
Taking these two propositions into account, the following proposition ensues:
Proposition 3.
Social welfare is the highest under pay-per-use pricing and the lowest under subscription pricing, that is,
Proof:
We know with simple calculation. □
Proposition 3 states that social welfare is the best under pay-per-use pricing although profits are the best under a two-part tariff pricing scheme. This is because profits gained under a two-part tariff scheme are lower than consumer surplus loss, as shown in Table 6 and Figure 4. These results contrast with those of a previous study [9] stating that social welfare is the best under a two-part tariff. Proposition 3 implies that a regulatory regime and consumers prefer a pay-per-use pricing scheme, but firms prefer a two-part tariff to pay-per-use pricing. From the perspective of social welfare, a regulatory regime can require firms to charge a lump-sum payment at least on basic service packages or to use a pay-per-use pricing scheme. The proposition also shows that subscription pricing is the lowest from the perspectives of the provider’s profits and social welfare.
Table 7 summarizes the results of this study using a numerical example when U = 20 and c = 0. The results show that the two-part tariff includes the other two pricing schemes. As we expected, consumer demand (or the total number of customers who buy services) is the lowest, and the total consumption of services by all customers is the highest under subscription pricing, which implies that subscription pricing cannot be efficiently utilized by consumers and leads to some losses in consumer surplus, compared with other pricing schemes.

Table 7.
Comparison of the results using a numerical example (when U = 20 and c = 0).
For a more graphical explanation, Figure 5 depicts a provider’s profits, consumer surplus, and social welfare, according to the price bundles of p and A under two-part tariff. It shows how a two-part tariff is related to the two other pricing schemes and summarizes the results of this study graphically. The optimal price bundle of (p, A) under two-part tariff is (4, 32), and the highest profit amounts to 640 at (p, A) = (4, 32). The left points in Figure 5 represent optimal solutions under subscription pricing, which is a special instance of the two-part tariff when a price bundle is (p, A) = (0, 88). The points on the right peaks represent the instance of pay-per-use pricing when a price bundle is (p, A) = (6.66, 0), which corresponds to the highest values of social welfare and consumer surplus.
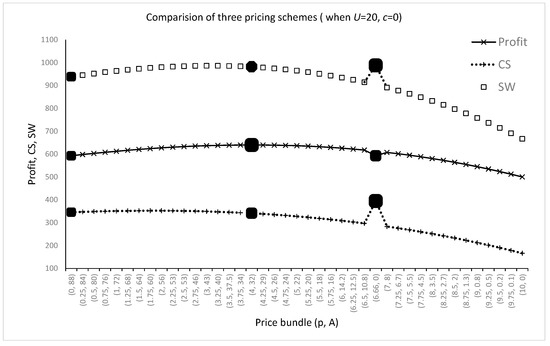
Figure 5.
Graphical view of the results in the case of two-part tariff.
5. Conclusions
Although many cloud service providers offer numerous online services, pricing schemes are different depending on service types and service levels. Previous research has focused on firms’ profitability with respect to the limitations of free services. This paper analyzed and compared three commonly used pricing schemes, i.e., subscription pricing, pay-per-use pricing, and two-part tariff pricing from the perspectives of a provider’s profit, consumer surplus, and social welfare. In particular, this paper showed how two-part tariff pricing can include the two other pricing schemes of subscription and pay-per-use pricing, that two-part tariff is the most profitable pricing scheme compared with the other two pricing schemes, and that pay-per-use pricing is the best pricing scheme from the perspective of consumer surplus and social welfare, which contrasts with the results of a previous study [9] stating that social welfare is maximized under a two-part tariff. Other results and implications of this study are summarized below.
Firstly, both the provider and consumers prefer pay-per-use pricing to subscription pricing. If the marginal cost of providing services is negligible, pay-per-use pricing and subscription pricing are the same for the provider. In reality, there are additional considerations, besides user benefits and cost structure. For example, metering service usage entails additional costs in the case of pay-per-use pricing. Therefore, if the additional metering cost is large, subscription pricing can be preferred to pay-per-use pricing in service models. Secondly, from the perspective of profit, firms prefer two-part tariffs to pay-per-use pricing. Thirdly, pay-per-use pricing is the most convenient for consumer surplus and social welfare if there is no additional metering cost, which implies that profit gains from a two-part tariff do not make up for the loss in consumer surplus when a provider changes his/her pricing scheme from pay-per-use pricing to two-part tariff. However, the government or consumers are concerned about social welfare or consumer surplus. Therefore, a regulatory regime may have the incentive to lead providers to use pay-per-use pricing or two-part tariff pricing with a minimum lump-sum fee for basic services and a unit price for usage.
This paper has a number of limitations with respect to customers’ contracts for pricing schemes. Thus, in future work, the choice of contract by customers and pricing differentiation for heterogeneous customers groups need to be analyzed.
Funding
This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2019S1A5A2A01046398).
Conflicts of Interest
The author declares no conflicts of interest.
References
- Buyya, R.; Yeo, C.S.; Venugopal, S.; Broberg, J.; Brandic, I. Cloud computing and emerging IT platforms: Vision, hype, and reality for delivering computing as the 5th utility. Future Gener. Comput. Syst. 2009, 25, 599–616. [Google Scholar] [CrossRef]
- Yeo, C.S.; Venugopal, S.; Chu, X.; Buyya, R. Autonomic metered pricing for a utility computing service. Future Gener. Comput. Syst. 2010, 26, 1368–1380. [Google Scholar] [CrossRef]
- Li, C.-F. Cloud computing system management under flat rate pricing. J. Netw. Syst. Manag. 2011, 19, 305–318. [Google Scholar] [CrossRef]
- Al-Roomi, M.; Al-Ebrahim, S.; Buqrais, S.; Ahmad, I. Cloud computing pricing models: A survey. Int. J. Grid Distrib. Comput. 2013, 6, 93–106. [Google Scholar] [CrossRef]
- Mazrekaj, A.; Shabani, I.; Sejdiu, B. Pricing schemes in cloud computing: An overview. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 80–86. [Google Scholar] [CrossRef]
- Weinhardt, C.; Anandasivam, A.; Blau, B.; Stößer, J. Business models in the service world. IT Prof. 2009, 11, 28–33. [Google Scholar] [CrossRef]
- Chun, S.-H.; Choi, B.-S. Service models and pricing schemes for cloud computing. Clust. Comput. 2014, 17, 529–535. [Google Scholar] [CrossRef]
- Chun, S.-H.; Choi, B.-S.; Ko, Y.W.; Hwang, S.H. The Comparison of Pricing Schemes for Cloud Services. In Frontier and Innovation in Future Computing and Communications. Lecture Notes in Electrical Engineering; Park, J., Zomaya, A., Jeong, H.Y., Obaidat, M., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 301. [Google Scholar]
- Wu, S.Y.; Banker, R.D. Best pricing strategy for information services. J. Assoc. Inf. Syst. 2010, 11, 339–366. [Google Scholar] [CrossRef]
- NIST Definition of Cloud Computing v15. Available online: http://www.nist.gov/itl/cloud/upload/cloud-def-v15.pdf (accessed on 10 November 2019).
- Durkee, D. Why cloud computing will never be free. Commun. ACM 2010, 53, 62–69. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, J. Parallel programming on cloud computing platforms. J. Converg. 2012, 3, 23–28. [Google Scholar]
- Walterbusch, M.; Martens, B.; Teuteberg, F. Evaluating cloud computing services from a total cost of ownership perspective. Manag. Res. Rev. 2013, 36, 613–638. [Google Scholar] [CrossRef]
- Osterwalder, A. The Business Model Ontology–A Proposition in a design science approach. Ph.D. Thesis, University of Lausanne, Lausanne, Switzerland, 2004. [Google Scholar]
- Samimi, P.; Patel, A. Review of pricing models for grid & cloud computing. In Proceedings of the 2011 IEEE Symposium on Computers & Informatics 2011, Kuala Lumpur, Malaysia, 20–23 March 2011; pp. 634–639. [Google Scholar]
- Ali, T.M.; Hany, H.A. Pricing models for cloud computing services, a survey. Int. J. Comput. Appl. Technol. Res. 2016, 5, 126–131. [Google Scholar]
- Jäätmaa, J. Financial Aspects of Cloud Computing Business Models. Master’s Thesis, Aalto University, Espoo, Finland, 2010. [Google Scholar]
- Chen, S.; Lee, H.; Moinzadeh, K. Pricing Schemes in Cloud Computing: Utilization-Based vs. Reservation-Based. Prod. Oper. Manag. 2019, 28, 82–102. [Google Scholar] [CrossRef]
- Available online: https://aws.amazon.com/ec2/pricing/on-demand (accessed on 10 November 2019).
- Available online: https://cloud.google.com/appengine/pricing (accessed on 10 November 2019).
- Lai, K. Markets are dead, long live markets. ACM SIGecom Exch. 2005, 5, 1–10. [Google Scholar] [CrossRef]
- Sharma, B.; Thulasiram, R.K.; Thulasiraman, P.; Garg, S.K.; Buyya, R. Pricing cloud compute commodities: A novel financial economic model. In Proceedings of the CCGRID’12, 2012 12th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Ottawa, ON, Canada, 13–16 May 2012; pp. 451–457. [Google Scholar]
- Macias, M.; Guitart, J. A genetic model for pricing in cloud computing markets. In Proceedings of the 2011 ACM Symposium on Applied Computing, TaiChung, Taiwan, 21–24 March 2011; pp. 113–118. [Google Scholar]
- Mihailescu, M.; Teo, Y.M. Dynamic resource pricing on federated clouds. In Proceedings of the 2010 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing, Melbourne, VIC, Australia, 17–20 May 2010. [Google Scholar] [CrossRef]
- Huang, J.; Kauffman, R.J.; Ma, D. Pricing strategy for cloud computing: A damaged services perspective. Decis. Support Syst. 2015, 78, 80–92. [Google Scholar] [CrossRef]
- Tirole, J. The Theory of Industrial Organization; The MIT Press: Cambridge, MA, USA; London, UK, 1995. [Google Scholar]
- Oi, W.Y. A Disneyland dilemma: Two-part tariffs for a Mickey Mouse monopoly. Q. J. Econ. 1971, 85, 77–96. [Google Scholar] [CrossRef]
- Schmalense, R. Monopolistic two-part pricing arrangements. Bell J. Econo. 1981, 12, 445–466. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).