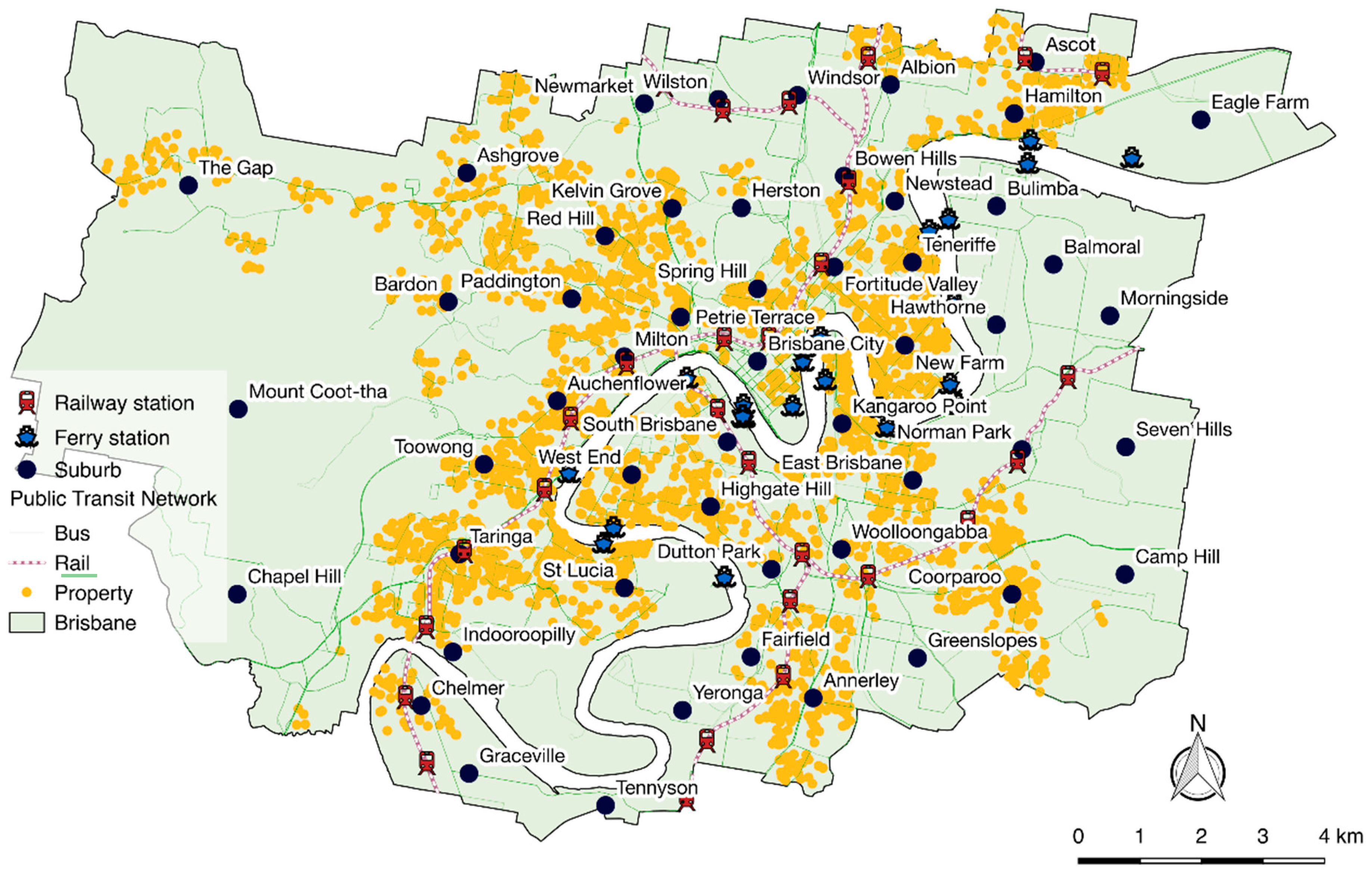
5.1. Global Models
To demonstrate that the property data exhibit a spatial process, the Breusch–Pagan (BP) test to detect heteroscedasticity and a Moran’s I test to detect spatial autocorrelation were carried out on the results of an OLS model. The tests indicated the presence of heteroscedasticity and spatial dependence in the OLS regression model (both tests have a
p-value of less than 0.001). Hence, to account for these violations of the OLS assumptions, it is appropriate to use the spatial lag model and the spatial error model to capture the effect of spatial dependence and use the GWR model to examine the effect of spatial heterogeneity in the estimates. The result of the GWR model is discussed in
Section 5.1. The Lagrange multiplier (LM) diagnostic tests for spatial dependence, see
Table 3, [
62,
63], further confirm the presence of spatial autocorrelation, as evidenced by the results of the LM error and robust LM error, and a missing spatially lagged dependent variable denoted by the result of the LM lag. The result of the LM robust lag is insignificant (
p-value greater than 0.05), so the null hypothesis of an omitted spatially lag dependent variable in the possible presence of spatial error autocorrelation can be rejected. Overall, the spatial error specification was better at addressing the problem since its statistical value was larger than the others. Alternatively, one could use the model selection method proposed by Elhorst [
64].
Interestingly, the travel time variability and delay variables were shown to be insignificant across all the regression approaches presented in this study (see
Table A1 in the
Appendix A), hence they were excluded. This may indicate that household long-term decisions, such as housing-related decisions, are affected by travel time, but not reliability indicators.
Variance inflation factors (VIF) were calculated to determine any multicollinearity that may be present in the models (see
Table A2 in the
Appendix A). The VIF result showed that there was no severe collinearity (VIF > 6) in any of the included independent variables.
As shown in
Table 4, both the spatial lag and the spatial error model provide better fit compared to the standard OLS model. The OLS model has an adjusted R-squared of 0.688 and AIC of −428.646, showing deficiencies compared to the higher adjusted R-squared values (0.693 and 0.71, respectively) and the smaller AIC values (−508.741 and −812.934, respectively) in the spatial lag and spatial error models. In the spatial lag model, the
-coefficient, which measures the strength of spatial dependence, is only mildly significant, in agreement with the modest improvement in the goodness of fit measures. However, in the spatial error model, the lambda coefficient is positive and highly significant, indicating spatially correlated errors. The Moran’s I test and the BP test indicate that only the spatial error model succeeded in eliminating the spatial autocorrelation, as shown by Moran’s I results (
p-value of 0.2047 for SE, <0.001 for SL, and <0.001 for OLS). This indicates that the problem is not directly from the spillover effect of neighbouring property values, but rather an unexplained correlated error of neighbouring properties. In addition, the BP test indicated that there was still spatial non-stationarity present in the spatial models. Overall, the coefficients of the independent variables among the three models are stable and show signs as expected from the literature. For the remainder of this section, the model interpretations are of the spatial error model, the model that best describes the relationships in the data.
All internal characteristics of the property are positively correlated to the property value and are highly significant. Their estimations also reveal that the property value is still largely governed by the internal characteristics of the property, despite the presence of neighbourhood characteristics and accessibility indicators in the models. This finding aligns well with other studies done on the same study area using hedonic modelling, see, for instance, [
12,
26]. The included socio-economic variables of the area also play a significant role in determining the premium on the property. The inclusion of neighbourhood traits in the models reveals that zones with a large proportion of high income individuals (Income), elderly residents (Age), household residential location mobility (Mobility), and population density (PopDen) experience premium property values. The proportion of unemployed persons (Unemp), which only includes people who are in the labour force, shows a positive correlation to property values. Generally, the unemployment rate in Brisbane is low, hence this may only reflect the number of young adults who still live in large family homes. In a similar study done by Tsai et al. [
26], to determine the value of ferry station proximity in Brisbane, they also found that the percentage of unemployed persons in each zone had a positive impact on property values.
The number of morning peak-hour trips (OMP) and the number of jobs accessible by public transport within a 30-min journey during morning peak hours (JobAccess) are found to have positive impacts on property values and are statistically significant. For every 1000 trips that took place during the morning peak-hour period, a property value can be affected by a premium of $14,389 AUD, or 2.46% of the mean property value. Furthermore, the 30-min job accessibility factor is shown to be statistically significant—every 1000 jobs positively influences the property value at the rate of 0.04%, translating to a monetary value of $234 AUD. For every kilometre away from the CBD, properties in the SA1 area experience a decrease in value, on average, of 4.25%, which is equivalent to $24,859 AUD of the mean property value. Although being within 400 m to a rail station confers a premium value of $12,517 AUD (at the mean property value), being within 800 m of a ferry station does not show any significant impact on property values. The insignificance of the evening peak (OEP) coefficient can be attributed to the preference for upscale homes in residential-oriented zones. The insignificance of transfers is not surprising since the interpretation is ambiguous, being either a measure of connectivity or related to difficulty in reaching a desired destination. Likewise, the number of trips to the CBD conflates several contradictory issues, such as the premium paid for living near the CBD and the inconvenience of travelling on transit to anywhere besides the CBD from more distant suburbs where prices are low. It should be noted that, since only a day’s worth of smart card data is available in this study, it is possible that there may be a censoring issue due to this limitation.
5.2. GWR Model
In a GWR model, the spatially-varying effects of the same variable can be logically explained by spatial heterogeneity in its relationship with the dependent variable. This differs from an OLS model, which assumes that a single model fits the entire study area. Hence, depending on other attributes, whether captured or omitted, the sign and scale of the GWR coefficients can change to reflect the spatial variation of the relationship.
Table 5 displays the ranges of significant parameters (
p-value less than 0.05) and goodness-of-fit values of the GWR model. The GWR model outperforms the three models discussed earlier by a substantially lower AIC (−1519.62) and higher adjusted R-squared of 0.741, after the degrees of freedom are taken into account. The Moran’s I test result indicates the residuals are spatially correlated, however, with only a subtle positive effect (Moran’s I statistics of 0.0017 and
p-value of 0.008). It should be noted that rectifying the spatial autocorrelation in residuals is not a direct goal of GWR.
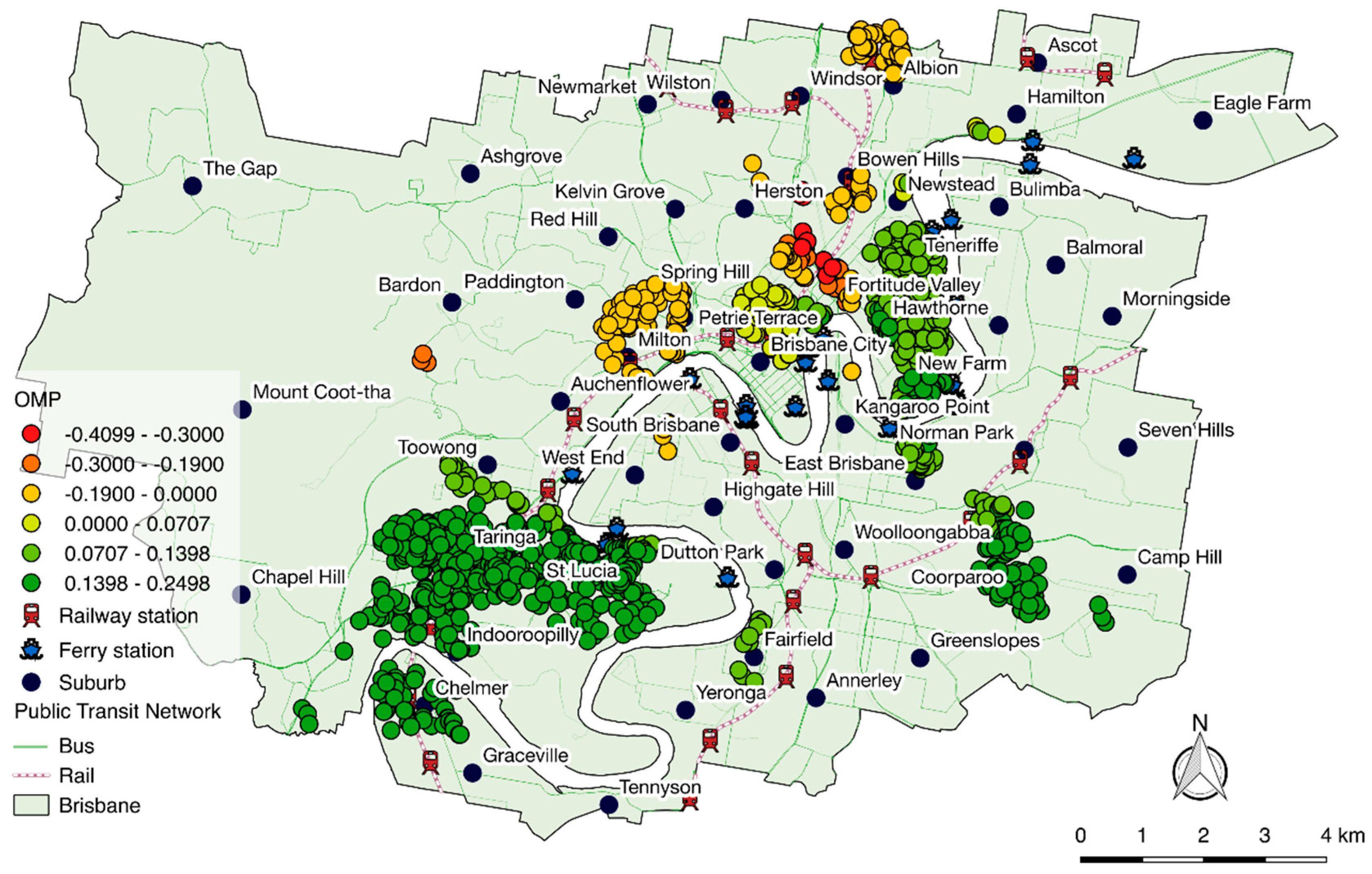
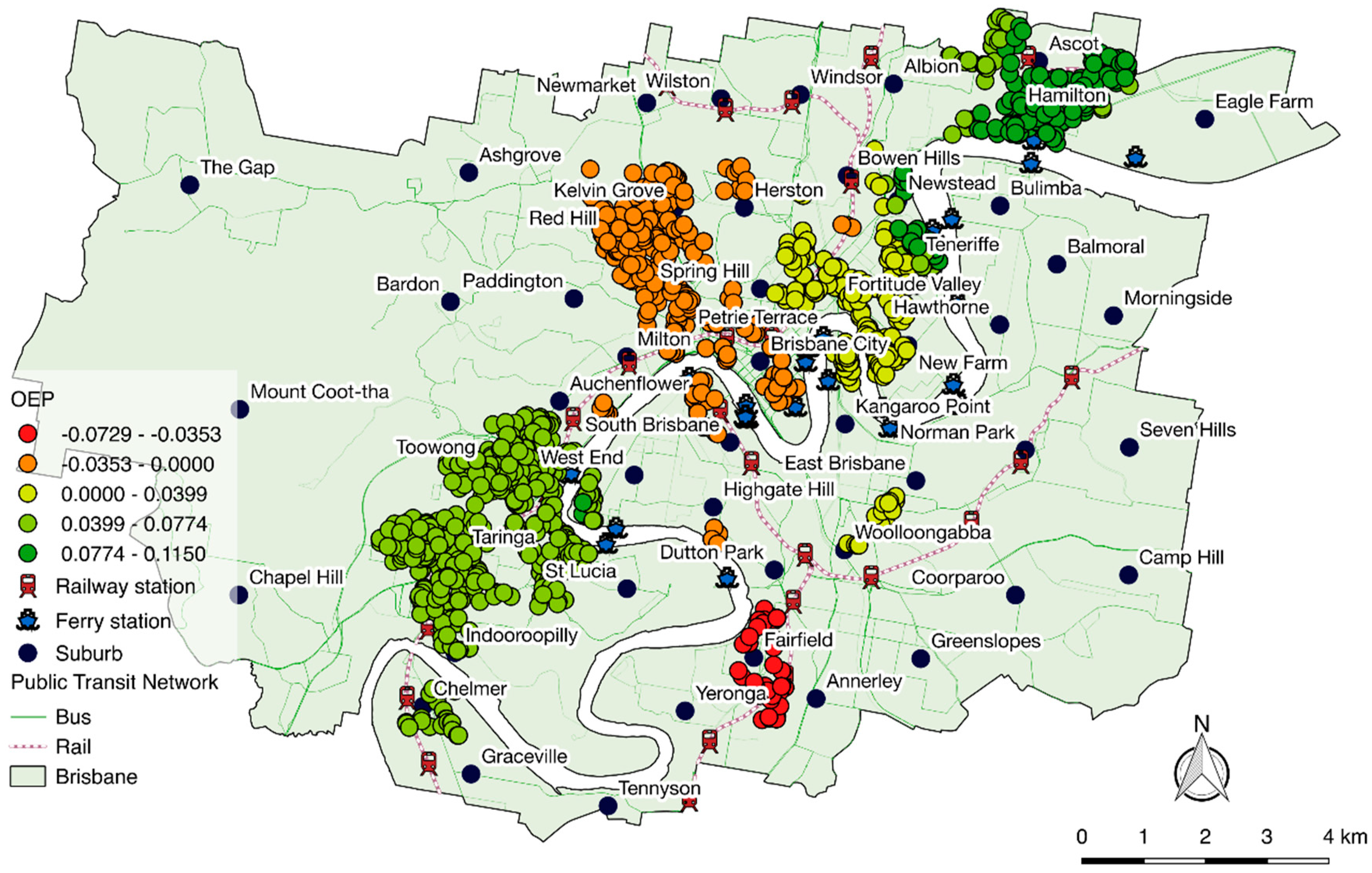
One of the many advantages of GWR is that coefficient estimations of the local model can be mapped (
Figure 4 for example). However, the focus of this paper is on transit accessibility variables—OMP, EMP, NTF, CBDTrips, Bus, JobAccess—hence, only the coefficients of these variables are shown. Note that all estimations shown in the following figures are found to be statistically significant at a
p-value lower than 0.05; those exceeding the
p-value threshold were omitted from the figures.
It is apparent from the maps in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9 that spatial variation exists in the estimates of the transit accessibility variables. In
Figure 4, the effect of morning peak trips, OMP, to property price varies from positive to negative across suburbs in contrast to the average effect found in the global estimate for the OLS model in
Table 4. The majority of properties are associated with a positive effect, with the premiums ranging from a 7% to 25% increase per 1000 morning trips, which is aligned with its global interpretation. It is also positive in the most attractive destination of the city, the CBD, where many transit commuters transfer. In south-western suburbs, low to medium density residential housing dominates and OMP positively influences property values. Areas near train stations are affected by the number of morning trips as they have a high level of accessibility to train stations where many bus passengers come to transfer, which is in accordance with other literature [
65]. It should be noted that both the south-western suburbs and the eastern suburbs, where a positive association between high property values and number of morning trips exist, have many young workers and students, which are the main demographics of public transport users in Brisbane [
66]. However, for those properties in the mixed-use areas around Paddington or Milton stations and in Fortitude Valley, Brisbane’s nightlife suburb, the number of morning trips has negative effects on property values.
Evening traffic is constituted mainly from non-work-related trips—including shopping, personal business, recreation, etc.—and returning home trips, as supported by the
How Queensland Travels report [
45]. In
Figure 5, the effect of the number of evening trips is shown. Most properties are affected by the number of evening trips occurring around them. Transit-accessible properties located near recreational areas with mixed-use in Chelmer, Taringa, and Toowong stations are positively affected by the number of departing trips in evening peak hours, up to 12% or
$64,339 AUD of the average property value for every 1000 trips. Hamilton, a suburb close to Brisbane Airport to the north-east of the CBD with low-medium residential buildings next to an industrial area just to the south of the airport, also experiences premiums. It is also well connected to public transport networks via a ferry station and two train stations. Similar results are present for suburbs with nightlife (Fortitude Valley), commercial, and recreational (Newstead) activities. The number of evening trips is the highest near job centres (evening commuters) or commercial and recreational activities (non-commute destinations)—areas with these attributes show positive relationship between land values and evening transit use. Interestingly, properties near the CBD show a negative relationship between the OEP variable and price. This suggests that congestion caused by the evening activities maybe a disincentivizing factor that pushes people away from living near the CBD area. Thus, it is reflected in decreased property values.
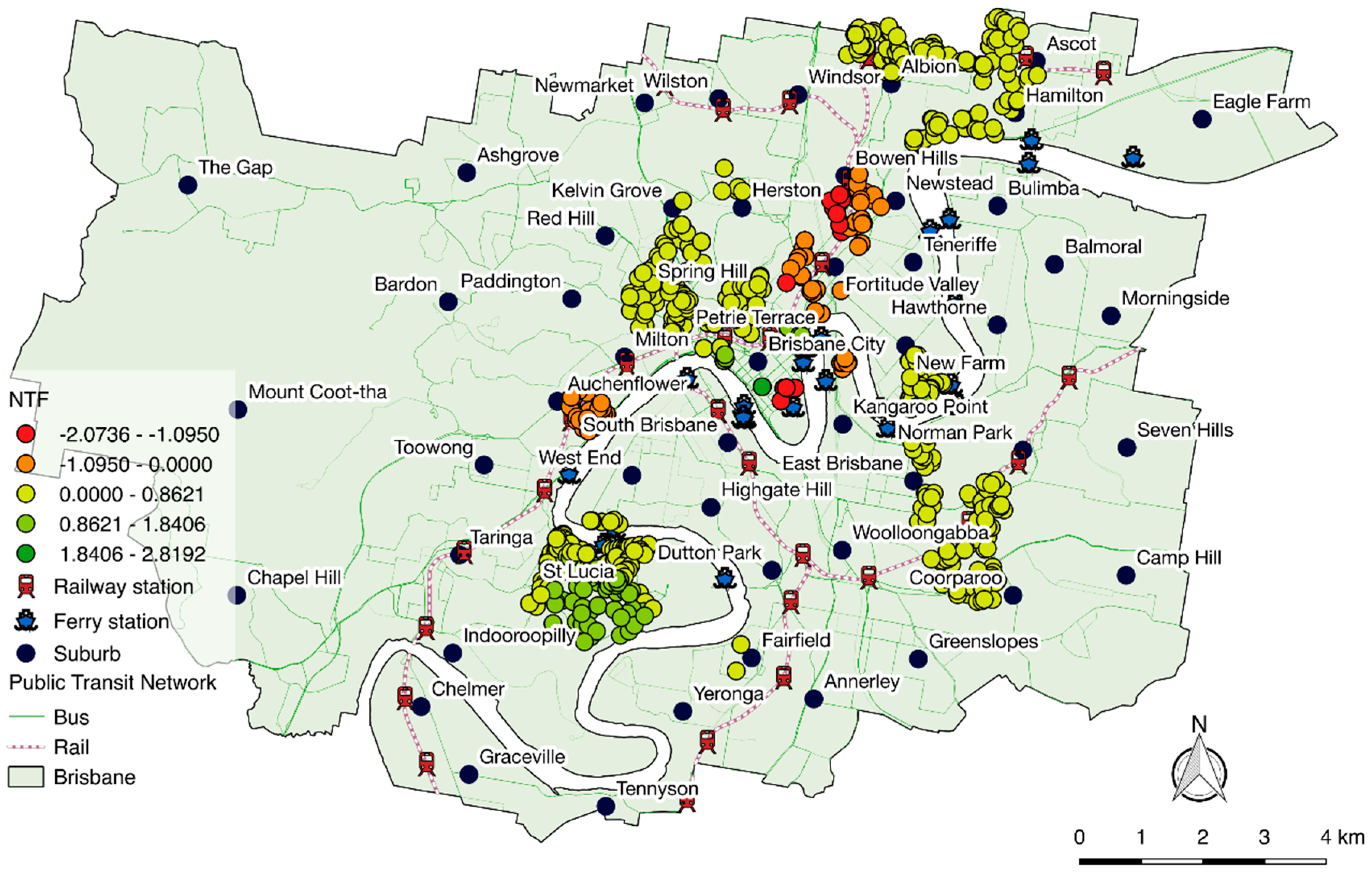
In
Figure 6, differences in property values in some areas can be seen to be associated with the fraction of trips having at least one transfer. The results for the transfer variable confirm the expected sign, with an average increase of 8% in property values for every 10% change in the transfer fraction variable. This can be translated into the dollar amount of approximately up to
$46,792 AUD of the mean property value. Clusters of negative associations near train stations indicate that transfers are not necessary in these highly-valued locations. Trips which consist of one or more transfers could indicate trip chaining as it is a very common travel behaviour for a trip to have more than one purpose [
67]. As discussed above, the proportion of trips with at least one transfer is ambiguous for accessibility. Several suburbs without train lines obtain premium values from the proportion of local departing passengers who made at least one transfer in their journeys. In these areas, feeder buses serve to connect residents to the rail network. While it would be interesting to see the effect of feeder buses on property values, it is difficult to distinguish between regular bus line and feeder buses from this data.
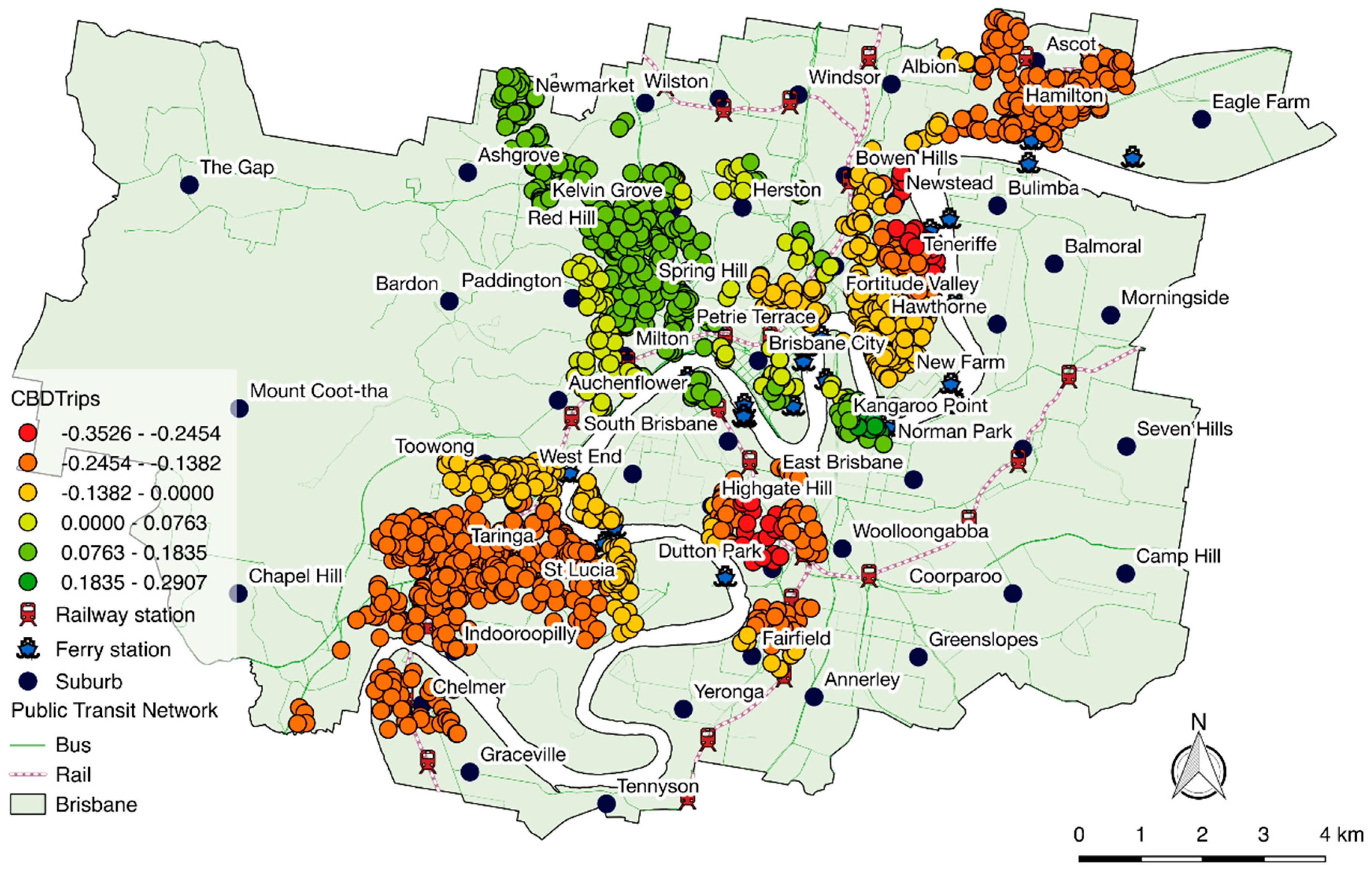
In
Figure 7, the relationship between the number of CBD trips via public transport and property values is shown. This variable can be thought of as a proxy to infer the degree of connectivity of a zone to the CBD and access to its employment opportunities and amenities. Negative associations between the number of trips headed to CBD and property values are observed for south and south-western suburbs, which reflects the importance of the University of Queensland, St. Lucia, as an employment and activity centre outside the CBD. Positive influences on property values due to the number of CBD trips occur mostly in the suburbs to the north-west of the CBD, where only bus services are available to public transport users. Perhaps this highlights that those areas that do not have access to the main rail network value CBD accessibility more than those well-off areas.
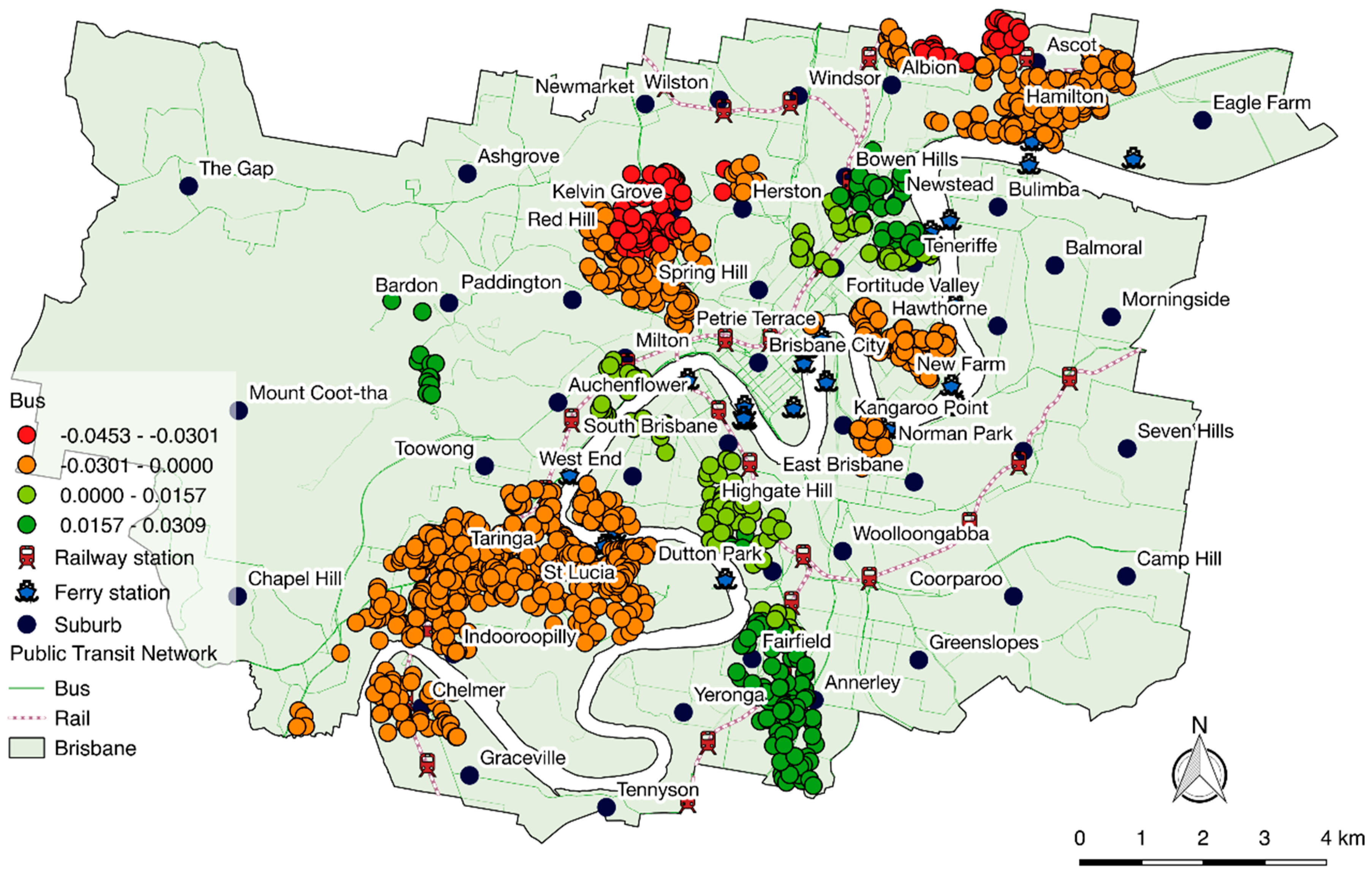
Figure 8 shows the number of bus stops within 400 m to the property and their impact on the value of properties across Brisbane. In total, 87% of public transport users in Brisbane will walk or cycle to the bus stop [
45]. While the global average effect of the variable shows a significant and positive relationship with the value of nearby properties which are conveniently located within a suitable walking or cycling range of bus transit nodes, the local results from GWR reveal a spatially mixed effect. Properties along the south-west rail line experience decreased property values, with the lowest at −4.5%, whereas properties on the south bank of the river experience premium values of up to 3% associated with more bus stops in the neighbourhood. Intuitively, a property that has access to many bus stops has positive effects (e.g., accessibility, attractiveness) and negative effects (e.g., noise, traffic-related air pollution, crime). Hence, this variable may need to be further investigated for its impacts affecting property values.
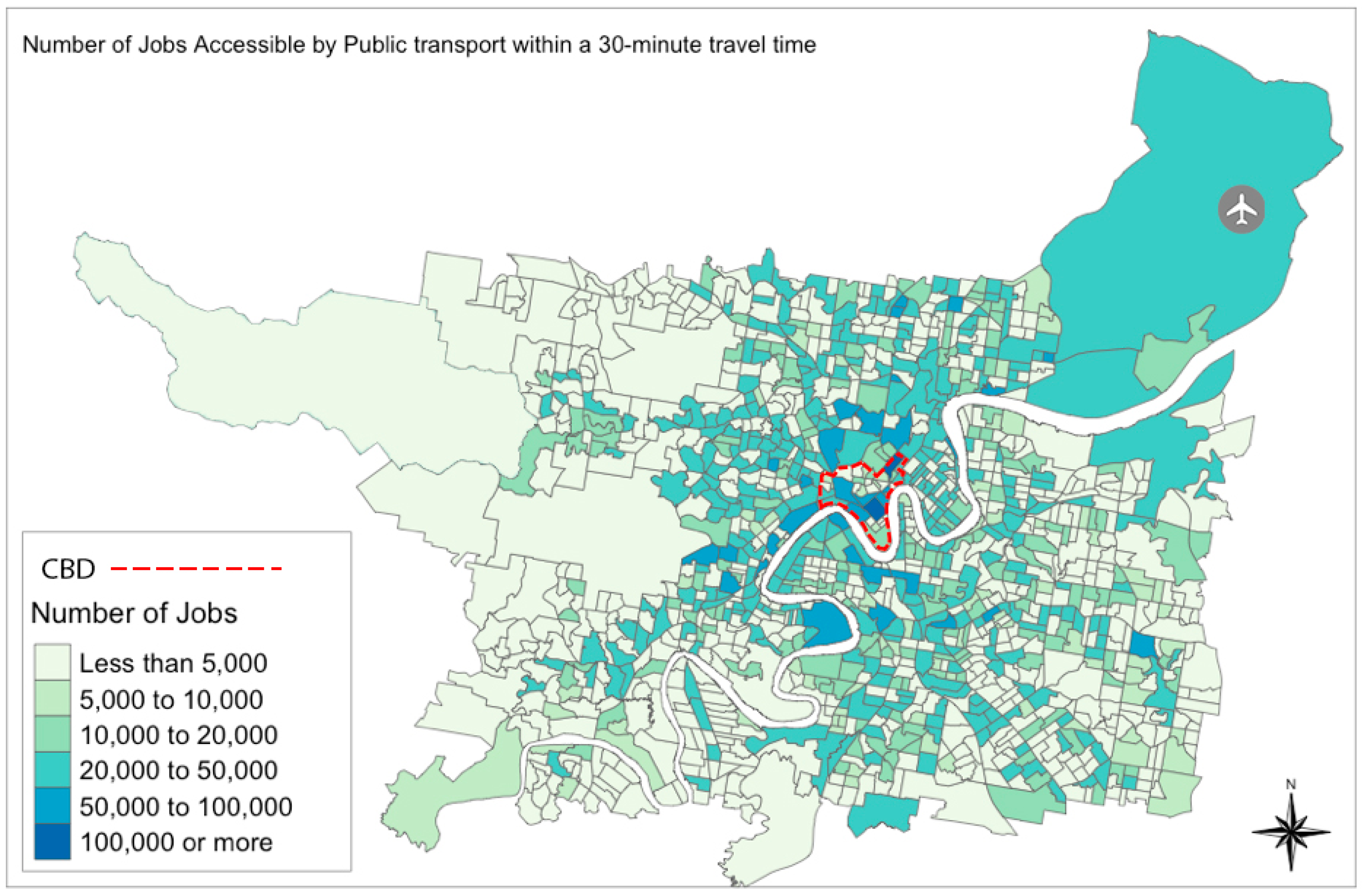
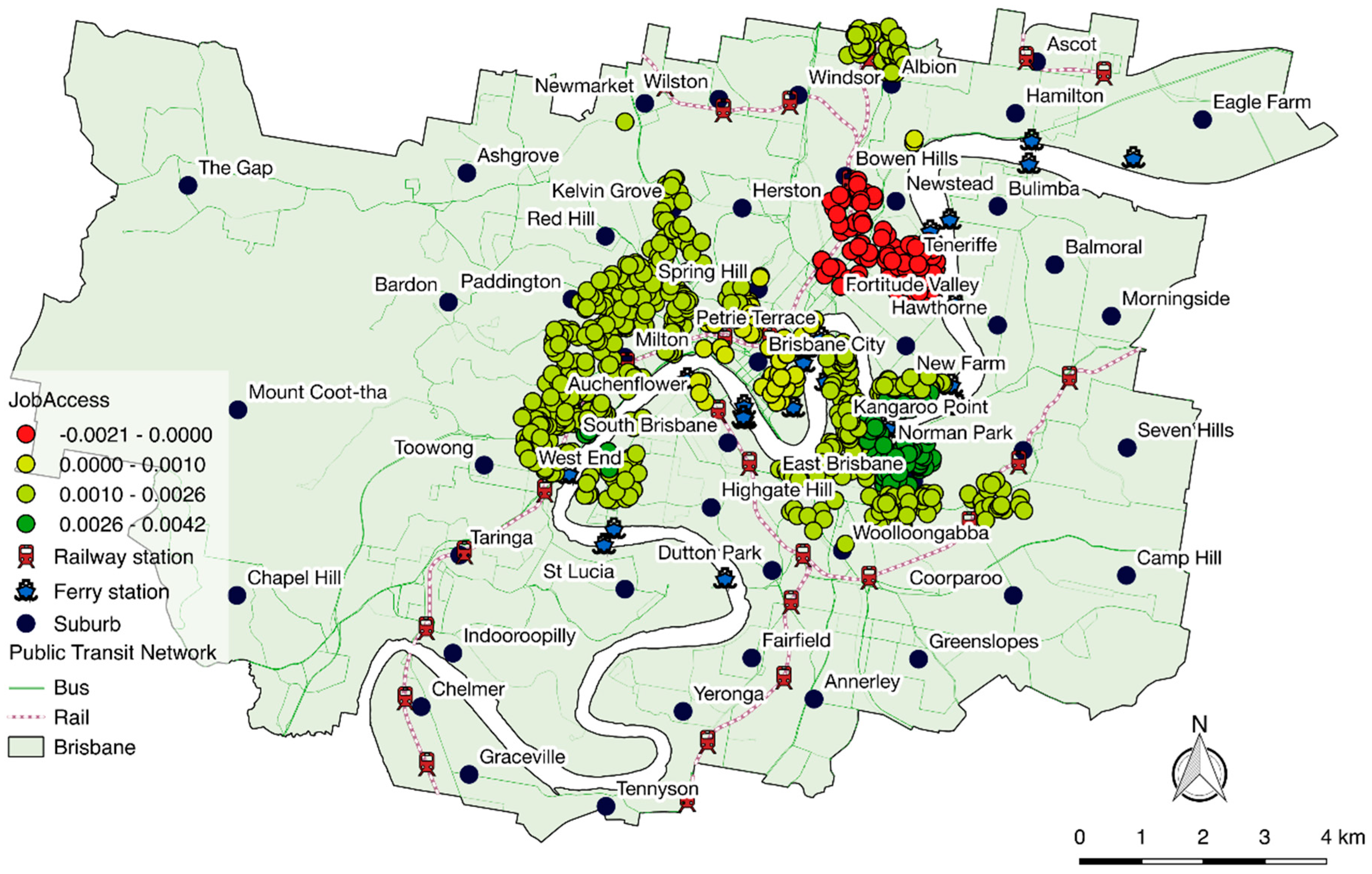
Finally, in
Figure 9, job accessibility is visualized. The number of jobs accessible by public transport services within 30 min of travel time shows a positive and significant impact on property values. A clear pattern can be observed in the figure, where most properties close to the CBD have high property values. The weak negative relationship observed in Newstead is driven, perhaps, by either low job accessibility or low property values. Living close to major bus routes, rail stations, and ferry stations affects the number of jobs accessible by public transport. Hence, those properties in close proximity to the major transport routes and the CBD show premiums in their values ranging from 0.1% to 0.42% per 1000 accessible jobs or
$585 to
$2457 in premium, at the mean property value.