Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems
Abstract
1. Introduction
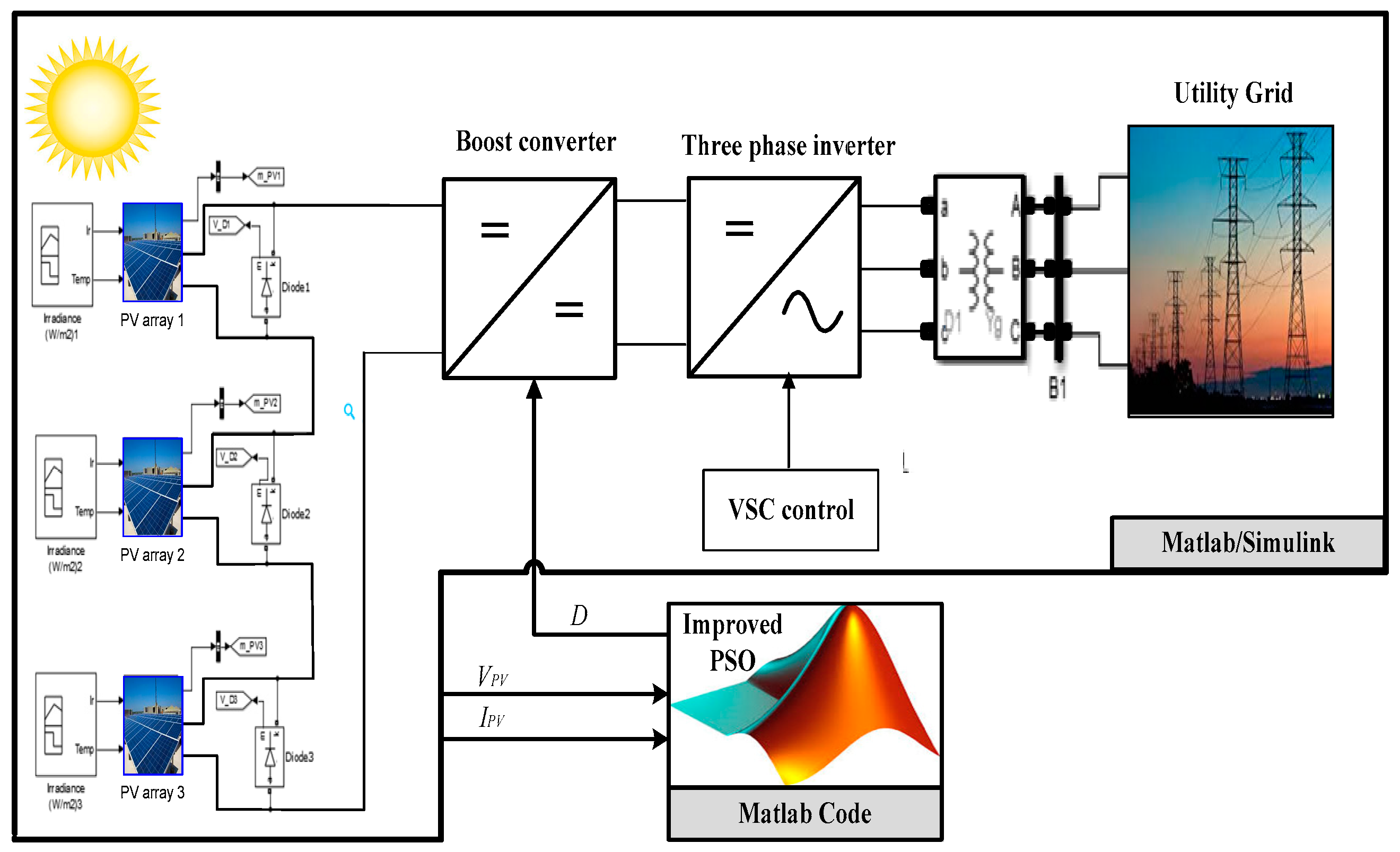
2. Description of the Partially Shaded Photovoltaic System
3. Global Peak Extraction Using Particle Swarm Optimization Technique
4. Proposed Particle Swarm Optimization Techniques
4.1. State of the Art PSO Methodology without Reinitialization (Case-1)
- Step 1:
- Initialize the PSO parameters (ω, c1, c2, and c3) and send the initial duty cycles sequentially to the partially shaded PV system (objective function) and gather the associated powers values.
- Step 2:
- Update the particles’ position and velocity ( and ) using Equations (1) and (5), respectively, then obtain the new duty cycles values of the converter.
- Step 3:
- Send new duty cycles (particles’ position) to the partially shaded PV system and gather the associated powers values.
- Step 4:
- Assess Pbest,i, Gbest and their related particles’ positions, then; go back to Step 2.
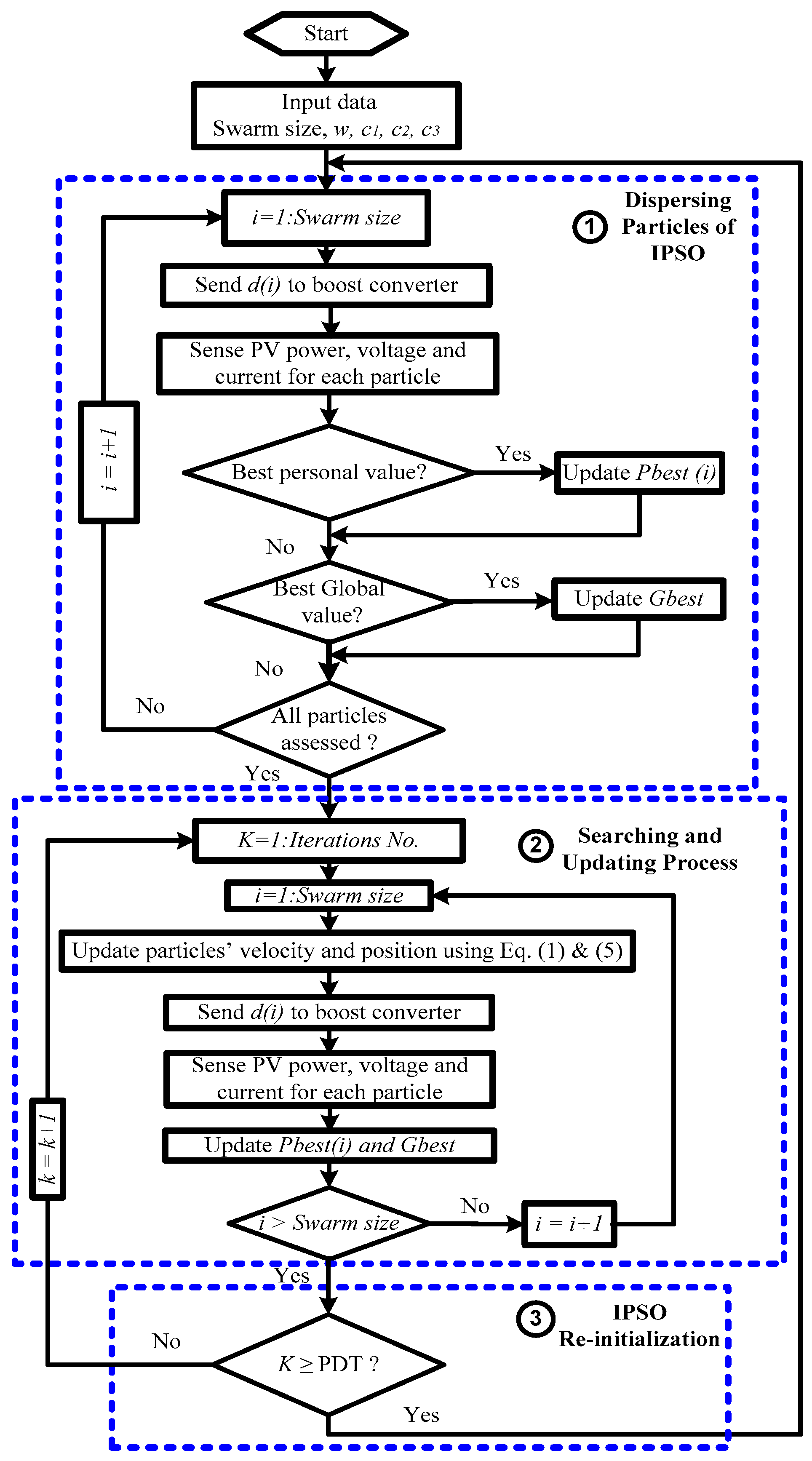
4.2. Improved PSO Reinitialization upon Predefined Time (Case-2)
- Step 1:
- Initialize the improved PSO parameters (ω, c1, c2, and c3), send the initial duty cycles sequentially to the partially shaded PV system (objective function), and gather the associated powers values.
- Step 2:
- Step 2: Update the particles’ position and velocity ( and ) using Equations (1) and (5), respectively, then obtain the new duty cycles values of the converter.
- Step 3:
- Send the new duty cycles (particles’ position) to the partially shaded PV system and gather the associated powers values.
- Step 4:
- Assess Pbest,i, Gbest and their related particle’s position, then check if the time is less than PDT (iteration < 100), go back to Step 2 otherwise go to Step 1.
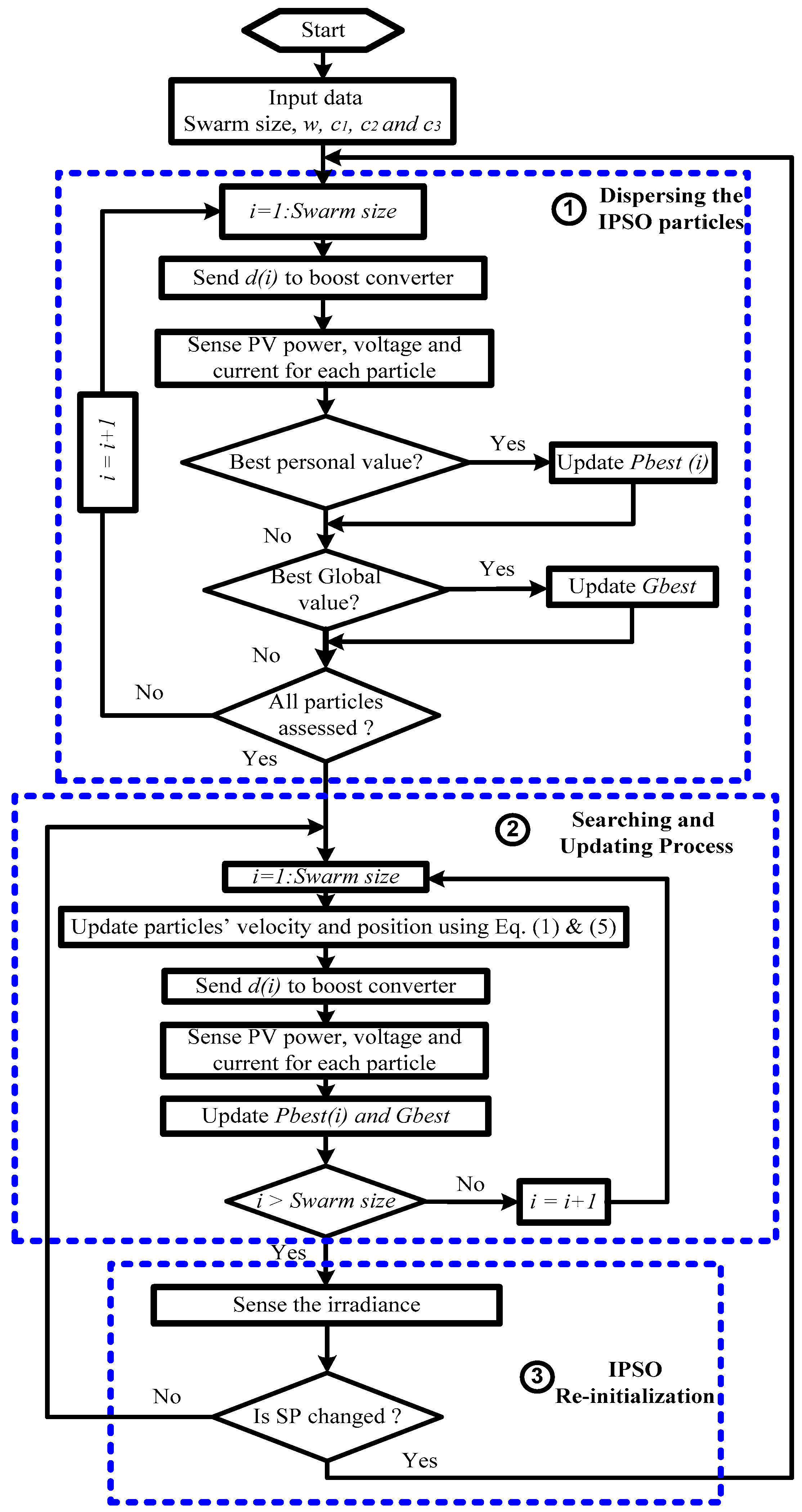
4.3. Improved PSO Reinitialization upon Shading Pattern Change (Case-3)
- Step 1:
- Initialize the improved PSO parameters (ω, c1, c2, and c3), send the initial duty cycles sequentially to the partially shaded PV system (objective function), and gather the associated powers values.
- Step 2:
- Update the particles’ position and velocity ( and ) using Equations (1) and (5), respectively, then obtain the new duty cycles values of the DC–DC converter.
- Step 3:
- Send the new duty cycles (particles’ position) to the partially shaded PV system and gather the associated powers values.
- Step 4:
- Assess Pbest,i, Gbest and their related particle’s position, then check if the SP of the PV system is not changed, go again to Step 2 otherwise go to Step 1.
5. Simulation Results and Discussion
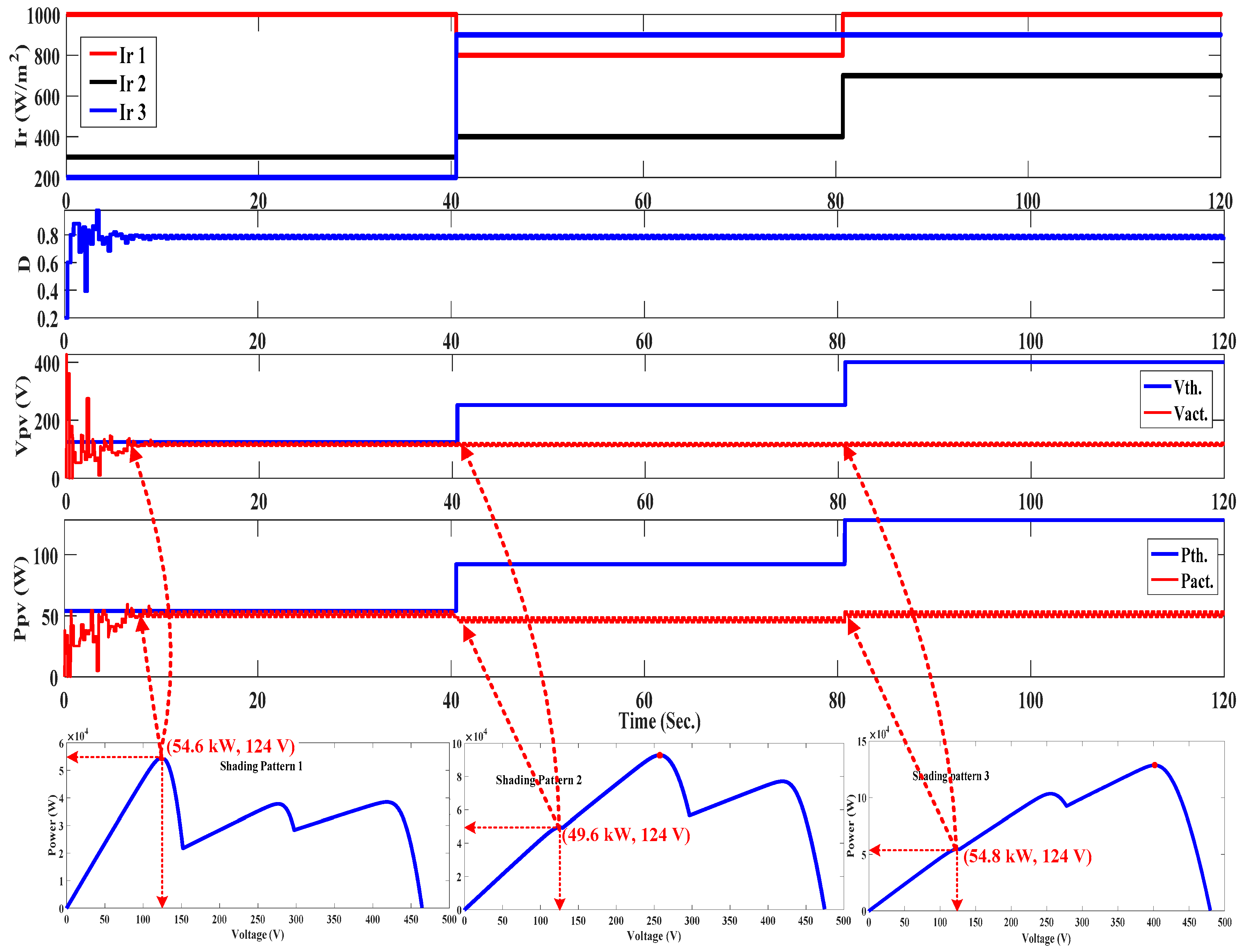
5.1. Conventional PSO without Reinitialization (Case-1)
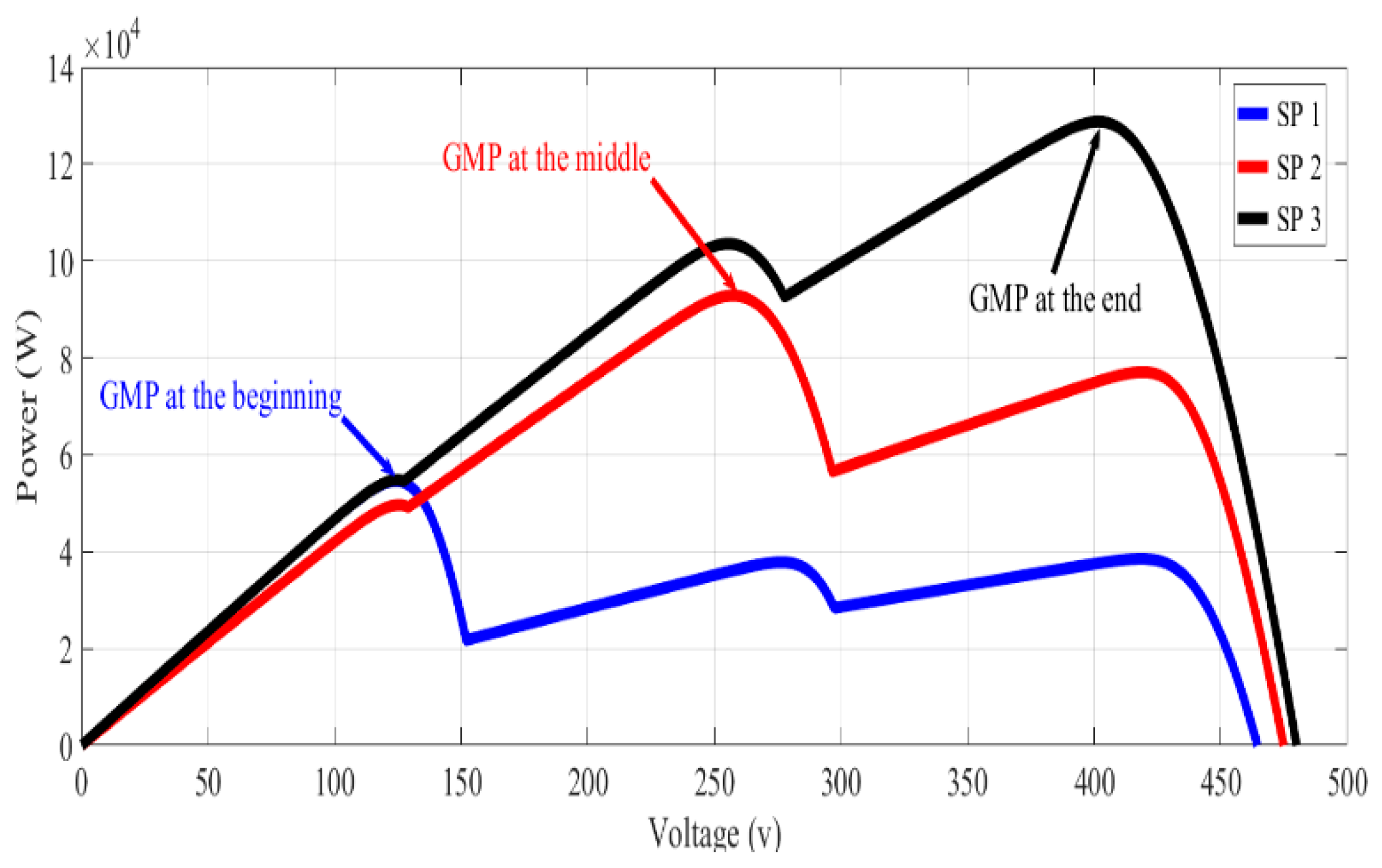
- From 0–40 s: PSO searches for the first GMP in a certain searching area and succeeds in catching the first GMP power (54.6 kW) for SP1 as illustrated in Figure 5.
- From 40–80 s: The partial shading pattern changed to SP2; hence, the GMP value (92.8 kW) and position (2nd GMP peak) also changed. Nevertheless, PSO cannot catch the new GMP power and remains in the first GMP searching area and its Gbest (d = 0.785). Therefore, it tracks the nearest peak in the same region of the first GMP (LMP equals to 49.6 kW); however, the current GMP is 92.8 kW for SP2. The reason is that the PSO reinitialization is not executed upon the SP change.
- From 80–120 s: In a similar manner, the partial shading pattern is changed (SP3); hence, the GMP value (128.8 kW) and position (3rd GMP peak) also changes. Nevertheless, PSO cannot catch the new GMP and remains in the first GMP searching area and its Gbest (d = 0.785). Therefore, it tracks the nearest peak at the same region of the first GMP (LMP equals to 54.8 kW); however, the current GMP is 128.8 kW for SP3. The reason is that the PSO reinitialization is not executed upon the SP change.
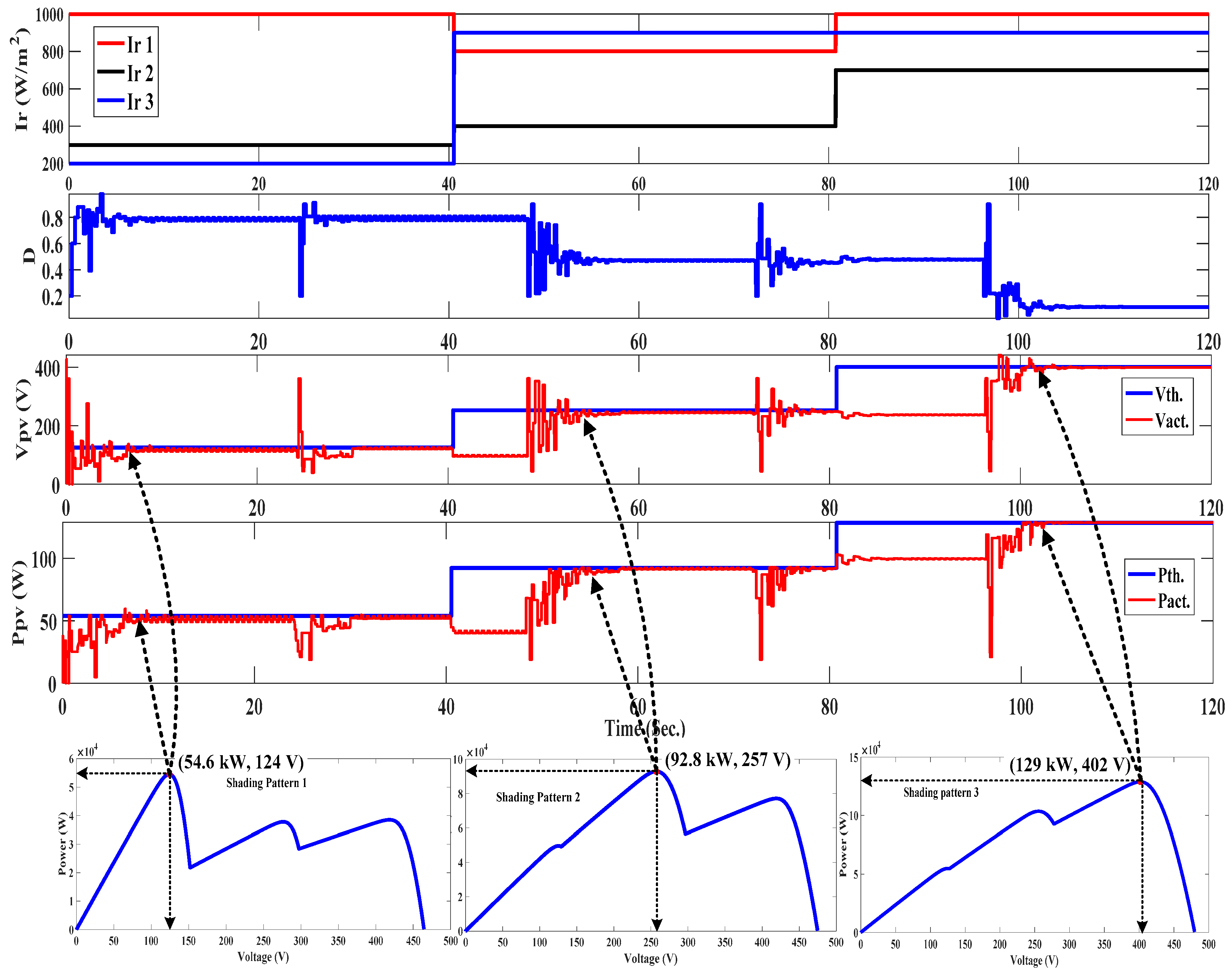
5.2. Improved PSO Reinitialization Based on Predefined Time (Case-2)
- From 0–24 s: The improved PSO caught the first GMP power (54.6 kW and 124 V) for SP1 as presented in Figure 6.
- From 24–40 s: The improved PSO reinitialization is executed, but the partial shading pattern has not changed; therefore, the system works again after reinitialization at the same situation (54.6 kW and 124 V). This reinitialization methodology has unwanted reinitialization that may disturb the PV system. Therefore, the reinitialization methodology upon PDT is no better in partial shading conditions.
- From 40–48 s: The partial shading pattern changes to SP2; hence, the GMP value and position also changes, but the improved PSO will not catch it until improved PSO reinitialization is executed. It remains at the nearest peak in the same region of the first GMP (LMP equals to 49.6 kW) until the improved PSO initialization is executed. This reinitialization has a delayed response to follow the new GMP of the new SP. Therefore, the reinitialization methodology upon PDT is no better in partial shading conditions.
- From 48–72 s: The particles are dispersed at the beginning of this period and the particles will catch the new GMP power (92.8 kW and 257 V) at d = 0.43.
- From 72–80 s: The improved PSO is reinitialized at the beginning of this period, but the SP has not changed; hence, the system will go again to the previous GMP point (92.8 kW and 257 V). Unwanted reinitialization occurs, which may disturb the PV system. Therefore, the reinitialization methodology upon PDT is no better in partial shading conditions.
- From 80–96 s: The partial shading pattern changes (SP3); hence, the GMP value and position also changes, but the improved PSO will not catch it until the improved PSO reinitialization is executed. It remains at the nearest peak in the same region of the second GMP (LMP equals to 100 kW) until PSO reinitialization is executed. A delayed response occurs in order to follow the new GMP of the new SP. Therefore, the reinitialization methodology upon PDT is no better in partial shading conditions.
- From 96 to 120 s: The improved PSO is reinitialized at the beginning of this period and the particles find the new GMP (129 kW at 402 V) for SP3.
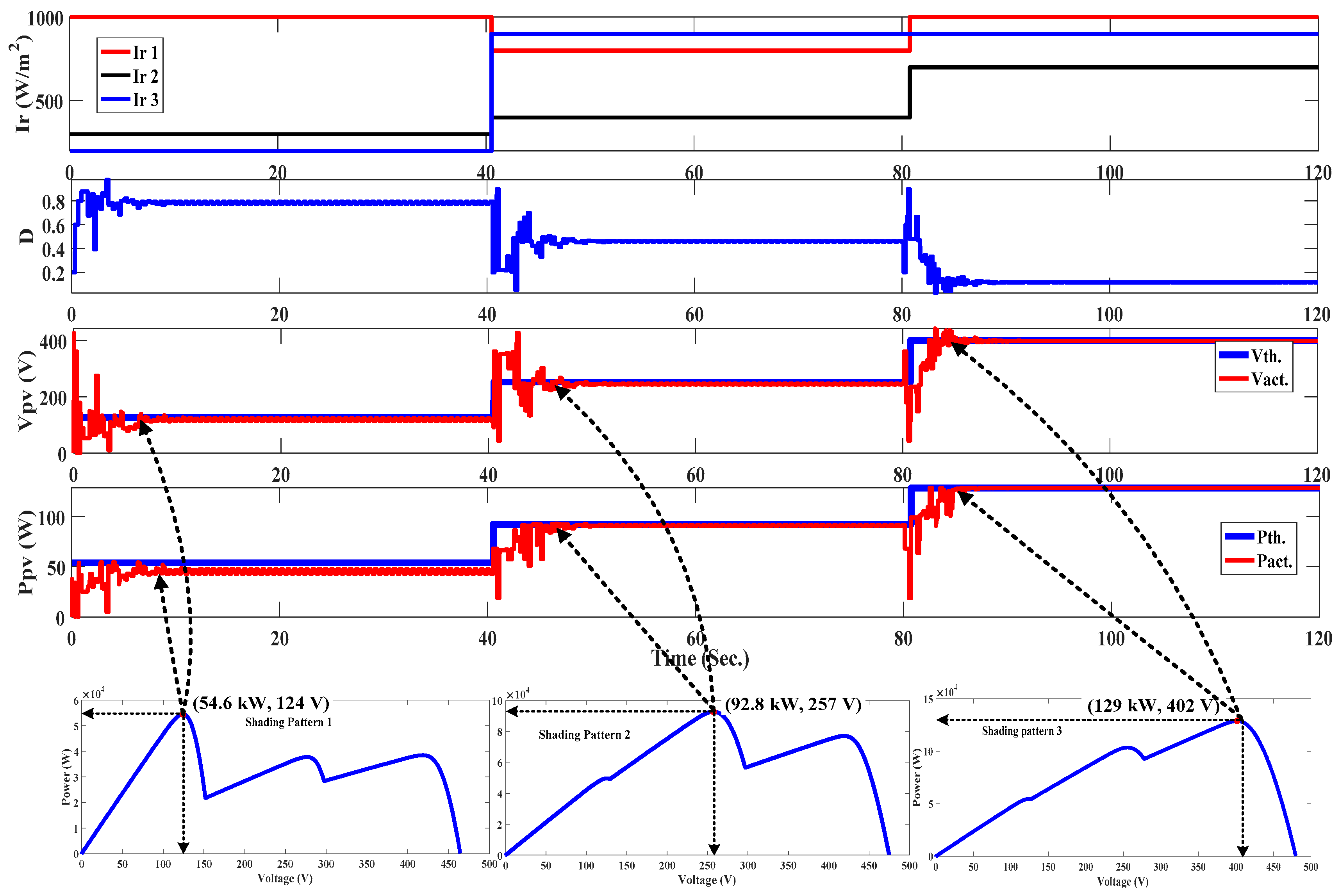
5.3. Improved PSO Reinitialization Upon the SP Change (Case-3)
- From 0–40 s: Improved PSO has successfully caught the first GMP power (54.6 kW and 124 V) for SP1 as shown in Figure 7.
- From 40–80 s: The partial shading pattern changed to SP2, both the GMP value (92.8 kW) and its position also changed (2nd GMP peak). PSO reinitialization is executed upon the SP change at t = 40 s. Improved PSO succeeded in finding the second GMP peak (92.8 kW) efficiently and accurately as shown in Figure 7.
- From 80–120 s: In a similar manner, the partial shading pattern changed to SP3. Reinitialization is executed upon the partial shading pattern change at t = 80 s. The improved PSO succeeded in finding the third GMP peak (128.8 kW) efficiently and accurately, as shown in Figure 7. The performance efficiency for this PV system is 100%, which reflects the effective performance of improved PSO reinitialization upon the partial shading pattern change. This reinitialization methodology solved the two shortcomings of the previous reinitialization methodology (PDT); unwanted reinitialization and delayed response.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| GMP | Global maximum power; |
| PV | Photovoltaic; |
| SP | Shading Pattern; |
| PSO | Particle swarm optimization; |
| PSC | Partial shading condition |
| Pbest,i | Personal best solution; |
| Gbest | Global best of Pbest,i; |
| xik | Position vector; |
| vik | Velocity vector; |
| ω | Inertia weight; |
| c1 and c2 | Acceleration coefficients; |
| r1, r2 | Random numbers; |
| MPPT | Maximum Power Point Tracker; |
| FPA | Flower pollination algorithm; |
| FA | Firefly algorithm; |
| CSO | Cuckoo search optimization; |
| ABC | Ant bee colony; |
References
- Farh, H.; Othman, F.; Eltamaly, A.M.; Al-Saud, M. Maximum Power Extraction from a Partially Shaded PV System Using an Interleaved Boost Converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef]
- Farh, H.M.; Othman, M.F.; Eltamaly, A.M. Maximum power extraction from grid-connected PV system. In Proceedings of the 2017 Saudi Arabia Smart Grid (SASG), Jeddah, Saudi Arabia, 12–14 December 2017. [Google Scholar]
- Eltamaly, A.M.; Farh, H.M.; Othman, M.F. A novel evaluation index for the photovoltaic maximum power point tracker techniques. Sol. Energy 2018, 174, 940–956. [Google Scholar] [CrossRef]
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of smart maximum power point tracker under partial shading conditions of photovoltaic systems. J. Renew. Sustain. Energy 2015, 7, 043141. [Google Scholar]
- Teo, J.; Tan, R.H.G.; Mok, V.H.; Ramachandaramurthy, V. Impact of Partial Shading on the PV Characteristics and the Maximum Power of a Photovoltaic String. Energies 2018, 11, 1860. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2019, 177, 306–316. [Google Scholar]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. A new robust, mutated and fast tracking LPSO method for solar PV maximum power point tracking under partial shaded conditions. Appl. Energy 2017, 201, 45–59. [Google Scholar]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)–based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Fathy, A. Reliable and efficient approach for mitigating the shading effect on photovoltaic module based on Modified Artificial Bee Colony algorithm. Renew. Energy 2015, 81, 78–88. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. A new global maximum power point tracking technique for solar photovoltaic (PV) system under partial shading conditions (PSC). Energy 2017, 118, 512–525. [Google Scholar]
- Chao, K.-H.; Lin, Y.-S.; Lai, U.-D. Improved particle swarm optimization for maximum power point tracking in photovoltaic module arrays. Appl. Energy 2015, 158, 609–618. [Google Scholar] [CrossRef]
- Rajasekar, N.; Vysakh, M.; Vilas, H.; Mohammed, T.S.; Muralidhar, A.K.; Paul, D.; Jacob, B.; Balasubramanian, K.; Babu, T.S. Application of modified particle swarm optimization for maximum power point tracking under partial shading condition. Energy Procedia 2014, 61, 2633–2639. [Google Scholar] [CrossRef]
- Babu, T.S.; Rajasekar, N.; Sangeetha, K. Modified particle swarm optimization technique based maximum power point tracking for uniform and under partial shading condition. Appl. Soft Comput. 2015, 34, 613–624. [Google Scholar] [CrossRef]
- Dileep, G.; Singh, S. An improved particle swarm optimization based maximum power point tracking algorithm for PV system operating under partial shading conditions. Sol. Energy 2017, 158, 1006–1015. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Chung, N.-Y.; Chao, K.-H.; Kao, J.-J. Smart Global Maximum Power Point Tracking Controller of Photovoltaic Module Arrays. Energies 2018, 11, 567. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Shamsudin, A.; Amjad, M. A direct control based maximum power point tracking method for photovoltaic system under partial shading conditions using particle swarm optimization algorithm. Appl. Energy 2012, 99, 414–422. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Peddapati, S.; Palani, S. MPPT of PV systems under partial shaded conditions through a colony of flashing fireflies. IEEE Trans. Energy Convers. 2014, 29, 463–472. [Google Scholar]
- Liu, Y.-H.; Salam, Z.; Shamsudin, A.; Amjad, M. A particle swarm optimization-based maximum power point tracking algorithm for PV systems operating under partially shaded conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Soufyane Benyoucef, A.; Chouder, A.; Kar, K.; Silvestre, S.; Aitsahed, O. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Sankar, P.; Nayak, P.S.R.; Simon, S.P.; Palani, S. Enhanced energy output from a PV system under partial shaded conditions through artificial bee colony. IEEE Trans. Sustain. Energy 2015, 6, 198–209. [Google Scholar] [CrossRef]
- Mirhassani, S.M. An improved particle swarm optimization based maximum power point tracking strategy with variable sampling time. Int. J. Electr. Power Energy Syst. 2015, 64, 761–770. [Google Scholar]
- Farh, H.M.; Eltamaly, A.M.; Othman, M.F. Hybrid PSO-FLC for dynamic global peak extraction of the partially shaded photovoltaic system. PLoS ONE. 2018, 13, e0206171. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of MPPT Techniques of Photovoltaic Systems Under Normal and Partial Shading Conditions. In Advances in Renew. Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 115–161. [Google Scholar]
- Titri, S.; Larbes, C.; Toumi, K.Y.; Benatchba, K. A new MPPT controller based on the Ant colony optimization algorithm for Photovoltaic systems under partial shading conditions. Appl. Soft Comput. 2017, 58, 465–479. [Google Scholar] [CrossRef]
- Soltani, I.; Sarvi, M.; Marefatjou, H. An intelligent, fast and robust maximum power point tracking for proton exchange membrane fuel cell. World Appl. Programm. 2013, 3, 264–281. [Google Scholar]
| SP No. Cases | SP#1 | SP#2 | SP#3 | |
|---|---|---|---|---|
| Irradiance (W/m2) | (1000, 300, 200) | (800, 400, 900) | (1000,700, 900) | |
| GMP value (kW) | 54.6 | 92.8 | 128.8 | |
| GMP place | 1st | 2nd | 3rd | |
| VPV at GMP (V) | 124 | 257 | 402 | |
| PSO without reinitialization | PPV (kW) | 54.6 | 49.6 | 54.8 |
| VPV (V) | 124 | 124 | 124 | |
| PSO Efficiency | 100% | 53% | 43% | |
| Improved PSO reinitialization upon PDT | PPV (kW) | 54.6 | 49.6–92.8 | 54.8–128.8 |
| VPV (V) | 124 | 124–257 | 257–402 | |
| Improved PSO Efficiency | 100% | 53% → 100% | 43% → 100% | |
| Improved PSO reinitialization upon SP change | PPV (kW) | 54.6 | 92.8 | 128.8 |
| VPV (V) | 124 | 257 | 402 | |
| Improved PSO Efficiency | 100% | 100% | 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltamaly, A.M.; M. H. Farh, H.; S. Al Saud, M. Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability 2019, 11, 2091. https://doi.org/10.3390/su11072091
Eltamaly AM, M. H. Farh H, S. Al Saud M. Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability. 2019; 11(7):2091. https://doi.org/10.3390/su11072091
Chicago/Turabian StyleEltamaly, Ali M., Hassan M. H. Farh, and Mamdooh S. Al Saud. 2019. "Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems" Sustainability 11, no. 7: 2091. https://doi.org/10.3390/su11072091
APA StyleEltamaly, A. M., M. H. Farh, H., & S. Al Saud, M. (2019). Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability, 11(7), 2091. https://doi.org/10.3390/su11072091






