Sustainable Financing for Sustainable Development: Agent-Based Modeling of Alternative Financing Models for Clean Energy Investments
Abstract
:1. Introduction
2. Literature Review
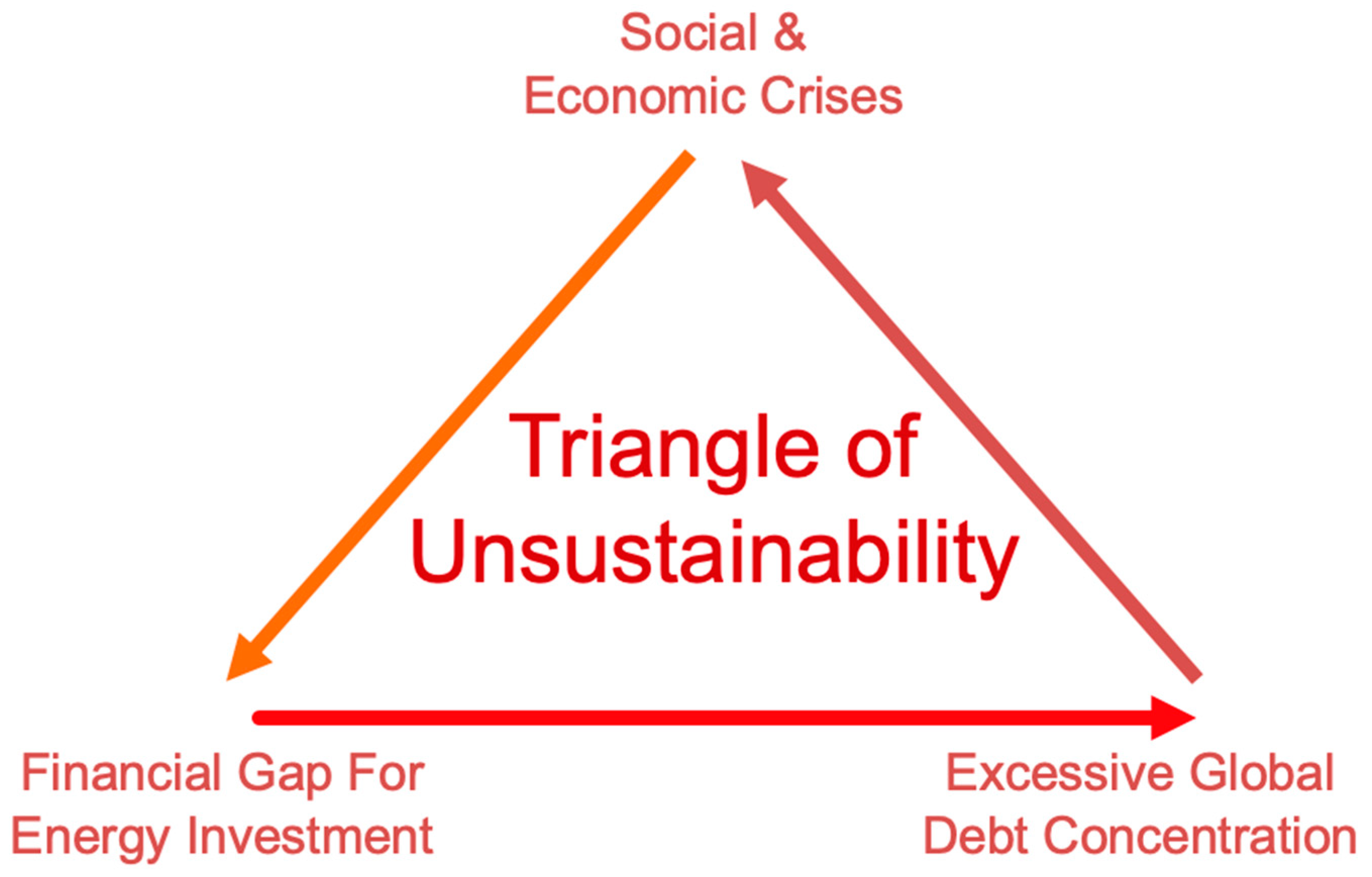
2.1. Sustainable Development and Global Debt Concentration
2.2. Wealth Inequality and Social Inequity
2.3. Financial Localization
2.4. Agent-Based Modeling
3. Methodology
3.1. Platform and Framework Description
- The individuals were prioritized to invest in a power plant as much as their savings.
- There were four types of shareholders that included individuals (IN), large enterprises (LE), a Bank, and an equity-based financial intermediary (EBIN). The shareholders were listed in a given order to participate in a power plant investment depending on their savings. For example, assume that the potential shareholders were listed, in order, as individuals and large enterprises. If the individuals did not have enough money for the entire investment, the remaining amount was provided by the large enterprises.
- The shareholders had an upper bound to join in the investment. This upper bound was usually one hundred percent for individuals. In other words, the individuals could invest up to 100% of the total investment of a power plant.
- The equity-based financial intermediary (EBIN) was designed to be a self-sufficient financial intermediary up to a certain limit according to the upper bound.
3.2. Agent-Based Model
3.2.1. Power Plant (PP) Agent-Type
3.2.2. Depositor/Investor (DI) Agent-Type
3.2.3. Loan Agent-Type
3.2.4. Bank Agent-Type
3.2.5. Equity-Based Financial Instrument (EBIS) Agent-Type
3.2.6. Equity-Based-Intermediary (EBIN) Agent-Type
3.2.7. Government Agent-type
3.2.8. Environment
Functions of the Environment
3.3. Model Implementation: A Solar Farm
Policy Scenarios
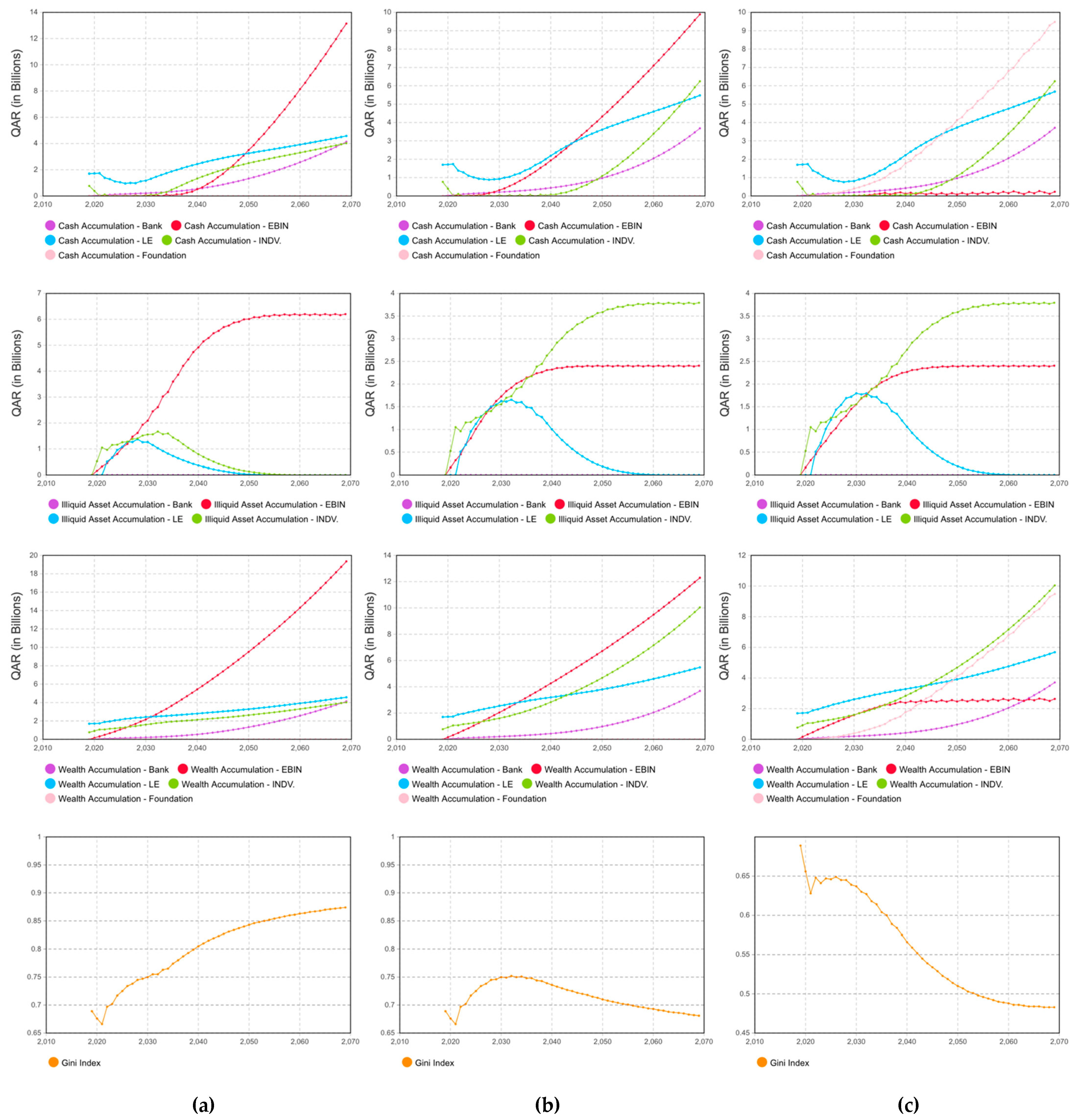
4. Results and Discussion
5. Key Findings
6. Future Work
7. Conclusions
- The literature focuses on alternative financing models to maintain debt sustainability, but there is a gap for studying wealth inequality and accumulation while reducing the debt. This study investigates sustainable financing models by not only reducing debt-burden on society, but also preventing social stress and redistributing the wealth more equitably.
- The literature advocates monetary reforms by establishing many small, local, not-for-profit financial intermediaries. However, there is a gap in the literature on timewise planning about when such financial intermediaries should be established. In this regard, this study investigates potential timelines for creating a bank or another type of financial intermediaries.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Functions of Loan Agent
Appendix B. Functions of Bank Agent
Appendix C. Functions of the EBIS Agent
Appendix D. Functions of the EBIN Agent
Appendix E. Variables and Constants of the Environment
References
- Samouilidis, J.-E.; Mitropoulos, C.S. Energy investment and economic growth. Energy Econ. 1983, 5, 237–246. [Google Scholar] [CrossRef]
- Munnell, A.H. Policy Watch: Infrastructure Investment and Economic Growth. J. Econ. Perspect. 1992, 6, 189–198. [Google Scholar] [CrossRef]
- IEA. World Energy Investment 2018. Available online: https://webstore.iea.org/world-energy-investment-2018 (accessed on 30 March 2019).
- OECD/IEA. IRENA Perspectives for the Energy Transition: Investment Needs for a Low-Carbon Energy System. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Mar/Perspectives_for_the_Energy_Transition_2017.pdf (accessed on 30 March 2019).
- UNFCCC Paris agreement. FCCC/CP/2015/L.9/Rev1. Available online: http://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf (accessed on 30 March 2019).
- Ari, I.; Koc, M. Sustainable financing for sustainable development: Understanding the interrelations between public investment and sovereign debt. Sustainability 2018, 10, 3901. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Statistics. 2017. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Jul/IRENA_Renewable_Energy_Statistics_2017.pdf (accessed on 30 March 2019).
- Piketty, T.; Zucman, G. Capital is back: Wealth-income ratios in rich countries 1700–2010. Quat.J. Econ. 2014, 129, 1255–1310. [Google Scholar] [CrossRef]
- Piketty, T. Capital in the Twenty-First Century; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Credit Suisse Global Wealth Databook 2018. Available online: https://www.credit-suisse.com/media/assets/corporate/docs/publications/research-institute/global-wealth-report-2018-en.pdf (accessed on 30 March 2019).
- The Future We Want; United Nations: New York, NY, USA, 2012.
- Transforming our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015.
- UNEP Green Finance for Developing Countries; United Nations: New York, NY, USA, 2016.
- UNEP The Financial System We Need; United Nations: New York, NY, USA, 2015.
- Gambetta, N.; Azadian, P.; Hourcade, V.; Reyes, M. The Financing Framework for Sustainable Development in Emerging Economies: The Case of Uruguay. Sustainability 2019, 11, 1059. [Google Scholar] [CrossRef]
- Scholtens, B. Finance as a driver of corporate social responsibility. J. Bus. Ethics 2006, 68, 19–33. [Google Scholar] [CrossRef]
- Kraus, S.; Burtscher, J.; Vallaster, C.; Angerer, M. Sustainable entrepreneurship orientation: A reflection on status-quo research on factors facilitating responsible managerial practices. Sustainability 2018, 10. [Google Scholar] [CrossRef]
- PWC. The Long View: How will the global economic order change by 2050? Available online: https://www.pwc.com/gx/en/world-2050/assets/pwc-world-in-2050-summary-report-feb-2017.pdf (accessed on 30 March 2019).
- MGI. Debt and (Not Much) Deleveraging. Available online: https://www.mckinsey.com/~/media/McKinsey/Featured%20Insights/Employment%20and%20Growth/Debt%20and%20not%20much%20deleveraging/MGI%20Debt%20and%20not%20much%20deleveragingFullreportFebruary2015.ashx (accessed on 30 March 2019).
- Tiftik, E.; Mahmood, K.; Gibbs, S.; Tran, H. Global Debt Monitor; The Institute of International Finance: Washington, DC, USA, 2017. [Google Scholar]
- Reinhart, C.M.; Rogoff, K.S. This Time is Different: Eight Centuries of Financial Folly; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- King, W.I. The Wealth and Income of the People of the United States; Macmillan: New York, NY, USA, 1915; p. 53. [Google Scholar]
- Shammas, C. A New Look at Long-Term Trends in Wealth Inequality in the United States. Am. Hist. Rev. 1993, 98, 412–431. [Google Scholar] [CrossRef]
- UNU-WIDER World Income Inequality Database (WIID4). 2018. Available online: https://www.wider.unu.edu/sites/default/files/WIID/WIID_19Dec2018.xlsx (accessed on 30 March 2019).
- Cagetti, M.; De Nardi, M. Wealth Inequality: Data and Models. Macroecon. Dyn. 2008, 12, 285–313. [Google Scholar] [CrossRef]
- Smith, A. An Inquiry into The Nature and Causes of The Wealth of Nations; Campbell, R.H., Skinner, A.S., Todd, W.B., Eds.; Liberty Classics: Indianapolis, IN, USA, 1981; Volume 1, ISBN 0865970084. [Google Scholar]
- Azzimonti, B.M.; De Francisco, E.; Quadrini, V. Financial Globalization, Inequality, and the Rising Public Debt. Am. Econ. Rev. 2014, 104, 2267–2302. [Google Scholar] [CrossRef]
- Röhrs, S.; Winter, C. Reducing Government Debt in the Presence of Inequality. J. Econ. Dyn. Control 2017, 82, 1–20. [Google Scholar] [CrossRef]
- Werner, R.A. International Review of Financial Analysis Towards a new research programme on ‘ banking and the economy’—Implications of the Quantity Theory of Credit for the prevention and resolution of banking and debt crises. Int. Rev. Financ. Anal. 2012, 25, 1–17. [Google Scholar] [CrossRef]
- Lee, K.; Werner, R.A. Reconsidering Monetary Policy: An Empirical Examination of the Relationship Between Interest Rates and Nominal GDP Growth in the U.S., Germany and Japan. Ecol. Econ. 2018, 146, 26–34. [Google Scholar] [CrossRef]
- Werner, R.A. How do banks create money, and why can other firms not do the same? An explanation for the coexistence of lending and deposit-taking. Int. Rev. Financ. Anal. 2014, 36, 71–77. [Google Scholar] [CrossRef]
- Werner, R.A. A lost century in economics: Three theories of banking and the conclusive evidence. Int. Rev. Financ. Anal. 2016, 46, 361–379. [Google Scholar] [CrossRef]
- Mkhaiber, A.; Werner, R. Funding of small firms: Are big banks less helpful and has the crisis changed this? In Proceedings of the European Financial Management Association 2018 Annual Meetings, Milan, Italy, 27–30 June 2018. [Google Scholar]
- Niemand, T.; Rigtering, C.; Kallmünzer, A.; Kraus, S.; Matijas, S. Entrepreneurial orientation and digitalization in the financial service industry: A contingency approach. In Proceedings of the 25th European Conference on Information Systems (ECIS 2017), Guimarães, Portugal, 5–10 June 2018; pp. 1081–1096. [Google Scholar]
- Tesfatsion, L. Introduction to the special issue on agent-based computational economics. J. Econ. Dyn. Control 2001, 25, 281–293. [Google Scholar] [CrossRef]
- Tesfatsion, L. Agent-Based Computational Economics: Growing Economies from the Bottom Up. Artif. Life 2002, 8, 55–82. [Google Scholar] [CrossRef]
- Tesfatsion, L.; Judd, K. Agent Based Computational Economics: A Constructive Approach to Economic Theory; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Epstein, J.M. Generative Social Science: Studies in Agent-Based Computational Modeling; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef]
- Chen, S.-H.; Chang, C.-L.; Du, Y.-R. Agent-based economic models and econometrics. Knowl. Eng. Rev. 2012, 27, 187–219. [Google Scholar] [CrossRef]
- Stoker, T.M. Empirical approaches to the problem of aggregation over individuals. J. Econ. Lit. 1993, 31, 1827–1874. [Google Scholar]
- Gallegati, M.; Palestrini, A.; Gatti, D.D.; Scalas, E. Aggregation of heterogeneous interacting agents: The variant representative agent framework. J. Econ. Interact. Coord. 2006, 1, 5–19. [Google Scholar] [CrossRef]
- Rahimiyan, M.; Mashhadi, H.R. Evaluating the efficiency of divestiture policy in promoting competitiveness using an analytical method and agent-based computational economics. Energy Policy 2010, 38, 1588–1595. [Google Scholar] [CrossRef]
- Ringler, P.; Keles, D.; Fichtner, W. Agent-based modelling and simulation of smart electricity grids and markets—A literature review. Renew. Sustain. Energy Rev. 2016, 57, 205–215. [Google Scholar] [CrossRef]
- Wu, J.; Mohamed, R.; Wang, Z. An Agent-Based Model to Project China’s Energy Consumption and Carbon Emission Peaks at Multiple Levels. Sustainability 2017, 9. [Google Scholar] [CrossRef]
- Liang, X.; Yu, T.; Hong, J.; Shen, G.Q. Making incentive policies more effective: An agent-based model for energy-efficiency retrofit in China. Energy Policy 2019, 126, 177–189. [Google Scholar] [CrossRef]
- Weidlich, A.; Veit, D. A critical survey of agent-based wholesale electricity market models. Energy Econ. 2008, 30, 1728–1759. [Google Scholar] [CrossRef]
- Abar, S.; Theodoropoulos, G.K.; Lemarinier, P.; Hare, G.M.P.O. Agent Based Modelling and Simulation tools: A review of the state-of-art software. Comput. Sci. Rev. 2017, 24, 13–33. [Google Scholar] [CrossRef]
- Bayram, I.S.; Saffouri, F.; Koc, M. Generation, analysis, and applications of high-resolution electricity load profiles in Qatar. J. Clean. Prod. 2018, 183, 527–543. [Google Scholar] [CrossRef]
- Qatar Second National Development Strategy 2018–2022; MDPS—Ministry of Development Planning and Statistics: Doha, Qatar, 2018.
- Henner, D. REN 21: Renewables 2017 Global Status Report; REN21: Paris, France, 2017. [Google Scholar]
- Al-Aali, M.; Bughenaim, S. Development of Solar IPP in Qatar. Master’s Thesis, Hamad Bin Khalifa University, Doha, Qatar, 2018. [Google Scholar]
- Strategy Department for Business. Energy and Industrial Business Population Estimates. 2017. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/663235/bpe_2017_statistical_release.pdf (accessed on 30 March 2019).
- IPCC Renewable Energy Sources and Climate Change Mitigation; Cambridge University Press: New York, NY, USA, 2012.
- Esty, B.C. Why Study Large Projects? An Introduction to Research on Project Finance. Eur. Financ. Manag. 2004, 10, 213–224. [Google Scholar] [CrossRef]
- Dittmer, K. 100 percent reserve banking: A critical review of green perspectives. Ecol. Econ. 2015, 109, 9–16. [Google Scholar] [CrossRef]
- Benes, J.; Kumhof, M. The Chicago Plan Revisited. IMF Work. Papers 2012, 12, 1–72. [Google Scholar] [CrossRef]
- Georgeff, M.; Pell, B.; Pollack, M.; Tambe, M.; Wooldridge, M. The Belief-Desire-Intention Model of Agency; Springer: Berlin, Germany, 1998; pp. 1–10. [Google Scholar]






| Country | Date (Income Inequality) | Income Inequality | Date (Wealth Inequality) | Wealth Iequality |
|---|---|---|---|---|
| Norway | 2015 | 23.9 | 2018 | 79.1 |
| Finland | 2015 | 25.2 | 2018 | 76.7 |
| Sweden | 2015 | 26.7 | 2018 | 86.5 |
| Agent | Variable | Abbreviation | Unit | Value |
|---|---|---|---|---|
| Power Plant 1 | Overnight capital cost | OCC | QAR 2 | 766,500,000 |
| Lifetime | LT | year | 25 | |
| Construction period | CP | year | 2 | |
| Power capacity | CAP | MWp | 300 | |
| Energy yield | EY | MWh/MW | 1655 | |
| Estimated O & M cost | OMC | QAR | 29.2 | |
| Decrease rate of O&M (first yr) | DOM | - | 0.01 | |
| Rate of plant availability | RPA | - | 0.99 | |
| Degradation factor (first year) | DF1 | - | 0.03 | |
| Degradation factor (others) | DFX | - | 0.002 | |
| Land lease | LL | QAR | 0 | |
| Rate of asset management cost | RAM | - | 0.30 | |
| Rate of insurance cost | RIN | - | 0.15 | |
| Rate of other expenses | ROE | - | 0.15 | |
| Depositor/Investor | Initial capital (IN) 3 | ICIN | QAR | 766,500,000 |
| Initial capital (LE) 4 | ICLE | QAR | 1,766,500,000 | |
| Population (IN) 5 | POPIN | people | 100,000 | |
| Population (LE) 6 | POPLE | people | 10 | |
| Loan | Interest rate | LIR | - | 0.04 |
| Loan period | LP | year | 10 | |
| Grace period | GP | year | LT | |
| Bank | Central bank rate | RCB | - | 0.0225 |
| Interest of required reserves | IORR | - | 0.0220 | |
| Prime-deposit interest rate | RPD | - | 0.0105 | |
| Default-deposit interest rate | RDD | - | 0.0095 | |
| Environment | Carbon intensity (NG) 7 | CIND | g CO2eq/kWh | 46 |
| Carbon intensity (Solar) 7 | CISolar | g CO2eq/kWh | 469 | |
| Construction frequency 8 | CF | year | 2 |
| Variable | Abbreviation | Value |
|---|---|---|
| Capital deposit share (pool/IN) | CDSIN, p | BANK = 1.0, EBIN = 0.0, SAFE = 0.0 |
| Capital deposit share (pool/LE) | CDSLE, p | BANK = 1.0, EBIN = 0.0, SAFE = 0.0 |
| Project developer share | DEVS | 0.15 |
| Equity intermediation share | EIS | 0.10 |
| Project Developer | Loan (%) | Equity (%) | Shareholder List 1 | Project Shares 2 [Shareholder Limits] | Non-Profit EBIN 3 | Foundation Share 4 | |
|---|---|---|---|---|---|---|---|
| 1 | LE 5 | 100 | 0 | (LE,Bank,IN,EBIN) | (1.0, 0.0, 0.0, 0.0) | - | - |
| 2 | LE 6 | 70 | 30 | (LE,Bank,IN,EBIN) | (1.0, 1.0, 1.0, 1.0) | False | 0.0 |
| 3 | LE 5,7 | 0 | 100 | (LE,Bank,IN,EBIN) | (1.0, 1.0, 1.0, 1.0) | False | 0.0 |
| 4 | EBIN | 0 | 100 | (EBIN,IN,LE,Bank) | (1.0, 1.0, 1.0, 1.0) | False | 0.0 |
| 5 | EBIN | 0 | 100 | (EBIN,IN,LE,Bank) | (0.20, 1.0, 1.0, 1.0) | False | 0.0 |
| 6 | EBIN | 0 | 100 | (EBIN,IN,LE,Bank) | (0.20, 1.0, 1.0, 1.0) | True | 0.5 |
| 7 | EBIN | 0 | 100 | (EBIN,IN,LE) 8 | (0.20, 1.0, 1.0) | True | 0.5 |
| Results | Policies for Comparison | Proposed Policy Implications | |||||
|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | Scenario 6 | Scenario 7 | |
| WA—Bank (QAR in Billions) 1 | 15.078 | 12.056 | 5.401 | 4.135 | 3.684 | 3.712 | 0.00 |
| WA—EBIN (QAR in Billions) | 0.00 | 1.792 | 4.318 | 19.346 | 12.296 | 2.636 | 2.636 |
| WA—LE (QAR in Billions) | 11.352 | 14.211 | 23.446 | 4.573 | 5.476 | 5.682 | 4.212 |
| WA—IN (QAR in Billions) | 1.230 | 1.23 | 1.23 | 4.027 | 10.041 | 10.041 | 9.343 |
| WA—FND 2 (QAR in Billions) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.482 | 9.482 |
| WA—Total (QAR in Billions) | 27.66 | 29.289 | 34.395 | 32.081 | 31.497 | 31.553 | 25.673 |
| Gini Index | 0.955 | 0.958 | 0.964 | 0.874 | 0.681 | 0.483 | 0.311 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ari, I.; Koc, M. Sustainable Financing for Sustainable Development: Agent-Based Modeling of Alternative Financing Models for Clean Energy Investments. Sustainability 2019, 11, 1967. https://doi.org/10.3390/su11071967
Ari I, Koc M. Sustainable Financing for Sustainable Development: Agent-Based Modeling of Alternative Financing Models for Clean Energy Investments. Sustainability. 2019; 11(7):1967. https://doi.org/10.3390/su11071967
Chicago/Turabian StyleAri, Ibrahim, and Muammer Koc. 2019. "Sustainable Financing for Sustainable Development: Agent-Based Modeling of Alternative Financing Models for Clean Energy Investments" Sustainability 11, no. 7: 1967. https://doi.org/10.3390/su11071967
APA StyleAri, I., & Koc, M. (2019). Sustainable Financing for Sustainable Development: Agent-Based Modeling of Alternative Financing Models for Clean Energy Investments. Sustainability, 11(7), 1967. https://doi.org/10.3390/su11071967





