Abstract
The longitudinal connectivity of many rivers is interrupted by man-made barriers preventing the up- and downstream migration of fishes. For example, dams, weirs, and hydropower plants (HPP) are insuperable obstructions for upstream migration if no special measures like fish passes are put into effect. While upstream fishways have been implemented successfully and are still being optimized, the focus of current research is more and more on effective fish protection and guiding devices for downstream migration. According to current knowledge fish guidance structures (FGS) have a high potential in supporting the downstream migration by leading fishes to a bypass as an alternative to turbine passage. This work presents a structured and straightforward approach for the evaluation of potential locations of FGS combining traditional dimensioning principles with computational fluid dynamics (CFD) and novel findings from etho-hydraulic research. The approach is based on three key aspects: fish fauna, structural conditions, and hydraulic conditions, and includes three assessment criteria, which are used in an iterative process to define potential FGS locations. The hydraulic conditions can be investigated by means of hydrodynamic 3D simulations and evaluated at cross sections of potential FGS positions. Considering fundamentals of fish biology and ethology allows for rating of the flow conditions and thus for a suitability assessment of various locations. The advantage of the proposed procedure is the possibility to assess FGS configurations without implementing the FGS in the numerical model, thus limiting the computational expense. Furthermore, the implementation of various operation conditions is straightforward. The conceptual approach is illustrated and discussed by means of a case study.
1. Introduction
Man-made barriers like hydropower plants (HPP), weirs, and dams interrupt the longitudinal connectivity of rivers, which hinders migration of fishes and delimitates their natural habitats [1]. The negative impacts on fish communities and consequently on the whole ecosystem underline the need to restore river connectivity allowing for up- and downstream migration of fishes again [2]. The importance of healthy river ecosystems is manifested by international regulations and guidelines. For instance, the EU’s Water Framework Directive states that impacted water bodies need to achieve “good ecological status” and national laws stipulate river restorations (e.g., Federal Act on the Protection of Waters in Switzerland). The upstream migration of fishes has been studied in detail during the last decades, leading to a considerable number of upstream fish passage designs [3,4]. They can be classified into nature-like structures (e.g., fish ramps), technical structures (e.g., vertical slot fishways), and special purpose structures (e.g., eel ladders) [5]. Devices improving a successful downstream migration have been investigated less and are a topic of current research [3,6,7,8,9,10]. The two main approaches for the reestablishment of downstream migration and guidance of fishes from the headwater into the tailwater of HPP are conveyance and bypass [8,11]. The former requires the application of fish-friendly turbines (e.g., minimum gap runner or Alden turbine) or a fish-friendly facility management. These measures can result in very high installation costs or considerable losses in energy production, respectively. The latter approach includes fish guidance structures (FGS) in terms of racks that block fish passage physically using narrow bar spacing or eliciting fish movement along the rack via generated flow fields as well as non-physical barriers like acoustic deterrents or strobe lights that cause fish deterrence. FGS have an especially high potential to support downstream migration [6,7,8,10,11,12,13,14,15,16]. Sensory systems are based on fish-specific behavior that shows high variation among different species [10,11,12].
FGS use the concept of guiding fishes along the rack or screen axis to a bypass. Usually they are positioned with a horizontal angle α < 45° to the approach flow to achieve the favorable ratio between the tangential velocity vt and normal velocity vn above one (Figure 1a), which is considered as a suitable criterion for guiding efficiency along the rack [8,13]. These so-called angled FGS can be installed either with horizontally or vertically oriented bars. The bar spacing of horizontal angled screens is usually between 10 and 20 mm so that fish with a body height greater than this cannot physically pass (Figure 1b). To date, horizontal FGS were mostly installed at HPP with design discharges below 100 m3/s (e.g., HPP Raghun, Germany with Q = 88 m3/s) to avoid normal velocities vn larger than the sustained fish swimming speed, which would press fish against the rack [12] (Section 2.1.1). The most common vertical screens are louvers and bar racks, which are frequently used in the north-eastern United States [14,15]. Louvers consist of vertical bars that are generally positioned perpendicular to the flow direction (Figure 1c), while the bars of bar racks are oriented normal to the rack plane (Figure 1d). The bar spacing of bar racks and louvers is usually larger than for horizontal screens so that a considerable share of the fish species can pass them. However, depending on fish size they may prevent physical passage as well [6,10,16].
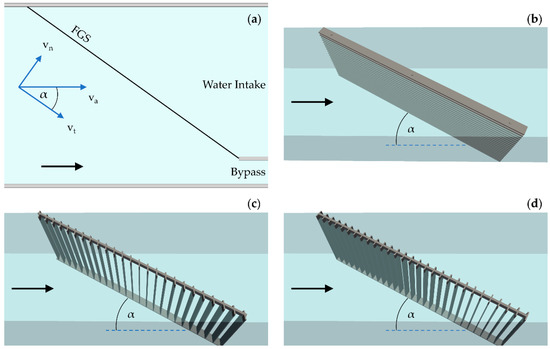
Figure 1.
(a) Layout of a fish guidance structure (FGS) with horizontal angle α with respect to the approach flow velocity va (velocity components vn and vt are normal and tangential to the rack, respectively); (b) example geometry of a horizontal FGS; (c) example geometry of a louver; (d) example geometry of a bar rack. The black arrows represent the flow direction.
Despite the relatively large bar spacing of vertical FGS, an avoidance effect is achieved by turbulent flow structures created by each bar and sensed by the fish when approaching the rack [10,16], while the guiding effect along the FGS comes from vt/vn > 1 [6,8]. The primary mechanisms for guiding fish movement at FGS are specified as follows:
- Of primary importance are the hydraulic cues caused by the rack bars, i.e., the turbulent zones and flow separation along the rack edges [16], triggering an avoidance reaction in fish. These turbulent structures cause only a few fish to swim through the FGS [10,17]. However, the avoidance reaction decreases with increasing bar spacing [12]. In fact, two fish species-specific reaction patterns could be observed in ethohydraulic experiments [10,17]. Some species, such as barbel, brown trout, and eel show investigative behavior and do not avoid rack contact. Instead, they hug the upstream rack surface and actively use it as a guidance structure but avoid passing. Grayling and spirlin, for example, behave differently as they avoid structures and only touch the screen in exceptional situations.
- The second mechanism is called sweeping flow, i.e., the parallel flow component vt actively drifting the fish towards the bypass. This mechanism is decisive for the functionality of FGS because otherwise the fishes are not directed towards the bypass. In case of exhaustion, the fish will be pressed against the bars of horizontal FGS and in case of FGS with vertical bars they can pass through the rack.
In addition to the classical bar rack, there exist further developments that are not arranged orthogonally to the rack axis, such as those with straight (Modified Bar Rack, MBR [10,17]) or curved bar cross-section shapes (Curved Bar Rack [18,19,20]). First investigations of this FGS type show a lower flow deflection and more symmetric flow field in the tailwater as well as lower hydraulic losses compared to conventional FGS.
Furthermore, screens can also be positioned with an inclination (“inclined racks”) or even horizontal to the riverbed plane. However, this type of FGS is dependent on a relatively shallow water depth, as the angle of inclination should be <10° [8]. For larger hydropower plants, this screen type is therefore usually unsuitable.
The proper positioning of FGS requires good knowledge of the hydraulic conditions prevailing at possible locations and a well-founded understanding of behavior patterns of the predominant fish communities [3,21]. Due to today’s computing power, computational fluid dynamics (CFD) has evolved as a powerful tool for investigating the flow under varying conditions and therefore has a high potential for fishway designs, for both up- and downstream migration. Various researchers applied CFD to investigate upstream fish passages, for example to assess the hydraulic conditions in pool-type fishways [22,23,24,25,26,27] or to optimize the attraction flow of fishway entrances [28,29]. However, downstream migration numerical simulations have been rarely used. A few authors implemented CFD models of turbine flows to assess fish mortality or injury rates [30,31]. Raynal et al. [32] investigated the hydraulic impacts of horizontal inclined bar racks in a rectangular channel by means of model- and real-scale CFD simulations. Mulligan et al. [33,34] performed numerical simulations and acoustic doppler velocimeter (ADV) measurements for surface partial-depth guiding walls in a laboratory flume to assess the guiding efficiency for surface-oriented fish species. A similar study was performed by Lundström et al. [35] who investigated the guiding potential of a surface guide wall at the Sikfors HPP in Sweden assessing the surface-orientated downstream migration of fish salmon smolts.
In contrast to most of the studies applying CFD to assess fishways, which focus on general facility optimization or are related to site-specific fish passage investigations, this paper presents a conceptual approach for the positioning of FGS using CFD, fish biology, and expert knowledge to support the planning of measures for fish downstream migration. The conceptual approach is illustrated and discussed by means of a case study of the HPP Brügg in Switzerland. Firstly, we will introduce the different aspects of the suggested approach and present a possible way to link the hydraulics with species-specific fish behavior patterns to rate the suitability of potential FGS configurations. Next, the application of the conceptual approach is introduced step by step for the HPP Brügg. Finally, we discuss the advantages and drawbacks of the conceptual approach, draw the main conclusions, and give recommendations for future research.
2. Methods
2.1. Conceptual Approach
The successful downstream guidance of fishes into the tailwater of HPP is a complex challenge, involving knowledge from different fields of research and concerns of various stakeholders [3]. In order to consider all essential aspects, the conceptual approach shown in Figure 2 is suggested to identify potential FGS positions. The approach is based on the three key aspects of fish fauna, structural conditions of HPP, and hydraulic and hydrologic conditions, and includes three assessment criteria, which are used in an iterative process to define potential FGS locations as described hereafter.
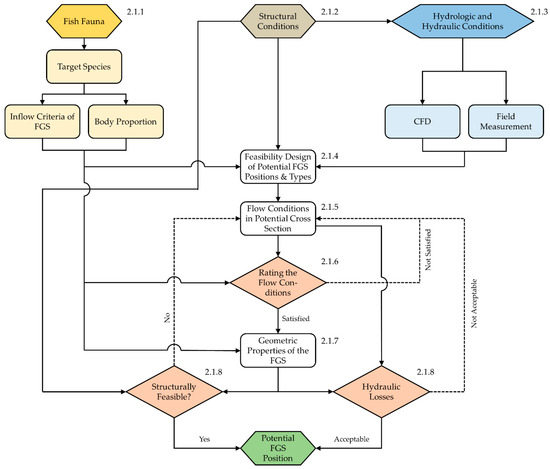
Figure 2.
Conceptual approach for the positioning of FGS using computational fluid dynamics (CFD) and expert knowledge.
2.1.1. Fish Fauna
Considering a river reach for restoration, awareness, and understanding of existing fish communities and their role in the ecosystem of the river is of major importance. This mainly includes knowledge of required habitats, migration behavior, and reproduction cycles. Based on the findings one or several target species may be identified. Subsequently, the fish biological fundamentals related to the defined target species must be scrutinized involving the migration period, body proportion, and species-specific swimming speed capabilities to be compared to the inflow conditions of the FGS.
Fish body proportions can be characterized by the relative body width wfish,rel and height hfish,rel as well as the proportion index P [12,36]. The relative body widths and heights are defined as the ratio between maximum width wfish and height hfish, respectively, and the total length L of the fishes, whereas the proportion index P is known as the ratio between hfish and wfish. For fishes with P > 1 the critical length Lcrit for the physical rack passage in relation to the bar spacing sbar can be determined as:
This criterion is strictly valid for vertically oriented bars. According to the present state of knowledge, fish change their natural body alignment only conditionally and rarely pass the barrier in a lateral position [37]. Therefore, for horizontal bars a higher protective effect can be expected for fishes having P > 1. As no general fish behavior patterns concerning the rack passage are known yet, it is recommended to use the same principles for horizontal bars as for vertical ones [12].
Various models have been developed for the design of incident flow velocities and horizontal angles of angled FGS, such as the approaches of Pavlov [36] and Bates and Vinsonhaler [14]. However, the method of O’Keeffe & Turnpenny [9] indicates the most favorable conditions for effective fish protection. They state that FGS must be designed in such a way that the normal speed vn perpendicular to the rack axis does not exceed the sustained swimming speed vsust of the fish:
The sustained swimming speed refers to the swimming activity that can be maintained by the fish over several hours (often t = 200 min is defined as the minimum characteristic duration) without fatigue [38,39]. Many empirical general and species-specific univariate and multivariate models were developed to estimate vsust. The works of Wolter and Arlinghaus [40], Peake [41], and Ebel [12] provide an overview of the relevant literature. Ebel [12] analyzed 785 studies from 21 countries including 80 fish species. Based on these data, he developed different multivariate models to quantify the sustained swimming speed vsust of European fish species and provide design recommendations for FGS and bypass systems at HPP. For a first assessment of vsust, the general multivariate model of Ebel can be applied, (derived from 225 datasets on 22 European fish species). In this model, L represents the body length [m], T the water temperature [°C], and t the swimming duration [s]:
For a more precise definition of vsust, Ebel proposes empirical multivariate approaches for rheophilic (4) and non-rheophilic species (5):
It should be noted that these approaches are not applicable to genera with special swimming styles such as lampreys (Petromyzontidae), sturgeons (Acipenseridae), or eels (Anguilidae) where species-specific models must be used. The swimming ability of lampreys can be assessed with the approach of Beamish [42], where p represents the body weight [g]:
For sturgeons the model of Peake et al. [43] applies:
and for eels the approach of Ebel [12] is suggested:
It must be mentioned that these models represent fish in optimal conditions, which is not the case when fish migrate.
With regard to permissible flow velocities, regulators of the US [8] and UK [9] provide some recommendations for FGS that are listed in Table 1. Both reports include many case studies, but most of their recommendations are not explicitly related to the behavior patterns of the target species. In the regulations for the UK [9], it is mentioned that vn should be smaller than the 90th percentile of the maximum sustained swimming speed, which is reasonably consistent with the recommendations of Ebel [12]. However, an overview of the sustained swimming speed vsust is only given for some fish species.

Table 1.
Recommendations concerning permissible flow velocities of the regulators of the US [8] and UK [9] (vn = normal velocity, va = approach flow velocity, vsust = sustained swimming speed).
2.1.2. Structural Conditions
The second pillar of the suggested approach represents the HPP and the associated structural conditions. It must be determined what type of HPP or migration obstacle is present, and its geometric dimensions must be specified. This includes the river width, the width and length of the headrace channel, the elevation difference to be overcome, and the prevailing flow depths.
2.1.3. Hydrologic and Hydraulic Conditions
The hydrologic and hydraulic conditions in the inflow area of the HPP also have to be assessed. In a first step, the flow duration curve of the investigated river stretch should be evaluated as to typical scenarios relevant for downstream migration of the target species, thereby accounting for their migration periods. From this, typical discharges result that should underlie the detailed hydraulic investigations. For this purpose, numerical modelling and field measurements can be used to determine the flow fields in detail for the relevant scenarios. Best knowledge of the prevailing hydraulic conditions can be achieved when both methods are combined, and field data can be used to calibrate and validate the numerical model. Considering FGS in real-scale numerical 3D-simulations of HPP is usually restricted to a smaller section, because the required grid resolution to resolve the whole FGS would lead to very large computing time making the conceptual approach inexpedient. Therefore, the hydraulic conditions of the present state without FGS are used as a reference, while the effects of FGS on the flow fields and on rack-near fish behavior known from detailed etho-hydraulic modelling [6,7,10,13,17,19,20,44,45,46,47] are taken into account separately in the assessment phase, see Section 2.3.
2.1.4. Feasibility Design of Potential FGS Positions and Types
Based on the numerical results, the HPP geometry, and an initial estimate of the fish biological conditions, advantageous regions in the headrace channel for the installation of FGS can be determined. First considerations about the FGS type should be undertaken as well. Overviews of the application range of different FGS types are given in References [8,9,12].
2.1.5. Flow Conditions in Cross Section of Potential Positions
In a next step, a possible FGS position is defined for each advantageous region. The hydraulic conditions obtained from the numerical model are then evaluated in the cross-section of the defined FGS position. For FGS with horizontally angled flow, the tangential velocities along the rack and the normal velocities perpendicular to the rack axis are of interest. In the case of non-angled racks, the subsequent evaluation is based on the approach flow velocity. For the definition of the relevant hydraulic parameters for other FGS types, References [8,9,12] can be used. It is important to select the FGS type with regard to the target species. For instance, investigations concerning the downstream migration of barbels showed that bar racks support a successful passage, while louvers are less suitable as a guiding device [13,17].
2.1.6. Rating the Flow Conditions with Respect to Target Species
The determined flow conditions, and thus the suitability of the rack positions to support the downstream migration of fish, can then be assessed using Equation (2) in combination with the decisive sustained swimming speeds vsust of the target species (Equations (3)–(8)). To achieve a good guiding efficiency along the rack, the ratio between the tangential velocity vt and normal velocity vn has to be above one [8].
This evaluation is considered as the primary assessment criterion for a potential FGS position. If the conditions are not fulfilled, the position of the FGS should be adjusted and the assessment must be carried out again.
2.1.7. Geometric Properties of FGS
After identifying a suitable position, the geometric characteristics of the FGS can be determined based on the fish biology, the site-specific conditions, and the chosen type of FGS. In the case of physically impassable barriers, the bar spacing must be defined in relation to the body proportions of the target species. To this end, Equation (1) can be rearranged to provide a criterion for the bar spacing sbar, which requires the definition of an appropriate value for Lcrit. It is recommended to choose the body length of the target fish species during its first migration stage in the life cycle as Lcrit. For vertical bars that are passable for fish, the negative correlation between the bar spacing and the protective effect must be taken into account [12]. The design of the rack geometry should also consider the rack stability, low susceptibility for rack vibration, and the installation of the rack cleaning system.
2.1.8. Structural Feasibility and Hydraulic Losses
Finally, the structural feasibility of the FGS realization and hydraulic losses caused by the FGS must be examined. Particular attention should be paid to the installation of a rack cleaning system and whether a certain configuration allows satisfactory connection with both bottom-near and surface-near bypass entrances. Basic dimensions for the bypass design and the rack cleaning system can be found in References [8,9,12]. Another important criterion to consider is the installation cost of the FGS.
For evaluation purposes, hydraulic head loss can be estimated with conventional formulas, like the approaches of Raynal et al. [13], Albayrak et al. [44], and Beck et al. [19] for vertical angled racks or the methods of Albayrak et al. [45] for horizontal angled racks. For inclined FGS the method of Raynal et al. [46] can be applied. The hydraulic head loss of FGS are particularly dependent on the flow velocity, the bar shape, and the bar spacing [13,44]. For HPP, these losses should be minimized to keep the deficits in electricity production as low as possible. If empirical equations are applied to estimate the hydraulic head loss, it must be noted that these formulae were developed based on laboratory tests or empirically from data sets, mainly for homogeneous inflow. Accordingly, for highly inhomogeneous approaches, flow condition deviations must be expected.
It is crucial that these two assessment criteria are appraised in close cooperation with the HPP operator. If a requirement is not met, the position of the FGS can be adjusted and the whole assessment must be carried out again starting with the evaluation of the hydraulic conditions in the adjusted cross-section. If no satisfactory FGS position is found even after repeated iteration through the concept, the investigated region should be excluded from the feasibility design. If this procedure is carried out for each region identified in the feasibility design, one or several potential FGS positions may be defined.
2.2. Numerical Modelling
The hydraulic conditions in the inflow area of HPP can be investigated by means of hydrodynamic 3D-simulations. To this end, the opensource CFD software OpenFOAM [48] constitutes a useful tool, which was used in the present study. For simulations of free-surface gravity flows the Eularian solver interFOAM is most suitable [49]. The interFOAM solver uses the Reynolds-averaged Navier-Stokes equations combined with a turbulence model acting as closure relation to the Reynolds-Stresses as governing flow equations [50]. The equations are solved with a finite volume method in combination with the PIMPLE algorithm for pressure-velocity coupling [50,51]. The interFOAM solver identifies the interface between water and air based on the volume of fluid (VOF) method, which is based on the water fraction parameter αw having values between 0 (air) and 1 (water). The interFOAM solver uses an artificial compression term in the transport equation of αw to define a fluid interface (αw = 0.5) and to avoid the use of interface reconstruction schemes. Detailed information about the VOF method and its implementation in the interFOAM solver can be found in References [26,51,52].
Another advantage of OpenFOAM besides its free availability is the use of an unstructured computational grid. The additional use of polyhedral cells (in addition to hexahedral cells) allows even complex geometries to be accurately mapped.
2.3. Influences of FGS on the Flow Field
The presented approach considers the hydraulic conditions without FGS. Hence, it is not possible to directly simulate the hydraulic effects of FGS on the flow field in its vicinity. Therefore, expert knowledge of these effects on the fish guidance efficiency should enter in this phase of the conceptual approach.
Raynal et al. [13,32] investigated the influences of angled bar racks on the flow field in their vicinity by means of laboratory investigations and numerical simulations in a rectangular channel. Based on systematic ethohydraulic model studies, Kriewitz [10] and Albayrak et al. [17] modified the classical angled bar racks by varying the bar angle β independent of α. Likewise, Beck et al. [19,20] developed curved bar racks and also tested these in laboratory flumes for both hydraulic and fish guidance performance. For all tested combinations of the horizontal angle α, the bar spacing, and the bar shape in the mentioned studies, a flow deflection and acceleration along the rack axis could be observed. The ratio of tangential to normal velocity increased continuously along the rack axis, mainly induced by increasing tangential velocities, as the normal velocities increased only slightly along the rack. These effects of the bar racks on the upstream flow field mainly increase with decreasing horizontal angle α, while the bar spacing and shape have minor influences on the hydraulic cues in the upstream near-rack zone.
In contrast to vertical angled bar racks, angled FGS with horizontal bars, particularly hydrodynamic bar shapes, which are the preferred types to minimize head losses, hardly affect the flow field, neither in the near-rack upstream nor downstream zones [47], except at flow depths close to the bed and to the surface if bottom and top overlays, respectively, are used.
Based on these findings it can be concluded that the evaluation of potential FGS positions following the suggested approach would not change fundamentally if the FGS could be included in the numerical models, as FGS mainly increase the tangential velocity along the rack axis.
3. Results: Application of Conceptual Approach to Case Study Hydropower Plant Brügg
HPP Brügg is located on the Aare river, a tributary of the Rhine river, about 2.2 km downstream of Lake Biel in Switzerland (Figure 3). It is a bay type HPP equipped with two double regulated Kaplan turbines having frontal approach flow. The HPP is placed next to the weir Port, which has five weir bays each equipped with a double hook gate. The design flow rate of the HPP is 220 m3/s. At higher flow rates, the additional discharge is spilled over the weir.
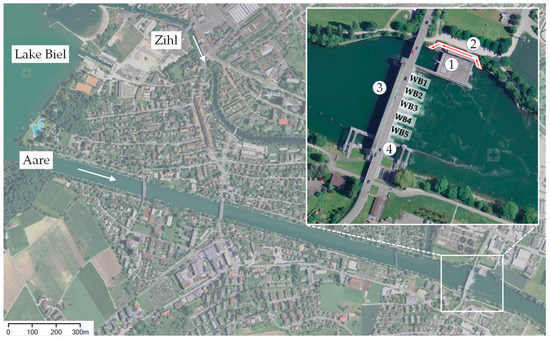
Figure 3.
Situation of hydropower plant (HPP) Brügg ①, upstream fishway ②, weir Port with weir bays WB1–WB5 ③, and ship lock ④. The white arrows indicate the flow direction (photos: map.geo.admin.ch).
The facility in Port/Brügg features an upstream fishway in the form of a vertical slot pass. However, this fish pass was not considered for the investigations of possible FGS positions, as it has to be rebuilt and the new exit will possibly be located upstream of the headrace channel.
Downstream migration of fish is currently only possible by passing through the Kaplan turbines, during weir operation, and for a limited time through the adjoining ship lock.
The revised Federal Act on the Protection of Waters in Switzerland requires restoration of the longitudinal connectivity of Swiss rivers [53]. Thus, obligations to improve the fish passage at the Port/Brügg facility are of a “very high” priority. Based on this prioritization, remediation measures are to be implemented by 2020. Hereafter, the results from applying the conceptual approach described in Section 2 to HPP Brügg are presented.
3.1. Fish Fauna
Through efforts to re-establish a self-sustaining salmon (Salmo salar) population in the Rhine river basin, this fish species is also expected in the Aare system in the long term. Therefore, salmon and barbel (Barbus barbus) have been defined as target species for the design of fishways along the Aare river. Salmon smolts in the life cycle state of first downstream migration have a body length between 10 and 20 cm considered as Lcrit [12,54]. The decisive body length of the barbel is estimated to be in the same range [55,56]. The relative body width wfish,rel is 0.10 and 0.11 for salmon and barbel, respectively. The proportion indices of salmon and barbel are P = 1.80 and P = 1.55, respectively [12]. The sustained swimming speeds vsust were assessed with Equation (3) for a swimming duration of t = 200 min and are between 0.36 and 0.85 m/s, depending on the water temperature (T = 5–15 °C).
3.2. Structural Conditions
Upstream of the HPP the river width is about 80 m. The headrace channel has a length of 46 m, a width of 24 m, and its entry width from the inlet pier to the left river bank is about 60 m. The water depth in the headrace channel is more than 6 m. The usable head of the HPP is 0.8–3.0 m, which leads to an annual electricity production of 25 GWh. The road bridge over the facility has a bridge pier placed in the middle of the headrace channel with a width of 1 m and a length of 3.5 m.
3.3. Hydrologic and Hydraulic Conditions
The five weir gates of HPP Brügg remain closed up to the design flow rate of 220 m3/s and the entire water volume is turbined. These conditions represent the most demanding situation for downstream migrating fish. Due to the closed weir, only the route via the powerhouse is possible and with the turbines running near full capacity, the flow velocities in the headrace channel are highest. HPP Brügg has an average annual runoff of 270 m3/s. The smallest average monthly discharge occurs in January and is 190–200 m3/s. Thus, the migration periods of fish play a subordinate role, as the relevant operational condition occurs throughout the year. Moreover, the goal of installing fish guidance structures at HPP Brügg is to ensure safe downstream migration for every native species all year long, which requires to consider the described operation condition to be decisive.
Accordingly, the hydraulic conditions were simulated for an operating condition with turbine operation at closed weir bays. The discharge was 195 m3/s and thus slightly below the design discharge. We did not simulate the whole design flow rate as no water level measurements to validate the numerical results were available for this operating condition. The hydraulic conditions in the inflow area of the HPP Brügg were investigated by means of hydrodynamic 3D-simulations using the opensource CFD software OpenFOAM (release v1712), as introduced in Section 2.2. The k-ε-RNG turbulence model was applied for the simulations performed herein.
For the sake of efficiency, a cascade of three simulations was carried out, whereby the model perimeter was reduced in size while the spatial resolution was increased. The model geometry of the first simulation (S1) includes the HPP Brügg, the weir Port, as well as 930 m of the Aare river upstream and 710 m downstream (Figure 4a). In the second simulation (S2), the HPP and weir were mapped (Figure 4b) and in the third simulation (S3), only the headrace channel and turbine admission flow area were included (Figure 4c). The initial resolutions of the computational grids are listed in Figure 4a–c. The computational grid of the S3 model, consisting of about 6.1 million cells, is shown in Figure 4d.
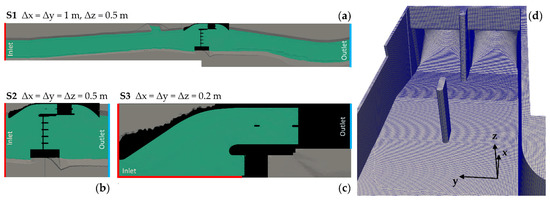
Figure 4.
(a–c) Model perimeters of the simulation sequence with the respective grid spacing; (d) Computational grid of the third simulation and orientation (coordinate system).
For simulation S1, different boundary conditions for water and air at the inflow and outflow borders were set based on the known water surface elevations (Table A1 in Appendix A). As initial conditions, different water surface elevations and flow velocities were applied for the head and tail waters. For simulations S2 and S3, the steady-state solution of the previous calculation was used as the initial condition and the boundary values αw, u, p, k, and ε were mapped accordingly.
In order to verify convergence of the solution to a steady state, the mass balances of water and the water surface elevation in the head and tail water were recorded over time. The solution was considered stationary when the mass balance was fulfilled, and constant water surface elevations were reached (Figure A1 in Appendix A).
The numerical models were validated using water level measurements in the head and tail waters of the HPP. The difference of the simulated and measured water surface elevations amounts to only a few centimeters and is thus in good agreement.
For simulation S3, the hydraulic conditions at steady state are shown in Figure 5. These results were used in the further application of the conceptual approach.
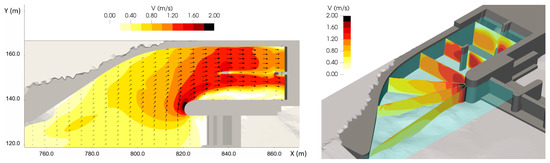
Figure 5.
Flow velocity contours in the headrace channel at steady state for simulation S3: (left) flow velocity at horizontal plane at water depth of 3 m; (right) flow velocity at different vertical cross sections. The light blue transparent plane represents the water surface at water fraction αw = 0.5.
3.4. Feasibility Design of Potential FGS Positions and Types
Prior to this study, two different studies concerning the installation of FGS at HPP Brügg had been carried out focusing on structural feasibility [57,58]. These studies spatially narrowed the feasibility of FGS implementation to the headrace channel. Due to the high flow depth of more than 6 m, inclined FGS are not an option, while angled FGS are considered to have the greatest potential of supporting fish downstream migration. Based on these findings and the simulated hydraulic conditions, two different regions for the installation of FGS in the headrace channel were defined (Figure 6).
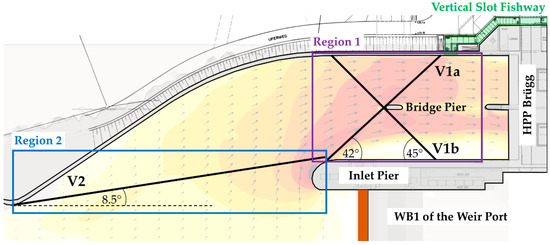
Figure 6.
Potential configurations of FGS in the headrace channel of HPP Brügg, where horizontal angles to main approach flow direction are indicated. The existing vertical slot fishway for upstream migration is shown in green. The black arrows indicate the flow direction and the arrow lengths represent the velocity magnitude.
3.5. Flow Conditions in Cross Sections of Potential Positions
Possible FGS configurations were defined for each region determined in Section 3.4. Two configurations were selected for region 1 (V1a and V1b), while there is only one configuration in region 2 (V2). From a qualitative point of view, configuration V1b is unfavorable, as it is placed almost perpendicular to the flow vectors. However, this configuration was still considered as it allows for a very short bypass inside the inlet pier of the HPP down to the tailwater. The downstream end of configuration V2 is positioned on the left side of the inlet pier since a bypass through weir bay 1 (WB1) is not possible. The FGS of all configurations are positioned horizontally angled to the main flow direction, to favor the ratio of tangential to normal velocities being above one. For these three positions, the hydraulic conditions obtained from the numerical model were evaluated in the corresponding cross-section (Figure A2 in Appendix A).
3.6. Rating the Flow Conditions with Respect to Target Species
The hydraulic conditions were rated with respect to the target species. To this end, Equation (2) was applied and the ratio of tangential to normal velocities was determined (Figure 7). Ethohydraulic experiments with various fish species have shown that vertical bar racks with horizontally angled approach flow guide fish to the bypass under laboratory conditions [10,17]. Thus, a rather high value of sustained swimming speed of vsust = 0.7 m/s, but within the range of 0.36 to 0.85 m/s determined in Section 3.1, was applied to rate the hydraulics.
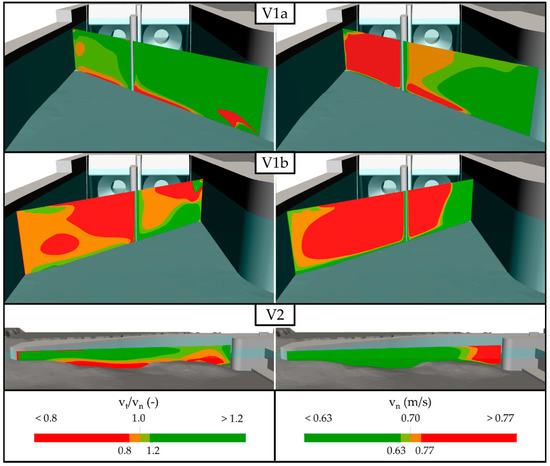
Figure 7.
Rating the flow conditions with respect to the target species: (left) ratio of tangential (vt) to normal velocities (vn); if the ratio is above unity, good fish guiding efficiency can be expected; (right) normal velocities compared to vsust = 0.7 m/s. The light blue transparent planes indicate the water surface at water fraction αw = 0.5.
The results show that a good guiding efficiency can be expected for configurations V1a and V2 since the tangential velocities of these configurations are mostly higher than the normal velocities. At configuration V1b the ratio between the tangential and normal velocities is largely below one, likely resulting in a lower guiding efficiency than for the other configurations. The rating of the flow conditions indicates that the normal velocities of configurations V1a and V1b exceed vsust, especially for the left half of the rack, which incorporates the risk of fish being jammed at the rack. The same applies to configuration V2 at the inlet pier of the HPP, where high normal velocities occur due to flow separation (see also Figure 5).
Consequently, none of the investigated configurations meets the assessment criteria concerning the hydraulic conditions. Since no other FGS configuration is possible in region 2, this area has not been considered further. Configuration V1b was initially considered because it would allow a favorable bypass connection. Since the rating of the hydraulic conditions is very negative and there would hardly be a better evaluation even with an adjusted position, this configuration was not further investigated. Configuration V1a only fails with regard to the normal velocities at the left half of the rack. To reduce the normal velocities in front of the left turbine inlet, a milder horizontal angle is required. Thus, an adjusted configuration of V1a, named V1a*, was investigated where the horizontal angle α of the left half of the rack was reduced from 42° to 30°. For this adjusted configuration, the hydraulic conditions were again evaluated in the corresponding cross-section and rated with the same assessment criteria as described above (Figure 8). The adjusted configuration shows potential for a good fish guiding efficiency and the normal velocities are mostly below the limit value of vsust. Consequently, this configuration meets the assessment criteria concerning the hydraulic conditions.
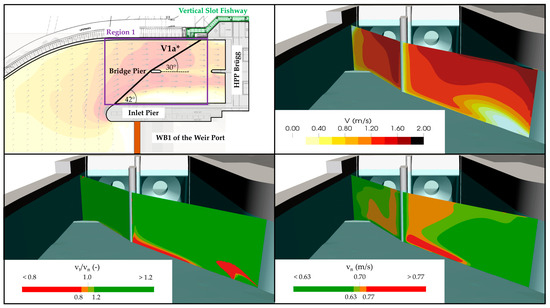
Figure 8.
Assessment of the adjusted configuration V1a*: (upper left) adjusted FGS position; (upper right) absolute flow velocities in the corresponding cross-section; (lower left) ratio of tangential (vt) to normal velocities (vn); (lower right) normal velocities compared to vsust = 0.7 m/s. The light blue transparent planes represent the water surface at water fraction αw = 0.5.
3.7. Geometric Properties of FGS
As described in Section 3.4 angled FGS are considered to have the greatest potential supporting the fish downstream migration. Configuration V1a* requires a rack length of approximately 42 m and a height of more than 6 m. According to Equation (1) a bar spacing sbar between 1.0 and 2.2 cm is required for FGS that are physically impassable. Since the proportion indices of salmon and barbel are above one, a high protective effect is to be expected with horizontal bars. For FGS with vertical bars (louvers and bar racks) there is no general rule about bar spacing. Bar spacings between a few centimeters up to more than 30 cm are reported in the literature [8,9,10]. For similar situations to HPP Brügg, a bar spacing in the order of 5–10 cm can be found in the same literature.
3.8. Structural Feasibility and Hydraulic Losses
Whether an FGS such as in configuration V1a* can be installed, it must be examined in detail in a further step, which is beyond the scope of this study. The bypass might be aligned similar to that of the existing fishway and its discharge can potentially be partly used as attraction flow for upstream migration. Special attention must be paid to the bridge pier to investigate how it affects the design and operation of the rack cleaning system.
Recent findings indicate lower hydraulic head losses for horizontal racks compared to vertically oriented bars, especially for hydrodynamic bar shapes [45,47]. Therefore the hydraulic head losses for configuration V1a* with horizontal bars were estimated based on the approach of Albayrak et al. [45], assuming rounded bar shape with a bar spacing of 1.5 cm, a bar thickness of 0.8 cm, and a bar depth of 8 cm. From the numerical simulations a mean approach flow velocity of 1.25 m/s was determined and the mean horizontal angle between the velocity vectors and the screen axis is about 30°. For such conditions the estimated hydraulic losses amount to 2–3 cm. To compare with the hydraulic head losses of configuration V1a* with vertical bars, we applied the approach of Beck et al. [19] for a curved bar rack with rounded bar tips. The calculation was performed for a bar spacing of 8 cm, a bar thickness of 0.8 cm, and a bar depth of 10 cm. The approach flow velocity and the mean angle between the velocity vectors were the same as for horizontal bars. With these assumptions, the resulting hydraulic head losses amount to 4–5 cm. In contrast to classical and modified angled bar racks with rather asymmetric and inhomogeneous flow fields downstream of the rack, curved bar racks (i) cause significantly reduced head losses and (ii) align the flow, ensuring a symmetric turbine admission flow [20]. This is particularly important for configuration V1a* as the rack is immediately upstream of the turbines. Note that in these examples, no bottom and top overlays were assumed.
However, these results must be considered with caution as the flow conditions in the headrace channel are highly inhomogeneous. It is the task of the HPP operator to define what hydraulic head losses due to FGS are acceptable. Thus, it cannot be definitively stated here whether the location V1a* represents a suitable FGS position concerning the two assessment criteria of structural feasibility and hydraulic losses.
4. Discussion
Silva et al. [3] developed a multidisciplinary approach providing a general framework to consider the interests of all stakeholders in the development and implementation of fishways. The presented approach in this work may be considered as a specification of this framework to address downstream fish migration by means of FGS involving essential aspects for a successful layout. With the proposed concept, we intend to provide a tool that combines traditional dimensioning principles of fish descent aids as reported in References [8,9,10,12] with computational fluid dynamics in order to evaluate suitable FGS configuration in a structured and straightforward way.
The proposed procedure uses the hydraulic conditions of the present state without FGS as a reference since the geometric representation of the FGS in the numerical models would require very small cell sizes (some millimeters) that would lead to a very high computing effort impeding an efficient layout procedure. On the one hand, omitting the FGS in the numerical simulations has the advantage that all possible FGS locations can be examined using the results of the same simulation, which reduces the computing effort considerably. On the other hand, the influences of the FGS on the surrounding flow field are not directly considered with this approach and have to be accounted for by expert judgement separately. As to the effect of FGS on the upstream flow field sensed by approaching fish, distinction should be made between FGS with vertical and horizontal bars. Based on findings on the flow impact of various kinds of vertical angled FGS in their vicinity [13,19,20,32], the suggested approach gives rather conservative results in terms of fish guidance efficiency, as the rack-parallel sweeping flow component tends to be intensified by the racks (“guidance effect”). Regarding angled FGS having horizontal bars without overlays, the flow field is quasi unaffected [47] so that the approach proposed herein is fully applicable. If bottom and/or top overlays are applied, the guidance effect for bottom- and surface-oriented fish is intensified, so that guidance efficiencies are again likely underestimated by the present approach. The overall assessment would thus not change considerably if FGS were included in the numerical models. However, further research on this topic involving numerical simulations and laboratory experiments for different FGS types is recommended to reduce uncertainties in the understanding of the impact caused by FGS on the upstream flow field.
The connection between hydraulics and the related behavioral responses of fishes is summarized in only one variable, which is vsust. This may be criticized as a too restrictive simplification of the complex behavioral pattern of fish species. Indeed, many authors claim that there are gaps in knowledge regarding species-specific behavior of fish, which must be approached in future research [1,3,59,60,61]. For example, the velocity increase along the rack is another important criterion, which can also be assessed easily based on the CFD results. The United States Bureau of Reclamation (USBR) [8] states that louvers should be operated with bypass-to-approach flow velocity ratios between 1.1 and 1.5. The ratio for vertical and horizontal FGS is in a similar, slightly lower range, but is still the subject of ongoing research. Nevertheless, the presented approach is structured in such a way that it is possible and desirable to consider future findings when rating the hydraulic conditions.
Fish downstream migration devices must incorporate four features [3]. Firstly, they must shield fish from the zones of potential injury, e.g., turbine passage. Secondly, they have to guide the fish to an alternative migration corridor. Thirdly, fishes must find their way into the bypass and last, but not least, fishes should successfully migrate through the bypass into the tailwater without damage. Thus, after finding a suitable configuration of an FGS by means of the presented approach, a proper design of the bypass is a crucial prerequisite for supporting a successful downstream migration. For the implementation of a bypass in the numerical model, flow obstruction by the FGS has to be taken into account. As discussed above, depending on the type of angled FGS, a part of the approach flow is diverted parallel to the FGS. This is reasonable from a hydrodynamic point of view, because flow obstruction first occurs at the most upstream part of the FGS causing a small increase of the water surface elevation, i.e., the tangential velocity will increase being in favor of fish guidance efficiency. As a first attempt, a similar behavior might be simulated with the numerical model by using a baffle at the location of the FGS and specifying a hydraulic head loss estimated by empirical approaches as given in the literature. However, the capability of baffles to reproduce the flow field near FGS must be validated by further investigations, and further research on how to consider FGS in a simplified manner is needed. Once this has been achieved, the presented concept can be extended by carrying out additional CFD simulations for the identified potential configurations, in which the bypass and the FGS are resolved and directly taken into account.
5. Conclusions
The successful downstream guidance of fishes into the tailwater of HPP by fish guidance structures (FGS) is a complex challenge. In order to consider all essential aspects, a structured and straightforward conceptual approach for the evaluation of potential FGS positions by means of CFD was presented. The applicability of the concept was illustrated and discussed based on the case study of HPP Brügg in Switzerland. The use of numerical models instead of field measurements to investigate the flow situation allows for assessing the hydraulic conditions in any desired section and for different scenarios and operating conditions. Furthermore, numerical results can be used for additional investigations, such as the evaluation and optimization of the turbine admission flow. In the present conceptual approach, potential FGS positions can be assessed without implementing the FGS in the numerical model to facilitate efficient application. However, this states also the main limitation because the hydrodynamic influence of FGS on the local flow field cannot be directly simulated but has to be assessed indirectly by considering recent findings form experimental etho-hydraulic and detailed numerical investigations (“expert judgement”). Future research has to develop new approaches to include FGS in a simplified manner while reproducing the main flow features near FGS at reasonable computational expense. Such a contribution would make the present approach more powerful. Furthermore, interactions between hydraulics and related species-specific behavioral responses of fishes are the subject of current research and related new findings can easily be included in the concept.
Applying the approach to HPP Brügg showed that the conceptual approach serves as an optimization tool for potential FGS configurations. A suitable configuration concerning the hydraulic conditions could be determined for which the normal velocities exceed the sustained swimming speed vsust of the target species only locally and which shows a ratio of tangential to normal velocity above one. Further steps in the design process, such as checking structural stability of the FGS and technical aspects of the rack cleaning system, are not part of the case study herein but are important in real-world applications.
Author Contributions
The numerical modelling and writing of the manuscript was performed by L.F. under the supervision of D.F.V., S.K. and R.M.B., C.R.K. provided the technical data of the hydropower plant Brügg and supported the feasibility assessment of the different alternatives. S.K. provided the boundary conditions and processed the bathymetry data of the Aare river as well as the model geometry of the hydropower plant Brügg. All authors were involved in editing the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Boundary conditions of the first OpenFOAM model (S1) for all hydraulic variables. An extended definition of their numerical implementation can be found in [62].
Table A1.
Boundary conditions of the first OpenFOAM model (S1) for all hydraulic variables. An extended definition of their numerical implementation can be found in [62].
| Boundary | αw | u | p | k | ε | nut |
|---|---|---|---|---|---|---|
| inlet water | fixedValue | flowrate-InletVelocity | fixedFlux-Pressure | fixedValue | fixedValue | calculated |
| inlet air | zeroGradient | noSlip | fixedFlux-Pressure | kqRWall-Function | epsilonWall-Function | nutkWall-Function |
| outlet water | fixedValue | inletOutlet | fixedValue | inletOutlet | inletOutlet | calculated |
| outlet air | inletOutlet | fixedValue | zeroGradient | inletOutlet | inletOutlet | calculated |
| atmosphere | inletOutlet | pressureInlet-OutletVelocity | totalPressure | inletOutlet | inletOutlet | calculated |
| walls | zeroGradient | noSlip | fixedFlux-Pressure | kqRWall-Function | epsilonWall-Function | nutkWall-Function |
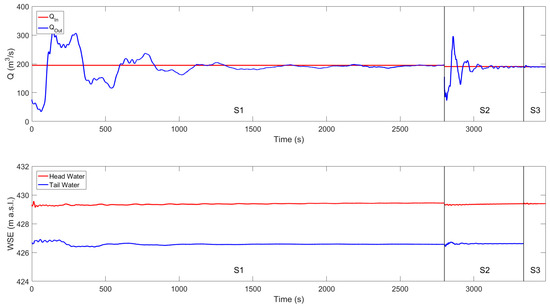
Figure A1.
Assessment of the convergence to a steady state for the three simulations (S1), (S2) and (S3): (top) mass balance of water over time; (bottom) water surface elevation over time in the head and tailwater of the HPP. For the simulation (S3), the tail water was not included in the model.
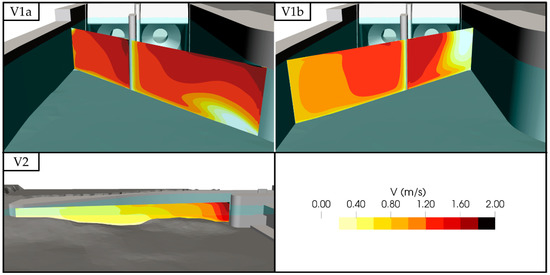
Figure A2.
Hydraulic conditions in the cross-sections of the defined FGS positions. The light blue transparent planes indicate the water surface at water fraction αw = 0.5.
References
- Katopodis, C.; Aadland, L.P. Effective dam removal and river channel restoration approaches. Int. J. River Basin Manag. 2006, 4, 153–168. [Google Scholar] [CrossRef]
- Lynch, A.J.; Myers, B.J.E.; Chu, C.; Eby, L.A.; Falke, J.A.; Kovach, R.P.; Krabbenhoft, T.J.; Kwak, T.J.; Lyons, J.; Paukert, C.P.; et al. Climate Change Effects on North American Inland Fish Populations and Assemblages. Fisheries 2016, 41, 346–361. [Google Scholar] [CrossRef]
- Silva, A.T.; Lucas, M.C.; Castro-Santos, T.; Katopodis, C.; Baumgartner, L.J.; Thiem, J.D.; Aarestrup, K.; Pompeu, P.S.; O’Brien, G.C.; Braun, D.C.; et al. The future of fish passage science, engineering, and practice. Fish Fish. 2017, 19, 340–362. [Google Scholar] [CrossRef]
- Clay, C.H. Design of Fishways and Other Fish Facilities, 2nd ed.; Lewis Publishers: Boca Raton, FL, USA, 1994. [Google Scholar]
- FAO/DVWK. Fish Passes—Design, Dimensions and Monitoring; FAO: Rome, Italy, 2002. [Google Scholar]
- Boes, R.; Albayrak, I. Fish guidance structures: New head loss formula and fish guidance efficiencies. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Szabo-Meszaros, M.; Navaratnam, C.U.; Aberle, J.; Silva, A.T.; Forseth, T.; Calles, O.; Fjeldstad, H.P.; Alfredsen, K. Experimental hydraulics on fish-friendly trash-racks: An ecological approach. Ecol. Eng. 2018, 113, 11–20. [Google Scholar] [CrossRef]
- U.S. Department of the Interior. Fish Protection at Water Diversions—A Guide for Planning and Designing Fish Exclusion Facilities; Water Resources Technical Publication, Bureau of Reclamation: Denver, CO, USA, 2006.
- O’Keeffe, N.; Turnpenny, W.H. Screening for Intake and Outfalls: A Best Practice Guide; Environment Agency: Bristol, UK, 2005. [Google Scholar]
- Kriewitz, C.R. Leitrechen an Fischabstiegsanlagen: Hydraulik und fischbiologische Effizienz (‘Guiding racks at fish descent systems: Hydraulics and fish biological efficiency’). In VAW-Mitteilungen 230; Boes, R., Ed.; Laboratory of Hydraulics, Hydrology and Glaciology (VAW), ETH Zürich: Zürich, Switzerland, 2015. (In German) [Google Scholar]
- Larinier, M.; Travade, F. Downstream migration: Problems and facilities. Bull. Fr. Peche Piscic. 2002, 364, 181–207. [Google Scholar] [CrossRef]
- Ebel, G. Fischschutz und Fischabstieg an Wasserkraftanlagen: Handbuch Rechen- und Bypasssysteme: Ingenieurbiologische Grundlagen, Modellierung und Prognose, Bemessung und Gestaltung (‘Fish Protection and Fish Downstream Migration at Hydropower Plants: Handbook on Rack and Bypass Systems: Fundamentals of Engineering Biology, Modelling and Forecasting, Dimensioning and Design’); Büro für Gewässerökologie und Fischereibiologie Dr. Ebel: Halle (Saale), Germany, 2013. (In German) [Google Scholar]
- Raynal, S.; Chatellier, L.; Courret, D.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 2. Angled trashracks. J. Hydraul. Res. 2013, 51, 67–75. [Google Scholar] [CrossRef]
- Bates, D.W.; Vinsonhaler, R. Use of Louvers for Guiding Fish. Trans. Am. Fish. Soc. 1957, 86, 38–57. [Google Scholar] [CrossRef]
- Amaral, S.V.; Winchell, F.C.; McMahon, B.J.; Dixon, D.A. Evaluation of angled bar racks and louvers for guiding silver phase American eels. Am. Fish. Soc. 2003, 33, 367–376. [Google Scholar]
- Electric Power Research Institute (EPRI); Dominion Millstone Laboratories (DML). Evaluation of Angled Bar Racks and Louvers for Guiding Fish at Water Intakes; Report No. 1005193; EPRI: Palo Alto, CA, USA, 2001. [Google Scholar]
- Albayrak, I.; Boes, R.M.; Kriewitz-Byun, C.R.; Peter, A.; Tullis, B. Fish guidance structures: Hydraulic performance and fish guidance efficiencies. J. Ecohydraulics 2019. in review. [Google Scholar]
- Beck, C.; Albayrak, I.; Boes, R. Improved hydraulic performance of fish guidance structures with innovative bar design. In Proceedings of the 12th International Symposium on Ecohydraulics (ISE 2018), Tokyo, Japan, 19–24 August 2018. [Google Scholar]
- Beck, C.; Albayrak, I.; Meister, J.; Boes, R.M. Hydraulic performance of fish guidance structures with curved bars—Part 1: Head loss assessment. J. Hydraul. Res. 2019. in review. [Google Scholar]
- Beck, C.; Albayrak, I.; Boes, R.M. Hydraulic performance of fish guidance structures with curved bars—Part 2: Flow fields. J. Hydraul. Res. 2019. in review. [Google Scholar]
- Wilkes, M.; Baumgartner, L.; Boys, C.; Silva, L.G.M.; O’Connor, J.; Jones, M.; Stuart, I.; Habit, E.; Link, O.; Webb, J.A. Fish-Net: Probabilistic models for fishway planning, design and monitoring to support environmentally sustainable hydropower. Fish Fish. 2018, 19, 677–697. [Google Scholar] [CrossRef]
- Khan, L.A. A three-dimensional computational fluid dynamics (CFD) model analysis of free surface hydrodynamics and fish passage energetics in a vertical-slot fishway. N. Am. J. Fish. Manag. 2006, 26, 255–267. [Google Scholar] [CrossRef]
- An, R.D.; Li, J.; Liang, R.F.; Tuo, Y.C. Three-dimensional simulation and experimental study for optimising a vertical slot fishway. J. Hydro-Environ. Res. 2016, 12, 119–129. [Google Scholar] [CrossRef]
- Quaranta, E.; Katopodis, C.; Revelli, R.; Comoglio, C. Turbulent flow field comparison and related suitability for fish passage of a standard and a simplified low-gradient vertical slot fishway. River Res. Appl. 2017, 33, 1295–1305. [Google Scholar] [CrossRef]
- Plymesser, K.; Cahoon, J. Pressure gradients in a steeppass fishway using a computational fluid dynamics model. Ecol. Eng. 2017, 108, 277–283. [Google Scholar] [CrossRef]
- Fuentes-Perez, J.F.; Silva, A.T.; Tuhtan, J.A.; Garcia-Vega, A.; Carbonell-Baeza, R.; Musall, M.; Kruusmaa, M. 3D modelling of non-uniform and turbulent flow in vertical slot fishways. Environ. Model. Softw. 2018, 99, 156–169. [Google Scholar] [CrossRef]
- Quaresma, A.L.; Romao, F.; Branco, P.; Ferreira, M.T.; Pinheiro, A.N. Multi slot versus single slot pool-type fishways: A modelling approach to compare hydrodynamics. Ecol. Eng. 2018, 122, 197–206. [Google Scholar] [CrossRef]
- Andersson, A.G.; Lindberg, D.E.; Lindmark, E.M.; Leonardsson, K.; Andreasson, P.; Lundqvist, H.; Lundstrom, T.S. A Study of the Location of the Entrance of a Fishway in a Regulated River with CFD and ADCP. Mod. Simul. Eng. 2012, 2012, 327929. [Google Scholar] [CrossRef]
- Gisen, D.C.; Weichert, R.B.; Nestler, J.M. Optimizing attraction flow for upstream fish passage at a hydropower dam employing 3D Detached-Eddy Simulation. Ecol. Eng. 2017, 100, 344–353. [Google Scholar] [CrossRef]
- Richmond, M.C.; Serkowski, J.A.; Ebner, L.L.; Sick, M.; Brown, R.S.; Carlson, T.J. Quantifying barotrauma risk to juvenile fish during hydro-turbine passage. Fish. Res. 2014, 154, 152–164. [Google Scholar] [CrossRef]
- Zangiabadi, E.; Masters, I.; Williams, A.J.; Croft, T.N.; Malki, R.; Edmunds, M.; Mason-Jones, A.; Horsfall, I. Computational prediction of pressure change in the vicinity of tidal stream turbines and the consequences for fish survival rate. Renew. Energy 2017, 101, 1141–1156. [Google Scholar] [CrossRef]
- Raynal, S.; Chatellier, L.; David, L.; Courret, D.; Larinier, M. Numerical Simulations of Fish-Friendly Angled Trashracks at Model and Real Scale. In Proceedings of the 35th IAHR World Congress, Vols I and Ii, Chengdu, China, 8–13 September 2013; pp. 2557–2566. [Google Scholar]
- Mulligan, K.B.; Towler, B.; Haro, A.; Ahlfeld, D.P. A computational fluid dynamics modeling study of guide walls for downstream fish passage. Ecol. Eng. 2017, 99, 324–332. [Google Scholar] [CrossRef]
- Mulligan, K.B.; Towler, B.; Haro, A.; Ahlfeld, D.P. Downstream fish passage guide walls: A hydraulic scale model analysis. Ecol. Eng. 2018, 115, 122–138. [Google Scholar] [CrossRef]
- Lundström, T.S.; Brynjell-Rahkola, M.; Ljung, A.L.; Hellstrom, J.G.I.; Green, T.M. Evaluation of Guiding Device for Downstream Fish Migration with in-Field Particle Tracking Velocimetry and CFD. J. Appl. Fluid Mech. 2015, 8, 579–589. [Google Scholar] [CrossRef]
- Pavlov, D.S. Structures Assisting the Migrations of Non-Salmonid Fish: USSR; FAO Fisheries Technical Paper 308, 97 S; Food and Agriculture Organisation of the United Nations: Rome, Italy, 1989. [Google Scholar]
- Stewart, J.; Ferrell, D.J. Escape panels to reduce by-catch in the New South Wales demersal trap fishery. Mar. Freshw. Res. 2002, 53, 1179–1188. [Google Scholar] [CrossRef]
- Webb, P.W. Hydrodynamics and Energetics of Fish Propulsion; Department of the Environment Fisheries and Marine Service: Ottawa, ON, Canada, 1975.
- Beamish, F.W.H. Swimming Capacity. In Fish Physiology 7; Hoar, W.S., Randall, D.J., Eds.; Academic Press: New York, NY, USA, 1978; pp. 101–187. [Google Scholar]
- Wolter, C.; Arlinghaus, R. Navigation impacts on freshwater fish assemblages: The ecological relevance of swimming performance. Rev. Fish Biol. Fish. 2003, 13, 63–89. [Google Scholar] [CrossRef]
- Peake, S. Swimming Performance and Behavior of Fish Species to Newfoundland and Labrador: A Literature Review for the Purpose of Establishing Design Water Velocity Criteria for Fishways and Culverts; Canadian Manuscript Report of Fisheries and Aquatic Sciences 1488-53872843; Department of Fisheries and Oceans: Ottawa, ON, Canada, 2008.
- Beamish, F.W.H. Swimming Performance of Adult Sea Lamprey, Petromyzon-Marinus, in Relation to Weight and Temperature. Trans. Am. Fish. Soc. 1974, 103, 355–358. [Google Scholar] [CrossRef]
- Peake, S.; Beamish, F.W.H.; McKinley, R.S.; Scruton, D.A.; Katopodis, C. Relating swimming performance of lake sturgeon, Acipenser fulvescens, to fishway design. Can. J. Fish. Aquat. Sci. 1997, 54, 1361–1366. [Google Scholar] [CrossRef]
- Albayrak, I.; Kriewitz, C.R.; Hager, W.H.; Boes, R.M. An experimental investigation on louvres and angled bar racks. J. Hydraul. Res. 2018, 56, 59–75. [Google Scholar] [CrossRef]
- Albayrak, I.; Maager, F.; Boes, R.M. An experimental investigation on fish guidance structures with horizontal bars. J. Hydraul. Res. 2019. accepted. [Google Scholar]
- Raynal, S.; Courret, D.; Chatellier, L.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 1. Inclined trashracks. J. Hydraul. Res. 2013, 51, 56–66. [Google Scholar] [CrossRef]
- Meister, J.; Fuchs, H.; Albayrak, I.; Boes, R.M. Horizontal bar rack bypass systems for fish downstream migration: State of knowledge, limitations, and gaps. In Proceedings of the 12th International Symposium on Ecohydraulics (ISE 2018), Tokyo, Japan, 19–24 August 2018. [Google Scholar]
- Greenshields, C.J. OpenFOAM: The Open Source CFD Toolbox—Programmer’s Guide; OpenFOAM Foundation Ltd. 2015. Available online: http://foam.sourceforge.net/docs/Guides-a4/ProgrammersGuide.pdf (accessed on 19 March 2019).
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces; Department of Mechanical Engineering Imperial College of Science, Technology & Medicine, University of London: London, UK, 1997. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and Openfoam®, 4th ed.; Holzmann CFD: Leoben, Austria, 2017. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (Vof) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Berberovic, E.; van Hinsberg, N.P.; Jakirlic, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef]
- Federal Act on the Protection of Waters of Switzerland (Gewässerschutzgesetz). SR 814.20 of 24 January 1991. 1 January 2017. Available online: https://www.admin.ch/opc/en/classified-compilation/19910022/201701010000/814.20.pdf (accessed on 19 March 2019).
- Morais, P.; Daverat, F. An Introduction to Fish Migration; Taylor & Francis Group, LLC: Boca Raton, FL, USA; London, UK, 2016. [Google Scholar]
- Hunt, P.C.; Jones, J.W. Population Study of Barbus-Barbus (L) in River Severn, England. 2. Movements. J. Fish. Biol. 1974, 6, 269–278. [Google Scholar] [CrossRef]
- Baras, E.; Lambert, H.; Philippart, J.C. A Comprehensive Assessment of the Failure of Barbus-Barbus Spawning Migrations through a Fish Pass in the Canalized River Meuse (Belgium). Aquat. Living Resour. 1994, 7, 181–189. [Google Scholar] [CrossRef]
- Höttges, A.; Sausen, S. Einsatz von Fischleitrechen am Aare-Kraftwerk Brügg (‘Use of Fish Guiding Screens at the Aare Power Plant in Brügg’). Master’ Thesis, Laboratory of Hydraulics, Hydrology and Glaciology (VAW), ETH Zürich, Zürich, Switzerland, 2016, unpublished. (In German). [Google Scholar]
- BKW. Vorstudien—Sanierung Fischgängigkeit am WKW Brügg (‘Prestudies—Remediation of fish migration at the HPP Brügg’); Bielersee Kraftwerke: Biel, Switzerland, 2016. (In German) [Google Scholar]
- Katopodis, C. Developing a toolkit for fish passage, ecological flow management and fish habitat works. J. Hydraul. Res. 2005, 43, 451–467. [Google Scholar] [CrossRef]
- Romao, F.; Quaresma, A.L.; Branco, P.; Santos, J.M.; Amaral, S.; Ferreira, M.T.; Katopodis, C.; Pinheiro, A.N. Passage performance of two cyprinids with different ecological traits in a fishway with distinct vertical slot configurations. Ecol. Eng. 2017, 105, 180–188. [Google Scholar] [CrossRef]
- Wilkes, M.A.; Webb, J.A.; Pompeu, P.S.; Silva, L.G.M.; Vowles, A.S.; Baker, C.F.; Franklin, P.; Link, O.; Habit, E.; Kemp, P.S. Not just a migration problem: Metapopulations, habitat shifts, and gene flow are also important for fishway science and management. River Res. Appl. 2018. [Google Scholar] [CrossRef]
- OpenFoam. Standard Boundary Conditions. Available online: https://www.openfoam.com/documentation/user-guide/standard-boundaryconditions.php (accessed on 2 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).