1. Introduction
Finding an optimal path to a sustainable and low-carbon economy is increasingly urgent to decrease the carbon emissions that are an important determinant of global warming. Infrastructure is an important part of the modern economy, promoting activities and transition dynamics of the economy and society [
1]. Therefore, future-ready sustainable infrastructure systems are especially needed. Transportation is needed as one of the key aspects of infrastructure to catalyze the shift toward climate-resilient economic growth [
2]. Due its heavy consumption of fossil energy, a sustainable and clean transportation system has long been advocated. Some researchers have investigated the impact of land use, demand management and operations management [
3,
4] on transportation; however, the rapid development of electric vehicles (EVs) is another important factor in sustainable transportation which ensures national energy security, reduces the consumption of petroleum energy, and minimizes the environmental pollution caused by automobile exhaust [
5]. EVs are being welcomed by increasing numbers of people. According to data from the China Automotive Industry Association, 1.27 million new energy vehicles were produced and 1.26 million were sold in in China in 2018, an increase of 60% and 61% in production and sales, respectively, when compared with the previous year. The author of [
6] showed that purchase subsidies, purchase restrictions, and driving restrictions were the most effective policies for EV promotion. However, the development of EVs in China is facing a dilemma due to deficient EV subsidy policies, weak EV market, local protectionism, insufficient charging infrastructure, short battery range, cost, and psychological factors [
6,
7,
8]. The insufficient charging infrastructure is posing a particular barrier. According to official data of Ministry of Public Security and China Electric Vehicle Charging Infrastructure Promotion Alliance, the inventory of new energy vehicles is 2.61 million, and the inventory of EV chargers was 299,752 at the end of 2018. Thus, the ratio of the total number of new energy vehicles to the total number of EV chargers was about 8.71:1.
There are many opportunities in China’s EV charger market and related support policies have been introduced. The State Grid Corporation of China has fully introduced a grid-connected project for distributed power, as well as various types of charging and switching facilities markets. According to China’s EV Infrastructure Development Annual Report (2016–2017), more than 30 provinces and cities have introduced subsidy policies for the construction of charging facilities. In 2015, China’s EV Charging Infrastructure Development Guide (2015–2020) estimated that more than 4.8 million decentralized EV chargers will be used by 2020 including 500,000 public and 4.3 million private chargers to meet the EV charging demand nationwide. Some researchers have investigated the economic efficiency of building charging stations or improving the technology in EVs [
9]. However, building charging stations is not only an economic problem, but also an environmental one. EV chargers are needed, considering future environmental protection and technology development, even though EV development is expensive.
Some obstacles exist in the construction of EV chargers. The first is consumers’ attitudes to new technology [
10,
11], which influences the expansion of EVs; therefore, the government should focus on long-term returns and not on the short-lived benefits derived from government regulations forcing the adoption of EVs. The second is the optimal construction site and the assignment problem; many researchers have tried to solve these problems using different operation methods [
12,
13,
14,
15] based on traffic density, geographical distribution, charging demand, and other factors. The number and location of EV chargers have been shown to be much more important than large charging stations [
8]. The charger type problem has also been investigated in the literature [
16,
17], and researchers have discussed how to integrate them properly to meet the different demands. Some researchers proposed an optimal battery recycling strategy [
18] to solve the energy management strategy. Aside from these technology, siting, or assignment problems, the business model and operation structure of an EV enterprise also affect the expansion and quantity of EV chargers, which can maintain the sustainable governance of the charging infrastructure.
Among all the obstacles and strategies in the process of developing charging infrastructures, the operation structure of the EV charger enterprise is a key factor, because it is related to the sustainable development of the EV charger industry. During the initial stage of the development of charging infrastructure in China, many high-quality EV chargers are needed, so creating a clear development route for EV charger enterprises is important. The right operation structure will encourage the high speed development and quality of charging infrastructure. Environmental factors, such as operation, supervision, and investment return, will affect the performance of different structures at different development stages. Which structure should the enterprises use to meet the need for widely distributed and high quality EV chargers? How can environmental factors at different developmental stages affect the optimal quality and quantity? What policies should the government adopt in the development of charging stations? This paper attempts to find answers to these questions by first comparing the difference in the optimal quantity and quality of EV chargers between different structures by constructing theoretical models, and then by simulating the conclusions we obtained from the theoretical model. We also conducted a comparative static analysis of the environmental factors that could affect the quantity and quality of EV chargers. Finally, policy recommendations about the operation structure are provided to guide the sustainable and effective development of the EV charger market.
We provide several contributions to the literature. First, most of the literature about the charging infrastructure of EVs has concentrated on the economic analysis of revenues and cost [
9], or the obstacles such as market adoption [
10,
11], construction site or assignment problems [
12,
13,
14,
15,
16,
17], and new technology to overcome these barriers [
18]. However, few studies have examined the choice of business operation structure by the enterprises in the process of infrastructure construction, which can affect the efficiency of investment, infrastructure safety, and infrastructure coverage (quantity), and then determined the sustainable development of the EV charger industry. A trade-off exists between the quantity and quality in different stages of the construction of charging infrastructure, and this also exists between the structures in general. Therefore, after comparing the optimal quantity and quality level in different operation structures theoretically, we selected the optimal operation structure for EV charger enterprises to meet the demand for a large number of EV chargers during different stages of the development of the charging infrastructure in China.
Few studies have explored the operating structure of charging infrastructure using a theoretical model or discussed the environmental factors affecting the charging infrastructure. We investigated the optimal quality and quantity in both company-owned and franchised structure enterprises by creating a theoretical model based on principle agency and contract model. We then created a sustainable development route for charging infrastructure according to our conclusions. We found that the franchised EV charger enterprises were more conducive to increasing the quantity to meet the needs of EVs at the beginning of the development. When the market became more saturated, and higher quality EV chargers were required, the company-owned structure performed better and will be required more to improve the quality.
Finally, operation, supervision, and profit factors are important in the construction of charging infrastructure. However, no discussion has occurred in the operation structure literature about how these factors at different development stages can affect the optimal quality and quantity. We used simulation and sensitivity analysis based on our theoretical model to examine the effect of these factors. According to our conclusions, we found that since there was insufficient experience in the operation and supervision of charging infrastructure, the franchised structure is recommended in the initial development stage of EV chargers as well, because the worst performance of the company-owned structure was observed when the operation and supervision costs were high.
The remainder of the paper is organized as follows.
Section 2 presents an overview of market and market models of EV chargers, and then the separate set-ups of the theoretical model of the company-owned and franchised type of EV charger enterprises are outlined.
Section 3 provides the simulation of the analytical solution.
Section 4 provides a discussion of the results when we improved management efficiency and further research are discussed as well.
Section 5 concludes and presents the policy implications.
2. Materials and Methods
2.1. Market Overview and Market Models of EV Chargers
Currently, the business model of China’s charging station can be divided into several types: (1) Leading EV charger operators, such as the State Grid Corporation of China (SGCC) and Potevio New Energy, that produce and operate EV chargers; (2) leading automobile enterprises, such as Tesla and BYD Auto, who create charging infrastructure in order to promote their EVs; (3) vehicle-station cooperation, such as Geely Auto and Tellus Power Group, who cooperate to provide a one-stop service that is more profitable; and (4) vehicles, piles, parking spaces, and internet service integral mode. For example, Win-sky expanded on a number of related businesses based on the charging network, vehicle internet, and parking spaces to increase profits. Other methods include (5) time-sharing renting and (6) crowd funding, which is represented by StarCharge, who is responsible for construction and operation, and enjoys the property rights of franchised EV chargers.
The above models are based on business, whereas we classified the EV charger enterprises into company-owned and franchised structure types according to how charging stations are operated based on the literature and existing operation structures in the EV charger market. This classification is commonly used in the operation literature; company-owned is a centralized structure, whereas the franchised structure is decentralized. Company-owned enterprises invest and build charging stations nationwide and self-manage them by hiring managers, such as SGCC and TGoods. The enterprise has the right to strictly standardize the management to enhance the quality and promote the operational efficiency of the whole company. The EV charger operator leading model, automobile enterprise leading model, and vehicle-station cooperation all belong to the company-owned structure. The relationship between the enterprise and each charging station manager in this type is that of the principal-agent, so each manager does not have the autonomy to operate the charging station, and thus, the incentive problem exists. The franchised type is represented by crowd funding firms like StarCharge, which experience less financial pressure. Under this mode, if the applicants can meet the requirements of having free spaces for parking five cars and extra capacity, the enterprise will provide the charging equipment and installment service for free and operate the EV chargers with the applicants and then they share revenue from the service fees of using EV chargers. This structure is useful to reduce the financial pressure on the EV charger enterprise. Each EV charger manager has its own profit, so the manager has a strong degree of autonomy. However, it is not convenient to uniformly manage and standardize the operation of each charging station because each franchised charging station manager has autonomy on the profit and operation, and they may sacrifice the quality of the EV chargers to pursue short-term profits.
Few theoretical models have been reported in the literature on EV charger industries. Wu et al. [
19] presented a monopolistic competition model for the differentiated products market to illustrate why the expected free market actually operates in a monopolistic competition market structure. However, besides from the market structure, determining how to arrange the operation or distribution structure of chargers is another key issue in the development of the charger market. The industrial economics literature has discussed how to arrange the supply chain or distribution structure, which consists of an integrated and decentralized structure in a competitive or uncompetitive market [
20], and has investigated the main factors that affect the distribution structure. First, product substitutability is important, and manufacturers will distribute their products through a company store for low degrees of substitutability, and use a decentralized distribution system for more highly competitive goods [
21,
22]. Second, demand and supply uncertainty have been examined in the choice of structure. An integrated or centralized structure is thought to be better when the demand uncertainty increases or is under a high supply risk, although centralization may decrease supply chain profits, resulting in the prisoner’s dilemma [
23,
24,
25]. Since variety can cause production and market costs, the variety and operation structure should be matched to produce better performance [
26]. Most analyses have been based on game theory models, and the price and quantity are common strategies depending on the goods’ substitutability [
27,
28,
29]; the competition intensities of the two variables significantly influence the equilibrium structure [
30]. However, quality selection, as an endogenous variable, has also been discussed. Cohen and Whang [
31] developed a product life-cycle model to study the price and quality choices of the manufacturers as they designed a joint product bundle for a product that may require maintenance and repair support after its sale. Zhao et al. [
32] researched how the structure of distribution channels may influence a firm’s quality and price strategies, and how they may in turn affect consumer welfare. They found that decentralization may reduce consumer welfare, but that decentralization in the high-quality channel hurts consumers more than it does in the low-quality channel. Some researchers used a multi-task model based on the principal agency model to analyze the operation structure, and stated that it is better to use dual channels because both structures have advantages in sales and brand maintenance, and mixing contracts is optimal [
33,
34,
35,
36,
37].
As for the construction of the charging infrastructure, multi-task models are not optimal because the needs and objectives are different during different development stages, especially in the early development period in China, so we must focus on one aspect: either quality or quantity. The operation, supervision, and profit factors cannot be ignored, and there has been no discussion about how these factors during different development stages affect the optimal quality and quantity in the optimal contract literature. These factors can affect the general results caused by the principal agency problem and free-riding problem in the two structures. We set up the theoretical models based on principle agency and the contract model [
34] considering these factors for both structures. We wanted to compare the differences in the optimal quantity and quality of EV chargers between the different structures, conduct a comparative static analysis of the environment factors that could affect the quantity and quality of EV chargers, and simulate the conclusions in the theoretical model, to determine the optimal development path during different stages in the development of the EV charger industry.
We separately established models to analyze the behavior of the company-owned and franchised EV charger enterprises and the optimal quantity and quality of EV chargers in the two structures. All of the critical factors in our model are listed in
Table 1.
2.2. Company-Owned EV Chargers
In the company-owned structure, we assumed that the EV charger enterprise built a total of
identical EV chargers, because the EV charger enterprise can centrally unify the funds and the business strategy. Since we were more concerned with the quality and the number of EV chargers due to the different operation structures and not the profit from the investment behavior, the investment profit of each EV charger was assumed to be constant,
, which was the same for the two kinds of EV charger structures. All the variables and parameters in our model have been explained in
Table 1 above. The investment profit changes at different development stages, which can similarly affect the quality and the number of EV chargers in both structures. Next, we investigated this effect by undertaking a comparative static analysis. The EV charger enterprise not only cares about the profits, but also the overall quality and safety of the EV chargers. We used the concept of comprehensive profit, which is equal to the product of profit and quality. Each EV charger has a manager hired by the enterprise, and the manager makes an effort,
, to maintain the quality and safety of the EV charger according to the requirements of the enterprise. According to the effort model of principal agency [
38], the quality production of the EV charger is
, and
,
to guarantee that quality increases with manager effort, and quality exhibits decreasing marginal production. Therefore, the comprehensive profit is
. Given information asymmetry, the enterprise cannot see the manager’s efforts based on the quality, so according to the principal agency model [
38], comprehensive profits are also affected by a normal random factor
, i.e.,
, where
is the variance of the random factor. The relationship between the enterprise and each manager is a principal-agent relationship [
39]. Managers do not have ownership and operational autonomy, and only receive wages from the EV charger enterprise headquarters, which consists of a fixed salary (denoted as
) and a performance-related salary. The performance-related salary is positively related to the comprehensive profit, and the incentive coefficient is
, where
is constant,
, and
is the supervision difficulty parameter for the enterprise. The incentive coefficient is inversely proportional to the difficulty parameter of supervising because the more difficult the supervision, the greater the influence of the uncertain information. So, the EV charger enterprise will be less motivated to offer incentives to the managers. Therefore, the salary of each EV charger manager is:
The greater the effort of the manager, the higher the quality of the EV charger, and then the higher the performance-related salary. Since it takes time and effort to operate the EV charger, we assume that the manager’s operation cost to maintain the quality of the EV charger is
. We assume
and
, so that the function increases with effort and performs an increasing margin cost.
is a parameter in cost function, and satisfies
: the larger the parameter
, the larger the operation cost. The utility function of the EV charger managers is:
The EV charger enterprise supervises the managers, and the supervision cost is
, with
,
, so that the cost function increases with the total number of EV chargers and displays an increasing margin cost.
is the supervision cost parameter we mentioned above that satisfies
, which means that the larger the
, the larger the supervision cost. Then, the profit of the EV charger enterprise equals the sum of the comprehensive profit of all
charging stations minus the salary of all charging station managers, and then its own supervision cost
is subtracted. The profit is:
Therefore, the optimization process in the principal agency relationship of the company owned structure charger enterprise is: given the coefficients of salary, which are
and
, the charging station managers will choose the level of effort to maximize their utility. The optimization problem of the EV charger manager is:
Then, the enterprise will select the appropriate number of charging stations to maximize the expected net profit condition on the manager’s optimal effort choice, which is the incentive condition (IC) of the manager of the EV charger. The enterprise will guarantee the manager’s participation, which forms the managers’ participation condition (PC).
To summarize, the optimization problem of the EV charger enterprise is:
Subjected to:
where Equations (5) and (6) are the manager’s PC condition and IC condition, respectively. Then, we solved the optimization problem backward: we found the optimal choice of the manager from Equation (6), and then we solved the optimal choice of the enterprise. We drew the following conclusions after derivation:
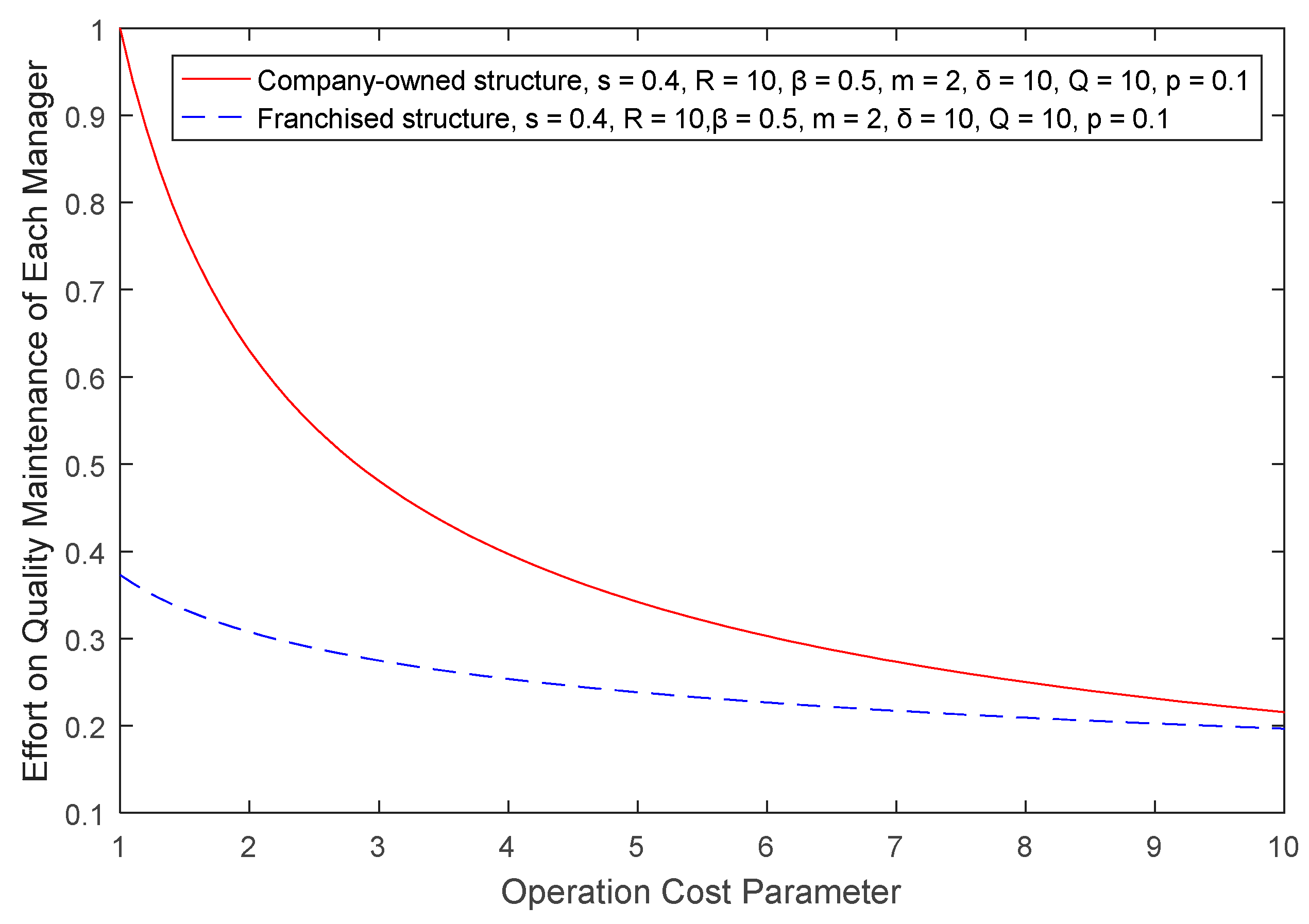
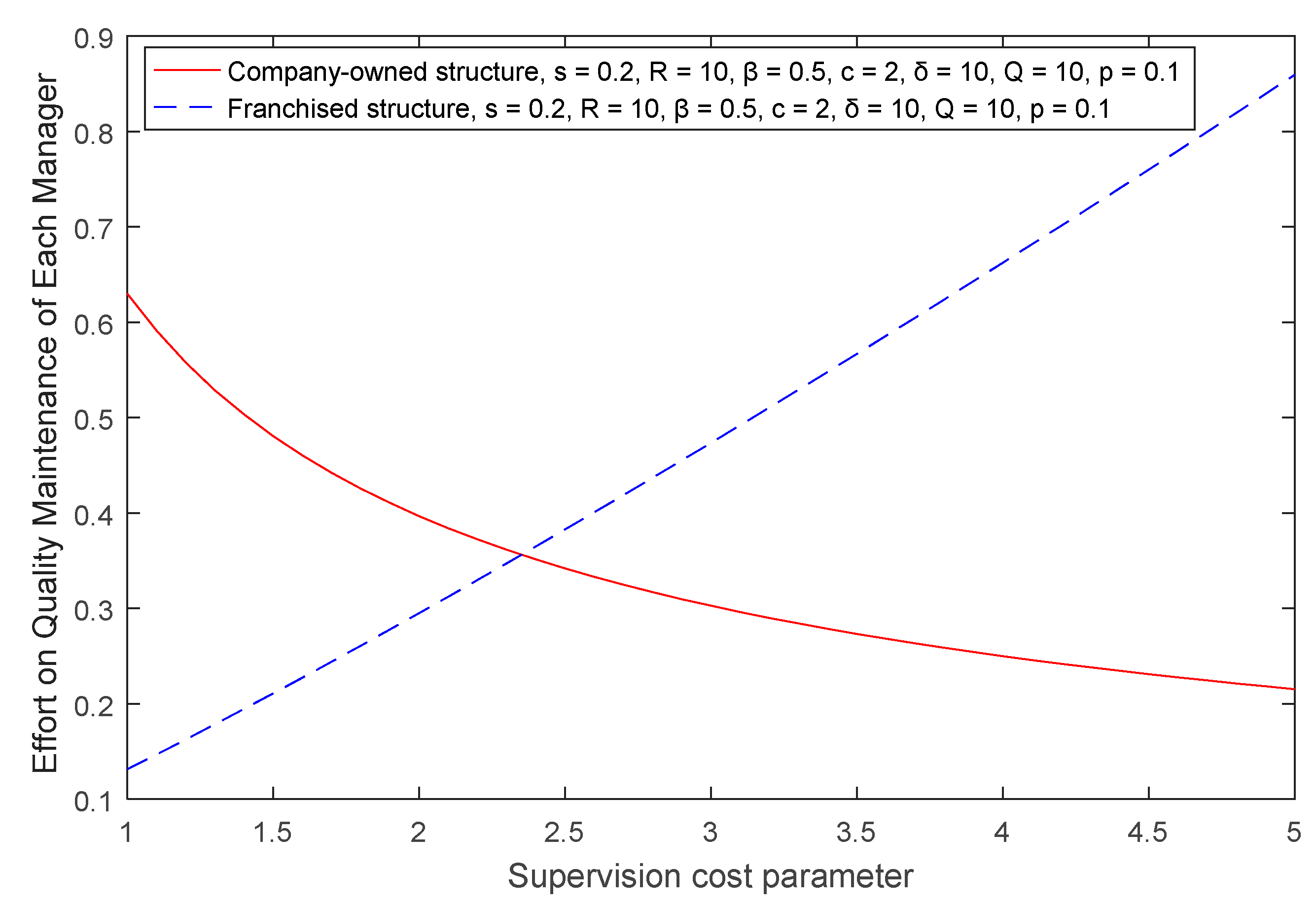
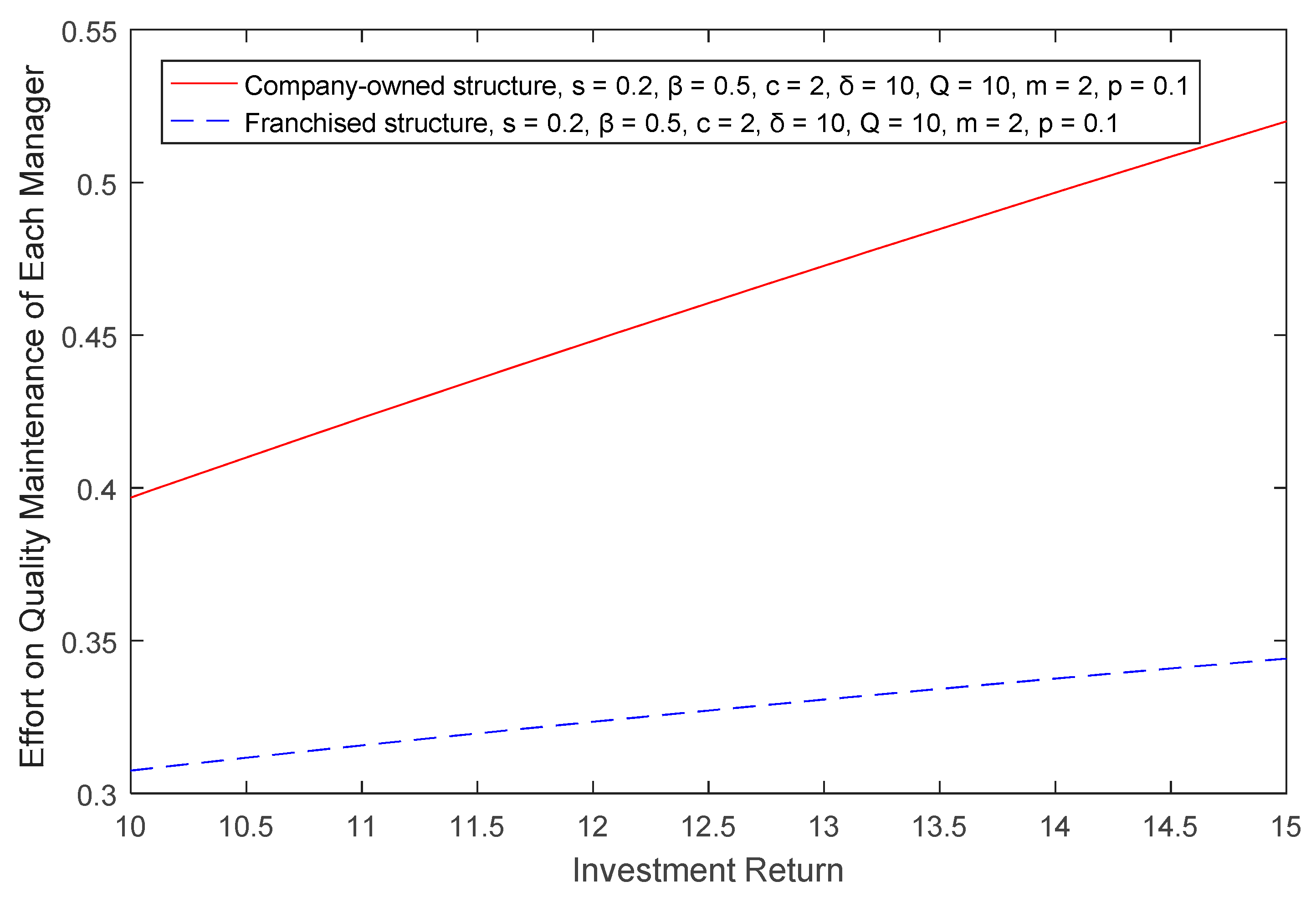
Lemma 1. For EV charger enterprises that use a company-owned structure, the quality of the EV chargers is positively correlated with the investment return, whereas it is negatively correlated with the operation cost of charging stations and the supervision difficulty of the enterprises.
Proof. Since the certainty equivalence of the manger is
, the best effort of the manager of the EV charger can be obtained from the following problem:
Take the partial derivative of the objective function with respect to variable
, we obtain the first-order condition:
Then, we take the partial derivative with the operation cost parameter
, investment return
, and supervision difficulty parameter
, and obtain, respectively:
Since , , , and , we know that , and from Equations (9)–(11), so we proved the conclusion. □
Lemma 2. The total number of EV chargers in the company-owned enterprise decreases with the increase of operation costs and the supervision difficulty of the enterprise, and increases with the increase of the investment return.
Proof. To ensure generality and convenience of solving problems, we assumed that
, then based on Equation (5), we obtain:
In order to easily obtain the solution, we further assumed that
,
and
, where
is the production elasticity of efforts and
. Therefore, the optimal level of effort is:
After incorporating Equations (12) and (13) into the objective function of the EV charger enterprise, the maximization problem of the enterprise becomes:
Taking the partial derivative of the function with respect to variable
, we obtain the optimal total number of chargers, which is:
Then, we easily obtain
and
. Taking the partial derivative of this function with respect to variable
:
When is large enough, for instants, , which means the supervision cost is large enough, and since , , and we know the first negative term in the bracket , which is negative, dominants in the value of all the terms, so the whole formula will be negative. □
2.3. Franchised EV Chargers
If the EV charger enterprise uses the franchised structure, the expansion is not directly planned and financially supported by the EV charger enterprise itself, but by the applicant who wants to build the EV charger. After obtaining franchise permission, the applicant invests in the place where the EV charger is needed, builds the EV charger with the help of the EV charger enterprise, and uses its brand to operate. The franchised station will be independent and the profits belong to the applicant. Since the EV charger enterprise does not participate in the specific operation of the charging station, the management and quality of all EV chargers cannot be regulated. The quality of the franchised EV charger depends on the average effort of all managers of the franchised EV charger. If each manager’s effort is
,
, and
is the number of franchised EV chargers, then the average level of effort is
. Similarly, the quality function is the same as the company-owned EV chargers, so the quality of the franchised EV chargers is
. We assumed that the investment of each EV charger was the same and the investment return is
, so the comprehensive income of each franchised EV charger is
considering the influence of the random factor
. The enterprise supervises the EV chargers to a certain extent. In the franchised structure, the charger manager has considerable autonomy, and they only pay the franchise fees to the EV charger enterprise, and keep the profits for themselves. When the EV charger has a quality problem, the operation of the franchised EV charger is stopped and the revenue of the manager is zero. If it is assumed that the probability that a franchised EV charger has a quality problem is
, then the probability that no quality problem is found is
. Therefore, the expected comprehensive income is:
This probability
can incentivize the manager of the franchised EV chargers. However, in the company-owned structure, the charger manager has no autonomy, and only receives a wage from the EV enterprise. When the EV charger has a quality problem, the wage of the manager will be low, and the operation of the EV charger will not be stopped. This is why there is no probability
in the company owned piles. The low quality leads to low comprehensive profits and low wages of the manager, which can incentivize the manager in the company-owned structures. Similarly, the manager’s operation cost of the franchise EV charger is still
. Therefore, the expected utility of the manager is:
The enterprise does not share the profits of the EV chargers and only charges the applicants the franchise fee, but also profits by providing construction and maintenance services to the franchised EV charger. The profit of the EV charger enterprise is denoted
. The enterprise also cares about the quality and safety of the EV chargers, so the enterprise’s comprehensive revenue generated from each franchise is
. The total revenue of all franchised stations is
. We assumed that the supervision cost of the enterprise under the franchise structure is still
. Then, the expected net profit of the enterprise is:
We still used backward induction to solve the optimal problem in the franchised structure charger firm. First, the franchised charging manager chooses the best effort to maximize their expected utility, and the optimization problem is:
Then, given the optimal effort level of the franchised charging station manager, the EV charger enterprise selects the optimal number of franchised EV chargers to maximize its expected profits. The optimization problem of the enterprise is:
After solving the optimization problem, we obtained the following conclusion:
Proposition 1. When the number of joining franchisees reaches a certain critical value, the quality and safety level of the franchised EV charger will always be lower than the company-owned chargers.
Proof. The certainty equivalent of the franchised EV charger manager is:
Therefore, the maximization problem of the franchised manager becomes choosing the optimal effort level to maximize Equation (20). Taking the derivative with respect to
in the above formula, we obtain:
where
. Since each franchisee is symmetrical, we have
. Then, the first-order condition is:
Comparing Equations (22) and (8), which is the first-order condition of the optimal effort of each manager of the company-owned EV charger, we know that when , i.e., , the marginal revenue of effort of the franchised EV charger manager is always less than the marginal revenue of effort of the company-owned EV charger manager. However, the marginal cost of the quality supervision is the same, so we obtain and then , which means the quality of the franchised EV charger will always be lower than the company-owned chargers.
The reason why the quality of the franchised EV charger deteriorates is that the quality of the franchised EV chargers depends on the average quality management effort of all the franchised managers, and each manager can only determine their own effort level, which means that their own effort has a small impact on the average effort and quality. Therefore, the optimal strategy of each franchised manager is to reduce their own effort level and be a free rider. Since each manager behaves in this way, the average effort level of the entire franchised EV chargers is reduced, as does the quality of the franchised EV chargers, which is consistent with the empirical conclusions in the literature [
40,
41].
The first-order condition of the franchise mode is
when
and
. Thus, the optimal effort level of the franchised manager is:
We substituted
into the objective function of the EV charger enterprise and obtained:
Taking the derivative with respect to
, we obtain:
Thus, we can determine the optimal total number of franchised EV chargers:
□
Comparing
and
, we obtain
, so we drew this conclusion:
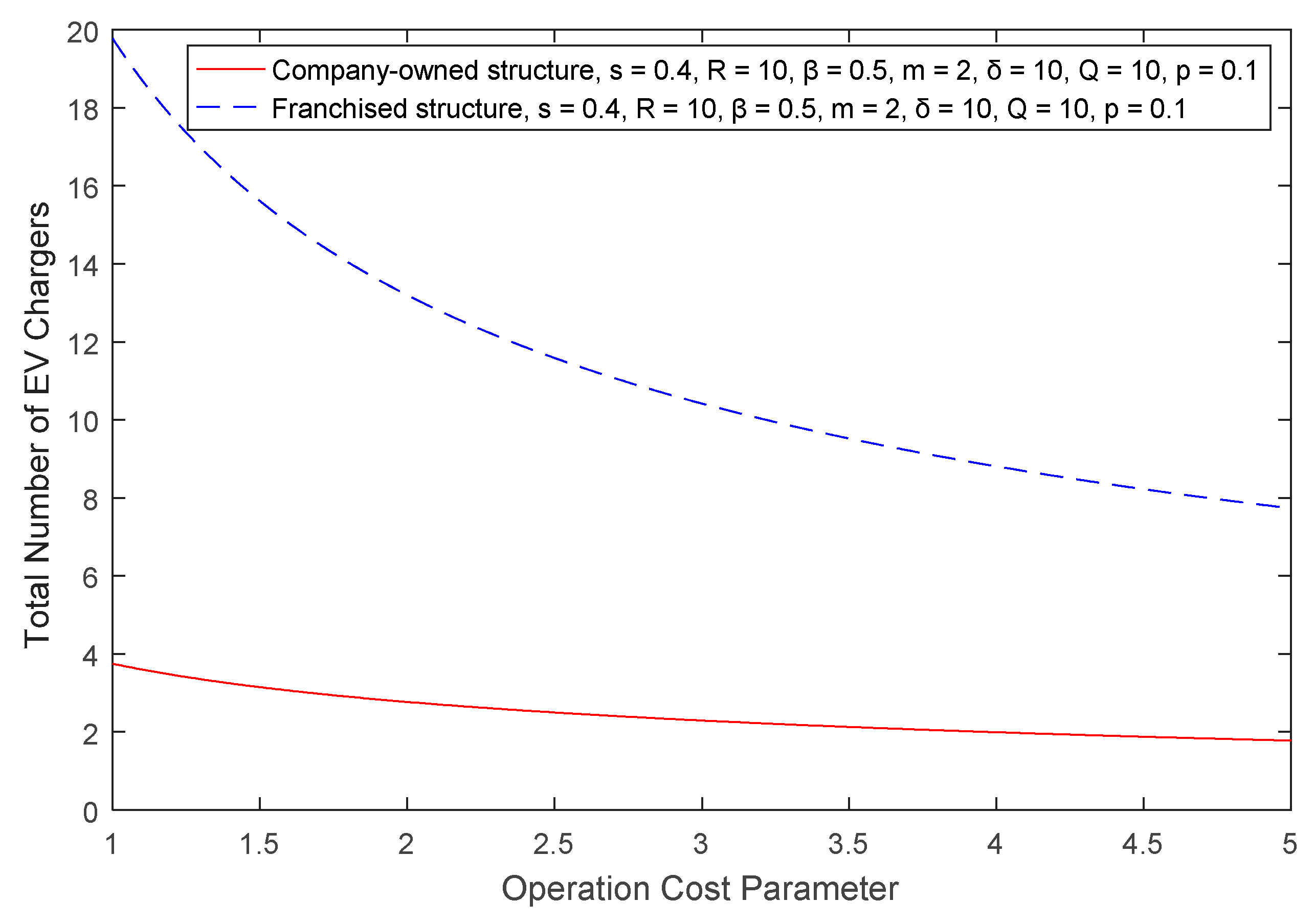
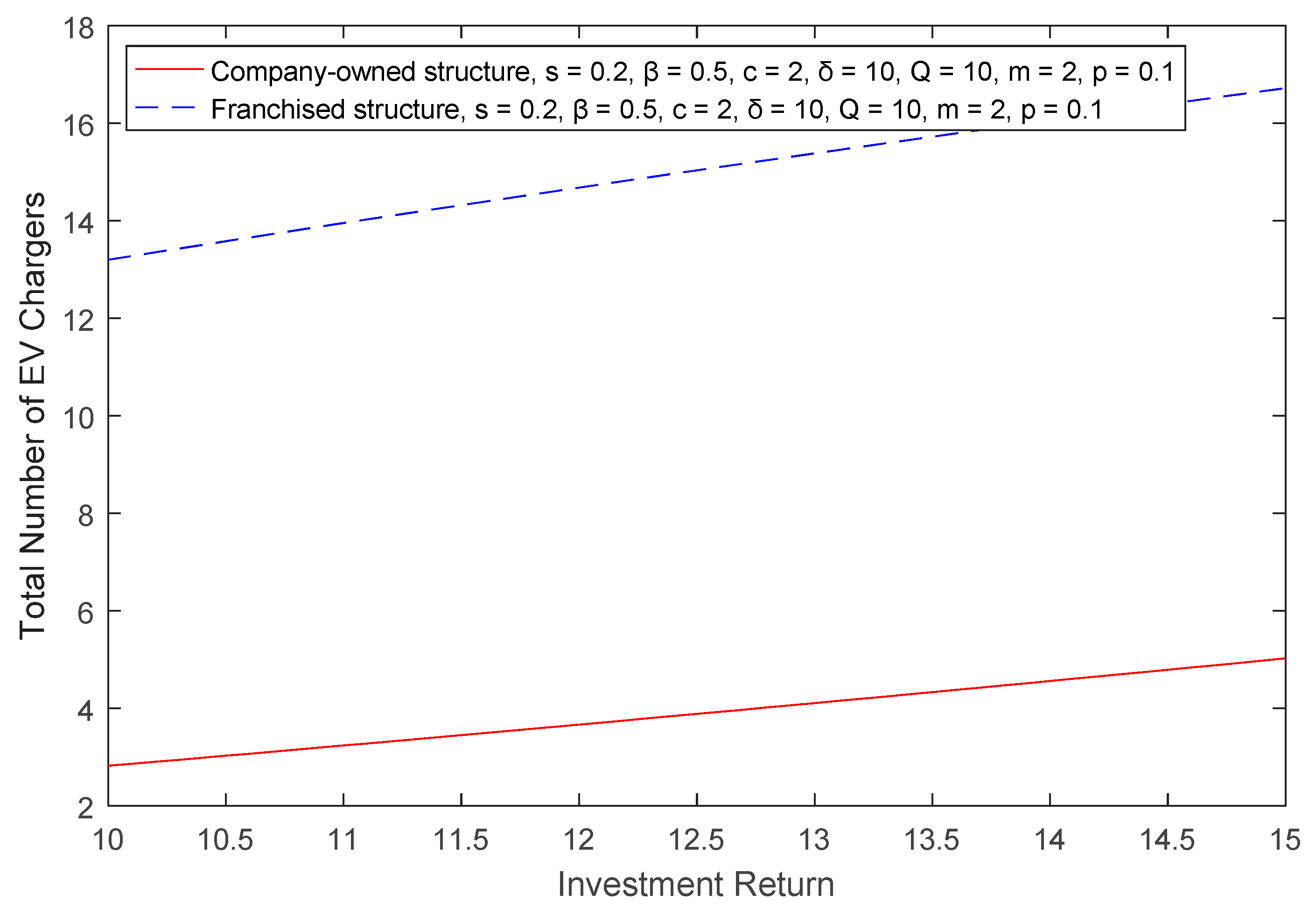
Proposition 2. The optimal total number of EV chargers in the franchised structure is greater than the total number in the company-owned structure.
After taking the derivative with respect to the operation cost parameter
in the formula of the number of EV chargers
, we obtain:
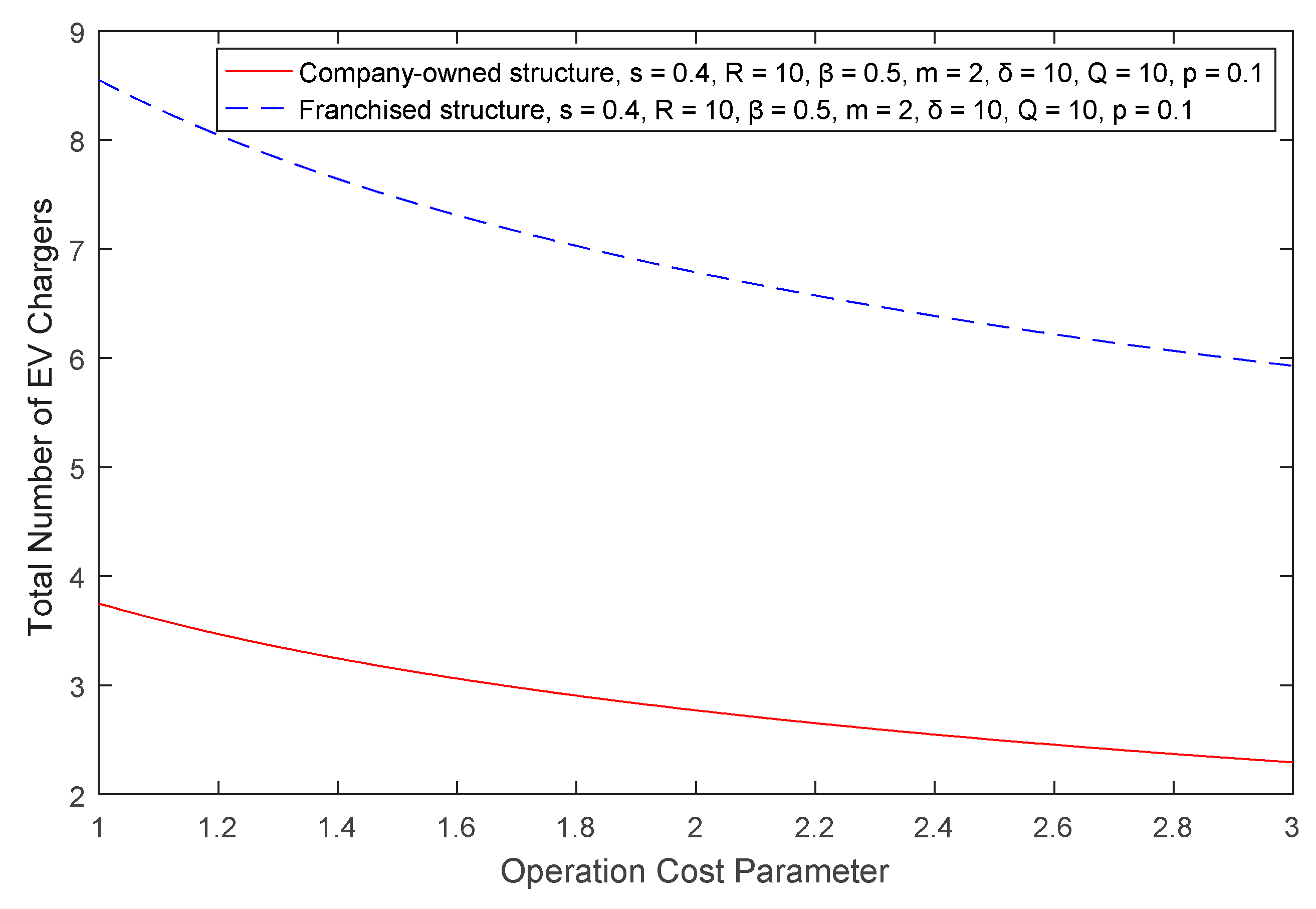
That is, the greater the operation cost, the smaller the optimal number of franchised EV chargers. By also taking the derivative with respect to the supervision cost parameter
in Equation (26), we obtain:
This means the number of optimal EV chargers is negatively correlated with the difficulty of the enterprise in supervising the franchised EV charger. Similarly, taking the derivative with respect to the investment return of each franchisee
, we obtain:
This means that as investment revenue increases, the number of joined EV chargers increases. Therefore, we summarize these conclusions into Lemma 3 below.
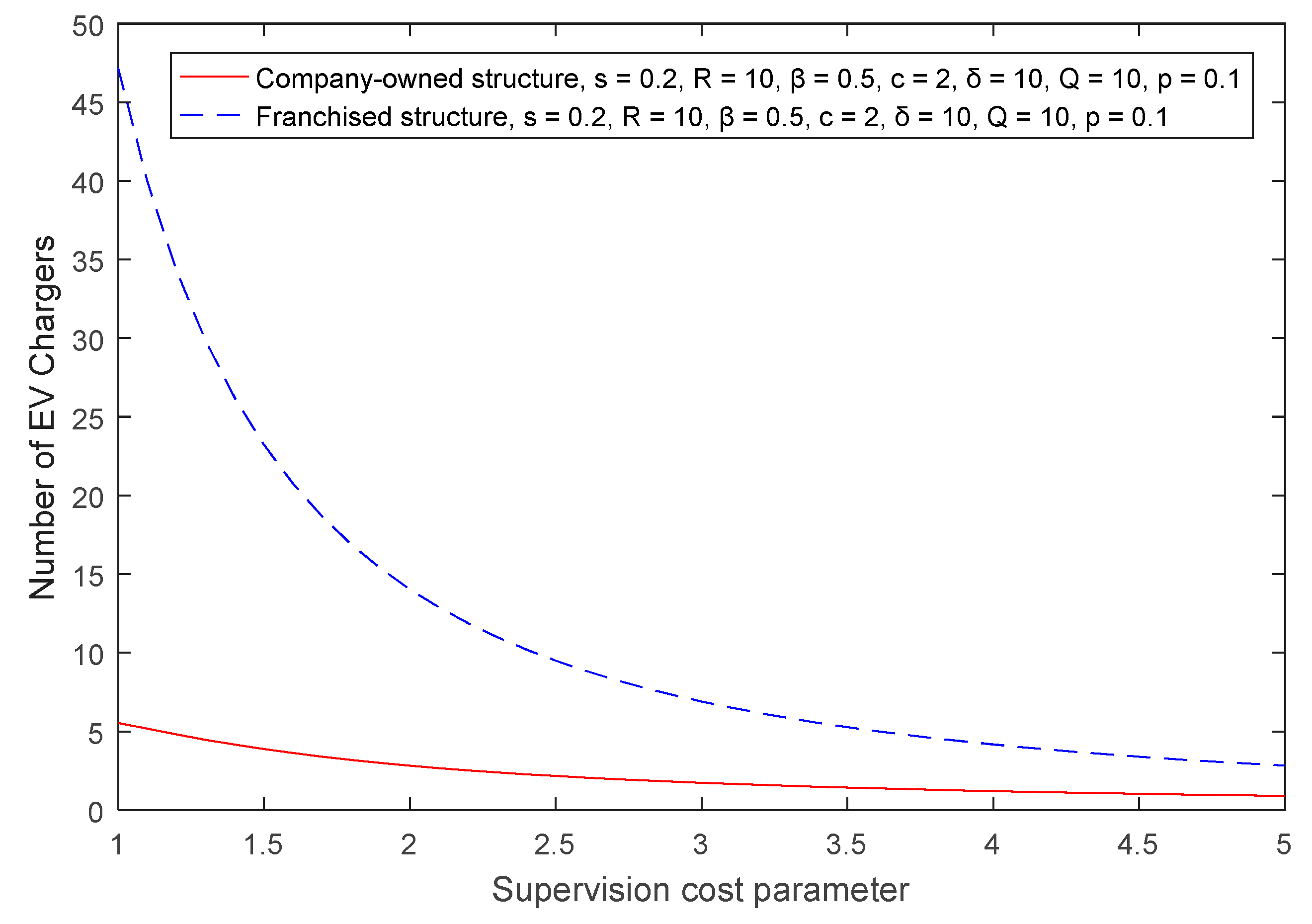
Lemma 3. The total number of franchised EV chargers decreases with the increase in operation and supervision costs, and increases with the increase in investment revenue.
Then, we considered the quality of the franchised EV charger. Substituting the optimal effort of the franchised EV charger manager with the quality function, and using the conclusion of Lemma 3, we can obtain:
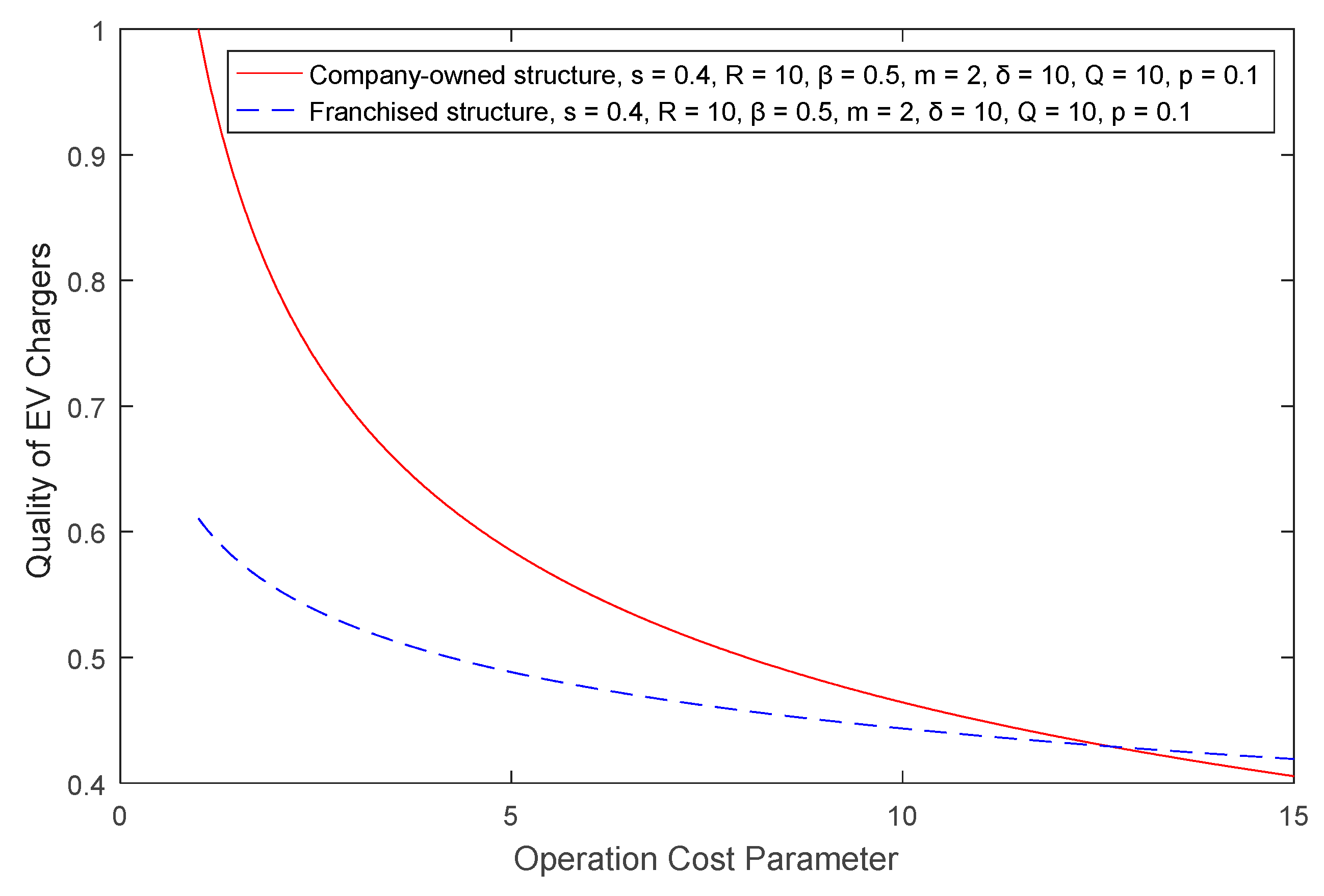
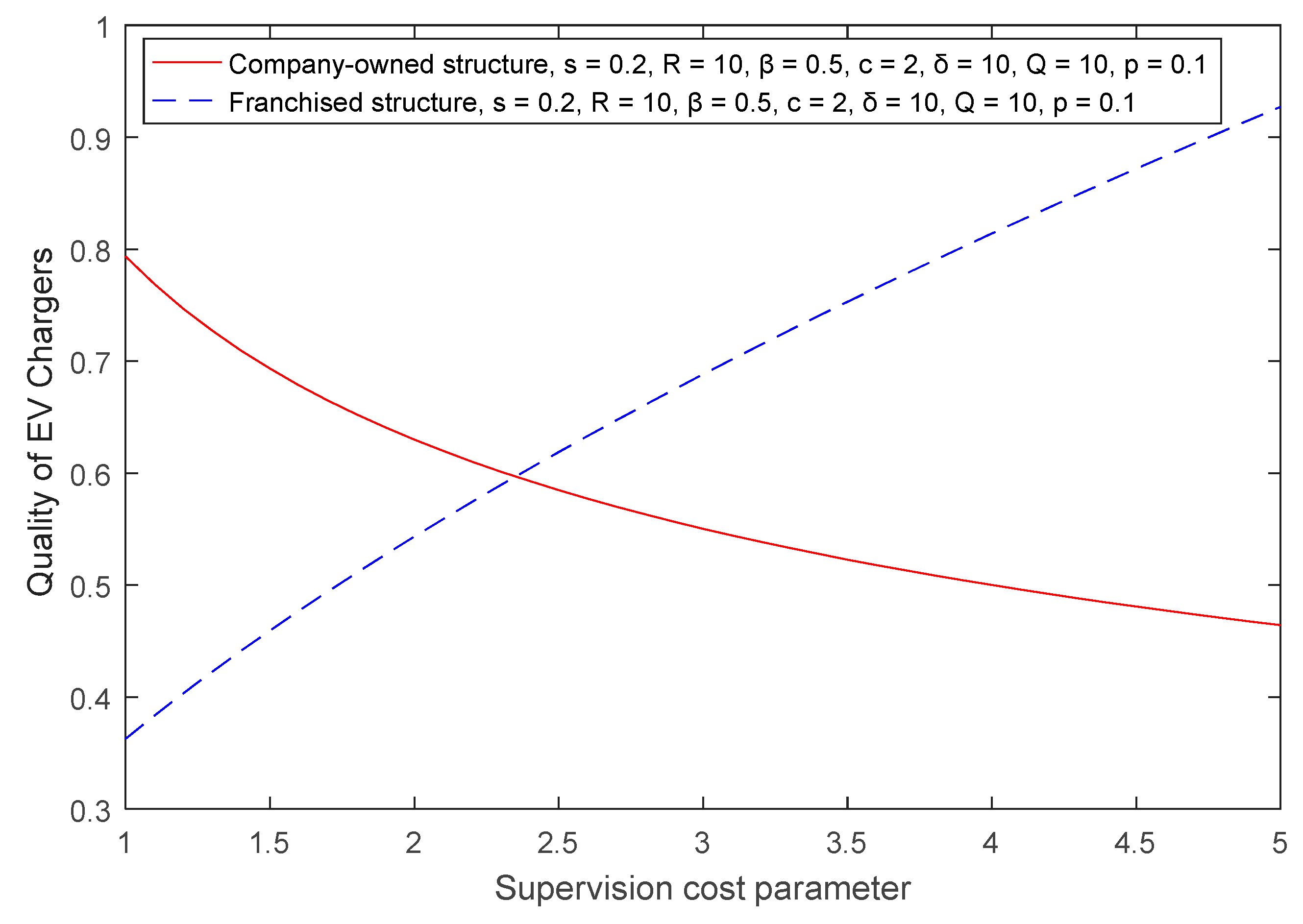
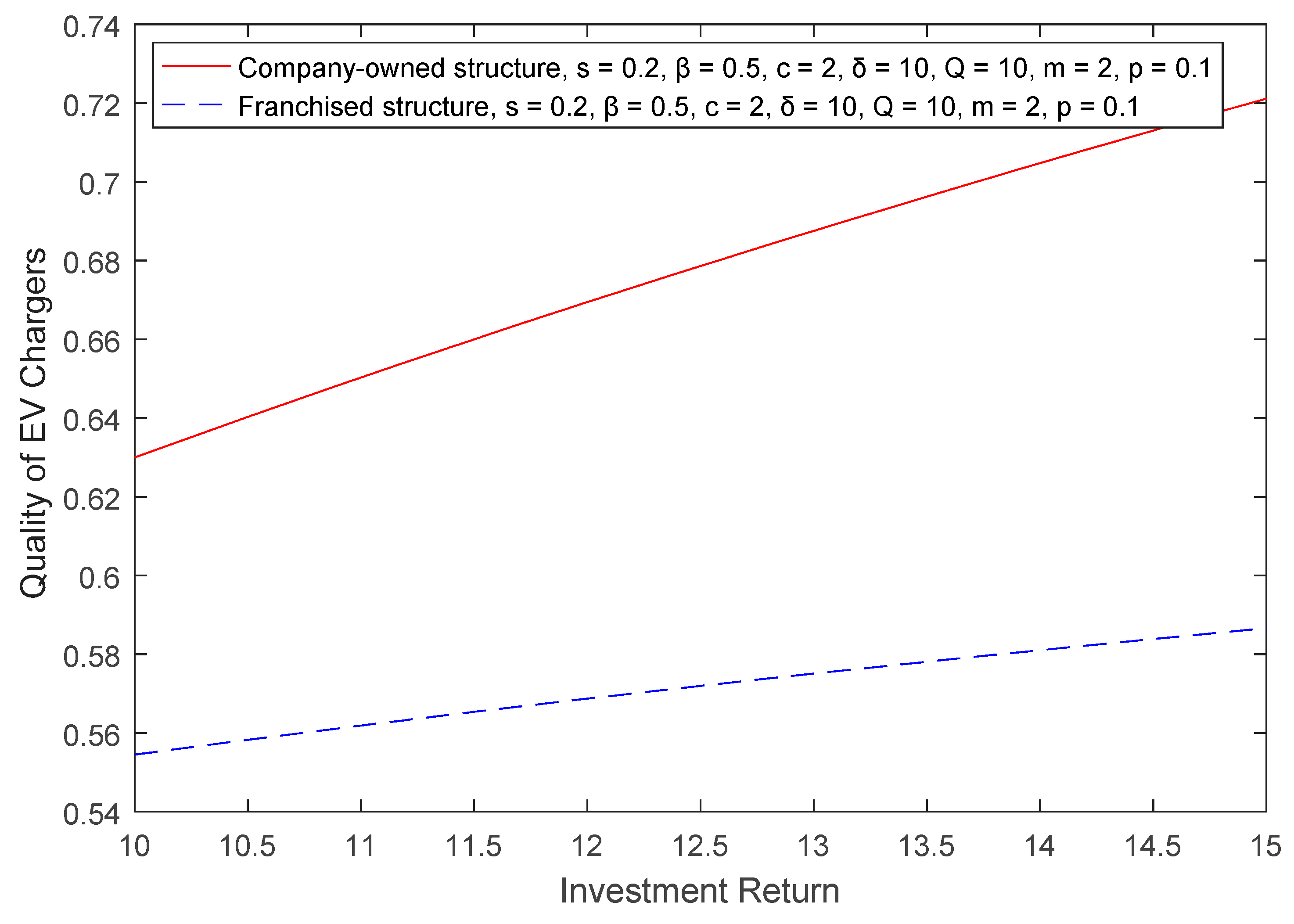
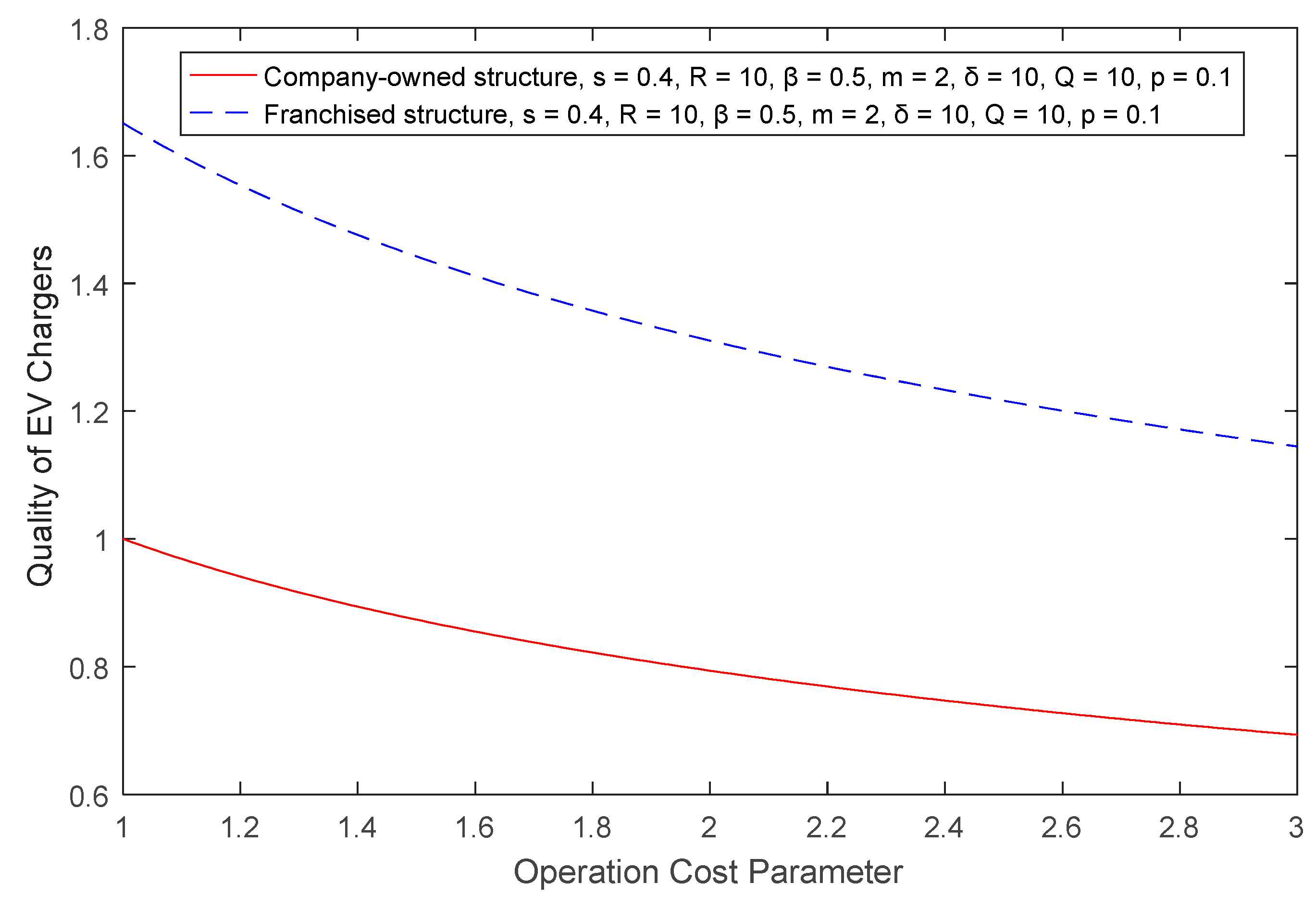
Lemma 4. When the total number of EV chargers is large enough, the quality of EV chargers in the franchise structure is negatively correlated with operation costs, and is positively correlated with the supervision costs and the investment return.
Proof. The quality of the EV chargers is:
Taking the derivate with respect to the operation cost
in Equation (30) above:
When the number of EV chargers
is large,
can be guaranteed to be positive and
, which means that the greater the operation cost, the worse the safety quality of the EV chargers. Then, taking the derivative with the supervision difficulty parameter
in Equation (30), we obtain:
As the enterprise experiences more difficulty in supervising the franchised EV charger, the optimal number of franchised EV chargers is reduced, so the free rider problem decreases, and the quality of the franchise improves. Similarly, we took the derivative with the investment return
and we obtained:
Since , the sign of depends on the difference in the values of and . When the investment revenue increases, the effort and the quality increase; however, the optimal number of franchised EV chargers also increases, which means that there are more free riders. When , which means that the effort increasing effect is larger than the free-riding effect, then . In this situation, the quality of the EV charger increases when the investment revenue increases; however, when , which means that the effort increasing effect is smaller than the free-riding effect, then there is , and the quality of EV charger decreases when the investment revenue increases. When the total number of charging files is large enough, the former situation occurs. □
5. Conclusions and Policy Implications
EVs have begun to enter the stage of market-oriented development in China, and will become the main component of the automotive market in the future under the advocacy of a low-carbon economy. However, the insufficiency of EV chargers has become a major factor restricting the effective development of EVs. Although the government has provided subsidies for the construction of EV chargers, the development plan of the distribution structure for EV chargers must be considered, and the quality and quantity of chargers under different structures must be investigated to guide the EV charger market toward healthy and effective development.
We analyzed the difference in the quality and quantity of EV chargers under company-owned and franchised structures by constructing theoretical models and discussed the trends of the quality and quantity of EV chargers in different market environments. First, the number of franchised EV chargers was larger in most cases, but the quality was worse when compared with the company-owned structure. Second, with the increase in operational costs, the optimal numbers and the quality of EV chargers declined in both structures. Third, with increasing supervision costs, the total number of all chargers decreased, as did the quality of the company-owned EV chargers; however, the quality of the franchised EV chargers increased due to the decreasing number of franchised chargers, which led to a decrease in free-riding behavior. Finally, a high investment return was more motivating in the company-owned structure because, although the quality and total number improved in both structures, the quality of the franchised chargers increased less than the company-owned ones.
Based on these results, we think that, in most cases, the franchised and company-owned structure face a trade-off between quantity and quality. However, in the initial development stage of the EV chargers, the operation and supervision costs are high because of insufficient experience, the franchised structure is more conducive to increasing the quantity to meet the increasing needs of EVs, and the quality is not necessarily lower. As the market becomes more saturated and a higher quality of EV charger is required, the company-owned structure will be needed to improve the quality. For the existing EV chargers constructed in the franchise structure, the supervision efficiency should be improved to avoid free-riding behavior, so that the number of EV chargers can be maintained while the quality can be guaranteed.