1. Introduction
As a healthy and environmentally friendly transportation mode, cycling has become more and more popular in the United States (US) over the past two decades [
1]. Previous research has indicated that cycling can provide substantial individual health benefits and alleviate negative impacts of motorized transportation, such as congestion and pollution [
2,
3,
4,
5]. Promoting the development of cycling could clearly benefit the social, environmental, and economic sustainability [
6]. According to the League of American Bicyclists, the number of bicycle commuters has been increased by 43% nationwide from 2000 to 2017 in US [
7]. However, the percentage of people commuting by bicycles is still low. The 2017 National Household Travel Survey (NHTS) reported that the bicycle mode share for commuting is only 1.1% [
8]. Compared with European cities, the bicycle ridership level is much lower in US [
9], indicating a substantial potential for increase.
Out of all the deterrents to bicycling, the safety concern has been identified as a primary hindrance [
10]. As non-motorists, bicyclists are more vulnerable when exposed to traffic crashes compared to drivers or passengers within vehicles [
11,
12]. When people have concerns about traffic safety, they would be less willing to travel by bicycles. As such, reducing vehicle-bicycle crashes could potentially increase the bicycle ridership and promote the sustainable development of urban transportation. Among various types of vehicle-bicycle crashes, the hit-and-run (HR) crashes are particularly dangerous. In such a case, the driver of the offending vehicle flees the crash scene without providing any assistance to the possible victim(s) or informing the traffic safety authority for an emergency response. Previous studies estimated that a 10 min reduction in the response time of an emergency medical service could reduce fatalities by one-third [
13]. Conversely, HR could significantly increase the potential for serious injuries or even fatalities owing largely to delayed or non emergency medical services. A recent report of the American Automobile Association (AAA) indicates that HR crashes have increased from 627,200 in 2010 to 737, 100 in 2015 by 17.5% in US [
14]. Meanwhile, number of bicyclist fatalities from HR crashes has increased from 94 to 129 by 37.2% during the same period, and more bicyclists have suffered from injuries [
14]. Therefore, it is imperative to identify factors contributing to HR in vehicle-bicycle crashes and develop effective means to limit such erroneous behavior.
While the investigations into crashes involving HR actions have drawn some attentions, most of these studies have focused on vehicle–vehicle or vehicle–pedestrian crashes [
15,
16,
17,
18,
19,
20,
21]. For instance, Tay et al. [
15] published one of the most notable studies on factors contributing to HR crashes. Using police-reported crash data in Singapore, a logistic regression model was applied to identify factors associated with HR actions. In this study, drivers were found to be more likely to flee from crash scenes when crashes occurred at night, on a straight road, and near shops. Crashes involving right turn and U-turn maneuvers were less likely to involve HR actions. In another study conducted by Tay et al. [
16], a logistic regression model was developed and factors including highway functional class, speed limit, lighting condition, and roadway profile were identified as key factors affecting HR in fatal crashes. To identify factors associated with HR pedestrian fatalities, Macleod et al. [
17] developed a logistic regression model using U.S. national fatal crash records from 1998 to 2007. Alcohol usage and invalid driving license were revealed as the leading factors contributing to HR pedestrian fatalities. Aidoo et al. [
18] conducted a study on HR crashes involving pedestrians using data from Ghana. Based on the calibrated logistic regression model, drivers tended to be more likely to flee crash scenes when crashes occurred in nighttime, on straight and flat road without medians, and at intersections. Zhang et al. [
19] studied HR crashes using a comprehensive dataset from Guangdong Province in China. Based on the calibrated logistic regression model, crashes occurring in dark environments, involving pedestrians, and caused by male and middle aged drivers were more likely to be involved with HR actions. Roshandeh et al. [
20] further investigated the effect of distractions on severe crashes caused by HR actions. In the study, the data set was split into two subsets according to crashes with and without driving distractions. It was found that non-distracted drivers were 27% less likely to flee crash scenes after crash occurrences compared to the behavior of distracted drivers. Unlike most of the previous research utilizing the maximum likelihood estimation of logistic regression models, Xie et al. [
21] employed real-time traffic data to investigate factors contributing to HR crashes. According to this study, the increase in upstream speed and average occupancy could potentially increase the possibility of HR actions. To identify factors contributing to HR in vehicle–bicycle crashes, Lopes et al. [
12] analyzed police reported crash data within Boston, Massachusetts from 2009 to 2012. Similar to most previous studies, this study also utilized logistic regression model. The results revealed that the probability of HR depended on the day of the week, time, and whether the vehicle was a taxi.
As shown in the literature, most of the existing studies regarding crashes involving HR actions have focused on vehicle–vehicle or vehicle–pedestrian crashes. Relatively little attention has been paid to factors affecting HR in vehicle–bicycle crashes, which has motivated the current study to conduct a thorough investigation. It should also be noted that the majority studies were performed using regression analysis. Of which, logistic regression analysis is predominant. However, logistic regression analysis maintains certain assumptions between crash contributing factors and crash occurrences, which needs to be validated before the calibrated models being used for predictions. To overcome this limitation, non-parametric classification algorithms such as the Classification and Regression Tree (CART) method have increasingly been adopted for traffic safety analysis [
22,
23,
24]. Nevertheless, classification algorithms only work well when the dataset is balanced, which means different classes are equally represented in the dataset. This is usually not the case for traffic crash datasets. In a typical traffic crash dataset, the number of minority instances (such as HR crashes) is much lower than that of majority instances (such as NHR crashes). If the data imbalance problem is left untreated, the classification model would classify the majority class more accurately while misclassifying the instances in the minority class, which makes the model fail to be informative in reality [
25,
26]. The main reason for this performance degradation is that traditional classification algorithms focus on achieving the highest overall accuracy. Additionally, when the dataset is imbalanced, the minority class hardly contributes to the accuracy compared with the majority class. For instance, if the majority class accounts for 90% of the data in an imbalanced dataset, a classification algorithm might easily acquire a 90% overall accuracy by assigning all the data to the majority class. Apparently, this high accuracy is pointless because the classification accuracy for the minority instances is 0%. This could be a serious problem when the identification of the minority class is of the interest. In the past decade, hundreds of algorithms have been proposed to treat data imbalance problems. These algorithms can be divided into two groups: Preprocessing and cost-sensitive learning. Preprocessing is usually performed to alleviate the imbalance problem in the input data before applying classification algorithms. Two classical techniques could be adopted for preprocessing: Resampling and feature selection. On the other hand, cost-sensitive learning assumes higher cost for the minority class misclassification with respect to the majority class misclassification. Additionally, the cost-sensitive learning can be incorporated at both the data and algorithm level. Please refer to Reference [
27] for a detailed review. The current study will adopt the resampling approach to treat the data imbalance problem. This is mainly because the resampling approach is independent of the selected classifier, which makes it more versatile.
The current study will contribute to existing literatures in several ways. First, it will extend previous HR studies by exploring various factors affecting HR in vehicle-bicycle crashes. Second, the CART method is introduced to overcome the limitations of logistic regression, which is the predominate model adopted by previous HR studies. Last, it will evaluate the impact of data imbalance on HR crash classification accuracy by incorporating a resampling algorithm. The remainder of this paper is organized as follows:
Section 2 describes the dataset and provides the descriptive statistics.
Section 3 introduces the main steps of the proposed methodology.
Section 4 presents analysis results and discussions. Finally,
Section 5 provides the summary and conclusion, and points out the study limitations.
2. Data Preparation
The data used in the current study is extracted from police-reported data within the jurisdiction of City of Chicago from September 2017 to August 2018 [
28]. As one of the best large cities in the US for bicycling, Chicago has more than 200 miles of on-street bike lanes, and more than 13,000 bike racks and bike parking areas at many rail stations [
29]. With substantial and sustained investment in bicycling infrastructures, Chicago has a national reputation as a bike-friendly city. Chicago has planned to establish a 645 miles network of bicycle facilities by 2020 and make bicycling an integral part of citizens’ daily life. To make that happen, the bicycle safety condition needs to be improved. From September 2017 to August 2018, there are 1,475 vehicle-bicycle crashes, of which 319 are identified as HR crashes, accounting for 21.6% of the total crashes. The original dataset contains detailed information about each crash, including roadway characteristics, crash time, the attributes of bicyclist, and vehicle involved in the crash, and so on. In the current study, the target variable is HR. For the modeling purpose, 18 independent variables are selected, including gender of bicyclist, age of bicyclist, bicyclist safety equipment, injury classification, bicyclist visibility, location of bicyclist, traffic control device, traffic control device condition, weather condition, lighting condition, traffic way type, roadway surface condition, crash hour, crash day of week, gender of driver, age of driver, driver action, and vehicle type. Please find the detailed summary statistics of variables in
Table 1.
3. Proposed Methodology
3.1. Classification and Regression Tree
In the current study, the Classification and Regression Tree (CART) method is employed to identify factors contributing to HR in vehicle-bicycle crashes. Originally proposed by Breiman et al. [
30], the CART method has become one of the most popular methods for data mining. As a non-parametric supervised learning method, the CART method can predict the outcome of a target variable by learning the decision rules inferred from a set of independent variables. Unlike the traditional regression models, such as logistic regression and ordered discrete outcome models, the CART model does not impose any predefined underlying relationship between the target variable and the crash contributing independent variables. Another major advantage of the CART model is that the analysis results could be visualized as a tree structure, making it easy to be interpreted and understood. A regression tree can be used for a continuous target variable and a classification tree can be built when it is categorical. In this study, the target variable refers to HR or NHR, which is discrete. Therefore, a classification tree is developed.
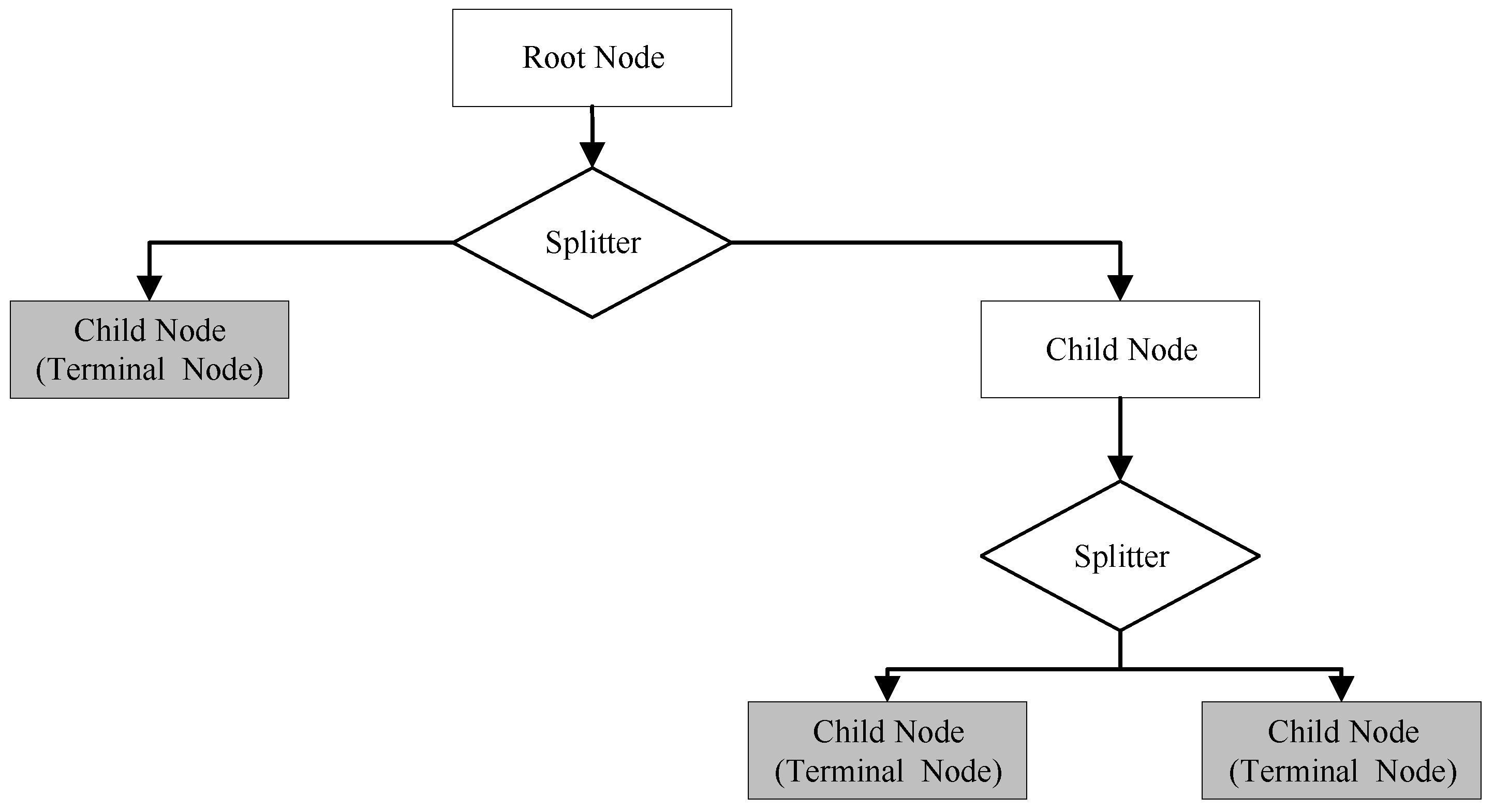
The execution of the CART method generally involves two major steps: Tree growing and pruning. Tree growing starts at the root node, which includes all data in the dataset. The root node is then divided into two child nodes by a splitter (independent variable), which yields the best improvement of purity of the two child nodes. In other words, the CART method chooses the splitter which can maximize the homogeneity of resultant child nodes. To select the best possible independent variable, a number of splitting criteria can be utilized. In the current study, the Gini index, which is the most common splitting criterion for nominal data, is used as the splitting criterion. If the root node
m is partitioned into two subset nodes (child nodes
n1 and
n2) by a candidate variable
θ, the Gini index for any child node is calculated as follows:
where
H(
n(
θ)) denotes the Gini index of the child node
n, and
p(
k|n) is the proportion of class
k records in node
n. Then the impurity at node
m can be calculated using the following function:
where
Nm is the total number of observations at node
m;
o1 and
o2 are numbers of observations in child node
n1 and
n2, respectively. The CART method seeks to split the root node
m by selecting the variable
θ* which can minimize the impurity at node
m:
This will create two child nodes that are as homogenous as possible. The tree growing process in execution of the CART method follows a binary recursive partitioning process. The term binary means each node in the tree can only be divided into two child nodes, in which case, the original node is called a parent node. The term recursive indicates that the above-mentioned binary partitioning process continues recursively for any resultant child node. Starting at the root node, the tree growing process goes on and on until it is impossible to split any node. At which point, the tree stops growing. This happens when all observations within each child node fall into an identical class or some preset constraint is met (for instance, the maximum depth of the tree).
Figure 1 illustrates the general structure of a decision tree.
The maximum tree created following the above procedure is most likely over fitting, lacking generalization ability. This means the tree corresponds too closely to a particular dataset and could result in high misclassification when classifying a new dataset. In this respect, tree pruning is an essential step to apply the CART method. The principle is to cut off branches which add little to the predictive value of the tree. In the current CART method application, the maximum tree is pruned by combing parameter tuning with
K-fold cross-validation. The solution algorithm for executing major steps of the CART method is coded in the Python scikit-learn (sklearn) library [
31]. Prior to executing the CART computational steps, several parameters such as max_depth (the maximum depth of the tree) and max_leaf_nodes (the maximum number of terminal nodes in a tree) could be customized to avoid the overfitting issue and increase the accuracy of classifications. In the fine-tuning of classification and recursive tree building process, the randomized search parameter tuning method is used. In a randomized parameter search, each parameter is assumed to follow a specific distribution. In the current paper, four parameters that have the most significant impacts on the predictive performance of the model are tuned, including min_sample_split, max_depth, min_samples_leaf, and max_leaf_nodes. Please refer to
Table 2 for the detailed definition and distribution of each parameter.
The program can sample a given number of candidate parameter sets from the parameter space. This number is set to 1000 in the current paper. Each sampled parameter set generates a corresponding tree. All generated decision trees are evaluated by K-fold cross-validation separately to output the tree with the highest accuracy level of classifications.
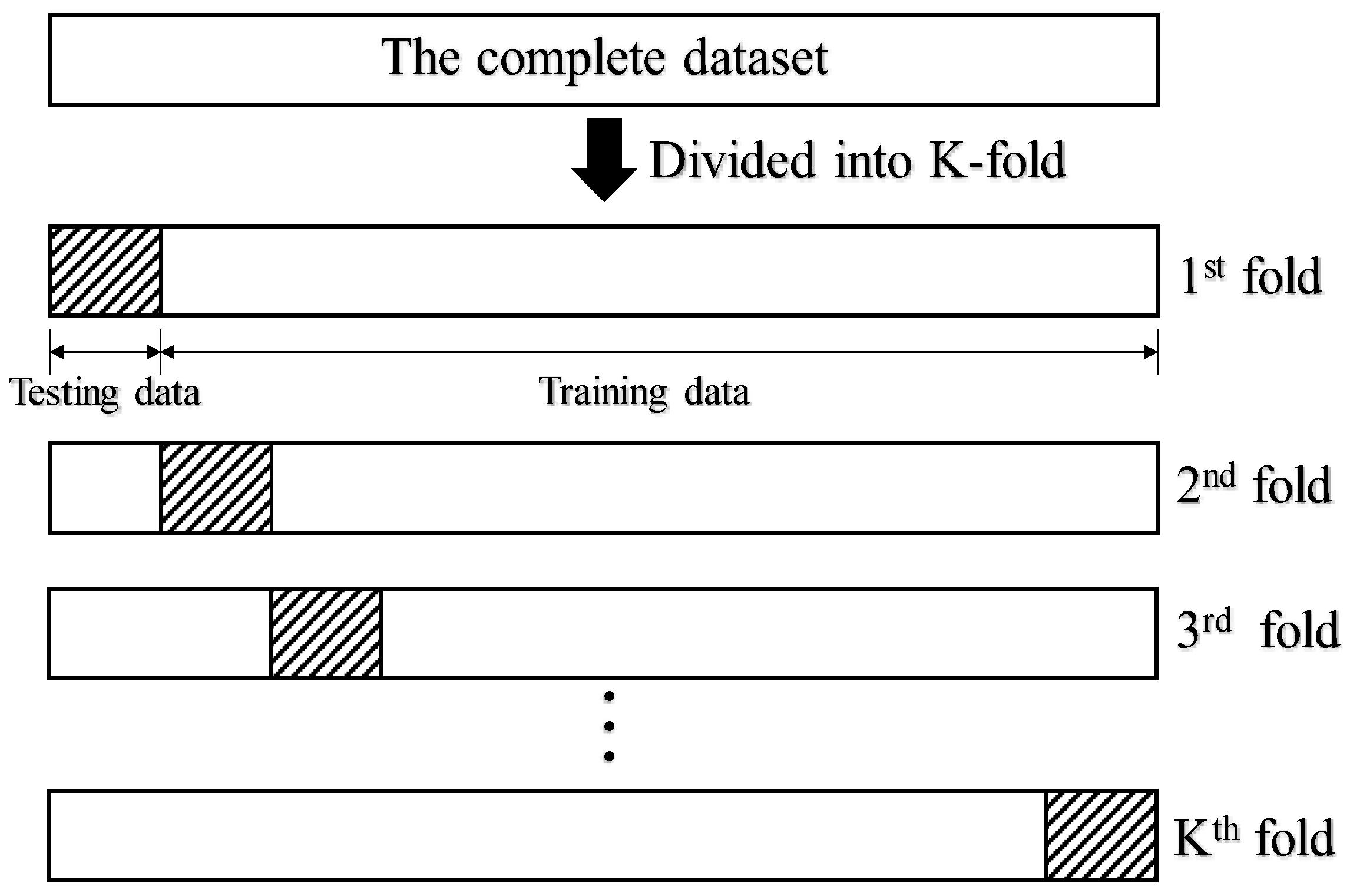
As demonstrated in
Figure 2, the
K-fold cross-validation randomly divides the entire dataset into the
K groups of data. One group of data is selected as the testing group, and the remaining
K-1 groups of data is combined to train the model. This process is repeated
K times, resulting in
K number of models. Each model is tested against an independent data subset.
The performance measure reported by K-fold cross-validation is the average classification accuracy of all folds. While K-fold cross-validation can be computationally expensive, it does not underuse the available data. This is a major advantage for cases with relatively small datasets. Without loss of generality, the value of K is set as five in the current study.
3.2. Data Imbalance Treatment
As mentioned before, traffic crash datasets are usually imbalanced. In the context of the current study, the ratio of NHR crashes to HR crashes is close to 4:1. Without any treatment, this unbalance will make the CART method fail in the detection of minority, but important instances. To address the data imbalance issue and improve the minority class recognition, the SVM-SMOTE (Support Vector Machine–Synthetic Minority Over-sampling Technique) algorithm is applied. Originally proposed by Nguyen et al. [
32], SVM-SMOTE is an improvement to the classical oversampling technique SMOTE. Generally speaking, SMOTE randomly generates artificial minority instances on the line segments connecting each minority instance with its
m nearest neighbors [
33]. By over-sampling the entire minority class, SMOTE tries to construct a more balanced dataset. Unlike SMOTE, SVM-SMOTE only generates artificial minority instances along the borderline separating different classes. This is due to the minority instances along the borderline are much more crucial for determining the optimal decision boundary than other minority instances. Previous studies have demonstrated that over-sampling only along the borderline generates better results [
32].
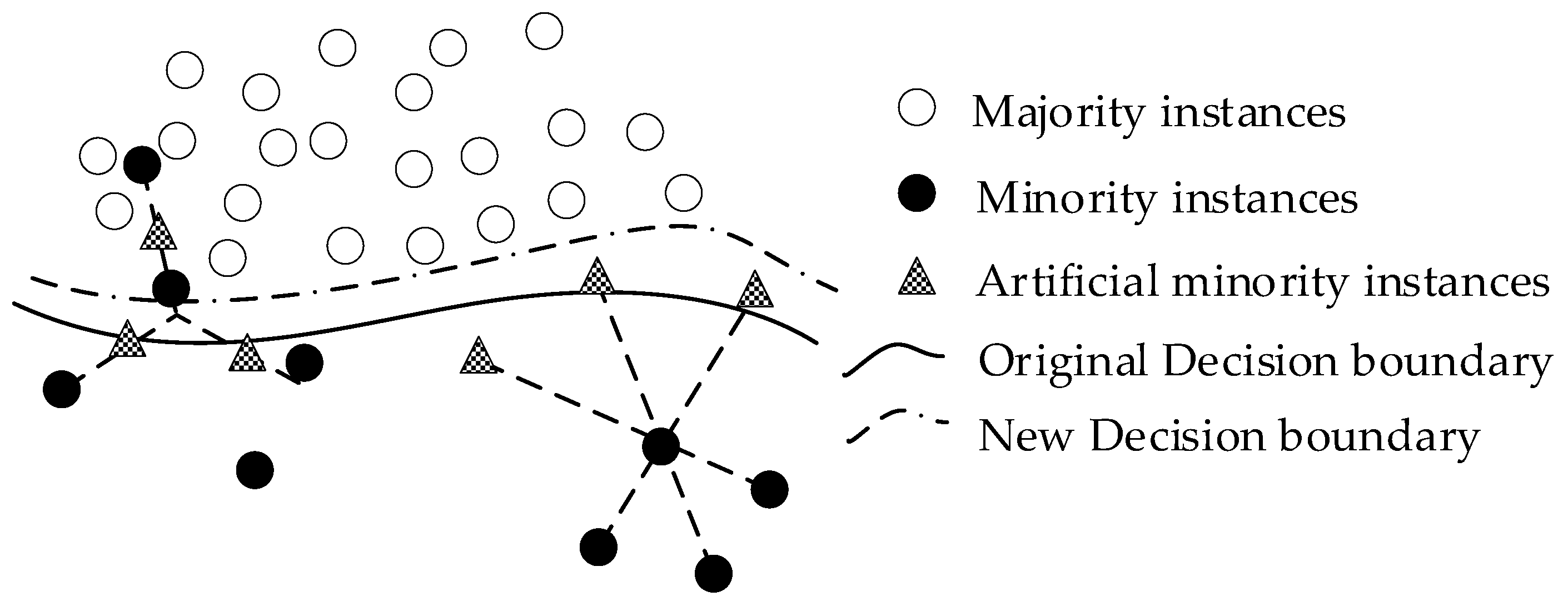
The basic idea of SVM-SMOTE is illustrated in
Figure 3. First of all, a standard SVM classifier is trained on the original imbalanced data to approximate the decision boundary and the borderline region. Without any oversampling, the decision boundary (the solid curve) is skewed toward the minority instances. Then, two different approaches are applied to generate artificial minority instances based on the location of existing minority instances within the borderline region.
For minority instances located far away from the decision boundary (minority instances on the right), an extrapolation technique is used to randomly generate artificial minority instances on the extension lines connecting existing minority instances. Due to the direction of expansion from the inside to the outside of the region being occupied by the minority instances, this will move minority instances towards the borderline region.
On the other hand, the minority instances on the left are closer to the decision boundary (surrounded by many majority instances), and an interpolation technique similar to SMOTE is applied to generate artificial minority instances. In this way, the artificial minority instances are randomly generated on lines connecting the minority instance and its
m nearest neighbors (in this case,
m = 3). After generating artificial minority instances, a new decision boundary (the dashed curve), which is moved toward majority instances, is created. Please refer to Reference [
32] for the algorithm details. In the current paper, the SVM-SMOTE algorithm is performed through the Python toolbox imbalanced-learn [
34].
With SVM-SMOTE, the number of artificial minority instances generated could be specified. To better understand the effect of data imbalance on classification accuracy, different ratios of minority instances to majority instances are tested, including 1.0, 0.9, 0.8, and 0.7.
It is very crucial to point out that the artificially more balanced data is only used to train the CART model. Specifically speaking, during each step of the K-fold cross-validation, the training data is first processed with SVM-SMOTE to generate a more balanced artificial dataset, which is used to train the CART model. Additionally, the remaining testing data, which is still imbalanced, is used to evaluate the performance of the trained CART model.
The overall accuracy is a commonly used evaluation metric for CART model, which can be calculated from the confusion matrix shown in
Table 3.
The overall accuracy is defined by
However, as mentioned in
Section 1, this metric could be inappropriate for imbalanced data. If the minority instances are significantly outnumbered by the majority instances, the overall accuracy might still be very high even when all minority instances are misclassified. To address the limitation of the overall classification accuracy, the G-mean (geometric mean) [
35] is used to evaluate the performance of the CART model. The G-mean can be calculated by the following equation:
By balancing the classification accuracy of the minority and majority instances, the G-mean could be used as a compact metric to evaluate the CART model performance.
To fully demonstrate the impact of data imbalance on the classification result, the whole data set is randomly partitioned into training and testing subsets. Without loss of generality, the ratio of training and testing data is set to 7:3. Then, the CART models with and without data imbalance treatment are trained on the training data with randomized parameter search correspondingly. After parameter tuning, the optimal CART models with and without data imbalance treatment are tested on the same imbalanced test data to compare the results.
4. Results Discussions
The Python program is run on a Windows workstation with 2.20 GHz Intel Xeon CPU and 64 GB RAM. The parameter tuning results based on the training data are shown in
Table 4.
After parameter tuning, the optimal CART models with and without data imbalance treatment are established. Then, these two models are tested on the same imbalanced testing data to compare the classification results. Please refer to
Table 5 for the testing results shown in confusion matrixes.
As can been seen from
Table 5, by incorporating data imbalance treatment, the classification results have been significantly changed. The original CART model without any data imbalance treatment has an overall classification accuracy of 78%. As expected, it classifies the majority instances (NHR crashes) more accurately (99%), but only 5% of the minority instances (HR crashes) are correctly predicted. Additionally, the G-mean is only 23%, which makes the model fail to be informative in reality.
On the other hand, by training the CART model on a more balanced synthetic training dataset generated by SVM-SMOTE, the CART model could have an overall classification accuracy of 71%, which is slightly lower than the original CART model. However, the classification accuracy for the minority instances (HR crashes) is increased from 5% to 49%. Further, the G-mean is increased from 23% to 61% by 171%. The model testing results indicate that the CART model incorporating SVM-SMOTE is much more robust when dealing with imbalanced datasets.
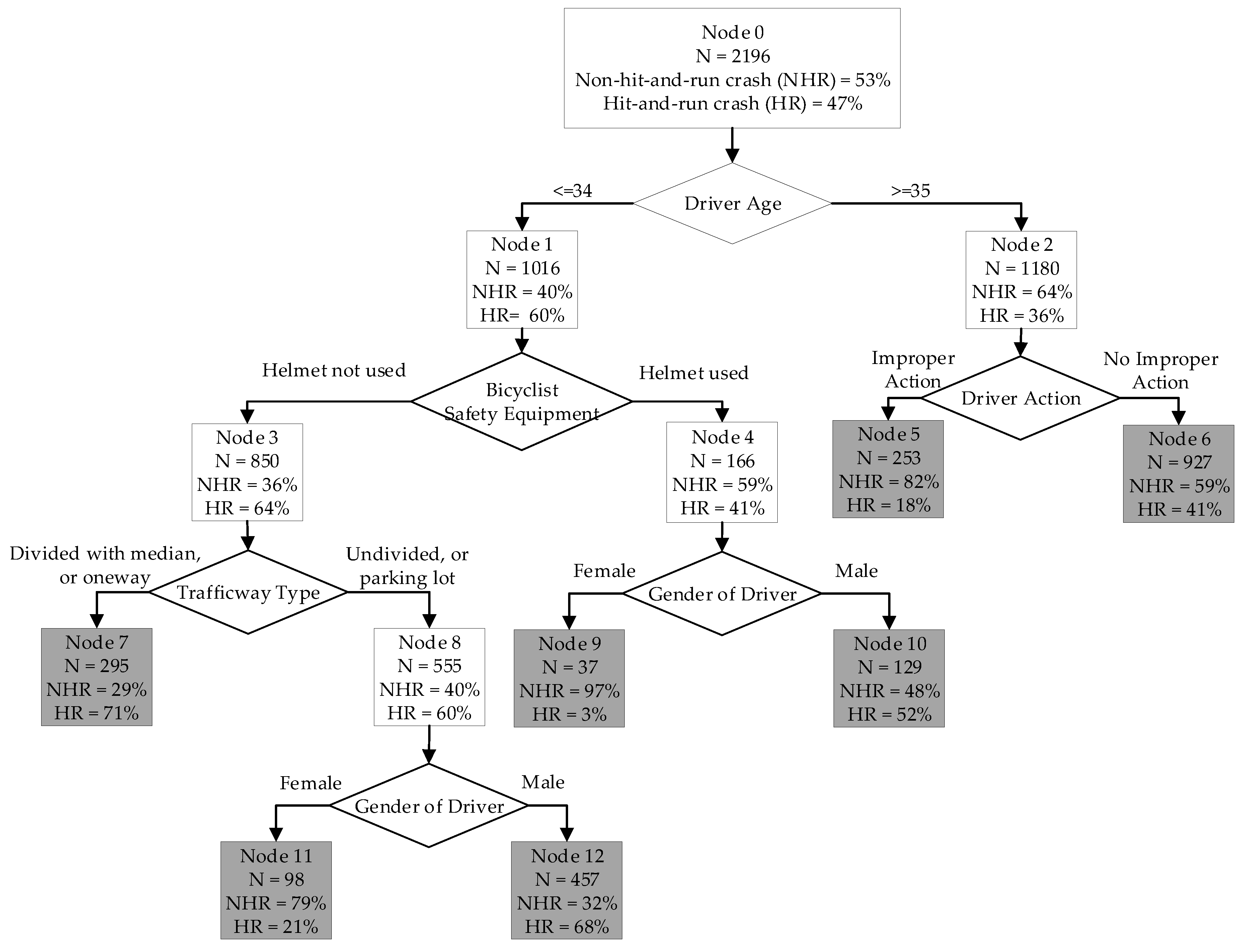
After model testing, the optimal CART model incorporating SVM-SMOTE is applied to the whole dataset to output the final decision tree, which is shown in
Figure 4.
The interpretation of the CART model results is relatively straightforward. Node 0 is the root node, which includes all the data. As can be seen from node 0, the original dataset is first oversampled by SVM-SMOTE to generate a more balanced synthetic dataset. According to the parameter setting, the ratio of minority instances to the majority instances is 0.9. As such, the synthetic dataset contains 1,156 NHR crashes and 1040 HR crashes. The tree has seven terminal nodes, which are marked as grey boxes in
Figure 4 (node 5, 6, 7, 9, 10, 11, and 12). It can be easily seen that driver age, bicyclist safety equipment, driver action, traffic way type, and gender of drivers are the primary splitters in the tree. The initial split is based on driver age. This indicates that driver age is the single most important variable to classify HR and NHR in vehicle-bicycle crashes. CART directs crashes caused by drivers less than or equal to 34 to node 1 and crashes caused by drivers over 35 to node 2. Comparing node 1 and node 2, crashes caused by drivers less than or equal to 34 shows greater propensity toward HR (60% versus 36%). This is probably because younger drivers (especially teenage drivers) are associated with higher crash risks compared with other age groups. The previous study has demonstrated that younger drivers lack driving experiences and tend to take more risks while driving [
36]. Thus, when they hit bicyclists, they are more likely to flee. Node 1 is further split into node 3 and 4 based on the safety equipment of bicyclists. CART sends crashes involving bicyclists not wearing helmets, to node 3 and crashes involving bicyclists wearing helmets to node 4. By simply wearing the helmets, the risk of HR could be reduced by 23%. Apparently, a helmet could offer more protection when a bicyclist smashes into the road. If the offending driver hit a bicyclist wearing a helmet, the perception that the victim might suffer from minor instead of severe injury could encourage he/she to stay. This further underlines the importance of wearing proper protection when cycling. CART continues to split node 3 into terminal node 7 and node 8 based on the traffic way type. While both node 7 and 8 are more prone to HR crashes, crashes occurring on undivided roads or parking lots have a less proportion of HR than crashes occurring on divided roads with median or one-way streets (60% versus 71%). Most parking lots in Chicago are covered with surveillance cameras, which makes fleeing drivers to get caught easily. This would force some of them to stay. Node 4 is further split into terminal node 9 and terminal node 10 based on the gender of the driver. Crashes caused by female drivers are directed to terminal node 9 and crashes caused by male drivers are sent to terminal node 10. Compared with male drivers, female drivers are highly unlikely to flee after crashes (3% versus 52%). CART divides node 8 into terminal node 11 and terminal node 12 according to the gender of drivers. Again, male drivers are much more prone to HR crashes compared with female drivers (68% versus 21%). This is consistent with the findings of Tay et al. [
15], who also pointed out that male drivers are more prone to other kinds of driving violations. Thus, it is not surprising that male drivers are more likely to flee the scenes compared to female drivers.
Turning to the right branch of the tree, node 2 is divided into terminal node 5 and terminal node 6 based on the driver action. When improper actions (including improper passing, turning, lane change, etc.) are involved in a crash, it is less likely to be a HR crash (18% versus 41%). This is probably due to drivers knowing that crashes occurred due to their improper driving behaviors, and running away could aggravate the punishment. Thus, they tend to stay.
Out of the 7 terminal nodes, 3 of them predicted the vehicle-bicycle crash is more likely to be a HR crash (node 7, 10 and 12), namely, proportion of HR crashes is higher than that of NHR crashes in these nodes. It should be noted that all 3 nodes are on the left branch of the tree, representing crashes caused by drivers less than or equal to 34 years old.
5. Conclusions
Targeting at exploring factors affecting HR and NHR in vehicle-bicycle crashes, this paper has introduced a CART method incorporating data imbalance treatment. Police-reported crash data within the jurisdiction of City of Chicago from September 2017 to August 2018 is collected for the modelling purpose. To avoid the over fitting problem and increase the classification accuracy, this study runs randomized search cross-validation to optimize the model parameters. In the original dataset, HR crashes and NHR crashes are imbalanced (1,156 versus 319), which might degrade the classification performance of the CART model. To fix this issue, SVM-SMOTE is applied to the original dataset to generate a more balanced synthetic dataset. It is very important to point out that the synthetic dataset is only used to train the CART model. To fully demonstrate the necessity of data imbalance treatment, both the CART models with and without data imbalance treatment are tested on the same imbalanced testing data.
The model testing results indicate that the overall classification accuracy of the original CART model is slightly higher than the CART model incorporating SVM-SMOTE (78% versus 71%). Nevertheless, only 5% of minority instances (HR crashes) are correctly predicted by the original CART model. As a contrast, the CART model incorporating SVM-SMOTE correctly predicts 49% of the minority instances. By data imbalance treatment, the G-mean has been increased from 23% to 61% by 171%, showing that the CART model incorporating SVM-SMOTE is much more robust when dealing with imbalanced datasets.
To generate the final decision tree, the optimal CART model incorporating SVM-SMOTE is applied to the whole dataset. The decision tree reveals that the following five variables play the most important roles in classifying HR and NHR crashes in vehicle-bicycle crashes: Driver age, bicyclist safety equipment, driver action, traffic way type, and gender of drivers. Out of the seven terminal nodes, three of them predicted the vehicle-bicycle crash is more likely to be an HR crash (node 7, 10, and 12). The associated decision rules and corresponding proportions of HR crashes are as follows:
Driver age ≤34 and not wearing a bike helmet and crashes occurred on divided roads with median or one-way (71%);
Driver age ≤34 and wearing a bike helmet and male driver (52%);
Driver age ≤34 and not wearing a bike helmet and crashes occurred on undivided roads or parking lots and male driver (68%).
It is also worth mentioning that crashes involving female drivers under the age of 34 and bicyclists wearing helmets are highly unlikely to be HR crashes. As indicated by node 9, only 3% of crashes are classified as HR crashes under this circumstance.
The issue of hit-and-run in vehicle-bicycle crashes might not be completely resolved in short term, but some countermeasures could still be undertaken to diminish the occurrences of these highly dangerous crashes. For instance, the results of this study further demonstrate the importance of wearing a helmet during cycling. Comparing node 3 and node 4, under the same circumstance, the risk of HR would be reduced by 23% by simply wearing a helmet (64% versus 41%). Nevertheless, there is no state law requiring adult bicyclists to use a helmet, and only several states require young riders to wear helmets. To improve cycling safety and to promote the social, environmental, and economic sustainability, it is recommended to enact state laws or regulations that require people to wear helmets during cycling. Moreover, safety education targeting at male drivers less than or equal to 34 years old should be reinforced.
The current study demonstrates that CART incorporating SVM-SMOTE is an appropriate method to identify risk factors contributing to hit-and-run in vehicle-bicycle crashes when the data is imbalanced. However, the methodology limitations should also be noted. Firstly, the confidence interval or probability level of risk factors is not available in CART. Secondly, it is difficult to use CART to conduct elasticity or sensitivity analysis. In addition, the CART model is generally unstable. Minor changes in the training dataset or different choice of CART parameters might create a completely different tree structure. The randomized parameter search and five-fold cross-validation adopted in the current study could help to alleviate this problem. Each of the 1,000 parameter settings sampled from the specified distributions is evaluated by 5-fold cross-validation to output the most accurate and stable tree. Moreover, the SVM-SMOTE does not work very well when dealing with high-dimensional imbalanced data. If more independent variables are included, the performance of the proposed methodology might decline. It should also be noted the SVM-SMOTE is an over-sampling method. Other imbalanced data classification approaches can also be tested, such as under-sampling, hybrid-sampling, and feature selection or extraction methods. Lastly, the quality of results for the current study is only as good as the input data. Many of the crash parameters are recorded by the police officers based on the best available information at the time, which might not be completely accurate. This could potentially affect the model results quality.