Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling
Abstract
1. Introduction
2. Materials and Methods
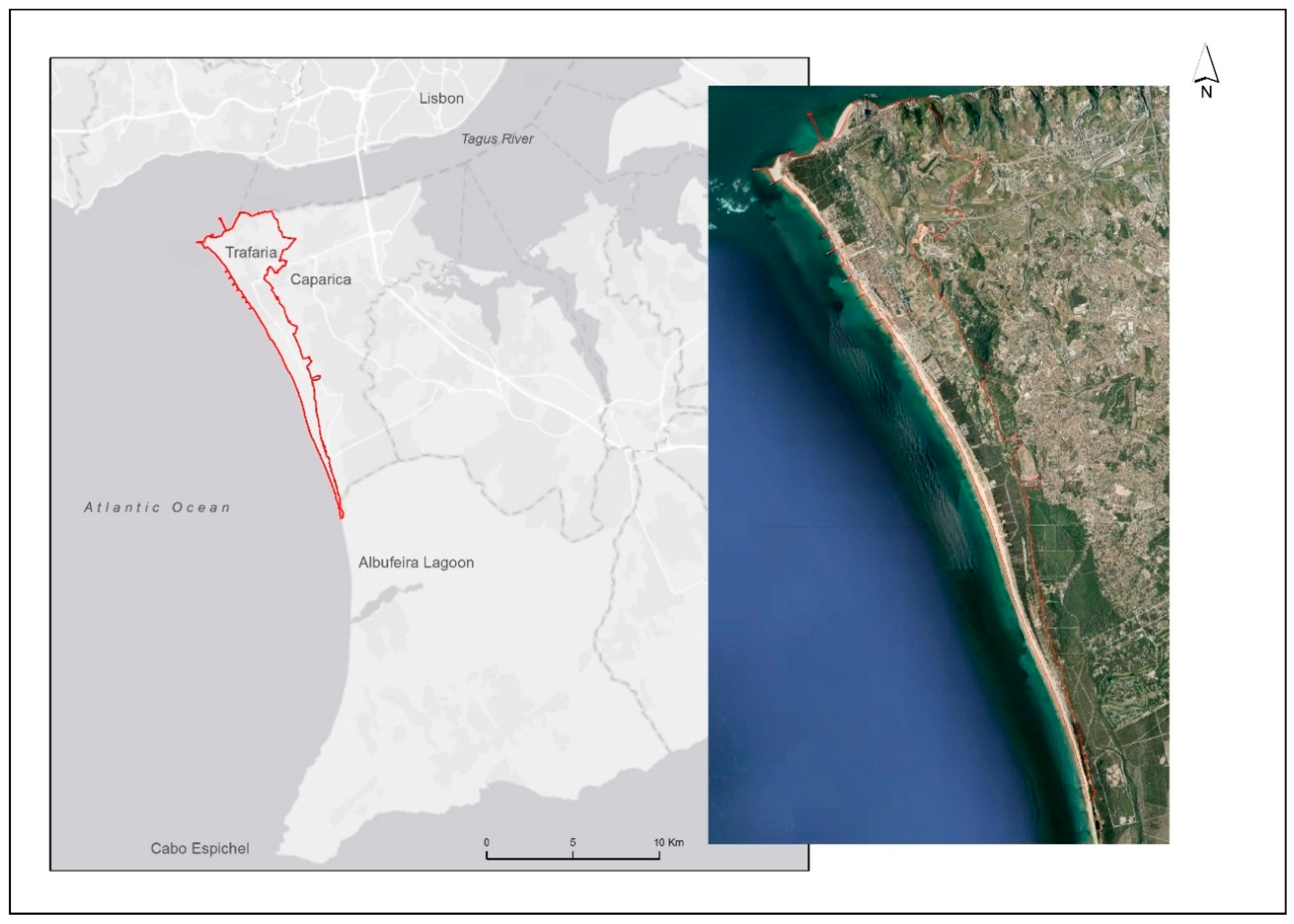
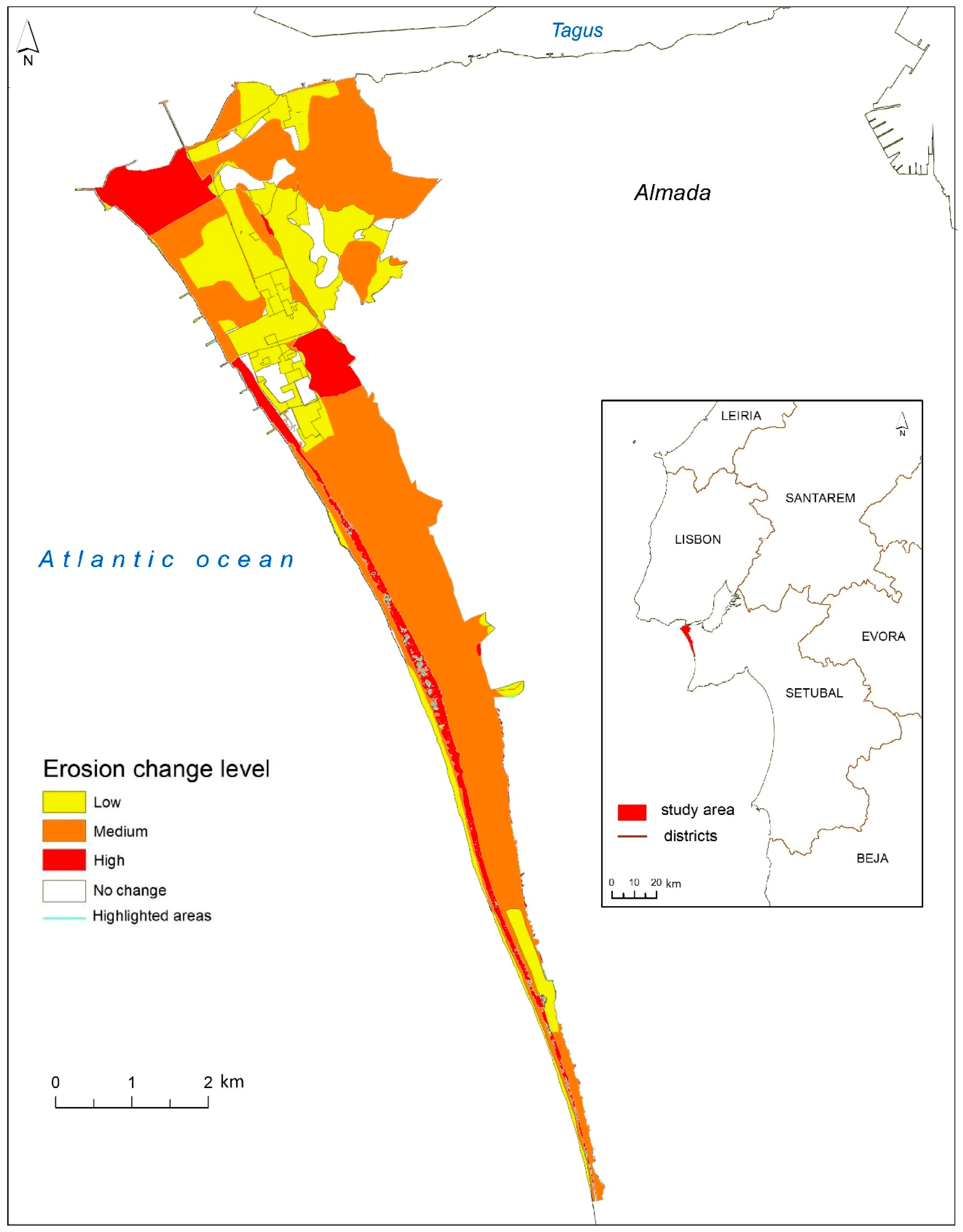
2.1. Study Area
2.2. Data
2.3. Methods
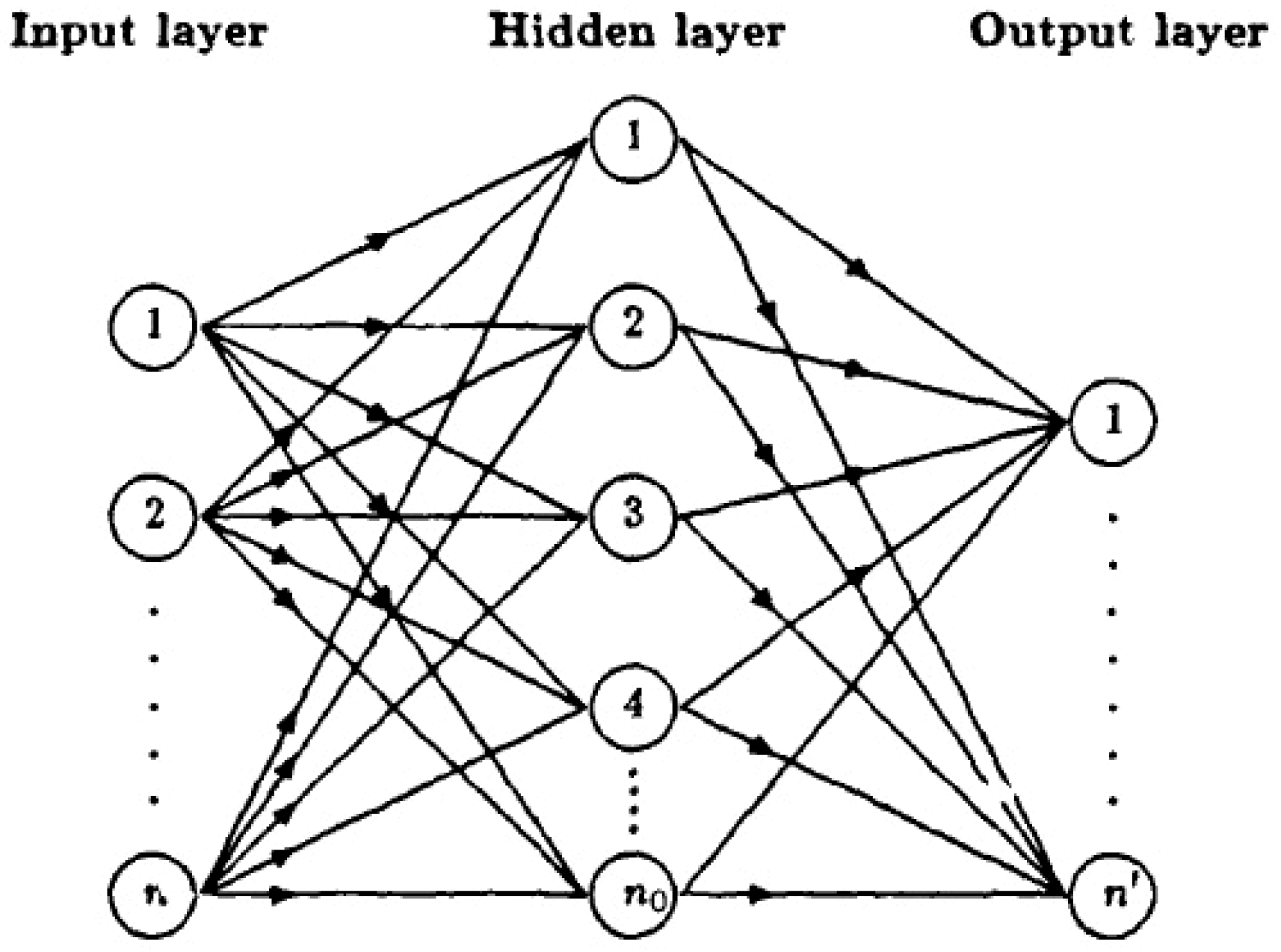
Artificial Neural Networks
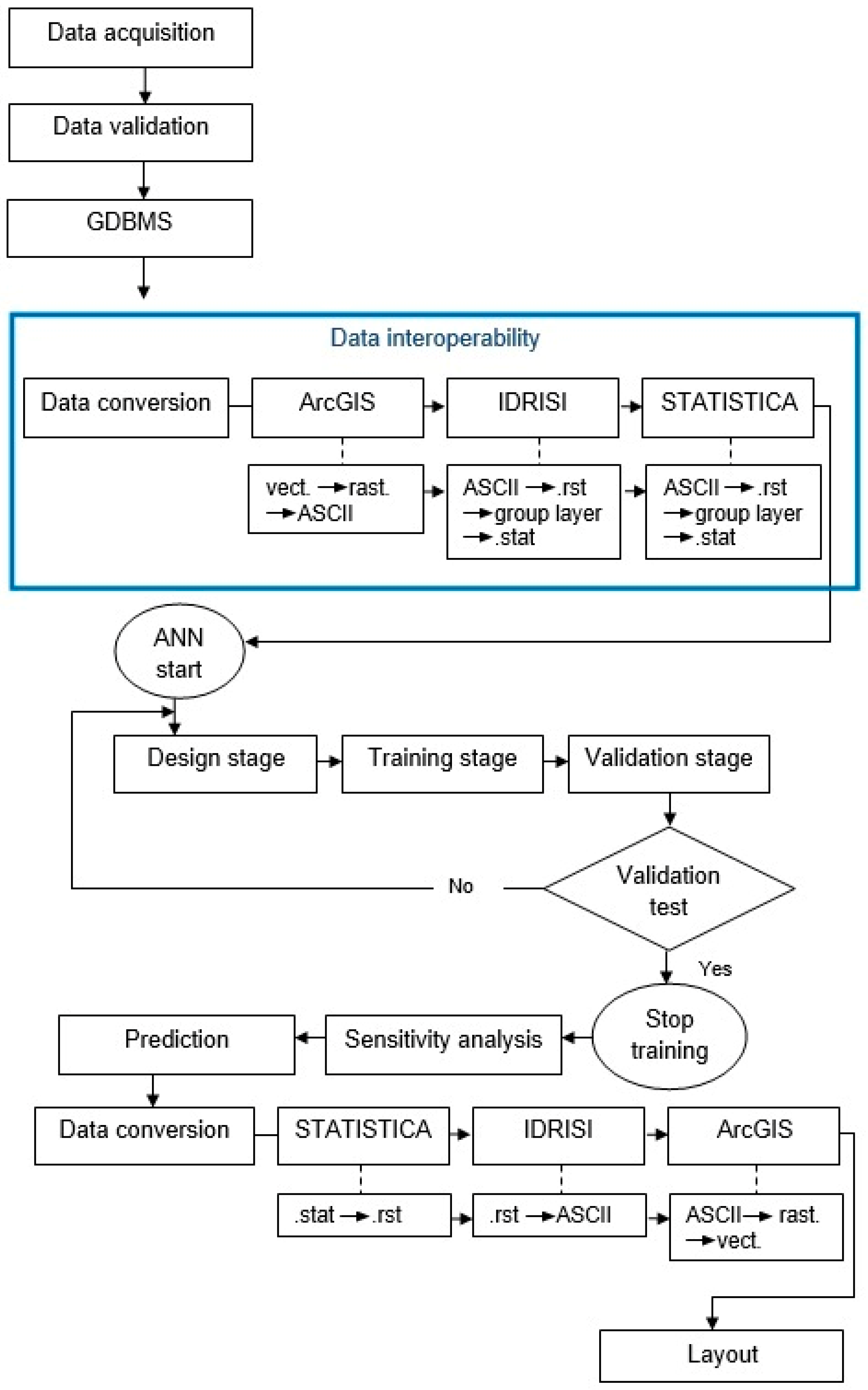
2.4. Model Implementation
3. Results
4. Conclusion and Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- NOEP. State of the U.S. Ocean and Coastal Economies 2016 Update; Middlebury Institute of International Studies at Monterey: Monterey, CA, USA, 2016. [Google Scholar]
- Qiang, H.; Mark, D.; Bertness, M.D.; Bruno, J.F.; Li, B.; Chen, G.; Coverdale, T.C.; Altieri, A.H.; Bai, J.; Sun, T.; et al. Economic development and coastal ecosystem change in China. Sci. Rep. 2014, 4, 5995. [Google Scholar] [CrossRef]
- Nicholls, R.J. Coastal flooding and wetland loss in the 21st century: Changes under the SRES climate and socio-economic scenarios. Glob. Environ. Chang. 2004, 14, 69–86. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Wong, P.P.; Burkett, V.; Codignotto, J.; Hay, J.; McLean, R.; Ragoonaden, S.; Woodroffe, C.D.; Abuodha, P.A.O.; Arblaster, J.; et al. Coastal systems and low-lying areas. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 315–356. [Google Scholar]
- Hanson, S.; Nicholls, R.; Ranger, N.; Hallegatte, S.; Corfee-Morlot, J.; Herweijer, C.; Chateau, J. A global ranking of port cities with high exposure to climate extremes. Clim. Chang. 2011, 104, 89–111. [Google Scholar] [CrossRef]
- Seto, K.C. Exploring the dynamics of migration to mega-delta cities in Asia and Africa: Contemporary drivers and future scenarios. Glob. Environ. Chang. 2011, 21, S94–S107. [Google Scholar] [CrossRef]
- Brown, S.; Nicholls, R.J.; Woodroffe, C.D.; Hanson, S.; Hinkel, J.; Kebede, A.S.; Neumann, B.; Vafeidis, A.T. Sea-level rise impacts and responses: A global perspective. In Coastal Hazards; Finkl, C.W., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 117–149. ISBN 978-94-007-5234-4. [Google Scholar]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future Coastal Population Growth and Exposure to Sea-Level Rise and Coastal Flooding—A Global Assessment. PLos ONE 2015, 10. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Liu, Y.; Fu, B.; Zhao, W. Driving forces and their contribution to the recent decrease in sedimentflux to ocean of major rivers in China. Sci. Total Environ. 2018, 634, 534–541. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Lazarus, E.D.; Ellis, M.A.; Murray, A.B.; Hall, D.M. An evolving research agenda for human–coastal systems. Geomorphology 2016, 256, 81–90. [Google Scholar] [CrossRef]
- Anfuso, G.; Martínez del Pozo, J.A. Towards management of coastal erosion problems and human structure impacts using GIS tools: Case study in Ragusa Province, Southern Sicily, Italy. Environ. Geol. 2005, 48, 646–659. [Google Scholar] [CrossRef]
- Kantamaneni, K.; Du, X.; Aher, S.; Singh, R.M. Building blocks: A quantitative approach for evaluating coastal vulnerability. Water 2017, 9, 905. [Google Scholar] [CrossRef]
- Aiello, A.; Canora, F.; Pasquariello, G.; Spilotro, G. Shoreline variations and coastal dynamics: A space time data analysis of the Jonian littoral, Italy. ECSA 2013, 129, 124–135. [Google Scholar] [CrossRef]
- Anders, F.J.; Byrnes, M.R. Accuracy of shoreline change rates as determined from maps and aerial photographs. Shore Beach 1991, 59, 17–26. [Google Scholar]
- Bheeroo, R.A.; Chandrasekar, N.; Kaliraj, S.; Magesh, N.S. Shoreline change rate and erosion risk assessment along the Trou Aux Biches–Mont Choisy beach on the northwest coast of Mauritius using GIS-DSAS technique. Environ. Earth Sci. 2016, 75, 444. [Google Scholar] [CrossRef]
- Joesidawati, M.L.; Suntoyo, S. Shoreline change in Tuban district, East Java using geospatial Digital Shoreline Analysis System (DSAS) techniques. IJOO 2016, 10, 235–246. [Google Scholar] [CrossRef]
- Gornitz, V.M.; Daniels, R.C.; White, T.W.; Birdwell, K.R. The development of a coastal risk assessment database: Vulnerability to sea-level rise in the U.S. Southeast. J. Coast. Res. 1994, 12, 327–338. [Google Scholar]
- Thieler, E.R.; Hammar-Klose, E.S. National Assessment of Coastal Vulnerability to Sea Level Rise: Preliminary Results for the US; Atlanta Coast USGS, 99-593; United States Geological Survey: Reston, VA, USA, 1999.
- Boruff, B.J.; Emrich, C.; Cutter, S.L. Erosion Hazard Vulnerability of US Coastal Counties. J. Coast. Res. 2005, 21, 932–942. [Google Scholar] [CrossRef]
- Sudha Rani, N.N.V.; Satyanarayana, A.N.V.; Bhaskaran, P.K. Coastal vulnerability assessment studies over India: A review. Nat. Hazards 2015, 77, 405–428. [Google Scholar] [CrossRef]
- Islam, M.A.; Mitra, D.; Dewan, A.; Akhter, S.H. Coastal multi-hazard vulnerability assessment along the Ganges deltaic coast of Bangladesh—A geospatial approach. Ocean Coast. Manag. 2016, 127, 1–15. [Google Scholar] [CrossRef]
- Jaranovic, B.; Trindade, J.; Ribeiro, J.; Silva, A. Using a Coastal Storm Hazard Index to assess storm impacts in Lisbon. Int. J. Saf. Secur. Eng. 2017, 7, 221–233. [Google Scholar] [CrossRef]
- Davidson, M.A.; Lewis, R.P.; Turner, I.L. Forecasting seasonal to multi-year Shoreline Change. Coast. Eng. 2010, 57, 620–629. [Google Scholar] [CrossRef]
- Pires, H.O.; Pessanha, V.E. Wave power climate of Portugal. In Hidrodynamics of Ocean Wave-Energy Utilization. Proceedings of the IUTAM Symposium, Lisbon, Portugal, 1985; Evans, D.V., de Falcão, A.F.O., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 157–167. [Google Scholar]
- Costas, S.; Jerez, S.; Trigo, R.M.; Goble, R.; Rebêlo, L. Sand invasion along the Portuguese coast forced by westerly shifts during cold climate events. Quat. Sci. Rev. 2012, 42, 15–28. [Google Scholar] [CrossRef]
- Veloso-Gomes, F.; Pinto, F.T. Eurosion Case Study: Cova do Vapor, Costa da Caparica (Portugal); Tech. Report; Instituto de Hidráulica e Recursos Hídricos—IHRH: Porto, Portugal, 2002. [Google Scholar]
- Taborda, R.; Freire de Andrade, C.; Nobre Silva, A.; Silveira, T.M.; Lira, C.; Freitas, M.C.; Pinto, C.A. Modelo de circulação sedimentar litoral no arco Caparica-Espichel. Comunicações Geológicas 2014, 101, 641–644. [Google Scholar]
- Schmidt, L.; Gomes, C.; Guerreiro, S.; O’Riordanb, T. Are we all on the same boat? The challenge of adaptation facing Portuguese coastal communities: Risk perception, trust-building and genuine participation. Land Use Policy 2014, 38, 355–365. [Google Scholar] [CrossRef]
- Sousa, N.F. Dinâmica da Linha de Costa e Vulnerabilidade à Erosão no Setor não Artificializado do Arco Caparica-Espichel. Master’s Thesis, University of Lisbon, Institute of Geography and Spatial Planning, Lisbon, Portugal, 2015. [Google Scholar]
- Rocha, J.; Ferreira, J.C.; Simões, J.; Tenedório, J.A. Modelling coastal and land use evolution patterns through neural network and cellular automata integration. J. Coast. Res. 2007, 50, 827–831. [Google Scholar]
- Veloso-Gomes, F.; Pinto, F.P.; Barbosa, J.P.; Costa, J.; Rodrigues, A. The Defensive Works at Costa da Caparica. In 2. as Jornadas de Hidráulica, Recursos Hídricos e Ambiente; SHRHR: Porto, Portugal, 2007; pp. 23–32. [Google Scholar]
- Moore, L. Shoreline Mapping Techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- Boak, E.; Turner, I. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Ferreira, O.; Garcia, T.; Matias, A.; Taborda, R.; Alvarinho Dias, J. An integrated method for the determination of set-back lines for coastal erosion hazards on sandy shores. Cont. Shelf Res. 2006, 26, 1030–1044. [Google Scholar] [CrossRef]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ergul, A. Digital Shoreline Analysis System (DSAS) Version 4.0—An ArcGIS Extension for Calculating Shoreline Change; Open-File Report 2008-1278; U.S. Geological Survey: Reston, VA, USA, 2009.
- Cenci, L.; Disperati, L.; Sousa, L.; Phillips, M.; Alves, F. Geomatics for Integrated Coastal Zone Management: Multitemporal shoreline analysis and future regional perspective for the Portuguese Central Region. J. Coast. Res. 2013, 65, 1349–1354. [Google Scholar] [CrossRef]
- Ford, M. Shoreline changes interpreted from multi-temporal aerial photographs and high resolution satellite images: Wotje Atoll, Marshall Islands. Remote Sens. Environ. 2013, 135, 130–140. [Google Scholar] [CrossRef]
- Calvao, T.; Pessoa, M.F.; Lidon, F.C. Impact of human activities on coastal vegetation—A review. Emir. J. Food Agric. 2013, 25, 926–944. [Google Scholar] [CrossRef]
- Openshaw, S.; Openshaw, C. Artificial Intelligence in Geography, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1997; ISBN 0471969915. [Google Scholar]
- Yalpir, S.; Durduran, S.S.; Unel, F.B.; Yolcu, M. Creating a Valuation Map in GIS through Artificial Neural Network Methodology: A Case Study. Acta Montan. Slovaca 2014, 19, 79–89. [Google Scholar]
- Open Geospatial Consortium, Inc. Technical Committee Policies and Procedures. Available online: http://docs.opengeospatial.org/pol/05-020r26/05-020r26.html (accessed on 18 April 2018).
- Noack, S.; Knobloch, A.; Etzold, S.H.; Barth, A.; Kallmeier, E. Spatial predictive mapping using artificial neural networks. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-2, 2014 ISPRS Technical Commission II Symposium, Toronto, ON, Canada, 6–8 October 2014; pp. 79–86. [Google Scholar] [CrossRef]
- Merkl, D. Partially Recurrent Neural Networks in Stock Forecasting. In Proceedings of the Artificial Intelligence in Economics and Management (AIEM4), Tel Aviv, Israel, 8–10 January 1996. [Google Scholar]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Carcano, E.C.; Bartolini, P.; Muselli, M.; Piroddi, L. Jordan recurrent neural network versus IHACRES in modeling daily streamflows. J. Hydrol. 2008, 362, 291–307. [Google Scholar] [CrossRef]
- Neagoe, V.E.; Neghina, M.; Datcu, M. Neural Network Techniques for Automated Land-Cover Change Detection in Multispectral Satellite Time Series Imagery. Math. Models Methods Appl. Sci. 2012, 1, 130–139. [Google Scholar]
- Zare, M.; Pourghasemi, H.R.; Vafakhah, M.; Pradhan, B. Landslide susceptibility mapping at Vaz Watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (MLP) and radial basic function (RBF) algorithms. Arab. J. Geosci. 2012, 6, 2873–2888. [Google Scholar] [CrossRef]
- Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Hernández, L. Performance Study of the Application of Artificial Neural Networks to the Completion and Prediction of Data Retrieved by Underwater Sensors. Sensors 2012, 12, 1468–1481. [Google Scholar] [CrossRef] [PubMed]
- LeCunn, Y.; Bengio, Y.; Geoffrey, H. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Systems 1988, 2, 321–355. [Google Scholar]
- Zhang, N.; Xiao, C.; Liu, B.; Liang, X. Groundwater depth predictions by GSM, RBF, and ANFIS models: A comparative assessment. Arab. J. Geosci. 2017, 10, 189. [Google Scholar] [CrossRef]
- Orr, M.J.L. Introduction to Radial Basis Function Networks; Centre for Cognitive Science, University of Edinburgh: Edinburgh, Scotland, 1996. [Google Scholar]
- Li, X.M.; Xiao, R.B.; Yuan, S.H.; Chen, J.A.; Zhou, J.X. Urban total ecological footprint forecasting by using radial basis function neural network: A case study of Wuhan city, China. Ecol. Indic. 2010, 10, 241–248. [Google Scholar] [CrossRef]
- Wu, C.M.; Lin, G.F. An Hourly Stream flow Forecasting Model Coupled with an Enforced Learning Strategy. Water 2015, 7, 5876–5895. [Google Scholar] [CrossRef]
- Csábrági, A.; Molnár, S.; Tanos, P.; Kovács, J. Application of artificial neural networks to the forecasting of dissolved oxygen content in the Hungarian section of the river Danube. Ecol. Eng. 2016, 100, 63–72. [Google Scholar] [CrossRef]
- Amid, S.; Gundoshmian, M.T. Prediction of output energies for broiler production using linear regression, ANN (MLP, RBF), and ANFIS models. Environ. Prog. Sustain. Energy 2017, 36, 577–585. [Google Scholar] [CrossRef]
- Mezaal, M.; Pradhan, B.; Sameen, M.; Shafri, H.; Yussof, Z. Optimized Neural Architecture for Automatic Landslide Detection from High-Resolution Airborne Laser Scanning Data. Appl. Sci. 2017, 7, 730. [Google Scholar] [CrossRef]
- Hossain, M.S.; Ong, Z.C.; Ismail, Z.; Khoo, S.Y. A comparative study of vibrational response based impact force localization and quantification using radial basis function network and multilayer perceptron. Expert Syst. Appl. 2017, 85, 87–98. [Google Scholar] [CrossRef]
- Maithani, S. A Neural Network based Urban Growth Model of an Indian City. J. Indian Soc. Remote Sens. 2009, 37, 363–376. [Google Scholar] [CrossRef]
- Gopal, S.; Fisher, M.M. Learning in single hidden-layer feedforward network models: Backpropagation in a spatial interaction modeling context. Geogr. Anal. 1996, 28, 38–55. [Google Scholar] [CrossRef]
- Morgado, P.; Gomes, E.; Costa, N. Competing visions? Simulating alternative coastal futures using a GIS-ANN web application. Ocean Coast. Manag. 2014, 101, 79–88. [Google Scholar] [CrossRef]
- Gopal, S. Artificial Neural Networks for Spatial Data Analysis. NCGIA Core Curriculum in GIScience. Posted 22 December 1998. Available online: http://www.ncgia.ucsb.edu/giscc/units/u188/u188.html (accessed on 21 May 2018).
- Bayram, S.; Ocal, M.E.; Oral, E.L.; Atis, C.D. Comparison of Multilayer perceptron (MLP) and Radial Basis Function (RBF) for Construction Cost Estimation: The Case of Turkey. J. Civ. Eng. Manag. 2016, 22, 480–490. [Google Scholar] [CrossRef]
- Tahani, M.; Vakili, M.; Khosrojerdi, S. Experimental evaluation and ANN modeling of thermal conductivity of graphene oxide nanoplatelets/deionized water nanofluid. Int. J. Heat Mass Transf. 2016, 76, 358–365. [Google Scholar] [CrossRef]
- Vakili, M.; Karami, M.; Delfani, S.; Khosrojerdi, S.; Kalhor, K. Experimental investigation and modeling of thermal conductivity of CuO–water/EG nanofluid by FFBP-ANN and multiple regressions. J. Therm. Anal. Calorim. 2017, 129, 629–637. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Kantamaneni, K.; Phillips, M.; Thomas, T.; Jenkins, R. Assessing coastal vulnerability: Development of a combined physical and economic index. Ocean Coast. Manag. 2018, 158, 164–175. [Google Scholar] [CrossRef]
| Code | Name | Units |
|---|---|---|
| RESID01_ | Resident population—2001 | Nº residents |
| RESID11_ | Resident population—2011 | Nº residents |
| CORNL00_ | Corine Land Cover—2000 | Level 1 CLC |
| CORN06_ | Corine Land Cover—2006 | Level 1 CLC |
| ALOJ01_3 | Households—2001 | Nº of households |
| ALOJ11_3 | Households—2011 | Nº of households |
| ER6080_R | Area of erosion plots—1967–1980 | Sq m |
| ER8090_R | Area of erosion plots—1980–1995 | Sq m |
| ER2008_R | Area of erosion plots—1995–2008 | Sq m |
| VEG_RCID | Area of vegetated and non-vegetated plots—currently | Sq m |
| A | Sensitivity Analysis—network 9:2:6:3:1 | ||||||||
| ALOJ01_3 | ALOJ11_3 | CORNL_00 | CORNL06_ | ER6080_R | ER8090_R | VEG_RCID | RESID01_ | RESID11_ | |
| Ratio | 1.000451 | 0.999655 | 0.999669 | 1.004549 | 1.017696 | 1.000097 | 1.007850 | 1.005299 | 1.000919 |
| Rank | 6 | 9 | 8 | 4 | 1 | 7 | 2 | 3 | 5 |
| B | Sensitivity Analysis—network 9:2:6:6:1 | ||||||||
| ALOJ01_3 | ALOJ11_3 | CORNL_00 | CORNL06_ | ER6080_R | ER8090_R | VEG_RCID | RESID01_ | RESID11_ | |
| Ratio | 1.047523 | 0.999605 | 1.002351 | 1.000591 | 1.018752 | 1.000064 | 1.011311 | 1.004844 | 0.999059 |
| Rank | 1 | 8 | 5 | 6 | 2 | 7 | 3 | 4 | 9 |
| C | Sensitivity Analysis—network 9:2:5:5:1 | ||||||||
| ALOJ01_3 | ALOJ11_3 | CORNL_00 | CORNL06_ | ER6080_R | ER8090_R | VEG_RCID | RESID01_ | RESID11_ | |
| Ratio | 1.012291 | 1.001607 | 0.998228 | 1.001061 | 1.013966 | 0.999958 | 1.001469 | 1.198692 | 1.003025 |
| Rank | 3 | 5 | 9 | 7 | 2 | 8 | 6 | 1 | 4 |
| D | Sensitivity Analysis—network 9:2:4:3:1 | ||||||||
| ALOJ01_3 | ALOJ11_3 | CORNL_00 | CORNL06_ | ER6080_R | ER8090_R | VEG_RCID | RESID01_ | RESID11_ | |
| Ratio | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| Rank | 4 | 7 | 2 | 5 | 3 | 9 | 8 | 1 | 6 |
| E | Sensitivity Analysis—network 9:1:7:1 | ||||||||
| ALOJ01_3 | ALOJ11_3 | CORNL_00 | CORNL06_ | ER6080_R | ER8090_R | VEG_RCID | RESID01_ | RESID11_ | |
| Ratio | 1.033375 | 1.002661 | 0.998286 | 1.019494 | 1.019418 | 1.000044 | 1.004505 | 1.262340 | 1.007049 |
| Rank | 2 | 7 | 9 | 3 | 4 | 8 | 6 | 1 | 5 |
| Index | Profile | Train Perf. | Select Perf. | Test Perf. | Train Error | Select Error | Test Error | Training/Members | Inputs | Hidden (1) | Hidden (2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
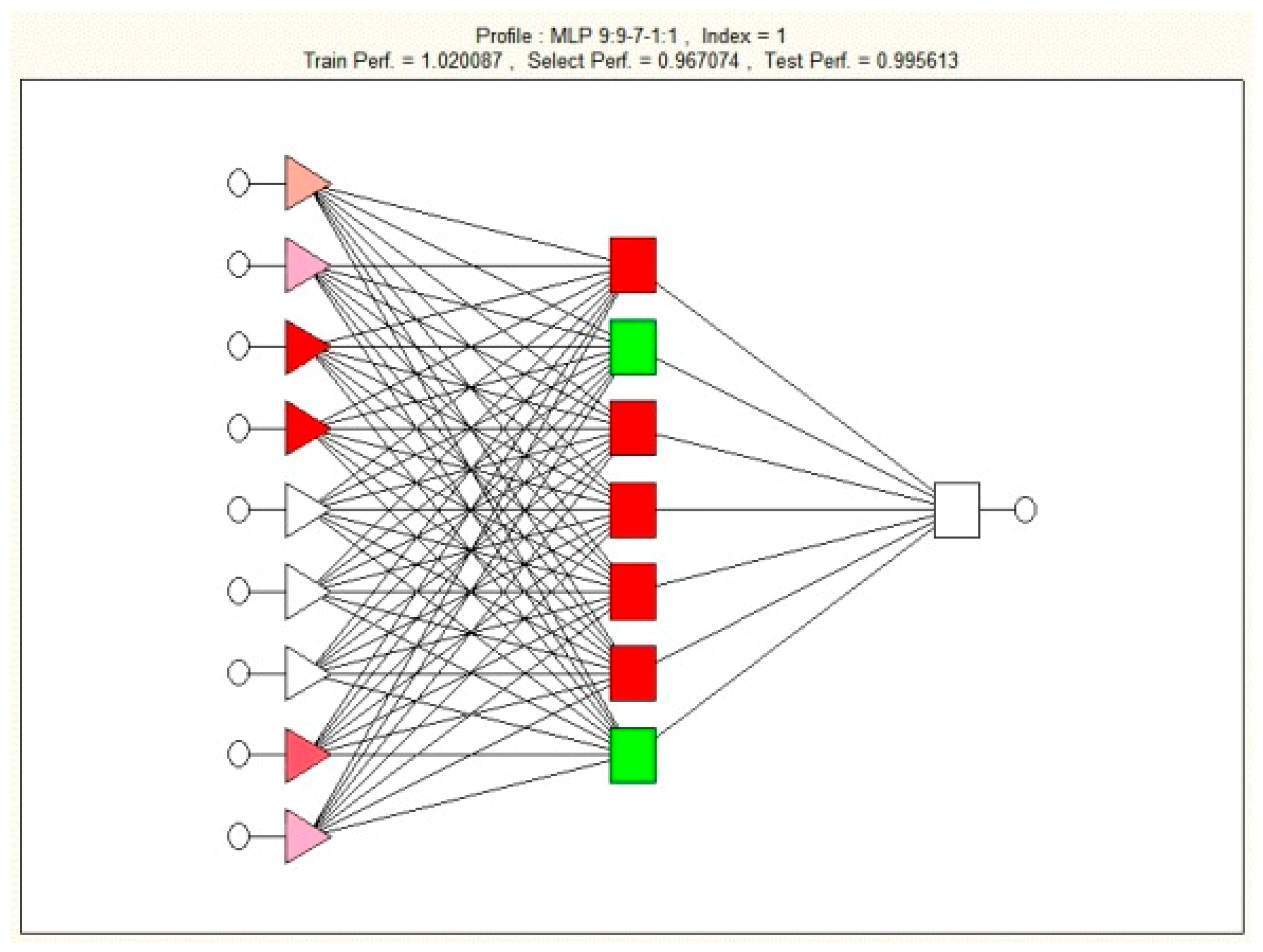
| 1 | MLP 9:9-7-1:1 | 1.020087 | 0.967074 | 0.995613 | 0.012059 | 0.034072 | 0.023768 | BP1b | 9 | 7 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peponi, A.; Morgado, P.; Trindade, J. Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability 2019, 11, 975. https://doi.org/10.3390/su11040975
Peponi A, Morgado P, Trindade J. Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability. 2019; 11(4):975. https://doi.org/10.3390/su11040975
Chicago/Turabian StylePeponi, Angeliki, Paulo Morgado, and Jorge Trindade. 2019. "Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling" Sustainability 11, no. 4: 975. https://doi.org/10.3390/su11040975
APA StylePeponi, A., Morgado, P., & Trindade, J. (2019). Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability, 11(4), 975. https://doi.org/10.3390/su11040975






