Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia
Abstract
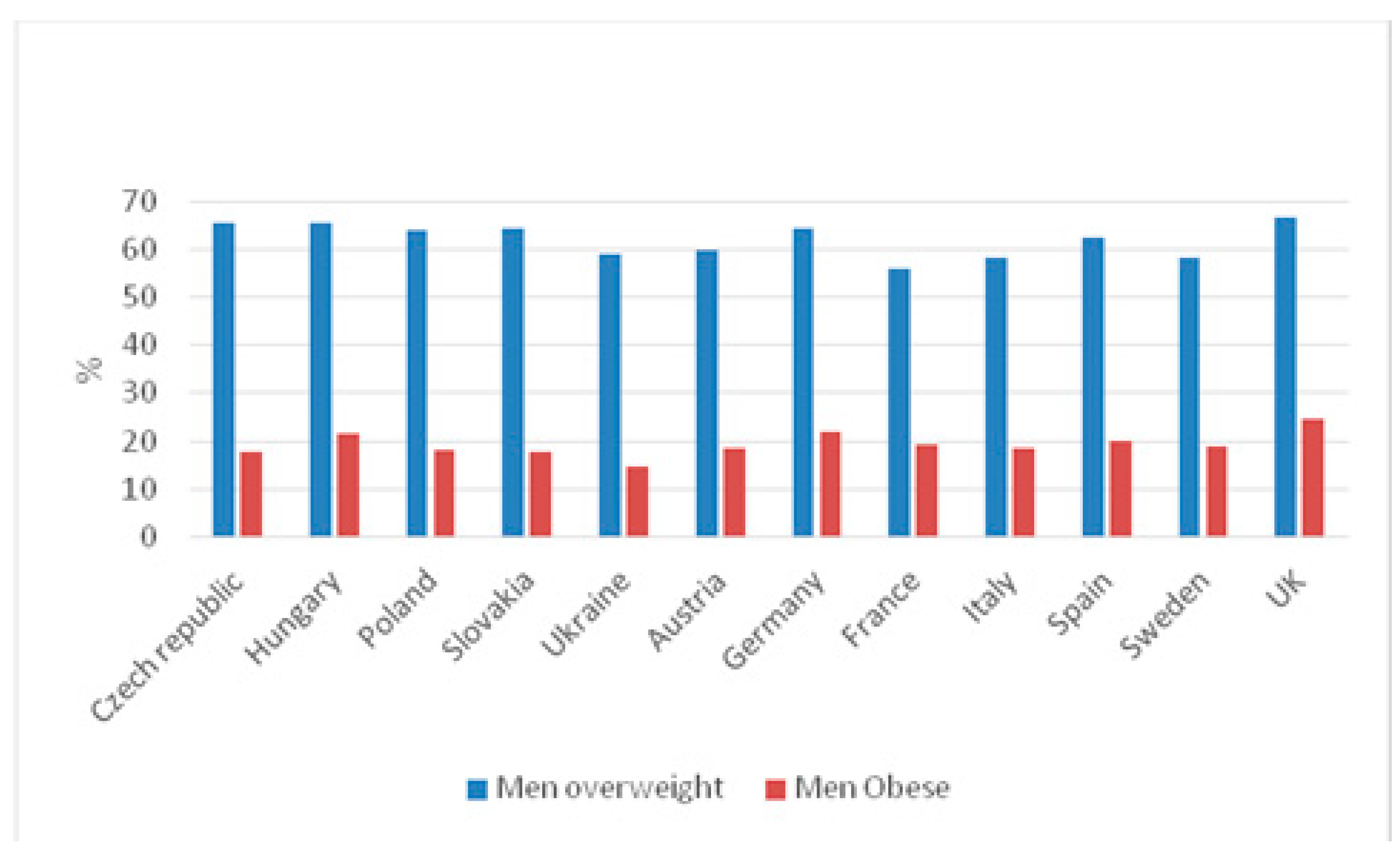
1. Introduction
2. Analysis Approach
2.1. Experimental Subjects
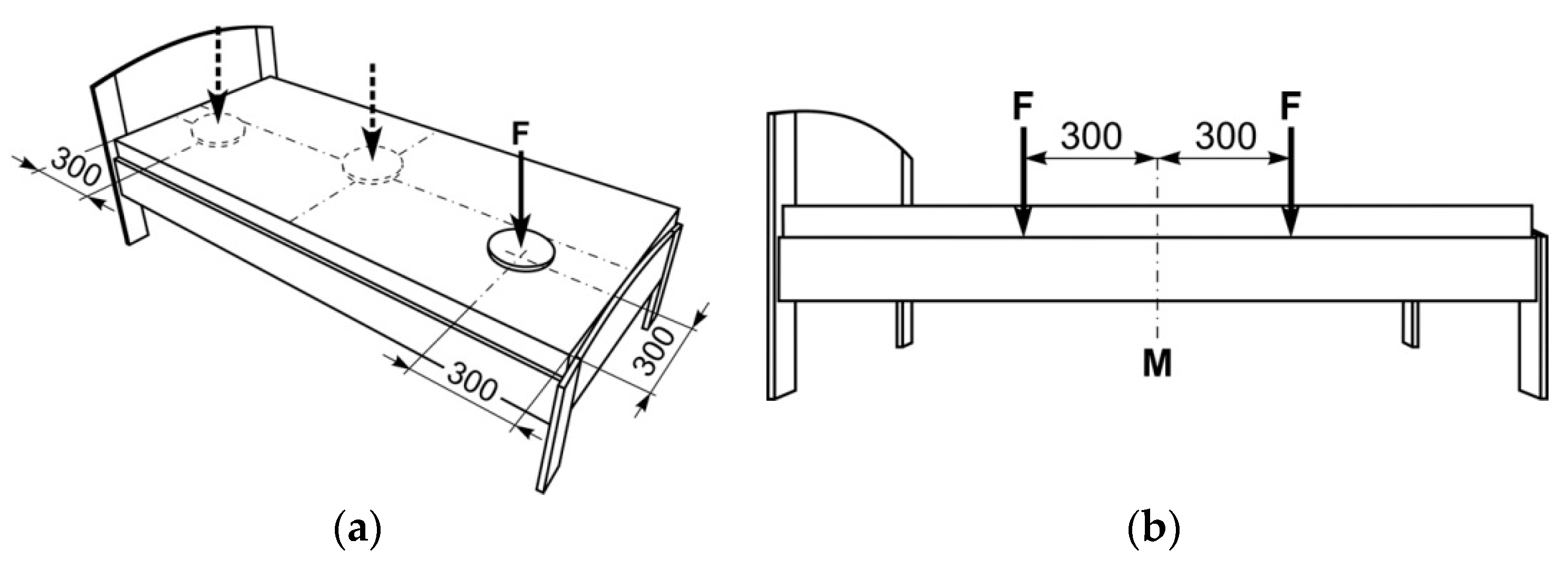
2.2. Static Load Test of Beds
2.3. Designing in Accordance with the Limit State
2.3.1. Strength of Elements
- σt,0,d—design tensile stress parallel to grains
- ft,0,d—design tensile strength of timber parallel (perpendicular) to grains, at which
- ft,0,k—typical tensile strength of timber parallel to grains (for spruce wood ft,0,k = 24 MPa, for beech wood ft,0,k = 42 MPa)
- γM—partial safety factor, γM = 1.3 for wood and wood materials
- kmod—modification factor dealing with the impact of the time of applying the load and the moisture content on the strength of material kmod = 1.10 for immediate load [55]
- σc,0,d—design compressive stress,
- fc,0,d—design compressive strength, at which
2.3.2. Element Bending
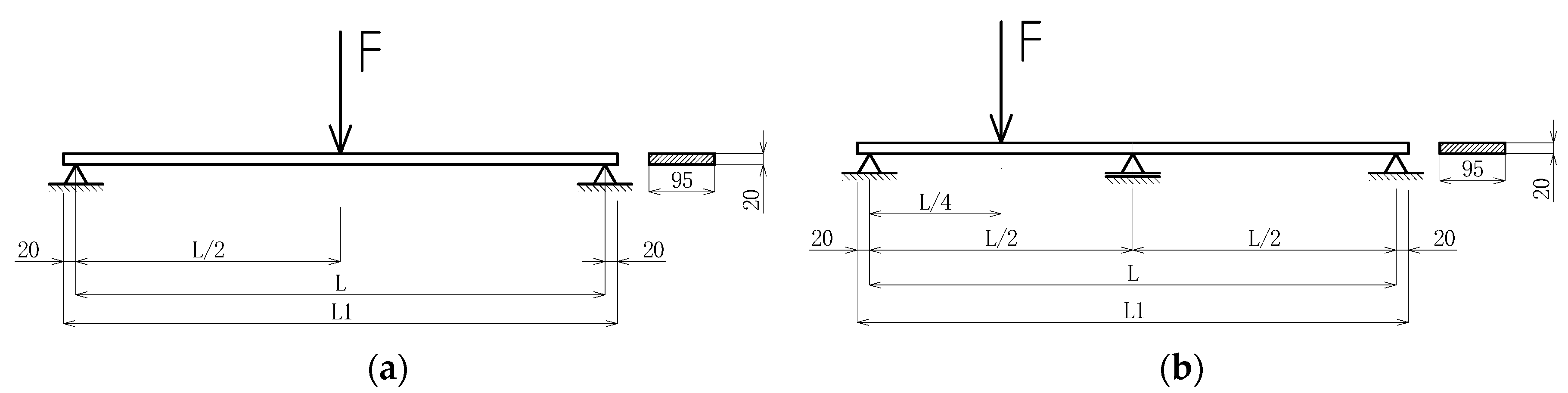
2.4. Methodology for Static Loading Testing of Bed Slats
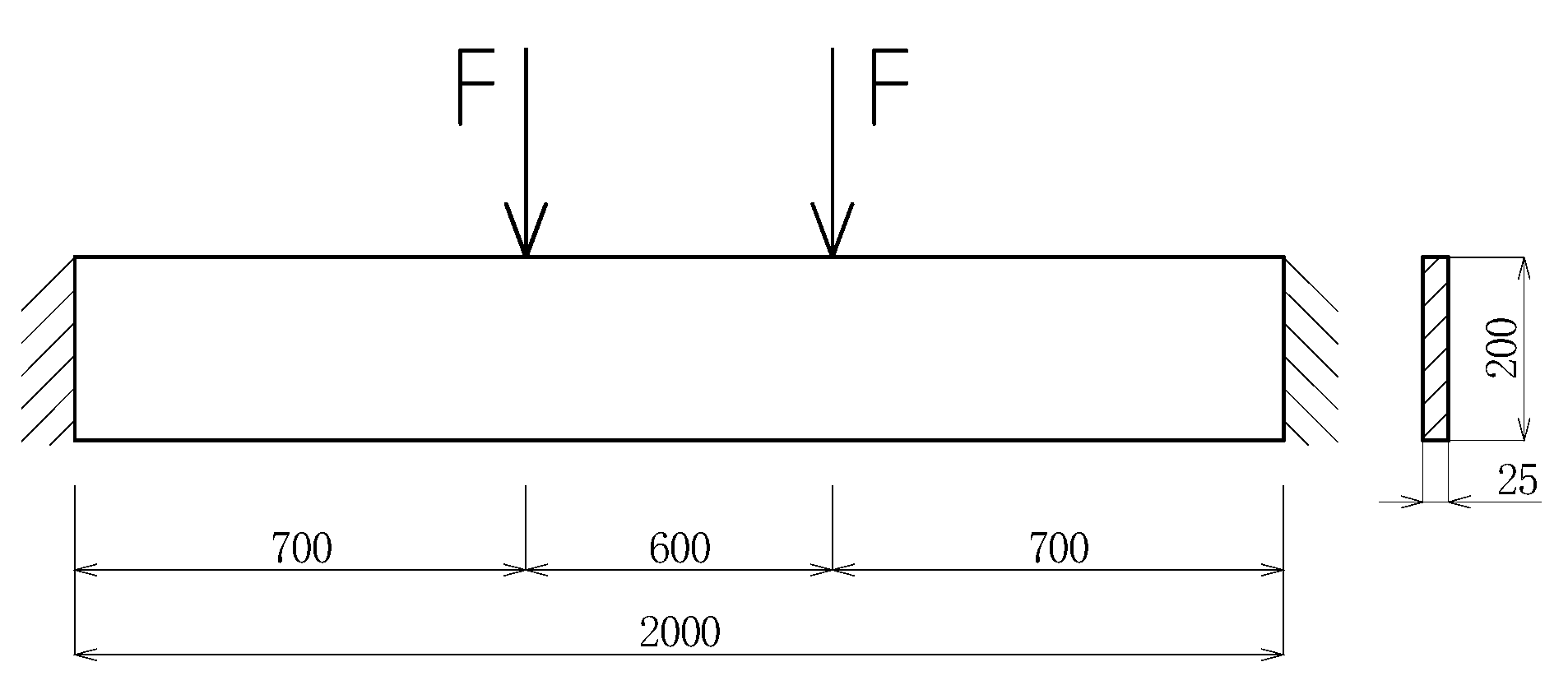
2.5. Methodology for Static Loading Testing of Sideboard
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Verhaert, V. Ergonomic analysis of integrated bed measurements: Towards smart sleep systems. Ergonomics 2011, 54, 169–178. [Google Scholar] [CrossRef]
- Navrátil, V. Čalunenie; Technical University in Zvolen: Zvolen, Slovakia, 2001. [Google Scholar]
- Camden, S.G. Nursing care of the bariatric patient. Bariatr. Nurs. Surg. Patient Care 2006, 1, 21–30. [Google Scholar] [CrossRef]
- Kornoš, P. Analýza Čaluneného Nábytku z Pohľadu Konštrukcie; Technical University in Zvolen: Zvolen, Slovakia, 2009. [Google Scholar]
- Hitka, M.; Hajduková, A. Antropometrická optimalizácia rozmerov lôžkového nábytku. Acta Facultatis Xylologiae Zvolen 2013, 55, 101–109. [Google Scholar]
- Wiggermann, N.; Smith, K.; Kumpar, D. What bed size does a patient need? The relationship between body mass index and space required to turn in bed. Nurs. Res. 2017, 66, 483–489. [Google Scholar] [CrossRef]
- Sedmák, R.; Hitka, M. Analýza zmien antropometrických údajov dospelej populácie na území Slovenska. In Proceedings of the Conference Management of Human Potential in the Enterprise, Zvolen, Slovakia, 18–19 May 2004. [Google Scholar]
- Sedmák, R.; Hitka, M. Dynamika zmien vybraných antropometrických znakov populácie Slovenska. Hum. Resour. Manag. Ergon. 2007, 3, 24–34. [Google Scholar]
- Malina, R.M. Secular trends in growth, maturation and physical performance: A review. Anthropol. Rev. 2004, 67, 3–31. [Google Scholar]
- Hauspie, R.C.; Vercauteren, M.; Susanne, C. Secular changes in growth and maturation: An update. Acta Paediatr. 1997, 423, 20–27. [Google Scholar] [CrossRef]
- Cole, T.J. Secular trends in growth. Proc. Nutr. Soc. 2000, 59, 317–324. [Google Scholar] [CrossRef]
- Cole, T.J. The secular trend in human physical growth: A biological view. Econ. Hum. Biol. 2003, 1, 161–168. [Google Scholar] [CrossRef]
- Sharp, M.A.; Patton, J.F.; Knapik, J.J.; Hauret, K.; Mello, R.P.; Ito, M.; Frykman, P.N. Comparison of the physical fitness of men and women entering the U.S. Army: 1978–1998. Med. Sci. Sports Exerc. 2002, 34, 356–363. [Google Scholar] [CrossRef]
- Knapik, J.J.; Sharp, M.A.; Darakjy, S.; Jones, S.B.; Hauret, K.G.; Jones, B.H. Temporal changes in the physical fitness of US Army recruits. Sports Med. 2006, 36, 613–634. [Google Scholar] [CrossRef]
- Yokota, M.; Barthalon, G.P.; Berglund, L.D. Assessment of male anthropometric trends and the effects on simulated heat stress responses. Eur. J. Appl. Psychol. 2008, 104, 297–302. [Google Scholar] [CrossRef] [PubMed]
- Bolstad, G.; Benum, B.; Rokne, A. Anthropometry of Norwegian light industry and Office workers. Appl. Ergon. 2001, 32, 239–246. [Google Scholar] [CrossRef]
- Hanson, L.; Sperling, L.; Gard, G.; Ipsen, S.; Vergara, C.O. Swedish anthropometrics for product and workplace design. Appl. Ergon. 2009, 40, 797–806. [Google Scholar] [CrossRef]
- Sundet, J.M. The Flynn Effect in Families: Studies of Register Data on Norwegian Military Conscripts and Their Families. J. Intell. 2014, 2, 106–118. [Google Scholar] [CrossRef]
- Barroso, M.P.; Arezes, P.M.; Da Costa, L.G.; Miguel, A.S. Anthropometric study of Portuguese workers. Int. J. Ind. Ergon. 2005, 35, 401–410. [Google Scholar] [CrossRef]
- Leitão, R.B.; Rodrigues, L.P.; Neves, L.; Carvalho, G.S. Development of adiposity, obesity and age at menarche: An 8-year follow-up study in Portuguese schoolgirls. Int. J. Adolesc. Med. Health 2013, 25, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Kayis, B.; Ozok, A.F. The anthropometry of Turkish army men. Appl. Ergon. 1991, 22, 49–54. [Google Scholar] [CrossRef]
- Jelačič, D.; Greger, K.; Grladinovič, T. Research on anthropometric characteristics of high school students and ergonomic characteristics of high school furniture. Drvna Ind. 2002, 53, 99–106. [Google Scholar]
- Martín-Merino, E.; Huerta-Álvarez, C.; Prieto-Alhambra, D.; Álvarez-Gutiérrez, A.; Montero-Corominas, D. Secular trends of use of anti-osteoporotic treatments in Spain: A population-based cohort study including over 1.5 million people and more than 12 years of follow-up. Bone 2017, 105, 292–298. [Google Scholar] [CrossRef]
- Myburgh, J.; Staub, K.; Ruhli, F.J.; Smith, J.R.; Steyn, M. Secular trend in stature of late 20th century white South Africans and two European populations. HOMO J. Comp. Hum. Biol. 2017, 68, 433–439. [Google Scholar] [CrossRef]
- Chuan, T.K.; Hartono, M.; Kumar, N. Anthropometry of the Singaporean and Indonesian populations. Int. J. Ind. Ergon. 2010, 40, 757–766. [Google Scholar] [CrossRef]
- Zhao, J.; Su, C.; Wang, H.; Wang, Z.; Wang, Y.; Zhang, B. Secular Trends in Energy and Macronutrient Intakes and Distribution among Adult Females (1991–2015): Results from the China Health and Nutrition Survey. Nutrients 2018, 10, 115. [Google Scholar] [CrossRef]
- Zheng, W.; Suzuki, K.; Yokomichi, H.; Sato, M.; Yamagata, Z. Multilevel longitudinal analysis of sex differences in height gain and growth rate changes in Japanese school-aged children. J. Epidemiol. 2013, 23, 275–279. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wang, M.J.J.; Wang, E.M. The comparisons of anthropometric characteristics among four peoples in East Asia. Appl. Ergon. 2004, 35, 173–178. [Google Scholar] [CrossRef]
- Zong, Y.; Xie, R.; Deng, N.; Liu, L.; Tan, W.; Gao, Y.; Yang, J.; Yang, Y. Secular trends in overweight and obesity among urban children and adolescents, 2003–2012: A serial cross-sectional study in Guangzhou, China. Sci. Rep. 2017, 7, 12042. [Google Scholar] [CrossRef]
- Kothyial, K.; Tettey, S. Anthropometry data of elderly people in Australia. Appl. Ergon. 2000, 31, 329–332. [Google Scholar] [CrossRef]
- dos Santos, F.K.; Maia, J.A.R.; Gomes, T.N.Q.F.; Daca, T.; Madeira, A.; Damasceno, A.; Katzmarzyk, P.T.; Prista, A. Secular Trends in Habitual Physical Activities of Mozambican Children and Adolescents from Maputo City. Int. J. Environ. Res. Public Health 2014, 11, 10940–10950. [Google Scholar] [CrossRef]
- Mokdad, M. Anthropometric study of Algerian farmers. Int. J. Ind. Ergon. 2002, 29, 331–341. [Google Scholar] [CrossRef]
- Wang, Y.; Beydoun, M.A. The obesity epidemic in the United States—Gender, age, socioeconomic, racial/ethnic, and geographic characteristics: A systematic review and meta-regression analysis. Epidemiol. Rev. 2007, 29, 6–28. [Google Scholar] [CrossRef]
- Stevens, G.A.; Singh, G.M.; Lu, Y.; Danaei, G.; Lin, J.K.; Finucane, M.M.; Bahalim, A.N.; McIntire, R.K.; Gutierrez, H.R.; Cowman, M.; et al. National, regional, and global trends in adult overweight and obesity prevalences. Popul. Health Metr. 2012, 10, 22. [Google Scholar] [CrossRef]
- Tremmel, M.; Gerdtham, U.-G.; Nilsson, P.M.; Saha, S. Economic Burden of Obesity: A Systematic Literature Review. Int. J. Environ. Res. Public Health 2017, 14, 435. [Google Scholar] [CrossRef]
- González-Rodríguez, L.G.; Perea Sánchez, J.M.; Aranceta-Bartrina, J.; Gil, Á.; González-Gross, M.; Serra-Majem, L.; Varela-Moreiras, G.; Ortega, R.M. Intake and Dietary Food Sources of Fibre in Spain: Differences with Regard to the Prevalence of Excess Body Weight and Abdominal Obesity in Adults of the ANIBES Study. Nutrients 2017, 9, 326. [Google Scholar] [CrossRef]
- Burke, N.L.; Shomaker, L.B.; Brady, S.; Reynolds, J.C.; Young, J.F.; Wilfley, D.E.; Sbrocco, T.; Stephens, M.; Olsen, C.H.; Yanovski, J.A.; et al. Impact of Age and Race on Outcomes of a Program to Prevent Excess Weight Gain and Disordered Eating in Adolescent Girls. Nutrients 2017, 9, 947. [Google Scholar] [CrossRef]
- Vuong, Q.-H.; Hoang, A.-D.; Vuong, T.-T.; La, V.-P.; Nguyen, H.K.T.; Ho, M.-T. Factors Associated with the Regularity of Physical Exercises as a Means of Improving the Public Health System in Vietnam. Sustainability 2018, 10, 3828. [Google Scholar] [CrossRef]
- Ogden, C.L.; Carroll, M.D.; Fryar, C.D.; Flegal, K.M. Prevalence of Obesity among Adults and Youth: United States, 2011–2014. NCHS Data Brief, 219, 1–8. 2015. Available online: https://www.cdc.gov/nchs/data/databriefs/db219.pdf (accessed on 4 December 2018).
- Finucane, M.M.; Stevens, G.A.; Cowan, M.J.; Danaei, G.; Lin, J.K.; Paciorek, C.J.; Singh, G.M.; Gutierrez, H.R.; Lu, Y.; Bahalim, A.N.; et al. Global burden of metabolic risk factors of chronic diseases collaborating group (body mass index). Lancet 2011, 377, 557–567. [Google Scholar] [CrossRef]
- de Onis, M.; Blössner, M.; Borghi, E. Global prevalence and trends of overweight and obesity among preschool children. Am. J. Clin. Nutr. 2010, 92, 1257–1264. [Google Scholar] [CrossRef]
- Chan, R.S.; Woo, J. Prevention of Overweight and Obesity: How Effective is the Current Public Health Approach. Int. J. Environ. Res. Public Health 2010, 7, 765–783. [Google Scholar] [CrossRef]
- Peltzer, K.; Pengpid, S.; Samuels, T.A.; Özcan, N.K.; Mantilla, C.; Rahamefy, O.H.; Wong, M.L.; Gasparishvili, A. Prevalence of Overweight/Obesity and Its Associated Factors among University Students from 22 Countries. Int. J. Environ. Res. Public Health 2014, 11, 7425–7441. [Google Scholar] [CrossRef]
- Flegal, K.M.; Carroll, M.D.; Ogden, C.L.; Curtin, L.R. Prevalence and trends in obesity among US adults, 1999–2008. JAMA 2010, 303, 235–241. [Google Scholar] [CrossRef]
- Rockholm, B.; Baker, J.L.; Sørensen, T.I.A. The levelling off of the obesity epidemic since the year 1999—A review of evidence and perspectives. Obes. Rev. 2010, 11, 835–846. [Google Scholar] [CrossRef] [PubMed]
- Odunitan-Wayas, F.; Okop, K.; Dover, R.; Alaba, O.; Micklesfield, L.; Puoane, T.; Uys, M.; Tsolekile, L.; Levitt, N.; Battersby, J.; et al. Food Purchasing Characteristics and Perceptions of Neighborhood Food Environment of South Africans Living in Low-, Middle- and High-Socioeconomic Neighborhoods. Sustainability 2018, 10, 4801. [Google Scholar] [CrossRef]
- Hitka, M.; Sedmák, R.; Joščák, P.; Ližbetinová, L. Positive Secular Trend in Slovak Population Urges on Updates of Functional Dimensions of Furniture. Sustainability 2018, 10, 3474. [Google Scholar] [CrossRef]
- Hitka, M.; Joščák, P.; Langová, N.; Krišťák, Ľ.; Blašková, S. Loar-Carrying Capacity and the Size of Chair Joints Determined for Users with a Higher Body Weight. Bioresources 2018, 13, 6428–6443. [Google Scholar] [CrossRef]
- Bellingar, T.A.; Benden, M.E. New ANSI/BIFMA standard for testing of educational seating. Ergon. Des. Q. Hum. Factors Appl. 2015, 23, 23–27. [Google Scholar] [CrossRef]
- Dvouletá, K.; Káňová, D. Utilization of anthropometry in the sphere of sitting and bed furniture. Acta Univ. Agric. Silvic. Mendel. Brun. 2014, 62, 81–90. [Google Scholar] [CrossRef]
- Muir, M.; Archer-Heese, G. Essentials of a bariatric patient handling program. OJIN Online J. Issues Nurs. 2009, 14. [Google Scholar] [CrossRef]
- Gourash, W.; Rogula, T.; Schauer, P.R. Essential Bariatric Equipment: Making Your Facility More Accommodating to Bariatric Surgical Patients; Springer: New York, NY, USA, 2007. [Google Scholar]
- Prokopec, M. Sedací a lehací čalouněný nábytek. Antropol. Ergon. Pohled. Lignum 1998, 2, 6–10. [Google Scholar]
- Benda-Prokeinová, R.; Dobeš, K.; Mura, L.; Buleca, J. Engel’s approach as a tool for estimating consumer behavior. E M Ekon. Manag. 2017, 20, 15–29. [Google Scholar] [CrossRef]
- Veselovský, J.; Baďura, R. Slovakian folk wooden cradle design, construction, typology and kinematics. Acta Fac. Xylologiae 2017, 59, 155–165. [Google Scholar] [CrossRef]
- Igaz, R.; Macek, Š.; Zemiar, J. The influence of unidirectional cyclic bend loading on initial relaxation speed of beech lamellas. Acta Fac. Xylologiae 2014, 56, 27–35. [Google Scholar]
- Gejdoš, M.; Tončíková, Z.; Němec, M.; Chovan, M.; Gergeľ, T. Balcony cultivator: New biomimicry design approach in the sustainable device. Futures 2018, 98, 32–40. [Google Scholar] [CrossRef]
- Irle, M.A.; Barbu, M.C.; Réh, R.; Bergland, L.; Rowell, R.M. Wood Composites; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Barbu, M.C.; Réh, R.; Irle, M.A. Wood-Based Composites; IGI Global: Hershey, PA, USA, 2014. [Google Scholar]
- Willard, D.T.; Loferski, J.R. Skateboards as a Sustainable Recyclable Material. Recycling 2018, 3, 20. [Google Scholar] [CrossRef]
- Smardzewski, J. Furniture Design; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Smardzewski, J.; Preklad, S. Stress distribution in disconnected furniture joints. Electron. J. Pol. Agric. Univ. 2002, 5, 1–7. [Google Scholar]
- Rohanová, A.; Nunez, E. Prediction models of Slovakian structural timber. Wood Res. 2014, 5, 757–767. [Google Scholar]
- Kasal, A.; Kuskun, T.; Haviarova, E.; Erdil, Y.Z. Static front to back loading capacity of wood chairs and relationships between chair strength and individual joint strength. Bioresources 2016, 11, 9359–9372. [Google Scholar] [CrossRef]
- Horman, I.; Hajdarevič, S.; Martinovič, S.; Vukas, N. Numerical analysis of stress and strain in a wooden chair. Drvna Ind. 2010, 61, 151–158. [Google Scholar]
- Horman, I.; Martinovič, S.; Hajdarevič, S. Finite volume method for analysis of stress and strain in wood. Drvna Ind. 2009, 60, 27–32. [Google Scholar]
- Gustafsson, S.I. Furniture design by use of finite element method. Holy Roh. Werkst. 1995, 53, 257–260. [Google Scholar] [CrossRef]
- Gustafsson, S.I. Finite element modelling versus reality for birch chairs. Holz Roh. Werkst. 1996, 54, 355–359. [Google Scholar] [CrossRef]
- Ministry of Health of the Slovak Republic. Report on health status in Slovakia. HEALTH 2016. Available online: http://health.gov.sk (accessed on 1 February 2018).
- Public Health Authority of the Slovak Republic. Annual Report on the Activities of the Public Health Office for 2017. Available online: http://uvzsr.sk/docs/vs/vyrocna_sprava_2017.pdf (accessed on 1 February 2018).
- Statistical Office of the Slovak Republic. View of Health Status of the Slovak Population and Its Determinants (Results of EHIS 2016). Available online: http://slovak.statistics.sk (accessed on 1 February 2018).
- Ng, M.; Fleming, T.; Robinson, M.; Tomson, B.; Graetz, N.; Margono, C.; Mullany, E.C.; Biryukov, S.; Abbafati, C.; Abera, S.F.; et al. Global, regional, and national prevalence of overweight and obesity in children and adults during 1980-2013: A systematic analysis for the Global Burden of Disease Study 2013. Lancet 2014, 384, 766–781. [Google Scholar] [CrossRef]
- Di Cesare, M.; Bentham, J.; Stevens, G.A.; Zhou, B.; Danaei, G.; Lu, Y.; Bixby, H.; Cowan, M.J.; Riley, L.M.R.; Hajifathalian, K.; et al. Trends in adult body-mass index in 200 countries from 1975 to 2014: A pooled analysis of 1698 population-based measurement studies with 19.2 million participants. Lancet 2016, 387, 1377–1396. [Google Scholar] [CrossRef]
- World Health Organization Regional Office for Europe. The Health Systems in Transition (HiT). Available online: http://euro.whoint/en/countries/slovakia (accessed on 1 February 2018).
- Tokarčíková, E.; Kucharčíková, A.; Ďurišová, M. Corporate social responsibility managers and their decision making. Turk. Online J. Educ. Technol. 2017, pp. 654–664. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-85048209196&origin=resultslist&sort=plf-f&src=s&st1=tokarcikova%2c+E.&st2=&sid=747c912fb7e26aef1630dbe062108b21&sot=b&sdt=b&sl=28&s=AUTHOR-NAME%28tokarcikova%2c+E.%29&relpos=0&citeCnt=0&searchTerm= (accessed on 10 November 2018).
- Vaňová, J.; Babeľová, Z.G.; Holková, A. Organizational information transfer as a tool for building-up employees economic awareness. In Proceedings of the European Conference on Knowledge Management, Famalicao, Portugal, 2–3 September 2010. [Google Scholar]
- Ližbetinová, L.; Lorincová, S.; Caha, Z. The application of the organizational culture assessment instrument (OCAI) to logistics enterprises. Nase More 2016, 63, 170–176. [Google Scholar] [CrossRef]
- EN 1725:1998 Domestic Furniture—Bed and Mattresses—Safety Requirements and Test Methods. Available online: https://furnitest.com/testing/furniture-testing/standards/en-17251998/ (accessed on 18 November 2018).
- Potkány, M.; Gejdoš, M.; Debnár, M. Sustainable innovation approach for wood quality evaluation in green business. Sustainability 2018, 10, 2984. [Google Scholar] [CrossRef]
- Matušková, M.; Klement, I. Colour change in high temperature drying of spruce wood. Acta Fac. Xylologiae 2009, 51, 47–53. [Google Scholar]
- Klement, I.; Huráková, T. The influence of drying characteristics and quality of spruce timber with content of reaction wood. Acta Fac. Xylologiae 2015, 57, 75–82. [Google Scholar]
- Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Štruktúra a Vlastnosti Dreva; Príroda a.s.: Bratislava, Slovakia, 1993. [Google Scholar]
- Klement, I.; Huráková, T. Determining the influence of sample thickness on the high-temperature drying of beech wood (Fagus sylvatica L.). BioResources 2016, 11, 5424–5434. [Google Scholar] [CrossRef]
- Čuta, M.; Kukla, L.; Novák, L. Modelling the development of body height (length) in children using parental height data. Československá Pediatrie 2010, 65, 159–166. [Google Scholar]
- Mitterpach, J.; Hroncová, E.; Ladomerský, J.; Štefko, J. Quantification of Improvement in Environmental Quality for Old Residential Buildings Using Life Cycle Assessment. Sustainability 2016, 8, 1303. [Google Scholar] [CrossRef]
- Lorincová, S.; Potkány, M. The proposal of innovation support in Small and Medium-sized Enterprises. In Production Management and Engineering Sciences; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Burton, P.J. Striving for Sustainability and Resilience in the Face of Unprecedented Change: The Case of the Mountain Pine Beetle Outbreak in British Columbia. Sustainability 2010, 2, 2403–2423. [Google Scholar] [CrossRef]
- May, N.; Guenther, E.; Haller, P. Environmental Indicators for the Evaluation of Wood Products in Consideration of Site-Dependent Aspects: A Review and Integrated Approach. Sustainability 2017, 9, 1897. [Google Scholar] [CrossRef]
- Delios, A. How can organizations be competitive but dare to care? Acad. Manag. Perspect. 2010, 24, 25–36. [Google Scholar] [CrossRef]
- Pfeffer, J. Building sustainable organizations: The human factor. Acad. Manag. Perspect. 2010, 24, 34–45. [Google Scholar]
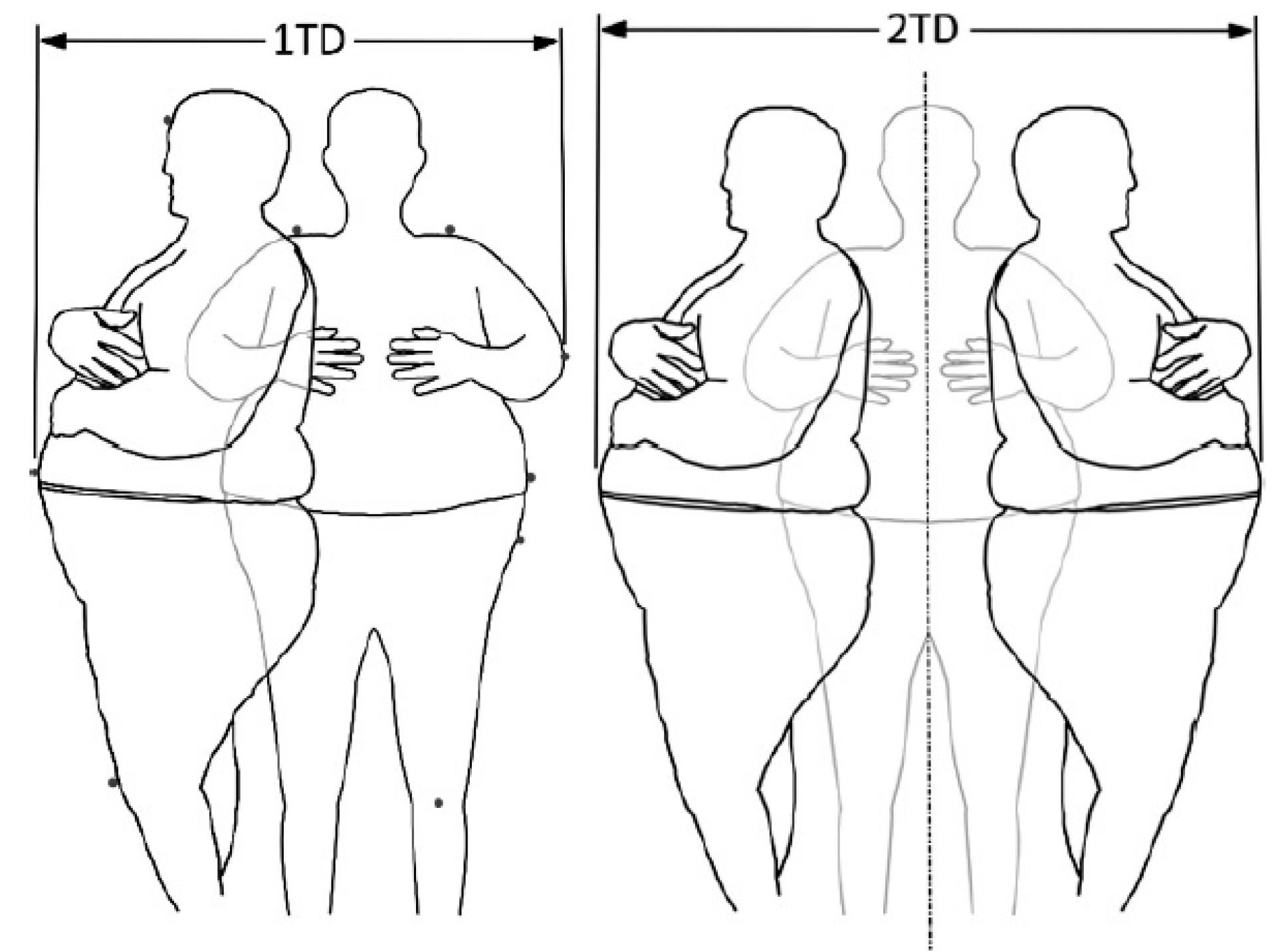
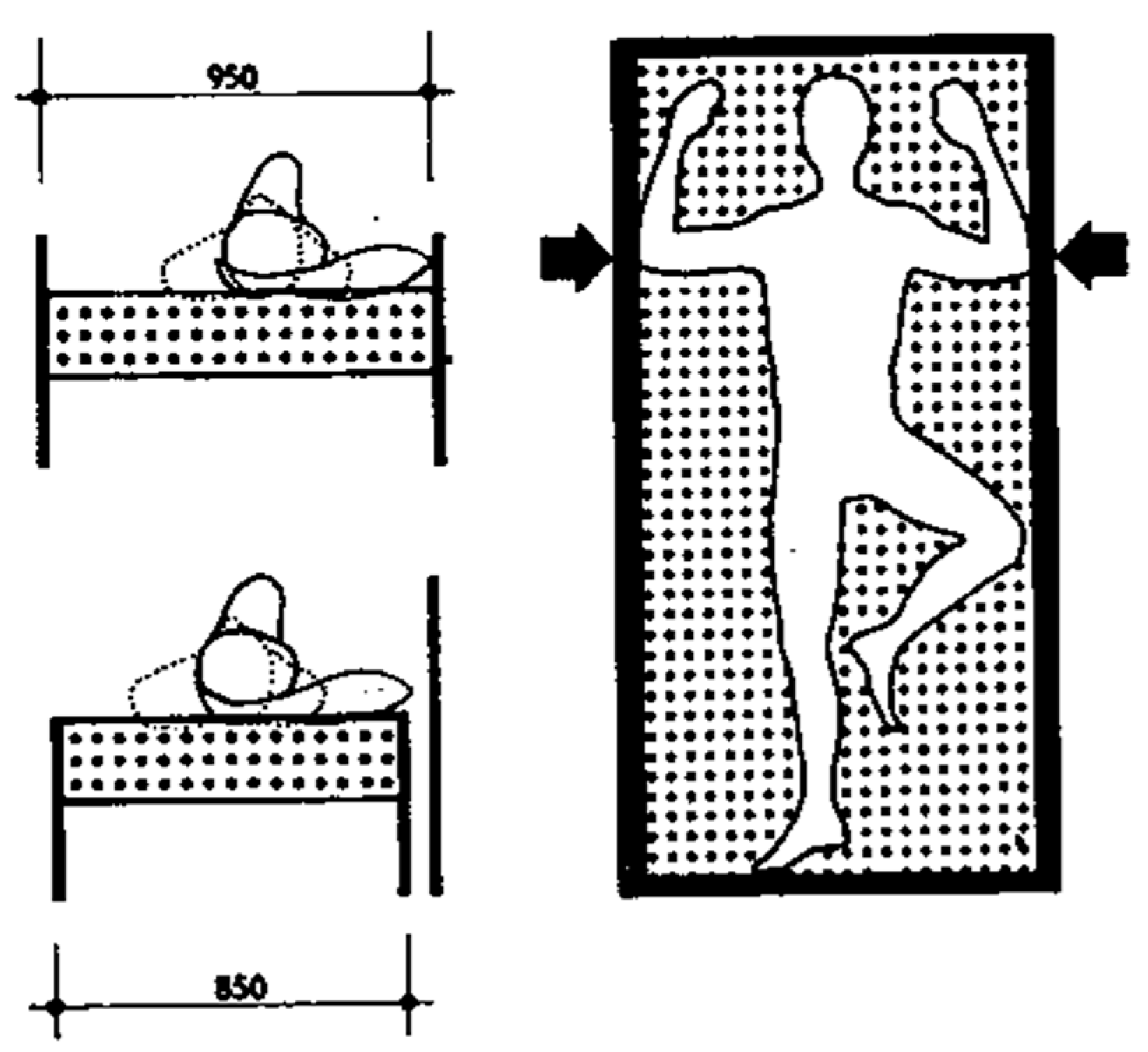
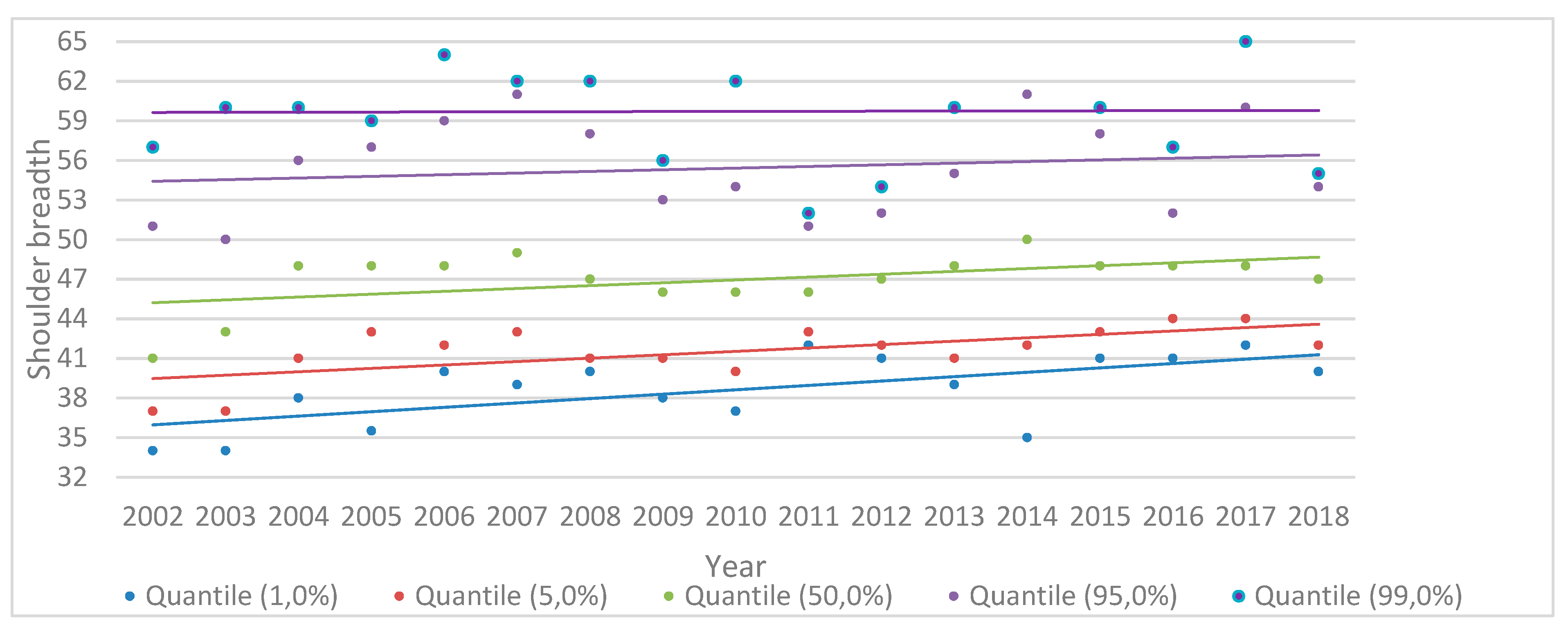
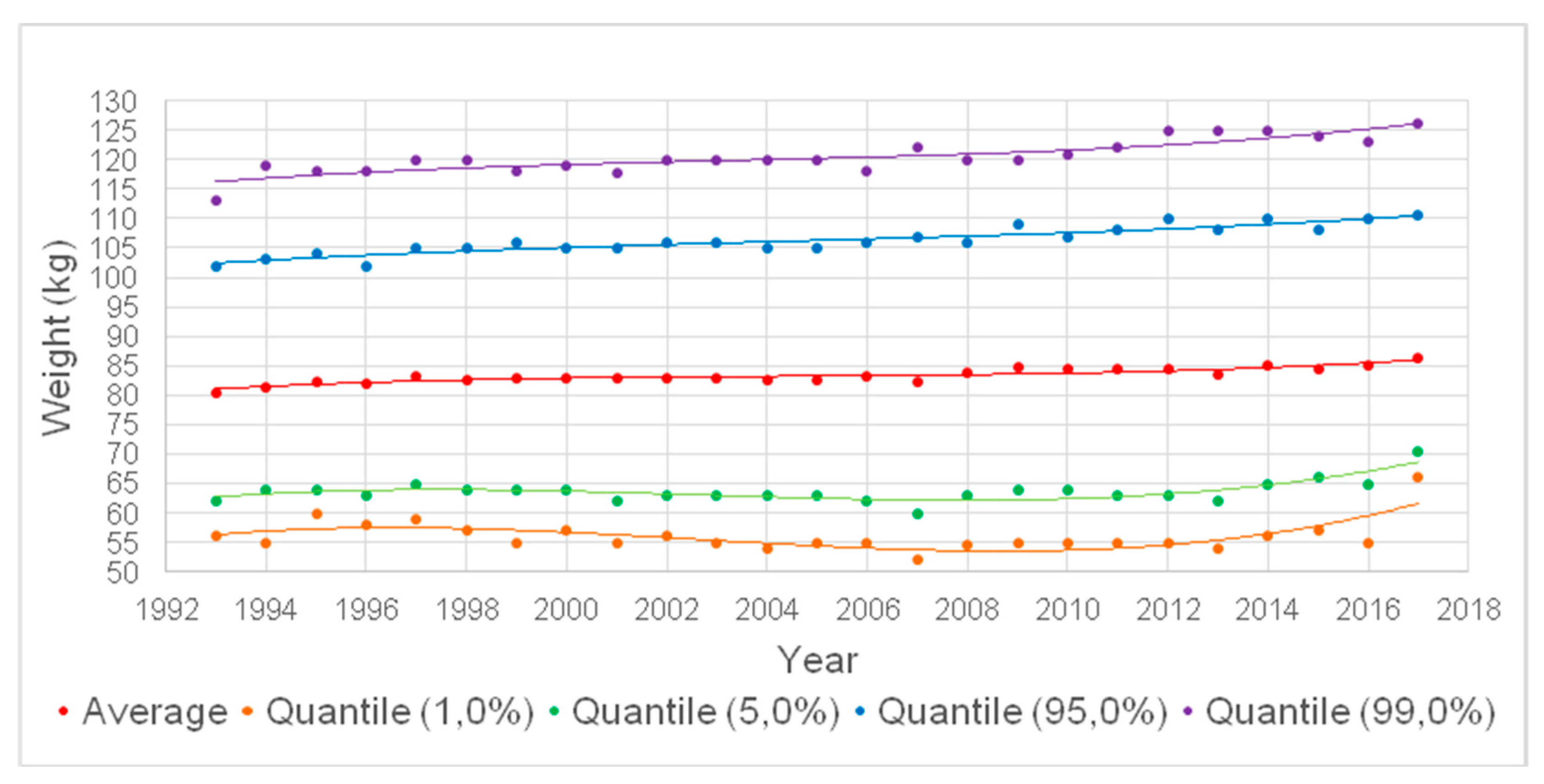

| Material constants for Norway spruce (Picea abies L.) | ||||||||
| Young’s Modulus (MPa) | Poisson’s Ratio | Shear Modulus (MPa) | ||||||
| Ex | EY | EZ | µXY | µYZ | µXZ | GXY | GYZ | GXz |
| 13,650.2 | 789.6 | 289.6 | 0.028 | 0.363 | 0.012 | 573.0 | 53.4 | 474.0 |
| Material constants for European beech (Fagus sylvatica L.) | ||||||||
| Young’s Modulus (MPa) | Poisson’s Ratio (-) | Shear Modulus (MPa) | ||||||
| Ex | EY | EZ | µXY | µYZ | µXZ | GXY | GYZ | GXz |
| 16,670.0 | 1130.0 | 630.0 | 0.044 | 0.33 | 0.027 | 1200.0 | 190.0 | 930.0 |
| Tensile Stress ft,0,d Along the Grain | Compressive Stress fc,0,d Along the Grain | Density ρ0 (kg/m3) | |
|---|---|---|---|
| Picea abies L. | 20.30 | 22.85 | 392.0 |
| Fagus sylvatica L. | 35.53 | 48.32 | 684.0 |
| Size/Material (mm) | Load 1400 N | Load 2100 N | ||
|---|---|---|---|---|
| Tensile Stress σt,0,d (MPa) | Compressive Stress σc,0,d (MPa) | Tensile Stress σt,0,d (MPa) | Compressive Stress σc,0,d (MPa) | |
| 95 × 20/800 Picea abies L. | 17.95 passed | 22.08 passed | 32.64 failed | 40.14 failed |
| 95 × 20/900 Picea abies L. | 24.02 failed | 29.574 failed | 36.03 failed | 44.361 failed |
| 95 × 20/1050 Picea abies L. | 28.021 failed | 24.021 failed | 42.031 failed | 51.031 failed |
| Size/Material | Load 1400 N | Load 2100 N | ||
|---|---|---|---|---|
| Tensile Stress U σt,0,d (MPa) | Compressive Stress σc,0,d (MPa) | Tensile Stress σt,0,d (MPa) | Compressive Stress σc,0,d (MPa) | |
| 95 × 20/800 Picea abies L. supported beam | 17.196 passed | 25.907 failed | ||
| 95 × 20/900 Picea abies L. supported beam | 15.072 passed | 16.138 passed | 22.608 failed | 24.207 failed |
| 95 × 20/1050 Picea abies L. supported beam | 18.301 passed | 18.73 passed | 27.452 failed | 28.096 failed |
| 95 × 20/900 Fagus sylvatica L. unsupported beam | 23.908 passed | 28.49 passed | 35.009 passed | 41.719 passed |
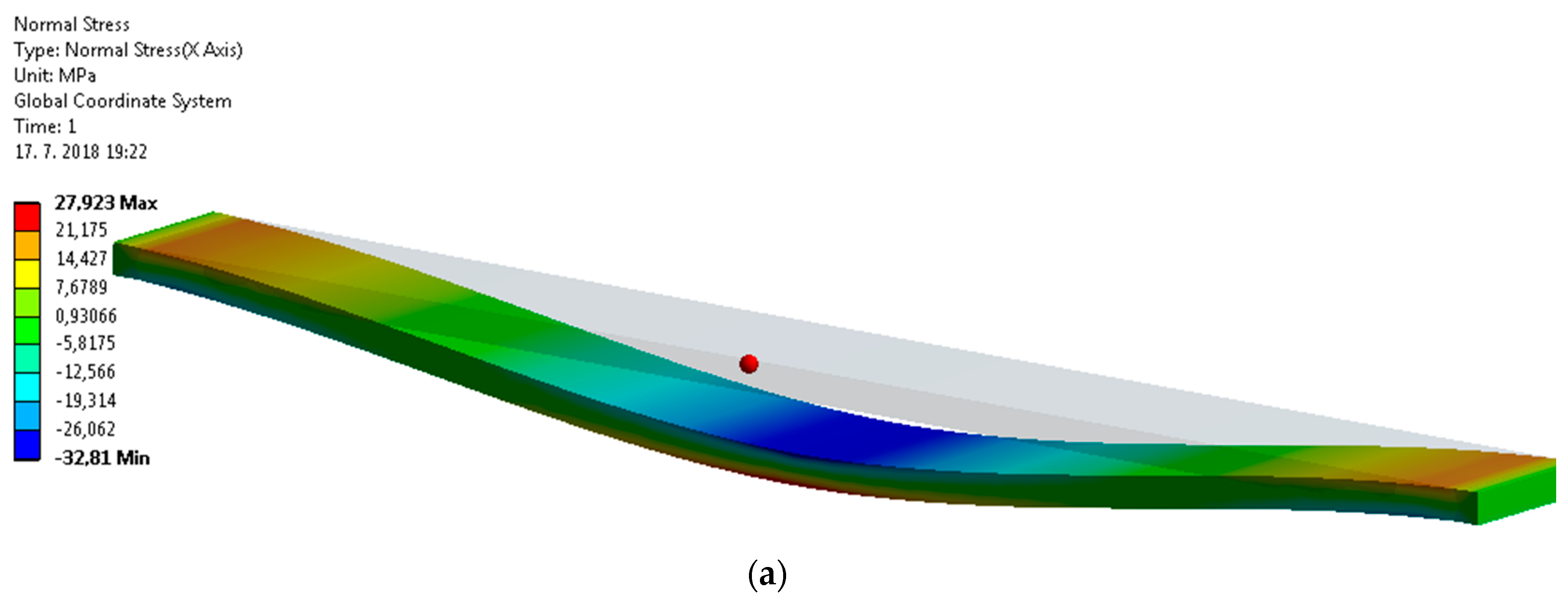
| 95 × 20/1050 Fagus sylvatica L. unsupported beam | 27.923 passed | 32.81 passed | 41.885 failed | 49.885 failed |
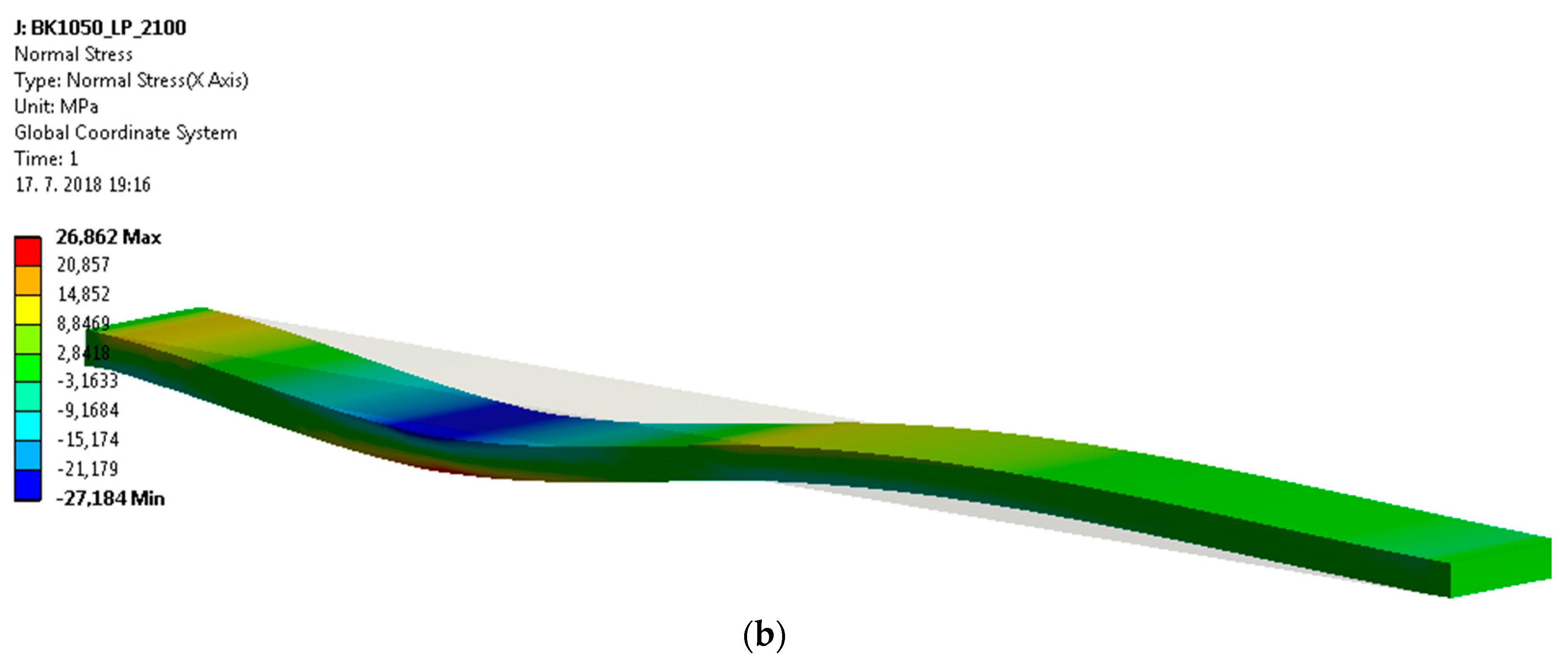
| 95 × 20/1050 Fagus sylvatica L. supported beam | 26.862 passed | 27.184 passed | ||
| Length of the Beam l = 2000 mm | ||
|---|---|---|
| F = 1200 N | F = 1800 N | |
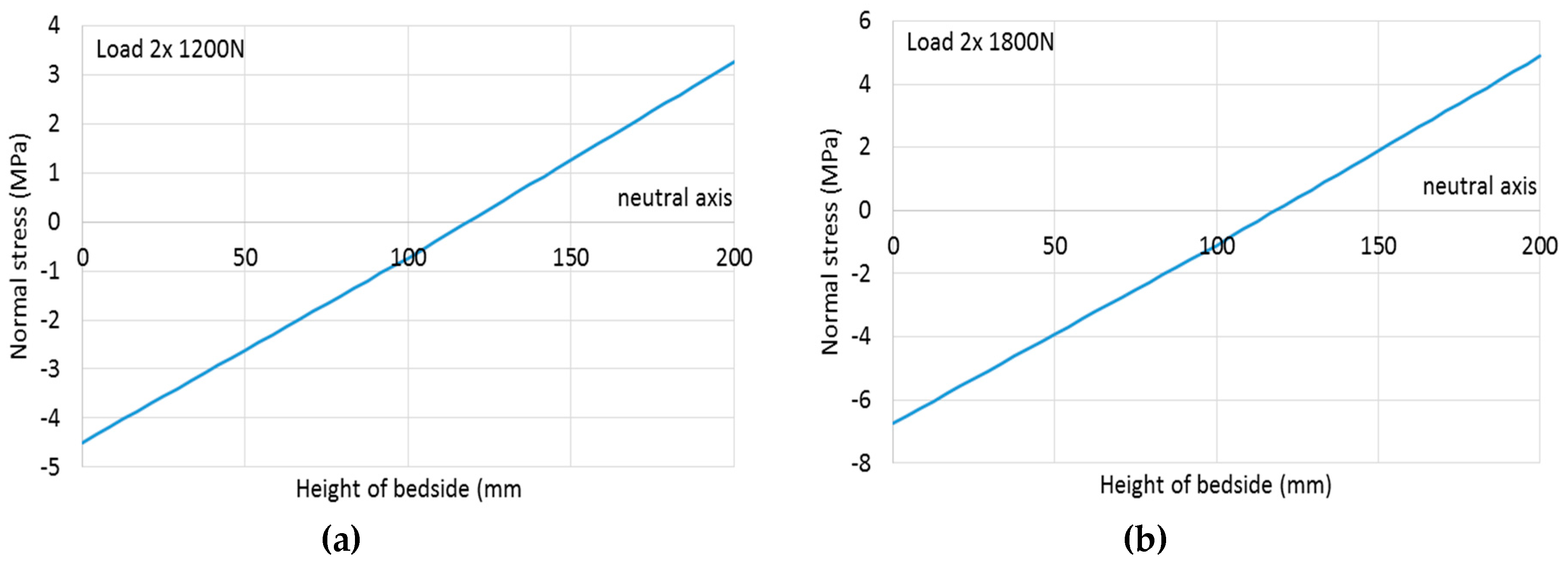
| Tensile stress σt,0,d (MPa) | 3.2535 | 4.8802 |
| Compressive stress σc,0,d (MPa) | 4.4929 | 6.7394 |
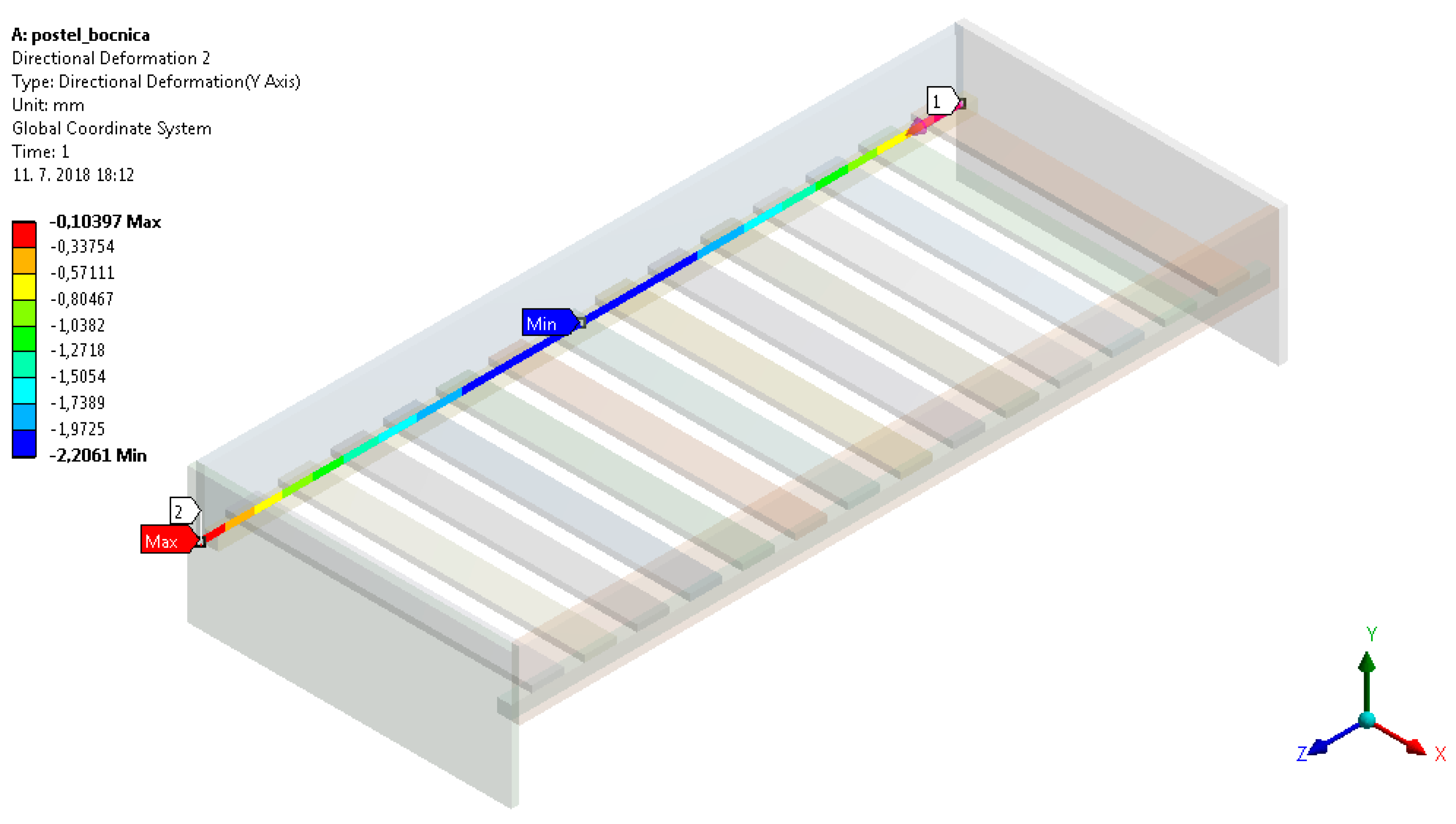
| Deformation y (mm) | 1.4707 | 2.2061 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Réh, R.; Krišťák, Ľ.; Hitka, M.; Langová, N.; Joščák, P.; Čambál, M. Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia. Sustainability 2019, 11, 624. https://doi.org/10.3390/su11030624
Réh R, Krišťák Ľ, Hitka M, Langová N, Joščák P, Čambál M. Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia. Sustainability. 2019; 11(3):624. https://doi.org/10.3390/su11030624
Chicago/Turabian StyleRéh, Roman, Ľuboš Krišťák, Miloš Hitka, Nadežda Langová, Pavol Joščák, and Miloš Čambál. 2019. "Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia" Sustainability 11, no. 3: 624. https://doi.org/10.3390/su11030624
APA StyleRéh, R., Krišťák, Ľ., Hitka, M., Langová, N., Joščák, P., & Čambál, M. (2019). Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia. Sustainability, 11(3), 624. https://doi.org/10.3390/su11030624





