Combined Experimental and Field Data Sources in a Prediction Model for Corrosion Rate under Insulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Historical Field Data Input
- (1)
- Determination of artificial neural network (ANN) parameters: Available parameters were operating temperature (°C), insulation type, pipe design, piping thickness (mm), type of pipe material, type of environment (weather condition either rainy or sunny), elapsed time (years), and CUI rate (mm/year) data. This surface profiler is suitable when the data contain more than one continuous factor. In this study, the operating temperature and corrosion rate were set as a continuous factor.
- (2)
- Definition of ANN architecture: The basic structure of the ANN was identified and determined. The layer of hidden nodes, the input parameter, and the output parameter were clearly prescribed. For this study, one hidden layer was used, and a hyperbolic tangent function (TanH) with a sigmoid type was used as an activation function for the ANN test.
- (3)
- Data normalization, filtration, and initialization: Field data collected from the actual plant in Kerteh, Malaysia, were simulated. Before that, the incomplete, missing information from the database or outlier values were removed to ensure only significant data were included. Usually, the field data are collected without the thickness measurement. Thus, data were simulated to generate sufficient data to continue with normalization and filtration. During this process, the range of CUI rate data was set from 0 to 1 mm/year based on ABB EUT.249A references as a common CUI rate occurrence [13].
- (4)
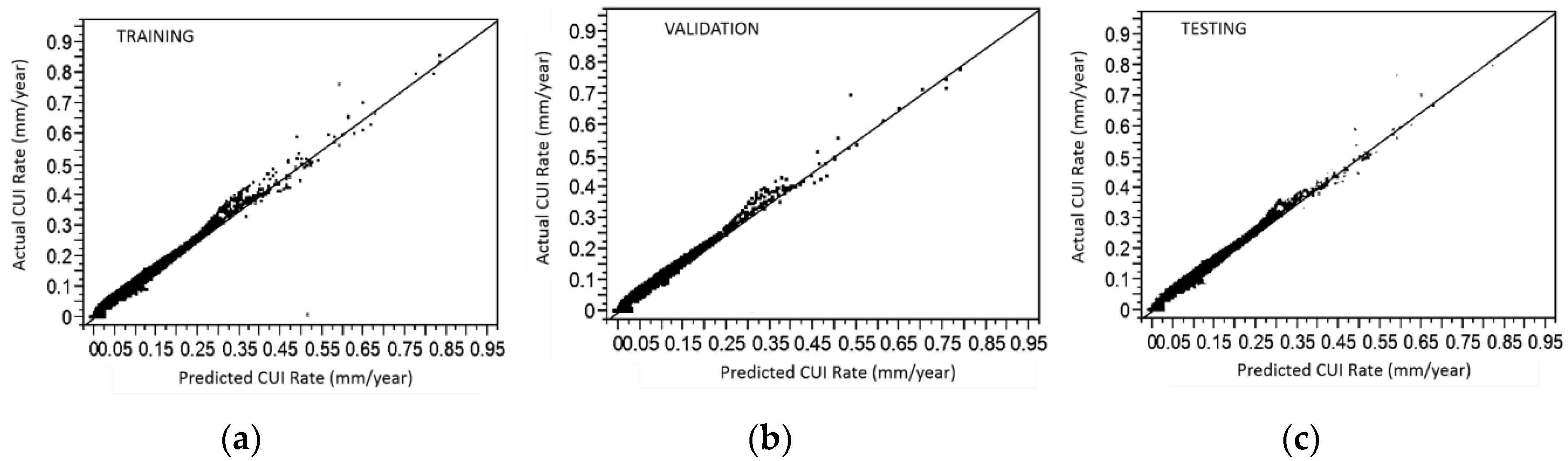
- ANN training and surface profiling: For training purposes, 70% of normalized data was used, while 15% for validation set and other 15% were for testing the basic model being developed. The surface profiling platform was used to plot points on the surface model after the ANN training completed. The points were selected based on the parameter and profiled the loss as a function of the parameters. The CUI rates were determined and tabulated in Excel sheets or in graphs.
2.2. Experimental Work Data Input
2.3. CUI Rate Prediction Modeling
3. Results
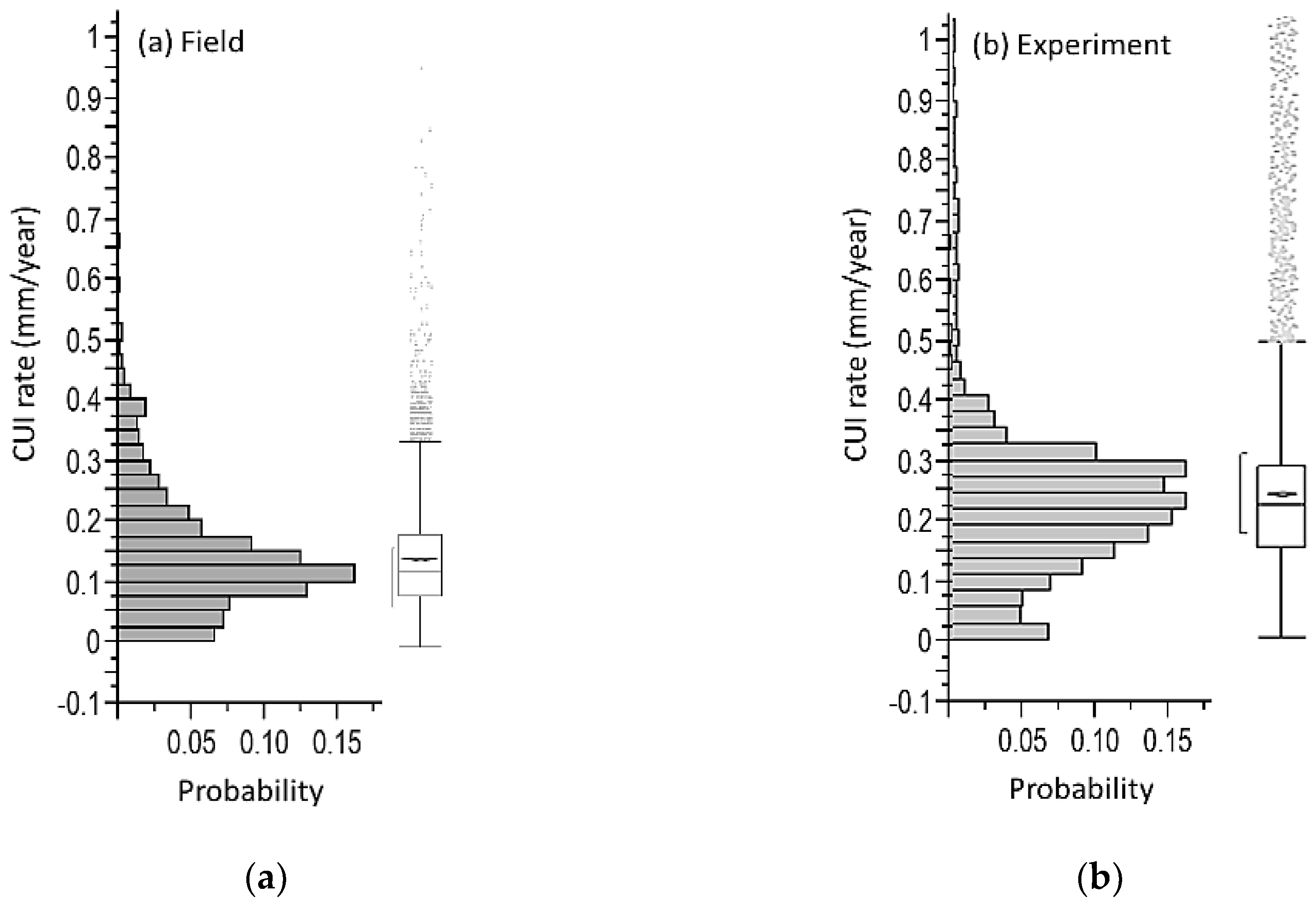
3.1. Historical Field Result
3.2. Experimental Work Result
3.3. CUI Rate Prediction Model
4. Discussion
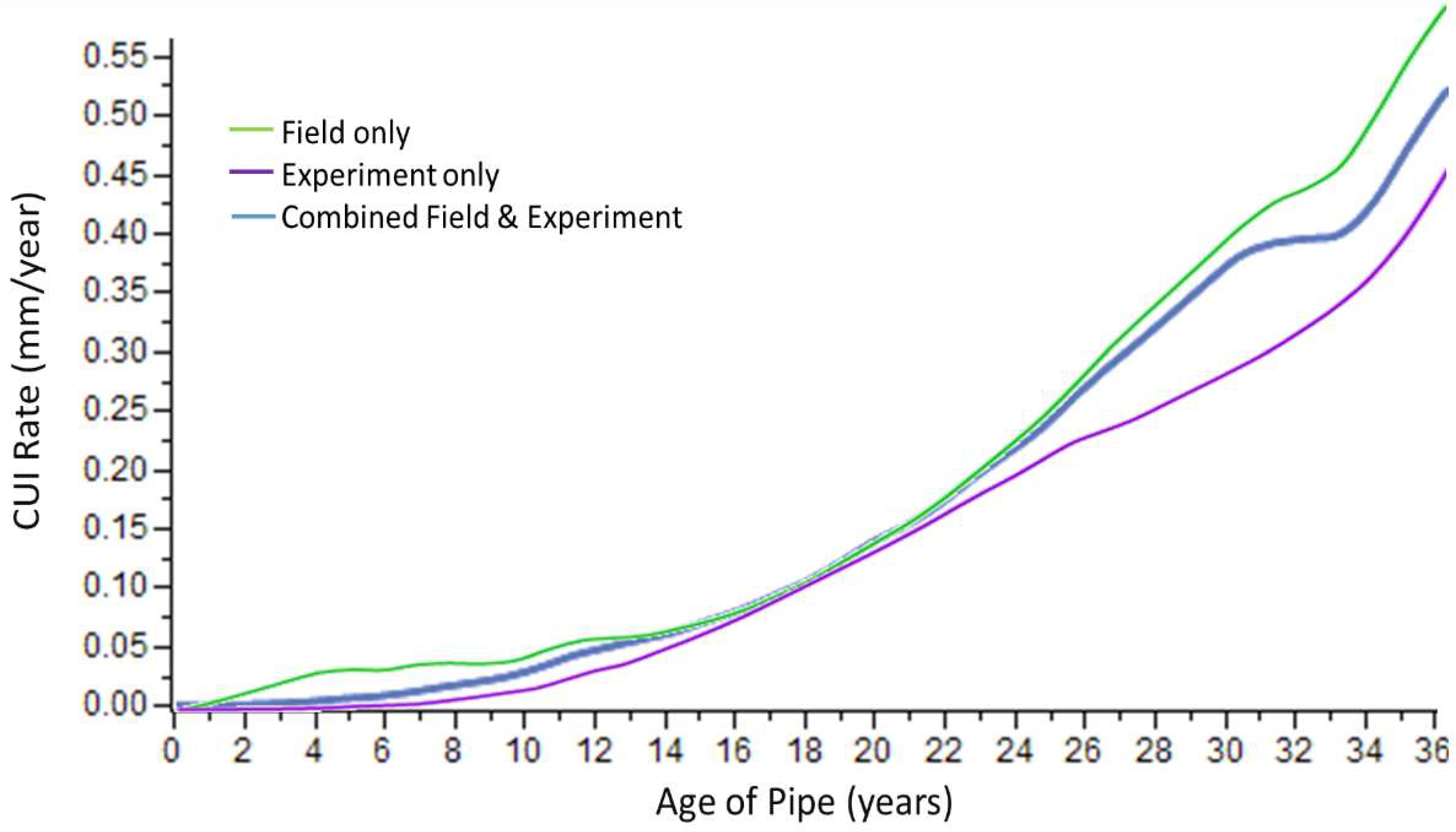
4.1. Comparison of Single Type Data and Combined Data in the CUI Rate Model
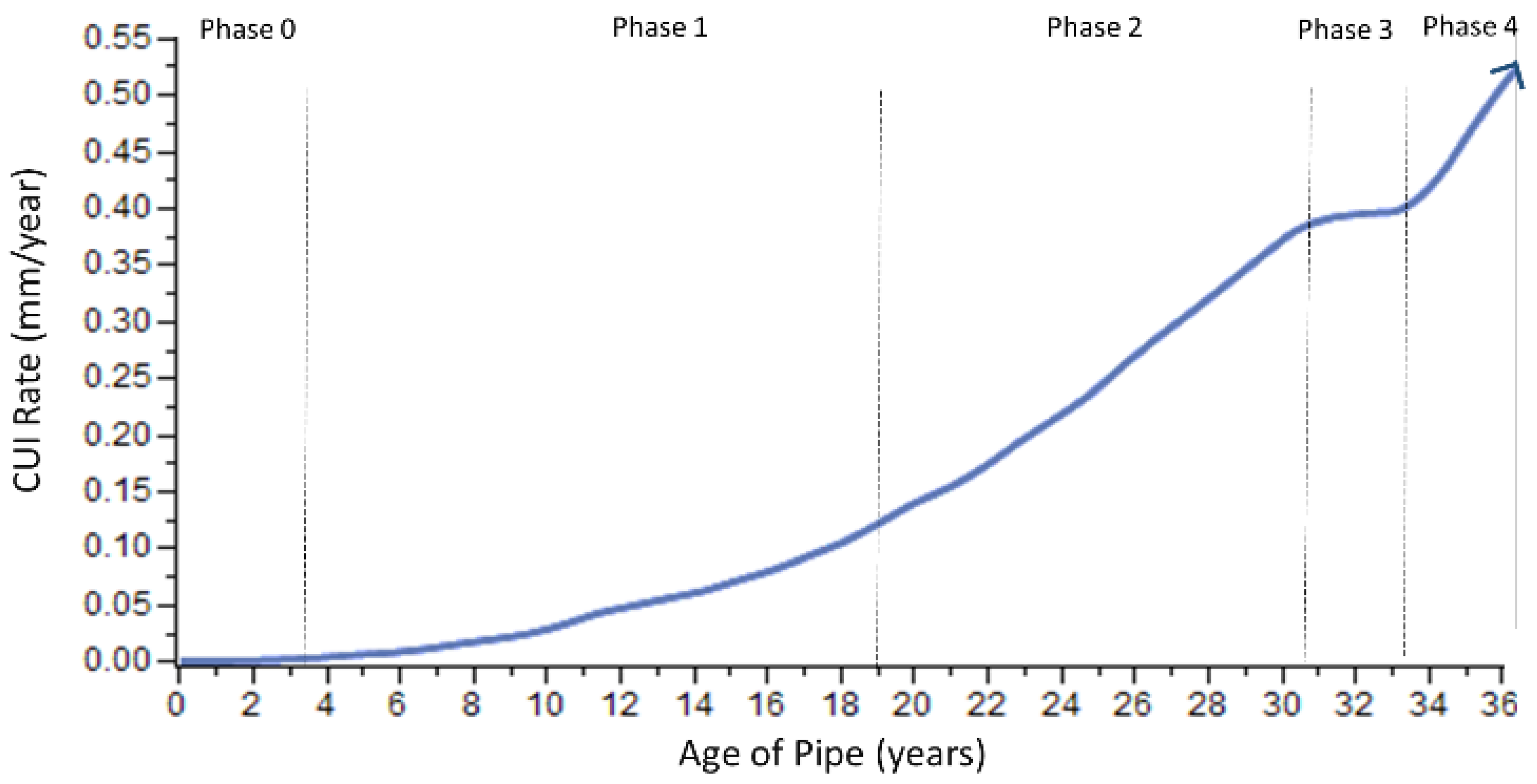
4.2. CUI Rate Model with Corrosion Phases
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- American Petroleum Institute Recommended Practice. API 581 Risk-Based Inspection, 2nd ed.; American Petroleum Institute: Washington, DC, USA, 2008. [Google Scholar]
- Datta, V.; Adlem, S.; Giardina, M.; de Varennes, N.; Gray, L.G.; Lachat, D.; Johnson, B. When Undercover Agents Can’t Stand the Heat: Coating in Action. J. Prot. Coat. Linings 2012, 29, 24–43. [Google Scholar]
- Marsh, J.; Ounnas, S.; Kenny, J.P.; Richardson, M. Corrosion management for aging pipelines-Experience from the forties field. In Proceedings of the Society of Petroleum Engineers International Oilfield Corrosion Conference, Aberdeen, UK, 28–29 May 2008; pp. 1–10. [Google Scholar]
- Fitzgerald, B.J.; Winnik, S. A Strategy for Preventing Corrosion Under Insulation on Pipeline in the Petrochemical Industry. J. Prot. Coat. Linings 2005, 22, 52–57. [Google Scholar]
- Kimberly, M.; Deepa, G. Corrosion under Insulation (CUI): A Nanotechnology Solution Explanation. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Quebec, Mexico, 13–18 July 2014; pp. 1–5. [Google Scholar]
- Tsai, Y.H.; Wang, J.; Chien, W.T.; Wei, C.Y.; Wang, X.; Hsieh, S.H. A BIM-based approach for predicting corrosion under insulation. J. Autom. Constr. 2019, 107, 102923. [Google Scholar] [CrossRef]
- Rachman, A.; Ratnayake, R.M.C. Machine learning approach for risk-based inspection screening assessment. J. Reliab. Eng. Syst. Saf. 2019, 185, 518–532. [Google Scholar] [CrossRef]
- Mohsin, K.M.; Mokhtar, A.A.; Tse, P.W. A fuzzy logic method: Predicting corrosion under insulation of piping systems with modelling of CUI 3D surfaces. Int. J. Press. Vessel. Pip. 2019, 175, 103929. [Google Scholar] [CrossRef]
- Helle, H.P.E. Five fatal flaws in API RP 581. In Proceedings of the 14th Middle East Corrosion Conference and Exhibition, Manama, Bahrain, 12–15 February 2012; p. 12. [Google Scholar]
- Bhandari, J.; Khan, F.; Abbassi, R.; Garaniya, V.; Ojeda, R. Modeling of pitting corrosion in marine and offshore steel structures—A technical review. J. Loss Prev. Process Ind. 2015, 37, 39–62. [Google Scholar] [CrossRef]
- Burhani, N.R.A.; Muhammad, M.; Ismail, M.C. Available Prediction Methods for Corrosion under Insulation (CUI): A Review. MATEC Web Conf. 2014, 13, 5005. [Google Scholar] [CrossRef]
- Javaherdashti, R. Corrosion under Insulation (CUI): A review of essential knowledge and practice. J. Mater. Sci. Surf. Eng. 2014, 1, 36–43. [Google Scholar]
- ABB. Guide for: Detection and Management of Corrosion under Insulation under Pressure Equipment; EUT.249A; ABB: Zürich, Switzerland, 2004. [Google Scholar]
- ASTM. Standard Guide for Laboratory Simulation of Corrosion under Insulation; G189-07; ASTM: West Conshohocken, PA, USA, 2008; pp. 1–11. [Google Scholar]
- Caines, S.; Khan, F.; Shirokoff, J.; Qiu, W. Experimental design to study corrosion under insulation in harsh marine environments. J. Loss Prev. Process Ind. 2015, 33, 39–51. [Google Scholar] [CrossRef]
- Burhani, N.R.A.; Muhammad, M.; Ismail, M.C.; Mahed, M.A. An Experimental Analysis using Taguchi Method in Resolving the Significant Factors subject to Corrosion under Insulation. ARPN J. Eng. Appl. Sci. 2016, 11, 11966–11970. [Google Scholar]
- Burhani, N.R.A.; Muhammad, M.; Mokhtar, A.A.; Ismail, M.C. Application of Logistic Regression in Resolving Influential Risk Factors Subject to Corrosion Under Insulation. In Proceedings of the 2016 International Conference on Industrial Engineering and Operations Management, Kuala Lumpur, Malaysia, 8–10 March 2016; pp. 1–6. [Google Scholar]
- Tuffery, S. Data Mining and Statistics for Decision-Making; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-97916-7. [Google Scholar]
- Demuth, H.B.; Beale, M.H.; Jess, O.D.; Hagan, M.T. Neural Network Design; PWS Publishing Co.: Boston, MA, USA, 1997. [Google Scholar]
- Vogels, T.P.; Rajan, K.; Abbott, L.F. Neural network dynamics. Annu. Rev. Neurosci. 2005, 28, 357–376. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.T. Springer Handbook of Engineering Statistics. Springer-Verlag: London, UK, 2007; Volume 49, p. 1120. ISBN 1-185233-806-0. [Google Scholar]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- You, J.S.; Wu, W.F. Probabilistic failure analysis of nuclear piping with empirical study of Taiwan’s BWR plants. Int. J. Press. Vessel Pip. 2002, 79, 483–492. [Google Scholar] [CrossRef]
- Khan, M.M.; Mokhtar, A.A.; Hussin, H. A fuzzy-based model to determine CUI corrosion rate for carbon steel piping systems. ARPN J. Eng. Appl. Sci. 2016, 11, 13325–13330. [Google Scholar]
- Melchers, R.E. Development of new applied models for steel corrosion in marine applications including shipping. Ships Offshore Struct. 2008, 3, 135–144. [Google Scholar] [CrossRef]
- Fontana, M. Corrosion Engineering, 3rd ed.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Valor, A.; Caleyo, F.; Alfonso, L.; Rivas, D.; Hallen, J.M. Stochastic modeling of pitting corrosion: A new model for initiation and growth of multiple corrosion pits. Corros. Sci. 2007, 49, 559–579. [Google Scholar] [CrossRef]




| Nodes | Training | Validation | Testing | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 1 | 0.84 | 0.024 | 0.87 | 0.024 | 0.85 | 0.024 |
| 2 | 0.85 | 0.018 | 0.89 | 0.018 | 0.86 | 0.018 |
| 3 | 0.85 | 0.016 | 0.88 | 0.016 | 0.87 | 0.016 |
| 4 | 0.86 | 0.015 | 0.89 | 0.015 | 0.87 | 0.015 |
| 5 | 0.87 | 0.014 | 0.88 | 0.015 | 0.88 | 0.013 |
| 6 | 0.88 | 0.012 | 0.89 | 0.014 | 0.87 | 0.014 |
| 7 | 0.87 | 0.011 | 0.88 | 0.012 | 0.89 | 0.009 |
| 8 | 0.99 | 0.009 | 0.90 | 0.010 | 0.91 | 0.009 |
| 9 | 0.88 | 0.009 | 0.87 | 0.010 | 0.89 | 0.010 |
| 10 | 0.89 | 0.008 | 0.87 | 0.011 | 0.86 | 0.011 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burhani, N.R.A.; Muhammad, M.; Rosli, N.S. Combined Experimental and Field Data Sources in a Prediction Model for Corrosion Rate under Insulation. Sustainability 2019, 11, 6853. https://doi.org/10.3390/su11236853
Burhani NRA, Muhammad M, Rosli NS. Combined Experimental and Field Data Sources in a Prediction Model for Corrosion Rate under Insulation. Sustainability. 2019; 11(23):6853. https://doi.org/10.3390/su11236853
Chicago/Turabian StyleBurhani, Nurul Rawaida Ain, Masdi Muhammad, and Nurfatihah Syalwiah Rosli. 2019. "Combined Experimental and Field Data Sources in a Prediction Model for Corrosion Rate under Insulation" Sustainability 11, no. 23: 6853. https://doi.org/10.3390/su11236853
APA StyleBurhani, N. R. A., Muhammad, M., & Rosli, N. S. (2019). Combined Experimental and Field Data Sources in a Prediction Model for Corrosion Rate under Insulation. Sustainability, 11(23), 6853. https://doi.org/10.3390/su11236853





