A Linear Programming Model with Fuzzy Arc for Route Optimization in the Urban Road Network
Abstract
1. Introduction
2. Materials and Methods
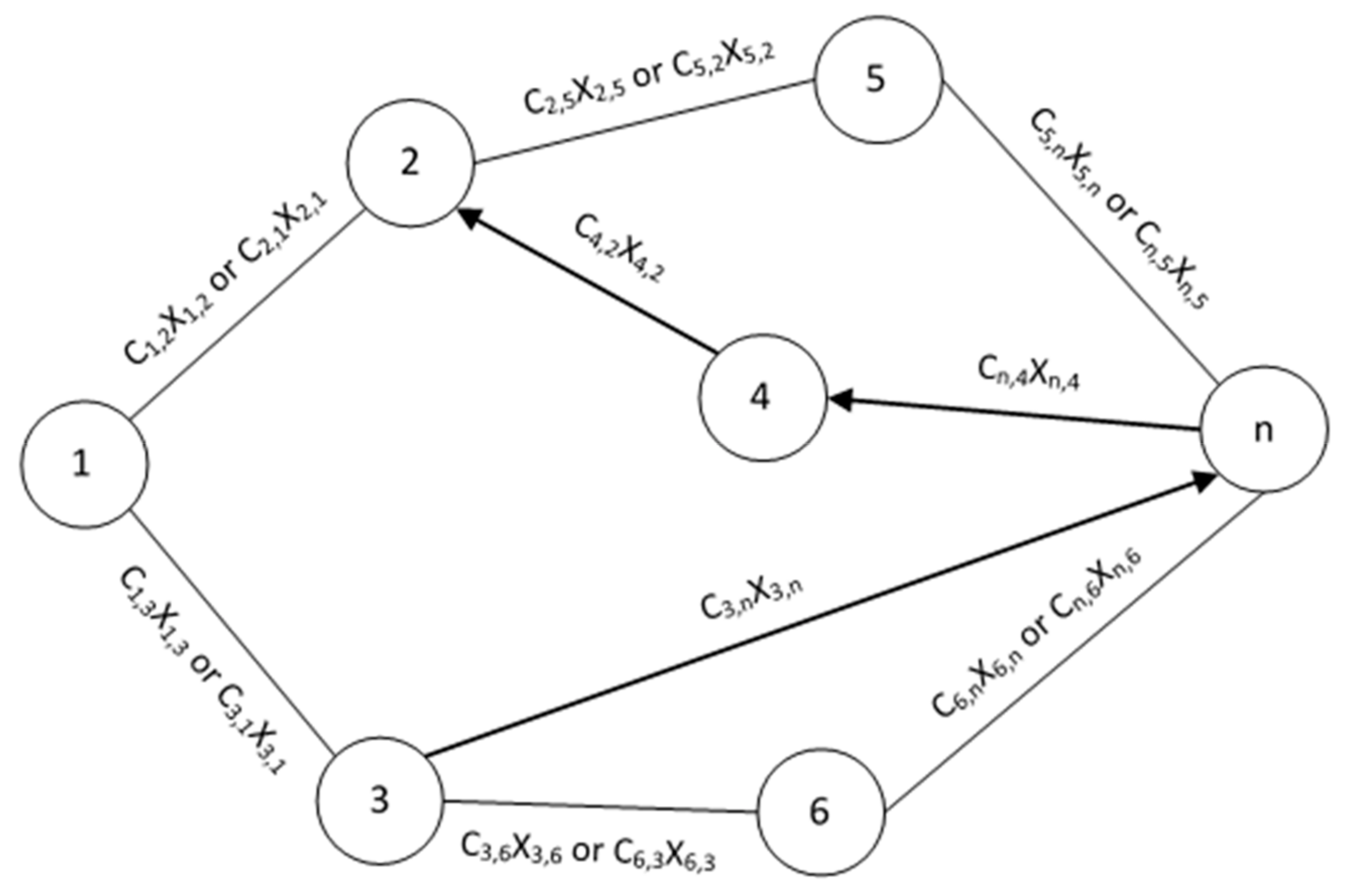
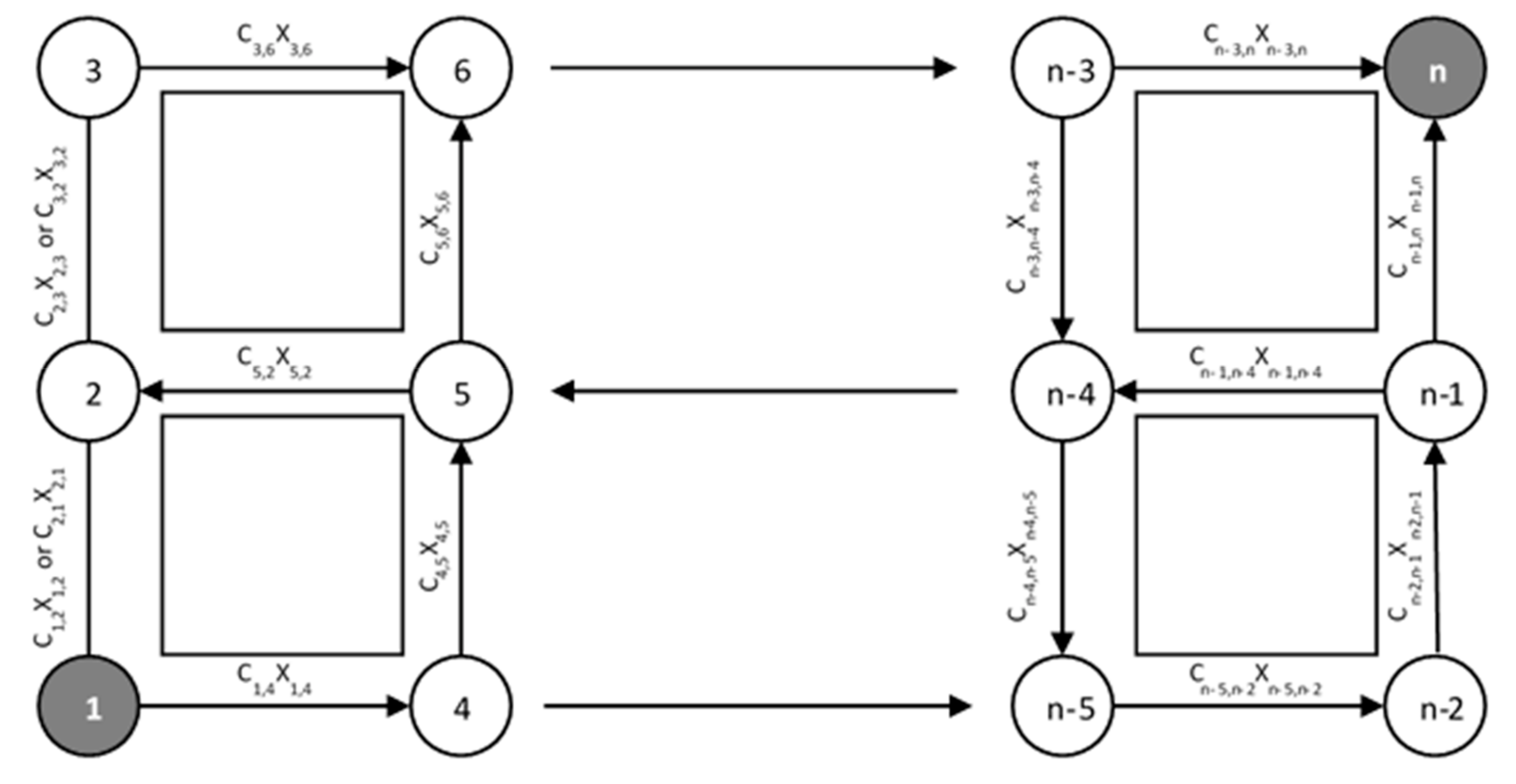
2.1. Linear Programming Formulation of the Shortest Path Problem
2.2. Proposed Model.
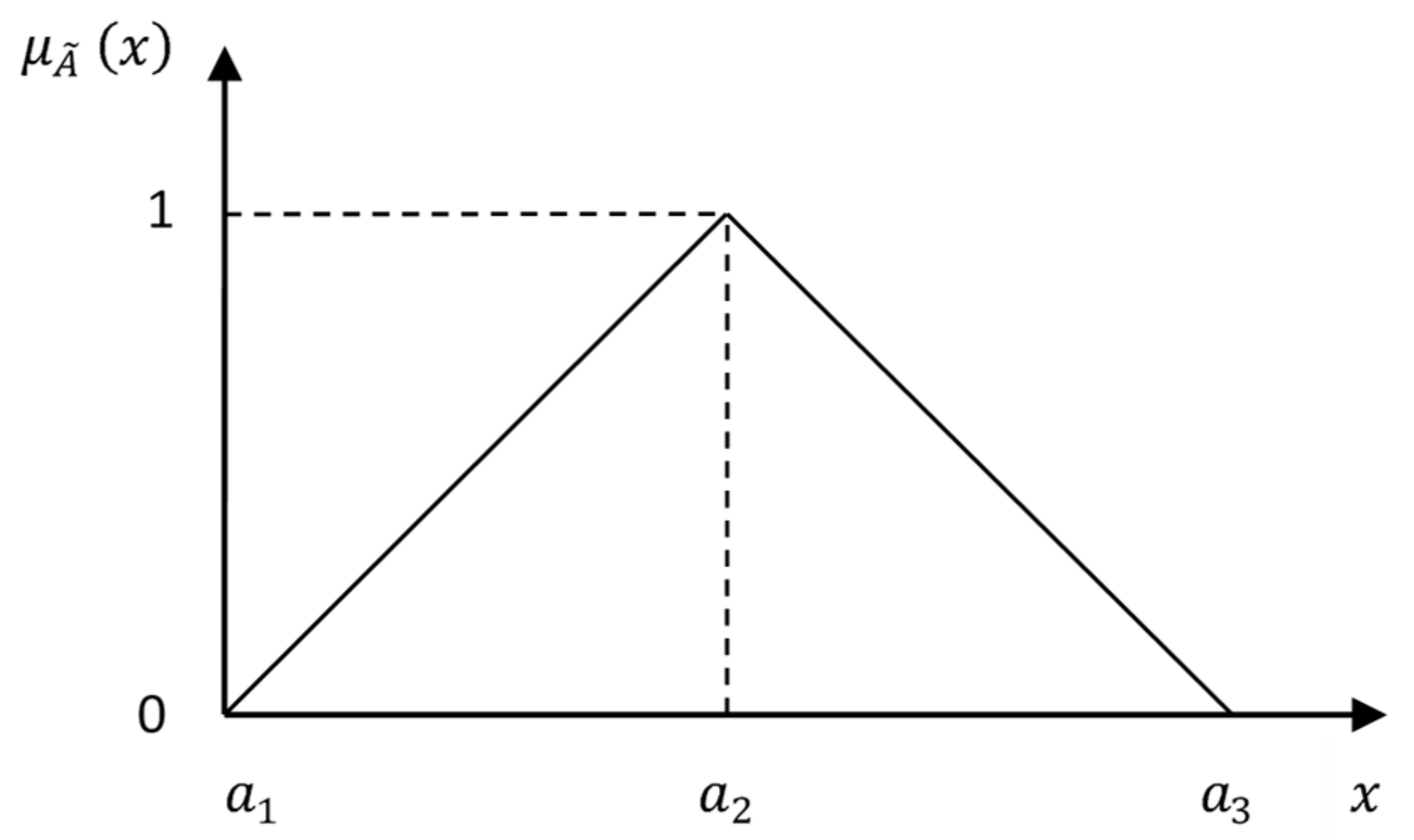
2.2.1. Fuzzy Coefficient Calculation
- 1)
- In regular figures, the area formed by the values of the fuzzy sets of the output variable was decomposed. To achieve this, the relationship between the membership grade of two adjacent fuzzy sets was analyzed, thereby defining two cases: The first case implied that the membership grade of the first fuzzy set was less than or equal to the value of belonging to the second set. For the second case, the membership grade of the first fuzzy set was greater than the membership grade of the second set. Four regular figures regarding the relationship between two adjacent fuzzy sets were formed.
- 2)
- The surface of each figure obtained in step 1 was calculated.
- 3)
- The centroid of each figure obtained in step 1 was determined.
- 4)
- The total centroid was calculated, with the result being the value of the defuzzification of the response variable (fuzzy coefficient, ).
2.2.2. Computing the Optimal Route
3. Results
3.1. Application to a Real Network
3.2. Results Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bellman, E. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connection with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Dantzig, G.B. On the shortest route through a network. Manag. Sci. 1960, 6, 187–190. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Butas, L.F. A directionally oriented shortest path algorithm. Transp. Res. 1968, 2, 253–268. [Google Scholar] [CrossRef]
- Johnson, D.B. Efficient algorithms for shortest paths in sparse networks. J. Assoc. Comput. Mach. 1977, 24, 1–13. [Google Scholar] [CrossRef]
- Zhan, F.B.; Noon, C.E. Shortest path algorithms: An evaluation using real road networks. Transp. Sci. 1998, 32, 65–73. [Google Scholar] [CrossRef]
- Zamirian, M.; Farahi, M.; Nazemi, H.A.R. An applicable method for solving the shortest path problems. Appl. Math. Comput. 2007, 190, 1479–1486. [Google Scholar] [CrossRef]
- An, P.T.; Hai, N.N.; Hoai, T.V. Direct multiple shooting method for solving approximate shortest path problems. J. Comput. Appl. Math. 2013, 244, 67–76. [Google Scholar] [CrossRef]
- Bode, C.; Irnich, S. The shortest-path problem with resource constraints with (k,2)-loop elimination and its application to the capacitated arc-routing problem. Eur. J. Oper. Res. 2014, 238, 415–426. [Google Scholar] [CrossRef]
- Duque, D.; Lozano, L.; Medaglia, A.L. An exact method for the biobjective shortest path problem for large-scale road networks. Eur. J. Oper. Res. 2015, 242, 788–797. [Google Scholar] [CrossRef]
- Marinakis, Y.; Migdalas, A.; Sifaleras, A. A hybrid particle swarm optimization-variable neighborhood search algorithm for constrained shortest path problems. Eur. J. Oper. Res. 2017, 261, 819–834. [Google Scholar] [CrossRef]
- Rostami, B.; Chassein, A.; Hopf, M.; Frey, D.; Buchheim, C.; Malucelli, F.; Goerigk, M. The quadratic shortest path problem: Complexity, approximability, and solutions methods. Eur. J. Oper. Res. 2018, 268, 473–485. [Google Scholar] [CrossRef]
- Arun Prakash, A. Pruning algorithm for the least expected travel time path on stochastic and time-dependent networks. Transp. Res. Part B 2018, 108, 127–147. [Google Scholar] [CrossRef]
- Chen, B.Y.; Li, Q.; Lam, W.H.K. Finding the k reliable shortest paths under travel time uncertainty. Transp. Res. Part B 2016, 94, 111–135. [Google Scholar] [CrossRef]
- Strehler, M.; Merting, S.; Schwan, C. Energy-efficient shortest routes for electric and hybrid vehicles. Transp. Res. Part B 2017, 103, 189–203. [Google Scholar] [CrossRef]
- Shi, N.; Zhou, S.; Wang, F.; Tao, Y.; Liu, L. The multi-criteria constrained shortest path problem. Transp. Res. Part E 2017, 101, 13–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, Z.M.; Song, S. Lagrangian relaxation for the reliable shortest path problem with correlated link travel times. Transp. Res. Part B 2017, 104, 501–521. [Google Scholar] [CrossRef]
- Cooke, K.L.; Halsey, E. The Shortest Route Through a Network with Time-Dependent Internodal Transit Times. J. Math. Anal. Appl. 1966, 14, 493–498. [Google Scholar] [CrossRef]
- Hernandes, F.; Lamata, M.T.; Verdegay, J.L.; Yamakami, A. The shortest path problem on networks with fuzzy parameters. Fuzzy Sets Syst. 2007, 158, 1561–1570. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Dou, Y.; Zhu, L.; Wang, H.S. Solving the fuzzy shortest path problem using multi-criteria decision method based on vague similarity measure. Appl. Soft Comput. 2012, 12, 1621–1631. [Google Scholar] [CrossRef]
- Kok, A.L.; Hans, E.W.; Schutten, J.M.J. Vehicle routing under time-dependent travel times: The impact of congestion avoidance. Comput. Oper. Res. 2012, 39, 910–918. [Google Scholar] [CrossRef]
- Farhanchi, M.; Hassanzadeh, R.; Mahdavi, I.; Mahdavi-Amiri, N. A modified ant colony system for finding the expected shortest path in networks with variable arc lengths and probabilistic nodes. Appl. Soft Comput. 2014, 21, 491–500. [Google Scholar] [CrossRef]
- Lakouari, N.; Ez-Zahraouy, H.; Benyoussef, A. Traffic flow behavior at a single lane roundabout as compared to traffic circle. Phys. Lett. A 2014, 378, 3169–3176. [Google Scholar] [CrossRef]
- Frank, H. Shortest paths in probabilistic graphs. Oper. Res. 1969, 17, 583–599. [Google Scholar] [CrossRef]
- Mirchandani, P.B. Shortest distance and reliability of probabilistic networks. Comput. Oper. Res. 1976, 3, 347–355. [Google Scholar] [CrossRef]
- Sigal, C.E.; Pritsker, A.A.B.; Solberg, J.J. The stochastic shortest route problem. Oper. Res. 1980, 28, 1122–1129. [Google Scholar] [CrossRef]
- Noorizadegan, M.; Chen, B. Vehicle routing with probabilistic capacity constraints. Eur. J. Oper. Res. 2018, 270, 544–555. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Algorithmes de plus courts chemins pour traiter des donnees floues. RAIRO Oper. Res. 1978, 12, 213–227. [Google Scholar] [CrossRef][Green Version]
- Chanas, S.; Kamburowski, J. The fuzzy shortest route problem. In Interval and Fuzzy Mathematics; Albrycht, J., Wisniewski, H., Eds.; Technology University of Poznan: Poznan, Poland, 1983; pp. 35–41. [Google Scholar]
- Chanas, S.; Delgado, M.; Verdegay, J.L.; Vila, M.A. Fuzzy optimal flow on imprecise structures. Eur. J. Oper. Res. 1995, 83, 568–580. [Google Scholar] [CrossRef]
- Klein, C.M. Fuzzy shortest paths. Fuzzy Sets Syst. 1991, 39, 27–41. [Google Scholar] [CrossRef]
- Dey, A.; Pal, A.; Pal, T. Interval type 2 Fuzzy Set in Fuzzy Shortest Path Problem. Mathematics 2016, 4, 62. [Google Scholar] [CrossRef]
- Tajdin, A.; Mahdavi, I.; Amiri, N.M.; Sadeghpour-Gildeh, B. Computing a fuzzy shortest path in a network with mixed fuzzy arc lengths using α-cuts. Comput. Math. Appl. 2010, 60, 989–1002. [Google Scholar] [CrossRef]
- Ramazani, H.; Shafahi, Y.; Seyedabrishami, S.E. A Shortest Path Problem in an Urban Transportation Network Based on Driver Perceived Travel Time. Trans. A Civ. Eng. 2010, 17, 285–296. [Google Scholar]
- Dai, L.; Fan, L.; Sun, L. Aggregate production planning utilizing a fuzzy linear programming. J. Integr. Des. Process Sci. 2003, 7, 81–95. [Google Scholar]
- Fung, R.; Tang, J.; Wang, D. Multiproduct Aggregate Production Planning with Fuzzy Demands and Fuzzy Capacities. IEEE Trans. Syst. Man Cybern. Part A 2003, 33, 302–313. [Google Scholar] [CrossRef]
- Sheng-Tun, L.; Yi-Chung, C. Deterministic Fuzzy Time Series Model for Forecasting Enrollments. Comput. Math. Appl. 2007, 53, 1904–1920. [Google Scholar]
- Castillo, O.; Melin, P. Automated mathematical modelling for financial time series prediction combining fuzzy logic and fractal theory. In Soft Computing for Financial Engineering; Kacprzyk, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 93–106. [Google Scholar]
- Escobar-Gómez, E.N.; Díaz-Núñez, J.J.; Taracena-Sanz, F.L. Model for Adjustment of Aggregate Forecasts using Fuzzy Logic. Ingeniería Investigación y Tecnología. 2010, 11, 289–302. [Google Scholar] [CrossRef][Green Version]
- Hosseini, R.; Dehmeshki, J.; Barman, S.; Mazinani, M.; Qanadi, S. A genetic type-2 fuzzy logic system for pattern recognition in computer aided detection system. In Proceedings of the 2010 IEEE World Congress on Computational Intelligence, Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Deng, Y.; Shi, W.K.; Du, F.; Liu, Q. A new similarity measure of generalized fuzzy numbers and its application to pattern recognition. Pattern Recognit. Lett. 2004, 25, 875–883. [Google Scholar]
- Bellman, R.E.; Kalaba, R.E.; Zadeh, L.A. Abstraction and pattern classification. J. Math. Anal. Appl. 1966, 13, 1–7. [Google Scholar] [CrossRef]
- Mitra, S.; Pal, S.K. Fuzzy sets in pattern recognition and machine intelligence. Fuzzy Sets Syst. 2005, 156, 381–386. [Google Scholar] [CrossRef]
- Pedrycz, W. Fuzzy sets in pattern recognition: Accomplishments and challenges. Fuzzy Sets Syst. 1997, 90, 171–176. [Google Scholar] [CrossRef]
- Mitchell, H.B. Pattern recognition using type-II fuzzy sets. Inf. Sci. 2005, 170, 409–418. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Image thresholding using type II fuzzy sets. Pattern Recognit. 2005, 38, 2363–2372. [Google Scholar] [CrossRef]
- Das, S. Pattern Recognition using the Fuzzy c-means Technique. Int. J. Energy Inf. Commun. 2013, 4, 1–14. [Google Scholar]
- Zadeh, L.A. Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications-two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Boulmakoul, A. Generalized path-finding algorithms on semirings and the fuzzy shortest path problem. J. Comput. Appl. Math. 2004, 162, 263–272. [Google Scholar] [CrossRef][Green Version]
- Mahdavi, I.; Nourifar, R.; Heidarzade, A.; Amiri, N.M. A dynamic programming approach for finding shortest chains in a fuzzy network. Appl. Soft Comput. 2009, 9, 503–511. [Google Scholar] [CrossRef]
- Ghatee, M.; Hashemi, S.M.; Zarepisheh, M.; Khorram, E. Preemptive priority based algorithms for fuzzy minimal cost flow problem: An application in hazardous materials transportation. Comput. Ind. Eng. 2009, 57, 341–354. [Google Scholar] [CrossRef]
- Ghatee, M.; Hashemi, S.M. Application of fuzzy minimum cost flow problems to network design under uncertainty. Fuzzy Sets Syst. 2009, 160, 3263–3289. [Google Scholar] [CrossRef]
- Keshavarz, E.; Khorram, E. A fuzzy shortest path with the highest reliability. J. Comput. Appl. Math. 2009, 230, 204–212. [Google Scholar] [CrossRef]
- Marien, E.J. The application of linear programming to a distribution system orientated toward service. Int. J. Phys. Distrib. 1972, 3, 191–204. [Google Scholar] [CrossRef]
- Ali, M.A.M.; Sik, Y.H. Transportation problem: A special case for linear programming problems in mining engineering. Int. J. Min. Sci. Technol. 2012, 22, 371–377. [Google Scholar] [CrossRef]
- García, J.; Florez, J.E.; Torralba, A.; Borrajo, D.; López, C.L.; García-Olaya, A.; Sáenz, J. Combining linear programming and automated planning to solve intermodal transportation problems. Eur. J. Oper. Res. 2013, 227, 216–226. [Google Scholar] [CrossRef]
- Luathep, P.; Sumalee, A.; Lam, W.H.K.; Li, Z.; Lo, H.K. Global optimization method for mixed transportation network design problem: A mixed-integer linear programming approach. Transp. Rese. Part B Methodol. 2011, 45, 808–827. [Google Scholar] [CrossRef]
- Faddel, S.; Aldeek, A.; Al-Awami, A.T.; Sortomme, E. ZAl-Hamouz, Ancillary Services Bidding for Uncertain Bidirectional V2G Using Fuzzy Linear Programming. Energy 2018, 160, 986–995. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–56. [Google Scholar] [CrossRef]
- Okada, S.; Soper, T. A shortest path problem on a network with fuzzy arc length. Fuzzy Sets Syst. 2000, 109, 129–140. [Google Scholar] [CrossRef]
- Buckley, J.J. Possibilistic linear programming with triangular fuzzy numbers. Fuzzy Sets Syst. 1988, 26, 135–138. [Google Scholar] [CrossRef]
- Foulds, L.R.; Nascimento, H.A.D.D.; Calixto, I.C.A.C.; Hall, B.R.; Longo, H. A fuzzy set-based approach to origin–destination matrix estimation in urban traffic networks with imprecise data. Eur. J. Oper. Res. 2013, 231, 190–201. [Google Scholar] [CrossRef]
- Ebrahimnejad, A.; Tavana, M. A novel method for solving linear programming problems with symmetric trapezoidal fuzzy numbers. Appl. Math. Model. 2014, 38, 4388–4395. [Google Scholar] [CrossRef]
- Zhu, G.; Song, K.; Zhang, P.; Wang, L. A traffic flow state transition model for urban road network based on Hidden Markov Model. Neurocomputing 2016, 214, 567–574. [Google Scholar] [CrossRef]
- Tian, Z.; Jia, L.; Dong, H.; Su, F.; Zhang, Z. Analysis of Urban Road Traffic Network Based on Complex Network. Procedia Eng. 2016, 137, 537–546. [Google Scholar] [CrossRef]

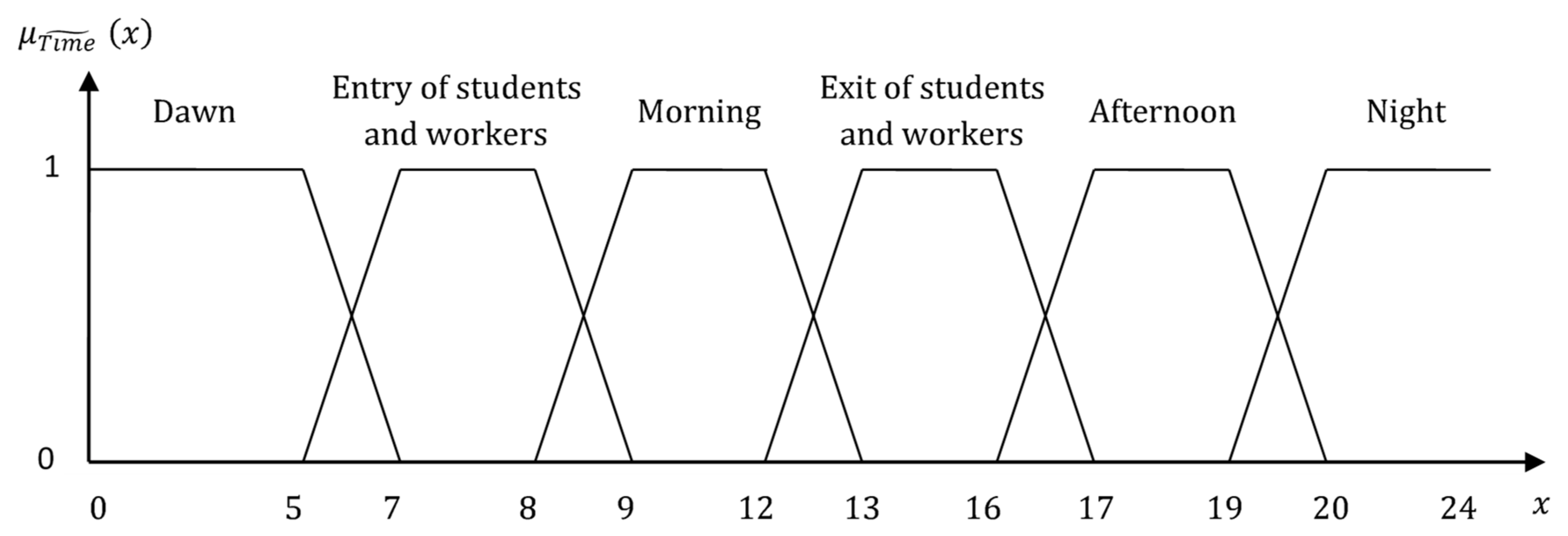


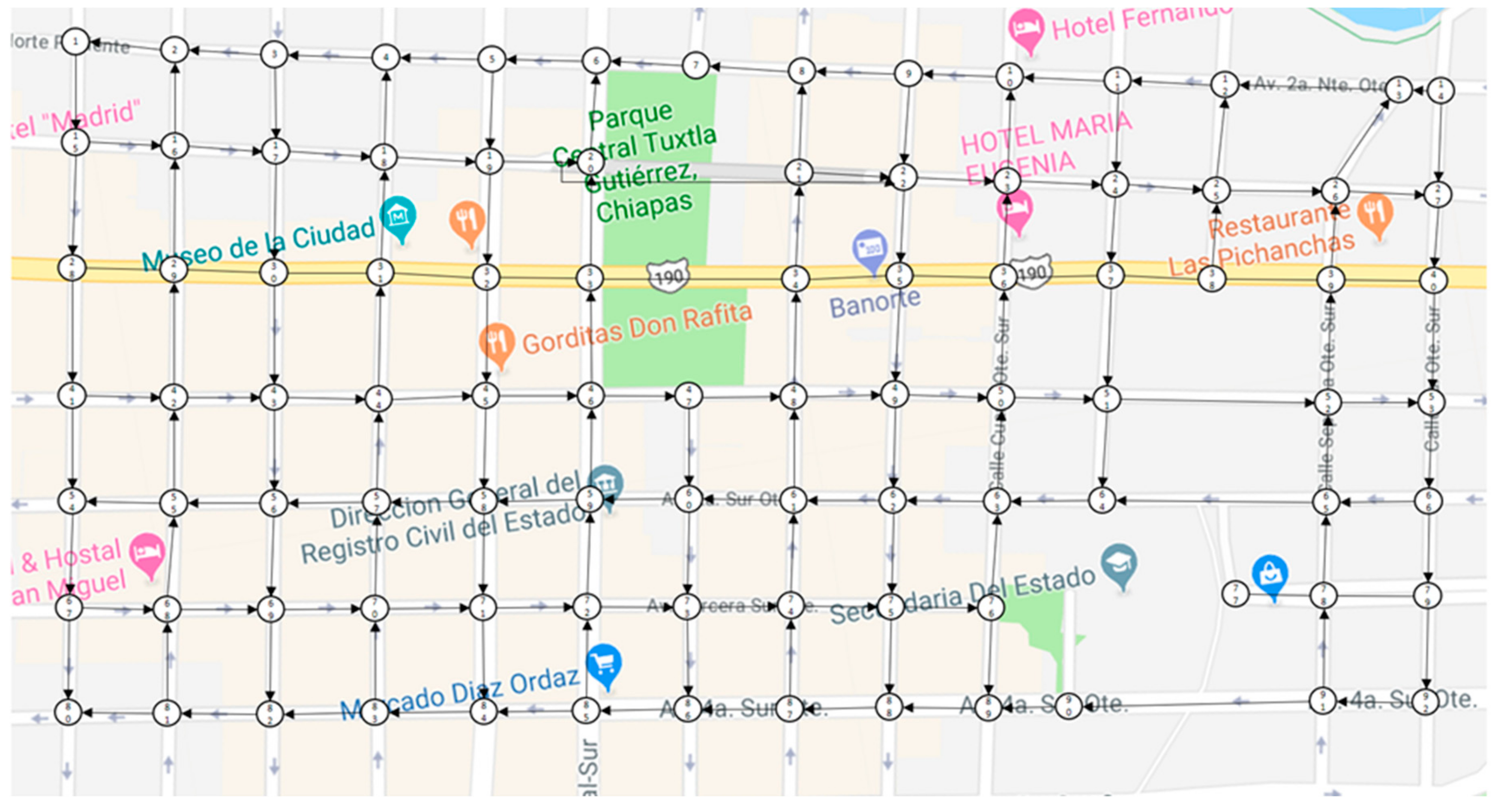
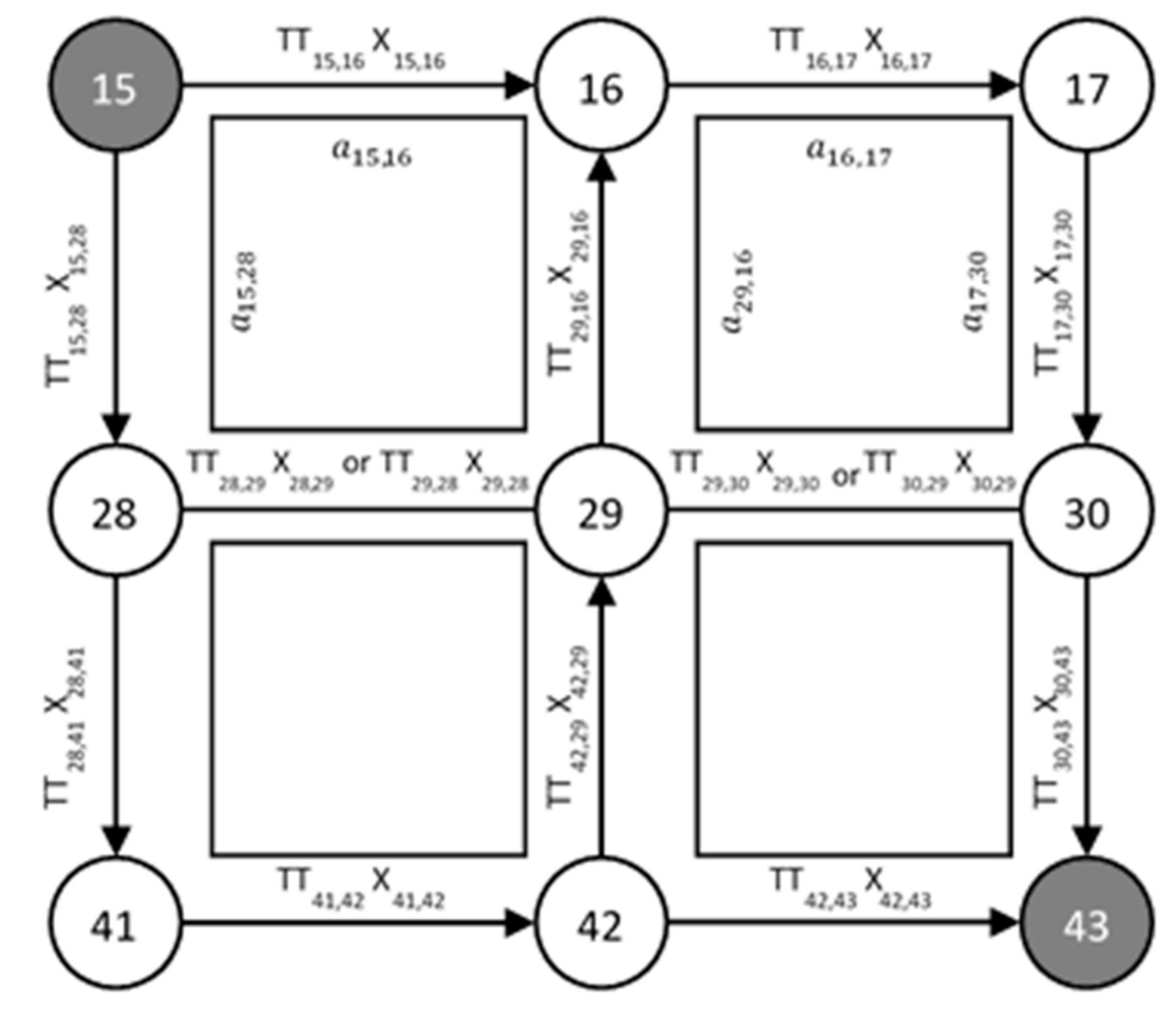
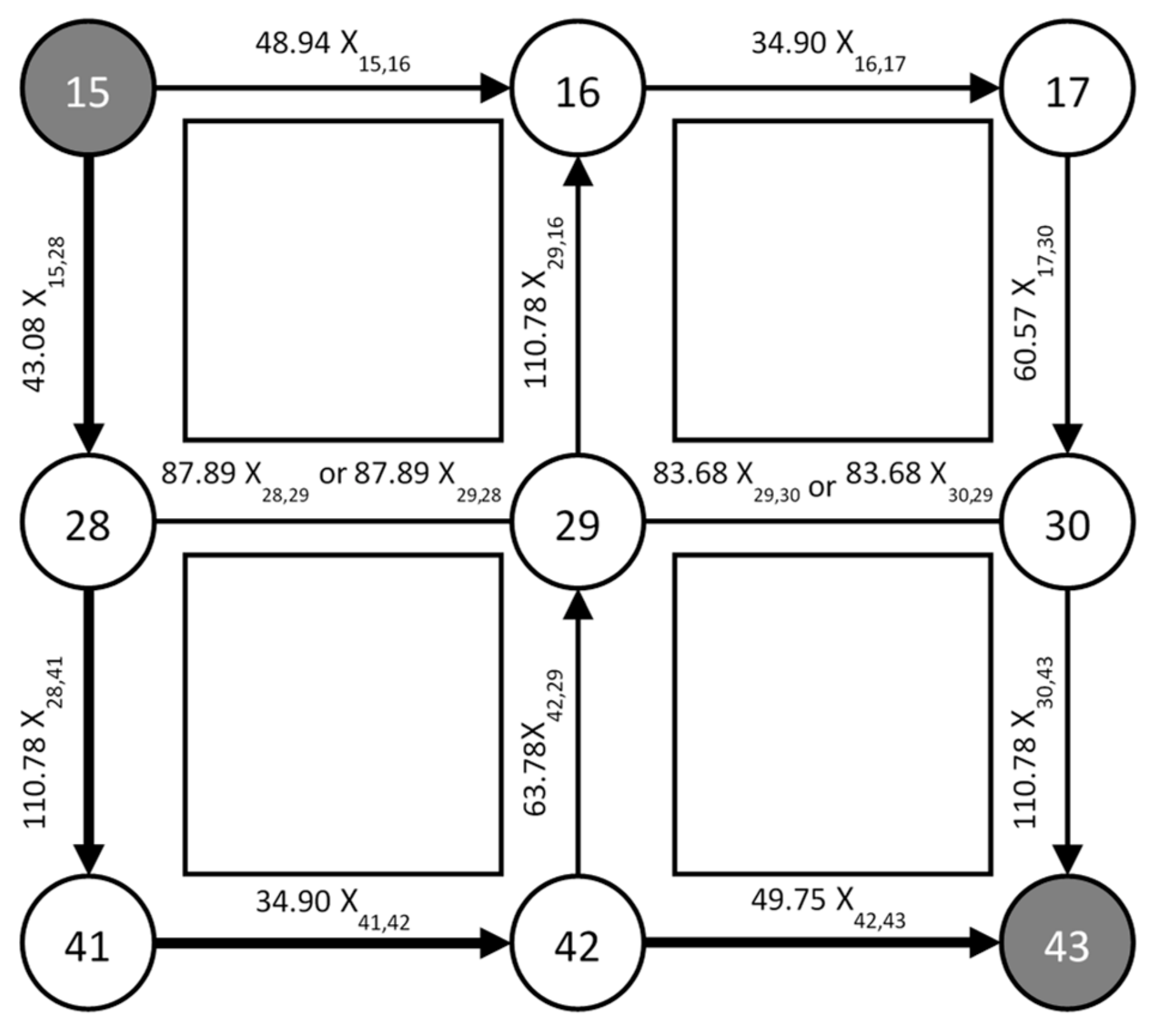
| Time of Day | |||||||
|---|---|---|---|---|---|---|---|
| Dawn | Entry of Students and Workers | Morning | Exit of Students and Workers | Afternoon | Night | ||
| Traffic density | Light | VQ | N | N | S | Q | VQ |
| Moderate | S | S | VS | N | |||
| Heavy | ES | VS | ES | VS | |||
| Type of Street Corner | Time in Seconds |
|---|---|
| Traffic light | 50 |
| Traffic light turn right | 53 |
| Traffic light turn left | 57 |
| No preference | 8 |
| Preference | 3 |
| Preference turn right | 6 |
| Preference turn left | 7 |
| One for one | 4 |
| One for one turn right | 6 |
| One for one turn left | 6 |
| Time of Day | Traffic Density | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 16 | 2 | 13:36:57 | 2 | 80 | 14 | 3.21 | 44.94 | 4 | 48.94 |
| 15 | 28 | 2 | 13:36:57 | 1.1 | 98 | 18 | 2.06 | 37.08 | 6 | 43.08 |
| 16 | 17 | 2 | 13:36:57 | 1.1 | 83 | 15 | 2.06 | 30.90 | 4 | 34.90 |
| 17 | 30 | 2 | 13:36:57 | 2 | 94 | 17 | 3.21 | 54.57 | 6 | 60.57 |
| 28 | 29 | 1 | 13:36:57 | 2.1 | 83 | 9 | 4.21 | 37.89 | 50 | 87.89 |
| 28 | 41 | 2 | 13:36:57 | 2 | 102 | 18 | 3.21 | 57.78 | 53 | 110.78 |
| 29 | 16 | 2 | 13:36:57 | 2 | 99 | 18 | 3.21 | 57.78 | 53 | 110.78 |
| 29 | 28 | 1 | 13:36:57 | 2.1 | 83 | 9 | 4.21 | 37.89 | 50 | 87.89 |
| 29 | 30 | 1 | 13:36:57 | 2.1 | 79 | 8 | 4.21 | 33.68 | 50 | 83.68 |
| 30 | 29 | 1 | 13:36:57 | 2.1 | 79 | 8 | 4.21 | 33.68 | 50 | 83.68 |
| 30 | 43 | 2 | 13:36:57 | 2 | 100 | 18 | 3.21 | 57.78 | 53 | 110.78 |
| 41 | 42 | 2 | 13:36:57 | 1.1 | 81 | 15 | 2.06 | 30.90 | 4 | 34.90 |
| 42 | 29 | 2 | 13:36:57 | 2 | 101 | 18 | 3.21 | 57.78 | 6 | 63.78 |
| 42 | 43 | 2 | 13:36:57 | 1.8 | 81 | 15 | 3.05 | 45.75 | 4 | 49.75 |
| Variable | Value | Cost (Time) |
|---|---|---|
| 0 | 48.94 | |
| 1 | 43.08 | |
| 0 | 34.90 | |
| 0 | 60.57 | |
| 0 | 87.89 | |
| 1 | 110.78 | |
| 0 | 110.78 | |
| 0 | 87.89 | |
| 0 | 83.68 | |
| 0 | 83.68 | |
| 0 | 110.78 | |
| 1 | 34.90 | |
| 0 | 63.78 | |
| 1 | 49.75 | |
| 238.51 | ||
| Route | Schedule | Real Travel Time | Calculated Time of the Classical Model (LP) | Absolute Percentage Error (LP) (%) | Calculated Time of the Fuzzy Model (FLP) | Absolute Percentage Error (FLP) (%) |
|---|---|---|---|---|---|---|
| 15–13 | 6:22:17 | 0:05:29 | 0:03:37 | 34.04 | 0:03:53 | 29.18 |
| 15–13 | 14:28:37 | 0:07:35 | 0:03:37 | 52.31 | 0:06:37 | 12.75 |
| 15–13 | 19:03:55 | 0:02:51 | 0:03:37 | 26.90 | 0:03:11 | 11.70 |
| 15–40 | 10:15:26 | 0:04:17 | 0:03:47 | 11.67 | 0:04:34 | 6.61 |
| 15–40 | 13:49:21 | 0:07:35 | 0:03:47 | 50.11 | 0:07:05 | 6.59 |
| 15–40 | 21:47:33 | 0:02:50 | 0:03:47 | 33.53 | 0:02:34 | 9.41 |
| 15–50 | 7:15:30 | 0:04:25 | 0:03:42 | 16.23 | 0:04:41 | 6.04 |
| 15–50 | 11:45:17 | 0:04:11 | 0:03:42 | 11.55 | 0:04:41 | 11.95 |
| 15–50 | 23:08:05 | 0:02:35 | 0:03:42 | 43.23 | 0:02:46 | 7.10 |
| 15–59 | 7:26:02 | 0:05:37 | 0:04:03 | 27.89 | 0:05:56 | 5.64 |
| 15–59 | 17:25:32 | 0:04:34 | 0:04:03 | 11.31 | 0:04:21 | 4.74 |
| 15–59 | 20:21:59 | 0:03:19 | 0:04:03 | 22.11 | 0:03:03 | 8.04 |
| 15–64 | 8:01:19 | 0:06:32 | 0:04:23 | 32.91 | 0:06:02 | 7.65 |
| 15–64 | 13:54:58 | 0:08:58 | 0:04:23 | 51.12 | 0:08:39 | 3.53 |
| 15–64 | 20:31:44 | 0:02:58 | 0:04:23 | 47.75 | 0:03:15 | 9.55 |
| 15–82 | 10:06:48 | 0:04:44 | 0:03:15 | 31.34 | 0:04:22 | 7.75 |
| 15–82 | 14:03:51 | 0:07:02 | 0:03:15 | 53.79 | 0:06:34 | 6.64 |
| 15–82 | 22:47:33 | 0:01:58 | 0:03:15 | 65.25 | 0:02:31 | 27.97 |
| 15–88 | 5:32:28 | 0:06:38 | 0:04:27 | 32.91 | 0:06:51 | 3.27 |
| 15–88 | 13:36:57 | 0:10:49 | 0:04:27 | 58.86 | 0:10:15 | 5.24 |
| 15–88 | 18:04:30 | 0:05:53 | 0:04:27 | 24.36 | 0:05:17 | 10.20 |
| Real Travel Time | Calculated Time from FLP | |
|---|---|---|
| Mean | 5.277777777 | 5.101587301 |
| Variance | 5.247425925 | 4.260914021 |
| Observations | 21 | 21 |
| Hypothesized Mean Difference | 0 | |
| Df | 20 | |
| t-stat | 1.506943922 | |
| p-value | 0.147458176 | |
| t-critical | 2.085963447 | |
| Absolute Percentage Error (LP) | Absolute Percentage Error (FLP) | |
|---|---|---|
| Mean | 35.199228509 | 9.597056757 |
| Variance | 264.135940142 | 46.574056590 |
| Observations | 21 | 21 |
| Hypothesized Mean Difference | 0 | |
| Df | 20 | |
| t-stat | 7.284123131 | |
| p-value | 2.403528976 × 10−7 | |
| t-critical | 1.724718243 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escobar-Gómez, E.; Camas-Anzueto, J.L.; Velázquez-Trujillo, S.; Hernández-de-León, H.; Grajales-Coutiño, R.; Chandomí-Castellanos, E.; Guerra-Crespo, H. A Linear Programming Model with Fuzzy Arc for Route Optimization in the Urban Road Network. Sustainability 2019, 11, 6665. https://doi.org/10.3390/su11236665
Escobar-Gómez E, Camas-Anzueto JL, Velázquez-Trujillo S, Hernández-de-León H, Grajales-Coutiño R, Chandomí-Castellanos E, Guerra-Crespo H. A Linear Programming Model with Fuzzy Arc for Route Optimization in the Urban Road Network. Sustainability. 2019; 11(23):6665. https://doi.org/10.3390/su11236665
Chicago/Turabian StyleEscobar-Gómez, Elías, J.L. Camas-Anzueto, Sabino Velázquez-Trujillo, Héctor Hernández-de-León, Rubén Grajales-Coutiño, Eduardo Chandomí-Castellanos, and Héctor Guerra-Crespo. 2019. "A Linear Programming Model with Fuzzy Arc for Route Optimization in the Urban Road Network" Sustainability 11, no. 23: 6665. https://doi.org/10.3390/su11236665
APA StyleEscobar-Gómez, E., Camas-Anzueto, J. L., Velázquez-Trujillo, S., Hernández-de-León, H., Grajales-Coutiño, R., Chandomí-Castellanos, E., & Guerra-Crespo, H. (2019). A Linear Programming Model with Fuzzy Arc for Route Optimization in the Urban Road Network. Sustainability, 11(23), 6665. https://doi.org/10.3390/su11236665






