1. Introduction
In many countries, providing (primary) education is a core task of local and/or state governments. In order to maintain sustainable government expenditure and foster the quality of education, governments are constantly seeking ways to deliver more value for their money, especially when faced with increasing enrolment. One of the main channels through which policy makers in amongst others the U.S. and Netherlands have sought to increase the efficiency of educational spending is through the consolidation of schools and/or school districts [
1,
2]. An important motivation of consolidation is the notion of economies of scale, i.e. that idea that bigger units have lower average (per-pupil) cost.
There is a large strand of literature on economies of scale in educational institutions and several review articles have emerged over the past decades [
2,
3]. While models, data and techniques vary, the vast body of these studies are concerned with estimating the relation between (average) cost and enrolment [
4,
5,
6,
7]. In general, while results differ across countries and methodologies, the smallest of schools and school districts are generally found to operate under economies of scale [
2,
3,
8,
9], although the tipping point (optimal size) varies. One issue with regards to economies of scale that has attracted less attention of empirical researchers is the distinction between the governing layer of school districts (U.S.) or boards (Netherlands) and the operational layer (schools). In the Netherlands, one board may govern up to thousands of pupils and tens of schools, while other boards govern only one school and 200 pupils. Similarly, some boards govern few large schools while other govern a larger number of smaller schools.
This paper departs from the observation that both layers matter for average (i.e. per-pupil) cost. From a policy perspective, this recognition has implications for policy makers and educational managers with regard to the size and number of school boards and schools. For example, given some level of enrolment, school boards (or districts) face the question of the optimal number of schools. The size and amount of school boards or districts is, in turn, a design choice influenced by national or local government. In other words, given the cost structure of schools and school boards, what is the optimal size of boards and schools in terms of enrolment and the number of schools governed by boards, and what does this imply for choices regarding consolidation or closure (when facing decreasing enrolment) of school (boards)?
Regarding the mechanisms that drive economies of scale at each level, school districts may e.g. benefit from scaling by requiring less overhead per governed school or pupil. At the school level, the potential effects of scale on cost include occupancy rates of school buildings, the spreading of fixed cost over a larger number of pupils or the specialization of teaching and managerial staff. Whereas the bundling of activities (joint purchases, integrated IT systems and manpower sharing) may be beneficial for all schools, the cost savings may be voided by increased managerial complexity, extra managerial layers, complex bureaucratic procedures, etc. In the study of economies of scale focusing on only one layer, bias may occur, for example, due to the fact that large school boards concentrated in densely-populated areas may also govern large schools. Possible observed (dis)economies of scale at the board layer may then be a result of the (dis)economies of scale of the associated schools instead of the board. In order to avoid any of these biases, the interdependency between the two layers should be integrated in the empirical model.
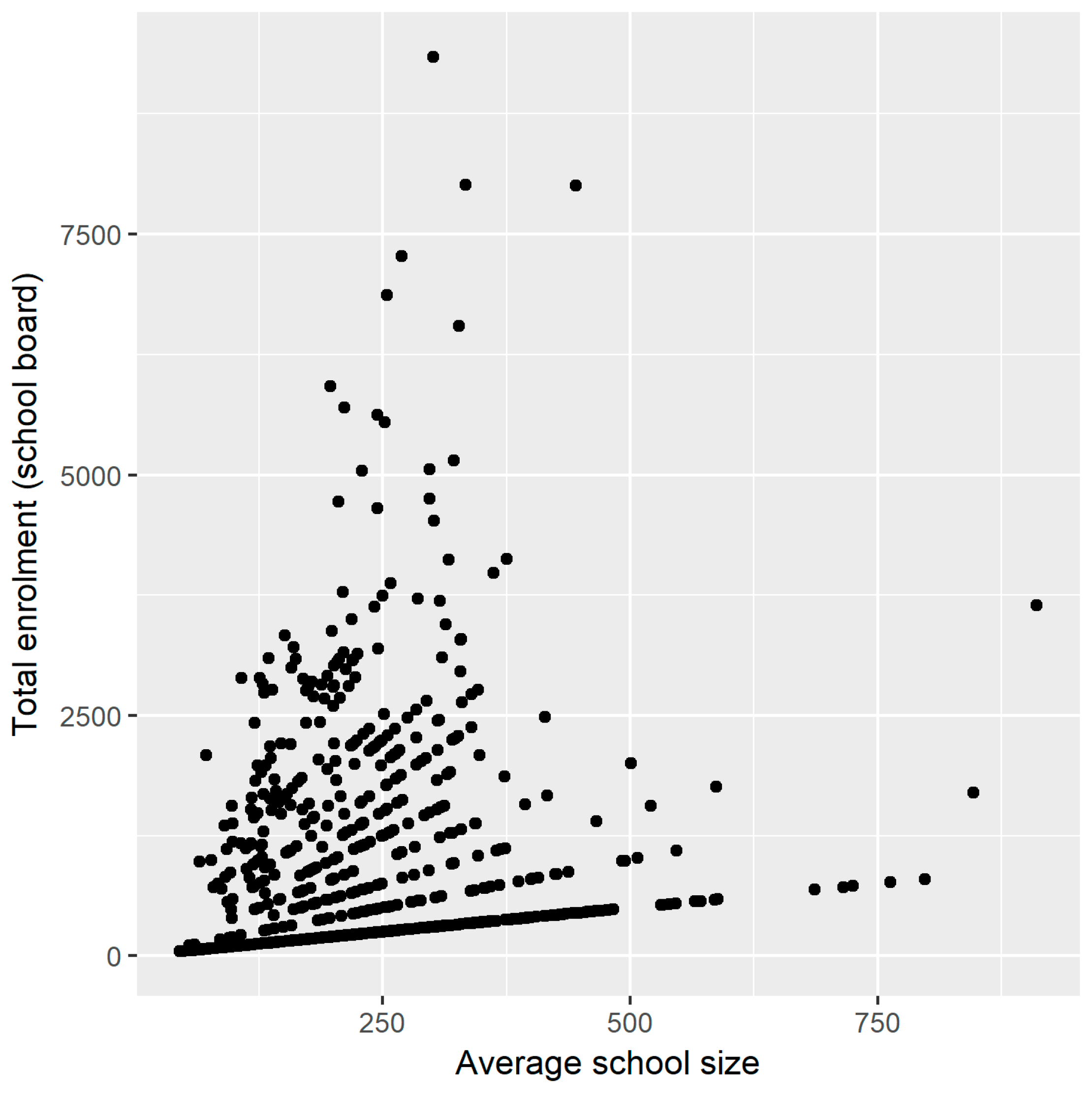
To see why the distinction is relevant especially in Dutch primary education, consider
Figure 1. Each dot represents a single school board. The vertical axis corresponds to the enrolment at each board. The horizontal axis corresponds to the average school size of the schools governed by a board. Both size indicators are only correlated weakly. That is, there are both small boards (in terms of enrolment) governing relatively large schools and large boards governing many relatively small schools.
Despite the lack of empirical analyses, multiple studies have recognized the importance of both layers. For example, Bickel & Howley [
10] perform a multi-level analysis to explore the relation between district and school scale and performance. In a more recent study, Schiltz & De Witte [
9] estimate district-level cost functions for Flemish schools and also note the potential joint influence of scale effects at both the district and the school level. Related is the analysis by Duncombe et al. [
7]. They model U.S. school district cost and include the median governed school size as an exploratory variable, shedding some light on the importance of school size and dynamics between the different layers. Most closely resembling this analysis is Wales [
11] which develops an simple but somewhat comparable aggregation approach to what we will do in this paper. In most previous studies, however, the unit of analysis typically is either the school district (or board) or school as determined by data availability: “although the school is the appropriate unit of analysis for investigating school costs, district-level data are often used, largely because school-level data are unavailable” [
8]. More generally, the observation that the administrative scale of public organizations may not correspond with the scale at which they produce or deliver services has been recognized in other domains as well, such as local governments. Blom-Hansen et al. [
12] for example distinguish between the administrative size of municipalities and the “plant” level of production, where economies of scale actually arise. In the realm of local governments, it has also motivated research into e.g. the effect of intermunicipal cooperation, a reform through which local governments can import economies of scale [
13,
14,
15].
To this end, this paper develops and estimate a model that allows for the simultaneous analysis of economies of scale at both the governing (districts or boards) and operational (school) level. This is done by modelling school board cost as an aggregation of school cost functions, so that individual school cost data is not required for estimation of the model.
Methodologically, solving this issue is a challenging task since it belongs to the class of aggregation problems. In case the structure of a micro unit (e.g., a school) is known, the question arises whether we are able to derive the structure of an aggregated unit. From the seminal work of Daal & Merkies [
16], we know that “aggregation is nearly always impossible” and that the aggregated function can be derived only under very specific conditions. In this paper we do not claim to solve this issue, but we can bypass the impossibility clause by aggregating individual cost functions through computational means. The model does not require individual school cost data. The research question, therefore, is whether it is possible to design an empirical model that takes into account the production technology and economic behaviour at both the school and school district level—and whether these can be estimated, even in the case of missing financial data at the school level.
The remainder of this paper is outlined as follows.
Section 2 outlines the methodology.
Section 3 discusses the data used for estimating the model.
Section 4 includes the results of the estimation.
Section 5 offers some conclusions and suggestions for further research.
2. Methodology
2.1. Model Design
To establish an empirical relationship between (minimum) cost and production (scale), it is common to apply a so-called cost function. Cost functions are a mathematical representation of this relationship, which may also include resource prices and a number of control variables. Cost functions eminently are suitable for deriving all kinds of economic relations, such as economies of scale and scope. For an explanation of this approach see [
17,
18]. Formally, a cost function can be written as:
where:
= (minimum) costs;
= vector services produced;
= vector of resource prices;
= vector of resources;
= set of feasible combinations of services produced and resources.
The parameters of cost functions are estimated on the basis of data on individual firms or other economic entities that can be indicated as Decision Making Units (DMUs). Other economic entities can refer to lower hierarchical functional entities (departments) or to higher entities (regions, boards, districts et cetera). The choice of DMU is a matter of perspective, depending on which policy or managerial issue is being addressed. In general, a pile of layers—each of them with specific responsibilities and discretionary power—can be distinguished. The relevant distinction here is between schools and boards. This distinction is in line with the distinction between the (primary) teaching process and the (secondary) general management process. The first directly refers to course content, education time and course schedules; whereas the latter refers to the administrative and financial tasks, labour contracts and building investment and maintenance. For obvious reasons these two different processes cannot be separated but may strongly interact.
Estimating cost functions that consider complex organisational structures still is a relatively unexplored area. As discussed in the introduction, there are conceptual similarities in many sectors, and several authors have dealt with analysing different scale layers (e.g., in health and local government). In the aforementioned study of Niaounakis & Blank [
19] on the effects of collaboration in local tax levying, data on the contributions of each municipality to municipal cooperation are available. In the preceding case of education, we lack this type of data. In this paper, data on production (enrolment, test scores, etc.) and environment of individual schools are available, but costs and other input data are not. Thus, in developing a suitable cost model, not only do we have to account for the complex organisational structure, we also must deal with a number of unobserved variables. The solution to this problem, putting it simply, is to sum up all the underlying cost functions of the associated schools to an aggregate cost function and estimate the parameters of the aggregated model. We will formally derive the relationship between schools and school board. Suppose that the minimum cost of an individual school
s connected to school board
b can be displayed as:
where:
= minimum costs of school s of school board b;
= vector of services of school s of school board b (e.g. number of pupils per type of training, education results);
= vector prices of resources used of school s of school board b (e.g. wage index, material price index);
= vector environmental factors of school s of school board b (e.g. social background).
This also includes costs for student administration, the ICT department, accounting, human resources and management. In case these (secondary) costs are carried by a separate body (the board), it is assumed that they can be allocated to the associated schools. This can be regarded as a school outsourcing these managerial and auxiliary activities to a third party (the board). It is assumed that secondary costs are directly related to services delivery and the size and quality of the board providing these services. In fact, the latter refers to the efficiency component of the school. Therefore, we may add to the minimum cost an efficiency term that is strongly correlated with a number of attributes of the board, such as the number of associated schools or the total services provided by the associated schools.
where:
The inefficiency term is a factor that inflates the minimum costs by a certain factor greater than one. This implies that the function g(.) must be so defined that it always produces outcomes greater than or equal to zero. Actual costs of school s of school board b then equal:
The total cost of board b is then the summation of costs of all associated schools of board b:
Or in logarithms:
The common procedure is that the (minimum) cost function is reflected by a mathematical equation (the functional specification), whose parameters can be estimated by an econometric method (e.g., nonlinear least squares). From the estimated parameters an estimate of scale effects can be derived.
The above equation now only includes observable variables. The left-hand side includes the total cost for all member schools, including the costs for management of the school board. The problem is now reduced to a statistical problem, because on the right side we find—in case there are many schools associated with a school board—a large number of terms. There are two solutions. The first solution is specifying a simple representation of the cost function, so that different terms can analytically be aggregated. There remains a simple regression equation consisting of terms such as the total number of pupils belonging to a school board. The second solution is based on the ability to solve the problem entirely numerically. The search for economies of scale requires a flexible functional form that allows scale elasticities to vary with size. The suggested simple solution does not meet this requirement and is therefore further ignored. We therefore entirely focus on the numerical solution.
As the parameters of and are empirically established, elasticities with respect to services produced by the school and with respect to the boards’ attributes can be calculated.
2.2. Functional Specification
For an empirical application of the economic model, we use the well-known translog cost function [
20]. The model includes first, second order and cross terms between outputs, and year dummies representing technical change. Because of the lack of accurate price indices for different resources, we ignore the possibility of price substitution. We divide actual cost by a general consumer price index to control for nominal developments. The translog cost function looks as follows:
Here,
and
are the parameters to be estimated. The model that will be estimated is obtained after substitution of (7) in (6).
3. Data
Data were sourced from the Education Executive Agency (DUO) of the Dutch Ministry of Education, Culture and Science. The agency publicly reports available datasets, including the annual financial statements of boards and enrolment at schools. Recall that the key issue in this paper is that enrolment and other pupil-related indicators are registered at the level of individual schools, while financial statements are observed at the board level.
The data set is constructed as follows. Each observation corresponds to a single school board and contains information on its cost. For board , let denote enrolment at school s. Furthermore, let Nb denote the number of schools governed by board . Then equals zero for . The largest number of schools governed by a single board in our sample equals 31.
In the actual data set, three enrolment variables are included. Dutch school boards are eligible for additional funding for enrolled pupils from a disadvantaged socio-economic background. To cater to their educational needs, schools with a large number of such pupils have smaller class sizes, implying higher cost. The three enrolment variables included correspond to the classification that is also used within the funding mechanism (SES-1, SES-2, SES-3).
Data are included for the years 2011–2015. Note that as the yearly (within-) variation of school boards - in terms of enrolment or cost - is limited in most cases, little additional information is gained from analysing multiple years. In 2015, there were 971 school boards governing schools providing elementary education. The final sample included for analysis contains 723 or roughly three quarters of these boards. In total, these boards govern 2601 different schools or 4.60 on average. Omissions are due to the fact that some boards in primary education may also govern one or more special needs education schools. Some boards even govern one or more vocational education schools. Their inclusion requires an extension of the cost function by additional output (enrolment) variables to account for the different pupils. While this offers the possibility to study economies of scope and a larger sample, the advantage of analysing a homogeneous group of boards outweighs the computational difficulties posed by including several poorly comparable school boards. In roughly thirty per cent of the schools, test scores were not available. For a board that governs both schools with test scores and without known test scores, the missing school scores a set equal to the average test scores of the other schools governed by the boards.
In addition to the cost and enrolment variables discussed, a number of additional indicators are included: i.e. the average test score at each school and the number of schools governed by each board.
Table 1 provides a set of summary statistics on the included variables.
4. Results
The main results are presented in
Table 2. The results were obtained by estimating Equation (6) after substituting Equation (7) using nonlinear least squares.
At first sight, the estimated model obviously appears to have a good fit (
. The first-order parameters have plausible positive signs and are estimated as significant at the 1% level. It should be noted that the standard errors have not been clustered. Due to the special aggregation structure and the high non-linearity of the model, it is cumbersome to exactly calculate the corrected standard errors. Therefore we apply a raw correction measure based on the intra correlation of the residuals only. The formula for this raw correction factor is:
where:
= correction factor least squares standard errors of estimated parameters;
= intra correlation of the residuals;
= average number of replications in the panel;
Note that formula (8) does not include any correction for the intra correlation of the independent variables in the model, implying that this this correction factor is overestimated and so are the corrected standard errors. The reported T-values therefore are underestimated. Note that in case of time dummies no correction need to be made, since no intra correlation exists and the estimated parameters are not biased due to the panel data structure. Most of the parameters show extremely low standard errors. Even in the case of inflating these standard errors by the correction factor, these standard errors still are very low. The exceptions are the parameters corresponding to the number of associated schools and the average test score. The standard errors of the remaining parameters b12 and b23 may be affected in such a way that they are no longer significant at the 5% level, but they still are at the 10% level. The parameters of the number of associated schools and square of associated schools are not significant at the 5% level after correction (the square term still is at the 10% level). The hypothesis of no relationship between number of associated schools therefore cannot be rejected. The parameters estimate of the average test score and square average test score are significant at the 5% level, even after the correction, implying that the hypothesis that there is no relationship between cost and average test score must be rejected. The requirements concerning monotonicity with respect to outputs are met (positive parameters). Note that requirements regarding input prices are not relevant here, since costs are deflated by a price index number.
As an indicator of the plausibility of the estimates, we estimated the marginal costs, presented in
Table 3, of the different enrolment categories. The marginal costs have been calculated for a fictional school. The fictional school is assigned 220 pupils (corresponding to an average school) with an average composition of pupils regarding SES (200, 12 and 8). Operating in the year 2011, this fictional school has an average score on educational quality and is associated with a board that consists of three schools. From the estimates of the year dummies’ parameters (significantly negative) we can also conclude that in 2011, 2012 and 2013 the conditional mean of costs were lower than in 2015, implying a substantial negative productivity change.
From these results, we note that the marginal cost of a pupil with SES-1 is about 4300 euro, about 7800 euro for a SES-2 pupil, and about 20,000 euro for a SES-3 pupil. These numbers are plausible, although the latter may be regarded as somewhat high. It must be noted that pupils in category SES-3 are rather rare.
We now turn to the key result of the analysis regarding economies of scale.
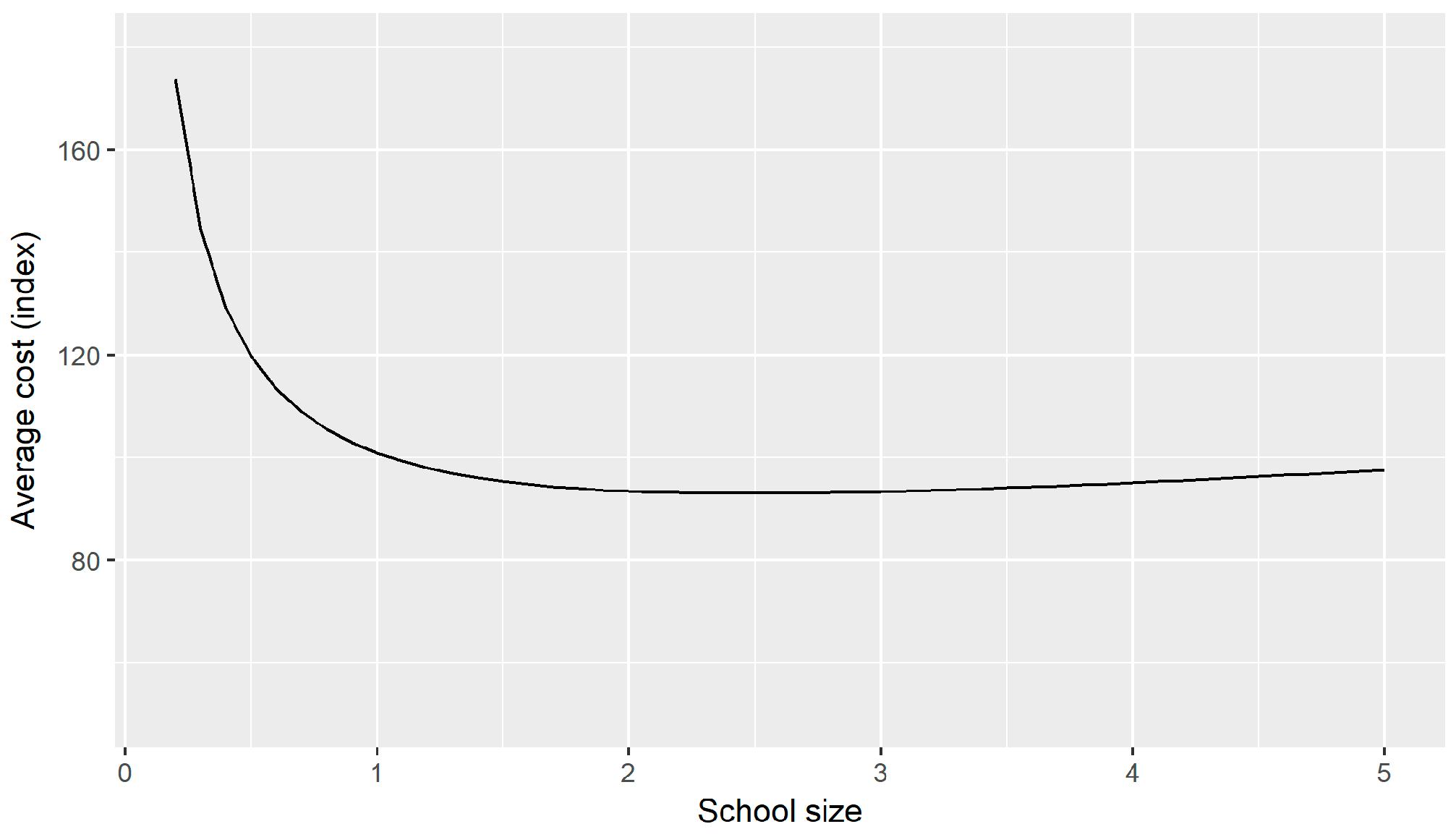
Figure 1 presents the estimated average cost curve at the school level.
Figure 1 is based on the average composition of a school with respect to SES (respectively 90% SES-1, 6% SES-2 and 4% SES-3). The size of the average school is set to 1. Furthermore, the average costs are presented in an index where the average cost of a school with average size is set to 100.
From
Figure 2, we conclude that the average cost for small schools—for example a school with a size less than one quarter of the average school size—is 60% higher than for the average school. The estimated average cost curve indicates substantial economies of scale for small schools. Average cost increases for schools larger than twice the average school size, implying that diseconomies of scale prevail though the rise in average cost is modest. From the estimated parameters in
Table 2, we can easily derive that, for a substantial number of (small) schools, scaling up is beneficial from a cost perspective.
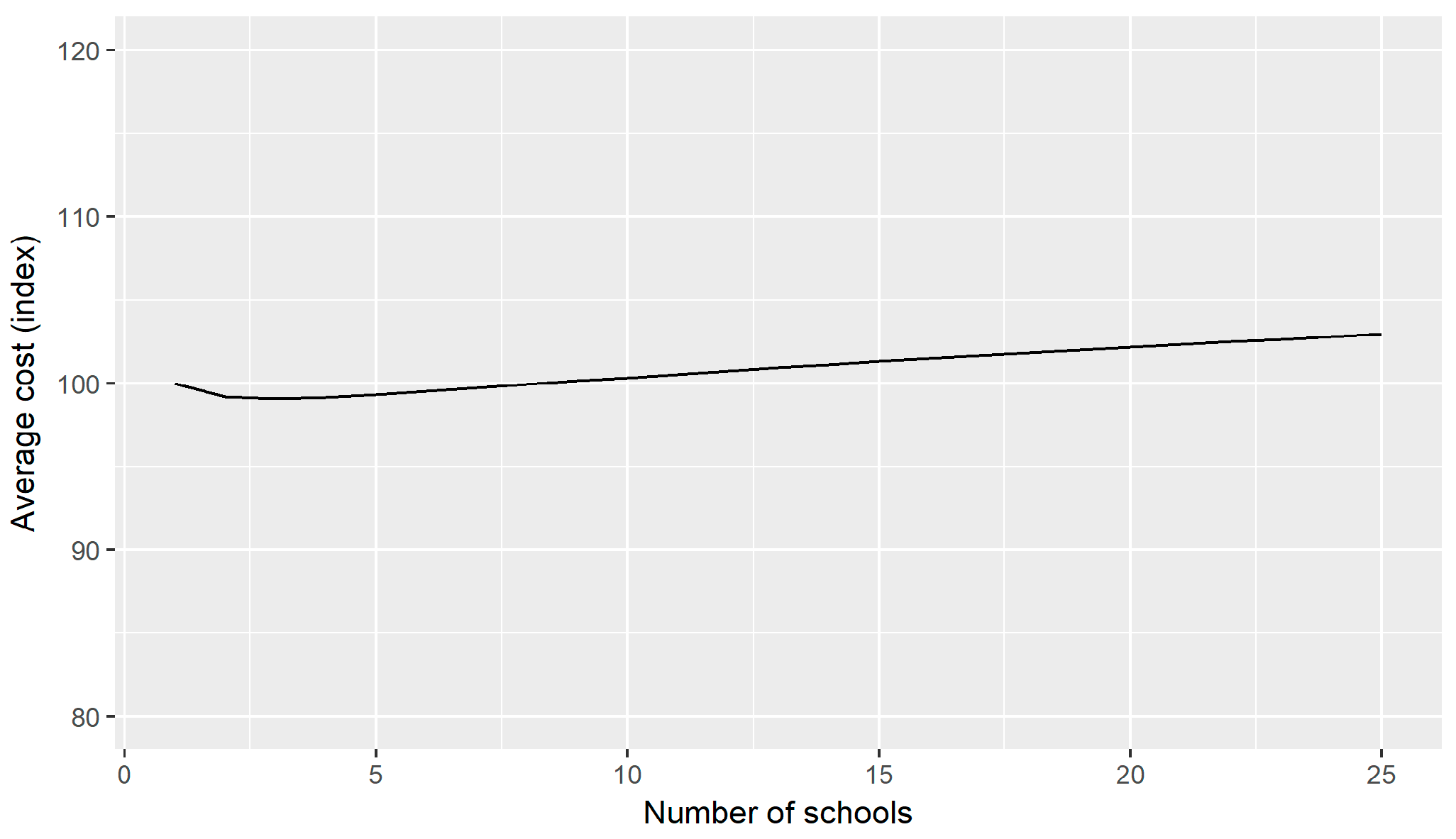
Figure 3 represents the average costs with respect to the number of associated schools in a school board. The reference category here is a school with an average number of pupils and with an average composition with respect to the SES-categories. The average cost is presented as an index and set to 100 in case the number of associated schools equals one.
From
Figure 3, we conclude that expanding a one-school school board by adding two extra schools leads to a decline in average cost of about 2%. However, as the number of associated schools increases beyond that, average cost also increases. The cost of a board with 25 or more associated schools has an average cost 5% higher than a board with three associated schools. Note that these outcomes are controlled for the size of the associated schools and purely reflect the effect of the number of associated schools. Although we may regard these as interesting outcomes, we need to put them in perspective. From the parameters presented in
Table 1, we can calculate the efficiency component due to the number of associated schools (and its statistical properties, such as standard errors and t-values). If we apply this to all observations, it shows that the efficiency of only 10% of the observations significantly differs (at 5% level) from the most efficient configuration (three schools in a board). In other words, the effect of board size is practically negligible. The policy implication that follows from this is that there is hardly any empirical evidence showing that board size matters for average cost.
5. Concluding Remarks
In many countries local governments face the question what the optimal configuration of school boards and schools is within their jurisdiction. From an economic perspective, the answers to these questions lays in the existence of (dis)economies of scale at the board level as well as the school level. However, these questions cannot be answered as easily as is suggested by many studies on economies of scale. Driven by data limitations, most studies only focus on the consequences of consolidation at the operational level (school) or at the governing level (school board). For obvious reasons these two levels are strongly intertwined, and their mutual dependency should be taken into account. In this paper we propose a model that connects both levels and meanwhile solves a data issue. The data issue concerns missing cost and input data at the school level which is addressed by estimated an aggregated cost function which only requires data at the board level.
The model is applied to a panel data set of primary schools in the Netherlands over the time (2011–2015). The results indicate that the cost structure of schools is characterized by substantial economies of scale at small sizes (say, fewer than 60 pupils). For schools with more than 60 pupils, average cost with respect to size flattens out. Optimal school size is estimated at 440 pupils. If school size increases further, then (modest) diseconomies of scale exist.
Regarding the size of school boards, a different picture arises. It shows that there might be some (board) economies of scale. Average cost declines in boards with the number of school managed up to three schools, but the effect is very modest. Boards with more than three associated schools show a modest increase of average cost. Only for the largest boards, with more than 25 schools, might we expect a significantly higher average cost than the optimal board (with three schools). Our results indicate that studies that find increasing economies of scale for small districts may in fact be driven by the (small) schools that these districts are governing. Given this possibility, it would be very useful to make a comparative analysis in the U.S. case, where district studies are common.
The optimal configuration indicated by the results is a board governing three schools of about 450 pupils each. From a cost point of view, schools smaller than 60 pupils should be avoided. In these cases, a merger could be considered. Mergers of schools greater than 200 pupils are not expected to exploit significant economies of scale. The number of schools per school board matters little for average cost, and other considerations may be more relevant here.
In the old days it was common to manage all public primary schools by one board (the municipality itself). Due to a change in legislation a municipality was allowed to form different schoolboards within their jurisdiction. However, many municipalities still operate from the original centralized perspective, but may consider to create at least three school boards with each of them their own discretionary authority. However, the cost savings from this strategy is limited. Far more important is the school size. Municipalities should monitor school size within their jurisdiction and in case pupil numbers shrink below 60 decide to encourage or force to merge or close down the school. However, due to considerations of proximity and respecting the spirit of the Freedom of Choice Act it is not very likely municipalities will be closing down or merge small schools. On the other hand, it is very interesting to know that these other public values come with a price.