Monetary Policy, Industry Heterogeneity and Systemic Risk—Based on a High Dimensional Network Analysis

Abstract

We utilized a high dimensional financial network to investigate the systemic risk contagion between different industries in China and to explore the impacts of monetary policy and industry heterogeneity factors. The empirical results suggest that the total level of systemic risk increased quite significantly during the 2008 global crisis and the 2015–2016 Stock Market Disaster. The energy, material, industrial, and financial sectors are the top systemic risk contributors. Industry heterogeneity variables such as the leverage ratio, book-to-market ratio, return on assets (ROA) and size have significant impacts on the systemic risk, but their effects on the systemic risk contribution are more pronounced than those on the systemic risk sensitivity. Moreover, monetary policy can effectively suppress the systemic risk diffusion derived from the leverage ratio. These results are essential for investors and regulators of risk management.

1. Introduction

Since the 2008 global financial crisis, systemic risk contagion and its influencing factors has become the focus of academic circles and regulatory authorities. Incentives for systemic risk may come from within the financial system (such as bank failure and the collapse of financial market prices) and from external financial systems (such as macroeconomic reform and the decline of a national economy’s pillar industries) [1,2,3]. Numerous studies have shown that non-financial industries are also associated with systemic risk [4,5,6,7]. In emerging markets, some non-financial industries may even play central roles in economy networks due to their special financing relationship and the socioeconomic system [8]. It is of great importance for investors and regulators to be able to understand systemic risk contagion, as well as to identify its influencing factors from a global industry perspective.

Despite the global financial crisis causing a worldwide recession in recent years, China’s economy has continued to grow rapidly and it is critical to global economic growth. For example, in the first half of 2019, China’s gross domestic product (GDP) growth rate was 6.3%, which ranked it first in the world. However, during the post-financial crisis, several serious market crashes occurred in the Chinese stock market, which damaged investor confidence and the entire economy. Impressively, China’s Shanghai Composite Index fell by more than 30% over 15 days in June 2015, and then fell by nearly 45% over the next two months. The index reached a peak of 5178 points on 15 June and plummeted to 2850 on 26 August 2015. The rapid growth of China’s economy and the dramatic fluctuations in the stock market during the post-crisis period have influenced the world economic and financial markets; this has attracted significant attention from international investors. Therefore, understanding China’s systemic risk during the post-crisis period is crucial for the world market. In general, the literature justifies systemic risk contagion during financial crisis, but little is known about it in emerging market economies during the post-crisis period. In this paper, we use the 2008–2016 Chinese stock market as an example to study dynamic systemic risk contagion.

The recent literature focuses on systemic risk contagion among financial institutions (see a review by Benoit et al. [9]), while the risk from sectors other than the financial sector are rarely mentioned. Bisias et al. [10] assumed that systemic risk arises endogenously within the financial system and provide a broad overview of quantitative measures of systemic risk. Glasserman and Young [11] proposed a theoretical framework for understanding the relationship between interconnections among financial institutions and financial stability. Kahou and Lehar [12] offer a literature review of macroprudential policies and address the link between the stability of the financial system and the performance of the overall economy. Since financial institutions and real enterprises are related through credit and debt, difficulties in financial institutions may lead to the collapse of the financial system or the increase of risk, and the same situation in a real sector (or enterprise) can have a similar effect. Chiu et al. [2] provide evidence of significant volatility and tail risk spillovers from the financial sector to many real sectors in the U.S. economy. The main reason why systemic risk can be contagious across industry is that investors tend to rely not only on the market but also tend to rely on industry-specific indices as important references for evaluating and predicting portfolio performance [13]. Thus, our goal here is to extend the study of systemic risk from the institutional level to the industry level.

The existing literature has proposed a number of methods to measure systemic risk based on publicly available market-data such as stock price. These methods can be broadly classified into three categories: financial asset correlation [14,15,16,17,18,19], tail-dependence [20,21,22,23,24], and sophisticated networks [25,26,27,28]. The representative measurements of financial asset correlation include the cross-correlation coefficient [15] and principal component analysis (PCA) [16]. There are four prominent examples of tail-risk measures: marginal expected shortfall (MES) and the systemic expected shortfall (SES) [23], the SRISK of Brownlees et al. [26], and the CoVaR of Adrian and Brunnermeier [22]. However, the above measurements may underestimate systemic risk among financial institutions since they cannot capture the risk spillovers found in financial network topologies [26]. Network theory provides a valuable tool for the analysis of systemic risk contagion because it can abstract the complex economic system into a network with a set of nodes and edges, revealing the inter-topological structure and complexity of the system [29,30]. Although the market-data may have no particular pre-specified graphical structure, we can recover the network structure as defined by the long-term variance decomposition network model (LVDN, Diebold and Yilmaz [25]). Another reason for adopting the complex network framework to study systemic risk is that the interconnectivity among institutions or industries often has a complicated dependency structure. For example, interdependency among the financial sector and other real economy sectors may not necessarily show monotonic linearity [31]. In addition, investigating systemic risk for a large number of samples can lead to severe statistical deficiencies in model estimation, including overfitting, inaccurate parameter estimates, and uninformed inferences (“dimensional disasters”). Barigozzi and Hallin [28] proposed LVDN methods based on the generalized dynamic factor model (GDFM) for the analysis of volatility interconnections in high dimensional series. Their method has two main advantages: (i) it is based on the GDFM, which is entirely non-parametric and model-free, thus it can overcome curse-of-dimensionality problems in large sample estimation, and (ii) given the economic interpretation of the network indicators, it has proven to be a powerful tool for analyzing systemic risk contagion.

Monetary policy plays an indispensable role in the stability of financial markets, but how monetary policy implementation affects systemic risk contagion at the industry level is inconclusive. According to Reinhart and Rogoff [32], systemic risk is closely related to monetary policy, and a tight money policy can lead to bank defaults, causing bank credit to tighten and leading to a sharp rise in systemic risk. Taylor believes that expansionary monetary policy is one of the main factors in systemic risk accumulation, which ultimately led to the global financial crisis [33]. Battiston et al. [1] found a correlation between debt defaults and systemic risk in the real economy. Chiu et al. [2] found that industry characteristics help to explain the size of tail spillovers. To the best of our knowledge, current research on systemic risk has not considered the interaction between monetary policy and industry characteristics. Therefore, we are trying to fill this research gap. We take monetary policy and industry heterogeneity factors into consideration and explore their influence on systemic risk sensitivity and contribution in various industries.

Here, we use the LVDN tool based on GDFM [28] to study system risk contagion in China. We used daily data from companies in the CSI 300 index from 4 January 2008 to 30 December 2016 to construct dynamic LVDNs and analyze the systemic risk sensitivity, systemic risk contribution, and the overall level of systemic risk from an industry perspective. Then, we studied the relationship between monetary policy, industry heterogeneity and systemic risk under the framework of panel regression analysis. The novelty of this paper is based on the following aspects:

• Using the LVDN tool based on GDFM, we expand on the current literature on measuring the systemic risk at the institutional level to focus on the industry level. We found that several industries including the energy, materials, industrial, and financial sectors are the top contributors to systemic risk due to their high levels of risk out-degree. Consumer, healthcare, IT, telecommunications, and utility industries are more susceptible to systemic risk due to their high levels of risk in-degree. This not only enables investors to better allocate portfolios across sectors to reduce risk exposure, but also helps regulators to target the most systemically important sectors, and monitor risk in the whole market.
• We found that the total connectedness of LVDNs increases significantly when the stability of the system exhibits distress. An increase in cross-industry connectedness caused the high systemic risk level during the 2008 global crisis and the 2015–2016 Stock Market Disaster in China. This suggests that regulatory commissions should focus on cross-industry connectedness and increase the coordination of their supervisory responsibilities.
• This paper revealed that monetary policy not only directly affects systemic risk but also indirectly affects the effect of the industry’s leverage ratio. Industry heterogeneity variables have significant impacts on systemic risk, but their effect on the systemic risk sensitivity is more pronounced than their effect on the systemic risk contribution.

In Section 2, we introduce the measure of systemic risk, i.e., the LVDN network based on the GDFM model and the panel regression models. We show the data and the empirical analysis in Section 3 and present our conclusions in Section 4.

2. Methodology

2.1. Measurement of Systemic Risk

The first step in investigating system risk contagion is to analyze the interdependences in volatility panels [25]. Firstly, we consider the panel of stocks and then from the daily adjusted closing price ${\{\mathrm{p}}_{it}\left|i=1,\dots ,n,t=1,\dots ,T\right.\}$, we compute the daily log-returns:

$$r_{it}=100\log (p_{it}/p_{it-1}),i=1,\dots ,n, t=1,\dots ,T$$

(1)

We assume that the stock return panel $r_n:=\{r_{nt}={(r_{1t}{r}_{2t}\dots r_{nt})}^{\prime }\left|t\in \mathbb{Z}\right.\}$ satisfies assumptions 1–3 from Barigozzi and Hallin [28], i.e., that it represents the generalized dynamic factor model (GDFM) decomposition:

$$r_{nt}={\chi }_{nt}+{\xi }_{nt},t\in \mathbb{Z}$$

(2)

where ${\chi }_n$ is driven by $q$ common shocks and ${\xi }_n$ is idiosyncratic (called level common and level idiosyncratic components, respectively). The Hallin and Liska [34] criterion yields $q^T=1$, i.e., a unique level common component. The two components ${\chi }_n, {\xi }_n$ represent the auto-regressive and sparse vector auto-regression (VAR) representations respectively:

$${\mathcal{F}}_n(L){\xi }_{nt}=v_{nt}=:{(v_{1t},\dots ,v_{nt})}^{\prime },t\in \mathbb{Z}$$

(3)

$${\mathcal{A}}_n(L){\chi }_{nt}=:{\eta }_{nt}=:{({\eta }_{1t},\dots ,{\eta }_{nt})}^{\prime },t\in \mathbb{Z}$$

(4)

where ${\mathcal{A}}_n$ is an auto-regressive filter and ${\mathcal{F}}_n$ is a VAR filter with sparse coefficients. Two volatility panels are defined as

$${\sigma }_{nt}:=\log ({\eta }_{nt}^2),{\omega }_{nt}:={\log (\mathrm{v}}_{nt}^2),t\in \mathbb{Z}$$

(5)

We assume those panels, in turn, satisfy assumptions 1–3 and hence, we admit the second-stage GDFM decomposition:

$${\dot{\sigma }}_{nt}:={\sigma }_{nt}-E[{\sigma }_{nt}]={\chi }_{\sigma ,nt}+{\xi }_{\sigma ,nt},t\in \mathbb{Z}$$

(6)

$${\dot{\omega }}_{nt}:={\omega }_{nt}-E[{\omega }_{nt}]={\chi }_{\omega ,nt}+{\xi }_{\omega ,nt},t\in \mathbb{Z}$$

(7)

where ${\chi }_{\sigma ,n}$ and ${\chi }_{\omega ,n}$ are driven by $q_{\sigma }$ and $q_{\omega }$ common shocks, and ${\xi }_n$ is idiosyncratic (called common and idiosyncratic volatility components, respectively). Again, the Hallin and Liska [34] criterion yields $q_{\sigma }^T=q_{\omega }^T=1$, i.e., a unique market shock, which is common to the two subpanels. The auto-regressive representation of the common volatility components is

$$\left(\begin{array}{cc}{A}_{\sigma ,n}(L)& 0_n\\ 0_n& A_{\omega ,n}(L)\end{array}\right)\left(\begin{array}{c}{\chi }_{\sigma ,n}\\ {\chi }_{\omega ,n}\end{array}\right)=\left(\begin{array}{c}{H}_{\sigma ,n}\\ H_{\omega ,n}\end{array}\right){\epsilon }_t,t\in \mathbb{Z}, {\epsilon }_t~wn(0,1)$$

(8)

and the sparse VAR representations of the idiosyncratic volatility components are

$$F_{\sigma ,n}(L){\xi }_{\sigma ,n}={\nu }_{\sigma ,nt},t\in \mathbb{Z},{\nu }_{\sigma ,nt}~\mathrm{wn}(0, {\mathrm{C}}_{\sigma ,n}^{-1})$$

(9)

$$F_{\omega ,n}(L){\xi }_{\omega ,n}={\nu }_{\omega ,nt},t\in \mathbb{Z},{\nu }_{\omega ,nt}~\mathrm{wn}(0, {\mathrm{C}}_{\omega ,n}^{-1})$$

(10)

Details on the estimators of (3), (4), (8), (9), and (10) are given in Forni et al. [35].

Following Diebold and Yilmaz [25], we define the vector moving average (VMA) of the common and idiosyncratic volatility components as

$$\begin{array}{l}{B}_{\sigma ,n}(L):=A_{\sigma ,n}{(L)}^{-1}{H}_{\sigma ,n}{K}_{\sigma },\\ B_{\omega ,n}(L):=A_{\omega ,n}{(L)}^{-1}{H}_{\omega ,n}{K}_{\omega },\end{array}$$

(11)

and

$$\begin{array}{l}{D}_{\sigma ,n}(L)=F_{\sigma ,n}{(L)}^{-1}{R}_{\sigma ,n},\\ D_{\omega ,n}(L)=F_{\omega ,n}{(L)}^{-1}{R}_{\omega ,n}.\end{array}$$

(12)

See Barigozzi and Hallin [28] for a more formal description and details. Next, we built the long-term variance decomposition (LVDN) networks based on the VAM representations of the two volatility components. Following Diebold and Yilmaz [25], we summarized the dependence up to the lag $h$ using the forecast error variance decomposition method and the ratios:

$$w_{ij}^h=({\displaystyle \sum _{k=0}^{h-1}{d}_{k,ij}^2}/{\displaystyle \sum _{l=1}^n{\displaystyle \sum _{k=0}^{h-1}{d}_{k,il}^2}})\times 100$$

(13)

For any $i$, note that $\frac{1}{100}{\displaystyle \sum _{j=1}^n{w}_{ij}^h}=1$. Thus, we can define the LVDN by

$${\mathcal{E}}_{LDVN}:=\{(i,j)\in {\{1\dots n\}}^2\left|w_{ij}^{LDVN}:=\underset{h\to \infty }{\lim }\right.w_{ij}^h\ne 0\}$$

(14)

In order to study a system’s risk and its determinants from the perspective of industry, this paper constructed the following three system risk measurement indicators based on network theory: the system risk sensitivity of each industry ($TI{C}^{IN}$), the system risk contribution of each industry ($TI{C}^{OUT}$), and the overall level of system risk (TC):

$$TI{C}_i^{IN}={\delta }_i^{from}={\displaystyle \sum _{j=1,j\ne i}^n{w}_{ij}^h},i=1,\dots ,n,$$

(15)

$$TI{C}_j^{OUT}={\delta }_j^{to}={\displaystyle \sum _{i=1,i\ne j}^n{w}_{ij}^h},j=1,\dots ,n,$$

(16)

$$TC={\delta }^{\mathrm{total}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\delta }_i^{from}}=\frac{1}{n}{\displaystyle \sum _{j=1}^n{\delta }_j^{to}}.$$

(17)

These three directional measures of the strength of the sector-conditional connectivity are used to measure the system risk sensitivity of each industry, the system risk contribution of each industry and the overall level of systemic risk, respectively. Among several prominent systemic risk measurement methods given in the recent literature, Adrian and Brunnermeier [22] suggested that the increase in tail-event interconnectedness can be used to identify systemic risk, and they proposed the conditional value at risk (CoVaR) measure. Acharya et al. [23] presented the marginal expected shortfall (MES) and systemic expected shortfall (SES) measures, which gave rise to the idea of identifying systemically important financial institutions (SIFIs). The economic interpretation of the network degree indicator in our model is related to the recently developed systemic risk measurements mentioned above, which is the main reason why we can use this method to measure systemic risk. In particular, the economic interpretation of the from-degree of series $i$ is closely related to the MES or SES, which measure the exposure of component $i$ to extreme events affecting all other components [23,28]. Also, the to-degree of series $j$ is related to the co-value at risk (CoVaR), which measures the impact of an extreme event affecting component $j$ on the whole panel [22,25]. Thus, the LVDN for the idiosyncratic volatility component is an ideal tool to measure system risk contagion.

2.2. Variable Description

This paper considers price-based instruments, which mainly refers to the interest rate and quantitative monetary policy instruments, a tool that primarily applies to reserve ratios., and The interest rate indicator (RATE) is expressed in the one-year deposit benchmark interest rate, and the reserve ratio indicator (RR) is the statutory reserve ratio based on the weighted average of large financial institutions.

Referring to Hoberg and Phillips [36], Adrian et al. [22], Chiu et al. [2], etc., we selected six industry heterogeneity indicators: the leverage ratio (LEV), book-to-market ratio (BM), total return on assets (ROA), debt cost (COST), increase in cash holdings (CASH), and size (SIZE). The leverage ratio is expressed as the total debt compared to the total assets, the debt cost is shown as the natural logarithm of the financial expense, and the size is expressed as the natural logarithm of the total assets. The industry heterogeneity variables are the arithmetic means of the industry sample stock. For the subsequent econometric analysis, the data frequency was adjusted quarterly. Also, we used the GDP growth rate indicators to reflect macroeconomic conditions.

2.3. Panel Regression Model

First, in order to study the relationship between monetary policy, industry heterogeneity, and systemic risk, we constructed the following panel regression model:

$$TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}=\alpha +{\beta }_{1}M{P}_{it}+{\beta }_{2}I{H}_{it}+{\beta }_{3}MA{C}_{it}+v_i+v_t+{\mu }_{it}$$

(18)

where $TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}$ is the system risk sensitivity and systemic risk contribution of industry $i$ at time $t$; $M{P}_{\mathrm{it}}$ is the monetary policy proxy variables, including the interest rate (RATE) and statutory reserve ratio (RATER); $I{H}_{it}$ is the industry heterogeneity indicators, including the six indicators described above; $MA{C}_{it}$ is the macroeconomic indicator, i.e., GDP; ${\alpha }_i$ is the individual factor; $v_i$ and $v_t$ are industry effects and quarter effects, respectively; ${\mu }_{it}$ is a random disturbance term, subject to independent and identically distributed (i.i.d.). In detail, model (18) is expressed as follows

$$\begin{array}{cc}\hfill TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}=\alpha & +{\beta }_{1}M{P}_{it}+{\beta }_{21}LE{V}_{it}+{\beta }_{22}M{B}_{it} +{\beta }_{23}RO{E}_{it}+{\beta }_{24}COS{T}_{it}\hfill \\ & +{\beta }_{25}CAS{H}_{it}+{\beta }_{26}SIZ{E}_{it}+{\beta }_{3}GD{P}_{it}+v_i+v_t+{\mu }_{it}\hfill \end{array}$$

(19)

Then, considering a correlation between the book market value ratio and other variables, we replace book market value ratio with the regression residual. Moreover, monetary policy factors restrict the financing of enterprises to a certain extent. Enterprises with fast credit growth will not be constrained by funds, and further expansion will reduce the probability of future default. Otherwise, the probability of default will increase. This will ultimately affect the system’s risk exposure in the industry. With the deepening of China’s “de-leveraging” policy, monetary policy may be biased for different industries or companies. Therefore, we added cross terms between the proxy variables of monetary policy and industry leverage ratios to the model to analyze the mechanism of monetary policy:

$$\begin{array}{cc}\hfill TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}=\alpha & +{\beta }_{1}RAT{E}_{it}+{\beta }_{21}LE{V}_{it}+{\beta }_{22}M{B}_{it} +{\beta }_{23}RO{E}_{it}+{\beta }_{24}COS{T}_{it}\hfill \\ & +{\beta }_{25}CAS{H}_{it}+{\beta }_{26}SIZ{E}_{it}+{\beta }_{3}GD{P}_{it}+\gamma RAT{E}_{it}\times LE{V}_{it}+v_i+v_t+{\mu }_{it}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}=\alpha & +{\beta }_{1}R{R}_{it}+{\beta }_{21}LE{V}_{it}+{\beta }_{22}M{B}_{it}+{\beta }_{23}RO{E}_{it}+{\beta }_{24}COS{T}_{it}\hfill \\ & +{\beta }_{25}CAS{H}_{it}+{\beta }_{26}SIZ{E}_{it}+{\beta }_{3}GD{P}_{it}+\gamma R{R}_{it}\times LE{V}_{it}+v_i+v_t+{\mu }_{it}\hfill \end{array}$$

(21)

Since the data in this paper is “large T small N” type panel data, to avoid sequence correlation, the feasible generalized least squares regression (FGLS) method was used for parameter estimation of (21). Also, due to the persistence of risk [37] and the endogeneity between variables, we constructed the following dynamic panel model:

$$TI{C}_{it}^{IN}/TI{C}_{it}^{OUT}=\alpha +\gamma TI{C}_{it-1}^{IN}/TI{C}_{it-1}^{OUT}+{\beta }_{1}M{P}_{it}+{\beta }_{2}I{H}_{it}+{\beta }_{3}MA{C}_{it}+v_i+v_t+{\mu }_{it}$$

(22)

Scholars have proposed many remedies to the endogeneity problem. Li [38] summarized the different methods to address endogeneity concerns and found that the generalized method-of-moments estimator (GMM) [39] has the most significant correction effect on the bias, followed by instrumental variables. However, the GMM and its extension methods are general estimators designed for situations with “small T, large N” panels, meaning few periods and many individuals. However, our situation is “small N, large T.” Both the GMM and instrumental variables estimators are susceptible to severe “small sample estimation bias” in particular customary finite sample situations [40]. Thus, for the dynamic panel model (22), we use the biased-corrected Least-Squares Dummy Variable (LSDVC) estimator, which has been proven to be more efficient than the GMM and IV estimators [40,41].

3. Empirical Analysis

3.1. Data Description

We used the LVDN tool based on GDFM [28] to study system risk contagion in China. We constructed dynamic LVDNs using daily data for companies in the CSI 300 index from 4 January 2008 to 30 December 2016, and analyzed their topological properties to identify the systemic risk sensitivity and contribution of different industries. Note that because the Shanghai and Shenzhen 300 Index adjusts its components each year, we needed to ensure continuity throughout the period to compare the evolution of the stock markets. In other words, the selected stocks needed to be included in the index at all times. In addition, a few stocks were suspended during trading time for long periods of time for specific reasons (such as asset restructuring or refunding). This is why the number of sample stocks was less than 300. In fact, we ended up with 100 industry-represented sample stocks from 10 different industries. The CSI 300, which stands for the China Securities Index 300 stock index, was jointly issued by the Shanghai and Shenzhen Stock Exchanges on April 8, 2005. The index compiles a sample of 300 A- share stocks listed on the Shanghai or Shenzhen stock market, and the total value of the stocks is approximately 70% of the total market capitalization of both stock exchanges. Therefore, the index is widely perceived to comprehensively reflect the performance and volatility of China A-share markets, and thus is a good representation of the equity market in terms of analyzing the system risk contagion. The constituents of the Shanghai and Shenzhen 300 Index were selected according to certain representative indicators. The composition of the index constituents was more evenly distributed across industries than the other indices, which is convenient for later research. Our data comprised the daily closing price of the sample stock indexes during the period from 4 January 2008, to 30 December, 2016 (a total of 2190 trading days). We selected data starting from 2008 because several prominent financial institutions were not listed on China’s A-share market until 2007. The stocks we considered belong to 10 different industries: energy, materials, industrial, optional consumer, major consumer, healthcare, financial, information technology, telecommunications services, and utilities. The industry classification was based on the China Securities Index industry classification. We obtained the stock prices through the Wind Financial database. Industry heterogeneity, monetary policy, and macroeconomic data were sourced from the China Stock Market and Accounting Research (CSMAR) database.

We calculated three systemic risk indicators as described above.

Table 1. Descriptive statistics.

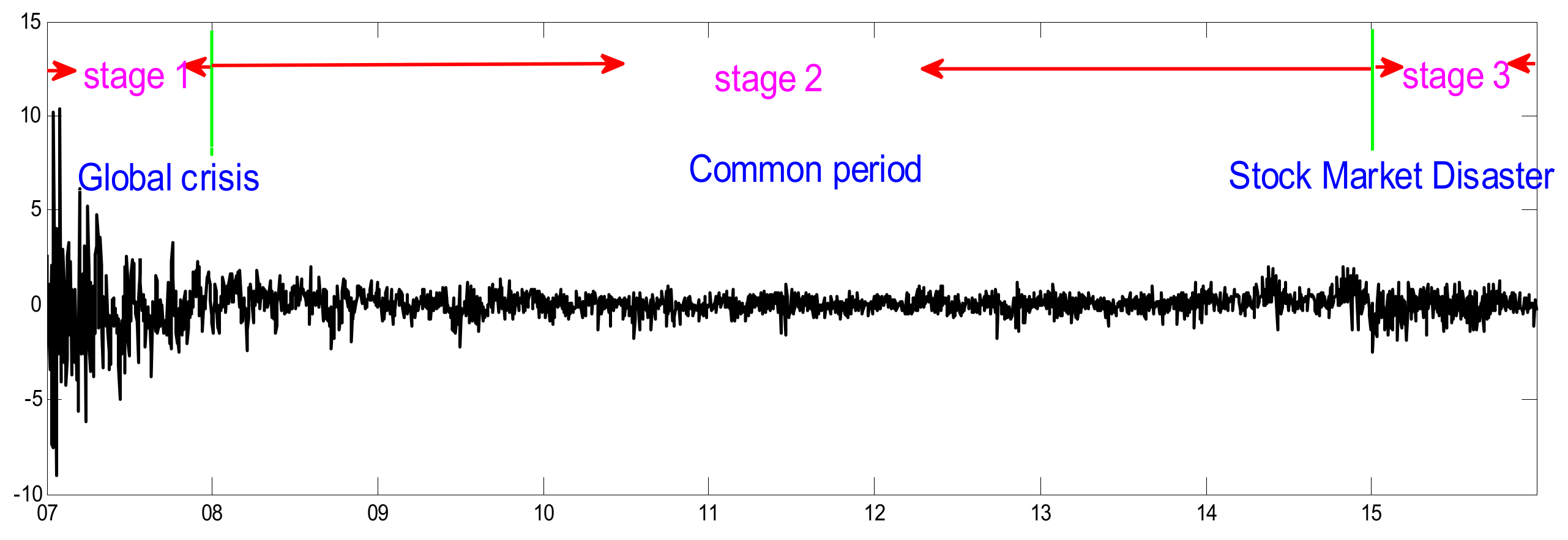
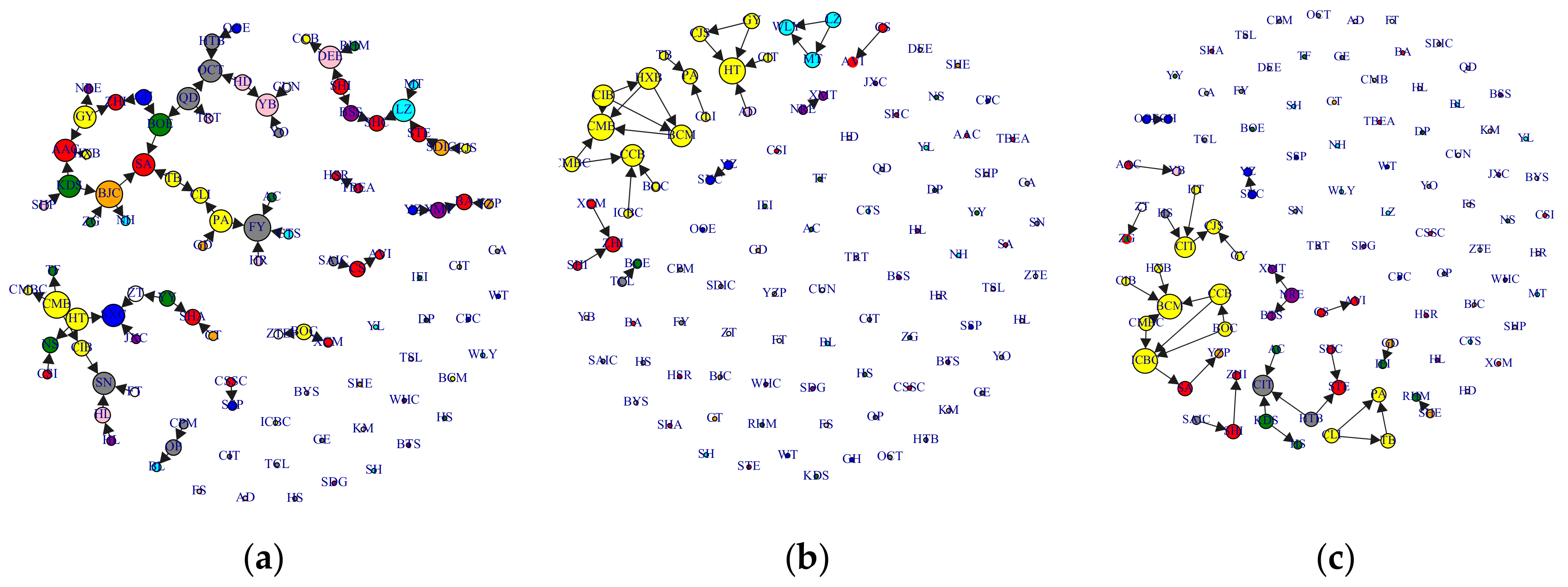
Variables	Mean	Standard Deviation	Min	1st Quartile	Median	3rd Quartile	Max
TC	10.052	6.613	4.987	9.678	10.068	14.763	26.556
$TI{C}^{IN}$	9.840	4.975	0.732	5.885	9.385	17.951	29.873
$TI{C}^{{}^{OUT}}$	10.245	9.917	0.000	3.414	9.948	16.951	47.591
RATE	2.500	0.646	1.500	2.250	3.000	3.000	3.500
RATER	0.183	0.195	0.150	0.170	0.180	0.200	0.215
LEV	0.523	0.236	0.034	0.401	0.558	0.699	0.966
MB	2.279	3.745	0.039	0.454	0.969	1.970	21.916
ROA	0.101	0.295	−1.060	0.011	0.043	0.115	4.659
COST	10.472	0.921	7.888	9.887	10.319	10.837	13.358
CASH	0.272	0.727	0.000	0.043	0.107	0.238	8.226
SIZE	10.108	0.962	7.897	9.492	9.912	10.496	13.346
GDP	0.085	0.017	0.0620	0.071	0.078	0.101	0.122

Note: TC, $TI{C}^{IN}$, and $TI{C}^{OUT}$ are calculated by Equations (17), (15), and (16), respectively. For an explanation of the remaining variables, see “Variable Descriptions” in Section 2.

summarizes the descriptive statistics for all variables incorporated into our analyses.

The mean value of the total systemic risk level (TC) was 10.052, but the maximum was 26.556, indicating that systemic risk increases rapidly in extreme cases. Secondly, the industry’s systemic risk contribution ($TI{C}^{OUT}$) had a higher standard deviation (9.917) than the industry’s systemic risk sensitivity ($TI{C}^{IN}$) (4.975), and the maximum value of $TI{C}^{OUT}$ (47.591) was much larger than the maximum value of $TI{C}^{IN}$ (29.873), indicating that $TI{C}^{OUT}$ fluctuates more severely than $TI{C}^{IN}$. This is consistent with the findings of Diebold and Yilmaz [25] and Härdle [42]. In terms of the industry heterogeneity variables, the book market value ratio, loan cost, and scale, as measured by the standard deviation, demonstrated broad distributions. The minimum value of the return on assets (ROA) was negative and the maximum value was positive. Together, these indicate that the sample selection was reasonable.

3.2. Analysis of the Generalized Dynamic Factor Model (GDFM)

During the sample period, the bankruptcy of the Lehman Brothers on 15 September 2008 represented the beginning of the global financial crisis. At the same time, the Chinese stock market experienced massive fluctuations. Furthermore, in June 2015, a stock market disaster occurred in the Chinese stock market. The Shanghai Composite Index fell to 3373 points from 5174 points, and the Shenzhen Composite Index dropped to 10,850 points from 18,182 points. Following this, many stocks fell sharply for a long time and this incident triggered the first large-scale government rescue action. Therefore, a high level of fluctuation and corresponding high volatility were found in two time periods during our sample period: the first one occurred from 4 January 2008 to 31 December 2008, 246 days in total; and the other was from 1 January 2015 to 30 December 2016, 487 days in total. We refer to these as the global crises and Stock Market Disasters, respectively. Moreover, the middle time period of 1457 days is referred to as the common period, since there was no systemic crisis in the Chinese stock market and the market was stable. Proceeding the estimation of the level-common and level-idiosyncratic shocks in Equation (2), we computed the estimated market shocks. The market shocks on the return of the sample stocks from 4 January 2008 to 30 December 2016 are shown in Figure 1. From this plot, we can easily observe two well-identified high periods: the 2008 global crisis and the 2015–2016 stock market disaster. It is evident that the most massive shocks over the sample period, by far, are those related to the 2008 global crisis. Therefore, as described in the following section, we divided the full sample period into three stages: stage 1 (2008, Global crisis), stage 2 (2009–2014, Common period), and stage 3 (2015–2016, Stock Market Disaster). In the following regression analysis, we made quarterly adjustments to the data to build quarterly risk networks.

3.3. Network Analysis

We focused on the LVDNs of the two idiosyncratic components ${\xi }_{\sigma ,n}^T$ and ${\xi }_{\omega ,n}^T$ of volatility given by Equations (9) and (10) to study the system risk. Since ${\xi }_{\sigma ,n}^T$ is completely unrelated, both serially and cross-sectionally (refer to Hallin and Liska [34] for details), we concentrated only on ${\xi }_{\omega ,n}^T$. According to the Bayesian information (BIC) criterion, we estimated a sparse VAR (5) model for ${\xi }_{\omega ,n}^T$. The graphs of LVDNs for the idiosyncratic volatilities ${\xi }_{\omega ,n}^T$ during the three sample stages are shown in Figure 2. Figure 2 shows the threshold LVDNs, with the optimal thresholds being 2.99, 1.48 and 2.59, respectively. In addition, we measured the systematic risk indicators based on the non-threshold LVDNs. Nodes of the same color belong to the same sector. The node size is expressed as the total degree. During the 2008 global financial crisis, as illustrated in Figure 2a, the connectedness of the whole network structures increased significantly, making the entire network more vulnerable to contagion. Moreover, during the stock market disaster, as illustrated in Figure 2c, the connectedness of the whole network structures also increased compared with that in the common period, as shown in Figure 2b. In the common period, as illustrated in Figure 2b, the network nodes were relatively scattered, and we found more interconnections within the sectors (nodes of the same color, such as yellow, red, and blue were linked together). These graphs reveal the importance of financial institutions (yellow nodes) in risk contagion. During the global crisis, the stock market disaster, and the relatively stable common period, the interconnections within financial institutions were very close.

Table 2. System risk indicators based on the long-term variance decomposition network model (LVDN) for ${\xi }_{\omega ,n}^T$.

Sector	Stage 1 (2008)		Stage 2 (2009–2014)		Stage 3 (2015–2016)
	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{I}\mathit{N}}$	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{O}\mathit{U}\mathit{T}}$	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{I}\mathit{N}}$	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{O}\mathit{U}\mathit{T}}$	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{I}\mathit{N}}$	$\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{O}\mathit{U}\mathit{T}}$
Energy	17.727	47.591	3.195	5.569	16.481	31.013
Materials	20.306	29.318	4.702	4.884	20.445	24.696
Industrial	24.570	27.630	3.982	4.446	16.353	17.904
Optional consumer	28.770	19.995	4.097	2.995	18.786	16.198
Major consumer	26.240	25.539	4.072	3.204	19.258	14.583
Healthcare	27.591	19.484	4.796	4.007	19.981	16.395
Financials	19.776	36.607	5.694	6.475	18.246	25.516
IT	26.331	17.942	4.476	4.658	19.208	12.499
Telecommunications	29.873	11.363	4.787	5.174	20.968	14.197
Utilities	29.547	15.546	4.849	3.458	16.068	12.301
TC	26.556		4.632		18.671

shows the system risk indicators in the threshold LVDN for ${\xi }_{\omega ,n}^T$. As shown in Table 2, we can see that the overall level of systemic risk spillover reached 20.176 in 2015, and the value TC reached 26,556 in 2008, three times higher than that in Stage 2. This was stimulated by the roller-coaster ups and downs of China’s stock market in 2015. In the first half of 2015, the stock market was in a “mad bull” state in which the excess liquidity in the market led to common risk exposure for most industries, and the potential risk transmission channels between industries widened rapidly, leaving the economy increasingly vulnerable. This process of potential systemic risk accumulation may not necessarily have an immediate and obvious impact on the economy, but a systemic crisis will be on the verge of breaking out when risks accumulate to a certain extent and negative impacts appear. In June 2015, the China Securities Regulatory Commission (CSRC) began to check the over-the-counter fund allocation. Due to the impact of rapid deleveraging, the risks accumulated in the first half of the year erupted instantly and the stock market plunged by more than 40%. Besides, there were significant differences in the input and output levels of systemic risk between different industries. The energy, materials, industrial, and financial industries showed high levels of systemic risk contribution, especially during the crisis, which was the main risk exporter. The industries with higher systemic risk sensitivity were the consumer, healthcare, IT, telecommunications, and utility industries, indicating that these industries are vulnerable to risk. Note that the system risk sensitivity/contribution indicators for the industrial sector were relatively large, and its system risk contribution was larger than the system risk sensitivity, which is different to other developed countries like the U.S. [28]. The industrial sector occupies a dominant position in China’s national economy, and it is necessary to target it as it is a systemically important sector, and effectively monitor and curb the risk that it accumulates. In addition, the system risk sensitivity of the financial sector was shown to be 19.78 in Stage 1 and 18.25 in Stage 3, whereas its system risk contribution was shown to be 36.61 in Stage 1 and 25.52 in Stage 3. The risk that financial institutions transmit to other real economic sectors was found to be greater than the risk that other sectors pass on to them. In the relatively stable Stage 2, the financial sector was shown to be the most central in the network. This once again proves the important position of financial institutions in risk contagion.

3.4. Regression Analysis

Table 3. Regression results of system risk indicators.

Variable	System Risk Sensitivity $\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{I}\mathit{N}}$			System Risk Contribution $\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{O}\mathit{U}\mathit{T}}$
Model	(1)	(2)	(3)	(4)	(5)	(6)
RATE		−1.1070 ** (0.012)			−0.7745 * (0.072)
RR			−0.9231 ** (0.023)			−0.7693 ** (0.024)
LEV	3.1309 ** (0.031)	11.3338 * (0.071)	9.8376 ** (0.046)	8.4922 *** (0.006)	4.4370 ** (0.047)	6.3611 ** (0.016)
RATE × LEV		−1.2265 ** (0.031)			−1.5642 * (0.055)
RR × LEV			−0.0407* (0.057)			−0.0672 * (0.059)
BM	0.2637 * (0.049)	0.1621 (0.190)	−0.0969 (0.254)	0.9427 ** (0.045)	0.8274 * (0.094)	0.7044 ** (0.046)
ROA	−2.1702 * (0.046)	−2.1140 * (0.057)	−1.749 * (0.093)	−2.5477 ** (0.029)	−2.9085 ** (0.035)	−3.0833 ** (0.027)
COST	−0.0612 (0.709)	0.0445 (0.787)	−0.0630 (0.237)	−0.0895 (0.114)	−0.0614 (0.982)	−0.0815 (0.496)
CASH	−0.0993 (0.209)	−0.0981 (0.212)	0.0957 (0.176)	−0.0821 (0.920)	−0.1248 (0.523)	−0.0631 (0.961)
SIZE	−0.6389 (0.439)	−0.5500 (0.504)	−0.4512 (0.583)	−0.4484 ** (0.044)	−0.4248 * (0.053)	−0.2057 * (0.097)
GDP	−4.8514 *** (0.000)	−5.4806 *** (0.000)	−3.956 *** (0.004)	−4.3967 *** (0.008)	−5.0943 ** (0.024)	−3.3957 ** (0.048)
_CONS	18.9773 (0.007)	31.2809 (0.000)	14.3496 (0.000)	20.8910 (0.000)	30.5027 (0.009)	19.4404 (0.000)
N	360	360	360	360	360	360

Note: *, **, and *** denote statistical significance at the 10%, 5%, and 1% levels, respectively.

presents the regression results for the system risk indicators ($TI{C}^{IN}$/$TI{C}^{OUT}$). We found a significant correlation between the systemic risk sensitivity and contribution of the industry and the industry’s heterogeneity variables. However, their correlations are different: the industry’s leverage ratio (LEV) was significantly positively correlated with both $TI{C}^{IN}$ and $TI{C}^{OUT}$, and the industry’s return on assets (ROA) was significantly negatively associated with both $TI{C}^{IN}$ and $TI{C}^{OUT}$. The book-to-market ratio (BM) was significantly positively correlated with $TI{C}^{OUT}$, and the size (SIZE) was significantly negatively correlated with $TI{C}^{OUT}$. However, except for model 1, the book-to-market ratio (BM) was not significantly related to $TI{C}^{IN}$, and the relationship between SIZE and $TI{C}^{IN}$ were not significant for models 1–3. This suggests that the relationship between the industry’s system risk contribution and industry characteristics is more significant. Our findings are similar to those of Berger et al. [43], who claimed that return on assets is positively related to systemic risk, Chiu et al. [2], who found that market-to-book ratios have a significant negative relationship with the industry system risk, and Zhu et al. [3], who found the firm size has a significantly negative effect on systemic risk contribution. The monetary policy proxy variables (RETE and RR) showed significant negative associations with system risk indicators, suggesting that an industry’s systemic risk-taking level will increase as the real interest rates or statutory reserve ratios decrease. This argument is similar to that of Ariccia et al. [44], who provided the theoretical foundations for the claim that prolonged periods of easy monetary conditions increase bank risk-taking. More importantly, the cross-terms of monetary policy proxy variables and leverage ratio show significant negative relationships with the systemic risk indicators.

Consequently, we argue that in the long run, whether a price-based monetary policy tool (interest rate) or a quantitative monetary policy tool (legal reserve ratio) is used, China’s monetary policy can effectively curb the systemic risk diffusion derived from the intra-industry leverage ratio. The absolute value of the coefficient $RATE\times LEV$ was found to be larger than the absolute value of the coefficient $RR\times LEV$, indicating that the interest rate instrument is generally more effective than the deposit reserve ratio instrument. In addition, the macroeconomic status proxy variable (GDP) was significantly negatively correlated with systemic risk indicators in all models, which means that the macroeconomic condition is a reliable guarantee against risk shocks.

Table 4. Dynamic panel regression results of system risk indicators.

Variable	System Risk Sensitivity $\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{I}\mathit{N}}$			System Risk Contribution $\mathit{T}\mathit{I}{\mathit{C}}^{\mathit{O}\mathit{U}\mathit{T}}$
Model	(1)	(2)	(3)	(4)	(5)	(6)
$TI{C}_{-1}^{IN}/TI{C}_{-1}^{OUT}$	0.1925 *** (0.004)	0.1875 *** (0.008)	0.1350 *** (0.000)	0.5806 *** (0.000)	0.5217 *** (0.000)	0.4753 *** (0.000)
RATE		−3.1672 *** (0.008)			−3.7020 *** (0.008)
RR			−1.1028 ** (0.036)			−1.1517 ** (0.036)
LEV	3.360 ** (0.040)	10.0586 ** (0.039)	9.3548 *** (0.009)	8.8306 ** (0.016)	9.3422 *** (0.009)	8.9068 *** (0.005)
RATE × LEV		−0.3219 ** (0.032)			−0.1806 * (0.054)
RR × LEV			−0.0312 ** (0.049)			−0.0330 * (0.066)
BM	0.2634 * (0.059)	0.1752 (0.289)	0.5760 (0.178)	1.0753 ** (0.045)	1.092 * (0.078)	1.034 ** (0.045)
ROA	−1.9500 ** (0.044)	−1.8701 * (0.065)	−2.0333 * (0.076)	−1.3203 ** (0.048)	−1.6542 ** (0.047)	−2.2654 * (0.075)
COST	0.0862 (0.798)	−0.0355 (0.443)	0.0795 (0.432)	−0.0652 (0.5706)	0.0935 (0.988)	0.0877 (0.727)
CASH	−0.0911 (0.256)	0.0050 (0.722)	−0.7503 (0.489)	0.3560 (0.490)	0.3003 (0.980)	0.5637 (0.606)
SIZE	−0.7369 (0.576)	0.5596 (0.837)	0.4594 (0.576)	−0.5107 ** (0.036)	−0.5086 ** (0.033)	−0.4980 * (0.054)
GDP	−4.963 *** (0.000)	−6.5806 *** (0.000)	−5.3675 *** (0.001)	−7.0302 *** (0.000)	−7.2611 *** (0.006)	−6.3186 *** (0.003)
_CONS	28.9306 *** (0.000)	17.2583 *** (0.000)	15.2951 *** (0.003)	25.0008 *** (0.000)	22.5635 *** (0.000)	20.0768 *** (0.000)
N	360	360	360	360	360	360

Note: *, **, and *** denote statistical significance at the 10%, 5%, and 1% levels, respectively.

shows the dynamic panel regression results of system risk indicators for Model (22). The coefficients of the variables RATE, RR, $RATE\times LEV$ and $RR\times LEV$ were found to be consistent in terms of variable significance and the direction of action, indicating that the above conclusions about monetary policy are robust. For the system risk sensitivity $TI{C}^{IN}$, only the industry heterogeneity variable LEV and ROA were significant, but for the system risk contribution $TI{C}^{OUT}$, the coefficients of the variables LEV, BM, ROA and SIZE were significant. This suggests that the system risk contribution is more sensitive to industry heterogeneity variables. This paper holds that vast discrepancies exist in the level of risk contribution in different industries because of the influences of several factors such as policy and the macro-economy. However, due to inter-industry involvement, the system risk sensitivity of different industries may be similar. Moreover, the stronger risk overflow of a single industry is shared by several industries. Thus, in most cases, the impact of industrial heterogeneity is not prominent. In fact, the discrepancy between risk sensitivity and contribution exactly proves the real existence of risk communication in industries. In addition to dynamic model testing, we also conducted a series of univariate model tests, such as adding lag terms to explanatory variables and introducing explanatory variables one by one, with robust results.

4. Conclusions

This paper seeks to shed new light on systemic risk contagion and its determinants from an industry perspective. We utilized the high dimensional financial network to capture the systemic risk contagion between different industries in China and to explore its relationships with monetary policy and industry heterogeneity factors. The results of the network analysis show that the total level of systemic risk increased significantly during the 2008 global crisis and the 2015–2016 Stock Market Disaster. The energy, materials, industrial, and financial industries are the top systemic risk contributors due to their high levels of risk output. Consumer, healthcare, IT, telecommunications, and utility industries are more susceptible to systemic risk due to their high levels of risk input. Combining the network theory and econometric analysis, we found that industry heterogeneity variables had significant impacts on systemic risk sensitivity and systemic risk contribution, but their effect on the systemic risk contribution was more pronounced. In particular, the effects of the leverage ratio and book-to-market ratio on the systemic risk contribution were positive, and the effects of the total return on assets and size on the systemic risk contribution were negative. However, for systemic risk sensitivity, only the effect of the leverage ratio and total return on assets were found to be robust. Moreover, monetary policy was shown to not only directly affect the systemic risk of the industry but also indirectly affect the effect of the industry’s leverage ratio, implying that China’s monetary policy can better restrain the adverse effects of leverage on market stability.

Our empirical study contributes to the literature on measuring systemic risk and has important economic implications in terms of asset pricing, risk management and policy making. For investors, the practical implications of our findings suggest that investment strategies should be adjusted accordingly to address risk contagion from the most influential industries to other industries. For regulators, we provide useful information when measuring the systemic risk and determining which industry are systemically important. In particular, we propose the following advice for risk supervision. Firstly, regulation should not only be placed on financial institutions but also on some entity industries. Secondly, great attention should be paid to connectivity among institutions or industries. The current economic and financial system demonstrates that more complex internal relevance and potential systematic risk attack is bound to influence entity industries through financial institutions, thus producing a scaling effect as well as a spillover effect. Ultimately, prudent regulation of monetary policy is necessary to prevent systematic risk in the mixed economy.

Our framework has several possible options for further study. First, the data used in our study do not include all publicly listed companies in China because we have eliminated companies that are not included in the CSI 300 and those that we only have limited data. Thus, developing new methods for analyzing systemic risk with limited data is a worthy goal. Another important extension would be the forecasting of systemic risk contagion in the networks. This effort could use the approach described by Barigozzi and Hallin [28], which provides volatility forecasts for the various stocks based on the GDFM approach. Moreover, the various variance decompositions and impulse-response functions of the GDFM approach open the way for systemic risk forecasting.