A Review of Information Fusion Methods for Gas Turbine Diagnostics
Abstract
1. Introduction
2. Background
3. Common Tools and Methods
3.1. Kalman Filters
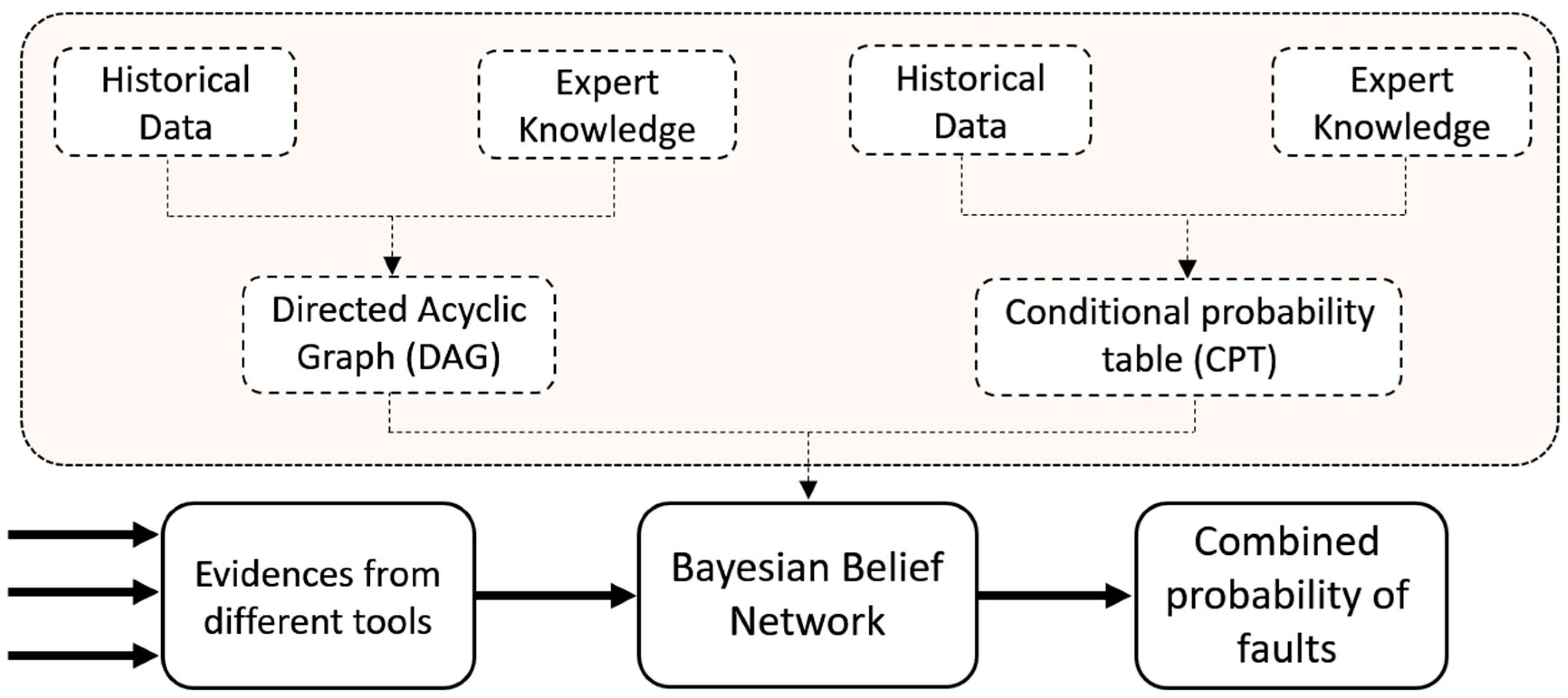
3.2. Bayesian Networks
3.3. Dempster–Schafer Theory
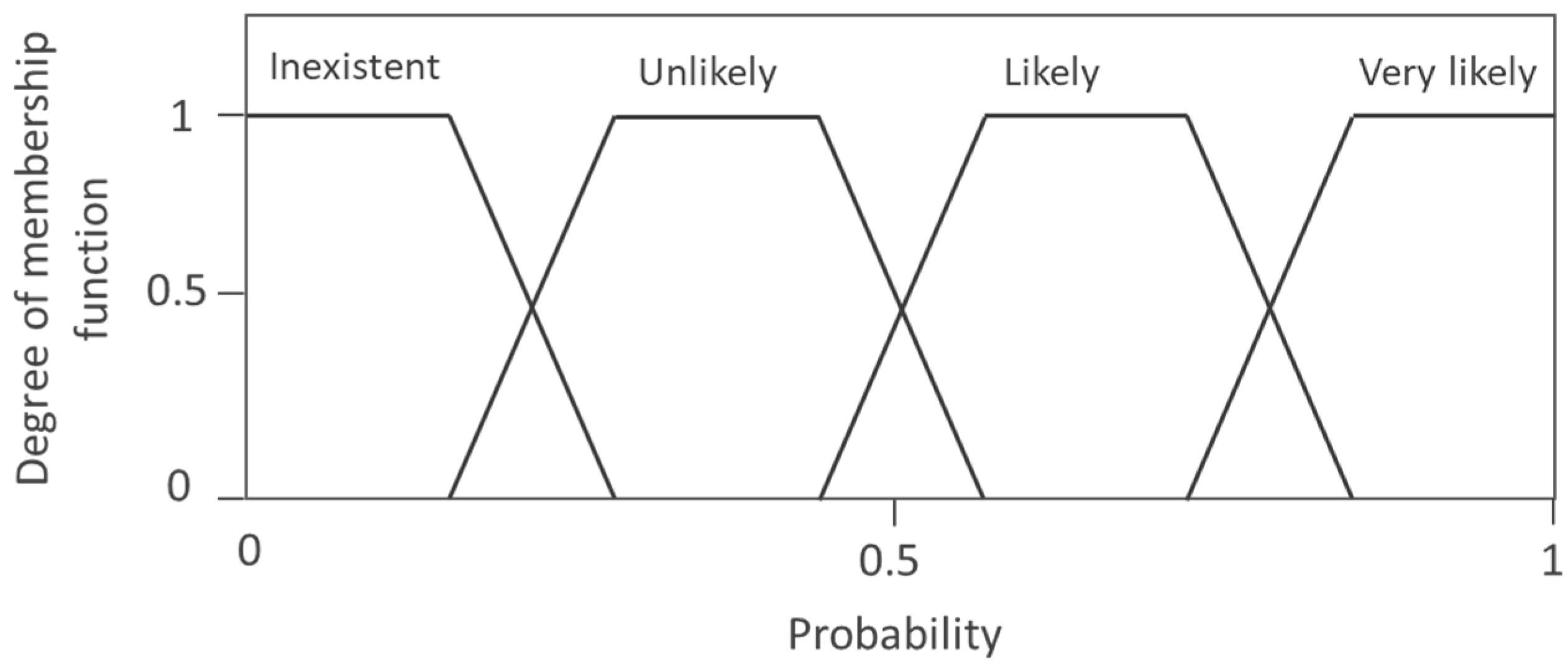
3.4. Fuzzy Inference
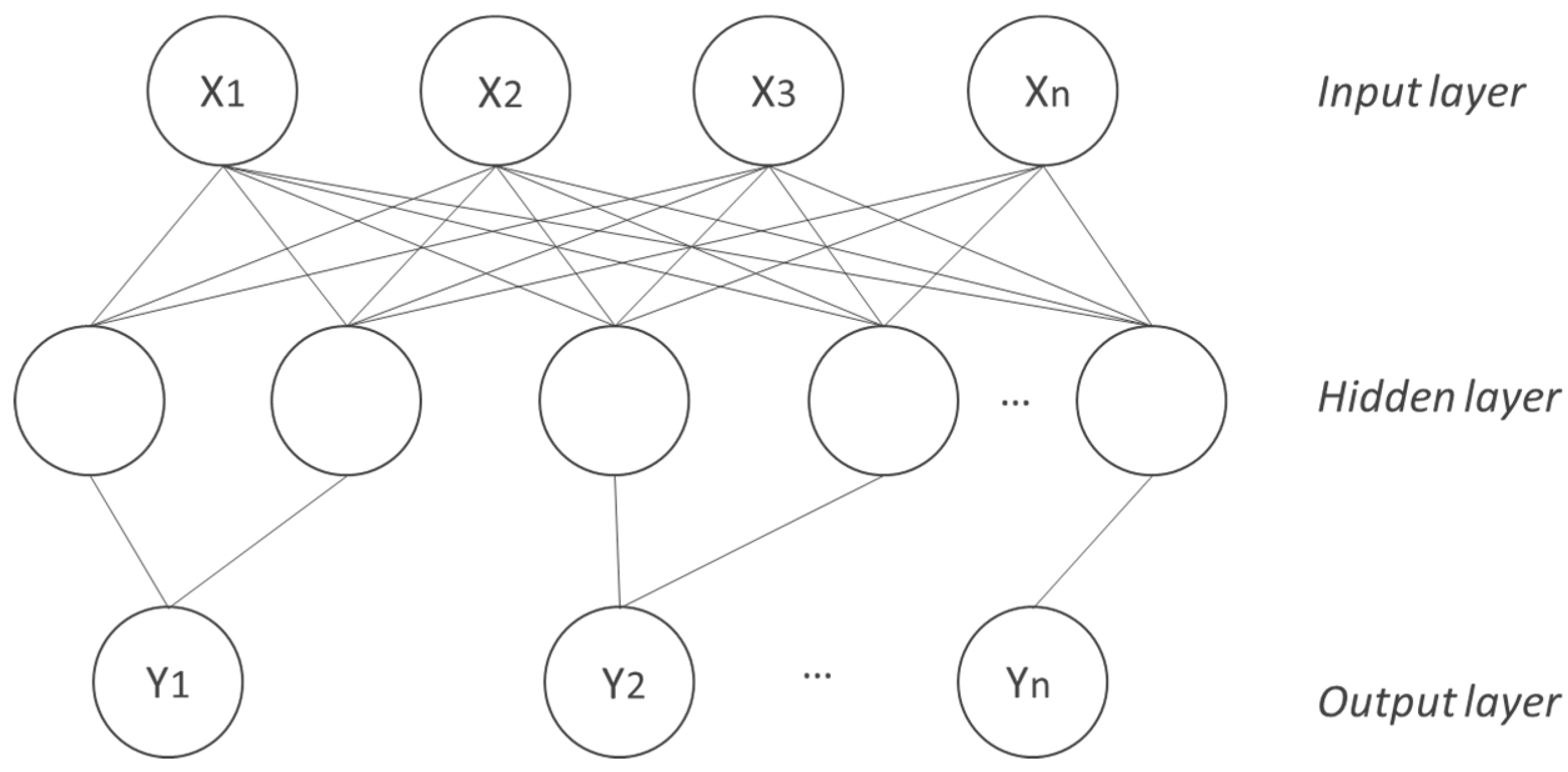
3.5. Probabilistic Neural Networks
4. Fusion Architectures
- Sensor-level fusion;
- Feature-level fusion;
- Decision-level fusion.
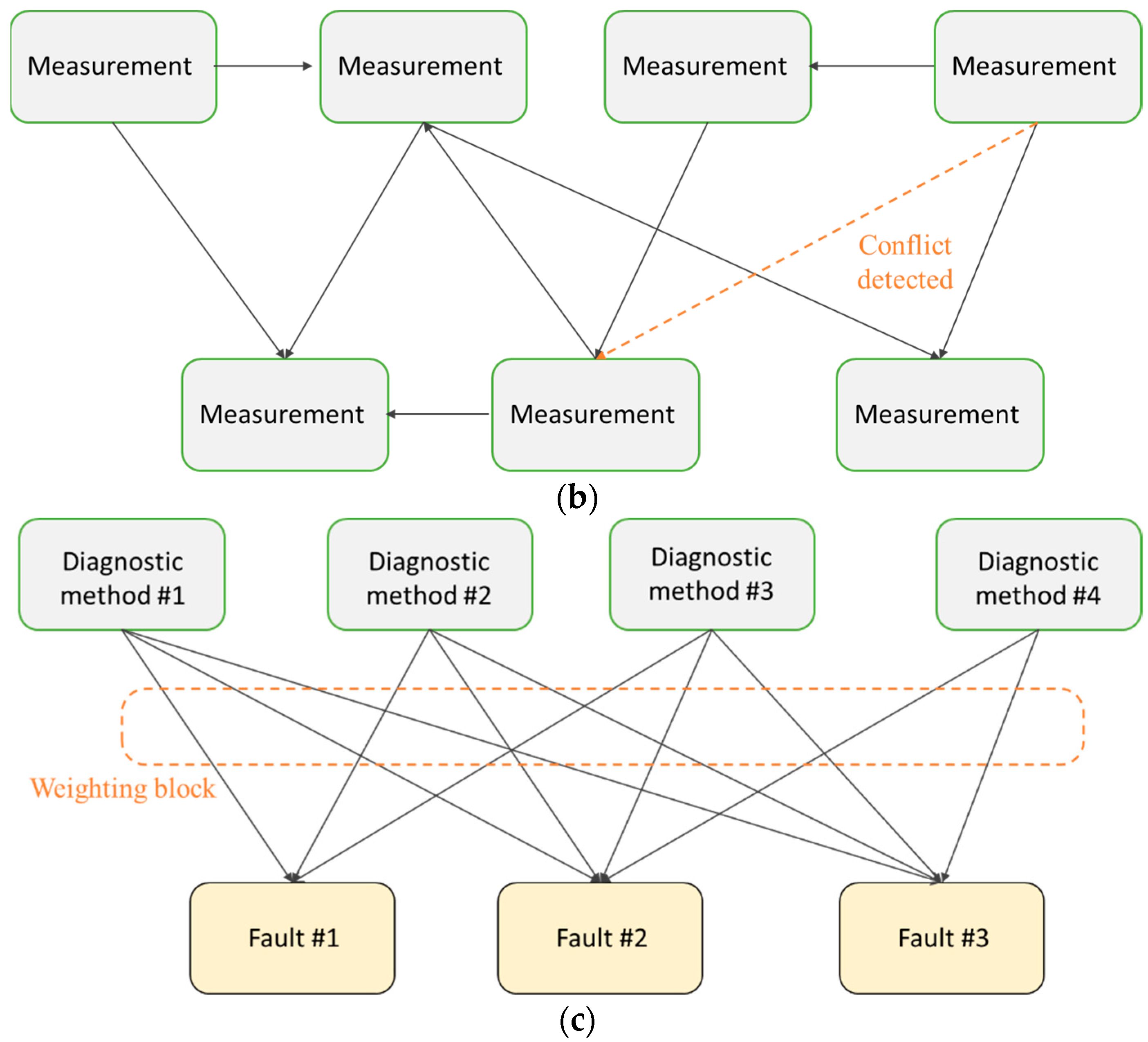
4.1. Sensor-Level Fusion
4.2. Feature-Level Fusion
4.3. Decision-Level Fusion
5. Discussion
- It can deal with incomplete and fuzzy information, including conflicting evidence;
- It does not require a priori knowledge of condition probabilities;
- It is robust toward measurement uncertainty;
- It provides a confidence level associated with the results.
Weights
6. Future Perspectives and Recommendations
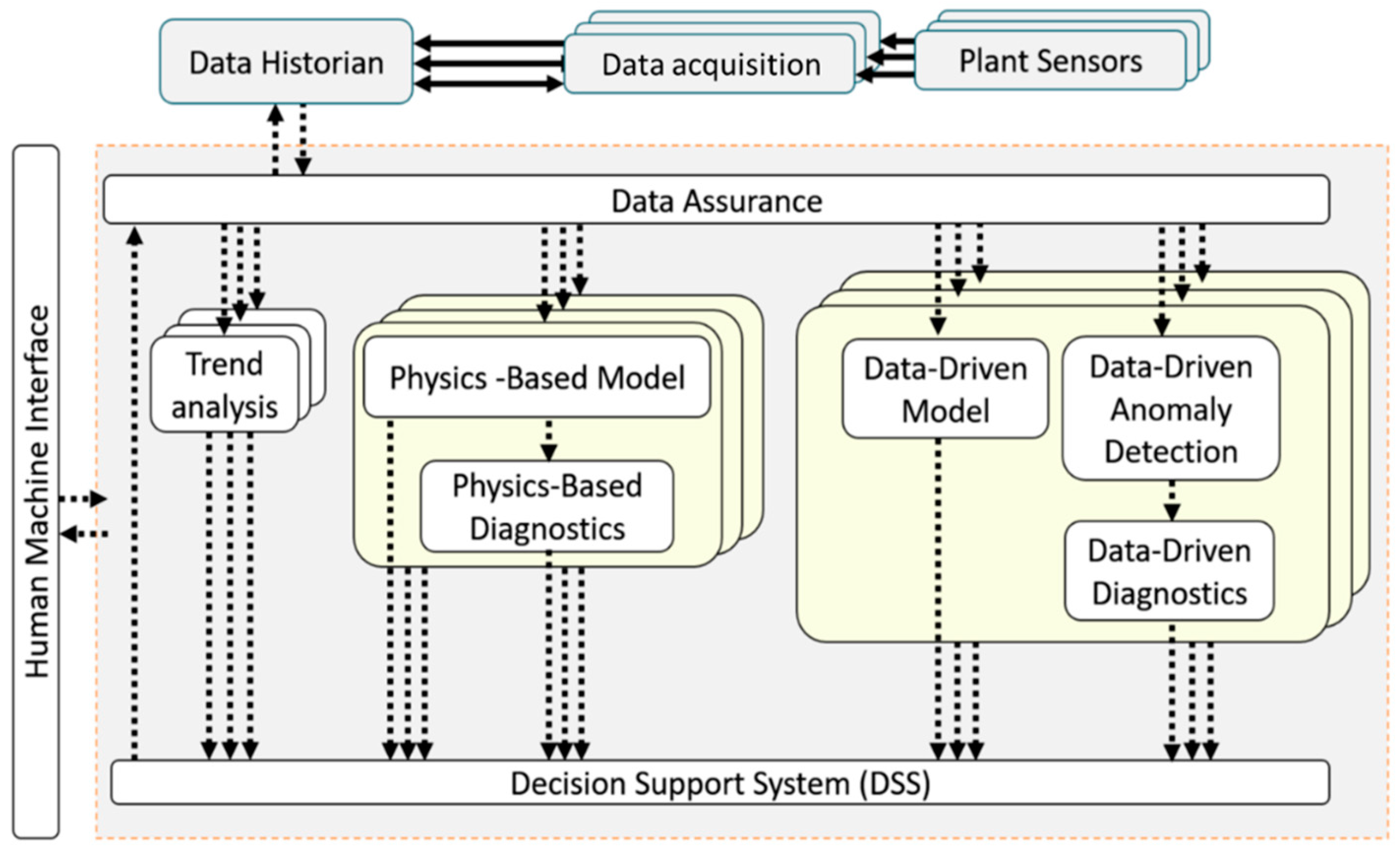
Micro Gas Turbine Diagnostics and Decision Support
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BBN | Bayesian belief network |
| CHP | Combined heat and power |
| DAG | Direct acyclic graph |
| DS | Dempster–Schafer |
| DDSS | Diagnostics and decision support system |
| FBN | Fuzzy belief network |
| FOD | Foreign object damage |
| GPA | Gas path analysis |
| HI | Health index |
| NN | Neural network |
| PCA | Principal component analysis |
| PNN | Probabilistic neural network |
| SVM | Support vector machine |
| VGV | Variable guide vane |
References
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Efficient Energy Management in a Microgrid with Intermittent Renewable Energy and Storage Sources. Sustainability 2019, 11, 3839. [Google Scholar] [CrossRef]
- Nami, H.; Akrami, E. Analysis of a gas turbine based hybrid system by utilizing energy, exergy and exergoeconomic methodologies for steam, power and hydrogen production. Energy Convers. Manag. 2017, 143, 326–337. [Google Scholar] [CrossRef]
- Cappelletti, A.; Martelli, F. Investigation of a pure hydrogen fuelled gas turbine burner. Int. J. Hydrogen Energy 2017, 42, 10513–10523. [Google Scholar] [CrossRef]
- Sung, T.; Kim, S.; Kim, K.C. Thermoeconomic analysis of a biogas-fueled micro-gas turbine with a bottoming organic Rankine cycle for a sewage sludge and food waste treatment plant in the Republic of Korea. Appl. Therm. Eng. 2017, 127, 963–974. [Google Scholar] [CrossRef]
- Grange, B.; Dalet, C.; Falcoz, Q.; Ferrière, A.; Flamant, G. Impact of thermal energy storage integration on the performance of a hybrid solar gas-turbine power plant. Appl. Therm. Eng. 2016, 105, 266–275. [Google Scholar] [CrossRef]
- Harun, N.F.; Tucker, D.; Adams, T.A., II. Open Loop and Closed Loop Performance of Solid Oxide Fuel Cell Turbine Hybrid Systems During Fuel Composition Changes. J. Eng. Gas Turbines Power 2017, 139, 061702. [Google Scholar] [CrossRef]
- Visser, W.P.J.; Shakariyants, S.A.; Oostveen, M. Development of a 3kW Microturbine for CHP applications. J. Eng. Gas Turbines Power 2011, 133, 042301. [Google Scholar] [CrossRef]
- Fallahi, Z.; Henze, G.P. Interactive Buildings: A Review. Sustainability 2019, 11, 3988. [Google Scholar] [CrossRef]
- Gorinevsky, D.; Matthews, B.; Martin, R. Aircraft Anomaly Detection using Performance Models Trained on Fleet Data. In Proceedings of the Conference on Intelligent Data Understanding, Boulder, CO, USA, 24–26 October 2012. [Google Scholar]
- Simon, D.L.; Rinehart, A.W. A model-based anomaly detection approach for analyzing streaming aircraft engine measurement data. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. GT2014–27172. [Google Scholar]
- Tolani, D.; Yasar, M.; Ray, A.; Yang, V. Anomaly Detection in Aircraft Gas Turbine Engines. J. Aerosp. Comput. Inf. Commun. 2006, 3, 44–51. [Google Scholar] [CrossRef]
- Liu, Y. Design of fault detection system for a heavy duty gas turbine with state observer and tracking filter. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. GT2017–64089. [Google Scholar]
- Tsoutsanis, E.; Meskin, N.; Benammr, M.; Khorasani, K. Transient Gas Turbine Performance Diagnostics through Nonlinear Adaptation of Compressor and Turbine Maps. J. Eng. Gas Turbines Power 2015, 137, 091201. [Google Scholar] [CrossRef]
- Hosseini, S.H.R.; Khaledi, H.; Solani, M.R. New Model Based Gas Turbine Fault Diagnostics Using 1D Engine Model and Nonlinear Identification Algorithms. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea and Air, Orlando, FL, USA, 8–12 June 2009. GT2009–59439. [Google Scholar]
- Mathioudakis, K.; Kamboukos, P.; Stamatis, A. Gas turbine component fault detection from a limited number of measurements. J. Power Energy 2004, 218, 609–618. [Google Scholar] [CrossRef]
- Jaw, L.C.; Lee, Y.J. Engine diagnostics in the eyes of machine learning. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. GT2014–27088. [Google Scholar]
- Vatani, A.; Khorasani, K.; Meskin, N. Health monitoring and degradation prognostics in gas turbine engines using dynamic neural networks. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montréal, QC, Canada, 15–19 June 2015. GT2015–44101. [Google Scholar]
- Tahan, M.; Tsoutsanis, E.; Muhammada, M.; Karim, Z.A.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A Review of Gas Turbine Gas-Path Diagnostics: State-of-the-Art Methods, Challenges and Opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Verbist, M.L.; Visser, W.P.J.; Van Buijtenen, J.P. Gas path analysis on KLM in-flight engine data. In Proceedings of the ASME Turbo Expo 2011: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. GT2011–45625. [Google Scholar]
- Marinai, L.; Singh, R. A bias-tolerant gas path diagnostics approach based on fuzzy logic. In Proceedings of the International Symposium of Air Breathing Engines (ISABE-2005-1285), Munich, Germany, 4–9 September 2005. [Google Scholar]
- Zarate, L.A.M.; Loboda, I. Computation and monitoring of the deviations of gas turbine unmeasured parameters. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montréal, QC, Canada, 15–19 June 2015. GT2015–43862. [Google Scholar]
- Volponi, A.J. Gas Turbine Parameter Corrections. ASME J. Eng. Gas Turbines Power 1999, 121, 613–621. [Google Scholar] [CrossRef]
- Jiang, X.; Foster, C. Plant performance monitoring and diagnostics–remote, real-time and automation. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. GT201–27314. [Google Scholar]
- Zhang, Y.; Martínez-García, M.; Latimer, A. Selecting optimal features for cross-fleet analysis and fault diagnosis of industrial gas turbines. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. GT2018–75286. [Google Scholar]
- Zhang, Y.; Jombo, G.; Latimer, A. A Knowledge Transfer Platform for Fault Diagnosis of Industrial Gas Turbines. In Proceedings of the 22nd IEEE International Conference on Intelligent Engineering Systems, Las Palmas de Gran Canaria, Spain, 21–23 June 2018. [Google Scholar]
- Romesis, C.; Li, Y.G. Condition-Based Maintenance for Gas Turbines Plants. 2013. Available online: https://www.semanticscholar.org/paper/CONDITION-BASED-MAINTENANCE-FOR-GAS-TURBINES-PLANTS-Romesis/90fb311a711721a6189f9ed2e88ca349b9fa11d8#citing-papers (accessed on 15 July 2019).
- Breese, J.S.; Horvitz, E.J.; Peot, M.A.; Gay, R.; Quentin, G.H. Automated Decision-Analytic Diagnosis of Thermal Performance in Gas Turbines. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992. 92–GT–399. [Google Scholar]
- Palmer, C.A. Combining Bayesian belief networks with gas path analysis for test cell diagnostics and overhaul. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, Stockholm, Sweden, 2–5 June 1998. 98–GT–168. [Google Scholar]
- Hansen, R.J.; Hall, D.L.; Kurtz, S.K. A new approach to the challenge of machinery prognostics. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, Hague, The Netherlands, 13–16 June 1994. 94–GT–003. [Google Scholar]
- Hall, D.L.; Hansen, R.J.; Lang, D.C. The Negative Information Problem in Mechanical Diagnostics. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, Birmingham, UK, 10–13 June 1996. 96–GT–035. [Google Scholar]
- Roemer, M.J.; Kacprzynski, G.J. Advanced Diagnostic and Prognostic Technologies for Gas Turbine Engine Risk Assessment. In Proceedings of the ASME Turbo Expo 2000, Munich, Germany, 8–11 May 2000. 2000–GT–30. [Google Scholar]
- Roemer, M.J.; Kacprzynski, G.J.; Schoeller, M.H. Improved Diagnostic and Prognostic Assessments Using Health Management Information Fusion. In Proceedings of the Autotestcon Proceedings IEEE Systems Readiness Technology Conference, Valley Forge, PA, USA, 20–23 August 2001; pp. 365–377. [Google Scholar]
- Sun, S.L.; Deng, Z.L. Multi-sensor optimal information fusion Kalman Filter. Automatica 2004, 40, 1017–1023. [Google Scholar] [CrossRef]
- Kjræulff, U.B.; Madsen, A.L. Bayesian Networks and Influence Diagrams: A Guide to Construction and Analysis; Springer: Berlin, Germany, 2013; ISBN 978-0-387-74101-7. [Google Scholar]
- Weber, P.; Simon, C. Benefits of Bayesian Network Models; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Martin, T.G.; Burgman, M.A.; Fidler, F.; Kuhnert, P.M.; Low-Choy, S.; Mcbride, M.; Mengersen, K. Eliciting expert knowledge in conservation science. Conserv. Biol. 2012, 26, 29–38. [Google Scholar] [CrossRef]
- Adel, T.; de Campos, C.P. Learning Bayesian networks with incomplete data by augmentation. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–10 February 2017. [Google Scholar]
- Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]
- Gou, K.X.; Jun, G.X.; Zhao, Z. Learning Bayesian Network Structure from Distributed Homogeneous Data. In Proceedings of the Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD 2007), Qingdao, China, 30 July–1 August 2007; pp. 250–254. [Google Scholar]
- Alonso-Barba, J.I.; delaOssa, L.; Gámez, J.A.; Puerta, J.M. Scaling up the Greedy Equivalence Search algorithm by constraining the search space of equivalence classes. Int. J. Approx. Reason. 2013, 54, 429–451. [Google Scholar] [CrossRef]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- Romessis, C.; Stamatis, A.; Mathioudakis, K. Setting up a belief network for turbofan diagnosis with the aid of an engine performance model. In Proceedings of the International Symposium of Air Breathing Engines (ISABE 2001), Bangalore, India, 2–7 September 2001; pp. 19–26. [Google Scholar]
- Romessis, C.; Mathioudakis, K. Bayesian network approach for gas path fault diagnosis. J. Eng. Gas Turbines Power 2004, 128, 64–72. [Google Scholar] [CrossRef]
- Lee, Y.K.; Mavris, D.N.; Volovoi, V.V.; Yuan, M.; Fisher, T. A fault diagnosis method for industrial gas turbines using Bayesian data analysis. J. Eng. Gas Turbines Power 2010, 132, 041602. [Google Scholar] [CrossRef]
- Ibarguengoytia Gonzales, P.H. Any Time Probabilistic Reasoning for Sensor Validation. Ph.D. Thesis, University of Salford, Manchester, UK, 1997. [Google Scholar]
- Kyriazis, A.; Mathioudakis, K. Gas turbines diagnostics using weighted parallel decision fusion framework. In Proceedings of the 8th European Turbomachinery Conference, Graz, Austria, 23–27 March 2009. [Google Scholar]
- Ganguli, R. Application of fuzzy logic for fault isolation of jet engines. In Proceedings of the ASME Turbo Expo 2001, New Orleans, LA, USA, 4–7 June 2001. 2001–GT–0013. [Google Scholar]
- Lipowsky, H.; Staudacher, S.; Nagy, D.; Bauer, M. Gas turbine fault diagnostics using a fusion of least squares estimations and fuzzy logic rules. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008. GT2008–50190. [Google Scholar]
- Aretakis, N.; Roumeliotis, I.; Alexiou, A.; Romesis, C.; Mathioudakis, K. Turbofan engine health assessment from flight data. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. GT2014–266443. [Google Scholar]
- Loboda, I.; Yepifanov, S. On the selection of an optimal pattern recognition technique for gas turbine diagnosis. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Simon, D.L.; Bourguet, S.; Léonard, O.; Zhang, X. Aircraft engine gas path diagnostic methods: Public benchmarking results. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Romesis, C.; Mathioudakis, K. Setting Up of a Probabilistic Neural Network for Sensor Fault Detection Including Operation with Component Faults. J. Eng. Gas Turbines Power 2003, 125, 634–642. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Romessis, C. Probabilistic neural networks for validation of on-board jet engine data. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2004, 218, 59–72. [Google Scholar] [CrossRef]
- Goebel, K.; Agogino, A.M. Fuzzy sensor fusion for gas turbine power plants. In Proceedings of the SPIE 1999-The International Society for Optical Engineering, Bellingham, WA, USA, 12 March 1999; Volume 3719, pp. 52–61. [Google Scholar] [CrossRef]
- Diallo, O.; Mavris, D. A data analytics approach to failure precursor detection of gas turbine. In Proceedings of the ASME Turbo Expo 2011, Vancouver, BC, Canada, 6–10 June 2011. GT2011–46019. [Google Scholar]
- Scheianu, D. Development of fault specific soft sensors with application to gas turbine diagnosis. In Proceedings of the ASME Turbo Expo, Copenhagen, Denmark, 11–15 June 2012. GT2012–69662. [Google Scholar]
- Lu, F.; Gao, T.; Huang, J.; Qiu, X. A novel distributed extended Kalman filter for aircraft engine gas-path health estimation with sensor fusion uncertainty. Aerosp. Sci. Technol. 2019, 84, 90–106. [Google Scholar] [CrossRef]
- Liu, K.; Gebraeel, N.Z.; Shi, J. A data-level fusion model for developing composite health indices for degradation modeling and prognostic analysis. IEEE Trans. Autom. Sci. Eng. 2013, 10, 652–664. [Google Scholar] [CrossRef]
- Liu, K.; Huang, S. Integration of data fusion methodology and degradation modeling process to improve prognostics. IEEE Trans. Autom. Sci. Eng. 2014, 13, 344–354. [Google Scholar] [CrossRef]
- Yan, H.; Liu, K. Multiple Sensor Data Fusion for Degradation Modeling and Prognostics Under Multiple Operational Conditions. IEEE Trans. Reliab. 2016, 65, 1416–1426. [Google Scholar] [CrossRef]
- Chen, S.; Wen, P.; Zhao, S.; Huang, D.; Wu, M.; Zhang, Y. A Data Fusion-based Methodology of Constructing Health Indicators for Anomaly Detection and Prognostics. In Proceedings of the International Conference on Sensing, Diagnostics, Prognostics, and Control 2018, Xi’an, China, 15–17 August 2018. [Google Scholar] [CrossRef]
- Li, Y.G. Gas Turbine Performance and Health Status Estimation Using Adaptive Gas Path Analysis. J. Eng. Gas Turbines Power 2010, 132, 041701. [Google Scholar] [CrossRef]
- Yan, W.; Goebel, K. Sensor Validation and Fusion for Gas Turbine Vibration Monitoring. In Proceedings of the SPIE-The International Society for Optical Engineering, Orlando, FL, USA, 8 August 2003. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Kyriazis, A.; Tsalavoutas, A.; Mathioudakis, K.; Bauer, M.; Johanssen, O. Gas Turbine Fault Identification by Fusing Vibration Trending and Gas Path Analysis. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June, 2009. GT2009–59942. [Google Scholar]
- Turso, J.A.; Litt, J.S. A Foreign Object Damage Event Detector Data Fusion System for Turbofan Engines. J. Aerosp. Comput. Inf. Commun. 2005, 2, 291–308. [Google Scholar] [CrossRef]
- Sarkar, S.; Sarkar, S.; Mukherjee, K.; Ray, A.; Srivastav, A. Multi-sensor information fusion for fault detection in aircraft gas turbine engines. J. Aerosp. Eng. 2012, 227, 1988–2001. [Google Scholar] [CrossRef]
- Volponi, A.; Brotherton, T.; Luppold, R.; Simon, D.L. Development of an Information Fusion System for Engine Diagnostics and Health Management. NASA/TM—2004-212924. In Proceedings of the 39th Combustion/27th Airbreathing Propulsion/21st Propulsion Systems Hazards/3rd Modeling and Simulation Joint Subcommittee Meeting sponsored by the Joint-Army-Navy-NASA-Air Force Interagency Propulsion Committee (JANNAF), Colorado Springs, CO, USA, 1–5 December 2003. [Google Scholar]
- Dewallef, P.; Romessis, C.; Léonard, O.; Mathioudakis, K. Combining Classification Techniques with Kalman Filters for Aircraft Engine Diagnostics. In Proceedings of the ASME Turbo Expo, Vienna, Austria, 14–17 June 2004. GT2004–53541. [Google Scholar]
- Kyriazis, A.; Arethkis, N.; Mathioudakis, K. Gas turbine fault diagnosis from fast response data using probabilistic methods and information fusion. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea and Air, Barcelona, Spain, 8–11 May 2006. GT2006–90362. [Google Scholar]
- Romessis, C.; Kyriazis, A.; Mathioudakis, K. Fusion of gas turbines diagnostic inference–the Dempster-Schafer approach. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea and Air, Montreal, QC, Canada, 14–17 May 2007. GT2007–27043. [Google Scholar]
- Romessis, C.; Mathioudakis, K. Estimation of gas turbines gradual deterioration through a Dempster-Schafer based fusion method. In Proceedings of the International Symposium of Air-Breathing Engines (ISABE), Montreal, QC, Canada, 7–11 September 2009. ISABE-2009–1301. [Google Scholar]
- Kyriazis, A.; Mathioudakis, K. Gas Turbine Fault Diagnosis Using Fuzzy-based Decision Fusion. J. Propuls. Power 2009, 25, 335–343. [Google Scholar] [CrossRef]
- Kyriazis, A.; Mathioudakis, K. Enhanced fault localization using probabilistic fusion with gas path analysis algorithms. J. Eng. Gas Turbines Power 2009, 131, 051601. [Google Scholar] [CrossRef]
- Xu, J. PHM-Oriented Integrated Fusion Prognostics for Aircraft Engines Based on Sensor Data. IEEE Sens. J. 2014, 14, 1124–1132. [Google Scholar] [CrossRef]
- Lu, F.; Wang, Y.; Huang, J.; Huang, Y. Gas Turbine Transient Performance Tracking Using Data Fusion Based on an Adaptive Particle Filter. Energies 2015, 8, 13911–13927. [Google Scholar] [CrossRef]
- Lu, F.; Jiang, C.; Huang, J.; Wang, Y.; You, C. A Novel Data Hierarchical Fusion Method for Gas Turbine Engine Performance Fault Diagnosis. Energies 2016, 9, 828. [Google Scholar] [CrossRef]
- Lu, F.; Wang, Y.; Huang, J.; Qiu, X. Gas turbine performance monitoring based on extended information fusion filter. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 483–497. [Google Scholar] [CrossRef]
- Yu, L.J.; Cleary, D.; Osborn, M.; Rajiv, V. Information fusion strategy for aircraft engine health management. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea and Air, Montreal, QC, Canada, 14–17 May 2007. GT2007–27174. [Google Scholar]
- Kodali, A.; Donat, W.; Singh, S.; Choi, K.; Pattipati, K. Dynamic Fusion and Parameter Optimization of Multiple Classifier Systems. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008. GT2008–51274. [Google Scholar]
- Visser, W.P.J.; Shakariyants, S.; De Later, M.T.L.; Ayed, A.H.; Kusterer, K. Performance optimization of a 3KW microturbine for CHP applications. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 619–628. [Google Scholar]
- European Commission. Putting Energy Efficiency First: Consuming Better, Getting Cleaner. MEMO/16/3986. 2016. Available online: http://europa.eu/rapid/press-release_MEMO-16-3986_en.htm (accessed on 7 August 2017).
- FUDIPO. Available online: https://fudipo.eu/whats-fudipo/ (accessed on 30 April 2019).
- Aslanidou, I.; Zaccaria, V.; Rahman, M.; Oostveen, M.; Olsson, T.; Kyprianidis, K.G. Towards an Integrated Approach for Micro Gas Turbine Fleet Monitoring, Control, and Diagnostics. In Proceedings of the Global Power and Propulsion Society Forum 2018, Zurich, Switzerland, 10–12 January 2018. [Google Scholar]
- Rahman, M.; Zaccaria, V.; Zhao, X.; Kyprianidis, K. Diagnostics-oriented modelling of micro gas turbines for fleet monitoring and maintenance optimization. Processes 2018, 6, 216. [Google Scholar] [CrossRef]
- Zaccaria, V.; Stenfelt, M.; Sjunnesson, A.; Hansson, A.; Kyprianidis, K. A model-based solution for gas turbine diagnostics: Simulations and experimental verification. In Proceedings of the ASME Turbo Expo 2019: Power for Land, Sea and Air, Phoenix, AZ, USA, 11–15 June 2019. GT2019–90858. [Google Scholar]



| [58] | [59,60,61] | [64] | [66] | [67] | |
|---|---|---|---|---|---|
| Data type | Performance + vibration | Performance | Vibration | Performance + vibration | Performance + vibration |
| Features extraction | Yes | No | Yes | Yes | Yes |
| Fusion method | PCA | Weighted HI | Aggregation of normalized amplitude | PDF integration and certainty factor | DS |
| Improvement from single sensor | 25% increase in detected anomalies | 20% decrease in error | Increased confidence level | Correct fault localized | Uncertainty identified for conflictual info |
| [71] | [72] | [74] | [75] | [47] | |
|---|---|---|---|---|---|
| Best single method | 0/24 (radial) | 2/15 (axial) | 1/12 (radial) | 4/15 (axial) | 0/24 (radial) |
| 0/16 (axial) | 0/16 (axial) | 2/15 (axial) | |||
| Worst single method | 6/24 | 3/15 | 3/12 | - | 6/24 |
| 1/16 | 4/16 | 4/15 | |||
| Best fusion method | 2/24 | 1/15 | 0/12 | 1/15 | 0/24 |
| 0/16 | 0/16 | 2/15 | |||
| Worst fusion method | 2/24 | - | 1/12 | - | 5/24 |
| 1/16 | 2/16 | 4/15 | |||
| Fusion method | BBN/PNN | DS | Fuzzy logic | Probabilistic fusion | BBN |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaccaria, V.; Rahman, M.; Aslanidou, I.; Kyprianidis, K. A Review of Information Fusion Methods for Gas Turbine Diagnostics. Sustainability 2019, 11, 6202. https://doi.org/10.3390/su11226202
Zaccaria V, Rahman M, Aslanidou I, Kyprianidis K. A Review of Information Fusion Methods for Gas Turbine Diagnostics. Sustainability. 2019; 11(22):6202. https://doi.org/10.3390/su11226202
Chicago/Turabian StyleZaccaria, Valentina, Moksadur Rahman, Ioanna Aslanidou, and Konstantinos Kyprianidis. 2019. "A Review of Information Fusion Methods for Gas Turbine Diagnostics" Sustainability 11, no. 22: 6202. https://doi.org/10.3390/su11226202
APA StyleZaccaria, V., Rahman, M., Aslanidou, I., & Kyprianidis, K. (2019). A Review of Information Fusion Methods for Gas Turbine Diagnostics. Sustainability, 11(22), 6202. https://doi.org/10.3390/su11226202








