Abstract
Unmanned aerial vehicles (UAVs) are expected to make groundbreaking changes in the logistics industry. Leading logistics companies have been developing and testing their usage of UAVs recently as an environmentally friendly and cost-effective option. In this paper, we investigate how much the UAV delivery service is environmentally friendly compared to the traditional ground vehicle (GV) delivery service. Since there are fuel (battery) and loadable weight restrictions in the UAV delivery, multi-hopping of UAV is necessary, which may cause a large consumption of electrical energy. We present a two-phase approach. In Phase I, a new vehicle routing model to obtain optimal delivery schedules for both UAV-alone and GV-alone delivery systems is proposed, which considers each system’s restrictions, such as the max loadable weight and fuel replenishment. In Phase II, CO2 emissions are computed as a sustainability measure based on the travelling distance of the optimal route obtained from Phase I, along with various GV travel-speeds. A case study finds that the UAV-alone delivery system is much more CO2 efficient in all ranges of the GV speeds investigated.
1. Introduction
Unmanned aerial vehicles (UAVs) are a class of the emerging technologies that are expected to make groundbreaking changes in the logistics industry. Leading logistics companies are developing and testing their services using UAVs. As a representative example, Amazon announced, in December 2013, the conception of the Prime Air service, which is based on home deliveries by UAVs [1]. In December 2016, they conducted their first trial of Prime Air in the UK [2]. In addition, DHL succeeded in a test for the delivery of medical supplies by UAVs called parcelcopters [3]. Such UAV-based services are expected to gradually expand. Teal group [4] anticipates that the civil unmanned aerial system (UAS) market will almost triple in size from around USD $5 billion in 2020 to USD $14.5 billion in 2028.
The strength of UAVs creates opportunities and applications. In comparison to the usual ground vehicle, they provide higher efficiency and flexibility, resulting in less cost. They move quickly with less interruption of obstacles than the ground vehicles, and a flexible path change is possible. According to Business Insider [5], as an illustrative comparison, delivering a typical shoebox costs just USD 0.05 per mile with drones, which is much cheaper than premium ground delivery services such as UPS or FedEx (USD $6.00 to $6.50 per mile) or USPS services (USD $2.00 per mile). Therefore, UAVs are being explored in a wide range of areas for future applications beyond the logistics industry. They can act promptly for disaster management and relief activity. They are useful for search and rescue missions, and the prevention and detection of disasters, such as wildfire. In addition, UAV technology is presently considered as an essential technology for 3D mapping [6,7].
There is no doubt that UAVs are more economical than the ground vehicles (GVs), as stated in previous literature [8]. Therefore, a variety of UAV logistic services, such as UAV only and truck-UAV hybrid services are emerging presently [9,10]. However, it is questionable if UAV service is truly sustainable. If one is truly sustainable, it must be environmentally friendly as well as economically efficient. If both consequences are not satisfied at the same time, the service may not last long. Much research has explored the economical use of UAVs for logistic services. However, quantitative investigations on the true sustainability of UAV logistic services have rarely represented. Therefore, in this study, we compare the UAV logistic service with the one using general ground vehicles (GVs) to quantitatively analyze the sustainability of the UAV logistic service and answer the question about how environmentally friendly the UAV logistic service is.
To compare the sustainability of the UAV logistic service with that of the GV logistic service, the following second question may arise: What routes do UAVs or GVs use to serve the same set of customers? We notice that UAVs are required to have multi-hops at depots due to the fuel (battery) and loadable weight restrictions of UAVs and, thus, UAVs should move differently from GVs. Therefore, we developed a mathematical model that provides two different delivery routes considering different fuel and loadable weight capacities. CO2 emissions are calculated based on the travelling distances obtained by the mathematical model. To discuss the sustainability of a vehicle, it is important to consider the travelling distance of the vehicle, which is directly related to pollutant emissions. However, to the best of our knowledge, the sustainability body of literature has hardly addressed on this issue.
A two-phase approach is adopted to investigate the sustainability of the UAV logistic service. In Phase I, a vehicle routing problem with multiple sharable depots and multiple trips (VRPMSDMT) is proposed to obtain delivery schedules of UAVs and GVs. The VRPMSDMT yields the UAV and GV delivery schedules to serve a set of customers given input parameters such as speed and loadable capacity. The total travelling distance of UAVs and GVs will serve as a key measure for environmental analysis. In Phase II, CO2 emissions are calculated based on information such as the total travelling distance and speed of the UAV and GV. In case of the GV logistic service, it is possible to directly measure CO2 emissions because it uses fossil fuel in general. However, since an UAV utilizes electrical energy, an environmental analysis was performed by estimating the amount of fossil fuels used to generate the electrical energy. As a result, we compared the CO2 emissions generated to serve a set of customers using an UAV and a GV to quantitatively show how environmentally friendly the UAV logistic service is. Most of the recent studies about UAV logistic services focus on the derivation of economic routing of UAVs for the last mile delivery. To the best of our knowledge, observing UAV logistic services both economically and environmentally has rarely been investigated. We believe it is a significant step for the future of sustainable UAV logistic services.
2. Literature Review
A vehicle routing problem (VRP) was first introduced in the 1950s by Dantzig and Ramser [11], and a huge amount of its variants have been proposed to address various real-world problems. VRPs can also be applied to UAV logistic services to generate optimal routes. We first share studies about UAV routing and, then, investigate another VRP variant that considers pollutant emissions.
2.1. Routing with UAVs
The studies on UAV routing have begun to attract research interests since the mid-2000s. Research in the early stage focused on UAV routing to facilitate military missions. Therefore, researchers paid less attention to UAV restrictions, such as travel time or distance, due to the sufficient fuel storage of military UAVs. Shima and Schumacher [12] posed a problem that assigns multiple UAVs to simultaneously perform cooperative tasks on consecutive targets. A team of UAVs acts as a sensor and a communication network to cooperatively track and attack moving targets on the ground. Zeng et al. [13] developed a nonlinear model to allocate and aggregate the available UAVs considering mission synchronization at a battlefield. Some researchers have investigated the routing issue of capacitated UAVs. In this case, the maximum flight time of UAVs is limited by fuel. Weinstein and Schumacher [14] suggested the capacitated UAV routing problem with a time window constraint. In the study, each UAV had its own maximum travel time, and tasks were defined with their locations, service times, and time windows. A mathematical optimization model was developed to find an optimal schedule for UAVs. Kim et al. [15] considered a problem with multiple tasks and UAVs with capacity limitations. A mathematical model was proposed, and two situations were considered, as follows: Whether a UAV returned or not. Alidaee et al. [16] proposed a mathematical model for real-time UAV scheduling and flight path selection. The proposed model was inspired by Kim et al. [15] and it enhanced the computational efficiency by constructing a new model using a smaller number of decision variables and constraints. Guerriero et al. [17] also addressed a UAV routing optimization problem with the rolling horizon concept to address dynamic situations. In other words, the problem allows cases where UAVs are not initially located at the depot, thereby enabling real-time scheduling based on the current location of the UAVs. The above studies addressed an embryonic routing issue of UAVs and some of them included limited UAV flight durations. However, the above studies only considered the case of non-persistent UAV routing. That means, if a UAV returns to the depot, the service or mission terminates. A persistent operation that provides a continuous service after replenishment has not been addressed.
Since the 2010s, with the development of technologies for commercial UAVs, researchers have paid more attention to the use of commercial UAVs. In the use of commercial UAVs, persistence is a critical factor that must be addressed. Due to the limited battery capacity and transport ability, the flight time and loadable products for a commercial UAV are extremely restricted. As a consequence, consideration on the persistent and capacitated UAV routing should be addressed to derive realistic UAV schedules for commercial uses. Sundar and Rathinam [18] suggested a mathematical model and algorithm for a persistent and capacitated UAV routing problem. The study considered refueling depots, as a UAV visits refueling depots for refueling and conducts missions persistently. However, the proposed model and algorithm were developed for a single UAV route. Troudi et al. [19] suggested a capacitated UAV routing problem that incorporates the battery charging issue. Homogeneous UAVs were considered, and each UAV can serve multiple delivery orders based on a single depot system. Liu et al. [20] proposed two-stage decision models for UAV fleet deployment and planning. Stochastic demands and multi-type delivery services were considered. Some researchers were interested in routing multiple and capacitated UAVs for persistent operations. Those authors suggested the use of multiple sharable depots. In this situation, UAVs can visit any depots in the field of operations and replenish their consumables. Afterwards, they can continue their services or missions persistently. Kim et al. [21] introduced the problem of multiple UAVs with multiple sharable depots. A mathematical model and genetic algorithm were proposed and tested for the large-size implementation. Song et al. [22] extended the above studies for real-time uses. A mathematical model that considers the current location and the battery and production information was suggested to derive UAV routing schedules in real time. A rolling horizon approach was employed, and a sequential task assignment heuristic was developed. Song et al. [23] extended the above mathematical model to reflect the effect of cargo weight on the flight ability and derive realistic UAV routing schedules for logistic services.
2.2. Sustainable VRPs
Now we turn our attention to sustainable vehicle routing problems (VRPs). VRPs that have additional attention on energy consumption are called green VRPs (GVRPs) [24,25]. A comparative study of the GVRP literature can be found in Poonthalir and Nadarajan [26]. GVRPs aim to optimize routes and they also consider environmental issues and related financial costs. Similarly, pollution routing problems (PRPs) consider a vehicle speed as a decision variable to reduce pollutant emissions [27]. Lin et al. [28] summarized various types of problems and their variants in the field of GVRPs and PRPs, and Chiang et al. [25] outlined the research trend of GVRPs. GVRPs usually set the objective to reduce the total travelling distance of vehicles since it is known that CO2 emissions and fuel consumption are proportional to the travelling distance. Besides the travelling distance, various factors are known to be influential on fuel consumptions [29]. A methodology for calculating transport emissions and energy consumption (MEET) [30] was provided using various factors, such as vehicle miles traveled, vehicle speed, load weight, and road gradient. Naderipour and Alinaghian [31] presented a comprehensive model modified to calculate pollution emissions more precisely in VRPs. As research on GVRP progresses, various factors including the travelling distance are considered in mathematical models. Kara et al. [32] presented an energy maximizing VRP (EMVRP), a variant of capacitated VRP (CVRP), which considers the load of a vehicle as well as the travelling distance. Later, the speed of vehicle was considered by Kuo [33] and Kuo and Wang [34] included the payload weight in addition to the speed. The speed of vehicle is also dependent on the degree of congestion of a route and, thus, traffic congestion was considered in their mathematical model. This type of problems is called time-dependent VRP (TDVRP). The vehicle speed in a TDVRP is not constant, but dependent on the departure time [35]. An emission-based TDVRP is called E-TDVRP, which includes travel time, fuel, and CO2 emissions [36]. Jabali et al. [36] presented a framework to model CO2 emissions in a TDVRP. Zhou and Lee [37] developed a TDVRP to minimize greenhouse gas emissions. A variety of factors such as three-dimensional customer locations, gravity, vehicle speed, vehicle operating time, vehicle capacity, rolling resistance, air density, road grade, and inertia were considered to estimate greenhouse gas emissions. Recently, Shen et al. [38] proposed a TDVRP that considers the driver’s salary and penalty costs in addition to fuel costs and carbon emission trading costs. Shen et al. [38] named it a low-carbon multi-depot open vehicle routing problem with time windows (MDOVRPTW). Open VRP has two kinds of vehicles, as follows: Company-owned and rental. Reverse logistics (the definition can be found in Dekker et al. [39]) was also considered as a kind of GVRP. However, a reverse logistics problem that considers pollution emissions has not been studied yet. Even though an approximation of the average energy and battery costs per kilometer for drones was proposed by D’Andrea [40], there is little research about the impact of UAVs on the environment. A possible reason is that UAVs have not yet been actively deployed in the delivery industry. As another field of VRP research that studies the environment, there are VRPs using alternative fuel vehicles (e.g., electric vehicles). Schneider et al. [41] and Lin et al [42] presented an electric VRP (EVRP). A VRP that uses a mixed fleet of electric vehicles and conventional (internal combustion engine) commercial vehicles was considered by Goeke & Schneider [43]. Recently, Macrina et al. [44] presented a GVRP with mixed vehicle fleets.
Recently, there have been studies on comparing the sustainability of UAVs with that of other transport, e.g., GVs. Goodchild and Toy [45] made a large-scale experiment considering real-world operations in Los Angeles region, and found the advantages of adopting UAVs in terms of reducing CO2 emissions. However, they did not address the VRP issues, such as generating optimal routes. Coelho et al. [46] suggested a multi-objective green UAV routing problem. The total travelling distance, total delivering time, number of UAVs used, maximum speed of UAVs, makespan, and total amount of necessary energy were simultaneously optimized based on the multi-objective optimization model. However, estimation of CO2 emissions was not taken into account. Chiang et al. [25] compared a GV-alone system and a GV-along-with-UAV system in terms of CO2 emissions and related costs when delivering goods to customers. Dukkanci et al. [47] presented a drone delivery problem that minimizes the total operational costs, which includes energy consumption during the delivery. Their system uses traditional delivery vehicles (GVs) as launch points for drones, which is also a GV-along-with-UAV system. Park et al. [48] compared drone and motorcycle deliveries of pizzas in rural and urban areas in terms of greenhouse gas emissions and exhausted particulates. The drone delivery as well as the motorcycle delivery have one destination from the departure point and, thus, neither multi-hopping of drones nor consideration of the travel route for both drones and motorbikes is necessary. Our work compares UAV-alone and GV-alone delivery systems to serve the same set of customers. We take into account the optimal delivery routes of each system, which reflects each system’s characteristics, such as a maximum weight to carry and a maximum trip travelling distance. The comparison is performed by means of CO2 emissions in each system’s optimal delivery scheme, which includes delivery routes and vehicle (GV or UAV) operations. Using this approach, we can directly and quantitatively compare two different logistic systems.
3. System Description and Methodologies
3.1. System Description
A quantitative comparison needs to be performed under the same systemic situation. In this study, the delivery schedules of UAVs and GVs were independently derived based on the same depot specifications and the same customer information. A proposed VRPMSDMT is able to independently obtain UAV and GV delivery schedules using different UAV and GV information, such as vehicle speed and loadable capacity, as input data. There are number of depots, number of delivery vehicles (UAVs or GVs), and number of customer delivery tasks. Delivery vehicle is characterized by its initial location (depot), travel speed (), maximum travelling distance (), and loadable capacity (). Customer is randomly distributed across the service area, and characterized by its location, demand quantity (), service process time (), and service time window ( and ). As a consequence, we obtain the delivery schedules of capacitated (for both travel distance and loadable product) delivery vehicles to serve customers with demands, specific process (service) times, and time window constraints. Under such situations, Phase I presents a VRPMSDMT that we proposed to obtain the delivery schedules of UAVs and GVs. Based on the system parameters and the result of Phase I, an environmental comparison between UAV and GV delivery logistics is performed in Phase II. Please refer to the following subsections for the details of Phase I and II.
3.2. Research Approaches
3.2.1. Phase I: Mathematical Optimization with Multiple Depots & Trips
Vehicle routing problems (VRPs) have been investigated since 1950s, and there are many variants of VRPs to obtain the delivery routes of vehicles. Presently, the use of UAVs for delivery services draws a great deal of interest due to the efficiency and economics of the UAV logistics. Leading logistics companies are investigating the use of UAVs and interesting applications are emerging. However, there are fundamental constraints behind a promising future of commercial UAV services. A commercial UAV has an extremely limited flight time and loadable capacity. Therefore, to provide a proper and timely UAV delivery service, UAVs should often visit depots to replenish their consumables, such as batteries and goods. To support these UAV behaviors and to provide persistent delivery services, we need a state-of-the-art mathematical model (VRPMSDMT) that allows multiple UAV trips using multiple sharable depots.
As stated in the literature review, diverse mathematical optimization models were developed to derive UAV schedules. However, those approaches are not suitable for dealing with persistent UAV services for the following reasons. First of all, those approaches do not allow multiple trips of multiple UAVs (see [12,13,14,15,16,17,18,49,50]). In other words, the mathematical models consider a single trip of a vehicle. In reality, a commercial UAV should be persistent through an iterative process of depot visits for fuel and deliverable replenishments. However, this persistence cannot be achieved using the previous mathematical models. Second, even though a target delivery area is usually large and vast, the previous mathematical models postulate that UAVs must start their services from their home depots and return to the home depots after services (see [12,13,14,15,49,50]). This home depot dependency limits the service flexibility and is not suitable for providing logistic services in a large area. In our mathematical model, UAVs freely visit any depots located in their service areas and replenish fuel and deliverables. Therefore, to develop a flexible and persistent delivery schedule of UAVs, multiple trips with multiple sharable depots are essential to deliver goods successfully [21,23,51]. In Phase I, a VRPMSDMT is adopted to obtain the delivery schedules of the vehicles (UAVs or GVs) wherein the VRPMSDMT allows multiple trips with multiple sharing depots. This is a prerequisite for persistent UAV logistic service and makes the delivery schedules realistic.
3.2.1.1. Notation
| System Parameters | ||
| i,j | : | Indices for customer tasks; |
| : | Index for depots; | |
| : | Index for delivery vehicles; | |
| : | Index for multiple trips; | |
| : | Number of customer tasks; | |
| : | Number of delivery vehicles in the system; | |
| : | Number of depots; | |
| : | Maximum number of trips per delivery vehicle during the time horizon; | |
| : | Large positive number; | |
| : | Location (latitude, longitude) of task ; | |
| : | Distance () from task (depot) i to task (depot); | |
| : | Maximum travelling time (minutes) of vehicle ; | |
| : | Loadable capacity () of vehicle ; | |
| : | Travel speed of vehicle ; | |
| : | Initial depot of vehicle ; | |
| : | Demand for task ; | |
| : | Processing time of task or replenishment time at depot ; | |
| : | Earliest start time of task ; | |
| : | Latest start time of task . | |
| Sets | ||
| ≔ | , set of tasks; | |
| ≔ | , set of start depots; | |
| ≔ | , set of end depots; | |
| ≔ | , set of all tasks and depots; | |
| ≔ | , set of vehicles; | |
| ≔ | set of delivery trips. | |
| Decision variables | ||
| : | Binary decision variable, equal to 1 if vehicle processes task or refuel/reload at depot after processing task or refuel/reload at depot , during the rth trip; 0, otherwise; | |
| : | Binary decision variable, equal to 1 if is task is assigned to vehicle during its rth trip; 0 otherwise; | |
| : | Real number decision variable, start time of task by the rth trip of vehicle . | |
Please note that each depot has two indices to distinguish the roles when a vehicle starts a trip from the depot and ends a trip at the depot. This distinction allows each vehicle to share multiple depots.
3.2.1.2. Mathematical Model
Based on the notations introduced in Section 3.2.1.1, a mixed integer linear programming (MILP) is proposed to obtain delivery schedules of UAV and GV. The MILP allows multiple sharable depots and multiple trips for each vehicle. Depending on the systemic parameters of UAV or GV logistics, the MILP can obtain a delivery schedule of UAV or GV logistics to serve the same customers for both scenarios. As a consequence, the result of the model in Phase I provides the basis for an environmental comparison of two delivery systems by obtaining two different delivery schedules of UAVs and GVs for the same service requests.
An objective function of the MILP is to minimize the total travelling distance for the multiple trips of delivery vehicles. In an environmental evaluation of vehicle routes, the total travelling distance is an important measure because more travelling distance causes more air pollutants. Therefore, to minimize the air pollutants, vehicles should travel to minimize the total travelling distance. Equation (1) shows the objective function of the MILP, as follows:
Equations (2) to (9) are used to determine delivery schedules, assigning delivery tasks to vehicles. Equation (2) ensures that each vehicle should start its first delivery trip from the depot where the vehicle is initially located. Equation (3) indicates that each vehicle moves to a customer (or an end depot in case of an idle vehicle) from a start depot. Equation (4) guarantees that each vehicle should finish its trips at an end depot. Multiple trips of each vehicle are linked via equation (5). By this equation, if vehicle finishes its rth trip at depot in , its (r+1)th trip should start at depot in . Note that depots in , and in indicate the same depot. Equation (6) ensures that a vehicle does not finish its trip at a task location and Equation (7) ensures that a vehicle does not finish its delivery trip at a start depot. Equation (8) states that all tasks should be served and Equation (9) links decision variables and .
Now we investigate Equations (10) to (13), focusing on a start time of task . Equation (10) states that the end time of vehicle ’s rth trip is equal to the start time of its (r+1)th trip. Equation (11) determines the start time of sequential tasks and considering the task processing time and travel time between the two tasks. Equation (12) guarantees that if task is not assigned to the rth trip of vehicle , the value of the corresponding decision variable becomes zero. Equation (13) describes the time window constraint of this study.
Equations (14) and (15) state that each delivery trip of a vehicle is limited by the maximum travel distance and loadable capacity. Equations (16) to (18) declare the decision variables of the mathematical model.
The mathematical model obtains UAV and GV delivery schedules, respectively, with specified vehicle input data, such as , , and . The delivery schedules (i.e., UAV and GV delivery schedules) are compared in Phase II.
3.2.2. Phase II: Environmental Analysis
This section shows how to measure and compare the sustainability of the two following alternatives: UAV-alone and GV-alone systems. As in the paper of Chiang et al. [25], we use CO2 emissions as a sustainability measure. It is known that the CO2 emissions for vehicles are proportional to the travelling distance and Chiang et al. [25] estimate them using the total travelling distance multiplied by the weighted average emission rate of the vehicles (WAER). Here, WAER is a speed-dependent weight parameter provided by Goodchild and Toy [45]. Chiang et al. [25] suggested adding the speed effect of vehicles on the travelling distance for the CO2 emission calculation. We use the same formula with Chiang et al. [25] for GVs. We set the WAER value for all vehicles to 0.6814 kg per kilometer (1.096575 kg per mile) assuming the speed of truck is fixed at 60 km/h (37.5 mi/h). The value was obtained using the linear interpolation based on Goodchild and Toy [45].
In the case of UAVs, the travelling distance and speed do not affect the CO2 emissions directly, because they use electricity. Instead, two different measures are introduced, as follows: The amount of CO2 emitted at power generation facilities per watt-hour (Wh), denoted by PGFER, and the average energy requirement of UAVs in Wh per kilometer (AER). The amount of CO2 emitted by UAVs per one kilometer can be obtained by PGFER times AER. Goodchild and Toy [45] also discussed the estimation of PGFER and AER. Since PGFER does not depend on the specification of GVs or UAVs, we use the same value 3.77 × 10−4 per Wh as in Chiang et al [25]. AER is mainly determined by the specification of a UAV, and we assume that our UAVs are similar to those of Chiang et al. [25]. Thus, AER in this study is set to 2.0712 Wh per kilometer (3.333 Wh per mile).
4. Case study
4.1. Case Study Description
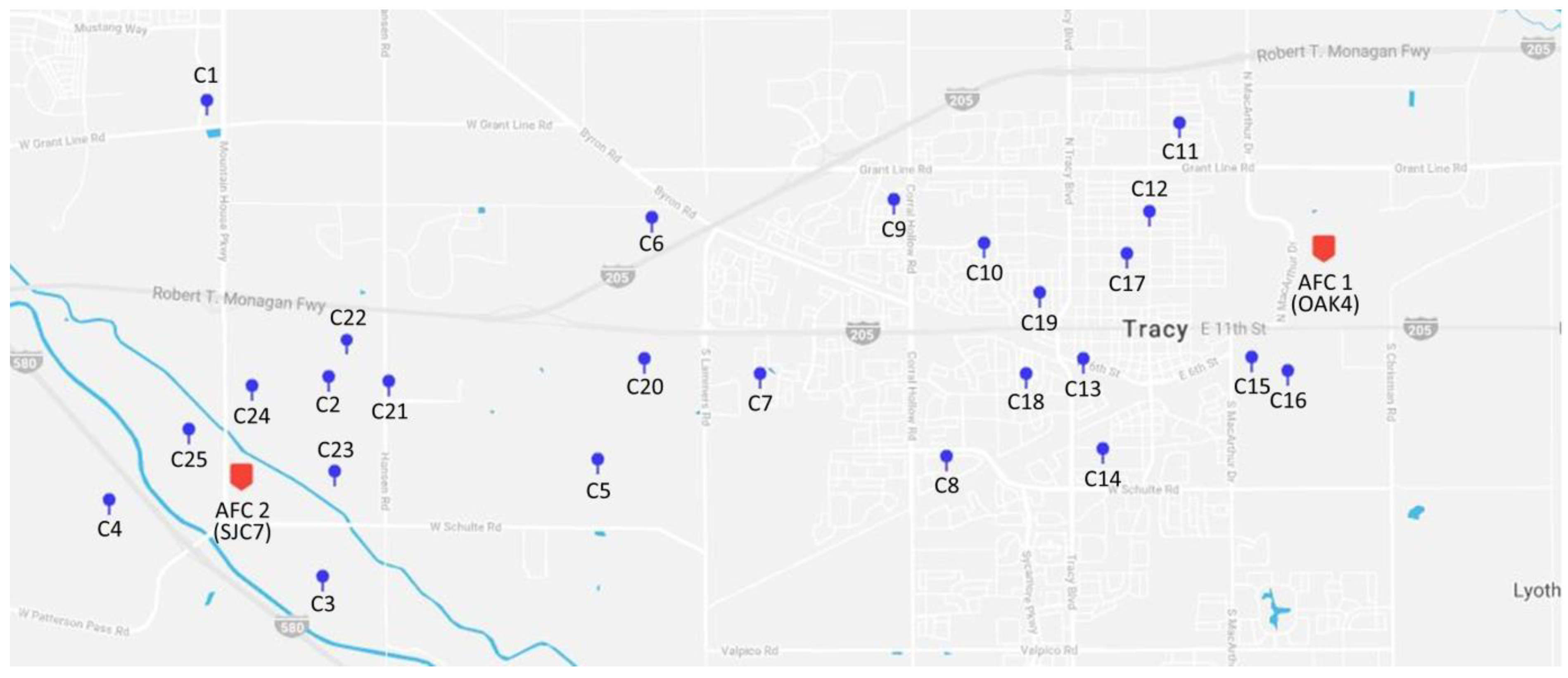
To validate the methodologies in this study and investigate the sustainability of UAV logistics, we present a realistic case study. Amazon is a leading company that actively tests and introduces UAV logistic services. Recently, Amazon revealed their new delivery drones and announced that their UAV delivery services will be implemented within months [52]. According to the description of their UAV delivery services, called Prime Air, UAVs take off from the Amazon Fulfillment Centers (AFCs) and provide delivery services to nearby customers. The case study deals with the actual Amazon AFCs and virtual nearby customers. Figure 1 graphically shows the two AFCs (OAK4 and SJC7) in Tracy, CA, USA and 25 customers (between 14:00 p.m. and 16:00 p.m.) near the AFCs. The Appendix A provides detailed descriptions for the locations (latitude and longitude), demand quantity, and time windows. With the same AFCs and customer information, delivery schedules of UAVs and GVs were obtained by phase I, respectively. The environmental effect of UAV logistic services is investigated in phase II. For the case study, we solve the mathematical model using CPLEX 12.4 on a personal computer with Intel i5-4460 CPU and 8 GB RAM.
Figure 1.
Graphical information of the case study.
4.2. Result of Phase I
Delivery schedules of UAVs and GVs were obtained, respectively, by solving the mathematical model in Phase I with the case study data inserted. The UAV and GV delivery schedules to serve the same set of customers can lead to a quantitative comparison between the two types of delivery services. For the UAV service, , , and were set to (30, 2.2, 80) in line with the Amazon’s new delivery services [52]. For the GV service, those were set to (300, 300, 60). Table 1 and Table 2 summarize the delivery schedules of UAVs and GVs to serve 25 customers with 2 AFCs.

Table 1.
Result of phase I: UAV delivery schedule.

Table 2.
Result of phase I: GV delivery schedule.
For the UAV service, 4 UAVs (two for each AFC) were used and the maximum number of trips () was set to 2 for each UAV. UAV 1 and 2 were initially located at AFC 1, while UAV 3 and 4 were located at AFC 2. All UAVs served 25 customers, sharing AFCs efficiently. For example, UAV 3 starts its second journey from AFC 2, serves customer 6, 7, 9, 10, and 17 and finishes its service at AFC 1. The total travelling distance of UAVs was 56.270 km and the computation time was 653.71 seconds.
For the GV service, two GVs are used (one for each AFC). Due to the sufficient maximum travelling time and loadable capacity of GVs, a second journey is not necessary for this case study. The total travelling distance of GVs was 47.633 km and the computation time was 6.34 seconds. The sufficient maximum travelling time and loadable capacity allow the algorithm to obtain an optimal solution in a short computation time. In addition, such benefits (i.e., sufficient maximum travelling time and loadable capacity) help the GVs reduce the total travelling distance because frequent replenishments of fuel and delivery products are not required.
In summary, due to the limited flight duration and loadable capacity of UAVs, the UAV service requires more travelling distance than the GV service. However, since UAVs consume electrical energy, it is uncertain if the long travel distance uses more CO2. Phase II analyzes the environmentally friendliness of the UAV service, based on the results of phase I.
4.3. Result of Phase II
The amount of CO2 emissions for each delivery unit was computed using the set of parameters described in Section 3.2.2 and the results in Section 4.2. If the goods are delivered by UAVs only, of CO2 are emitted. In case of GVs only of CO2 are produced. That means the GV-alone delivery system gives off 746 times more CO2 than the UAV-alone system. It is evident that CO2 emissions per kilometer of a UAV is significantly smaller than that of a GV.
A sensitivity analysis of AER values on the dominance of UAVs over GVs along with GV-speed was performed. In the case study above, the AER value for UAVs is 2.0712 Wh/km, which was obtained from Goodchild and Toy [45]. In addition, the speed of ground vehicles was set to 60 km/h. In that instance, UAVs significantly outperformed GVs in terms of the amount of CO2 emissions. Table 3 summarizes how GVs produce CO2 as their speed increases from 40 to 80 km/h and in each case, critical AER values by which UAVs maintain the dominance over GVs in producing CO2 are given. When we compute the CO2 emissions of GVs in Table 3, the optimal route obtained from Phase I stays the same. That means the table shows the varying CO2 emissions by the speed of vehicles. The threshold of AER values, however, was much larger than the original case regardless of the speed of GVs. Allowable AER values (i.e., AER values that UAVs may have, to use the same amount of CO2 as GVs) were more than 683 (, when the GV speed is 80 km/h) times the original case. A UAV becomes less sustainable than an 80 km/h GV if a UAV consumes more than 683 times the amount of electric energy used for UAVs in the case study.

Table 3.
Changes in CO2 emissions with the speeds of GV change.
Many researchers anticipate that UAV logistics is environmentally friendly and the UAV service is in the limelight as the next generation logistics system. However, no quantitative comparison has been conducted on the eco-friendliness of UAV services compared to that of GV services under the same condition. Through phase I, delivery schedules of UAVs and GVs were obtained to serve the same set of customers. Phase II quantitatively analyzed the eco-friendliness of the UAV service using the result of phase I. In our case study, it is found that UAV service is at least 683 times eco-friendlier than GV logistics. Throughout phases I and II, we provide a quantitative analysis on eco-friendliness of the UAV service and suggest a future guideline to investigate the true sustainability of UAV logistics.
5. Concluding Remarks
In this study, we investigated how environmentally friendly UAV delivery service is compared to GV delivery service. To perform such a comparison, we first obtained an optimal delivery schedule that minimized the total travelling distance for each service. Since there are different levels of fuel and loadable capacity restrictions for the UAV and GV delivery services, delivery routes for the two services are also different. UAVs need more fuel replenishments and have a lower weight capacity, which causes more hops than GVs. We present a new mathematical model to obtain an optimal delivery schedule for each delivery service under such restrictions. Based on the optimal delivery information obtained, CO2 emissions of the UAV-alone and GV-alone delivery systems are computed. The case study found that the GV-alone delivery generated at least 683 times more CO2 than the UAV-alone delivery in all ranges of the GV speeds tested.
We stress the implications and limitations of this study. The presentations in this study answer the following question: How many UAVs are environmentally friendly if the UAV delivery system is implemented in the logistics industry. Since UAVs, compared to GVs, have different limitations and restrictions for delivering goods, the question must be addressed from the understanding of different characteristics of UAVs and GVs, and their resultant delivery schemes. The two-phase methodology proposed in this study is needed to provide different routes for the two different types of vehicles and to analyze their sustainability in terms of the CO2 emissions of their travels. We believe the methodology and the results of this study provide a guideline to further investigate the true sustainability of UAV logistic services and facilitate the use of UAVs for delivery services. There are, however, two limitations in this study. First, we focused on CO2 emissions only during the vehicle’s travel. It is easy to think that manufacturing and disposal processes of vehicles (including batteries) also cause greenhouse gas (GHG) emissions. Second, this study postulates a specific scenario that uses stationary depots and one type of vehicle (UAVs or GVs) in each delivery system. It is possible and natural to mix the two types of vehicles in one delivery system. Those limitations of this study are expected to be overcome by future research.
We contemplate future research based on the limitations of this research. First, it may be possible to additionally consider greenhouse gas (GHG) emissions during manufacturing and disposal processes of UAVs and GVs. Stolaroff et al. [53] presented the life cycle GHG emissions represented by CO2-equivelent per package delivered by UAVs and GVs. They consider CO2-equivelent emissions during all stages of a vehicle’s life cycle, but do not consider the distance a vehicle should travel for each service. Since the battery life of a UAV is much shorter than the engine life of a GV and the travelling distance of a UAV is longer than that of a GV, the dominance of UAV over GV CO2 emissions can be possibly weakened under the lifecycle assessment (LCA). Second, this sustainability analysis of the UAV delivery service can be applied to various types of logistic services. With respect to vehicle types, there is a UAV-GV combined logistic service. With respect to depot mobility, there exist movable depots that are different from stationary depots postulated in this study. Since various types of logistic systems with UAVs are being developed and tested, we believe that the sustainability analysis of those systems is also required. Even though there is a lack of the sustainable VRP literature so far, this paper may serve as a guideline that triggers research activities on the topic.
Author Contributions
This paper is the result of the joint work by all authors. J.E., B.D.S., and S.L. designed the methodologies. B.D.S. conducted the CPLEX experiment of the mathematical model. D.-E.L. conducted the CO2 emission analysis. J.E., B.D.S., and D.-E.L. wrote the original draft. S.L. and D.-E.L. supervised all research processes. J.E., B.D.S., S.L., and D.-E.L. reviewed and edited the final version of the manuscript.
Acknowledgments
The second author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government(2019R1F1A1060289). The third author was financially supported by Hansung University. The fourth author was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2017R1D1A3B03028784).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Detail information of Amazon Fulfillment Centers (AFCs) and customer nodes.
Table A1.
Detail information of Amazon Fulfillment Centers (AFCs) and customer nodes.
| Component | Latitude | Longitude | Ai (kg) | Ei (time) | Li (time) | Pi (min) |
|---|---|---|---|---|---|---|
| AFC 1 (OAK4) | 37.745554 | −121.405899 | − | − | − | 3 |
| AFC 2 (SJC7) | 37.724946 | −121.529487 | − | − | − | 3 |
| C1 | 37.758957 | −121.533522 | 0.5 | 14:05 | 14:08 | 2 |
| C2 | 37.733929 | −121.519634 | 1.0 | 14:10 | 14:15 | 1 |
| C3 | 37.715911 | −121.520369 | 0.3 | 14:20 | 14:26 | 1 |
| C4 | 37.722765 | −121.544745 | 0.3 | 14:23 | 14:28 | 1 |
| C5 | 37.726434 | −121.488956 | 1.1 | 14:25 | 14:30 | 2 |
| C6 | 37.748291 | −121.482774 | 0.3 | 14:30 | 14:36 | 2 |
| C7 | 37.734170 | −121.470416 | 0.4 | 14:34 | 14:40 | 1 |
| C8 | 37.726698 | −121.449134 | 0.8 | 14:38 | 14:45 | 1 |
| C9 | 37.749915 | −121.455130 | 0.4 | 14:43 | 14:48 | 1 |
| C10 | 37.745974 | −121.444830 | 0.5 | 14:48 | 14:53 | 2 |
| C11 | 37.756825 | −121.422498 | 0.2 | 14:53 | 14:57 | 1 |
| C12 | 37.748816 | −121.425940 | 0.2 | 14:58 | 15:04 | 1 |
| C13 | 37.735515 | −121.433507 | 0.7 | 15:05 | 15:09 | 2 |
| C14 | 37.727368 | −121.431281 | 0.4 | 15:10 | 15:15 | 2 |
| C15 | 37.735640 | −121.414277 | 0.6 | 15:13 | 15:18 | 1 |
| C16 | 37.734443 | −121.410023 | 0.2 | 15:17 | 15:22 | 2 |
| C17 | 37.745062 | −121.428390 | 0.2 | 15:21 | 15:24 | 1 |
| C18 | 37.734207 | −121.439899 | 0.7 | 15:26 | 15:29 | 1 |
| C19 | 37.741537 | −121.43835 | 0.4 | 15:30 | 15:34 | 1 |
| C20 | 37.735574 | −121.483496 | 0.3 | 15:37 | 15:41 | 2 |
| C21 | 37.733535 | −121.512674 | 0.2 | 15:43 | 15:46 | 2 |
| C22 | 37.737334 | −121.517482 | 0.2 | 15:45 | 15:50 | 1 |
| C23 | 37.725357 | −121.518890 | 0.5 | 15:50 | 15:54 | 1 |
| C24 | 37.733093 | −121.528331 | 0.4 | 15:53 | 15:57 | 1 |
| C25 | 37.729156 | −121.535539 | 0.6 | 15:56 | 16:00 | 2 |
References
- Banker, S.; Amazon and drones. Here Is Why it Will Work. Forbes Magazine. Available online: https://www.forbes.com/sites/stevebanker/2013/12/19/amazon-drones-here-is-why-it-will-work (accessed on 26 August 2019).
- Perlow, B. Amazon Completes 1st Drone Delivery. ABC News. Available online: https://abcnews.go.com/US/amazon-completes-drone-delivery/story?id=44185981 (accessed on 26 August 2019).
- Bryan, V. Drone Delivery: DHL ‘Parcelcopter’ Flies to German Isle. Reuters. Available online: www.reuters.com/article/us-deutsche-post-drones/drone-deliverydhl-parcelcopter-flies-to-german-isle-idUSKCN0HJ1ED20140924 (accessed on 26 August 2019).
- Teal Group. 2019 World Civil Unmanned Aerial Systems Market Profile & Forecast. Available online: http://tealgroup.com/images/TGCTOC/WCUAS2019TOC_EO.pdf (accessed on 26 August 2019).
- Business Insider. The Most Staggering Part About Amazon’s Upcoming Drone Delivery Service. Available online: https://www.businessinsider.com/cost-savings-from-amazon-drone-deliveries-2016-6 (accessed on 26 August 2019).
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Siebert, S.; Teizer, J. Mobile 3D mapping for surveying earthwork projects using an Unmanned Aerial Vehicle (UAV) system. Automat. Constr. 2014, 41, 1–14. [Google Scholar] [CrossRef]
- Carlsson, J.G.; Song, S. Coordinated logistics with a truck and a drone. Manag. Sci. 2018, 64, 3971–4470. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Song, B.D.; Lee, S. Truck-drone hybrid delivery routing: Payload-energy dependency and No-Fly zones. Int. J. Prod. Econ. 2019, 214, 220–233. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Shima, T.; Schumacher, C. Assignment of cooperating UAVs to simultaneous tasks using genetic algorithms. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 5829. [Google Scholar] [CrossRef]
- Zeng, J.; Yang, X.; Yang, L.; Shen, G. Modeling for UAV resource scheduling under mission synchronization. J. Syst. Eng. Electron. 2010, 21, 821–826. [Google Scholar] [CrossRef]
- Weinstein, A.; Schumacher, C. UAV scheduling via the vehicle routing problem with time windows. In Proceedings of the AIAA Infotech@ Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007; p. 2839. [Google Scholar] [CrossRef]
- Kim, Y.; Gu, D.W.; Postlethwaite, I. Real-time optimal mission scheduling and flight path selection. IEEE Trans. Autom. Control 2007, 52, 1119–1123. [Google Scholar] [CrossRef]
- Alidaee, B.; Wang, H.; Landram, F. A note on integer programming formulations of the real-time optimal scheduling and flight path selection of UAVs. IEEE Trans. Control Syst. Technol. 2009, 17, 839–843. [Google Scholar] [CrossRef]
- Guerriero, F.; Surace, R.; Loscri, V.; Natalizio, E. A multi-objective approach for unmanned aerial vehicle routing problem with soft time windows constraints. Appl. Math. Model 2014, 38, 839–852. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for routing an unmanned aerial vehicle in the presence of refueling depots. IEEE Trans. Autom. Control 2013, 11, 287–294. [Google Scholar] [CrossRef]
- Troudi, A.; Addouche, S.A.; Dellagi, S.; Mhamedi, A. Sizing of the drone delivery fleet considering energy autonomy. Sustainability 2018, 10, 3344. [Google Scholar] [CrossRef]
- Liu, M.; Liu, X.; Zhu, M.; Zheng, F. Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service. Sustainability 2019, 11, 3871. [Google Scholar] [CrossRef]
- Kim, J.; Song, B.D.; Morrison, J.R. On the scheduling of systems of UAVs and fuel service stations for long-term mission fulfillment. J. Intell. Robot. Syst. 2013, 70, 347–359. [Google Scholar] [CrossRef]
- Song, B.D.; Kim, J.; Morrison, J.R. Rolling horizon path planning of an autonomous system of UAVs for persistent cooperative service: MILP formulation and efficient heuristics. J. Intell. Robot. Syst. 2016, 84, 241–258. [Google Scholar] [CrossRef]
- Song, B.D.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Chiang, W.-C.; Li, Y.; Shang, J.; Urban, T.L. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Appl. Energy 2019, 242, 1164–1175. [Google Scholar] [CrossRef]
- Poonthalir, G.; Nadarajan, R. Green vehicle routing problem with queues. Expert Syst. Appl. 2019, 138, 112823. [Google Scholar] [CrossRef]
- Bektas, T.; Laporte, G. The pollution-routing problem. Transp. Res. B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of green vehicle routing problems: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- US Department of Energy. Fuel Economy Guide. Available online: http://www.fueleconomy.gov (accessed on 11 October 2019).
- European Commission. Directorate-General Transp. In MEET: Methodology for Calculating Transport Emissions and Energy Consumption; European Commission: Brussels, Belgium, 1999; ISBN 978-92-8286-785-3. [Google Scholar]
- Naderipour, M.; Alinaghian, M. Measurement, evaluation and minimization of CO2, NOx, and CO emissions in the open time dependent vehicle routing problem. Measurement 2016, 90, 443–452. [Google Scholar] [CrossRef]
- Kara, I.; Kara, B.Y.; Yetis, M.K. Energy minimizing vehicle routing problem. In Proceedings of the International Conference on Combinatorial Optimization and Applications, Xian, China, 14–16 August 2007; pp. 62–71. [Google Scholar]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Kuo, Y.; Wang, C.C. Optimizing the VRP by minimizing fuel consumption. Manag. Environ. Qual. Int. J. 2011, 22, 440–450. [Google Scholar] [CrossRef]
- Malandraki, C.; Daskin, M.S. Time dependent vehicle routing problems: Formulations, properties and heuristic algorithms. Transp. Sci. 1992, 26, 185–200. [Google Scholar] [CrossRef]
- Jabali, O.; Van Woensel, T.; De Kok, A.G. Analysis of travel times and CO2 emissions in time-dependent vehicle routing. Prod. Oper. Manag. 2012, 21, 1060–1074. [Google Scholar] [CrossRef]
- Zhou, Y.; Lee, G. A Lagrangian relaxation-based solution method for a green vehicle routing problem to minimize greenhouse gas emissions. Sustainability 2017, 9, 776. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Wang, S. Multi-depot open vehicle routing problem with time windows based on carbon trading. Int. J. Environ. Res. Public Health 2018, 15, 2025. [Google Scholar] [CrossRef]
- Dekker, R.; Fleischmann, M.; Inderfurth, K.; van Wassenhove, L.N. (Eds.) Reverse Logistics: Quantitative Models for Closed-Loop Supply Chains; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- D’Andrea, R. Guest editorial can drones deliver? IEEE Trans. Autom. Sci. Eng. 2014, 11, 647–648. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Lin, J.; Zhou, W.; Wolfson, O. Electric vehicle routing problem. Transp. Res. Procedia 2016, 12, 508–521. [Google Scholar] [CrossRef]
- Goeke, D.; Schneider, M. Routing a mixed fleet of electric and conventional vehicles. Eur. J. Oper. Res. 2015, 245, 81–99. [Google Scholar] [CrossRef]
- Macrina, G.; Pugliese, L.D.P.; Guerriero, F.; Laporte, G. The green mixed fleet vehicle routing problem with partial battery recharging and time windows. Comput. Oper. Res. 2019, 101, 183–199. [Google Scholar] [CrossRef]
- Goodchild, A.; Toy, J. Delivery by drone: An evaluation of unmanned aerial vehicle technology in reducing CO2 emissions in the delivery service industry. Transp. Res. Part D Transp. Environ. 2018, 61, 58–67. [Google Scholar] [CrossRef]
- Coelho, B.N.; Coelho, V.N.; Coelho, I.M.; Ochi, L.S.; Haghnazar, R.; Zuidema, D.; Lima, M.S.F.; da Costa, A.R. A multi-objective green UAV routing problem. Comput. Oper. Res. 2017, 88, 306–315. [Google Scholar] [CrossRef]
- Dukkanci, O.; Kara, B.Y.; Bektas, T. The Drone Delivery Problem. Available online: https://ssrn.com/abstract=3314556 (accessed on 10 January 2019).
- Park, J.; Kim, S.; Suh, K. A comparative analysis of the environmental benefits of drone-based delivery services in urban and rural areas. Sustainability 2018, 10, 888. [Google Scholar] [CrossRef]
- Kim, S.; Moon, I. Traveling salesman problem with a drone station. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 42–52. [Google Scholar] [CrossRef]
- Coutinho, W.P.; Battarra, M.; Fliege, J. The unmanned aerial vehicle routing and trajectory optimisation problem, a taxonomic review. Comput. Ind. Eng. 2018, 120, 116–128. [Google Scholar] [CrossRef]
- Song, B.D.; Kim, J.; Kim, J.; Park, H.; Morrison, J.R.; Shim, D.H. Persistent UAV service: An improved scheduling formulation and prototypes of system components. J. Intell. Robot. Syst. 2014, 74, 221–232. [Google Scholar] [CrossRef]
- Lee, D.; Amazon to Deliver by Drone ‘within Months’. BBC NEWS. Available online: https://www.bbc.com/news/technology-48536319 (accessed on 26 August 2019).
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nat. Commun. 2018, 9, 409. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).