1. Introduction
Maintaining a comfortable thermal environment for occupants in an indoor space is the most important goal of an heating, ventilation, and air conditioning (HVAC) system [
1]. In order to evaluate thermal comfort, many indices have been presented, including effective temperature (ET), operative temperature (OT), standard effective temperature (SET), and even a thermoregulation model [
2,
3]. In particular, the predicted mean vote (PMV) model proposed by Fanger [
4], applied to ASHRAE Standard 55 [
5], is the most widely used for evaluating thermal comfort. The PMV model is based on a mathematical equation and is limited in that it does not reflect the physiological characteristics of each occupant [
6]. Nonetheless, the PMV model is still the most-used model for thermal comfort evaluation and HVAC system control.
The PMV model evaluates thermal comfort by using six factors: air temperature, mean radiant temperature, relative humidity, air velocity, clothing thermal insulation, and metabolic rate. Among those six factors, the human factors, clothing thermal insulation and metabolic rate, are known to be difficult to measure. Accurate clothing thermal insulation can only be determined through precise measurements in the laboratory [
7]. However, since this process is laborious, major international standards provide a table established by measuring the thermal insulation of several clothing items in advance [
5,
8], which has been significantly adopted by industry and academia. In practice, one [
9,
10], two [
11,
12,
13,
14,
15], or three [
16] clothing ensembles have been assumed and the total clothing thermal insulation calculated by referring to the tables to evaluate thermal comfort or control an HVAC system based on the PMV model.
However, in reality, clothing ensembles vary individually and seasonally [
17,
18]. In addition, a clothing ensemble could be changed within a short period of time with an option of putting clothes on or taking them off. Accordingly, the conventional method that adopts a fixed representational clothing (clo) value—without consideration of a clothing ensemble value, dynamically changing over time—may contribute to causing errors in thermal comfort prediction [
19].
Evaluating the clo value dynamically is also important for energy savings. Newsham [
20] reported that increasing clothing flexibility could affect energy consumption. Lee and Schiavon [
21] showed that the energy analysis results for PMV model control could be incorrect when using a conventional method for applying 0.5 clo and 1.0 clo for the cooling and heating seasons, respectively.
Several recent studies have been conducted to predict clo values dynamically. De Carli et al. [
22] and Schiavon et al. [
11] constructed a model that predicts clo values based on the outdoor temperature at 6 a.m., because people mainly decide on their clothing ensemble according to the weather in the morning. However, these predictive models do not reflect the fact that occupants can change their clothing ensemble depending on the situation.
Some researchers used a heat balance model, rather than the outdoor temperature, to predict clo values in real time. M. Konarska et al. [
23] measured the skin temperature of each part of the human body and applied these temperatures to the heat balance model to calculate the clo value. Lee et al. [
24] and Miura et al. [
25] suggested a predictive model for evaluating the clo value by measuring several local skin temperatures and clothing surface temperatures using an infrared camera and calculating the heat balance equation. These studies showed the possibility of using a predictive model to estimate clo values in real time. However, since the heat balance model adopted in the predictive models discussed above depends on predefined computational formulas, they have a significant limitation in that they do not consider individual physiological characteristics, such as body mass index (BMI) [
26]. Previous studies have reported that the clothing thermal insulation predicted by the heat balance model was significantly different from the actual one [
27,
28,
29]. In addition, many studies of thermal comfort [
6,
30,
31,
32,
33] have proposed a more accurate model that predicts thermal comfort by using physiological factors.
In recent years, a data-driven approach has been actively used to evaluate personal thermal comfort by considering physiological factors [
34]. Jiang and Yao [
35] modeled the individual’s thermal sensation using the C-support vector classification algorithm, which is a type of data-driven method. They showed that the accuracy of the predictive model was above 89% against the measured data. Ghahramani et al. [
36] predicted the individual’s thermal comfort using infrared thermography of the human face and collected thermal comfort votes. Through statistical analysis, this study revealed that four points of the human face—front face, cheekbone, nose, and ear—played an important role in predicting personal thermal comfort. Recently, Choi and Yeom [
6] developed a data-driven thermal sensation prediction model as a function of local body skin temperatures. They showed that a combination of the waist, arm, and wrist (front), as well as BMI and gender, could be used to estimate overall thermal sensation with 95.87% accuracy. However, to the authors’ knowledge, there has not yet been an attempt to estimate clothing insulation using data-driven methods, not thermal comfort.
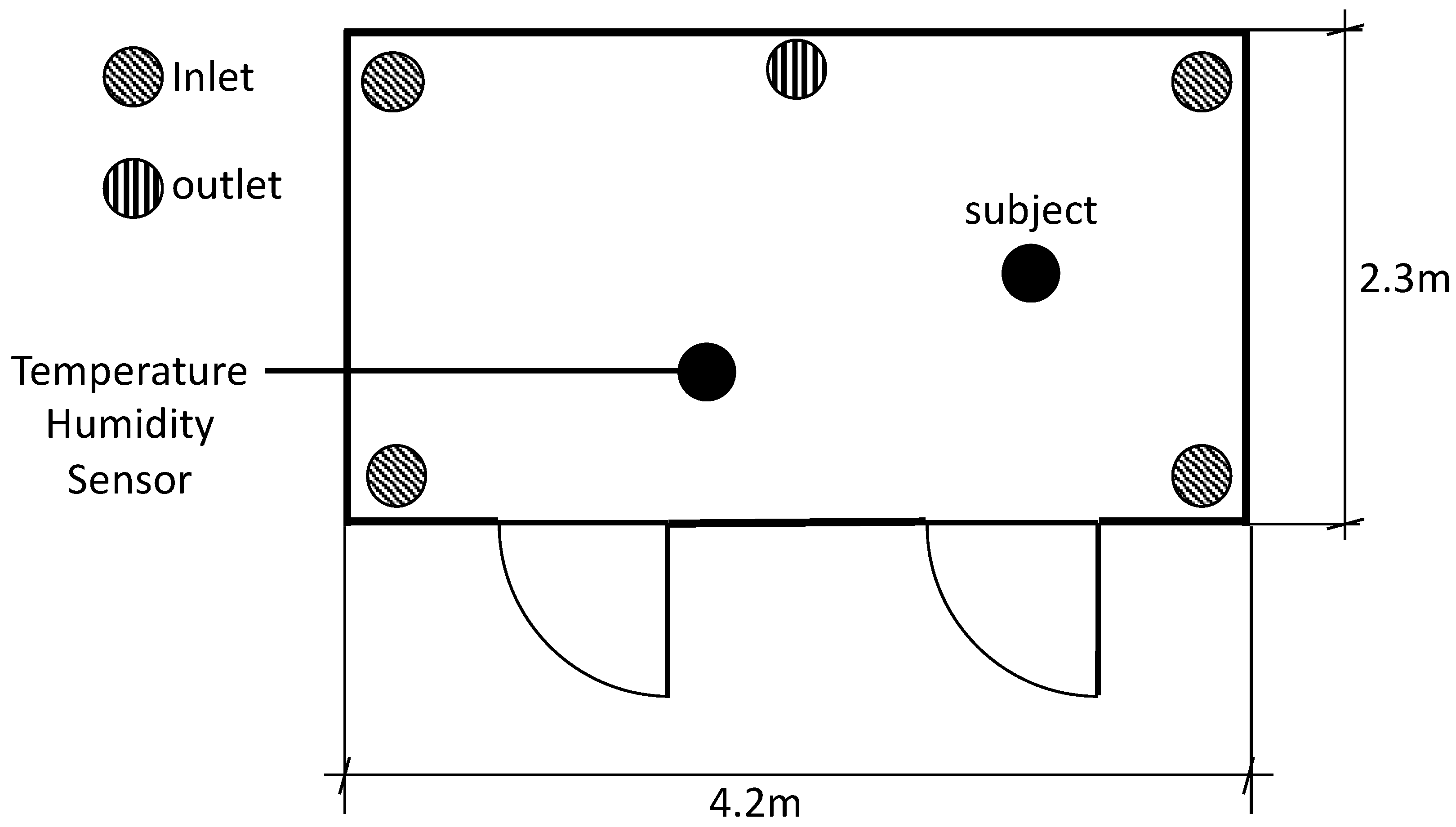
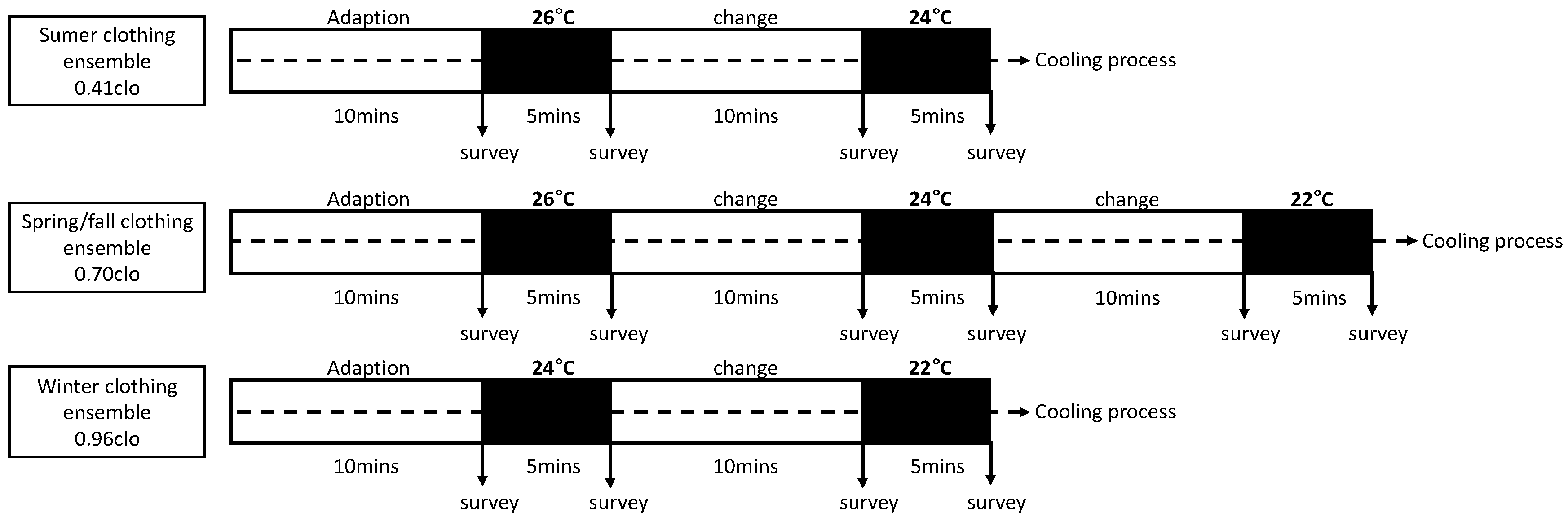
Thus, the purpose of this study was to establish a data-driven model that predicts the clo value with the consideration of individual physiological factors in real time. A series of experiments in an environmental chamber with multiple test participants were carried out to measure the skin and clothing surface temperatures of each subject. The environmental conditions and individual physiological data of the subjects were applied by data-driven methods.
4. Conclusions
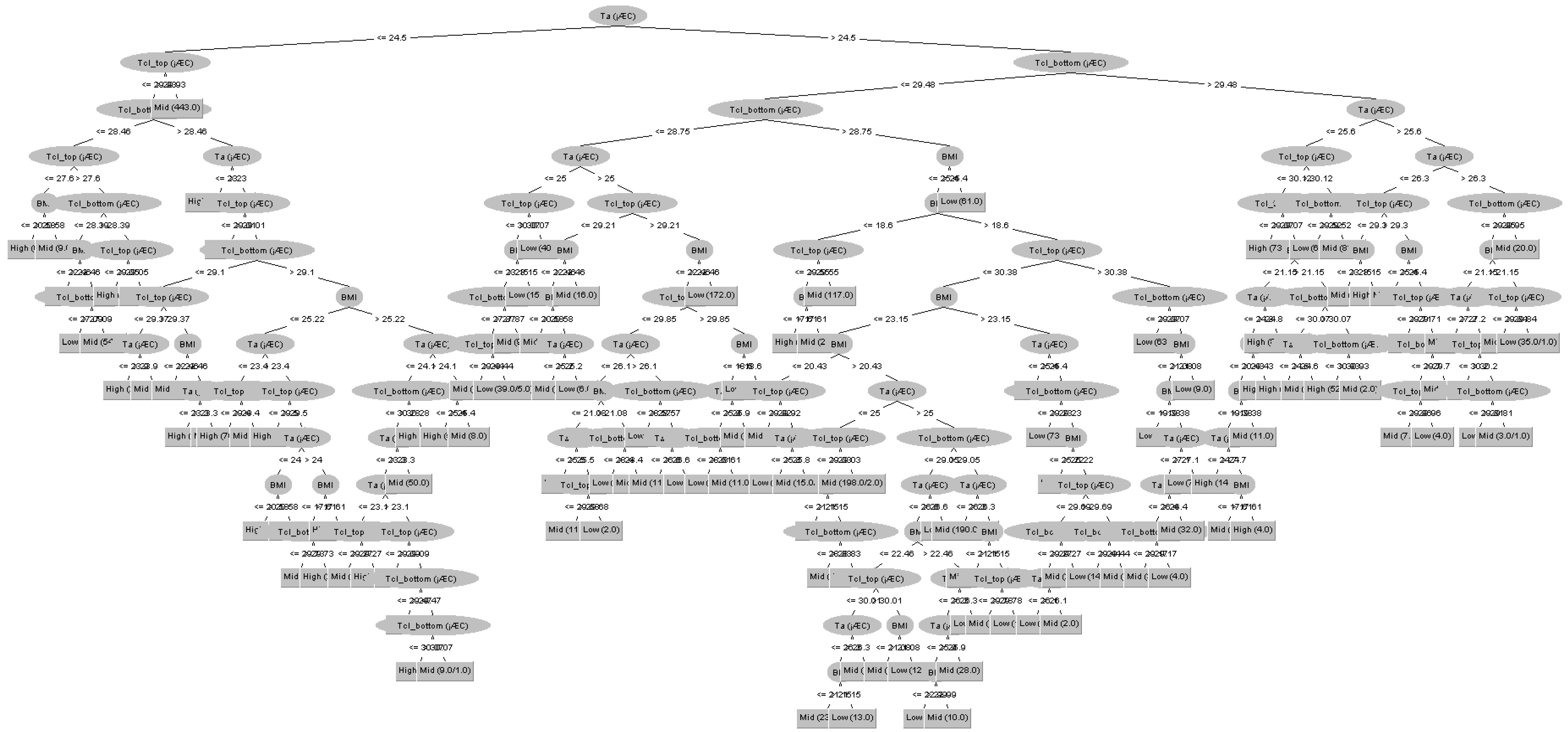
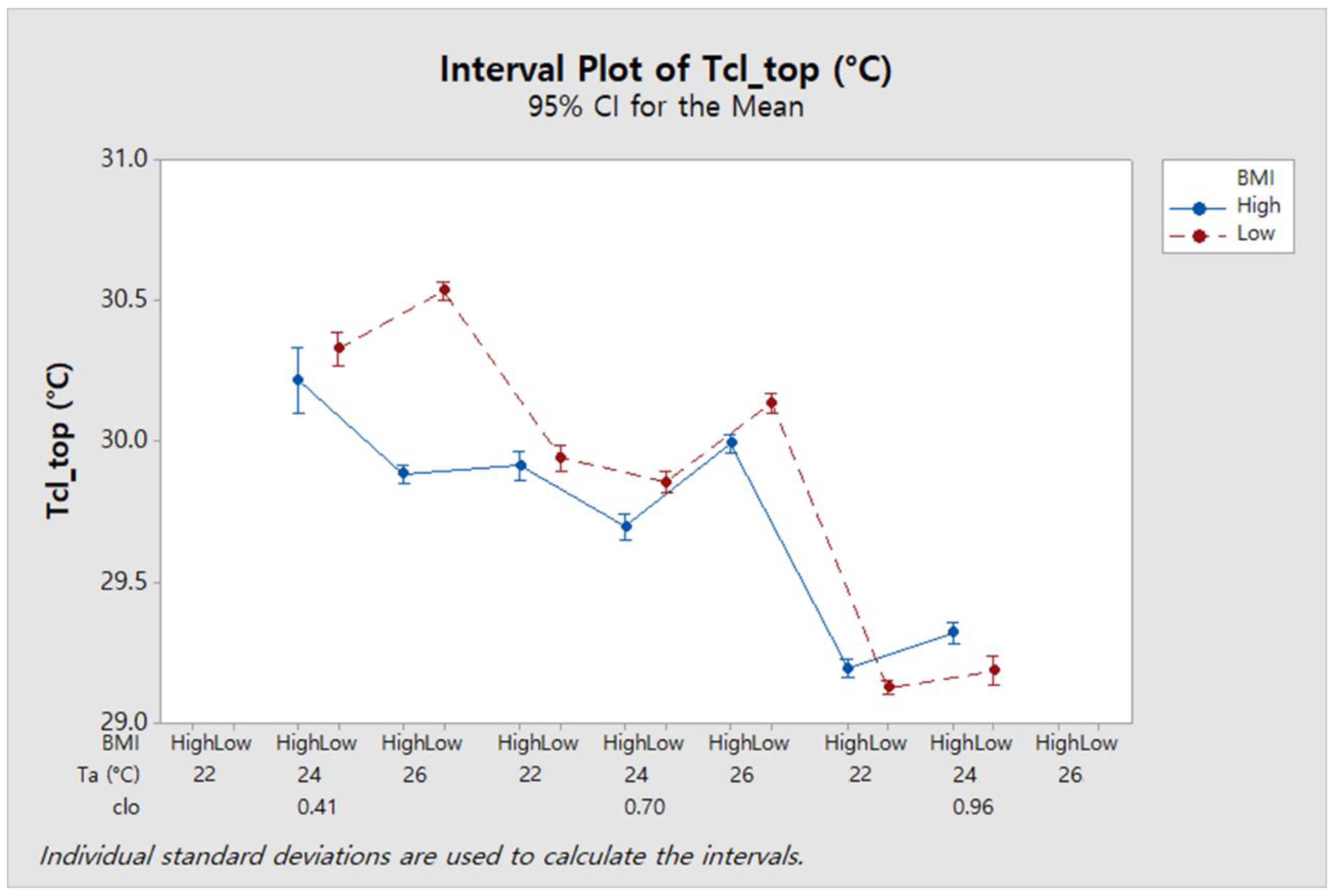
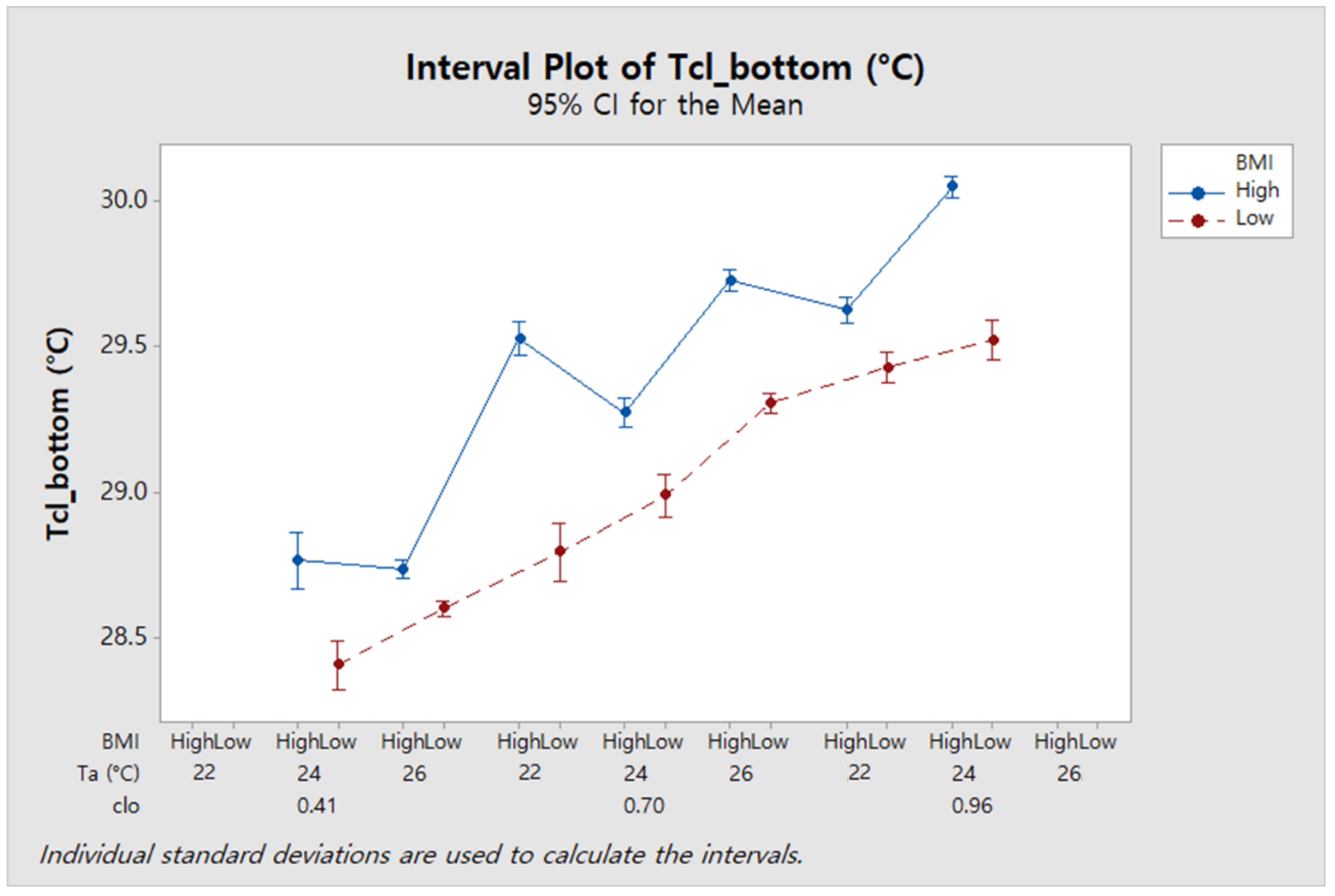
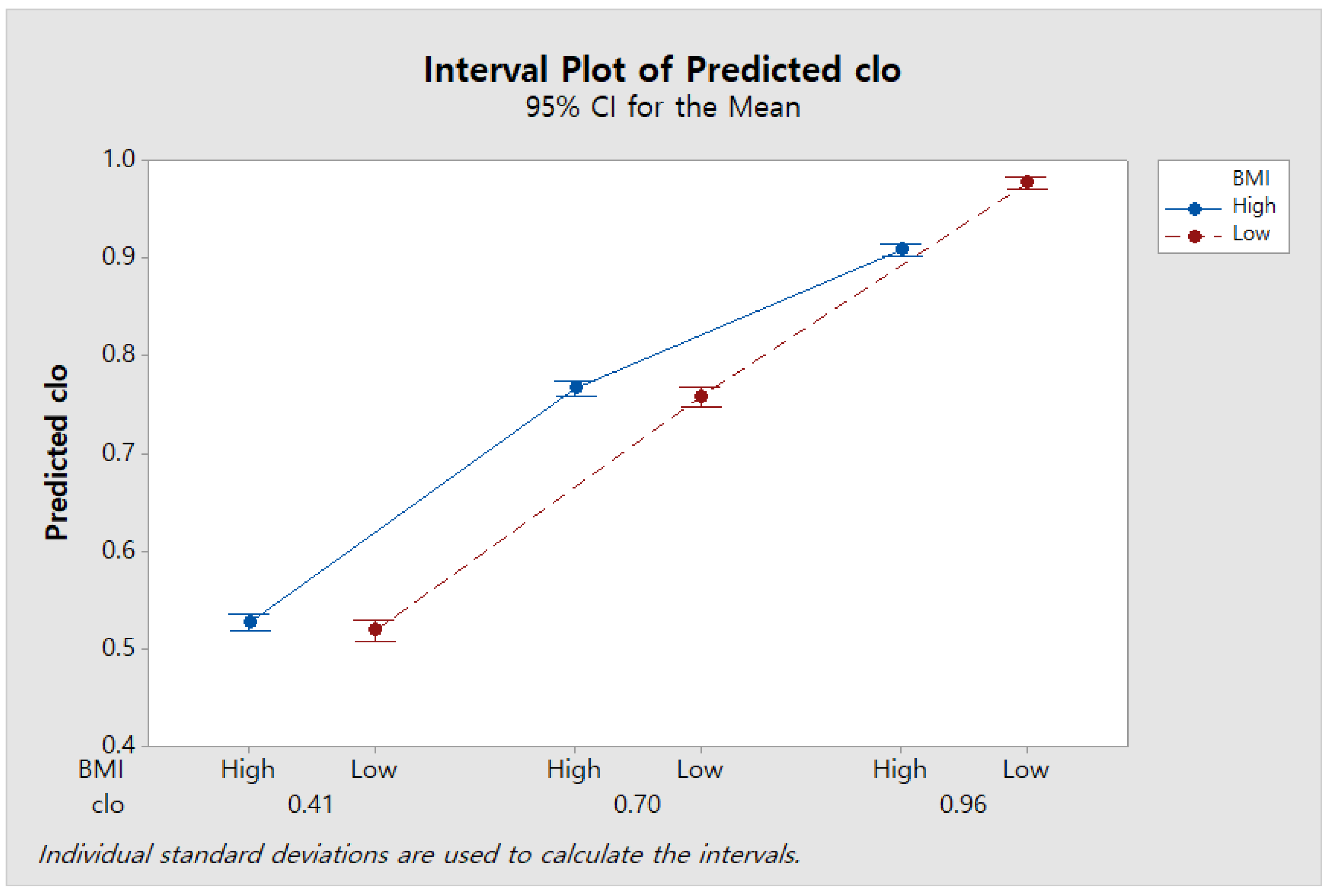
The clo value plays an important role not only in thermal comfort but also in energy saving. In this study, a predictive model that can predict the clo value in real time was developed. To this end, the environmental factors and individual factors of subjects were measured in various clothing conditions through the human experiment. The data obtained from the experiment were applied to the stepwise regression and decision tree algorithms. The results of this study are as follows.
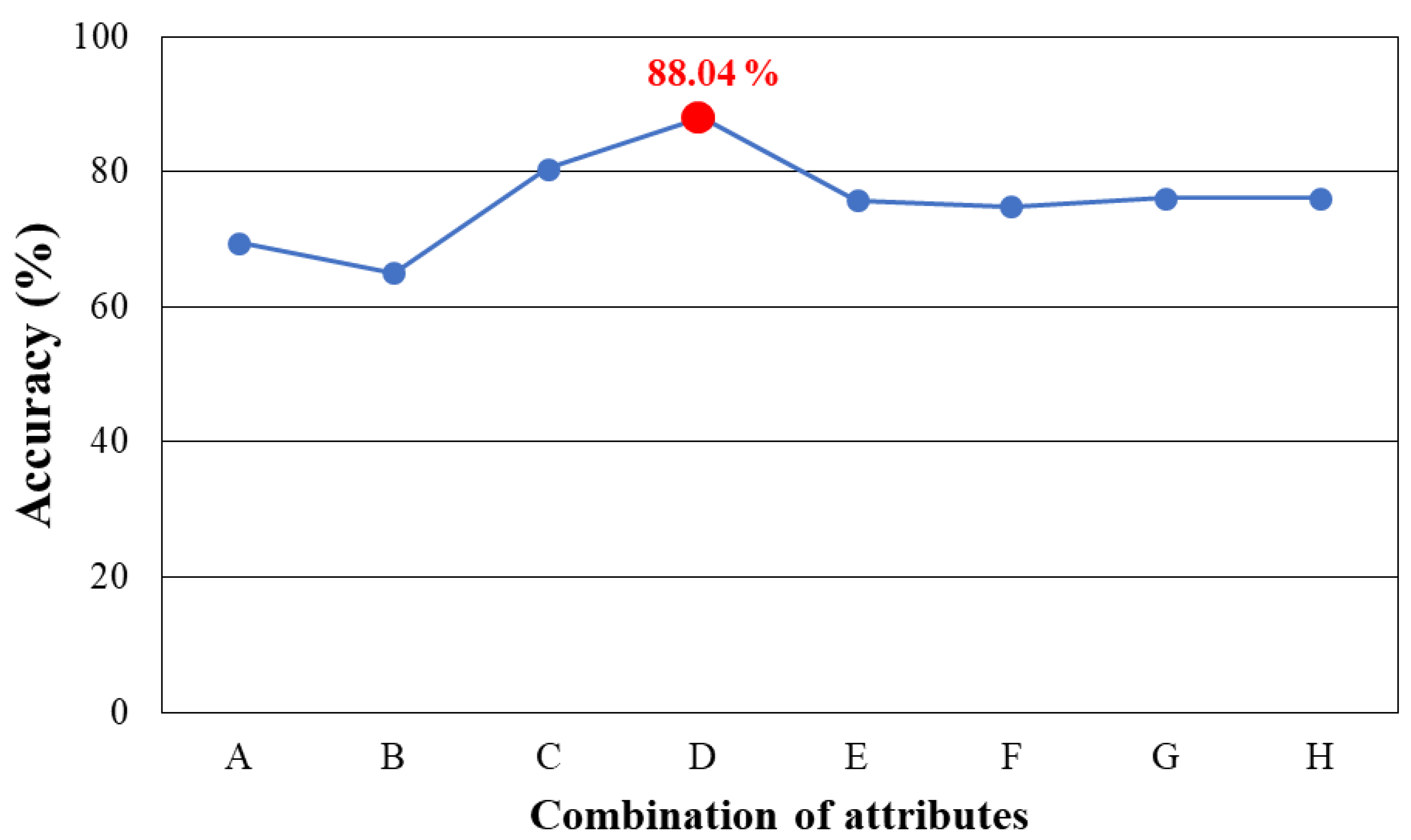
The predictive model using the decision tree algorithm showed an accuracy of 88.04% when using air temperature, top and bottom clothing surface temperatures, and BMI.
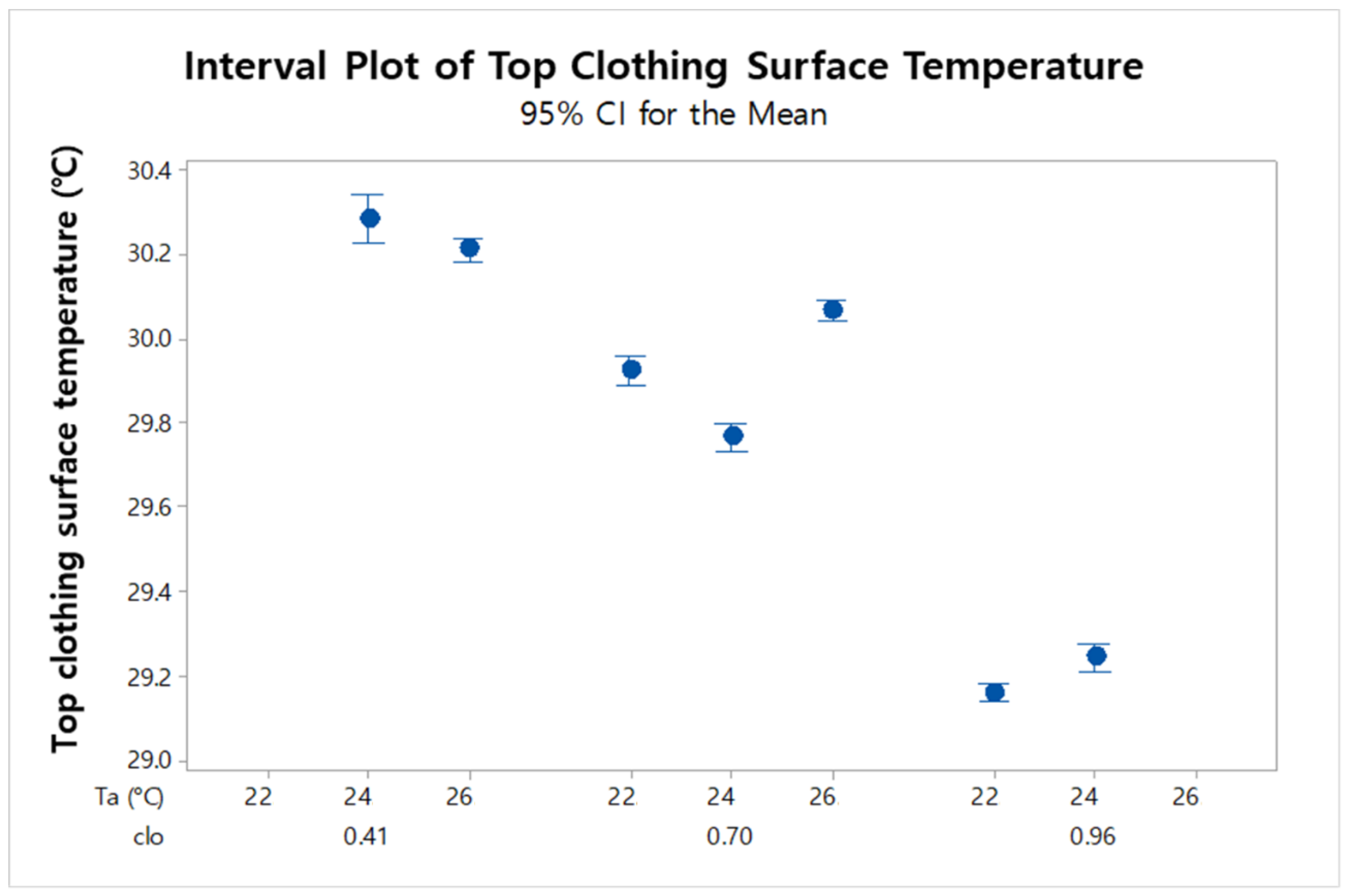
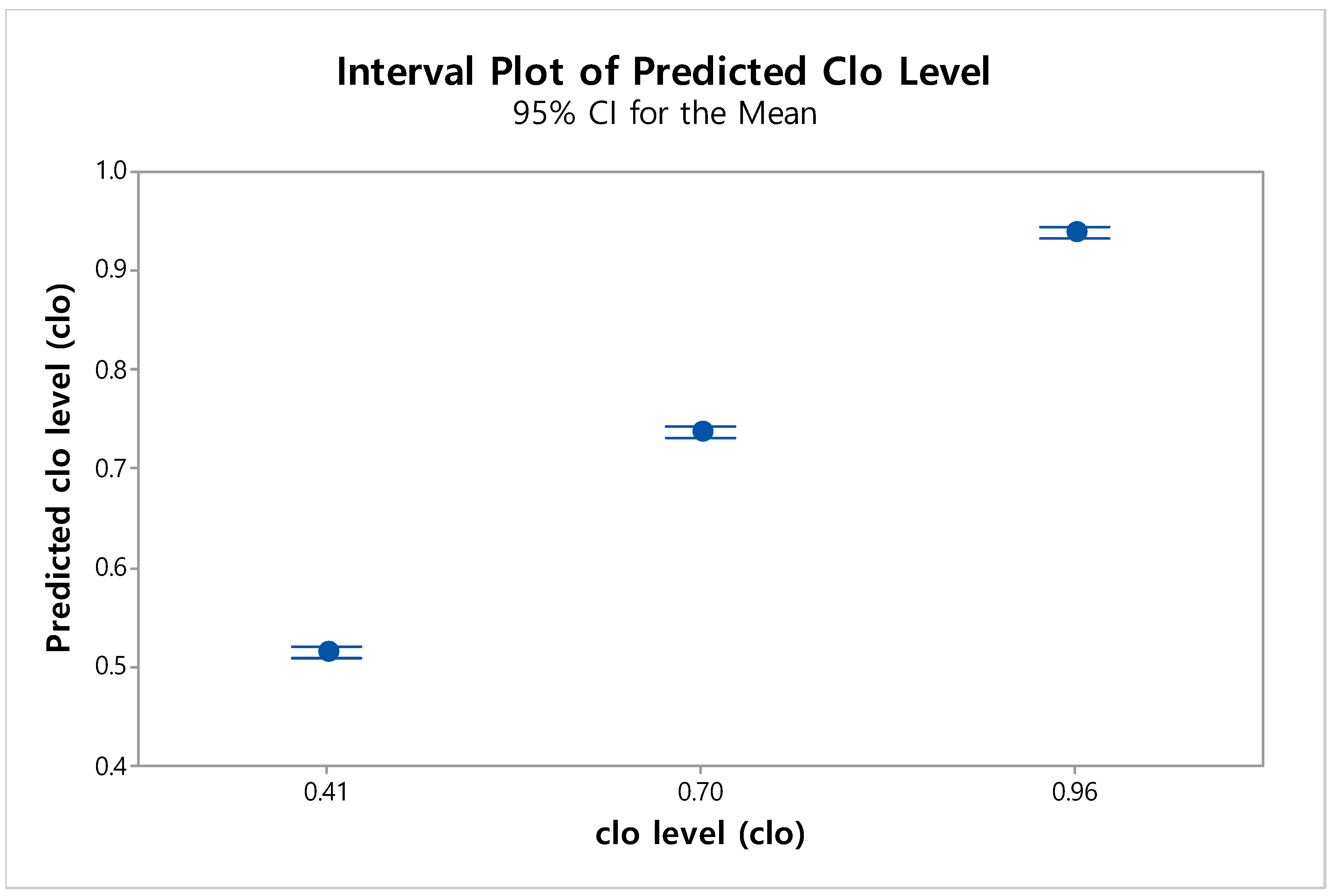
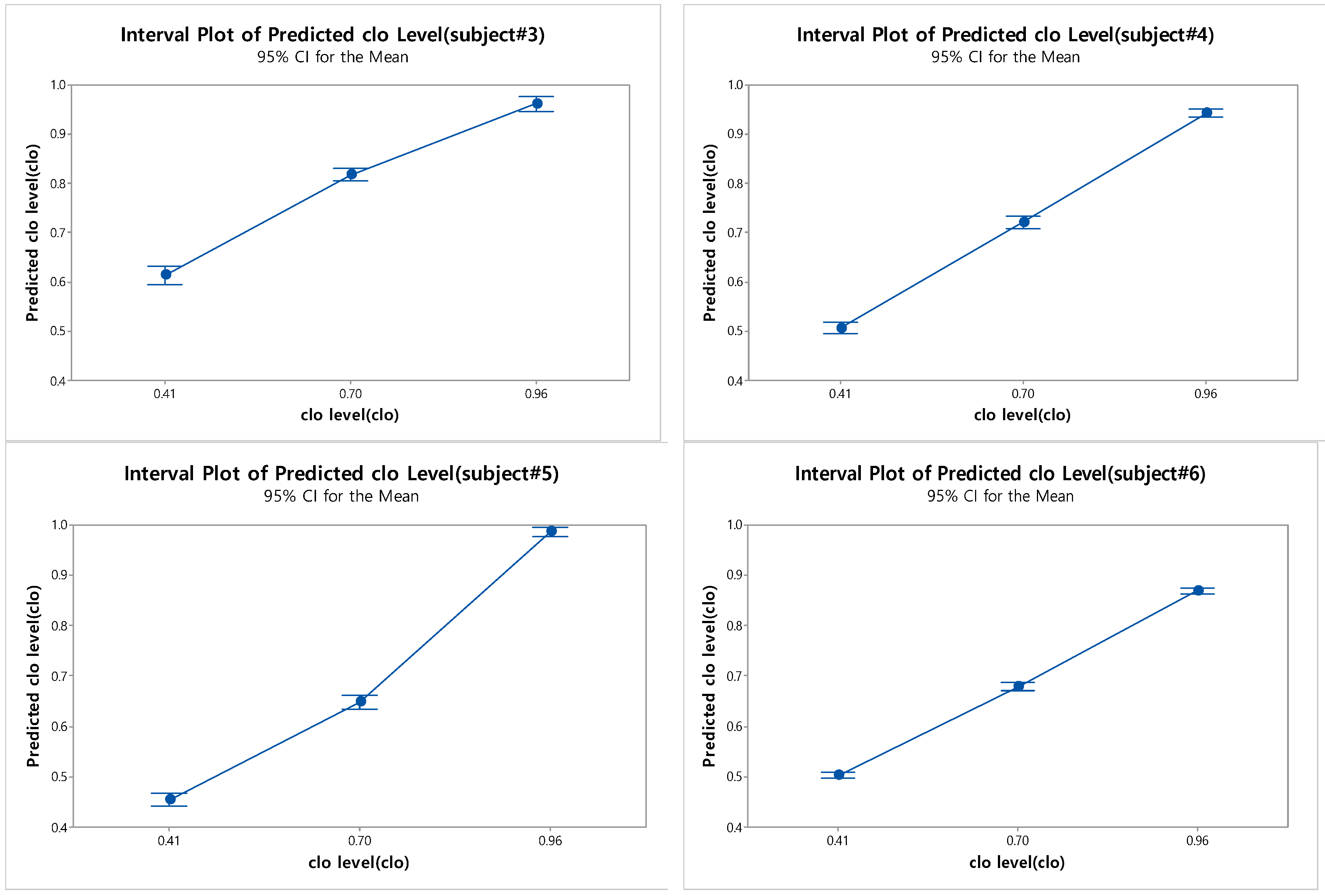
For both predictive models, the higher the clo value, the higher the precision of the clo value prediction.
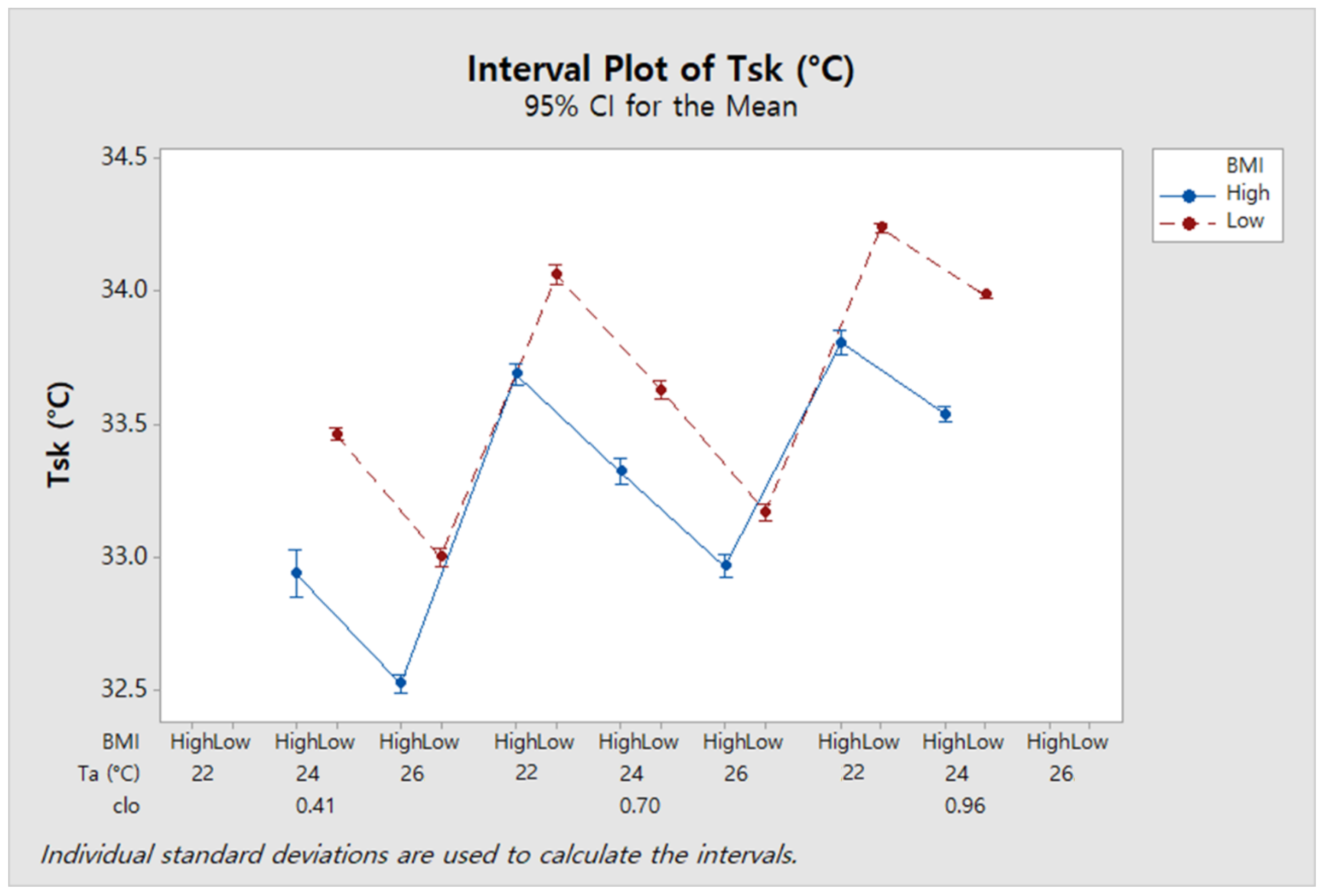
According to BMI group, there was a difference in the accuracy of the clo value prediction model, especially for the highest clo value (0.96 clo).
For practical application of the predictive model established in this paper, it is necessary to obtain various data, such as skin temperatures and clothing temperatures, in real time. Such a practical application can be technically implemented by the use of sensory devices, such as infrared cameras and PMV meters, which have been frequently adopted in existing studies [
23,
24,
25]. In recent years, sensor technology has been developed, and inexpensive sensors with good performance have been introduced. Therefore, considering that these sensors will be actively used in the future, the results of this research have high potential to be adopted for evaluating individual clothing insulation and, furthermore, thermal comfort in real time. Also, it is necessary to reduce the number of sensing points and simplify the computational algorithm to achieve a cost-effective approach.
In this study, the predictive models were constructed through a data-driven method, but there were limitations. Twenty human subjects were used as a sample, and a statistically meaningful deduction resulted. However, a larger sample size would have increased the accuracy and validity of the results, especially considering the differences in BMI. The experiment was carried out only for cooling. Therefore, it is necessary to carry out the experiment using heating in the future. In addition, only three clothing ensembles were selected for each season. In the future, it will be necessary to construct more sophisticated prediction models by using more clothing ensembles with a larger dataset for better performance.