Individually Optimized Commercial Road Transport: A Decision Support System for Customizable Routing Problems
Abstract
1. Introduction
How can a customizable VRP be implemented into a DSS enabling route optimization for urban logistics applications of several industries?
2. Methodology
3. VRP Attributes and Related Work
4. Multi-Attribute Vehicle Routing Decision Support System (MAVRDSS)
4.1. Requirements
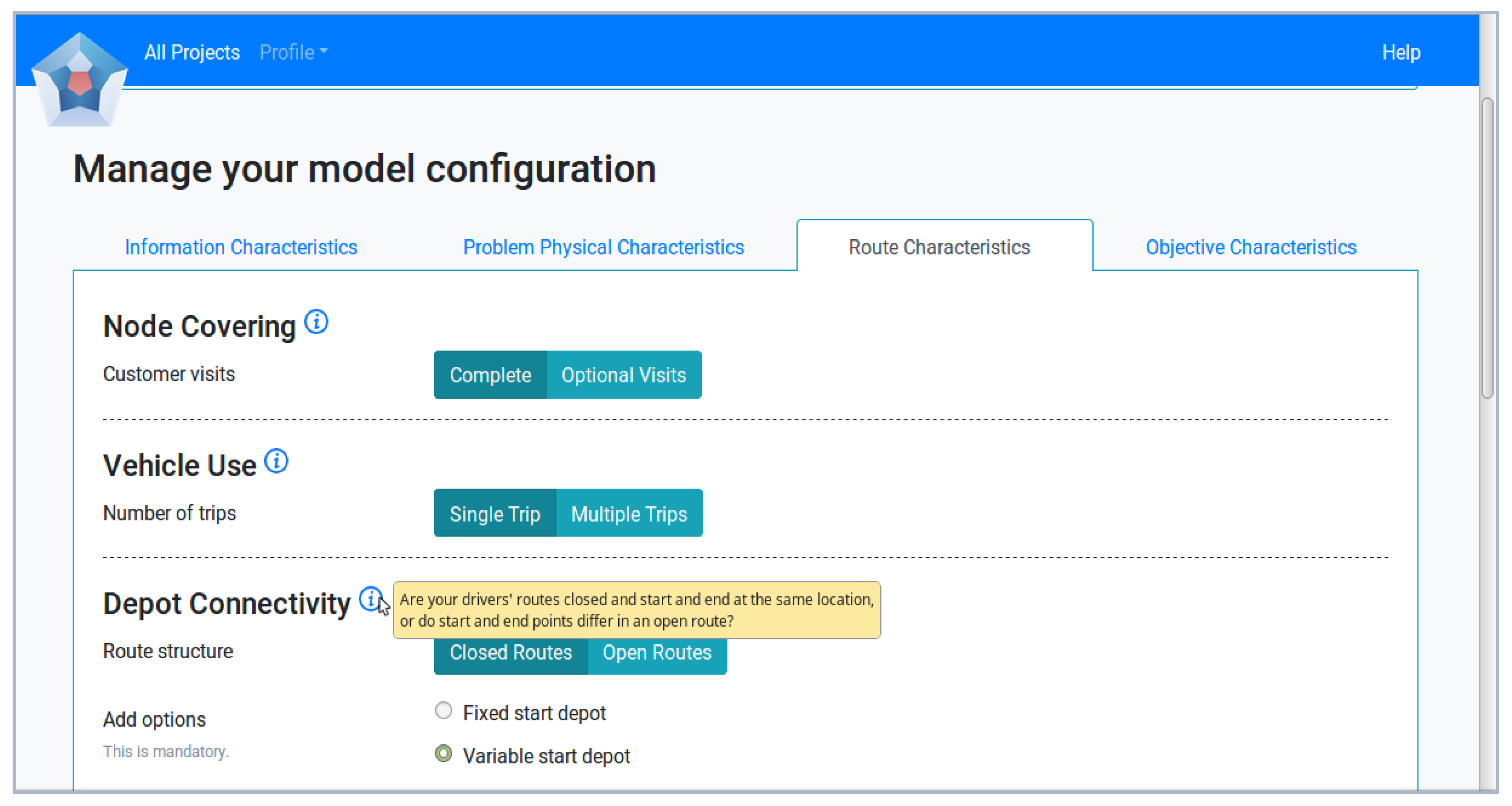
4.2. Functionality and User Interaction
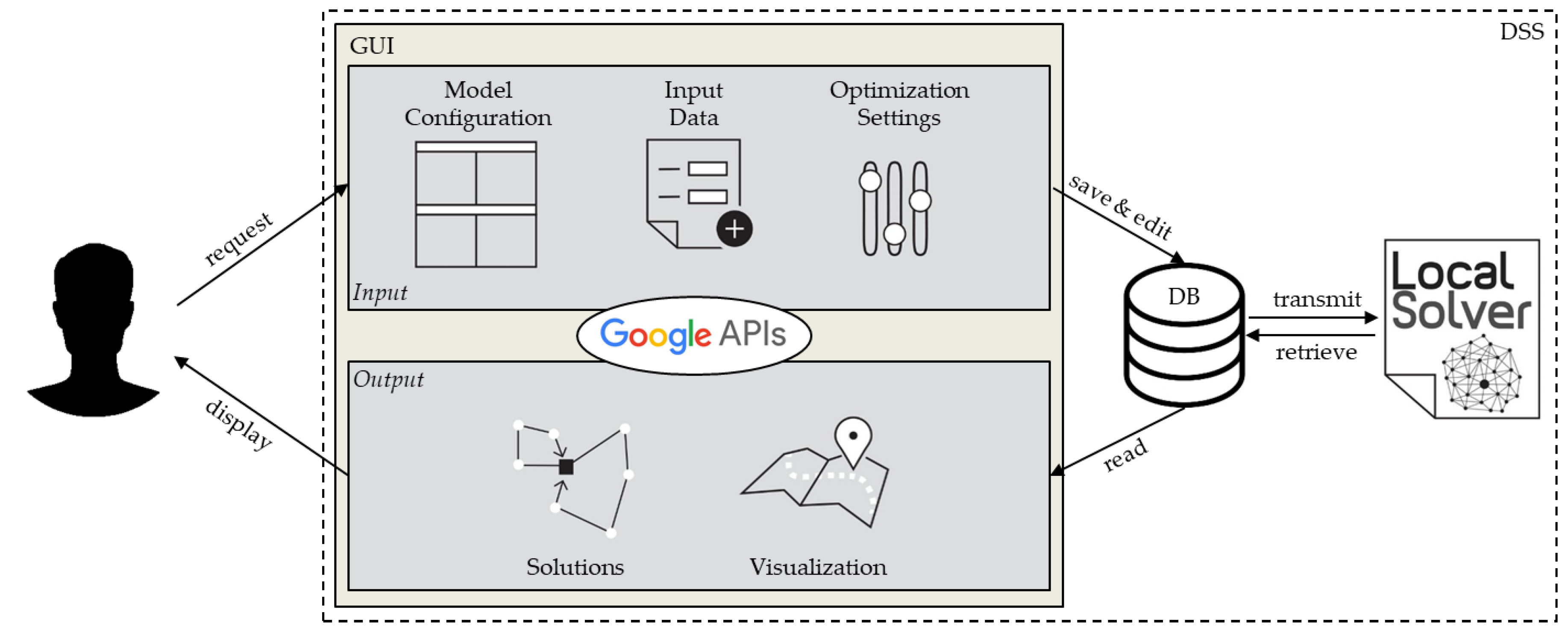
4.3. System Components and Implementation
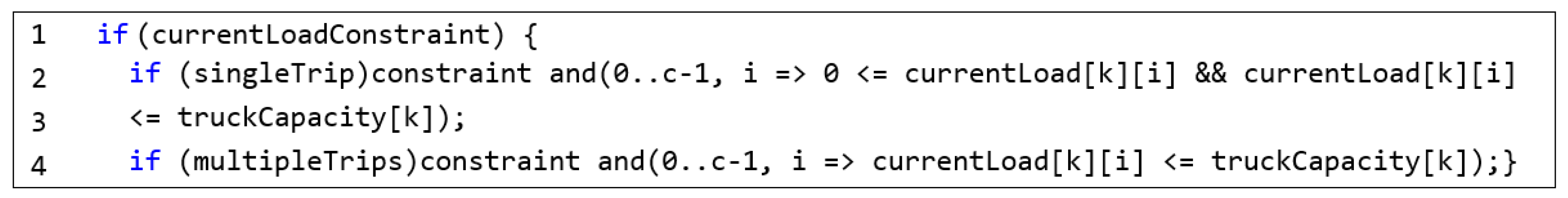

5. Results
5.1. Benchmark Calculations
5.2. Real-World Simulations
6. Discussion and Contributions
7. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Drexl, M. Rich vehicle routing in theory and practice. Logist. Res. 2012, 5, 47–63. [Google Scholar] [CrossRef]
- Hasle, G.; Kloser, O. Industrial vehicle routing. In Geometric Modelling, Numerical Simulation, and Optimization; Hasle, G., Lie, K.-A., Quak, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 397–436. [Google Scholar]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Cattaruzza, D.; Absi, N.; Feillet, D.; González-Feliu, J. Vehicle routing problems for city logistics. Eur. J. Transp. Logist. 2017, 6, 51–79. [Google Scholar] [CrossRef]
- Laporte, G. Fifty years of vehicle routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Lahyani, R.; Khemakhem, M.; Semet, F. Rich vehicle routing problems. From a taxonomy to a definition. Eur. J. Oper. Res. Soc. 2015, 241, 1–14. [Google Scholar] [CrossRef]
- Rademeyer, A.L.; Lubinsky, D.J. A decision support system for strategic, tactical and operational visit planning for on-the-road personnel. S. Afr. J. Ind. Eng. 2017, 28, 57–72. [Google Scholar]
- Hartl, R.F.; Hasle, G.; Janssens, G.K. Special issue on rich vehicle routing problems. Cent. Eur. J. Oper. Res. 2006, 14, 103–104. [Google Scholar] [CrossRef]
- Lahyani, R.; Coelho, L.C.; Khemakhem, M.; Laporte, G.; Semet, F. A multi-compartment vehicle routing problem arising in the collection of olive oil in Tunisia. Omega 2014, 51, 1–10. [Google Scholar] [CrossRef]
- Gregor, S.; Hevner, A.R. Positioning and presenting design science research for maximum impact. MIS Q 2013, 37, 337–355. [Google Scholar] [CrossRef]
- Dedrick, J. Green IS: Concepts and issues for information systems research. Commun. Assoc. Inf. Syst. 2010, 27, 173–184. [Google Scholar] [CrossRef]
- Watson, R.T.; Boudreau, M.C.; Chen, A.J. Information systems and environmentally sustainable development: Energy informatics and new directions for the IS community. Manag. Inf. Syst. Q. 2010, 34, 23–38. [Google Scholar] [CrossRef]
- Malhotra, A.; Melville, N.P.; Watson, R.T. Spurring impactful research on information systems for environmental sustainability. Manag. Inf. Syst. Q. 2013, 37, 1265–1274. [Google Scholar] [CrossRef]
- Gholami, R.; Watson, R.T.; Molla, A.; Hasan, H.; Bjørn-Andersen, N. Information systems solutions for environmental sustainability: How can we do more? J. Assoc. Inf. Syst. 2016, 17, 521–536. [Google Scholar] [CrossRef]
- Hassan, N.R. Value of IS research: Is there a crisis? Commun. Assoc. Inf. Syst. 2014, 34, 801–816. [Google Scholar] [CrossRef]
- Hevner, A.R.; March, S.T.; Park, J.; Ram, S. Design science in information systems research. Manag. Inf. Syst. Q. 2004, 28, 75–105. [Google Scholar] [CrossRef]
- Hevner, A.R. A three cycle view of design science research. Scand. J. Inf. Syst. 2007, 19, 87–92. [Google Scholar]
- Venable, J.; Pries-Heje, J.; Baskerville, R. FEDS: A framework for evaluation in design science research. Eur. J. Inf. Syst. 2016, 25, 77–89. [Google Scholar] [CrossRef]
- Baldacci, R.; Battarra, M.; Vigo, D. Routing a heterogeneous fleet of vehicles. In The Vehicle Routing Problem: Latest Advances and New Challenges; Golden, B.L., Raghavan, S., Wasil, E.A., Eds.; Operations Research/Computer Science Interfaces, Series; Springer: New York, NY, USA, 2008; Volume 43, pp. 3–27. [Google Scholar]
- Crainic, T.G.; Crisan, G.C.; Gendreau, M.; Lahrichi, N.; Rei, W. A concurrent evolutionary approach for rich combinatorial optimization. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference, Montreal, QC, Canada, 8–12 July 2009; ACM: New York, NY, USA; pp. 2017–2022. [Google Scholar]
- Caceres-Cruz, J.; Riera, D.; Juan, A.; Arias, P.; Guimarans, D. Rich vehicle routing problem: Survey. ACM Comput. Surv. 2015, 47, 1–29. [Google Scholar] [CrossRef]
- Crainic, T.G.; Crisan, G.C.; Gendreau, M.; Lahrichi, N.; Rei, W. Multi-thread integrative cooperative optimization for rich combinatorial problems. In Proceedings of the 23rd IEEE International Parallel and Distributed Processing Symposium, Rome, Italy, 23–29 May 2009; IEEE: New York, NY, USA; p. 8. [Google Scholar]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Lahrichi, N.; Rei, W. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- Kitchenham, B.; Brereton, O.P.; Budgen, D.; Turner, M.; Bailey, J.; Linkman, S. Systematic literature reviews in software engineering—A systematic literature review. Inf. Softw. Technol. 2009, 51, 7–15. [Google Scholar] [CrossRef]
- Webster, J.; Watson, R. Analyzing the past to prepare for the future: Writing a literature review. Manag. Inf. Syst. Q. 2002, 26, 13–23. [Google Scholar]
- Armas, J.; Melián-Batista, B.; Moreno-Pérez, J.A.; Brito, J. GVNS for a real-world rich vehicle routing problem with time windows. Eng. Appl. Artif. Intell. 2015, 42, 45–56. [Google Scholar] [CrossRef]
- Eksioglu, B.; Vural, A.V.; Reisman, A. The vehicle routing problem. A taxonomic review. Comput. Ind. Eng. 2009, 57, 1472–1483. [Google Scholar] [CrossRef]
- Amorim, P.; Parragh, S.N.; Sperandio, F.; Almada-Lobo, B. A rich vehicle routing problem dealing with perishable food: A case study. TOP 2014, 22, 489–508. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D. The multi-trip vehicle routing problem with time windows and release dates. Transp. Sci. 2016, 50, 676–693. [Google Scholar] [CrossRef]
- Ceselli, A.; Righini, G.; Salani, M. A column generation algorithm for a rich vehicle-routing problem. Transp. Sci. 2009, 43, 56–69. [Google Scholar] [CrossRef]
- Coelho, V.N.; Grasas, A.; Ramalhinho, H.; Coelho, I.M.; Souza, M.J.F.; Cruz, R.Z. An ILS-based algorithm to solve a large-scale real heterogeneous fleet VRP with multi-trips and docking constraints. Eur. J. Oper. Res. Soc. 2016, 250, 367–376. [Google Scholar] [CrossRef]
- Derigs, U.; Kurowsky, R.; Vogel, U. Solving a real-world vehicle routing problem with multiple use of tractors and trailers and EU-regulations for drivers arising in air cargo road feeder services. Eur. J. Oper. Res. Soc. 2011, 213, 309–319. [Google Scholar] [CrossRef]
- Derigs, U.; Pullmann, M.; Vogel, U. A short note on applying a simple LS/LNS-based metaheuristic to the rollon–rolloff vehicle routing problem. Comput. Oper. Res. 2013, 40, 536–546. [Google Scholar] [CrossRef]
- Goel, A. A column generation heuristic for the general vehicle routing problem. In Proceedings of the International Conference on Learning and Intelligent Optimization, Venice, Italy, 18–22 January 2010; p. 9. [Google Scholar]
- Hemmelmayr, V.; Doerner, K.F.; Hartl, R.F.; Rath, S. A heuristic solution method for node routing based solid waste collection problems. J. Heuristics 2013, 19, 129–156. [Google Scholar] [CrossRef]
- Holland, C.; Levis, J.; Nuggehalli, R.; Santilli, R.; Winters, J. UPS optimizes delivery routes. INFORMS J. Appl. Anal. 2017, 47, 8–23. [Google Scholar] [CrossRef]
- Ibeas, A.; Moura, J.L.; Dell’Olio, L. Planning school transport: Design of routes with flexible school opening times. Transp. Plan. Technol. 2009, 32, 527–544. [Google Scholar] [CrossRef]
- Kovacs, A.A.; Golden, B.L.; Hartl, R.F.; Parragh, S.N. The generalized consistent vehicle routing problem. Transp. Sci. 2015, 49, 796–816. [Google Scholar] [CrossRef]
- López-Sánchez, A.D.; Hernández-Díaz, A.G.; Vigo, D.; Caballero, R.; Molina, J. A multi-start algorithm for a balanced real-world open vehicle routing problem. Eur. J. Oper. Res. Soc. 2014, 238, 104–113. [Google Scholar] [CrossRef]
- Oppen, J.; Løkketangen, A.; Desrosiers, J. Solving a rich vehicle routing and inventory problem using column generation. Comput. Oper. Res. 2010, 37, 1308–1317. [Google Scholar] [CrossRef]
- Osaba, E.; Yang, X.-S.; Diaz, F.; Onieva, E.; Masegosa, A.D.; Perallos, A. A discrete firefly algorithm to solve a rich vehicle routing problem modelling a newspaper distribution system with recycling policy. Soft Comput. 2017, 21, 5295–5308. [Google Scholar] [CrossRef]
- Prescott-Gagnon, E.; Desaulniers, G.; Rousseau, L.-M. Heuristics for an oil delivery vehicle routing problem. Flexible Serv. Manuf. J. 2014, 26, 516–539. [Google Scholar] [CrossRef]
- Rais, A.; Alvelos, F.; Carvalho, M.S. New mixed integer-programming model for the pickup-and-delivery problem with transshipment. Eur. J. Oper. Res. Soc. 2014, 235, 530–539. [Google Scholar] [CrossRef]
- Rasmussen, M.S.; Justesen, T.; Dohn, A.; Larsen, J. The home care crew scheduling problem. Preference-Based Visit Clustering and Temporal Dependencies. Eur. J. Oper. Res. Soc. 2012, 219, 598–610. [Google Scholar] [CrossRef]
- Rieck, J.; Zimmermann, J. A new mixed integer linear model for a rich vehicle routing problem with docking constraints. Ann. Oper. Res. 2010, 181, 337–358. [Google Scholar] [CrossRef]
- Santillán, C.G.; Reyes, L.C.; Rodriguez, M.L.M.; Barbosa, J.J.G.; López, O.C.; Zarate, G.R.; Hernández, P. Variants of VRP to optimize logistics management problems. In Logistics Management and Optimization through Hybrid Artificial Intelligence Systems; Zezzatti, O., Ochoa, C.A., Chira, C., Hernandez, A., Basurto, M., Eds.; IGI Global: Hershey, PA, USA, 2012; pp. 207–237. [Google Scholar]
- Schmid, V.; Doerner, K.F.; Laporte, G. Rich routing problems arising in supply chain management. Eur. J. Oper. Res. Soc. 2013, 224, 435–448. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Bektaş, T. The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations. Int. J. Prod. Econ. 2015, 164, 366–378. [Google Scholar] [CrossRef]
- Stenger, A.; Schneider, M.; Goeke, D. The prize-collecting vehicle routing problem with single and multiple depots and non-linear cost. Eur. J. Transp. Logist. 2013, 2, 57–87. [Google Scholar] [CrossRef]
- Wen, M.; Cordeau, J.-F.; Laporte, G.; Larsen, J. The dynamic multi-period vehicle routing problem. Comput. Oper. Res. 2009, 37, 1615–1623. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.H.G. Complexity of vehicle routing and scheduling problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of green vehicle routing problem. Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Gendreau, M.; Laporte, G.; Potvin, J.V.; Semet, F. A guide to vehicle routing heuristics. J. Oper. Res. Soc. 2002, 53, 512–522. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation, 74th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Laporte, G. The vehicle routing problem. An overview of exact and approximate algorithms. Eur. J. Oper. Res. Soc. 1992, 59, 345–458. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Kritzinger, S.; Doerner, K.F.; Hartl, R.F.; Kiechle, G.; Stadler, H.; Manohar, S.S. Using traffic information for time-dependent vehicle routing. Procedia Soc. Behav. Sci. 2012, 39, 217–229. [Google Scholar] [CrossRef][Green Version]
- Bräysy, O.; Gendreau, M. Vehicle routing with time windows, part 1: Route construction and local search algorithms. Transp. Sci. 2005, 39, 104–118. [Google Scholar] [CrossRef]
- Hartl, M. Ruby on Rails Tutorial: Learn Wen Development with Rails. Available online: https://www.railstutorial.org/book/ (accessed on 10 August 2019).
- Gardi, F.; Benoist, T.; Darlay, J.; Estellon, B.; Megel, R. Local Search for 0-1 Nonlinear Programming. In Mathematical Programming Solver Based on Local Search; Gardi, F., Benoist, T., Darlay, J., Estellon, B., Megel, R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 29–51. [Google Scholar]
- Belenguer, J.M.; Martinez, M.C.; Mota, E. A lower bound for the split delivery vehicle routing problem. Oper. Res. 2000, 48, 801–810. [Google Scholar] [CrossRef]
- Silva, M.M.; Subramanian, A.; Ochi, L.S. An iterated local search heuristic for the split delivery vehicle routing problem. Comput. Oper. Res. 2015, 53, 234–249. [Google Scholar] [CrossRef]
- Aleman, R.E.; Zhang, X.; Hill, R.R. A ring-based diversification scheme for routing problems. Int. J. Math. Oper. Res. 2009, 1, 163–190. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Maischberger, M. A parallel iterated tabu search heuristic for vehicle routing problems. Comput. Oper. Res. 2010, 39, 2033–2050. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Gendreau, M.; Laporte, G. A tabu search heuristic for periodic and multi-depot vehicle routing problems. Networks 1997, 30, 105–119. [Google Scholar] [CrossRef]
- Yu, V.F.; Lin, S.-W.; Lee, W.; Ting, C.-J. A simulated annealing heuristic for the capacitated location routing problem. Comput. Ind. Eng. 2010, 58, 288–299. [Google Scholar] [CrossRef]
- Prins, C.; Prodhon, C.; Wolfler Calvo, R. A memetic algorithm with population management (MA| PM) for the capacitated location-routing problem. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization, Budapest, Hungary, 10–12 April 2006; Gottlieb, J., Raidl, G.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 183–194. [Google Scholar]
- Prins, C.; Prodhon, C.; Ruiz, A.; Soriano, P.; Wolfler Calvo, R. Solving the capacitated location-routing problem by a cooperative lagrangean relaxation-granular tabu search heuristic. Transp. Sci. 2007, 41, 470–483. [Google Scholar] [CrossRef]
- Barreto, S.S. Analysis and modelling of location-routing problems. Ph.D. Thesis, Aveiro University, Aveiro, Portugal, October 2004. (In Portuguese). [Google Scholar]
- Holguin-Veras, J.; Hodge, S.; Wojtowicz, J.; Singh, C.; Wang, C.; Jaller, M.; Aros-Vera, F.; Ozbay, K.; Weeks, A.; Replogle, M.; et al. The New York City off-hour delivery program: A business and community-friendly sustainability program. INFORMS J. Appl. Anal. 2018, 48, 70–86. [Google Scholar] [CrossRef]
- Shao, S.; Guan, W.; Ran, B.; He, Z.; Bi, J. Electric vehicle routing problem with charging time and variable travel time. Math. Probl. Eng. 2017, 5098183, 1–13. [Google Scholar] [CrossRef]
- Arnott, D.; Pervan, G. Design science in decision support systems research: An assessment using the Hevner, March, Park, and Ram guidelines. J. Assoc. Inf. Syst. 2012, 13, 923–949. [Google Scholar] [CrossRef]
- Figliozzi, M. Vehicle routing problem for emissions minimization. Transp. Res. Rec. 2010, 2197, 1–7. [Google Scholar] [CrossRef]
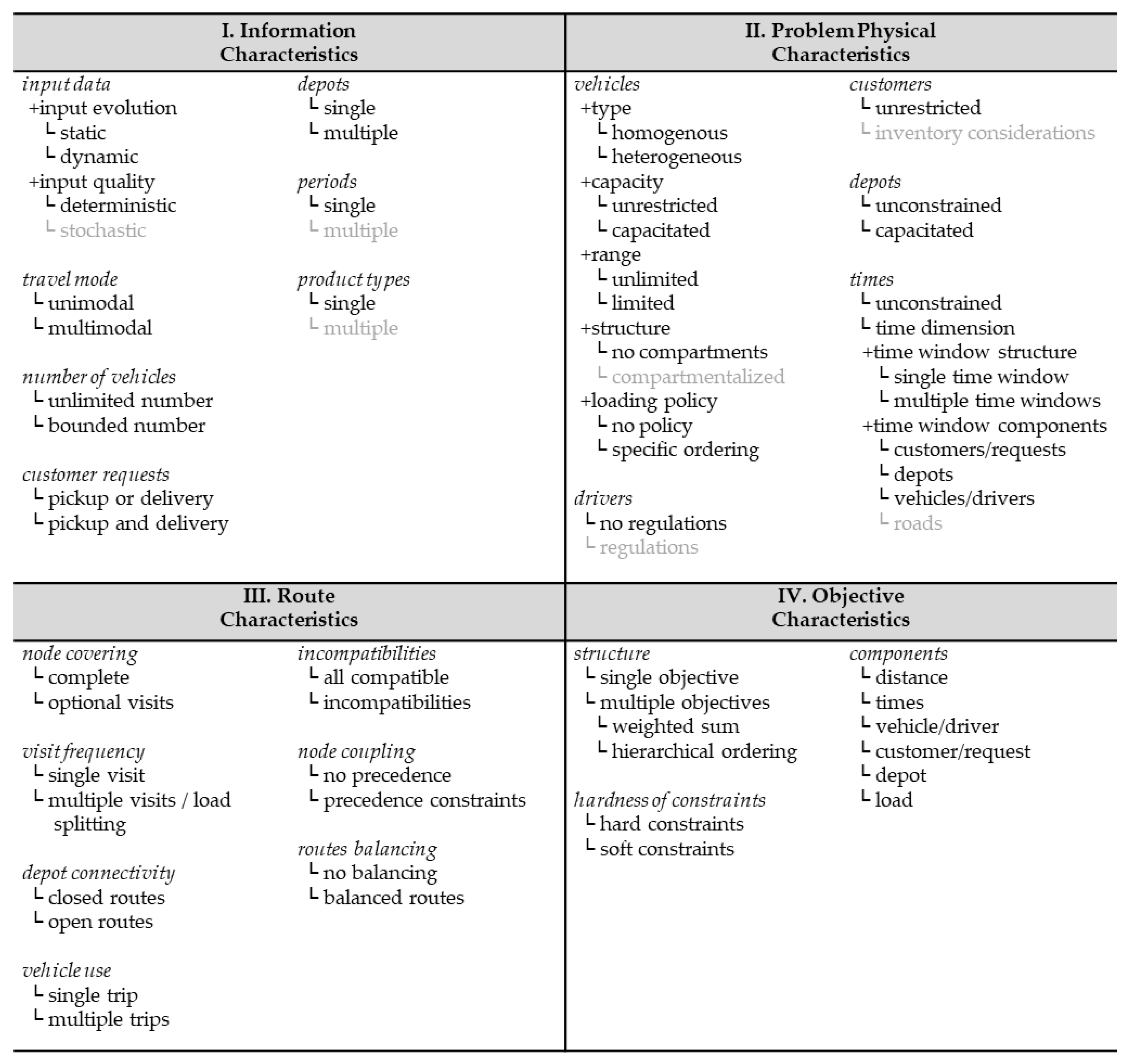
| Attribute | Abbr. | Description |
|---|---|---|
| Pickup and delivery | PD | Customers may have pickup and delivery requests to be served in sequential, separate or simultaneous manner |
| Multiple depots | MD | There is more than one node without a request; vehicle trips depart from and/or arrive at more than one node |
| Multiple periods | MP | The planning horizon covers more than one period and requests are served according to visitation patterns |
| Multiple products | MC | Vehicles can carry different types of products/commodities (e.g., dry, liquid, frozen) |
| Heterogeneous vehicles | HV | Vehicles have different properties (e.g., costs, capacity, maximum travel distance, travel speed and distance) |
| Capacitated vehicles | CV | Vehicles have limited loading capacities |
| Limited range | LR | The length of a route is restricted (e.g., limited fuel, emissions) |
| Compartmentalized vehicles | VC | Different product types are carried in separate vehicle compartments |
| Loading policy/specific ordering | LP | Routing must respect possible ordering of visits induced by a loading policy (e.g., last-in-first-out) |
| Driver regulations | DR | Routing must respect legislation on driver working hours and safety (e.g., rest periods) |
| Inventory considerations | IN | Requests base on customers’ inventory levels (typically: avoiding stock-out situations) |
| Capacitated depots | CD | Depots have limited storing capacities |
| Multiple time windows | MW | Customers are associated with more than one time window, in which the request can be served (equivalently: The planning period is interrupted by at least one break time) |
| Time window | ||
| component -customer/requests -depots -vehicles/drivers -roads | CT DT VT RT | Time restrictions on -customer/requests (e.g., opening hours, break times) -depots (e.g., closing hours) -vehicles/drivers (e.g., working hours, lunch breaks) -roads (e.g., time dependent access restriction) |
| Optional visits | OV | Decision consists in choosing which requests to serve as visits are not mandatory |
| Multiple trips | MT | Vehicles can perform more than one trip in a planning period (equivalently: A tour includes at least one intermediate depot visit) |
| Multiple visits/split-deliveries | MV | Vehicles can visit customers more than once and may serve a fraction of demand at each visit |
| Open routes | OR | Start and end node of a vehicle’s tour may not be equal |
| Incompatibilities | IC | Node sequencing must respect physical inclusion or exclusion restrictions between, e.g., vehicle-customer, vehicle-depot, vehicle-product, or customer-depot |
| Precedence constraints | PC | Routing must respect a possible visiting order due to physical or service considerations (e.g., dial-a-ride, loading issues) |
| Balanced routes | BR | The workload of routes must be balanced (e.g., in terms of distance, duration, loaded quantities, or cost) |
| Objective components | ||
| -distance -times/durations -vehicle/driver -customer/request -facility/depot -loads | DO TO VO CO FO LO | Optimization targets can include -distance (e.g., minimize total travel distance or cost of travel) -times/durations (e.g., minimize travel durations or time windows) -vehicle/driver (e.g., minimize number of operated vehicles/drivers) -customer/request (e.g., maximize number of visits) -facility/depot (e.g., minimize number of necessary locations) -loads (e.g., minimize number or cost of loadings) |
| Multiple objectives | MO | There is more than one optimization target (e.g., minimize fixed vehicle cost and distance cost); multiple targets are prioritized either by weights or by a hierarchical ordering (includes several weighted sum objectives) |
| Soft constraints | SC | Problem constraints addressed in objective function (e.g., penalty fee) |
| Authors | Routing Attributes | Objective Function | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PD | MD | MP | MC | HV | LR | VC | LP | BR | DR | IN | CD | MW | CT | DT | VT | RT | OV | MT | MV | OR | IC | PC | DO | TO | VO | CO | FO | LO | MO | SC | |
| Amorim et al. [28] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Armas et al. [26] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| Cattaruzza et al. [29] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||||
| Ceselli et al. [30] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||
| Coelho et al. [31] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Derigs et al. [32] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||||
| Derigs et al. [33] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||||
| Goel [34] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||
| Hemmelmayr et al. [35] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||||
| Holland et al. [36] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||
| Ibeas et al. [37] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||||
| Kovacs et al. [38] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Lahyani et al. [9] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||
| López-Sánchez et al. [39] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||||
| Oppen et al. [40] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Osaba et al. [41] | ✓ | ✓ | ✓ | ||||||||||||||||||||||||||||
| Prescott-Gagnon et al. [42] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||
| Rais et al. [43] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||||
| Rasmussen et al. [44] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||
| Rieck and Zimmermann [45] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||
| Santillán et al. [46] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Schmid et al. [47] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||
| Soysal et al. [48] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||||||||||
| Stenger et al. [49] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||
| Wen et al. [50] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||||||||
| Number of Customers | Aleman et al. | SplitILS | MAVRDSS | |||
|---|---|---|---|---|---|---|
| Gap | CT | Gap | CT | Gap | CT | |
| 22 | 0.0 | 2.6 | 0.0 | 0.2 | 0.0 | 19 |
| 23 | 0.1 | 1.6 | 0.0 | 0.1 | 0.4 | 12 |
| 30 | 0.0 | 7.5 | 0.0 | 0.2 | 0.4 | 9 |
| 33 | 0.1 | 8.4 | 0.0 | 0.5 | 1.5 | 22 |
| 51 | 0.1 | 49.8 | 0.0 | 1.8 | 1.2 | 17 |
| 76 | 0.2 | 91.4 | 0.0 | 51.8 | 4.2 | 45 |
| 101 | 0.2 | 298.2 | 0.0 | 38.9 | 8.8 | 117 |
| |N| × |M| × |K| | ALNS | CGL | ITS/1 | MAVRDSS | ||||
|---|---|---|---|---|---|---|---|---|
| Gap | CT | Gap | CT | Gap | CT | Gap | CT | |
| 50 × 4 × 4 | 0.0 | 29 | 0.0 | 15 | 0.0 | - | 0.0 | 12 |
| 50 × 4 × 2 | 0.0 | 28 | 0.1 | 50 | 0.0 | - | 0.0 | 14 |
| 75 × 5 × 3 | 0.0 | 64 | 0.6 | 17 | 0.1 | - | 0.0 | 22 |
| 80 × 2 × 5 | 0.1 | 75 | 0.1 | 1 | 0.0 | - | 0.0 | 42 |
| 100 × 2 × 5 | 0.3 | 120 | 0.4 | 79 | 0.2 | - | 3.4 | 31 |
| 100 × 2 × 8 | 0.5 | 88 | 0.6 | 336 | 0.5 | - | 1.5 | 32 |
| 100 × 3 × 6 | 0.7 | 93 | 0.2 | 293 | 0.4 | - | 3.4 | 48 |
| 100 × 4 × 4 | 0.8 | 88 | 1.1 | 427 | 0.7 | - | 1.9 | 40 |
| 160 × 4 × 5 | 0.0 | 179 | 0.4 | 539 | 0.0 | - | 7.1 | 28 |
| 240 × 6 × 5 | 0.3 | 315 | 0.0 | 10 | 0.3 | - | 5.5 | 54 |
| 249 × 2 × 14 | 0.8 | 333 | 2.5 | 1175 | 2.2 | - | 7.0 | 102 |
| 249 × 3 × 12 | 0.5 | 361 | 1.6 | 419 | 1.7 | - | 5.4 | 88 |
| 249 × 4 × 8 | 0.5 | 363 | 2.3 | 984 | 1.7 | - | 5.2 | 89 |
| 249 × 5 × 6 | 0.8 | 357 | 1.0 | 1040 | 1.0 | - | 3.5 | 110 |
| 360 × 9 × 5 | 0.5 | 582 | 1.1 | 1786 | 0.7 | - | 0.9 | 78 |
| |N| × |M| | MAPM | LRGTS | SALRP | MAVRDSS | ||||
|---|---|---|---|---|---|---|---|---|
| Gap | CT | Gap | CT | Gap | CT | Gap | CT | |
| 21 × 5 | 0.0 | 0.3 | 0.0 | 0.2 | 0.0 | 18.3 | 0.0 | 1 |
| 22 × 5 | 4.6 | 0.3 | 0.4 | 0.2 | 0.0 | 16.6 | 0.0 | 1 |
| 27 × 5 | 0.0 | 1.0 | 0.1 | 0.3 | 0.0 | 23.3 | 0.0 | 2 |
| 29 × 5 | 0.0 | 0.8 | 0.0 | 0.4 | 0.0 | 23.9 | 0.0 | 1 |
| 32 × 5 | 6.0 | 1.0 | 0.1 | 0.5 | 0.0 | 25.1 | 0.0 | 2 |
| 36 × 5 | 5.4 | 1.4 | 3.5 | 0.7 | 0.0 | 31.7 | 0.0 | 2 |
| 50 × 5 | 0.0 | 3.8 | 3.7 | 2.4 | 0.0 | 52.8 | 0.0 | 18 |
| 75 × 10 | 8.4 | 9.4 | 8.1 | 10.1 | 0.4 | 126.8 | 2.2 | 94 |
| 88 × 8 | 1.5 | 34.2 | 5.2 | 17.5 | 0.0 | 226.9 | 0.8 | 65 |
| 100 × 10 | 3.9 | 44.5 | 3.0 | 28.2 | 0.6 | 330.8 | 2.2 | 86 |
| 134 × 8 | 9.7 | 110.5 | 7.1 | 48.3 | 0.0 | 552.4 | 3.4 | 9 |
| 150 × 10 | 1.4 | 255.0 | 2.3 | 119.2 | 2.7 | 577.0 | 6.0 | 80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leyerer, M.; Sonneberg, M.-O.; Heumann, M.; Kammann, T.; Breitner, M.H. Individually Optimized Commercial Road Transport: A Decision Support System for Customizable Routing Problems. Sustainability 2019, 11, 5544. https://doi.org/10.3390/su11205544
Leyerer M, Sonneberg M-O, Heumann M, Kammann T, Breitner MH. Individually Optimized Commercial Road Transport: A Decision Support System for Customizable Routing Problems. Sustainability. 2019; 11(20):5544. https://doi.org/10.3390/su11205544
Chicago/Turabian StyleLeyerer, Max, Marc-Oliver Sonneberg, Maximilian Heumann, Tim Kammann, and Michael H. Breitner. 2019. "Individually Optimized Commercial Road Transport: A Decision Support System for Customizable Routing Problems" Sustainability 11, no. 20: 5544. https://doi.org/10.3390/su11205544
APA StyleLeyerer, M., Sonneberg, M.-O., Heumann, M., Kammann, T., & Breitner, M. H. (2019). Individually Optimized Commercial Road Transport: A Decision Support System for Customizable Routing Problems. Sustainability, 11(20), 5544. https://doi.org/10.3390/su11205544






