Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Rapeseed
Abstract
:1. Introduction
2. Materials and Methods
2.1. Method of Construction of Neural Models
2.2. Methodology for Validating the Neural Models
- RAE—relative approximation error:
- RMS—root mean square error:
- MAE—mean absolute error:
- MAPE—mean absolute percentage error:where,
- n—number of observations;
- —actual values obtained during research; and
- —values given by the model.
2.3. Neural Network Sensitivity Analysis
3. Results
Network Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gonzalez-Sanchez, A.; Frausto-Solis, J.; Ojeda-Bustamante, W. Attribute selection impact on linear and nonlinear regression models for crop yield prediction. Sci. World J. 2014, 2014, 509249. [Google Scholar] [CrossRef] [PubMed]
- Kantanantha, N.; Serban, N.; Griffin, P. Yield and price forecasting for stochastic crop decision planning. J. Agric. Biol. Environ. Stat. 2010, 15, 362–380. [Google Scholar] [CrossRef]
- Domínguez, J.A.; Kumhálová, J.; Novák, P. Winter oilseed rape and winter wheat growth prediction using remote sensing methods. Plant Soil Environ. 2015, 61, 410–416. [Google Scholar] [CrossRef]
- Bussay, A.; van der Velde, M.; Fumagalli, D.; Seguini, L. Improving operational maize yield forecasting in Hungary. Agric. Syst. 2015, 141, 94–106. [Google Scholar] [CrossRef]
- Nelson, G.C.; Valin, H.; Sands, R.D.; Havlík, P.; Ahammad, H.; Deryng, D.; Elliott, J.; Fujimori, S.; Hasegawa, T.; Heyhoe, E. Climate change effects on agriculture: Economic responses to biophysical shocks. Proc. Natl. Acad. Sci. USA 2014, 111, 3274–3279. [Google Scholar] [CrossRef] [PubMed]
- Khairunniza-Bejo, S.; Mustaffha, S.; Ishak, W.; Ismail, W. Application of Artificial Neural Network in Predicting Crop Yield: A Review. J. Food Sci. Eng. 2014, 4, 1–9. [Google Scholar] [CrossRef]
- Mohsen, N.; Seyed Ahmad, S.-N.; Moslem, A. Modeling the seed yield of Ajowan (Trachyspermum ammi L.) using artificial neural network and multiple linear regression models. Ind. Crops Prod. J. 2018, 117, 224–234. [Google Scholar] [CrossRef]
- Abdipour, M.; Younessi-Hmazekhanlu, M.; Ramazani, S.H.R.; Omidi, A.H. Artificial neural networks and multiple linear regression as potential methods for modeling seed yield of safflower (Carthamus tinctorius L.). Ind. Crops Prod. 2019, 127, 185–194. [Google Scholar] [CrossRef]
- Park, S.J.; Hwang, C.S.; Vlek, P.L.G. Comparison of adaptive techniques to predict crop yield response under varying soil and land management conditions. Agric. Syst. 2005, 85, 59–81. [Google Scholar] [CrossRef]
- Bongiovanni, R.; Lowenberg-Deboer, J. Precision agriculture and sustainability. Precis. Agric. 2004, 5, 359–387. [Google Scholar] [CrossRef]
- Neruda, M.; Neruda, R. To contemplate quantitative and qualitative water features by neural networks method. Plant Soil Environ. 2002, 2002, 322–326. [Google Scholar] [CrossRef]
- Grahovac, J.; Jokić, A.; Dodić, J.; Vućurović, D.; Dodić, S. Modelling and prediction of bioethanol production from intermediates and byproduct of sugar beet processing using neural networks. Renew. Energy 2016, 85, 953–958. [Google Scholar] [CrossRef]
- Mueller, W.; Idziaszek, P.; Boniecki, P.; Zaborowicz, M.; Koszela, K.; Kujawa, S.; Kozłowski, R.J.; Przybył, K.; Niedbała, G. An IT system for the simultaneous management of vector and raster images. In Proceedings of the Eighth International Conference on Digital Image, Chengu, China, 20–22 May 2016; pp. 10033–100332. [Google Scholar]
- Kung, H.Y.; Kuo, T.H.; Chen, C.H.; Tsai, P.Y. Accuracy analysis mechanism for agriculture data using the ensemble neural network method. Sustainability 2016, 8, 735. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Chen, X.; Wang, J. Artificial Combined Model Based on Hybrid Nonlinear Neural Network Models and Statistics Linear Models—Research and Application for Wind Speed Forecasting. Sustainability 2018, 10, 4601. [Google Scholar] [CrossRef]
- Niedbała, G. Simple model based on artificial neural network for early prediction and simulation winter rapeseed yield. J. Integr. Agric. 2019, 18, 54–61. [Google Scholar] [CrossRef]
- Niedbała, G.; Mioduszewska, N.; Mueller, W.; Boniecki, P.; Wojcieszak, D.; Koszela, K.; Kujawa, S.; Kozłowski, R.J.; Przybył, K. Use of computer image analysis methods to evaluate the quality topping sugar beets with using artificial neural networks. In Proceedings of the Eighth International Conference on Digital Image, Chengu, China, 20–22 May 2016; pp. 10033–100332. [Google Scholar]
- Wojciechowski, T.; Niedbala, G.; Czechlowski, M.; Nawrocka, J.R.; Piechnik, L.; Niemann, J. Rapeseed seeds quality classification with usage of VIS-NIR fiber optic probe and artificial neural networks. In Proceedings of the ICOIP 2016 International Conference on Optoelectronics and Image Processing, Warsaw, Poland, 10–12 June 2016. [Google Scholar]
- Niedbała, G.; Kozłowski, R.J. Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Wheat. J. Agric. Sci. Technol. 2019, 21, 51–61. [Google Scholar]
- Bartoszek, K. Usefulness of MODIS data for assessment of the growth and development of winter oilseed rape. Zemdirb. Agric. 2014, 101, 445–452. [Google Scholar] [CrossRef]
- Saluja, R.K.; Kumar, V.; Sham, R. Stability of biodiesel–A review. Renew. Sustain. Energy Rev. 2016, 62, 166–181. [Google Scholar] [CrossRef]
- Gilardelli, C.; Stella, T.; Frasso, N.; Cappelli, G.; Bregaglio, S.; Chiodini, M.E.; Scaglia, B.; Confalonieri, R. WOFOST-GTC: A new model for the simulation of winter rapeseed production and oil quality. Field Crops Res. 2016, 197, 125–132. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). FAOSTAT Online Statistical Service. Available online: http://faostat.fao.org (accessed on 5 November 2018).
- Gabrielle, B.; Denoroy, P.; Gosse, G.; Justes, E.; Andersen, M.N. Development and evaluation of a CERES-type model for winter oilseed rape. Field Crops Res. 1998, 57, 95–111. [Google Scholar] [CrossRef]
- Zeleke, K.T.; Luckett, D.; Cowley, R. Calibration and testing of the FAO AquaCrop model for canola. Agron. J. 2011, 103, 1610–1618. [Google Scholar] [CrossRef]
- Deligios, P.A.; Farci, R.; Sulas, L.; Hoogenboom, G.; Ledda, L. Predicting growth and yield of winter rapeseed in a Mediterranean environment: Model adaptation at a field scale. Field Crops Res. 2013, 144, 100–112. [Google Scholar] [CrossRef]
- Zeleke, K.T.; Luckett, D.J.; Cowley, R.B. The influence of soil water conditions on canola yields and production in Southern Australia. Agric. Water Manag. 2014, 144, 20–32. [Google Scholar] [CrossRef]
- StatSoft Inc. Statistica. Data Analysis Software System, Version 7.1. Available online: www.statsoft.pl (accessed on 5 November 2018).
- Emamgholizadeh, S.; Parsaeian, M.; Baradaran, M. Seed yield prediction of sesame using artificial neural network. Eur. J. Agron. 2015, 68, 89–96. [Google Scholar] [CrossRef]
- Grzesiak, W.; Błaszczyk, P.; Lacroix, R. Methods of predicting milk yield in dairy cows-Predictive capabilities of Wood’s lactation curve and artificial neural networks (ANNs). Comput. Electron. Agric. 2006, 54, 69–83. [Google Scholar] [CrossRef]
- Li, F.; Qiao, J.; Han, H.; Yang, C. A self-organizing cascade neural network with random weights for nonlinear system modeling. Appl. Soft Comput. 2016, 42, 184–193. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Iqbal, J.; Omid, M.; Badrul, N.; Wahab, A.W.A. A Comparative Study Between Artificial Neural Networks and Adaptive Neuro-Fuzzy Inference Systems for Modeling Energy Consumption in Greenhouse Tomato Production: A Case Study in Isfahan Province. J. Agric. Sci. Technol. 2015, 17, 49–62. [Google Scholar]
- Safa, M.; Samarasinghe, S.; Nejat, M. Prediction of Wheat Production Using Artificial Neural Networks and Investigating Indirect Factors Affecting It: Case Study in Canterbury Province, New Zealand. J. Agric. Sci. Technol. 2015, 17, 791–803. [Google Scholar]
- Huang, N.; Li, R.; Lin, L.; Yu, Z.; Cai, G. Low redundancy feature selection of short term solar irradiance prediction using conditional mutual information and Gauss process regression. Sustainability 2018, 10, 2889. [Google Scholar] [CrossRef]
- Zhang, G.P.; Patuwo, E.B.; Michael, Y.H. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Peng, J.; Kim, M.; Kim, Y.; Jo, M.; Kim, B.; Sung, K.; Lv, S. Constructing Italian ryegrass yield prediction model based on climatic data by locations in South Korea. Grassl. Sci. 2017, 63, 184–195. [Google Scholar] [CrossRef]
- Kaiser, B.N.; Gridley, K.L.; Brady, J.N.; Phillips, T.; Tyerman, S.D. The role of molybdenum in agricultural plant production. Ann. Bot. 2005, 96, 745–754. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, E.J.; Bolle-Jones, E.W. Molybdenum as a Plant Nutrient: I. The Influence of Molybdenum on the Growth of Some Brassica Crops in Sand Culture. J. Hortic. Sci. 1952, 27, 245–256. [Google Scholar] [CrossRef]
- Hale, K.L.; McGrath, S.P.; Lombi, E.; Stack, S.M.; Terry, N.; Pickering, I.J.; George, G.N.; Pilon-Smits, E.A.H. Molybdenum Sequestration in Brassica Species. A Role for Anthocyanins? Plant Physiol. 2001, 126, 1391–1402. [Google Scholar] [CrossRef] [PubMed]
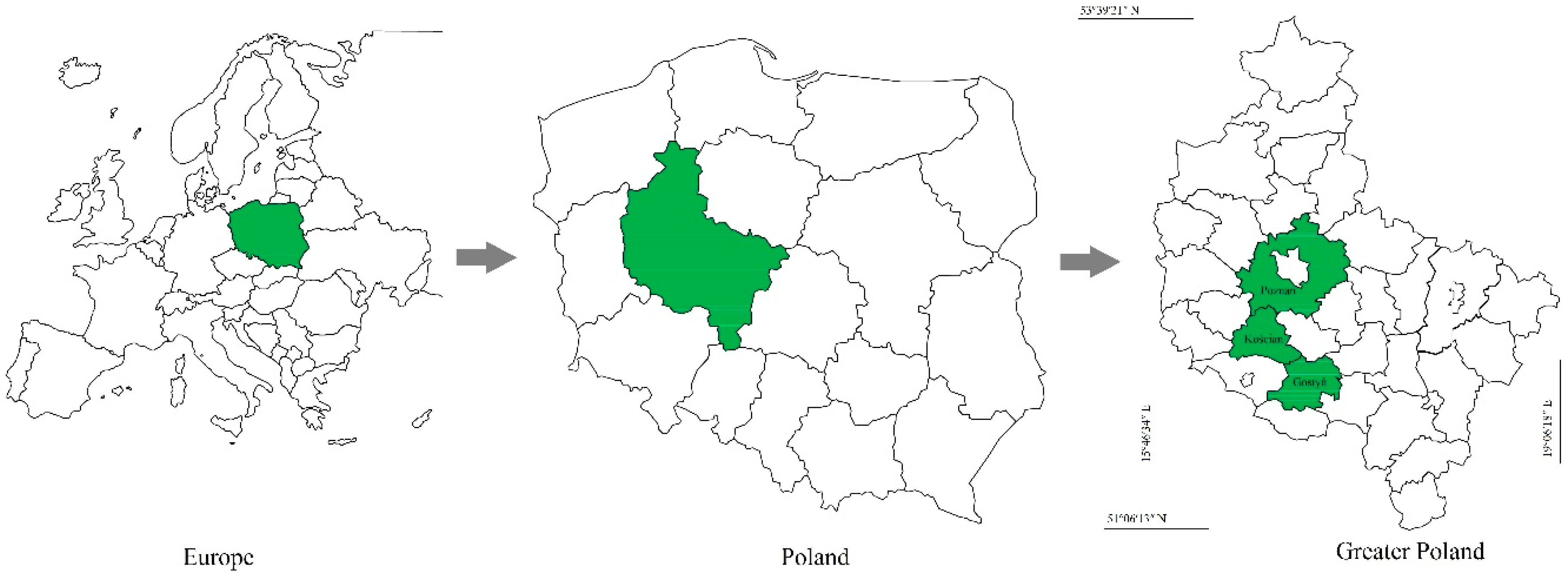
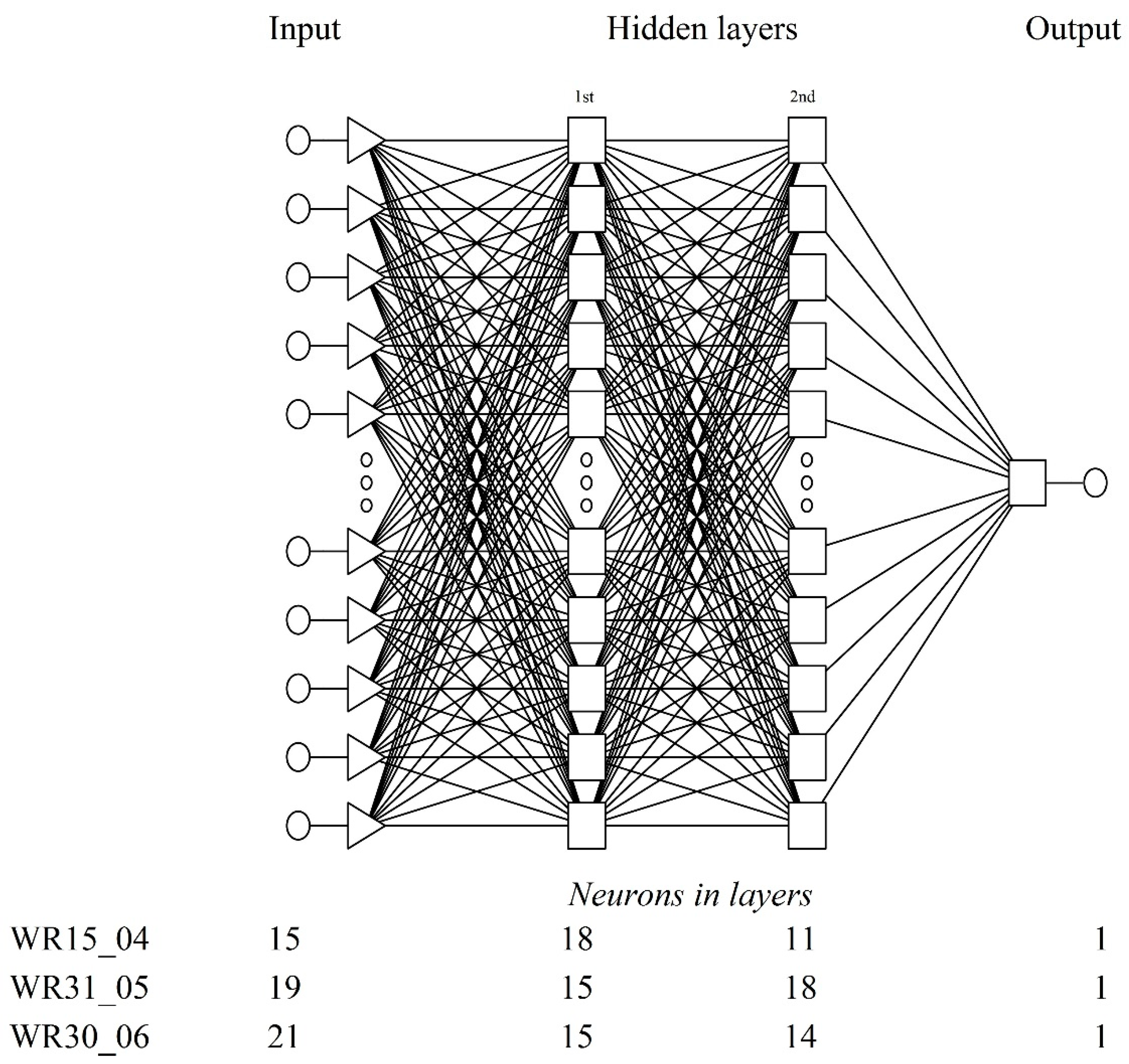
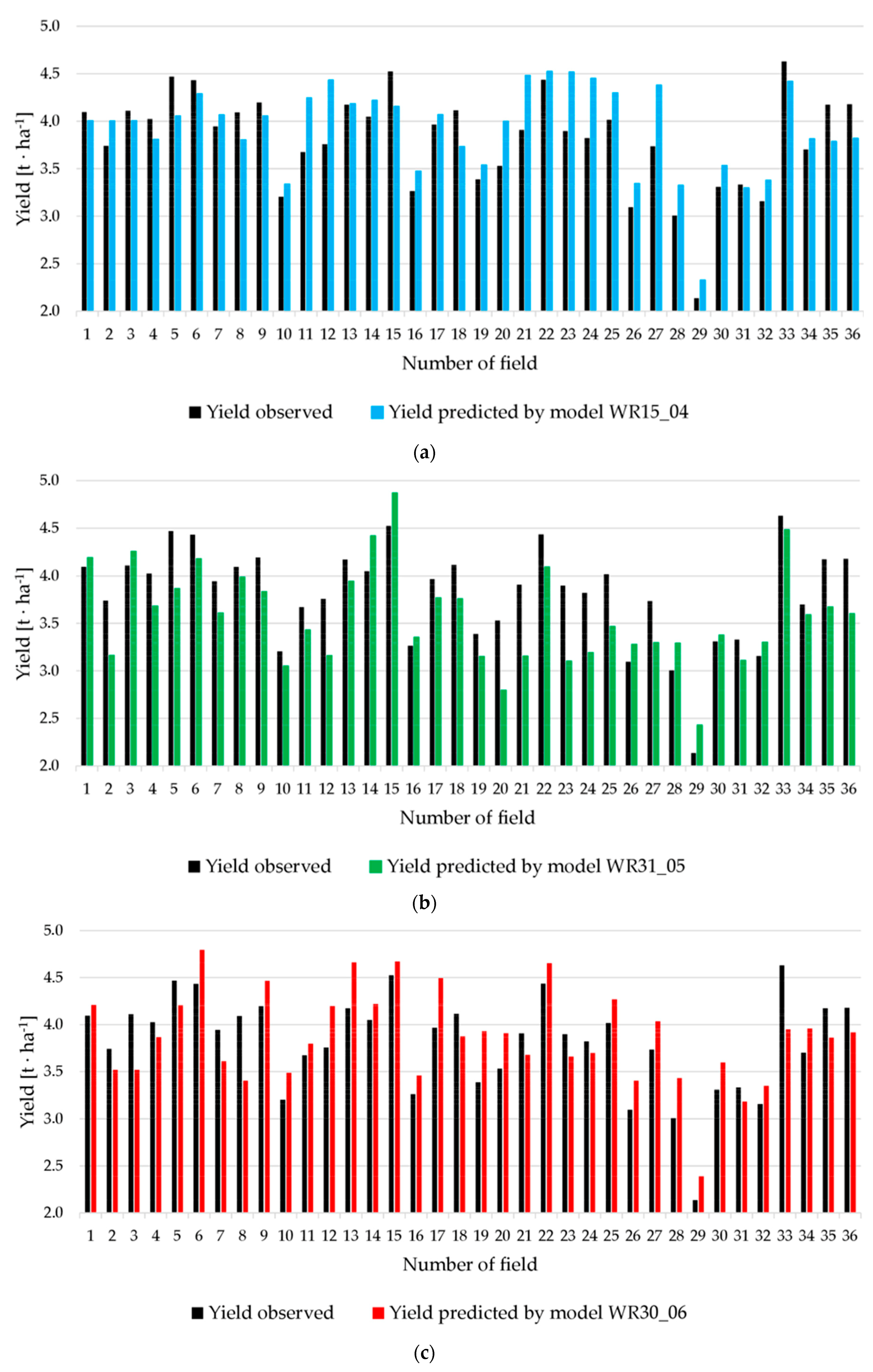
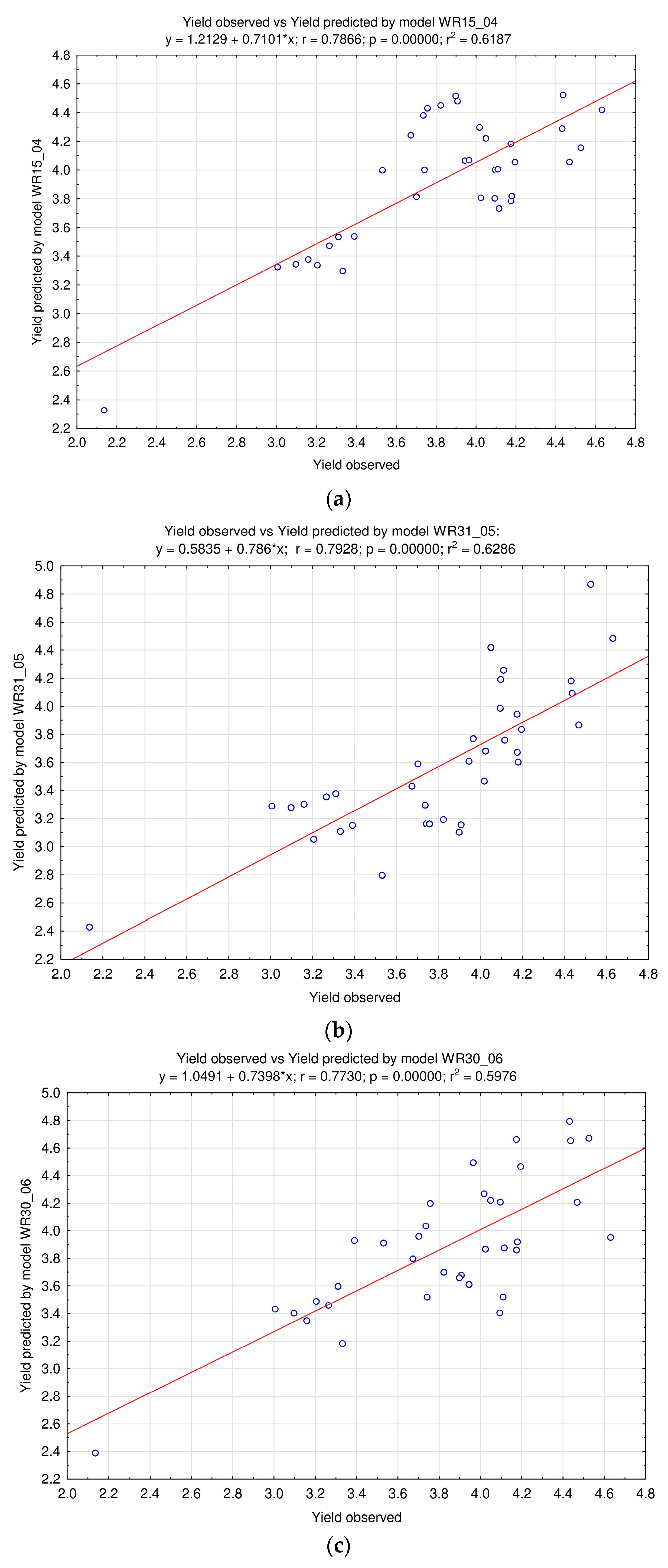
| Set A | Set B | |||||||
|---|---|---|---|---|---|---|---|---|
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| Number of fields | 32 | 49 | 48 | 50 | 45 | 28 | 40 | 36 |
| Symbol | Unit of Measure | Variable Name | Model WR15_04 | Model WR31_05 | Model WR30_06 | The Scope of Data |
|---|---|---|---|---|---|---|
| R9-12_LY | mm | The sum of precipitation from 1 September to 31 December of the previous year | + | + | + | 63–234 |
| T9-12_LY | °C | The average air temperature from 1 September to 31 December of the previous year | + | + | + | 4.9–9.4 |
| R1-4_CY | mm | The sum of precipitation from 1 January to 15 April of the current year | + | + | + | 59–185 |
| T1-4_CY | °C | The average air temperature from 1 January to 15 April of the current year | + | + | + | −0.4–4.9 |
| R4_CY | mm | The sum of precipitation from 1 April to 30 April of the current year | - | + | + | 8.7–60.4 |
| T4_CY | °C | The average air temperature from 1 April to 30 April of the current year | - | + | + | 5.9–12.2 |
| R5_CY | mm | The sum of precipitation from 1 May to 31 May of the current year | - | + | + | 14.2–132.5 |
| T5_CY | °C | The average air temperature from 1 May to 31 May of the current year | - | + | + | 11.8–16.2 |
| R6_CY | mm | The sum of precipitation from 1 June to 30 June of the current year | - | - | + | 15–121 |
| T6_CY | °C | The average air temperature from 1 June to 30 June of the current year | - | - | + | 14.2–19.6 |
| N_LY | kg ha−1 | The sum of N fertilization—autumn in the previous year | + | + | + | 0–41 |
| N_CY | kg ha−1 | The sum of N fertilization—spring in the current year | + | + | + | 0–175 |
| P2O5_CY | kg ha−1 | The sum of P2O5 fertilization in the current year | + | + | + | 0–104 |
| K2O_CY | kg ha−1 | The sum of K2O fertilization in the current year | + | + | + | 0–234 |
| MGO_CY | kg ha−1 | The sum of MgO fertilization in the current year | + | + | + | 0–298 |
| SO3_CY | kg ha−1 | The sum of sulfate ions (VI) fertilization in the current year | + | + | + | 14–115 |
| B_CY | g ha−1 | The sum of B fertilization in the current year | + | + | + | 0–3.66 |
| CU_CY | g ha−1 | The sum of Cu fertilization in the current year | + | + | + | 10–487 |
| MN_CY | g ha−1 | The sum of Mn fertilization in the current year | + | + | + | 70–600 |
| MO_CY | g ha−1 | The sum of Mo fertilization in the current year | + | + | + | 0–60 |
| ZN_CY | g ha−1 | The sum of Zn fertilization in the current year | + | + | + | 10–560 |
| WR15_04 | WR31_05 | WR30_06 | |
|---|---|---|---|
| Neural Network Structure | MLP 15:15-18-11-1:1 | MLP 19:19-15-18-1:1 | MLP 21:21-15-14-1:1 |
| Learning error | 0.1229 | 0.1053 | 0.0924 |
| Validation error | 0.0625 | 0.1051 | 0.1053 |
| Test error | 0.1283 | 0.1258 | 0.1277 |
| Mean | 3.3626 | 3.3626 | 3.3626 |
| Standard deviation | 1.0703 | 1.0703 | 1.0703 |
| Average error | 0.0762 | −0.0401 | −0.0245 |
| Deviation error | 0.7183 | 0.6264 | 0.6098 |
| Mean Absolute error | 0.5819 | 0.5021 | 0.4771 |
| Quotient deviations | 0.6711 | 0.5852 | 0.5697 |
| Correlation | 0.7413 | 0.8127 | 0.8218 |
| Model | RAE [-] | RMS [t ha−1] | MAE [t ha−1] | MAPE [%] |
|---|---|---|---|---|
| WR15_04 | 0.075 | 0.337 | 0.282 | 7.51 |
| WR31_05 | 0.091 | 0.401 | 0.344 | 7.85 |
| WR30_06 | 0.081 | 0.341 | 0.306 | 8.12 |
| Variable | Model | |||||
|---|---|---|---|---|---|---|
| WR15_04 | WR31_05 | WR30_06 | ||||
| Quotient | Rank | Quotient | Rank | Quotient | Rank | |
| R9-12_LY | 1.1669 | 3 | 1.3693 | 1 | 1.1508 | 1 |
| T9-12_LY | 1.1933 | 2 | 1.0366 | 10 | 1.0529 | 9 |
| R1-4_CY | 1.0224 | 6 | 1.0599 | 6 | 1.0252 | 16 |
| T1-4_CY | 1.0250 | 5 | 1.0689 | 5 | 1.1034 | 3 |
| R4_CY | - | - | 1.0698 | 4 | 1.0906 | 4 |
| T4_CY | - | - | 1.0403 | 9 | 1.0376 | 12 |
| R5_CY | - | - | 1.1412 | 3 | 1.0881 | 5 |
| T5_CY | - | - | 1.2512 | 2 | 1.0340 | 14 |
| R6_CY | - | - | - | - | 1.0527 | 10 |
| T6_CY | - | - | - | - | 1.0471 | 11 |
| N_LY | 0.9966 | 14 | 1.0031 | 17 | 1.0296 | 15 |
| N_CY | 1.0124 | 10 | 1.0167 | 12 | 1.0163 | 19 |
| P2O5_CY | 1.0000 | 12 | 0.9796 | 19 | 0.9854 | 21 |
| K2O_CY | 0.9975 | 13 | 1.0043 | 15 | 1.0086 | 20 |
| MGO_CY | 1.0143 | 8 | 1.0550 | 7 | 1.1308 | 2 |
| SO3_CY | 1.0340 | 4 | 1.0295 | 11 | 1.0655 | 6 |
| B_CY | 1.0034 | 11 | 0.9911 | 18 | 1.0357 | 13 |
| CU_CY | 0.9905 | 15 | 1.0103 | 14 | 1.0200 | 18 |
| MN_CY | 1.0138 | 9 | 1.0033 | 16 | 1.0589 | 8 |
| MO_CY | 1.1935 | 1 | 1.0540 | 8 | 1.0650 | 7 |
| ZN_CY | 1.0220 | 7 | 1.0135 | 13 | 1.0239 | 17 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niedbała, G. Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Rapeseed. Sustainability 2019, 11, 533. https://doi.org/10.3390/su11020533
Niedbała G. Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Rapeseed. Sustainability. 2019; 11(2):533. https://doi.org/10.3390/su11020533
Chicago/Turabian StyleNiedbała, Gniewko. 2019. "Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Rapeseed" Sustainability 11, no. 2: 533. https://doi.org/10.3390/su11020533
APA StyleNiedbała, G. (2019). Application of Artificial Neural Networks for Multi-Criteria Yield Prediction of Winter Rapeseed. Sustainability, 11(2), 533. https://doi.org/10.3390/su11020533





