Collection of Solid Waste in Municipal Areas: Urban Logistics
Abstract
1. Introduction
2. Literature Review
2.1. Reverse Logistics
2.2. Municipal Solid Waste (MSW Collection)
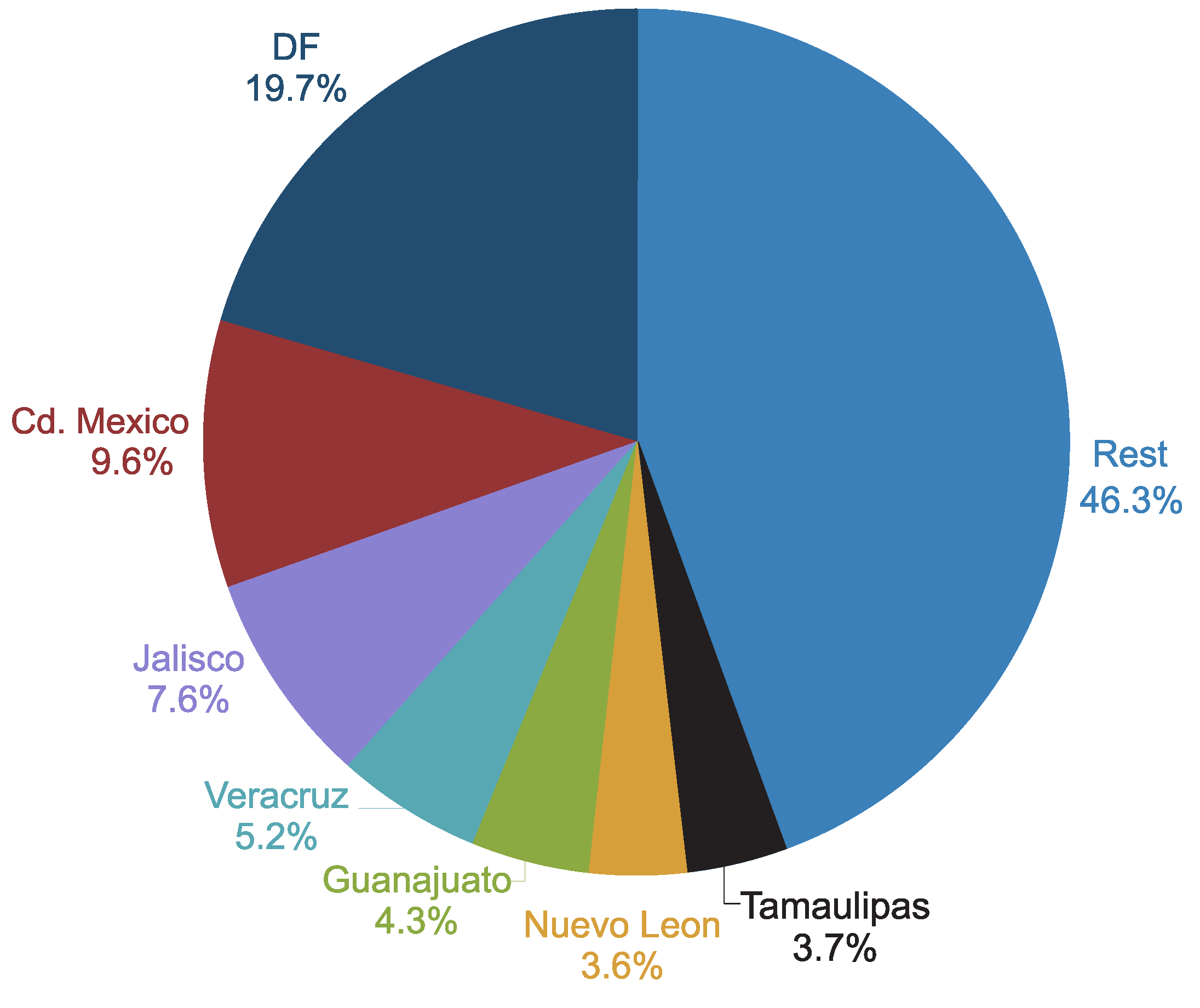
3. Case Study: San Nicolas De Los Garza
3.1. Model 1
3.2. Model 2
3.3. Other Considerations
4. Results And Analysis
4.1. Results of Model 1
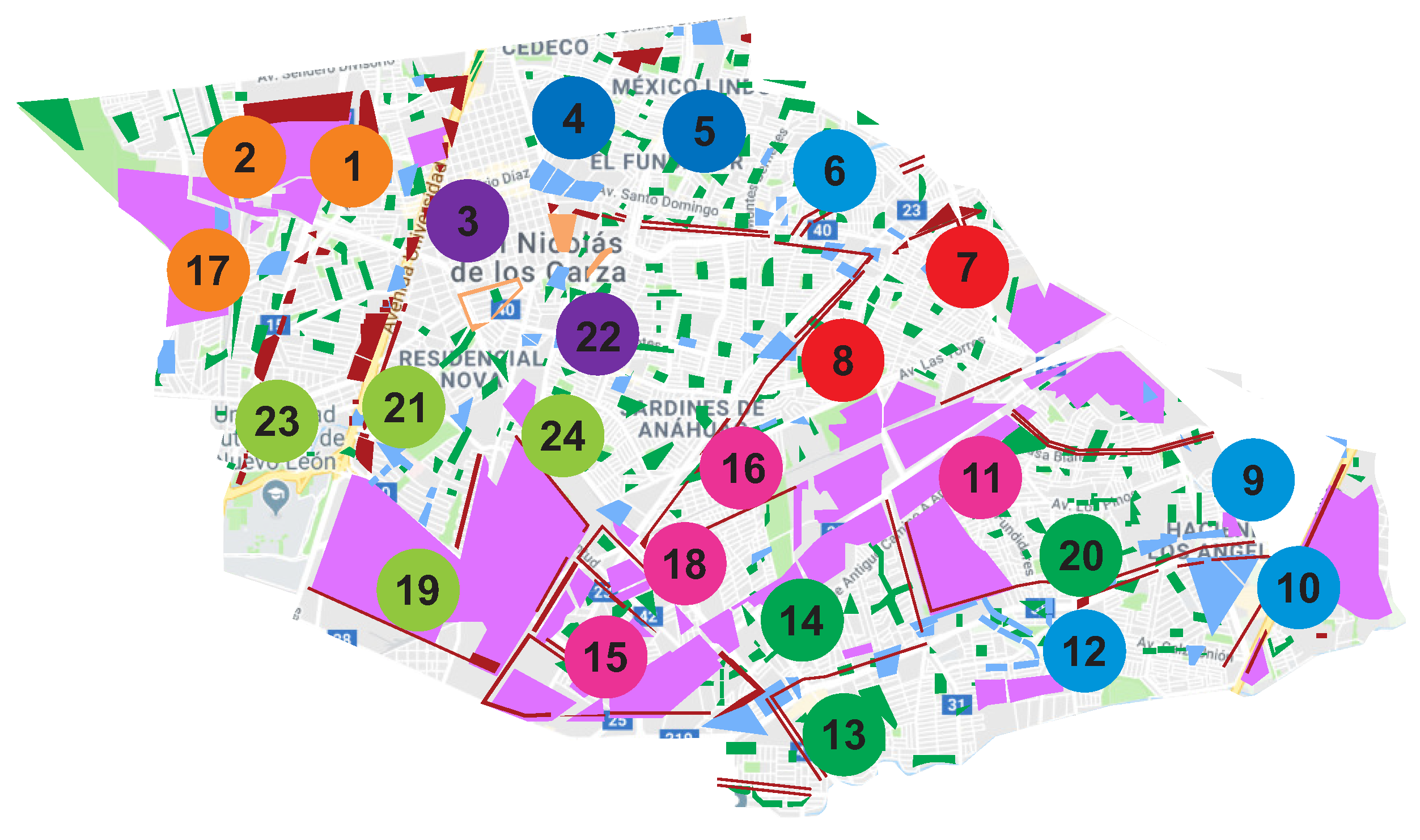
4.2. Results of Model 2
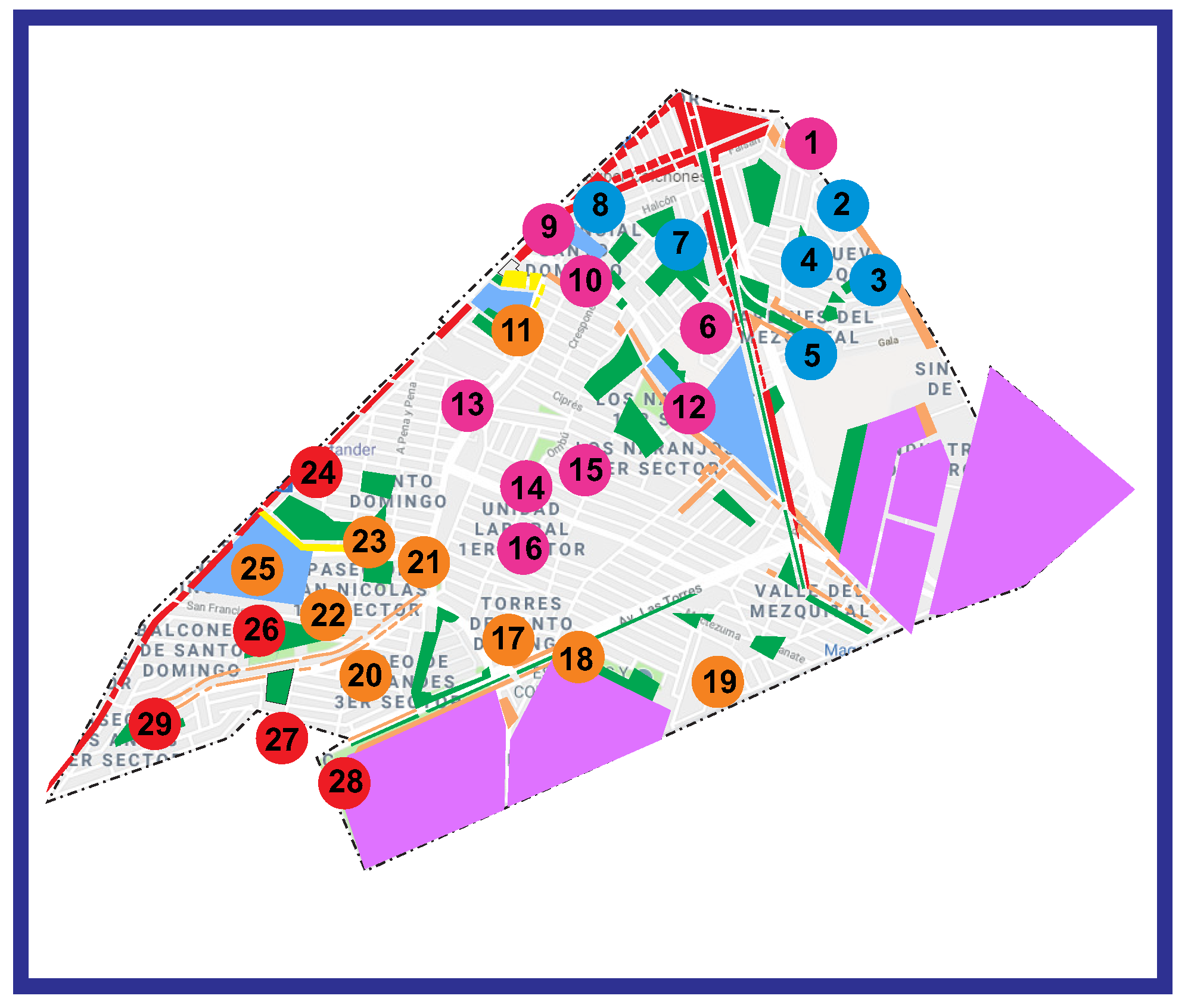
4.3. Results Algorithm: Allocation of Non-Contiguous Parks
5. Conclusions
6. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Robusté, F.; Campos, J.M.; Galván, D. Nace la Logistica Urbana. In Proceedings of the Actas del IV Congreso de Ingeniería del Transporte, Valencia, Spain, 7–9 June 2000; Volume 2, pp. 683–691. [Google Scholar]
- Taniguchi, E.; Thompson, R.G.; Yamada, T. Recent Trends and Innovations in Modelling City Logistics. Procedia Soc. Behav. Sci. 2014, 125, 4–14. [Google Scholar] [CrossRef]
- Winkenbach, M.; Kleindorfer, P.R.; Spinler, S. Enabling Urban Logistics Services at La Poste through Multi-Echelon Location-Routing. Transp. Sci. 2015, 50, 1–21. [Google Scholar]
- Macário, R.; Galelo, A.; Martins, P.M. Business Models in Urban Logistics. Ing. Desarro. 2008, 24, 77–96. [Google Scholar]
- Villamizar, A.M.; Torres, J.M.; Padilla, N.H. Mathematical Programming Modeling and Resolution of the Location-Routing Problem in Urban Logistics1. Ing. Univ. 2014, 18, 271–289. [Google Scholar]
- Álvarez, J.; Eslava, A. La logística urbana, la ciudad logística y el ordenamiento territorial logístico. Reto 2016, 4, 21–40. [Google Scholar]
- Dotoli, M.; Epicoco, N. A Vehicle Routing Technique for Hazardous Waste Collection. IFAC Pap. Online 2017, 50, 9694–9699. [Google Scholar] [CrossRef]
- Buhrkal, K.; Larsen, A.; Ropke, S. The Waste Collection Vehicle Routing Problem with Time Windows in a City Logistics Context. Procedia Soc. Behav. Sci. 2012, 39, 241–254. [Google Scholar] [CrossRef]
- INEGI. Banco de Indicadores; Technical Report; Instituto Nacional de Estadistica y Geografia: Mexico City, Mexico, 2015; Available online: http://mapserver.inegi.org.mx/ambiental/map/indexV3FFM.html (accessed on 1 October 2019).
- Arriaga, E.P.; Morenoz, J.R.; Caro, G.V. Los sistemas de recolección de residuos sólidos (Los métodos y sus aplicaciones). CienciaUAT 2007, 1, 58–60. [Google Scholar]
- Galicia, F.G. Análisis del Sistema de Recolección de Residuos Sólidos Urbanos en el Centro Histórico de Morelia, aplicando Sistemas de Información Geográfica (SIG). Master’s Thesis, Universidad Nacional Autónoma de México, Mexico City, Mexico, 2008. [Google Scholar]
- SEDESOL. Manual Para el Diseño de Rutas de Recolección de Residuos Sólidos Municipales; Secretaría de Desarrollo Social. 1997. Available online: http://www.inapam.gob.mx/work/models/SEDESOL/Resource/1592/1/images/ManualTecnicosobreGeneracionRecoleccion.pdf (accessed on 1 October 2019).
- Mercado, L. Logística Inversa; Technical Report; Revista Industria al dia; Universidad de Cordoba: Cordoba, Colombia, 2005; Available online: http://www.unicordoba.edu.co/revistas/vieja_industrialaldia/documentos/ed.1/logistica_inversa.pdf (accessed on 1 October 2019).
- Purkayastha, D.; Majumder, M.; Chakrabarti, S. Collection and recycle bin location-allocation problem in solid waste management: A review. Pollution 2015, 1, 175–191. [Google Scholar]
- Group, W.B. What a Waste 2.0 A Global Snapshot of Solid Waste Management to 2050; Technical report; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Uriarte-Miranda, M.L.; Caballero-Morales, S.O.; Martinez-Flores, J.L.; Cano-Olivos, P.; Akulova, A.A. Reverse Logistic Strategy for the Management of Tire Waste in Mexico and Russia: Review and Conceptual Model. Sustainability 2018, 10, 3398. [Google Scholar] [CrossRef]
- Hage, O.; Soderholm, P.; Berglund, C. Norms and economic motivation in household recycling: Empirical evidence from Sweden. Resour. Conserv. Recycl. 2015, 53, 155–165. [Google Scholar] [CrossRef]
- Castillo, L.D.R.; Gallardo Izquierdo, A.; Pinero Guilamany, A. La distancia del domicilio al contenedor como un factor influyente en la frecuencia de separación de residuos urbanos. In Hacia la sustentabilidad: Los Residuos Solidos Como Fuente de Energía y Materia Prima; Red iberoamericana en gestion y aprovechamiento de residuos (REDISA), 2011; pp. 209–213. Available online: http://www.redisa.net/doc/artSim2011/GestionYPoliticaAmbiental/La%20distancia%20del%20domicilio%20al%20contenedor%20como%20un%20factor%20influyente%20en%20la%20frecuencia%20de%20separaci%C3%B3n%20de%20residuos%20urbanos.pdf (accessed on 1 October 2019).
- Chang, N.B.; Wei, Y.L. Strategic Planning of Recycling Drop-Off Stations and Collection Network by Multiobjective Programming. Environ. Manag. 1999, 24, 247–263. [Google Scholar] [CrossRef]
- Gautam, A.K.; Kumar, S. Strategic planning of recycling options by multi-objective programming in a GIS environment. Clean Technol. Environ. Policy 2005, 7, 306–316. [Google Scholar] [CrossRef]
- Alonso, A.B. Localizacion optima de contenedores de residuos solidos urbanos en Alcalá de Henares. M+A Rev. Electrón. Medioambiente 2016, 17, 1–23. [Google Scholar]
- Simon, S.; Demaldé, J.; Hernandez, J.; Carnero, M. Optimización de Recorridos para la Recolección de Residuos Infecciosos. Inf. Tecnol. 2012, 23, 125–132. [Google Scholar] [CrossRef]
- Bing, X.; de Keizer, M.; Bloemhof-Ruwaard, J.M.; van der Vorst, J.G. Vehicle routing for the eco-efficient collection of household plastic wastes. Waste Manag. 2014, 34, 719–729. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, A.A.; Butrón, E.G. Asignación de rutas de vehículos para un sistema de recolección de residuos sólidos en la acera. Rev. Ing. 2001, 13, 5–11. [Google Scholar] [CrossRef]
- Aguilar, J.A.A.; Zambrano, M.E.J. Mejora del servicio de recolección de residuos sólidos urbanos empleando herramientas SIG: Un caso de estudio. Ingeniería 2015, 19, 118–1128. [Google Scholar]
- Pastor, J.M. Optimizacion de la localizacion y recogida de residuos sólidos urbanos (RSU). Master’s Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2013. [Google Scholar]
- Regidor, M.P.M.; de Lacalle, J.G.L. Estado del arte en procesos de zonificación. Rev. GeoFocus 2009, 11, 155–181. [Google Scholar]
- Zoltners, A.; Sinha, P. Sales territory alignment: A review and model. Manag. Sci. 1983, 29, 1237–1256. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.Z.; Fernández, E. A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Comput. Oper. Res. 2009, 36, 755–776. [Google Scholar] [CrossRef]
- Armstrong, M.; Honey, R. A spatial decision support system for school redistricting. URISA J. 1993, 5, 40–52. [Google Scholar]
- Muyldermans, L.; Cattrysse, D.; Oudheusden, D.V.; Lotan, T. Districting for salt spreading operations. Eur. J. Oper. Res. 2002, 139, 521–532. [Google Scholar] [CrossRef]
- Tiede, D.; Strobl, J. Polygon-based regionalisation in a GIS environment. In Proceedings of the Trends in Knowledge-Based Landscape Modeling, Dessau, Germany, 18–20 May 2006; pp. 54–59. [Google Scholar]
- Kalcsics, J.; Nickel, S.; Schröder, M. A Generic Geometric Approach to Territory Design and Districting; Berichte des Fraunhofer ITWM; Fraunhofer-Institut fur Techno: Kaiserslautern, Germany, 2009; pp. 1–32. [Google Scholar]
- Benabdallah, S.; Wright, J.R. Multiple subregion allocation models. Asce J. Urban Plan. Dev. 1992, 118, 24–40. [Google Scholar] [CrossRef]
- García, E.R.; Andrade, M.A.G. Compacidad en celdas aplicada al diseño de zonas electorales. Supplement 2008, 5, 73–95. [Google Scholar]
- Díaz, A.; Bernábe, B.; Luna, D. Relación lagrangeana para el problema de particionamiento de áreas geográficas. Rev. Mat. Teor. Apl. 2012, 19, 169–181. [Google Scholar]
- Phuntsho, S.; Dulal, I.; Yangden, D.; Tenzin, U.; Herat, S.; Shon, H.; Vigneswaran, S. Studying municipal solid waste generation and composition in the urban areas of Bhutan. Waste Manag. Res. 2010, 28, 545–551. [Google Scholar] [CrossRef] [PubMed]
- Jayakody, K.P.K.; Jayakody, L.L.; Karunarathna, A.K.; Basnayake, B.F. Municipal Solid Waste Management System and Solid Waste Characterization at Hikkaduwa Secretariat; Technical Report; Department of Agricultural Engineering, University of Peradeniya: Peradeniya, Sri Lanka, 2008. [Google Scholar]
- Kaosol, T. Sustainable Solutions for Municipal Solid Waste Management in Thailand. Int. J. Environ. Ecol. Eng. 2009, 3, 399–404. [Google Scholar]
- Ayantoyinbo, B.B.; Adepoju, O.O. Analysis of Solid Waste Management Logistics and Its Attendant Challenges in Lagos Metropolis. Logistics 2018, 2, 11. [Google Scholar] [CrossRef]
- Laureri, F.; Minciardi, R.; Robba, M. An algorithm for the optimal collection of wet waste. Waste Manag. 2010, 48, 56–63. [Google Scholar] [CrossRef]
- Son, L.H.; Louati, A. Modeling municipal solid waste collection: A generalized vehicle routing model with multiple transfer stations, gather sites and inhomogeneous vehicles in time windows. Waste Manag. 2016, 52, 34–49. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Bhattacharyya, B.K. Optimization of municipal solid waste collection and transportation routes. Waste Manag. 2015, 43, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Gobierno-Municipal, S. Plan de Desarrollo Urbano Sustentable 2013–2033 San Nicolás de Los Garza. 2013. Available online: http://transparencia.sanicolas.gob.mx/LTAINL/dic13/plan%20de%20desarrollo%20sustentable.pdf (accessed on 15 December 2016).
- Calva, L.F.L.; de la Torre, R.; Reyes, A.G.; Chamussy, L.R.; Garcia, C.R.; Dominguez, F.V. El desarrollo humano de los municipios en México. Technical Report. 2015. Available online: http://www.mx.undp.org/content/mexico/es/home/library/poverty/informe-de-desarrollo-humano-municipal-2010-2015--transformando-.html (accessed on 1 October 2019).
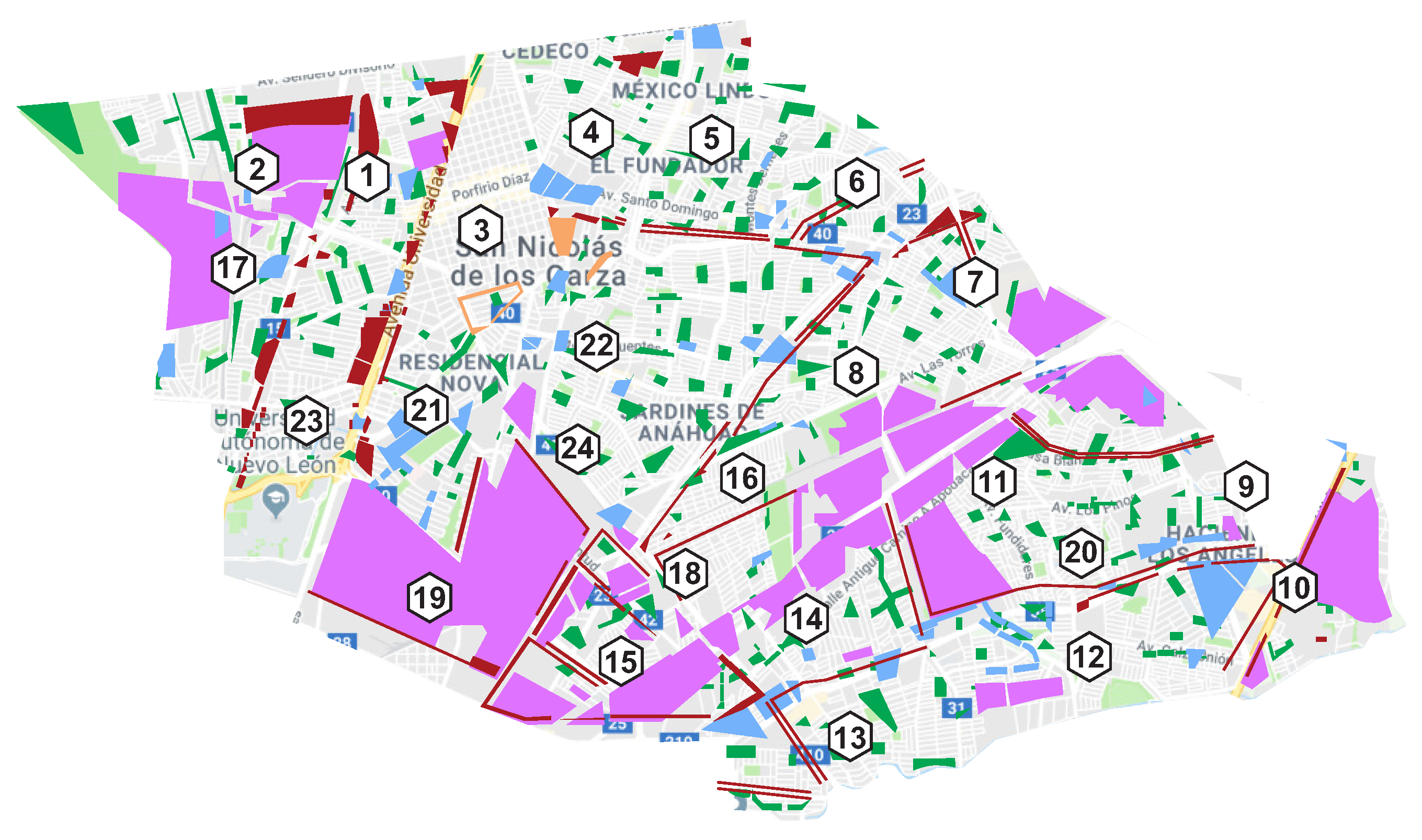


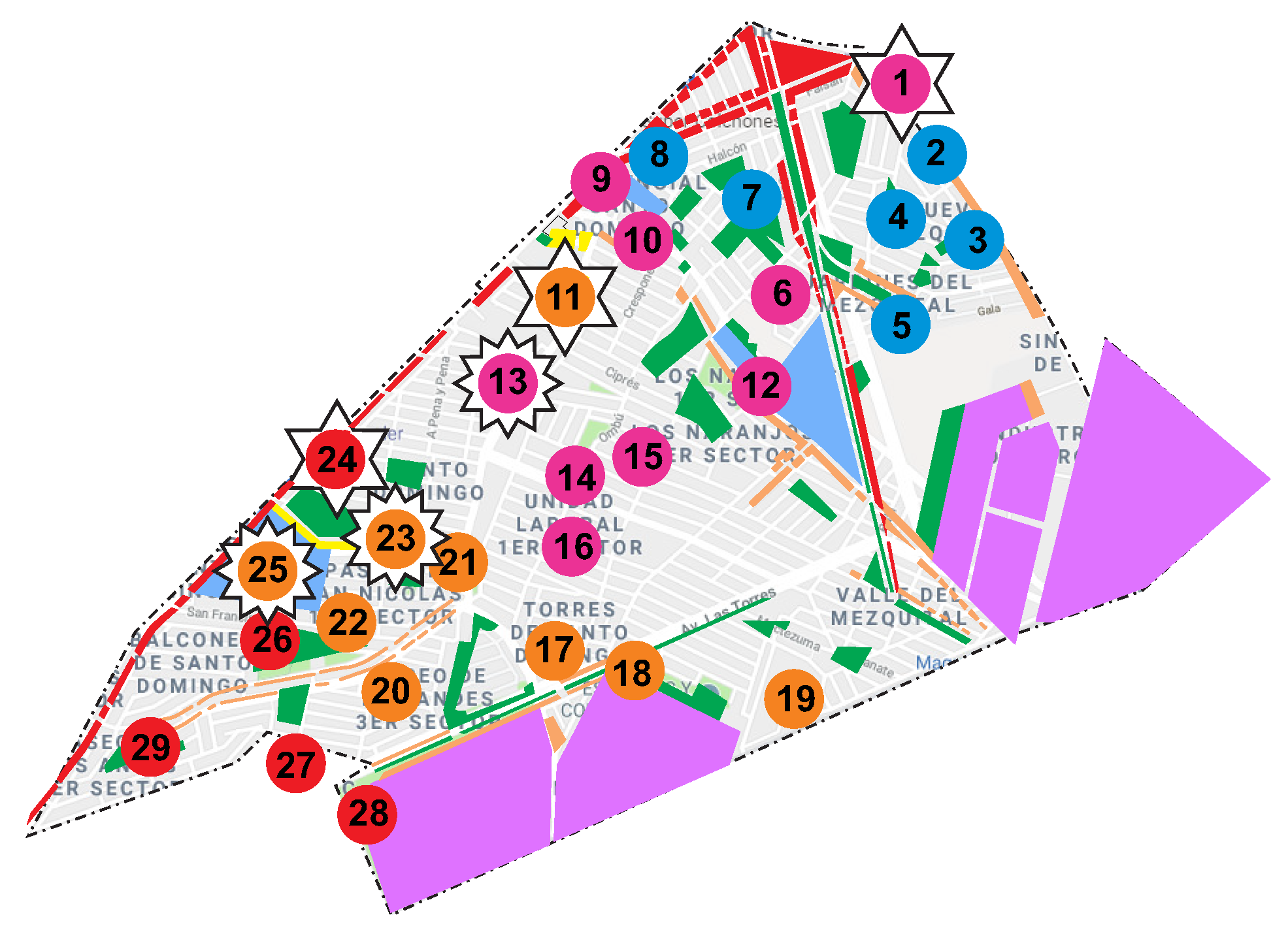
| Districts | Parks | Activity Measure m | % m |
|---|---|---|---|
| 1. Casa Bella | 11 | 71,344.02 | 5% |
| 2. Balcones | 3 | 25,901.85 | 1.8% |
| 3. Centro | 2 | 11,771.30 | 0.8% |
| 4. CEDECO | 18 | 82,428.73 | 5.7% |
| 5. El Refugio | 20 | 51,673.84 | 3.6% |
| 6. Vicente Guerrero | 10 | 74,529.20 | 5.2% |
| 7. Santo Domingo | 12 | 89,845.99 | 6.3% |
| 8. Del Paseo | 17 | 10,6051.64 | 7.4% |
| 9. San Cristobal | 7 | 27,787.56 | 1.9% |
| 10. La Fe | 4 | 27,285.80 | 1.9% |
| 11. Casa Blanca | 13 | 95,637.52 | 6.7% |
| 12. Talaverna | 14 | 130,072.60 | 9.1% |
| 13. Del Vidrio | 14 | 52,549.01 | 3.7% |
| 14. Constituyentes | 19 | 33,960.43 | 2.4% |
| 15. Nogalar | 8 | 45,471.45 | 3.2% |
| 16. Pedregal | 5 | 25,059.05 | 1.7% |
| 17. Residencial Anahuac | 7 | 51,956.72 | 3.6% |
| 18. La Grange | 6 | 8417.01 | 0.6% |
| 19. Industrial | 0 | 0 | 0% |
| 20. Andalucia | 19 | 97,414.25 | 6.8% |
| 21. Cuauhtemoc | 12 | 77,329.98 | 5.4% |
| 22. Las Puentes | 20 | 137,946.42 | 9.6% |
| 23. Anahuac | 11 | 42,991.38 | 3% |
| 24. Jardines de Anahuac | 13 | 67,664.64 | 4.7% |
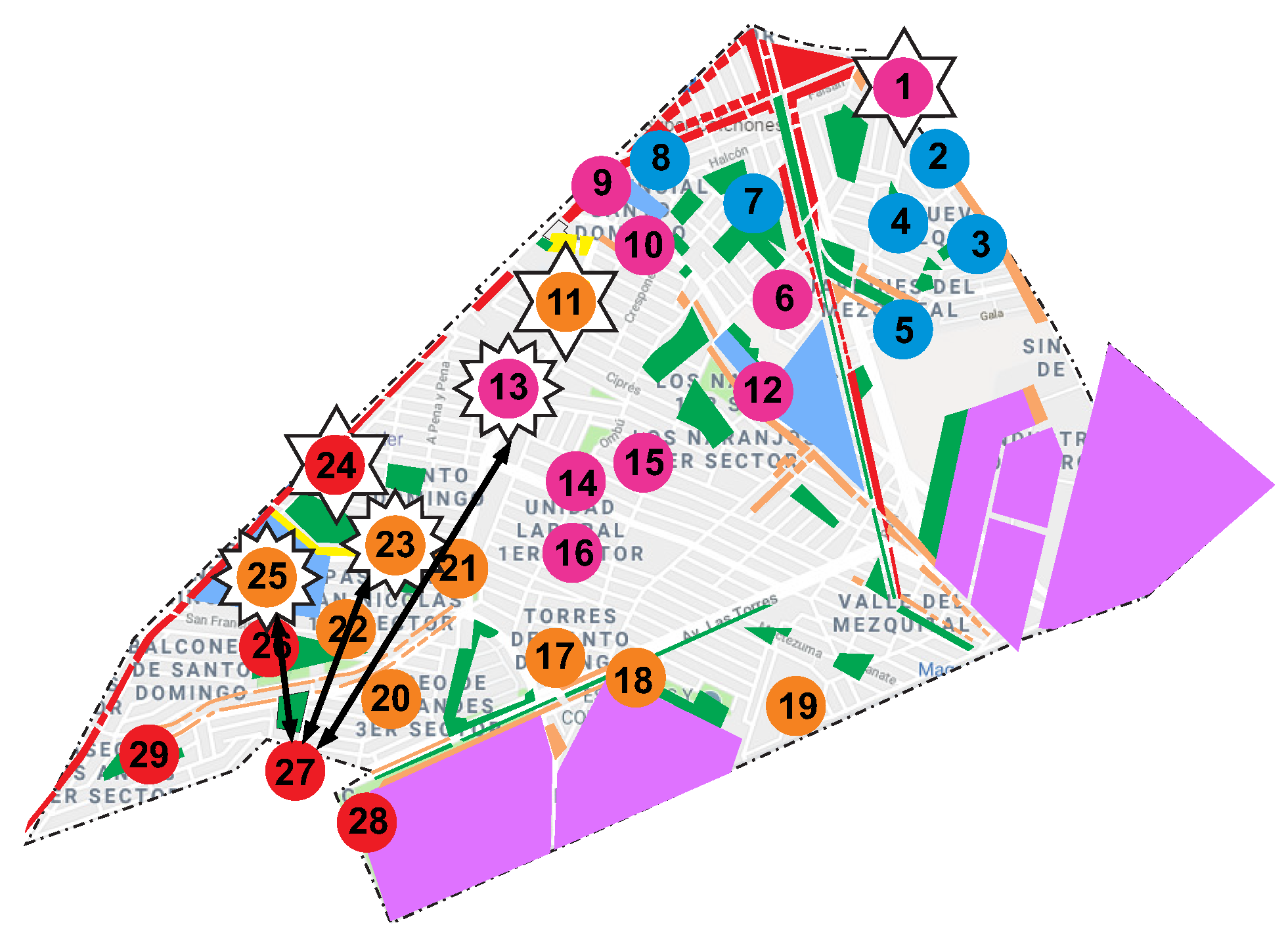
| Algorithm: Allocation of Non-Contiguous Parks |
|---|
| Input: Matrix of adjacency of the parks in each formed territory, where an element takes the value of 1 if the parks are adjacent and 0 otherwise; Adjacency matrix of all district parks; Matrix of distances between each park; Table of results of model 2 containing the measure of activity of each territory. |
| Output: Contiguous parks. |
| 1. While Criterion of contiguity is not met do |
| 2. Identify a territory that contains at least one non-contiguous park. |
| 3. Select a non-contiguous territory. |
| 4. Search the adjacent parks of the park selected from the previous step. |
| 5. for Adjacent parks do |
| Comparison between distances from the parks to the center of territory. |
| end for |
| 6. Select the park with the shortest distance to the center of territory. |
| 7. To realize interchange between the park with smaller distance to the center of territory and the non-contiguous park. |
| 8. Calculate the activity measure of the two territory formed. |
| 9. Evaluate criterion of contiguity. |
| end while |
| 10. return Compliance with the criterion of contiguity of the parks and new territories formed. |
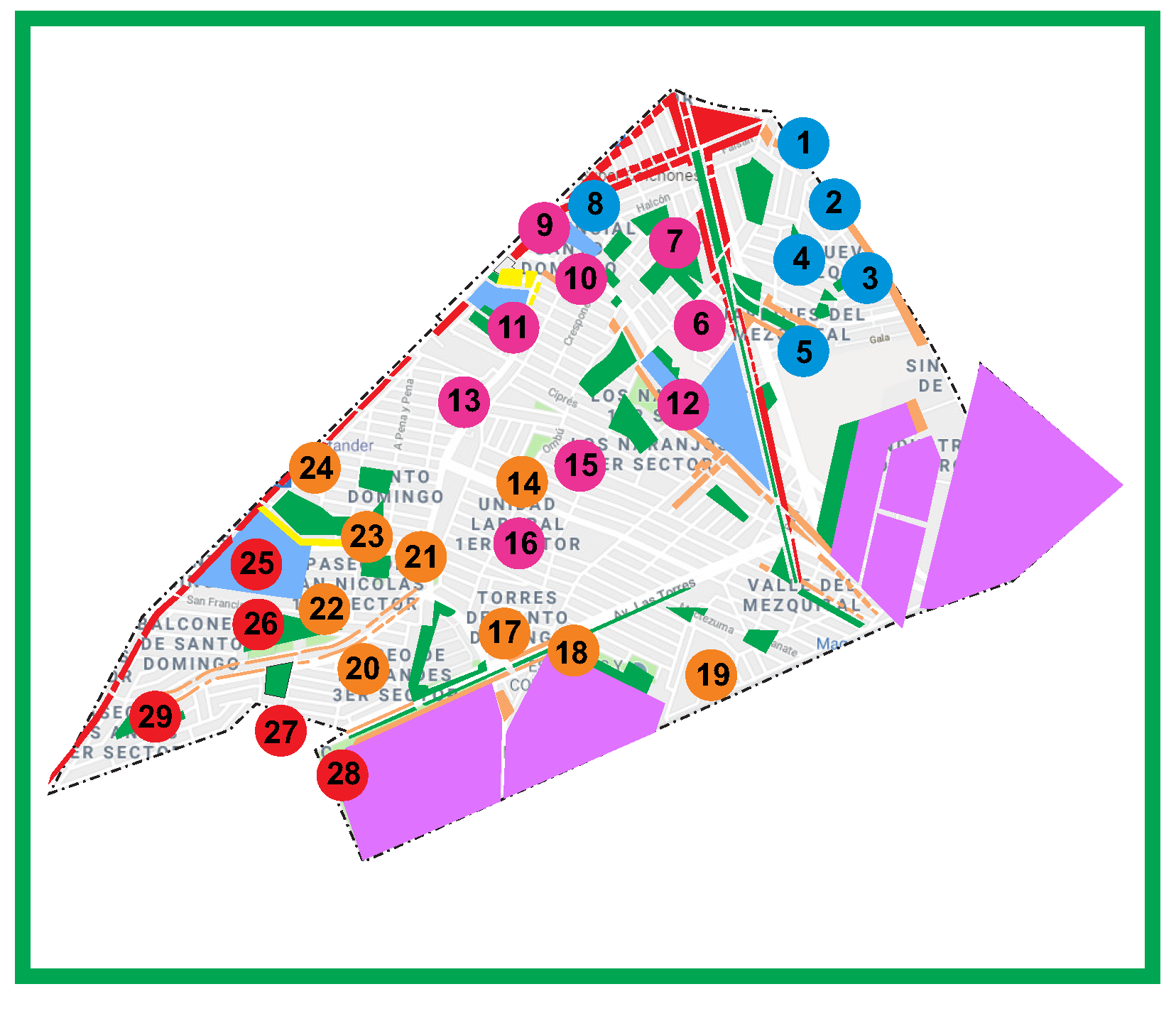
| Districts | Provider | Parks | Activity Measure m |
|---|---|---|---|
| 1, 2, 17 | Provider A | 21 | 149,202.59 |
| 4, 5, 6 | Provider B | 48 | 208,631.77 |
| 3, 22 | Provider C | 22 | 149,717.72 |
| 19, 21, 23, 24 | Provider D | 36 | 187,986 |
| 11, 15, 16, 18 | Provider E | 32 | 174,585.03 |
| 7, 8 | Provider F | 29 | 195 897.63 |
| 13, 14, 20 | Provider G | 52 | 183,923.69 |
| 9, 10, 12 | Provider H | 25 | 185,145.96 |
| Weeks | Parks | Activity Measure m |
|---|---|---|
| Week 1 | 1–11, 17, 21 | 53,658.57 |
| Week 2 | 12–16, 18, 19, 22 | 52,728.17 |
| Week 3 | 20, 23, 32–36 | 52,708.06 |
| Week 4 | 24–31 | 46,947.11 |
| Week | Parks | Activity Measure m |
|---|---|---|
| Week 1 | 2–5, 7, 8 | 52,387 |
| Week 2 | 1, 6, 9, 10–16 | 48,546 |
| Week 3 | 11, 17–23, 25 | 50,697 |
| Week 4 | 24, 26–29 | 44,265 |
| Week | Parks | Activity Measure m |
|---|---|---|
| Week 1 | 1–5, 8 | 43,580 |
| Week 2 | 6, 7, 9, 10–13, 15, 16 | 56,877 |
| Week 3 | 14, 17–24 | 48,893 |
| Week 4 | 25–29 | 46,546 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saucedo Martinez, J.A.; Mendoza, A.; Alvarado Vazquez, M.d.R. Collection of Solid Waste in Municipal Areas: Urban Logistics. Sustainability 2019, 11, 5442. https://doi.org/10.3390/su11195442
Saucedo Martinez JA, Mendoza A, Alvarado Vazquez MdR. Collection of Solid Waste in Municipal Areas: Urban Logistics. Sustainability. 2019; 11(19):5442. https://doi.org/10.3390/su11195442
Chicago/Turabian StyleSaucedo Martinez, Jania Astrid, Abraham Mendoza, and Maria del Rosario Alvarado Vazquez. 2019. "Collection of Solid Waste in Municipal Areas: Urban Logistics" Sustainability 11, no. 19: 5442. https://doi.org/10.3390/su11195442
APA StyleSaucedo Martinez, J. A., Mendoza, A., & Alvarado Vazquez, M. d. R. (2019). Collection of Solid Waste in Municipal Areas: Urban Logistics. Sustainability, 11(19), 5442. https://doi.org/10.3390/su11195442






