Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area
Abstract
1. Introduction
- Construct and compare changes in network indicators across unimodal networks of subway and bus, in conjunction with an integrated network of both bus and subway, using link distances as weights.
- Analyze if the networks being studied show small-world and scale-free features, which are indicators of network resilience.
2. Literature Review
2.1. Application of Graph Theory in the Public Transportation Field
2.2. Contribution to the Literature
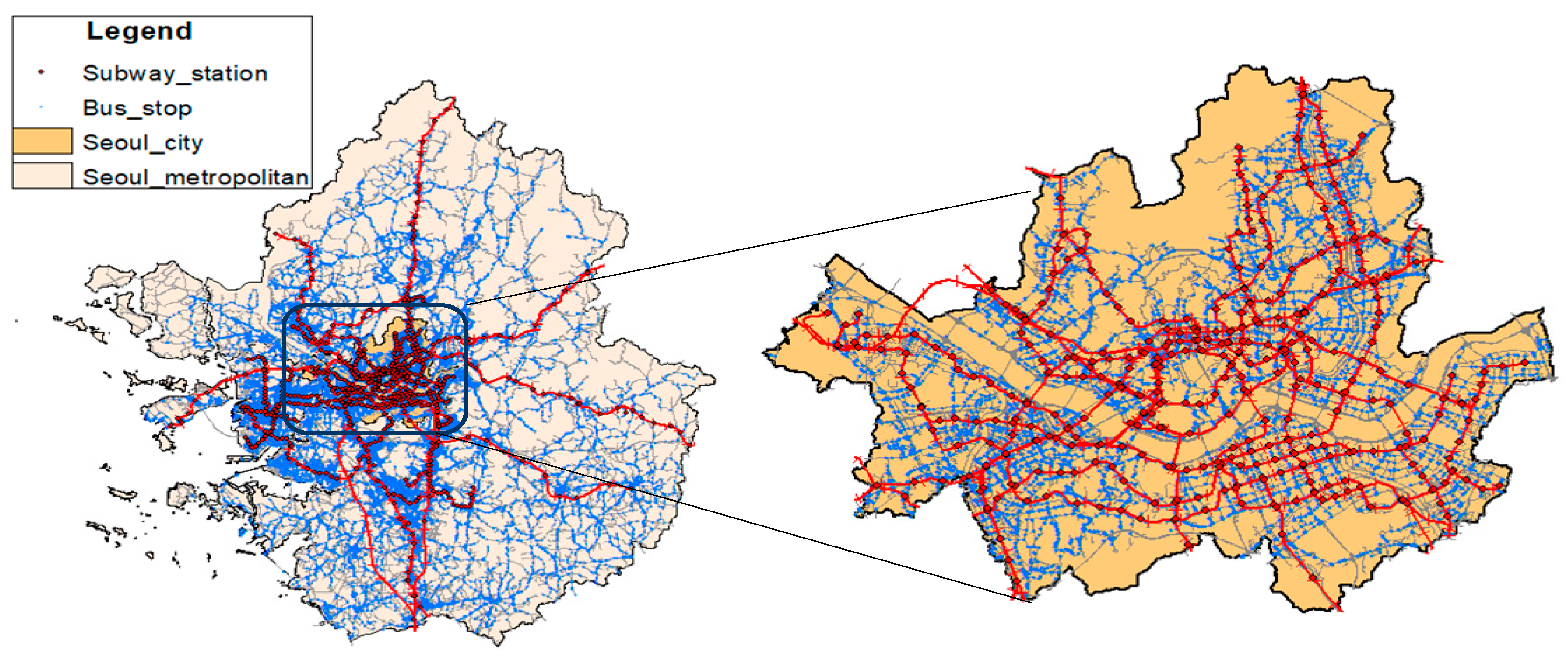
3. Case Study: The Public Transportation System in the Seoul Metropolitan Area
4. Network Analysis of Public Transportation Networks in the SMA
4.1. Data Preprocessing and Graph Generation
4.2. Network Indicators
4.2.1. Basic Network Properties
4.2.2. Average Path Length and Clustering Coefficient
4.2.3. Community Detection within the Networks in the SMA
4.2.4. Degree Assortativity
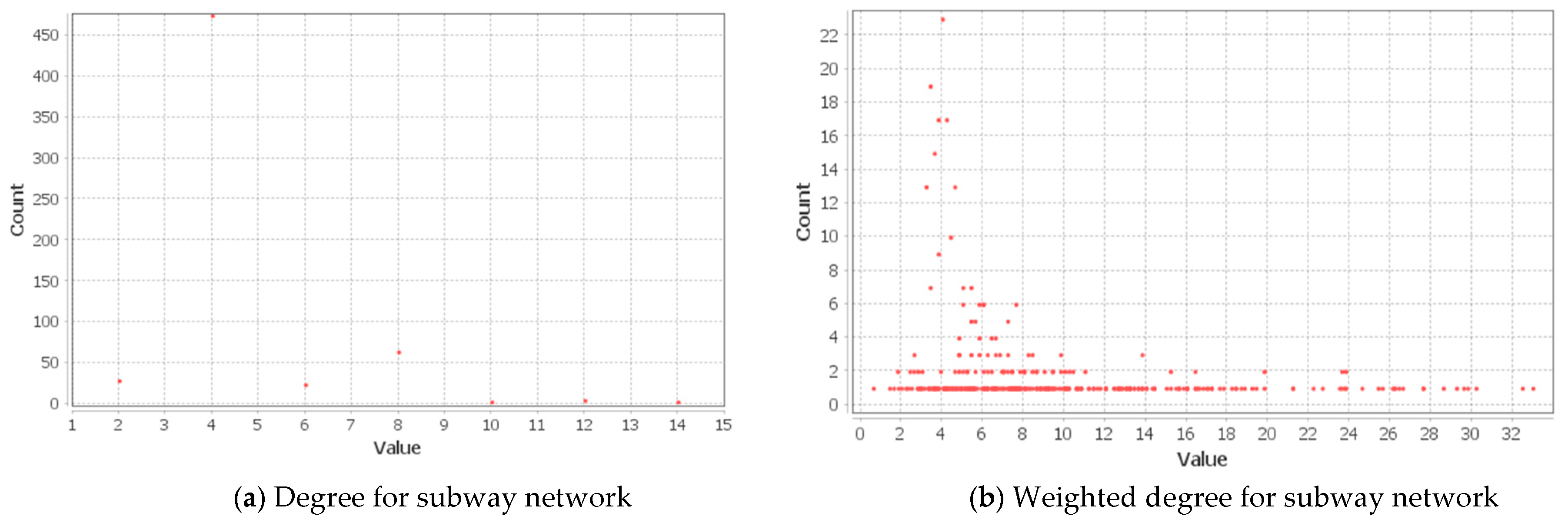
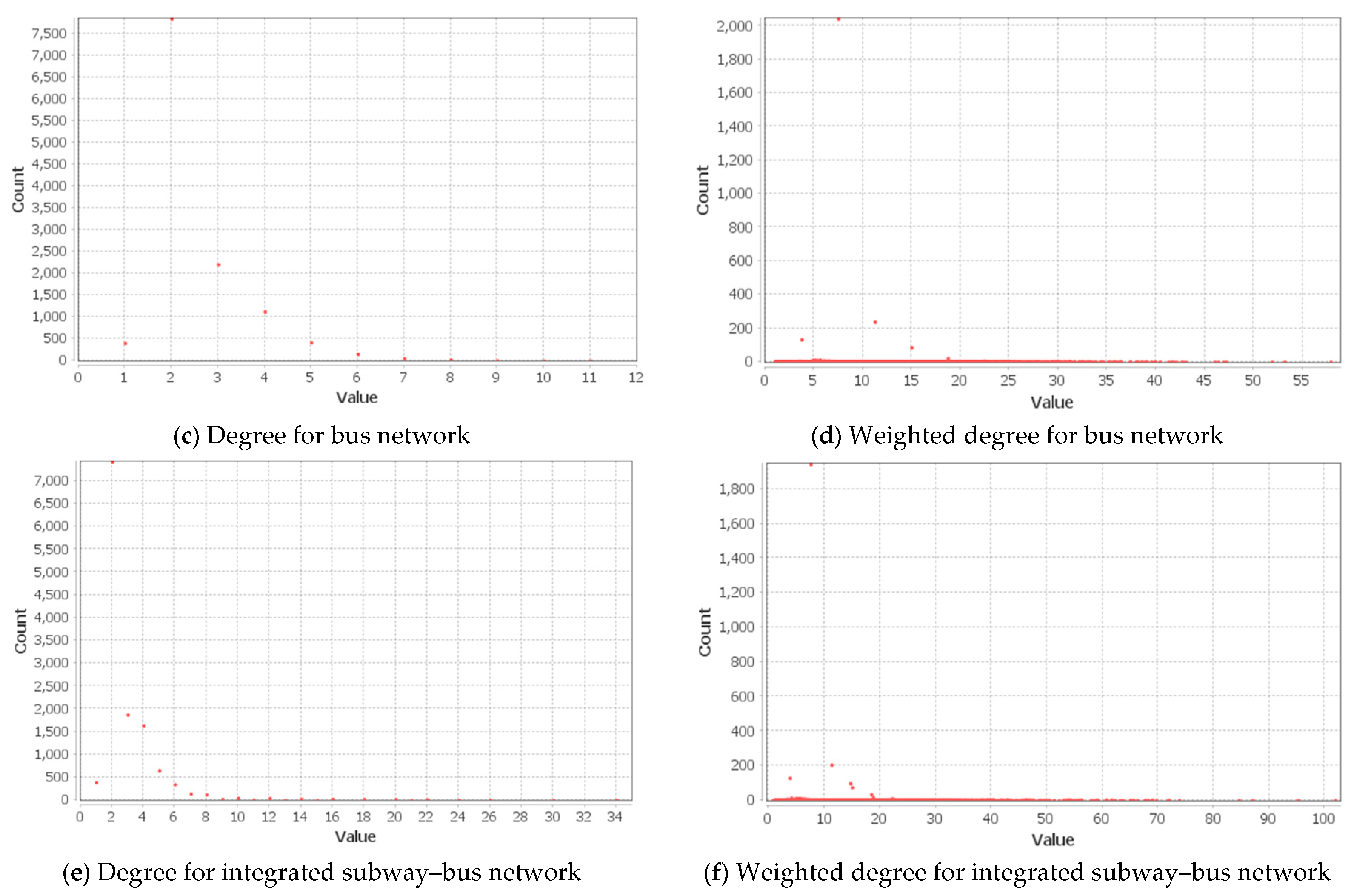
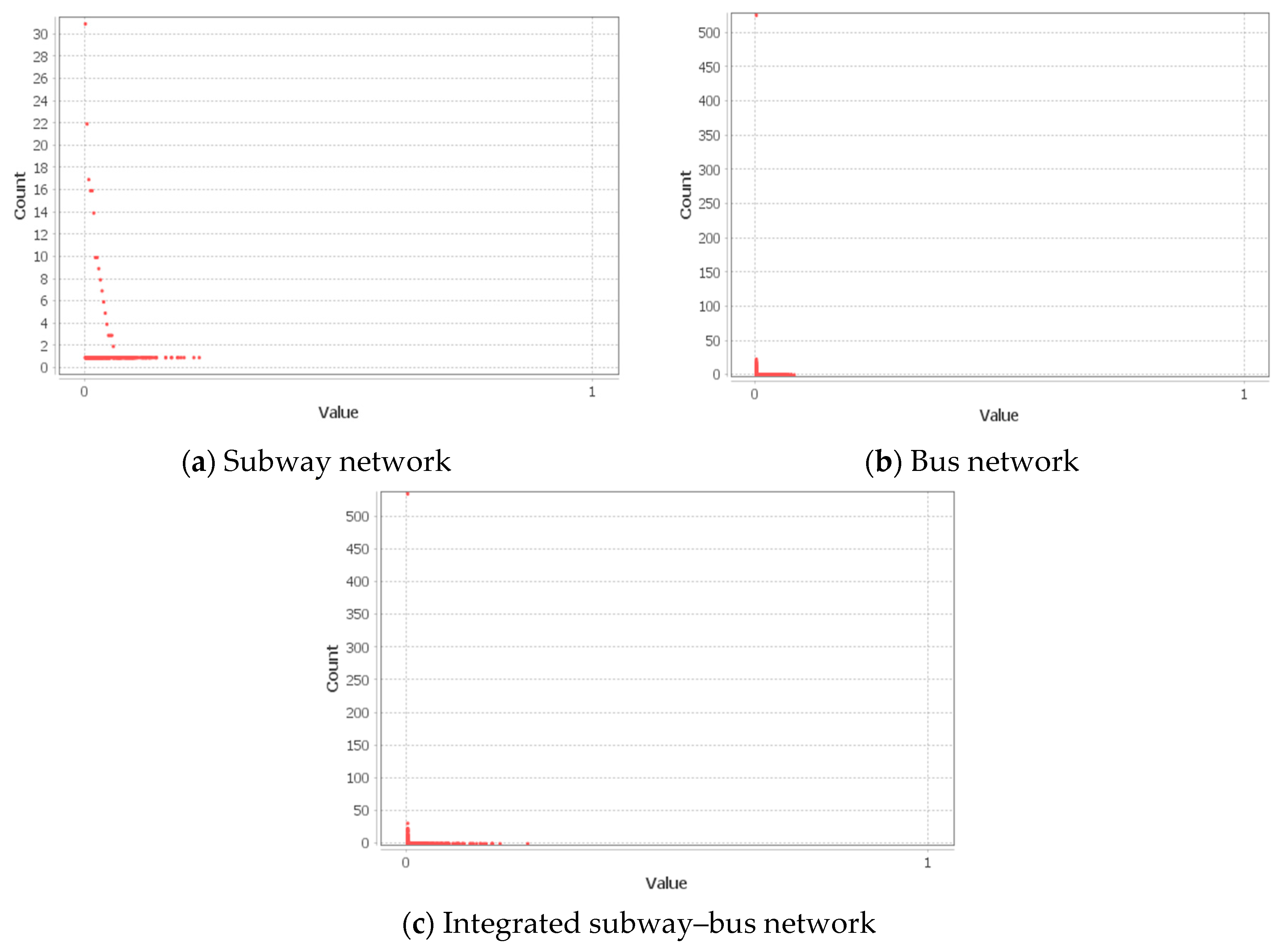
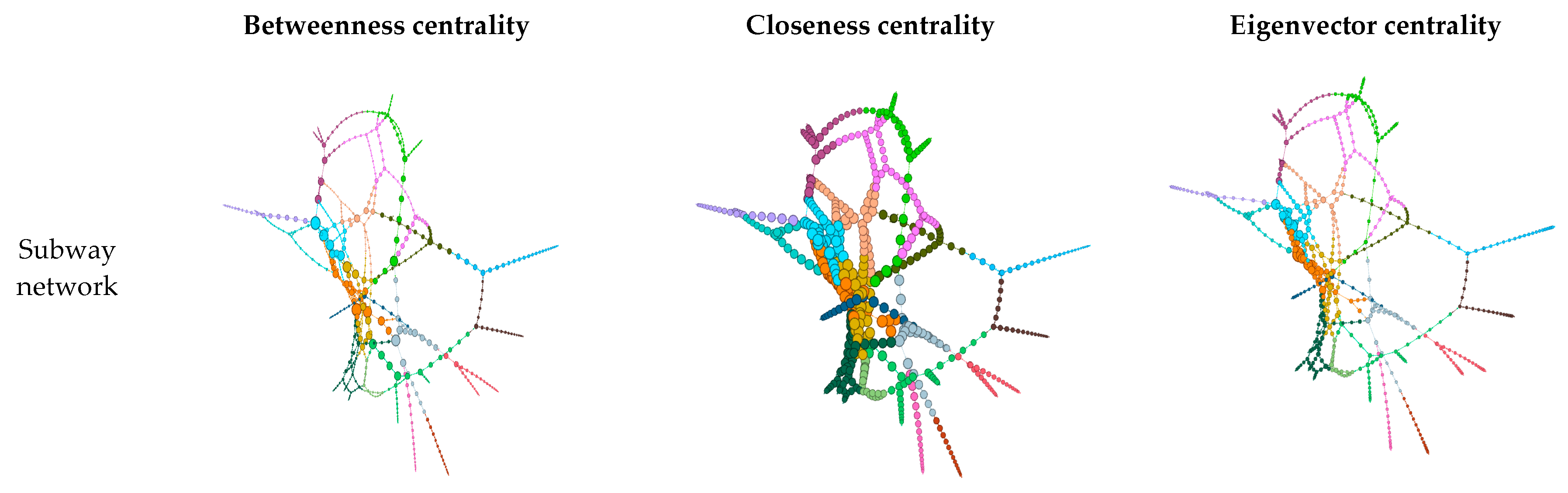
4.2.5. Centrality and Connectivity in the Public Transportation Networks in the SMA
5. Discussion of Results
6. Conclusions and Future Work
- Both bus and subway networks in the SMA have no small-world characteristics and even after integrating them, the resulting network did not show a small-world property. Also, only the bus network is a scale-free network, indicating the presence of highly connected hubs.
- The average path length, the clustering coefficient, and the degree of connectivity of nodes (subway stations or bus stops) reflected the intensity of interconnectivity and improved accessibility within the integrated public transportation network.
- The outcomes of the degree centrality, weighted degree centrality, closeness centrality, and eccentricity centrality show that, on average, the nodes (subway stations or bus stops) within the integrated network are easily reachable. The average betweenness and eigenvector centralities decreased with network size, meaning fewer public transportation nodes are seen to have high centrality values. Hence, averagely, the stations in the subway network were strategically located in the network and effectively linked several nodes together.
- From the average network centrality values, we identified that the subway network has a high effect on network integration, which highlights the need to connect bus stops with subway stations to obtain the full benefits of public transportation network integration.
Author Contributions
Funding
Conflicts of Interest
References
- Sutton, J.C. GIS applications in transit planning and operations: A review of current practice, effective applications and challenges in the USA. Transp. Plan. Technol. 2005, 28, 237–250. [Google Scholar] [CrossRef]
- Batool, K.; Niazi, M.A. Towards a methodology for validation of centrality measures in complex networks. PLoS ONE 2014, 9, e90283. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Chen, J.; Yan, X. Space‒time evolution analysis of the Nanjing metro network based on a complex network. Sustainability 2019, 11, 523. [Google Scholar] [CrossRef]
- de Bona, A.A.; Fonseca, K.V.O.; Rosa, M.O.; Lüders, R.; Delgado, M.R.B.S. Analysis of public bus transportation of a Brazilian city based on the theory of complex networks using the P-Space. Math. Probl. Eng. 2016, 2016, 3898762. [Google Scholar] [CrossRef]
- Chatterjee, A.; Manohar, M.; Ramadurai, G. Statistical analysis of bus networks in India. PLoS ONE 2016, 11, e0168478. [Google Scholar] [CrossRef] [PubMed]
- Shanmukhappa, T.; Ho, I.W.H.; Tse, C.K. Bus transport network in Hong Kong: Scale-free or not? In Proceedings of the International Symposium on Nonlinear Theory and Its Applications, Yugawara, Japan, 27–30 November 2016.
- Chopra, S.S.; Dillon, T.; Bilec, M.M.; Khanna, V. A network-based framework for assessing infrastructure resilience: A case study of the London metro system. J. R. Soc. Interface 2016, 13, 20160113. [Google Scholar] [CrossRef] [PubMed]
- Bell, D.C.; Atkinson, J.S.; Carlson, J.W. Centrality measures for disease transmission networks. Soc. Netw. 1999, 21, 1–21. [Google Scholar] [CrossRef]
- Landherr, A.; Friedl, B.; Heidemann, J. A critical review of centrality measures in social networks. Bus. Inf. Syst. Eng. 2010, 2, 371–385. [Google Scholar] [CrossRef]
- Veres, P.; Bányai, T.; Illés, B. Intelligent transportation systems to support production logistics. In Vehicle and Automotive Engineering; Jarmai, K., Bollo, B., Eds.; Springer: Cham, Switzerland, 2017; pp. 245–256. [Google Scholar]
- Wang, J.; Jiang, C.; Zhang, K.; Quek, T.Q.; Ren, Y.; Hanzo, L. Vehicular sensing networks in a smart city: Principles, technologies and applications. IEEE Wirel. Commun. 2017, 25, 122–132. [Google Scholar] [CrossRef]
- Errampalli, M.; Patil, K.S.; Prasad, C.S.R.K. Evaluation of integration between public transportation modes by developing sustainability index for Indian cities. Case Stud. Transp. Policy 2018. [Google Scholar] [CrossRef]
- Geurs, K.T.; La Paix, L.; van Weperen, S. A multi-modal network approach to model public transport accessibility impacts of bicycle-train integration policies. Eur. Transp. Res. Rev. 2016, 8, 25. [Google Scholar] [CrossRef]
- Shi, J.; Wen, S.; Zhao, X.; Wu, G. Sustainable development of urban rail transit networks: A vulnerability perspective. Sustainability 2019, 11, 1335. [Google Scholar] [CrossRef]
- Aziz, A.; Nawaz, M.S.; Nadeem, M.; Afzal, L. Examining suitability of the integrated public transport system: A case study of Lahore. Transp. Res. Part A Policy Pract. 2018, 117, 13–25. [Google Scholar] [CrossRef]
- One Card Fits All: Integrated Public Transport Fare System. Available online: https://www.seoulsolution.kr/en/content/one-card-fits-all-integrated-public-transport-fare-system (accessed on 25 August 2019).
- Integrated Public Transport Systems Make Travel Easier and More Affordable. Available online: http://www.worldbank.org/en/news/press-release/2015/04/07/integrated-public-transport-systems-make-travel-easier-and-more-affordable (accessed on 17 June 2019).
- Pucher, J.; Park, H.; Kim, M.H.; Song, J. Public transport reforms in Seoul: Innovations motivated by funding crisis. J. Public Transp. 2005, 8, 41–62. [Google Scholar] [CrossRef]
- Zahedi, Z.; Mawengkang, H.; Masri, M.; Ramon, H.; Putri, Y.M. Mathematical fallacies and applications of graph theory in electrical engineering. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1255. [Google Scholar]
- Black, W.R. Sustainable transportation: A US perspective. J. Transp. Geogr. 1996, 4, 151–159. [Google Scholar] [CrossRef]
- Hong, J.Y. Spatio-Temporal Models Incorporating Network Topology Measures for Pedestrian Exposure Estimation. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2015. [Google Scholar]
- Lin, J.; Ban, Y. Complex network topology of transportation systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Physica A 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Liu, J.G.; Ren, Z.M.; Guo, Q. Ranking the spreading influence in complex networks. Physica A 2013, 392, 4154–4159. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.S.; Zhang, Y.C.; Zhou, T. Identifying influential nodes in complex networks. Physica A 2012, 391, 1777–1787. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Soh, H.; Lim, S.; Zhang, T.; Fu, X.; Lee, G.K.K.; Hung, T.G.G.; Di, P.; Prakasam, S.; Wong, L. Weighted complex network analysis of travel routes on the Singapore public transportation system. Physica A 2010, 389, 5852–5863. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Deng, J.; Wang, T. Research on Hub node identification of the public transport network of Guilin based on complex network theory. In CICTP 2014: Safe, Smart, and Sustainable Multimodal Transportation Systems; Ma, J., Pan, D., Huang, H., Yin, Y., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 1302–1309. [Google Scholar]
- Mishra, S.; Welch, T.F.; Jha, M.K. Performance indicators for public transit connectivity in multi-modal transportation networks. Transp. Res. A Policy Pract. 2012, 46, 1066–1085. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Fu, B.B.; Li, S.B. Dynamics analysis for the hour-scale based time-varying characteristic of topology complexity in a weighted urban rail transit network. Physica A 2019, 527, 121280. [Google Scholar] [CrossRef]
- Rommel, J. Topological Analysis of the Evolution of Public Transport Networks. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Humphries, M.D.; Gurney, K. Network ‘small-world-ness’: A quantitative method for determining canonical network equivalence. PLoS ONE 2008, 3, e0002051. [Google Scholar] [CrossRef]
- Wu, J.; Gao, Z.; Sun, H.; Huang, H. Urban transit system as a scale-free network. Mod. Phys. Lett. B 2004, 18, 1043–1049. [Google Scholar] [CrossRef]
- Scheurer, J.; Porta, S. Centrality and connectivity in public transport networks and their significance for transport sustainability in cities. In World Planning Schools Congress, Global Planning Association Education Network; GPEAN: Rio de Janeiro, Brazil, 2006. [Google Scholar]
- Tsiotas, D.; Polyzos, S. Introducing a new centrality measure from the transportation network analysis in Greece. Ann. Oper. Res. 2015, 227, 93–117. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Lee, R.K.W.; Lim, E.P.; Zhu, F. Measuring centralities for transportation networks beyond structures. In Applications of Social Media and Social Network Analysis; Kazlenko, P., Chawla, N., Eds.; Springer International Publishing AG: Cham, Switzerland, 2015; pp. 23–39. [Google Scholar]
- Liu, J.; Xiong, Q.; Shi, W.; Shi, X.; Wang, K. Evaluating the importance of nodes in complex networks. Physica A 2016, 452, 209–219. [Google Scholar] [CrossRef]
- Du, Y.; Gao, C.; Hu, Y.; Mahadevan, S.; Deng, Y. A new method of identifying influential nodes in complex networks based on TOPSIS. Physica A 2014, 399, 57–69. [Google Scholar] [CrossRef]
- Derrible, S. Network centrality of metro systems. PLoS ONE 2012, 7, e40575. [Google Scholar] [CrossRef]
- Chen, A.; Yang, C.; Kongsomsaksakul, S.; Lee, M. Network-based accessibility measures for vulnerability analysis of degradable transportation networks. Netw. Spat. Econ. 2007, 7, 241–256. [Google Scholar] [CrossRef]
- Caschili, S.; de Montis, A. Accessibility and complex network analysis of the US commuting system. Cities 2013, 30, 4–17. [Google Scholar] [CrossRef]
- Rubulotta, E.; Ignaccolo, M.; Inturri, G.; Rofè, Y. Accessibility and centrality for sustainable mobility: Regional planning case study. J. Urban Plan. Dev. 2012, 139, 115–132. [Google Scholar] [CrossRef]
- Dash, S.P. BRT System: An approach for sustainable public transport system for Mangalore city. J. Civ. Eng. Environ. Technol. 2018, 4, 192–197. [Google Scholar]
- Cao, W.; Feng, X.; Zhang, H. The structural and spatial properties of the high-speed railway network in China: A complex network perspective. J. Rail Transp. Plan. Manag. 2019, 9, 46–56. [Google Scholar] [CrossRef]
- Lu, Q.C.; Lin, S. Vulnerability analysis of urban rail transit network within multi-modal. Sustainability 2019, 11, 2109. [Google Scholar] [CrossRef]
- Cats, O.; Krishnakumari, P.; Tundulyasaree, K. Rail network robustness: The role of rapid development and a polycentric structure in withstanding random and targeted attacks. In Proceedings of the Transportation Research Board 98th Annual Meeting, Washington, DC, USA, 13–17 January 2019. [Google Scholar]
- Jiang, R.; Lu, Q.C.; Peng, Z.R. A station-based rail transit network vulnerability measure. J. Transp. Geogr. 2018, 66, 10–18. [Google Scholar] [CrossRef]
- Shanmukhappa, T.; Ho, I.W.H.; Tse, C.K. Spatial analysis of bus transport networks using network theory. Physica A 2018, 502, 295–314. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, N.; Liu, Y.; Xu, W. Exploring spatiotemporal variation in hourly metro ridership at station level: The influence of built environment and topological structure. Sustainability 2018, 10, 4564. [Google Scholar] [CrossRef]
- Wu, X.; Dong, H.; Tse, C.K.; Ho, I.W.; Lau, F.C. Analysis of metro network performance from a complex network perspective. Physica A 2018, 492, 553–563. [Google Scholar] [CrossRef]
- Yang, Y.; He, Z.; Song, Z.; Fu, X.; Wang, J. Investigation on structural and spatial characteristics of taxi trip trajectory network in Xi’an, China. Physica A 2018, 506, 755–766. [Google Scholar] [CrossRef]
- Zhang, H. Structural analysis of bus networks using indicators of graph theory and complex network theory. Open Civ. Eng. J. 2017, 11. [Google Scholar] [CrossRef]
- Chatterjee, A. Studies on the structure and dynamics of urban bus networks in Indian cities. arXiv 2015, arXiv:1512.05909. [Google Scholar]
- Ding, R.; Ujang, N.; Hamid, H.B.; Wu, J. Complex network theory applied to the growth of Kuala Lumpur’s public urban rail transit network. PLoS ONE 2015, 10, e0139961. [Google Scholar] [CrossRef] [PubMed]
- King, D. Analytical Approaches to Investigating Transit Network Resilience. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2015. [Google Scholar]
- Mohmand, Y.T.; Wang, A. Complex network analysis of Pakistan railways. Discret. Dyn. Nat. Soc. 2014, 2014, 126261. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Y. Complexity modeling and stability analysis of urban subway network: Wuhan city case study. Procedia Soc. Behav. Sci. 2013, 96, 1611–1621. [Google Scholar] [CrossRef]
- Jang, S.; An, Y.; Yi, C.; Lee, S. Assessing the spatial equity of Seoul’s public transportation using the Gini coefficient based on its accessibility. Int. J. Urban Sci. 2017, 21, 91–107. [Google Scholar] [CrossRef]
- Cervero, R.; Kang, C.D. Bus rapid transit impacts on land uses and land values in Seoul, Korea. Transp. Policy 2011, 18, 102–116. [Google Scholar] [CrossRef]
- Seoul Open Data Plaza. Available online: https://data.seoul.go.kr/ (accessed on 20 July 2019).
- Hong, J.; Shankar, V.N.; Venkataraman, N. A spatially autoregressive and heteroskedastic space-time pedestrian exposure modeling framework with spatial lags and endogenous network topologies. Anal. Methods Accid. Res. 2016, 10, 26–46. [Google Scholar] [CrossRef]
- Telesford, Q.K.; Joyce, K.E.; Hayasaka, S.; Burdette, J.H.; Laurienti, P.J. The ubiquity of small-world networks. Brain Connect. 2011, 1, 367–375. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef]
- Ji, X.; Machiraju, R.; Ritter, A.; Yen, P.Y. Examining the distribution, modularity, and community structure in article networks for systematic reviews. In AMIA Annual Symposium Proceedings Archive; American Medical Informatics Association: Washington, DC, USA, 2015. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Thedchanamoorthy, G.; Piraveenan, M.; Kasthuriratna, D.; Senanayake, U. Node assortativity in complex networks: An alternative approach. Procedia Comput. Sci. 2014, 29, 2449–2461. [Google Scholar] [CrossRef]
- Noldus, R.; van Mieghem, P. Assortativity in complex networks. J. Complex Netw. 2015, 3, 507–542. [Google Scholar] [CrossRef]
- Armour, C.; Fried, E.I.; Deserno, M.K.; Tsai, J.; Pietrzak, R.H. A network analysis of DSM-5 posttraumatic stress disorder symptoms and correlates in US military veterans. J. Anxiety Disord. 2017, 45, 49–59. [Google Scholar] [CrossRef]
- Xu, Q.; Mao, B.H.; Bai, Y. Network structure of subway passenger flows. J. Stat. Mech. Theory Exp. 2016, 2016, 033404. [Google Scholar] [CrossRef]
- Krnc, M.; Sereni, J.S.; Škrekovski, R.; Yilma, Z.B. Eccentricity of networks with structural constraints. Discuss. Math. Graph Theory 2018. [Google Scholar] [CrossRef]
- Ruhnau, B. Eigenvector-centrality—A node-centrality? Soc. Netw. 2000, 22, 357–365. [Google Scholar] [CrossRef]
- Seoul, Republic of Korea Disaster Risk Management Profile. 2016. Available online: https://www.alnap.org/help-library/disaster-risk-management-profile-seoul-republic-of-korea (accessed on 12 August 2019).
- Wang, Y.; Deng, Y.; Ren, F.; Zhu, R.; Wang, P.; Du, T.; Du, Q. Analysing the spatial configuration of urban bus networks based on the geospatial network analysis method. Cities 2020, 96, 102406. [Google Scholar] [CrossRef]


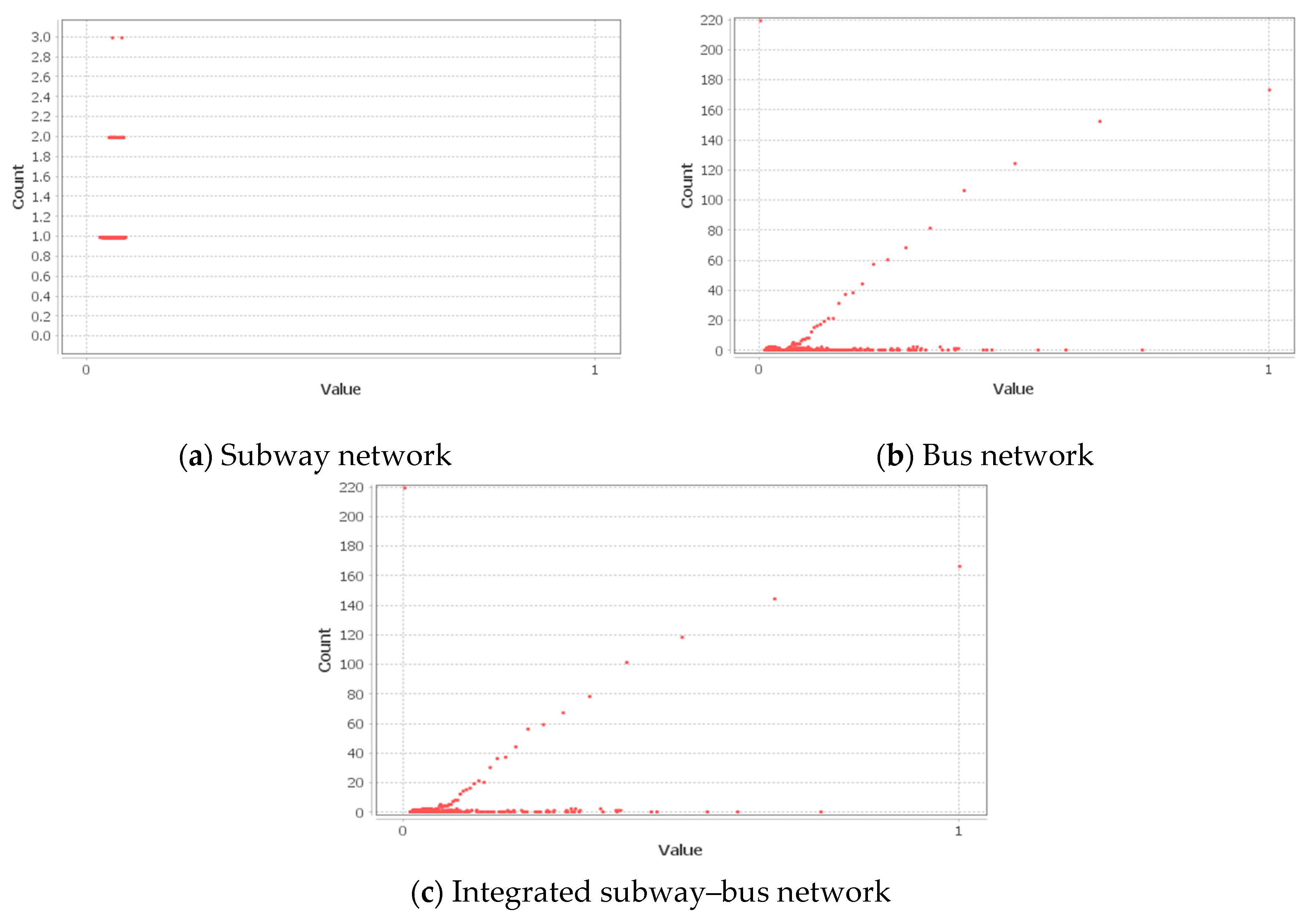
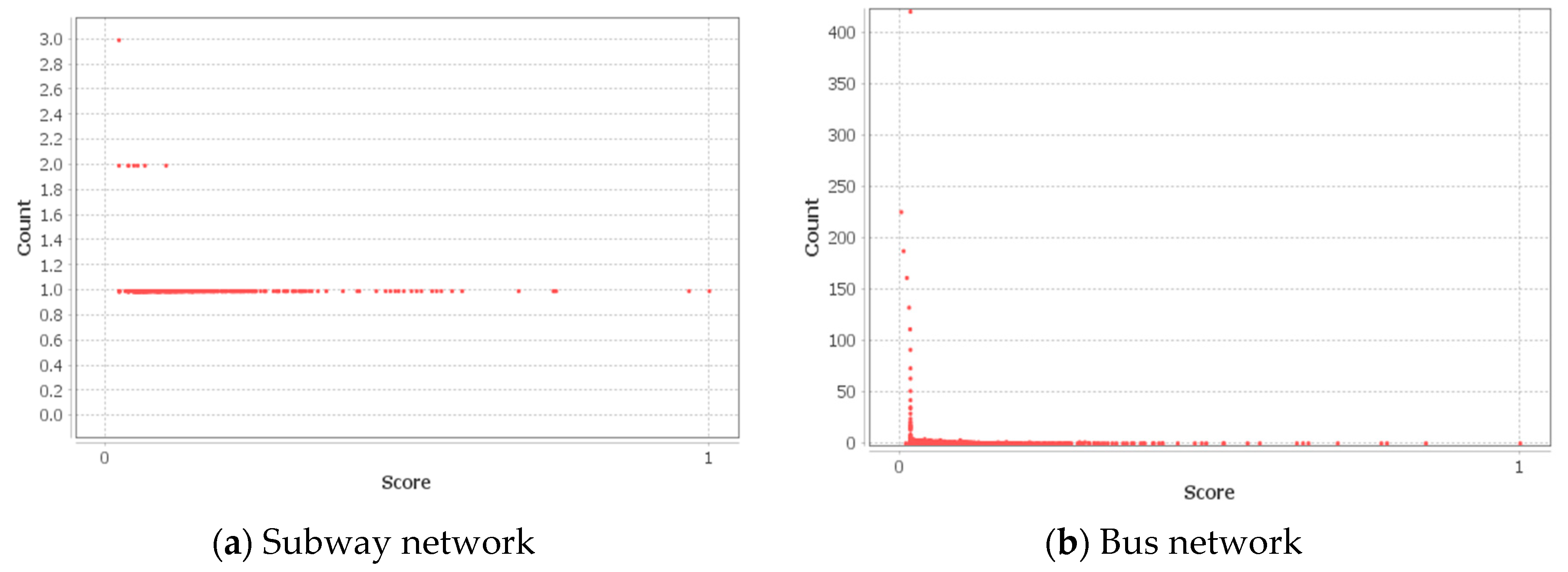
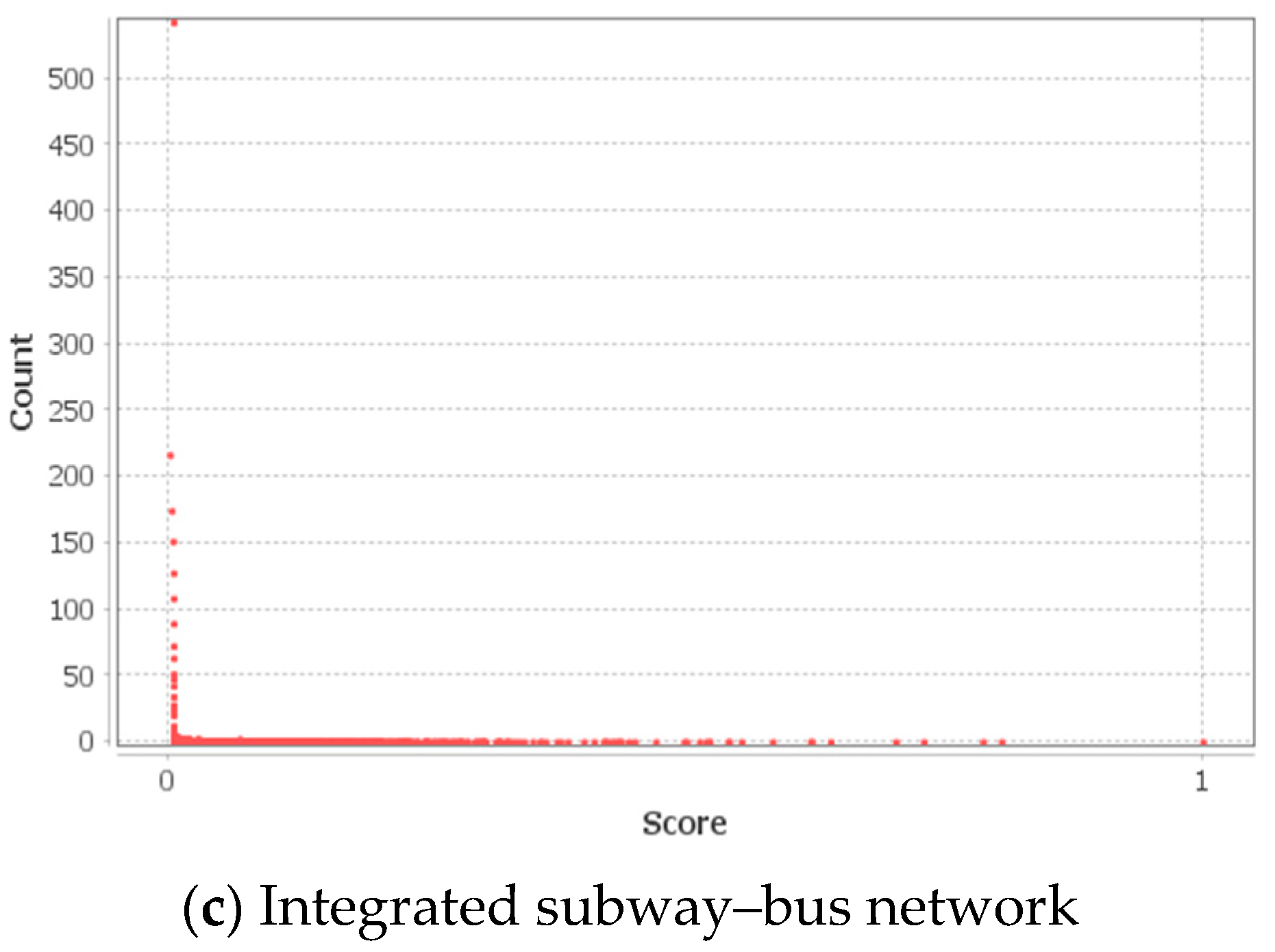

| Author | Network Type | Network Indicators |
|---|---|---|
| Cao et al., 2019 [44] | High speed railway | Degree, strength, betweenness |
| Lu et al., 2019 [45] | Rail | Degree, connectivity index |
| Yu et al., 2019 [3] | Metro | Degree, network density, network average distance, network clustering coefficient |
| Zhang et al., 2019 [30] | Rail | Strength, clustering coefficient, average shortest path length |
| Cats et al., 2019 [46] | Rail | Degree, betweenness |
| Jiang et al., 2018 [47] | Metro | Closeness |
| Shanmukhappa et al., 2018 [48] | Bus | Degree, eigenvector, betweenness, hub and authority centrality, clustering coefficient, average shortest path length, small world network, efficiency |
| Shi et al., 2018 [49] | Metro | Degree, closeness |
| Wu et al., 2018 [50] | Metro | Node occupying probability (centrality) |
| Yang et al., 2018 [51] | Taxi | Clustering coefficient, degree centrality, density, |
| Zhang, H., 2017 [52] | Bus | Degree, modularity, correlation coefficient, efficiency, average shortest path, average transfer time |
| Chopra et al., 2016 [7] | Metro | Clustering coefficient, characteristic path length, passenger strength, modularity, assortativity |
| Shanmukhappa et al., 2016 [6] | Bus | Degree |
| Xu et al., 2016 | Subway | Station throughflow |
| Chatterjee, 2015 [53] | Bus | Betweenness, closeness, clustering coefficient, average path length |
| Ding et al., 2015 [54] | Rail | Closeness, betweenness, clustering coefficient, global efficiency, complexity of network growth |
| King, 2015 [55] | Subway | Betweenness, degree, global efficiency, density, size, order |
| Mohmand et al., 2014 [56] | Railways | Degree, betweenness, closeness |
| Rommel, 2014 [31] | Rail | Degree, betweenness, closeness |
| Liu and Tan, 2013 [57] | Subway | Degree, clustering coefficient, average shortest path length |
| Derrible, 2012 [39] | Metro | Betweenness |
| Soh et al., 2010 [27] | Bus, rail (nonintegrated) | Strength, degree, degree–degree correlations, clustering coefficient, eigenvector, |
| Network Indicator | Subway | Bus | Integrated Subway and Bus |
|---|---|---|---|
| Network-based measurements | |||
| Number of stations, | 602 | 12,271 | 12,873 |
| Number of links, | 1371 | 15,548 | 19,354 |
| Network diameter, | 66 | 174 | 149 |
| Ave. clustering coefficient, | 0.007 | 0.016 | 0.028 |
| Ave. path length, | 20.304 | 43.631 | 28.169 |
| Assortativity, | 0.068 | 0.394 | 0.362 |
| Degree of connectivity, | 0.762 | 0.422 | 0.501 |
| Modularity, | 0.891 | 0.937 | 0.933 |
| Number of communities | 24 | 63 | 59 |
| Method | Criteria | Result | |
|---|---|---|---|
| 1 | 1 | Subway | |
| Bus | |||
| Integrated | |||
| 2 | 2 | Subway | |
| Bus | |||
| Integrated | |||
| Measures | Subway Network | Bus Network | Integrated Network |
|---|---|---|---|
| p-value | 0.0000 | 0.1298 | 0.0000 |
| 1 | 5.5968 | 6.7507 | 3.7699 |
| 4 | 6 | 4 |
| Centrality Measures | Subway Network | Bus Network | Integrated Network | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg. | Min. | Max. | Avg. | Min | Max | Avg. | Min. | Max. | |
| Degree, | 4.554 | 2.000 | 14.000 | 2.534 | 1.000 | 11.000 | 3.007 | 1.000 | 34.000 |
| Weighted degree, | 7.747 | 0.604 | 33.000 | 8.881 | 1.000 | 57.890 | 10.180 | 0.604 | 101.840 |
| Betweenness centrality, | 0.032 | 0.000 | 0.224 | 0.003 | 0.000 | 0.078 | 0.002 | 0.000 | 0.230 |
| Closeness centrality, | 0.052 | 0.023 | 0.074 | 0.066 | 0.000 | 1.000 | 0.073 | 0.000 | 1.000 |
| Eigenvector centrality, | 0.111 | 0.019 | 1.000 | 0.035 | 0.000 | 1.000 | 0.019 | 0.000 | 1.000 |
| Eccentricity centrality, | 0.022 | 0.015 | 0.029 | 0.042 | 0.000 | 1.000 | 0.040 | 0.000 | 1.000 |
| Eccentricity, | 46.078 | 35.000 | 66.000 | 97.468 | 0.000 | 174.000 | 85.663 | 0.000 | 149.000 |
| Integration Type | Average Centrality Measures | ||||
|---|---|---|---|---|---|
| Degree | Weighted Degree | Closeness Centrality | Betweenness Centrality | Eigenvector Centrality | |
| Subway–Bus | 5.30 | 20.35 | 0.05 | 0.001 | 0.09 |
| Bus–bus | 2.73 | 9.59 | 0.07 | 0.001 | 0.01 |
| All stations | 3.01 | 10.18 | 0.07 | 0.002 | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, J.; Tamakloe, R.; Lee, S.; Park, D. Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area. Sustainability 2019, 11, 5404. https://doi.org/10.3390/su11195404
Hong J, Tamakloe R, Lee S, Park D. Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area. Sustainability. 2019; 11(19):5404. https://doi.org/10.3390/su11195404
Chicago/Turabian StyleHong, Jungyeol, Reuben Tamakloe, Soobeom Lee, and Dongjoo Park. 2019. "Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area" Sustainability 11, no. 19: 5404. https://doi.org/10.3390/su11195404
APA StyleHong, J., Tamakloe, R., Lee, S., & Park, D. (2019). Exploring the Topological Characteristics of Complex Public Transportation Networks: Focus on Variations in Both Single and Integrated Systems in the Seoul Metropolitan Area. Sustainability, 11(19), 5404. https://doi.org/10.3390/su11195404






