A Hybrid Artificial Intelligence Model to Predict the Elastic Behavior of Sandstone Rocks
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
2.1.1. Wire-Lined Log Data Analysis
2.1.2. Core Data Generation
2.2. Quality Check and Data Filtration
2.3. Correction for the Depth Shifting Between Wireline-Logged Depth and Core Depth
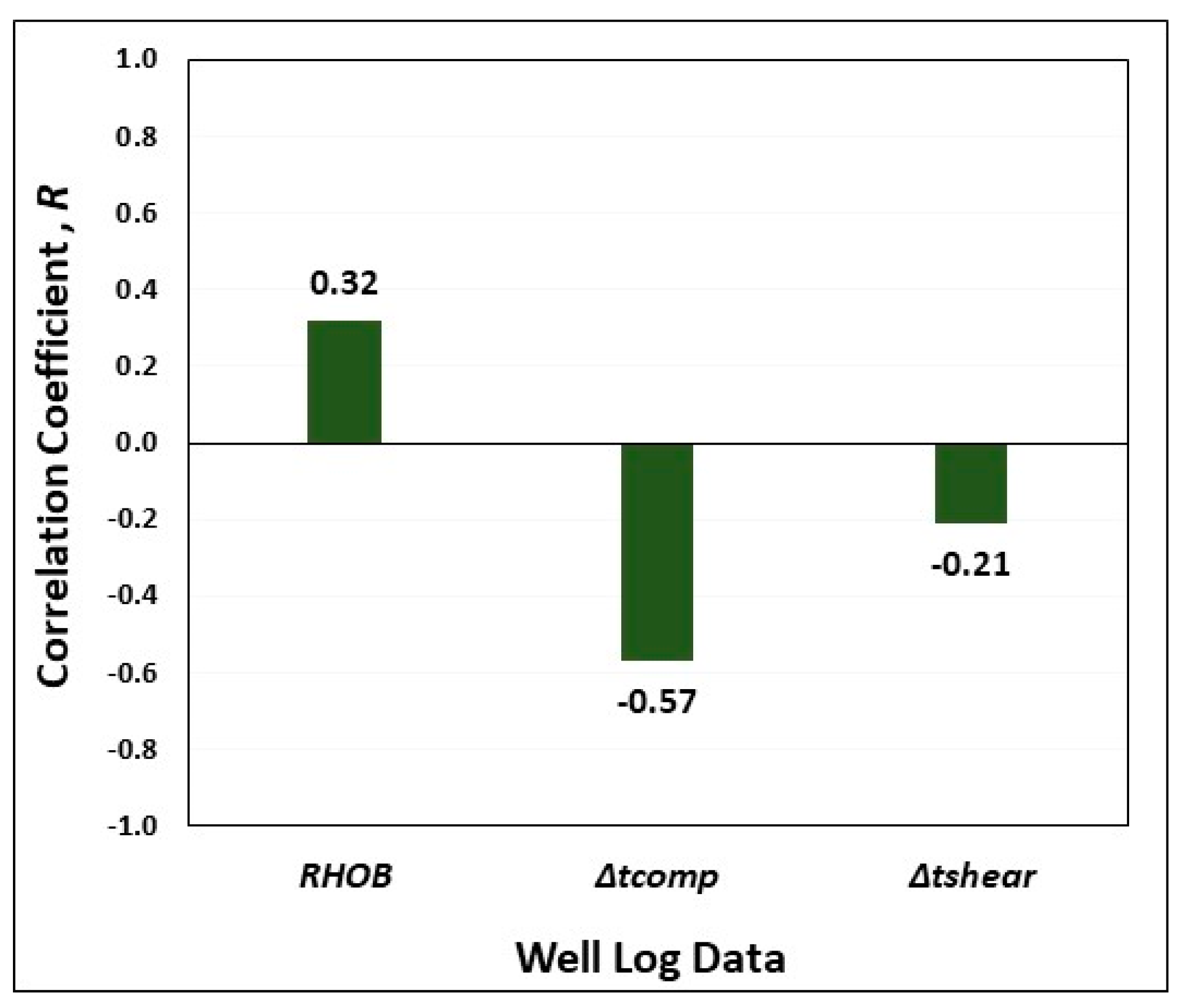
2.4. Inputs/Output Relative Importance
2.5. The Proposed Prediction Approach
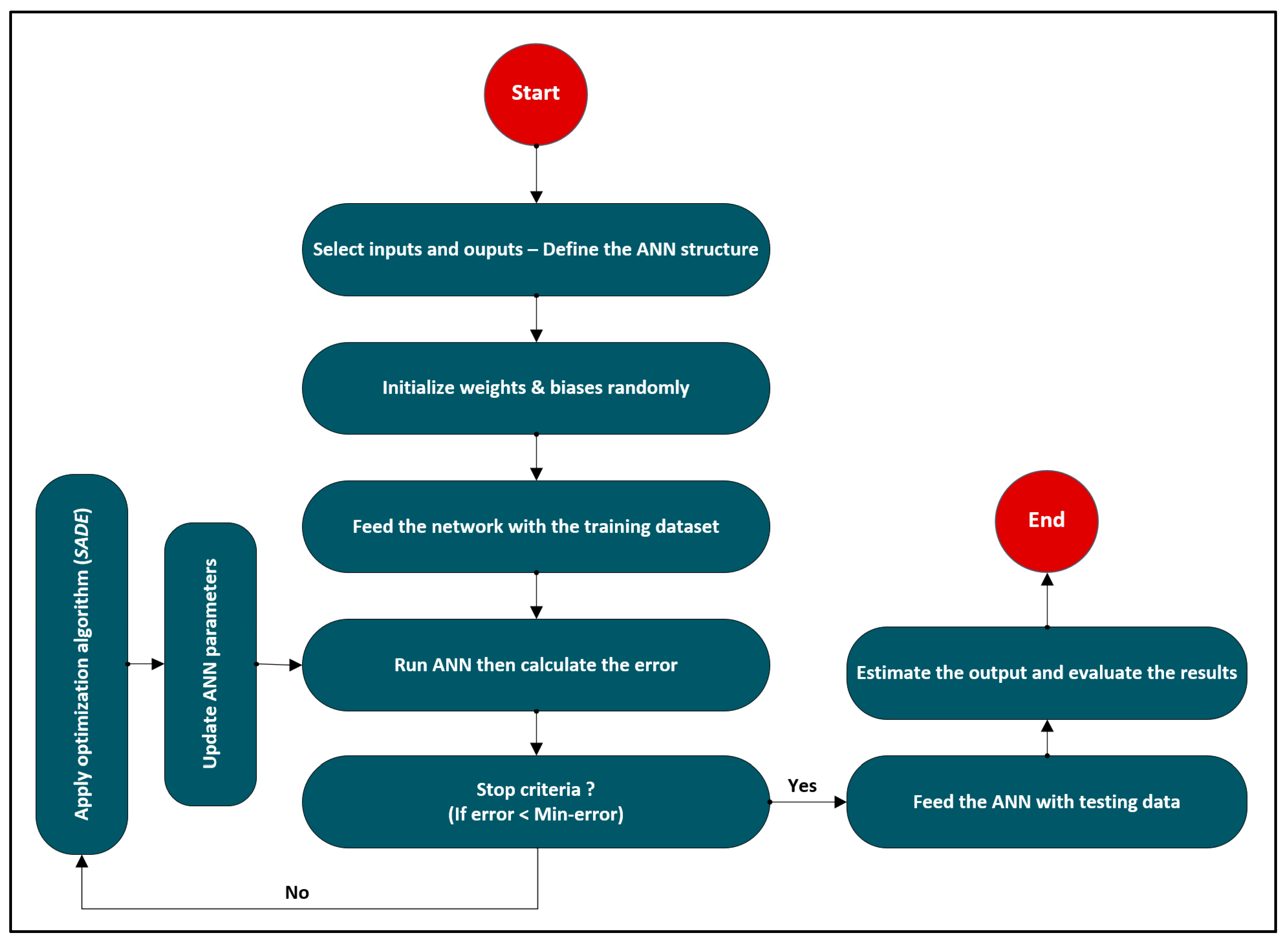
2.5.1. Artificial Neural Network (ANN)
2.5.2. The Self-Adaptive Differential Evolution (SADE) Algorithm
2.5.3. Building and Implementing of ANN to Predict PRstatic Values
- Correlation coefficient (R)
- Mean absolute percentage error (MAPE)
- Coefficient of determination (R2)
3. Results and Discussion
3.1. Sensitivity Analysis
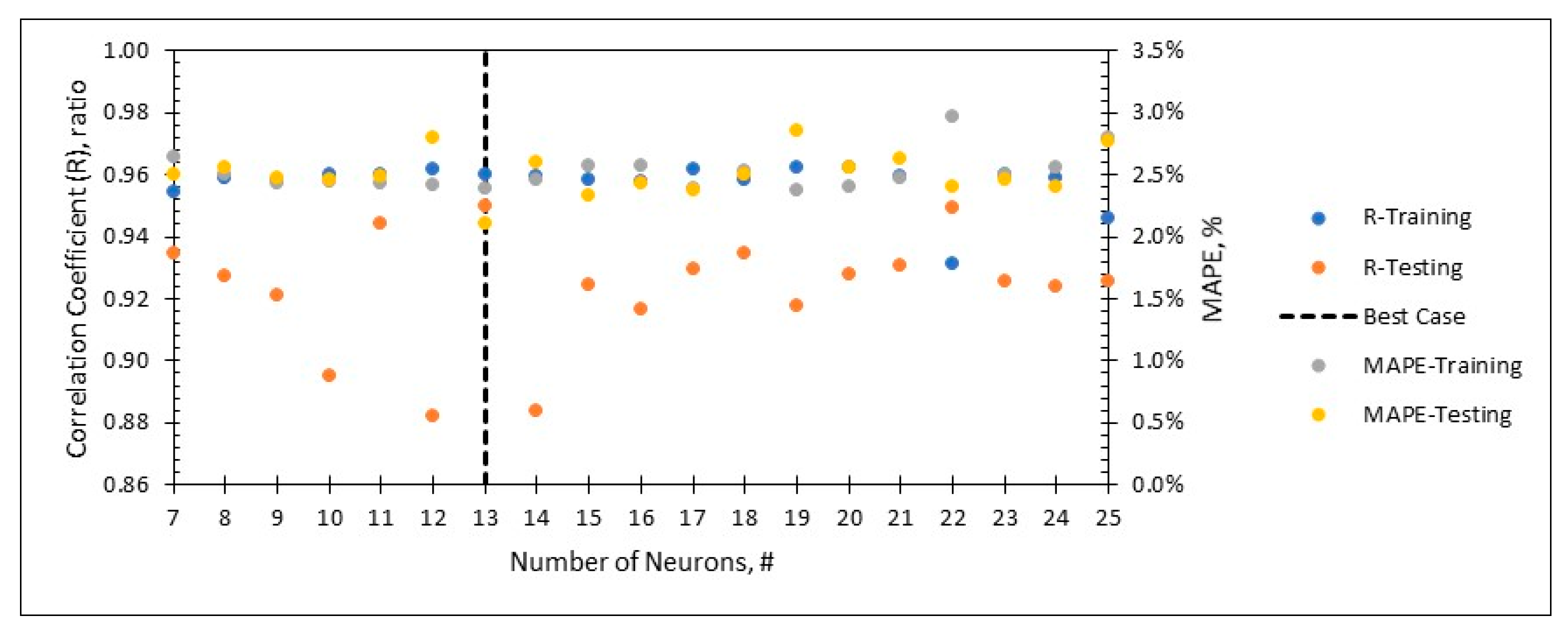
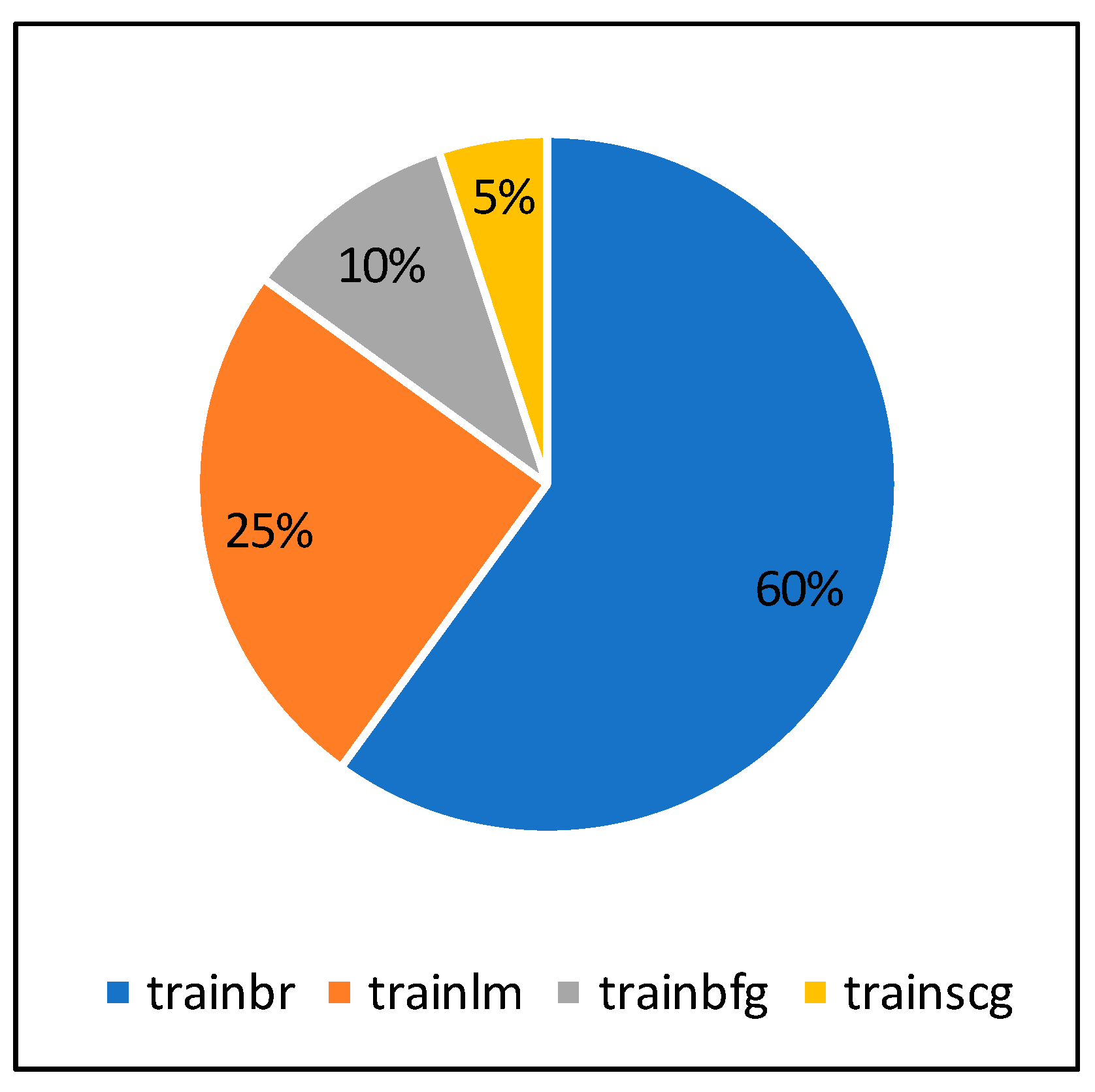
3.2. Optimization Process Findings
- Only one hidden layer with 13 neurons
- A Bayesian regularization backpropagation (trainbr) training algorithm
- An optimized learning rate of 0.12
- An input/hidden layer transfer function that is Elliot symmetric sigmoid (elliotsig)
- A hidden/output layer transfer function that is pure-linear
3.3. Development of an ANN-Based Mathematical Model
3.4. Procedure to Use the Developed Empirical Equation to Predict PRstatic Values
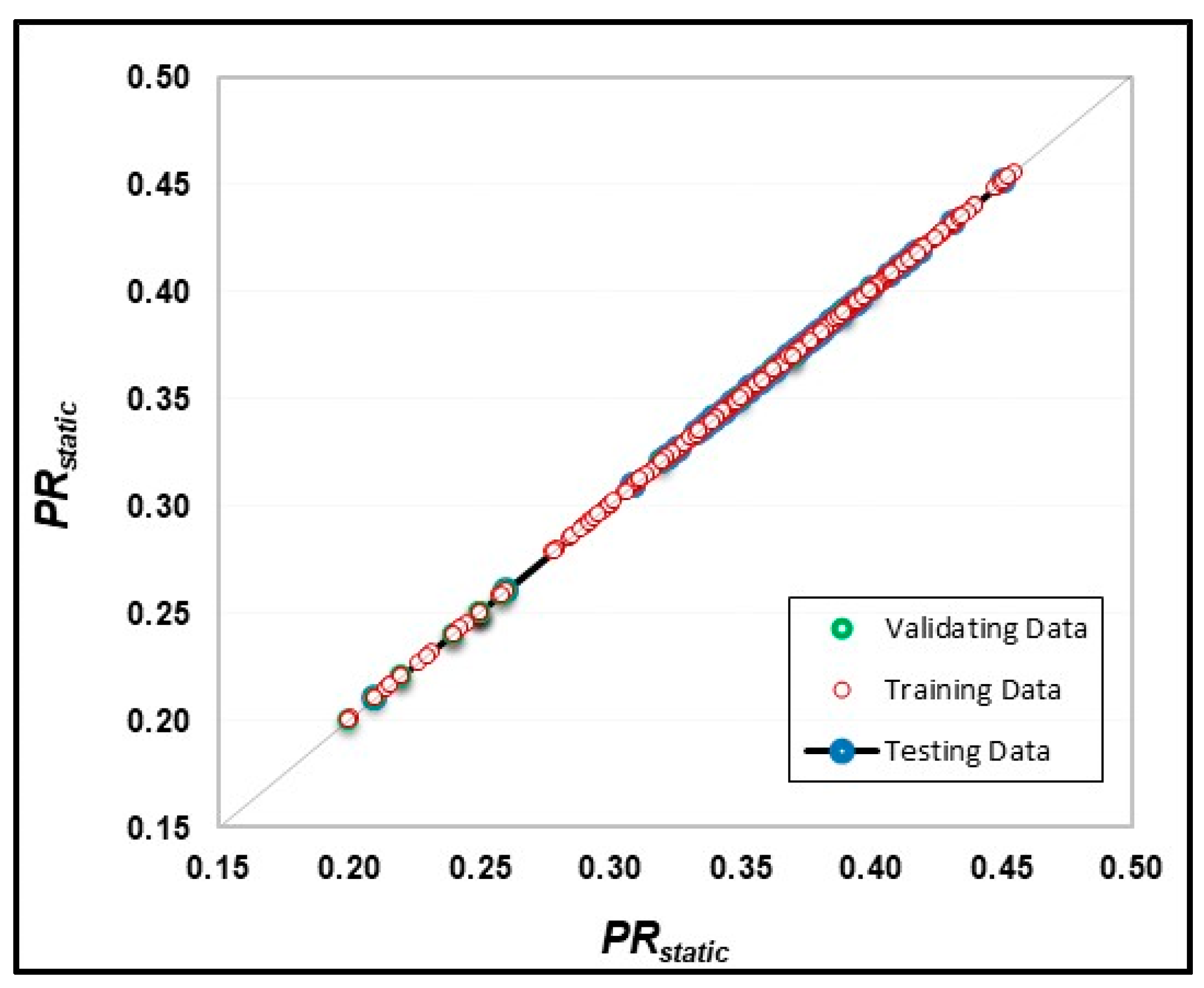
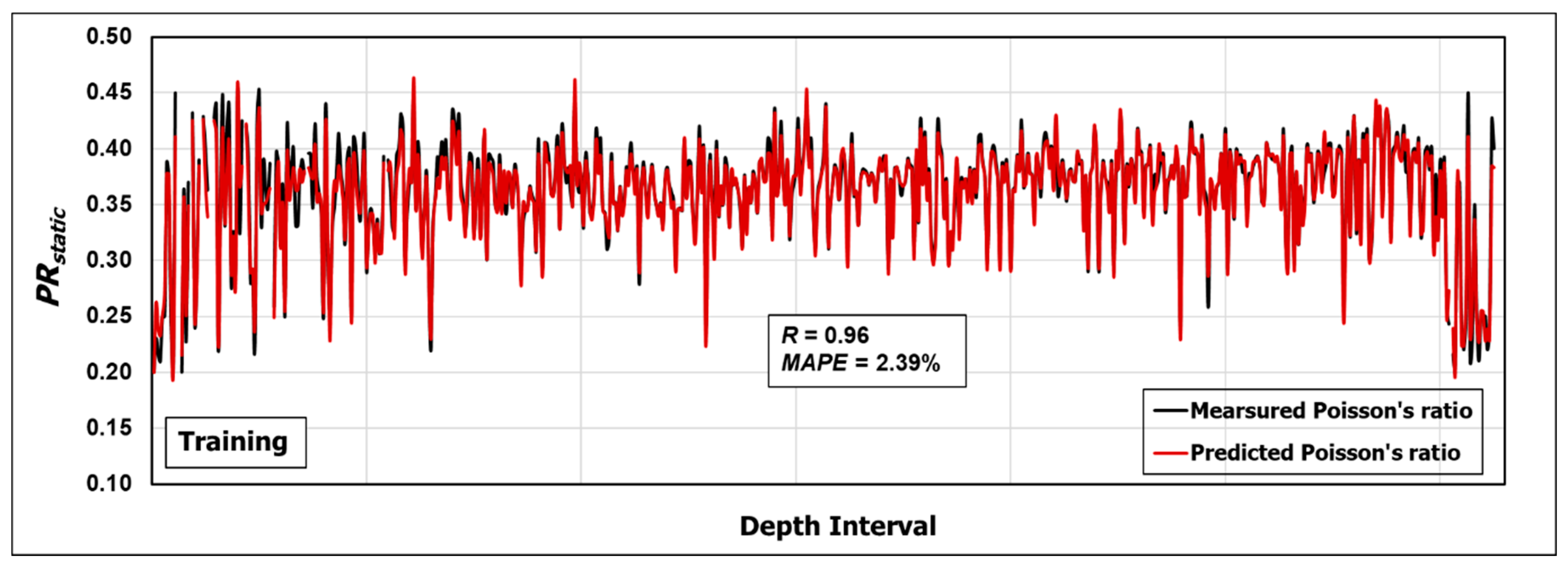
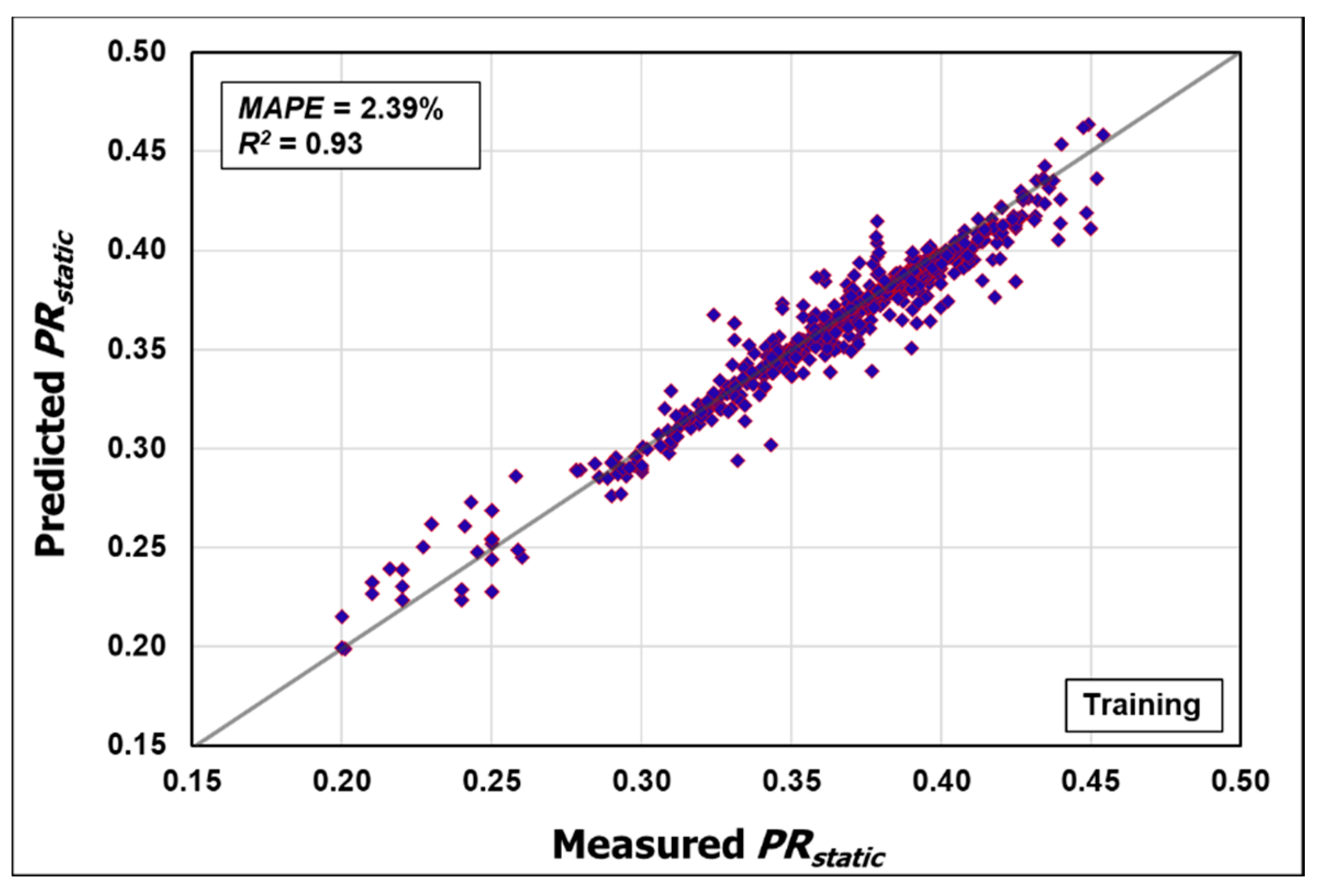
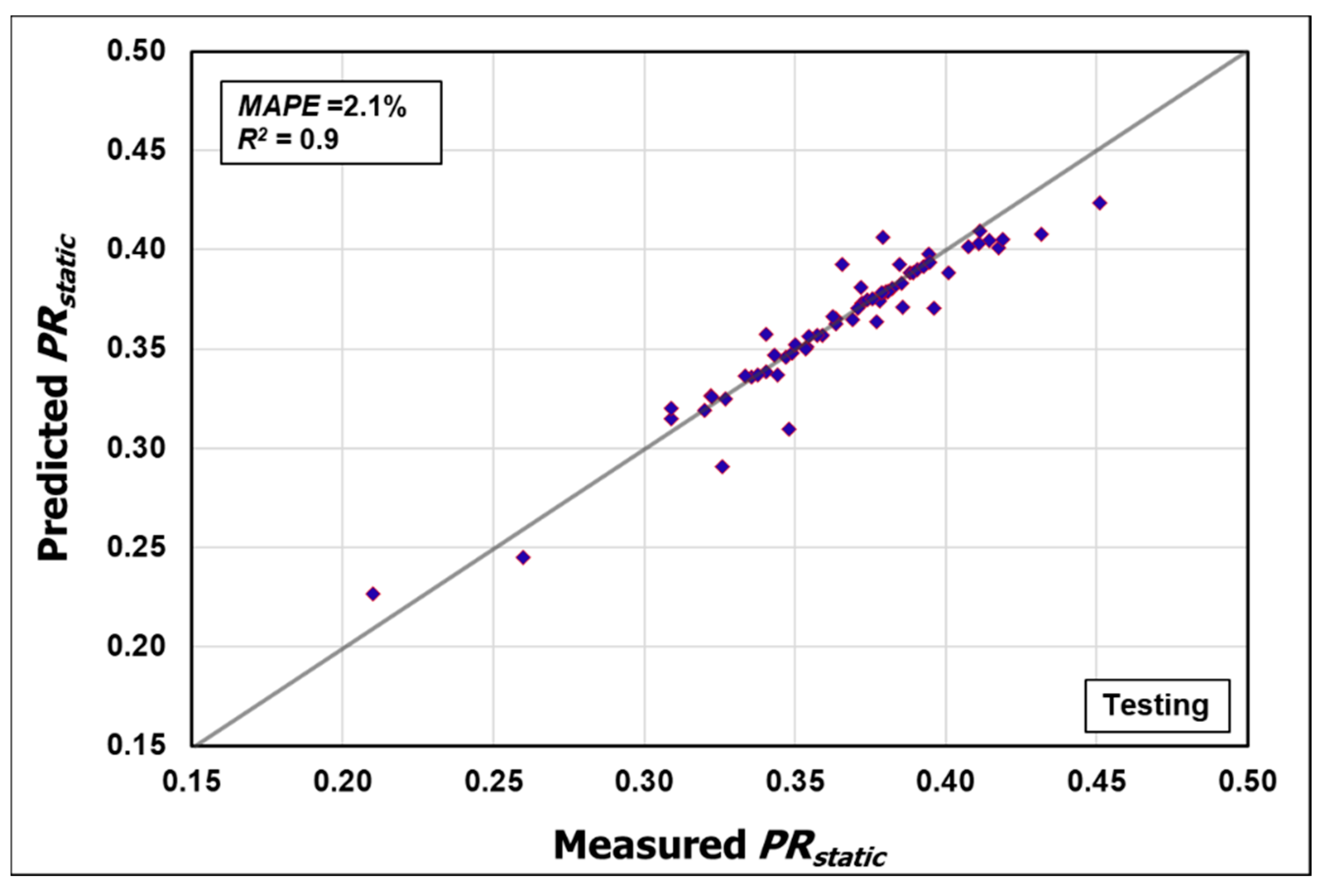
3.5. Validation of the Developed ANN Model and the Extracted Equation
- Phase 1:
- includes using unseen data from other drilled wells within the same area to predict PRstatic and comparing the results with the actual values.
- Phase 2:
- validates the developed model vs. common previous approaches.
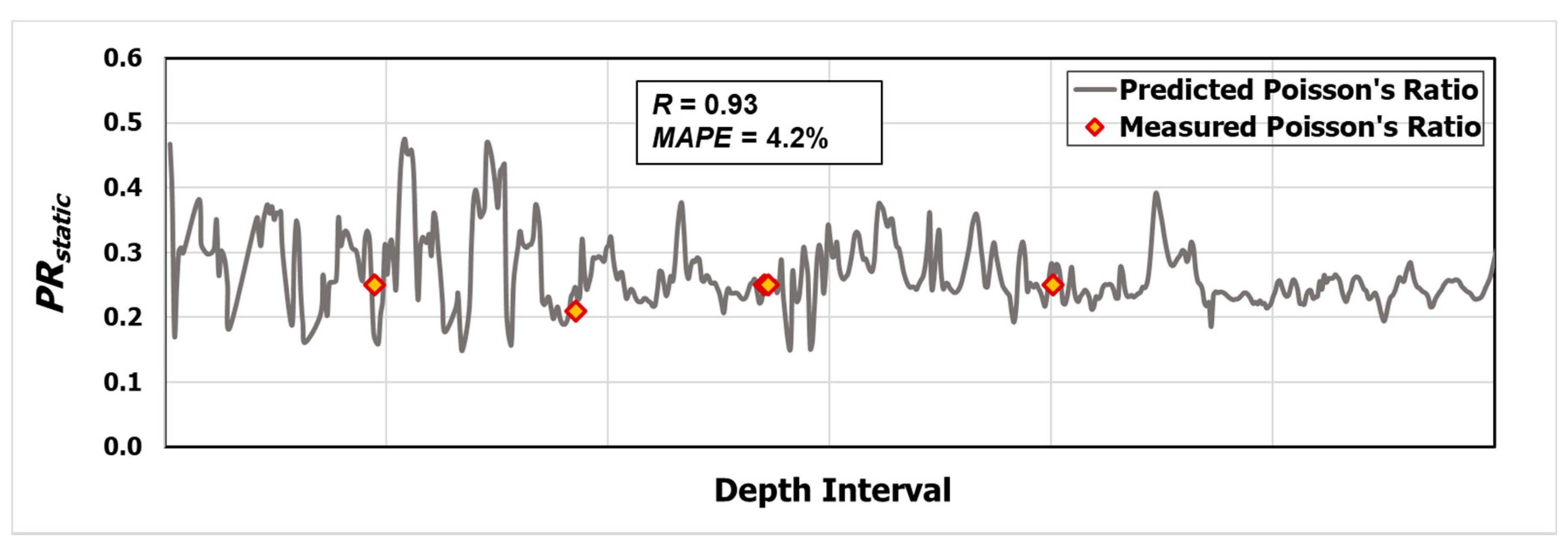
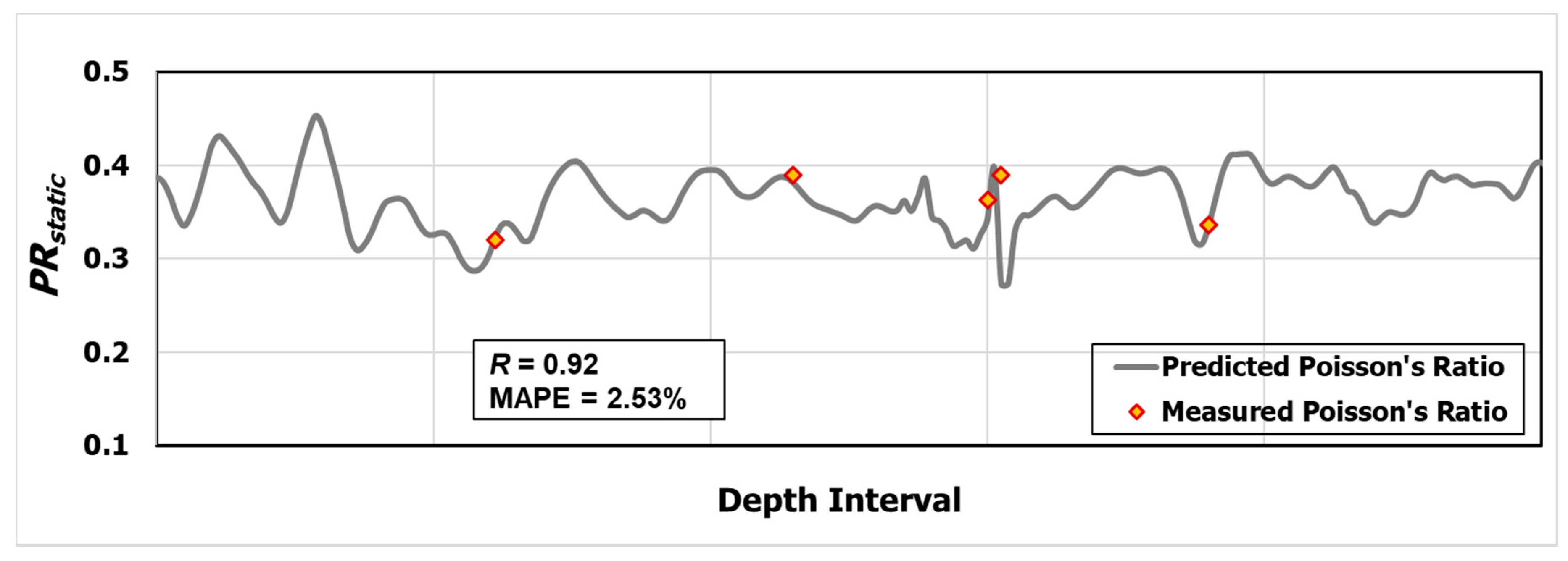
3.5.1. Phase: Validation Using Field Data
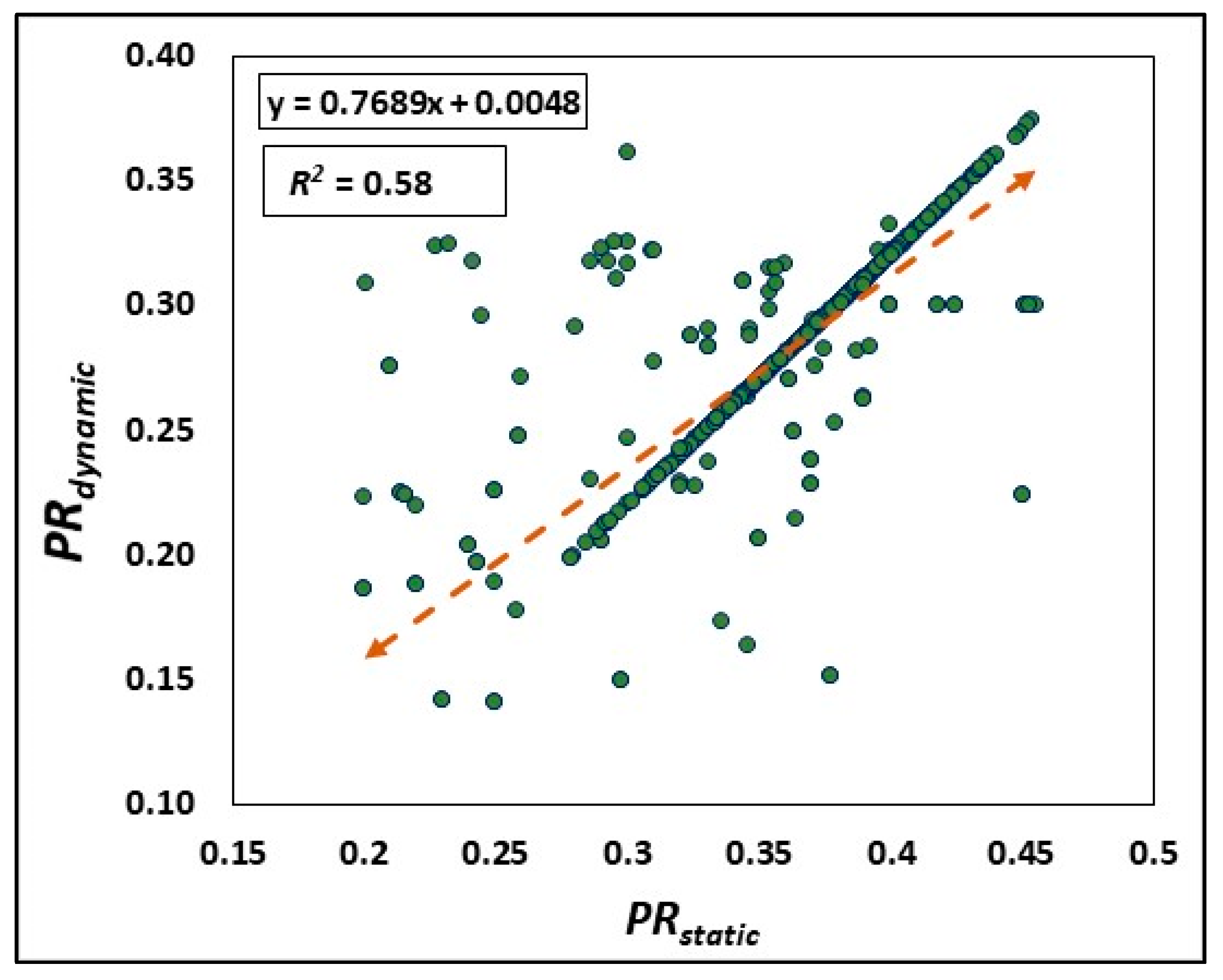
3.5.2. Phase 2: Validation by Comparing the Predictions of the ANN Model with Common Previous Approaches
4. Conclusions
- The developed ANN model has the leading predictive efficiency for the static Poisson’s ratio compared with other approaches.
- Petrophysical log data, namely RHOB, , and are used as input parameters for the developed model to produce a continuous profile of PRstatic values whenever these log data are available.
- The extracted ANN-based empirical equation makes the implementation of the developed ANN model easier and more practical, without the need to run the ANN model using any software.
- The developed ANN model allows the estimation of PRstatic values of retrieved sandstone samples without destroying them, which makes them available for more tests.
- The developed ANN-based equation is considered a timely and economically effective tool to estimate PRstatic values, especially when core data are not available.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AI | Artificial intelligence |
| MAPE | Mean absolute percentage error |
| UCS | Unconfined compressive strength |
| ANN | Artificial neural network |
| SADE | self-adaptive differential evolution |
| Tansig | Hyperbolic tangent sigmoid transfer function |
| Hardlim | Hard-limit transfer function |
| Logsig | Log-sigmoid transfer function |
| Pure-linear | Linear transfer function |
| Elliotsig | Elliot symmetric sigmoid transfer function |
| Tribas | Triangular basis transfer function |
| Satlin | Saturating linear transfer function |
| Radbas | Radial basis transfer function |
| Trainlm | Levenberg–Marquardt backpropagation |
| Trainbfg | BFGS quasi-Newton |
| Trainbr | Bayesian regularization backpropagation |
| Trainscg | Scaled conjugate gradient backpropagation |
| List of Symbols | |
| R2 | Coefficient of determination |
| PRstatic | Static Poisson’s ratio |
| PRdynamic | Dynamic Poisson’s ratio |
| RHOB | Formation bulk density |
| P-wave | Compressional wave |
| S-wave | Shear wave |
| P-wave transit time | |
| S-wave transit time | |
| T | Tensile strength |
| Overburden stress | |
| Horizontal stress | |
| Vp | P-wave velocity |
| Vs | S-wave velocity |
| Es | Static Young’s modulus |
| b1 | Input layer biases |
| b2 | Output layer bias |
| N | Number of neurons in the hidden layer |
| R | Correlation coefficient |
| w1 | Weights linking inputs and hidden layer |
| w2 | Weights linking output and hidden layer |
| Subscripts | |
| i | Index of each neuron in the hidden layer |
| n | Normalized value |
Appendix A
References
- Anifowose, F.; Adeniye, S.; Abdulraheem, A.; Al-Shuhail, A. Integrating seismic and log data for improved petroleum reservoir properties estimation using non-linear feature-selection based hybrid computational intelligence models. J. Pet. Sci. Eng. 2016, 145, 230–237. [Google Scholar] [CrossRef]
- Anifowose, F.A.; Labadin, J.; Abdulraheem, A. Ensemble model of non-linear feature selection-based extreme learning machine for improved natural gas reservoir characterization. J. Nat. Gas Sci. Eng. 2015, 26, 1561–1572. [Google Scholar] [CrossRef]
- Helmy, T.; Hossain, M.I.; Adbulraheem, A.; Rahman, S.M.; Hassan, M.R.; Khoukhi, A.; Elshafei, M. Prediction of non-hydrocarbon gas components in separator by using hybrid computational intelligence models. Neural Comput. Appl. 2017, 28, 635–649. [Google Scholar] [CrossRef]
- Al-Bulushi, N.I.; King, P.R.; Blunt, M.J.; Kraaijveld, M. Artificial neural networks workflow and its application in the petroleum industry. Neural Comput. Appl. 2012, 21, 409–421. [Google Scholar] [CrossRef]
- Tariq, Z.; Elkatatny, S.; Mahmoud, M.; Ali, A.Z.; Abdulraheem, A. A new technique to develop rock strength correlation using artificial intelligence tools. In SPE Reservoir Characterisation and Simulation Conference and Exhibition; Society of Petroleum Engineers: Calgary, AB, Canada, 2017. [Google Scholar] [CrossRef]
- Nes, O.M.; Fjær, E.; Tronvoll, J.; Kristiansen, T.G.; Horsrud, P. Drilling time reduction through an integrated rock mechanics analysis. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar]
- Zhang, H.; Qiu, K.; Fuller, J.; Yin, G.; Yuan, F.; Chen, S. Geomechanical Evaluation Enabled Successful Stimulation of a HPHT Tight Gas Reservoir in Western China. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 19–22 January 2014. [Google Scholar]
- Tutuncu, A.N.; Sharma, M.M. Relating Static and Ultrasonic Laboratory Measurements to Acoustic Log Measurements in Tight Gas Sands. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar] [CrossRef]
- Gatens, J.M., III; Harrison, C.W., III; Lancaster, D.E.; Guidry, F.K. In-situ stress tests and acoustic logs determine mechanical propertries and stress profiles in the devonian shales. SPE Formation Eval. 1990, 5, 248–254. [Google Scholar] [CrossRef]
- Najibi, A.R.; Ghafoori, M.; Lashkaripour, G.R.; Asef, M.R. Empirical relations between strength and static and dynamic elastic properties of Asmari and Sarvak limestones, two main oil reservoirs in Iran. J. Pet. Sci. Eng. 2015, 126, 78–82. [Google Scholar] [CrossRef]
- Tariq, Z.; Mahmoud, M.; Abdulraheem, A. Core log integration: A hybrid intelligent data-driven solution to improve elastic parameter prediction. Neural. Comput. Appl. 2019, 1–21. [Google Scholar] [CrossRef]
- Nawrocki, P.A.; Dusseault, M.B. Modelling of Damaged Zones around Boreholes Using a Radius Dependent Young’s Modulus. J. Can. Pet. Technol. 1996, 35, 31–35. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.S.; Xiong, Y.; Winterfeld, P.H.; Huang, Z. Geomechanics coupling simulation of fracture closure and its influence on gas production in shale gas reservoirs. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TA, USA, 23–25 February 2015. [Google Scholar]
- Ameen, M.S.; Smart, B.G.; Somerville, J.M.; Hammilton, S.; Naji, N.A. Predicting rock mechanical properties of carbonates from wireline logs (a case study: Arab-D reservoir, Ghawar field, Saudi Arabia). Mar. Pet. Geol. 2009, 26, 430–444. [Google Scholar] [CrossRef]
- Elkatatny, S.; Mahmoud, M.; Mohamed, I.; Abdulraheem, A. Development of a new correlation to determine the static Young’s modulus. J. Pet. Explor. Prod. Technol 2018, 8, 17–30. [Google Scholar] [CrossRef]
- Spain, D.R.; Gil, I.R.; Sebastian, H.M.; Smith, P.; Wampler, J.; Cadwallader, S.; Graff, M. Geo-engineered completion optimization: An integrated, multi-disciplinary approach to improve stimulation efficiency in unconventional shale reservoirs. In Proceedings of the SPE Middle East Unconventional Resources Conference and Exhibition, Muscat, Oman, 26–28 January 2015. [Google Scholar]
- Mahmoud, M.; Elkatatny, S.; Ramadan, E.; Abdulraheem, A. Development of lithology-based static Young’s modulus correlations from log data based on data clustering technique. J. Pet. Sci. Eng. 2016, 146, 10–20. [Google Scholar] [CrossRef]
- Tariq, Z.; Elkatatny, S.; Mahmoud, M.; Abdulraheem, A. A new artificial intelligence based empirical correlation to predict sonic travel time. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 14–16 November 2016. [Google Scholar]
- Tariq, Z.; Elkatatny, S.; Mahmoud, M.; Ali, A.Z.; Abdulraheem, A. A new technique to develop rock strength correlation using artificial intelligence tools. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 8–10 May 2017. [Google Scholar]
- Tariq, Z.; Elkatatny, S.M.; Mahmoud, M.A.; Abdulraheem, A.; Abdelwahab, A.Z.; Woldeamanuel, M. Estimation of Rock Mechanical Parameters Using Artificial Intelligence Tools; American Rock Mechanics Association: San Francisco, CA, USA, 2017. [Google Scholar]
- Elkatatny, S.; Tariq, Z.; Mahmoud, M.; Abdulraheem, A.; Mohamed, I. An integrated approach for estimating static Young’s modulus using artificial intelligence tools. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- D’Andrea, D.V.; Fischer, R.L.; Fogelson, D.E. Prediction of Compressive Strength from Other Rock Properties; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1965; Volume 6702.
- Kumar, J. The effect of Poisson’s ratio on rock properties. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, New Orleans, LA, USA, 3–6 October 1976. [Google Scholar]
- Edimann, K.; Somerville, J.M.; Smart, B.G.D.; Hamilton, S.A.; Crawford, B.R. Predicting rock mechanical properties from wireline porosities. In Proceedings of the SPE/ISRM Rock Mechanics in Petroleum Engineering, Trondheim, Norway, 8–10 July 1998. [Google Scholar]
- Kumar, A.; Jayakumar, T.; Raj, B.; Ray, K.K. Correlation between ultrasonic shear wave velocity and Poisson’s ratio for isotropic solid materials. Acta Mater. 2003, 51, 2417–2426. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. Effects of testing methods and conditions on the elastic properties of limestone rock. Eng. Geol. 2004, 74, 139–156. [Google Scholar] [CrossRef]
- Singh, V.; Singh, T.N. A Neuro-Fuzzy Approach for Prediction of Poisson’s Ratio and Young’s Modulus of Shale and Sandstone. In Proceedings of the 41st US Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 17–21 June 2006. [Google Scholar]
- Shalabi, F.I.; Cording, E.J.; Al-Hattamleh, O.H. Estimation of rock engineering properties using hardness tests. Eng. Geol. 2007, 90, 138–147. [Google Scholar] [CrossRef]
- Al-Anazi, A.; Gates, I.D. A support vector machine algorithm to classify lithofacies and model permeability in heterogeneous reservoirs. Eng. Geol. 2010, 114, 267–277. [Google Scholar] [CrossRef]
- Abdulraheem, A. Prediction of Poisson’s Ratio for Carbonate Rocks Using ANN and Fuzzy Logic Type-2 Approaches. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26 March 2019. [Google Scholar]
- ASTM D2664-04. Standard Test Method for Triaxial Compressive Strength of Undrained Rock Core Specimens without Pore Pressure Measurements. 2005. Available online: https://www.astm.org/Standards/D2664.htm (accessed on 3 April 2019).
- Gercek, H. Poisson’s ratio values for rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 1–13. [Google Scholar] [CrossRef]
- Dawson, R. How Significant Is A Boxplot Outlier? J. Stat. Educ. 2011, 19. [Google Scholar] [CrossRef]
- Thirumalai, C.S.; Manickam, V.; Balaji, R. Data analysis using Box and Whisker Plot for Lung Cancer. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies, Vellore, Tamil Nadu, India, 21–22 April 2017. [Google Scholar] [CrossRef]
- Fontana, E.; Iturrino, G.J.; Tartarotti, P. Depth-shifting and orientation of core data using a core–log integration approach: A case study from ODP–IODP Hole 1256D. Tectonophysics 2010, 494, 85–100. [Google Scholar] [CrossRef]
- Nadezhdin, O.; Zairullina, E.; Efimov, D.; Savichev, V. Algorithms of Automatic Core-Log Depth-Shifting In Problems of Petrophysical Model Construction, Proceedings of the SPE Russian Oil and Gas Exploration & Production Technical Conference and Exhibition; Society of Petroleum Engineers: Moscow, Russia, 16 October 2014. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin, Genmany, 2009; pp. 1–4. [Google Scholar]
- Sudakov, O.; Burnaev, E.; Koroteev, D. Driving Digital Rock towards Machine Learning:predicting permeability with Gradient Boosting and Deep Neural Networks. Comput. Geosci. 2018, 127, 91–98. [Google Scholar] [CrossRef]
- Chauhan, S.; Rühaak, W.; Anbergen, H.; Kabdenov, A.; Freise, M.; Wille, T.; Sass, I. Phase segmentation of X-ray computer tomography rock images using machine learning techniques: An accuracy and performance study. Solid Earth 2016, 7, 1125–1139. [Google Scholar] [CrossRef]
- Chauhan, S.; Rühaak, W.; Khan, F.; Enzmann, F.; Mielke, P.; Kersten, M.; Sass, I. Processing of rock core microtomography images: Using seven different machine learning algorithms. Comput. Geosci. 2016, 86, 120–128. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Javadpour, F.; Sahimi, M. Data mining and machine learning for identifying sweet spots in shale reservoirs. Expert Syst. Appl. 2017, 88, 435–447. [Google Scholar] [CrossRef]
- Mousavi Nezhad, M.; Gironacci, E.; Rezania, M.; Khalili, N. Stochastic modelling of crack propagation in materials with random properties using isometric mapping for dimensionality reduction of nonlinear data sets. Int. J. Numer. Methods Eng. 2017, 113, 656–680. [Google Scholar] [CrossRef]
- Keller, L.M.; Schwiedrzik, J.J.; Gasser, P.; Michler, J. Understanding anisotropic mechanical properties of shales at different length scales: In situ micropillar compression combined with finite element calculations. J. Geophys. Res. Solid Earth 2017, 122. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, 381–392. [Google Scholar] [CrossRef]
- Rable, B. The Future is Here: 3 Ways AI Roots Itself in O&G in the Surge Magazine. 2017. Available online: http://thesurge.com/stories/future-artificial-intelligence-roots-oil-gas-industry (accessed on 3 April 2019).
- Anifowose, F.A.; Labadin, J.; Abdulraheem, A. Ensemble machine learning: An untapped modeling paradigm for petroleum reservoir characterization. J. Pet. Sci. Eng. 2017, 151, 480–487. [Google Scholar] [CrossRef]
- Lippman, R.P. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Nakamoto, P. Neural Networks and Deep Learning: Deep Learning Explained to Your Granny a Visual Introduction for Beginners Who Want to Make Their Own Deep Learning Neural Network (Machine Learning); CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2017. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Niculescu, S. Artificial neural networks and genetic algorithms in Qsar. J. Mol. Struct. 2003, 622, 71–83. [Google Scholar] [CrossRef]
- Yılmaz, I.; Yuksek, A.G. An example of artificial neural network (ANN) application for indirect estimation of rock parameters. Rock Mech. Rock Eng. 2008, 41, 781–795. [Google Scholar] [CrossRef]
- Rao, S.; Ramamurti, V. A hybrid technique to enhance the performance of recurrent neural networks for time series prediction. In Proceedings of the IEEE international conference on neural networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 52–57. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1995, 23, 341–359. [Google Scholar]
- Goudos, S.K.; Baltzis, K.B.; Antoniadis, K.; Zaharis, Z.D.; Hilas, C.S. A comparative study of common and self-adaptive differential evolution strategies on numerical benchmark problems. Procedia Comput. Sci. 2011, 3, 83–88. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-adaptive differential evolution algorithm for numerical optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–4 September 2005; Volume 2, pp. 178–1791. [Google Scholar]
- Vesterstrom, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004. [Google Scholar]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Foroud, T.; Baradaran, A.; Seifi, A. A comparative evaluation of global search algorithms in black box optimization of oil production: A case study on Brugge field. J. Pet. Sci. Eng. 2018, 167, 131–151. [Google Scholar] [CrossRef]
- Abdelgawad, K.; Elkatatny, S.; Moussa, T.; Mahmoud, M.; Patil, S. Real-Time Determination of Rheological Properties of Spud Drilling Fluids Using a Hybrid Artificial Intelligence Technique. J. Energy Resour. Technol. 2019, 141, 032908. [Google Scholar] [CrossRef]
- Smith, G. Essential Statistics Regression and Econometrics; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Yale, D.P. Static and Dynamic Rock Mechanical Properties in the Hugoton and Panoma Fields, Kansas. In Proceedings of the SPE Mid-Continent Gas Symposium, Amarillo, TX, USA, 22–24 May 1994. [Google Scholar]
- Montmayeur, H.; Graves, R.M. Prediction of static elastic/mechanical properties of consolidated and unconsolidated sands from acoustic measurements: Correlations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. [Google Scholar]







| Parameter | RHOB, g/cm3 | |||
|---|---|---|---|---|
| Minimum | 2.24 | 44.34 | 73.19 | 0.20 |
| Maximum | 2.98 | 80.49 | 145.60 | 0.46 |
| Range | 0.74 | 36.15 | 72.42 | 0.26 |
| Standard deviation | 0.13 | 7.59 | 11.80 | 0.05 |
| Variance | 0.02 | 57.63 | 139.35 | 0.00 |
| Parameter | Ranges | |
|---|---|---|
| Number of Neurons | 5–25 | |
| Inputs Number | 3 | |
| Output Number | 1 | |
| Number of Hidden Layers | 1–3 | |
| Learning Rate | 0.01–0.9 | |
| Input Layer Transfer Function | tansig | |
| elliotsig | ||
| tribas | ||
| Output Layer Transfer Function | pure-linear | |
| Training Algorithm | trainlm | trainscg |
| trainbr | trainbfg | |
| Neuron Index | Input Layer Weights | Hidden Layer Weights | Input Layer Biases | ||
|---|---|---|---|---|---|
| i | |||||
| 1 | −2.020 | −4.310 | 3.000 | 1.551 | −5.071 |
| 2 | 4.057 | 1.753 | 2.032 | −0.689 | 4.269 |
| 3 | −1.519 | −4.775 | 3.168 | 1.309 | 4.943 |
| 4 | −5.682 | −2.829 | −1.652 | 1.235 | 3.583 |
| 5 | −0.388 | −1.805 | 1.971 | 0.088 | 1.466 |
| 6 | 0.165 | −1.357 | 3.607 | −1.041 | −4.866 |
| 7 | 2.678 | −4.758 | 2.102 | 1.225 | −4.560 |
| 8 | 1.961 | −2.012 | −4.199 | 1.508 | −5.459 |
| 9 | −2.979 | 3.590 | −1.195 | −1.485 | −6.104 |
| 10 | −1.352 | 3.028 | 6.392 | −1.405 | −3.564 |
| 11 | 0.982 | 2.406 | −3.062 | 1.549 | −3.602 |
| 12 | 3.043 | −1.423 | 0.093 | 2.899 | −3.161 |
| 13 | −3.225 | −1.833 | 1.484 | −2.479 | −2.090 |
| Model | R | MAPE, % | R2 |
|---|---|---|---|
| ANN_SADE | 0.97 | 4.88 | 0.96 |
| Standard Workflow | 0.67 | 53.5 | 0.45 |
| Kumar’s Model | 0.94 | 16.13 | 0.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gowida, A.; Moussa, T.; Elkatatny, S.; Ali, A. A Hybrid Artificial Intelligence Model to Predict the Elastic Behavior of Sandstone Rocks. Sustainability 2019, 11, 5283. https://doi.org/10.3390/su11195283
Gowida A, Moussa T, Elkatatny S, Ali A. A Hybrid Artificial Intelligence Model to Predict the Elastic Behavior of Sandstone Rocks. Sustainability. 2019; 11(19):5283. https://doi.org/10.3390/su11195283
Chicago/Turabian StyleGowida, Ahmed, Tamer Moussa, Salaheldin Elkatatny, and Abdulwahab Ali. 2019. "A Hybrid Artificial Intelligence Model to Predict the Elastic Behavior of Sandstone Rocks" Sustainability 11, no. 19: 5283. https://doi.org/10.3390/su11195283
APA StyleGowida, A., Moussa, T., Elkatatny, S., & Ali, A. (2019). A Hybrid Artificial Intelligence Model to Predict the Elastic Behavior of Sandstone Rocks. Sustainability, 11(19), 5283. https://doi.org/10.3390/su11195283






