Dynamics of Upwelling Annual Cycle in the Equatorial Pacific Ocean
Abstract
Key points:
- The linear framework of the Zebiak–Cane ocean model for upwelling annual cycle works well in the Pacific through observed and Coupled Model Intercomparison Project Phase 5 (CMIP5) results.
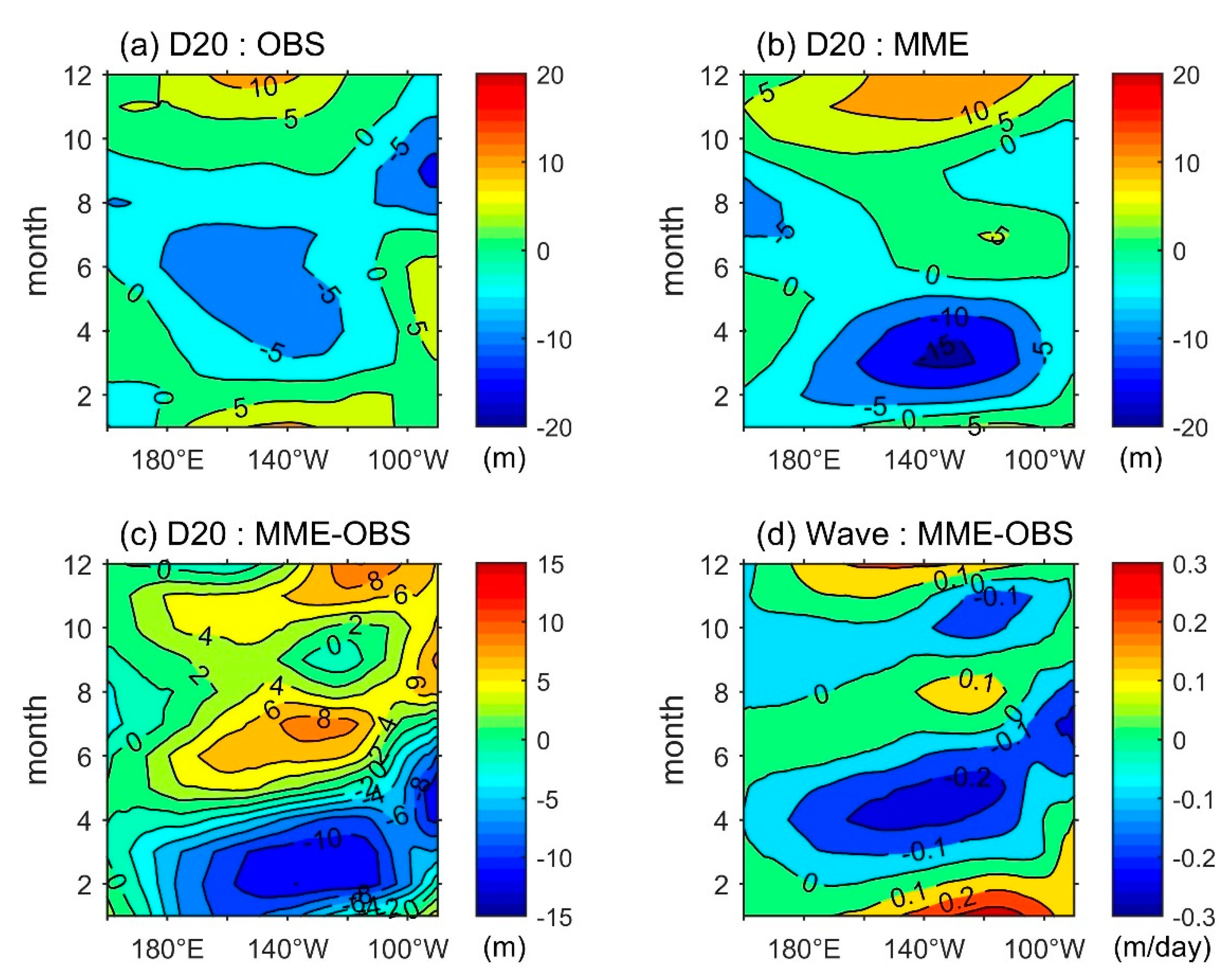
- In observation, the equatorial Pacific upwelling annual cycle is dominated by local wind-driven Ekman effects.
- In CMIP5 simulations, the amplified westward-shift wave upwelling overtakes Ekman effects and plays a crucial role in the equatorial Pacific upwelling annual cycle.
1. Introduction
2. Model and Data
3. Results and Discussion
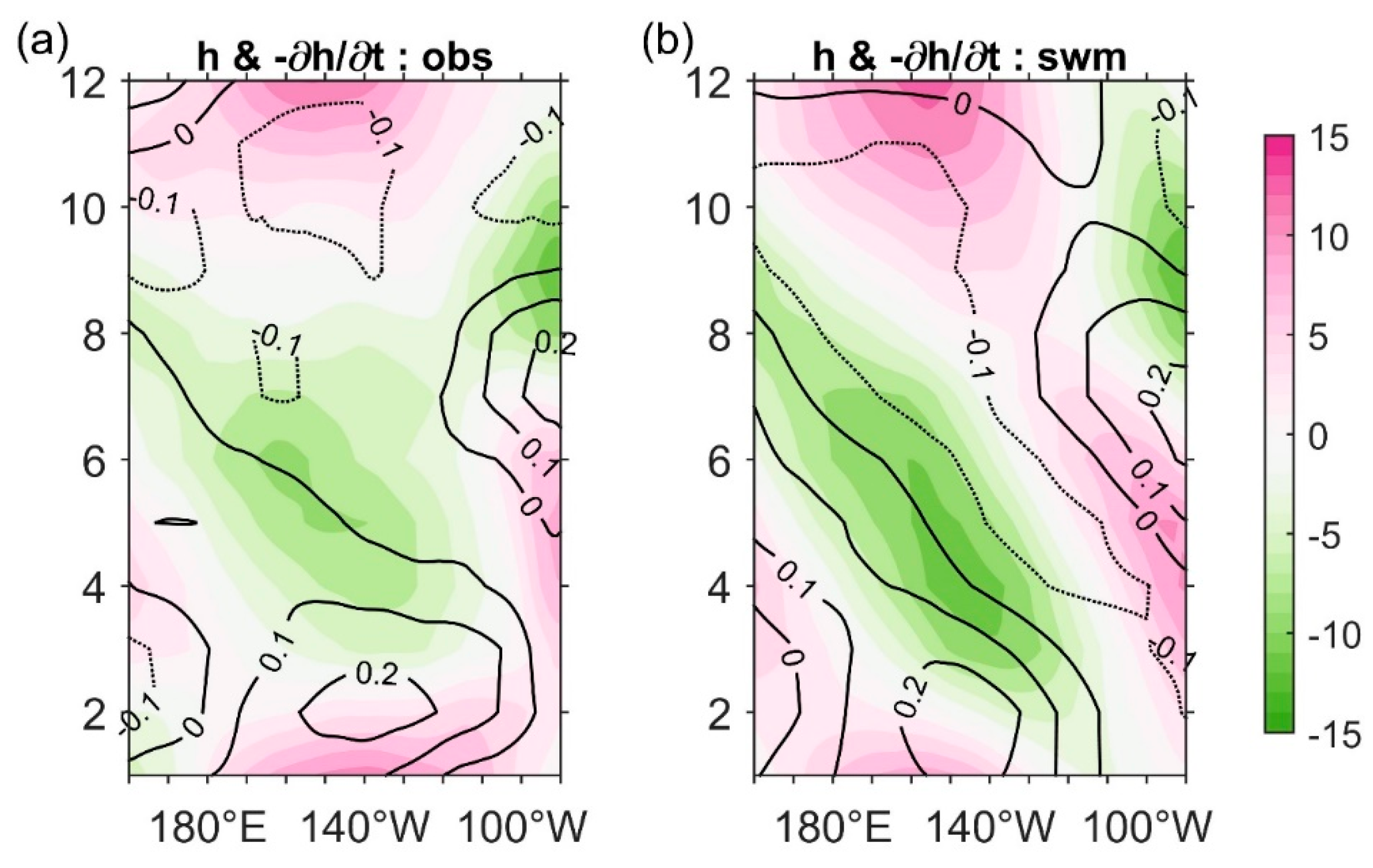
3.1. The Theoretical Formation of Upwelling Annual Cycles
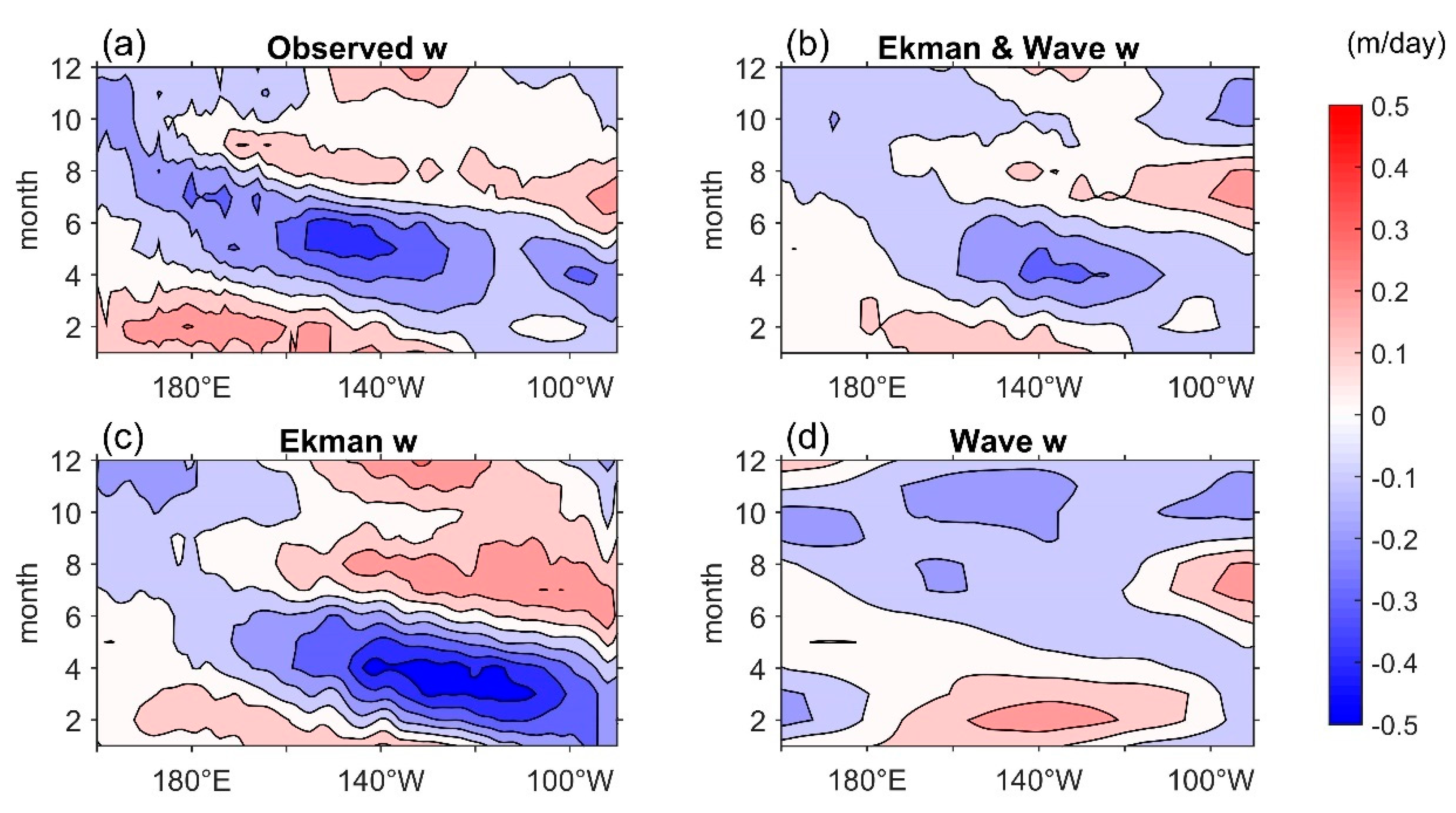
3.2. Validation in Observation
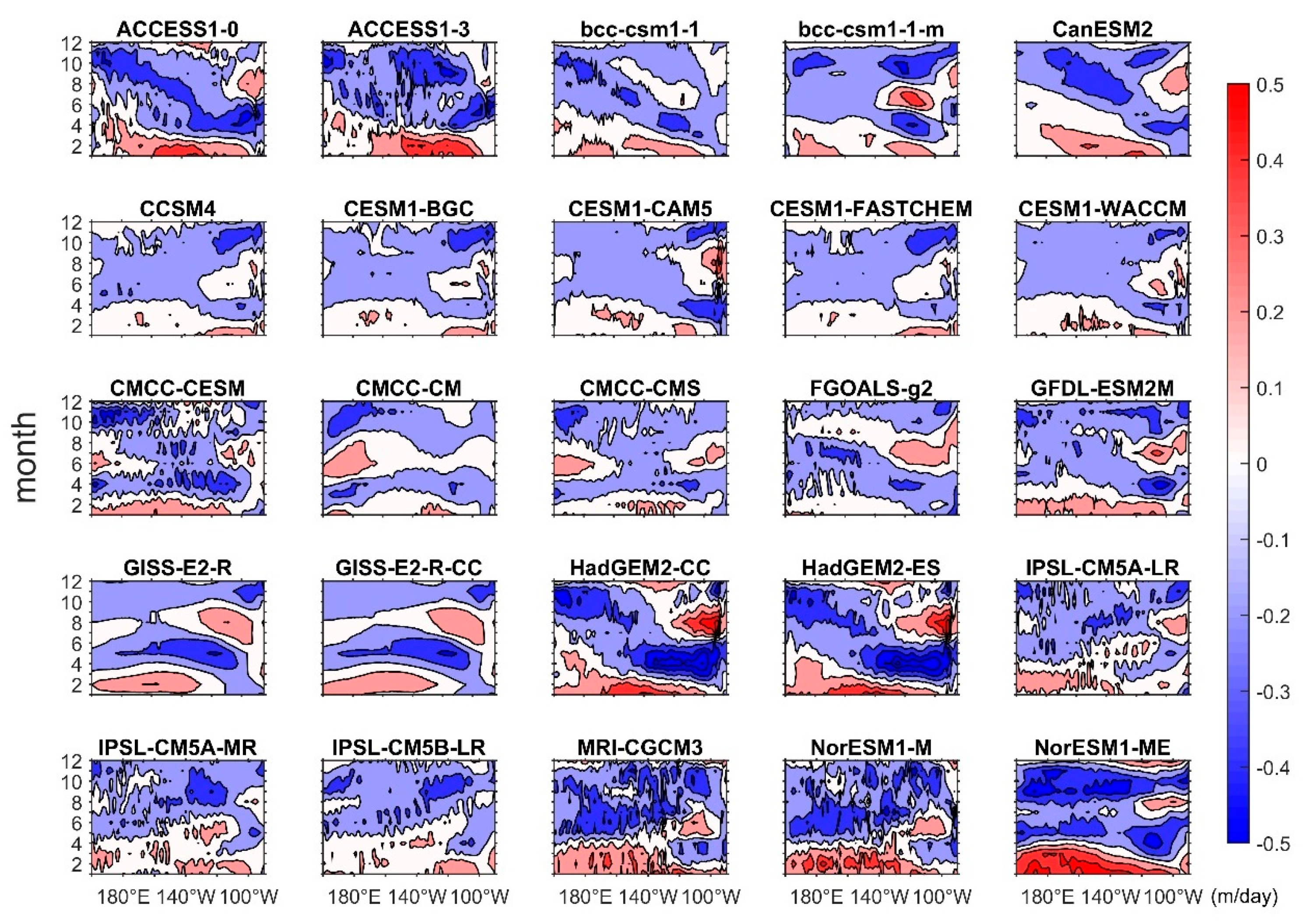
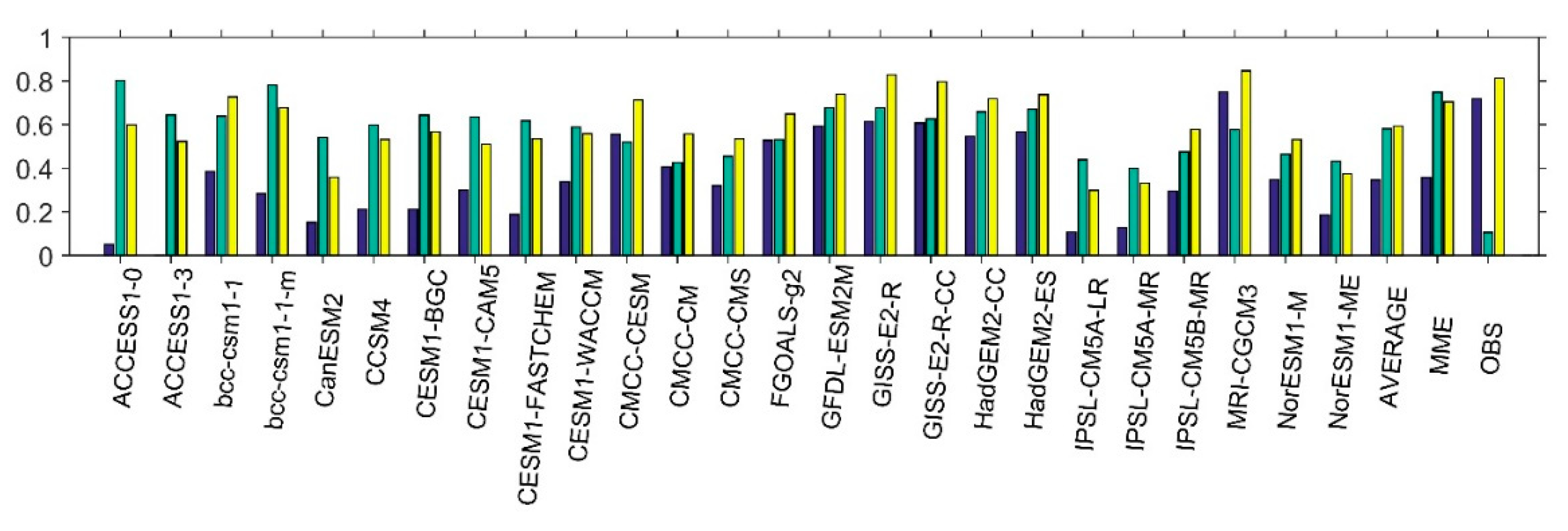
3.3. Validation in CMIP5 Simulations
3.4. The Dynamical Bias in CMIP5 Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xie, S.-P. Ocean–atmosphere interaction in the making of the Walker circulation and equatorial Pacific cold tongue. J. Clim. 1998, 11, 189–201. [Google Scholar] [CrossRef]
- Li, G.; Xie, S.-P. Tropical Biases in CMIP5 Multimodel Ensemble: The Excessive Equatorial Pacific Cold Tongue and Double ITCZ Problems. J. Clim. 2014, 27, 1765–1780. [Google Scholar] [CrossRef]
- Clement, A.C.; Seager, R.; Cane, M.; Zebiak, S.E. An ocean dynamical thermostat. Oceanogr. Lit. Rev. 1997, 6, 556. [Google Scholar] [CrossRef]
- An, S.-I.; Kim, J.-W.; Im, S.-H.; Kim, B.-M.; Park, J.H. Recent and future sea surface temperature trends in tropical Pacific warm pool and cold tongue regions. Clim. Dyn. 2012, 39, 1373–1383. [Google Scholar] [CrossRef]
- Dandonneau, Y.; Deschamps, P.-Y.; Nicolas, J.-M.; Loisel, H.; Blanchot, J.; Montel, Y.; Thieuleux, F.; Bécu, G. Seasonal and interannual variability of ocean color and composition of phytoplankton communities in the North Atlantic, equatorial Pacific and South Pacific. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 303–318. [Google Scholar] [CrossRef]
- Weingartner, T.J.; Weisberg, R.H. On the Annual Cycle of Equatorial Upwelling in the Central Atlantic Ocean. J. Phys. Oceanogr. 1991, 21, 68–82. [Google Scholar] [CrossRef]
- Richter, I.; Xie, S.-P. On the origin of equatorial Atlantic biases in coupled general circulation models. Clim. Dyn. 2008, 31, 587–598. [Google Scholar] [CrossRef]
- Hagos, S.M.; Cook, K.H. Development of a Coupled Regional Model and Its Application to the Study of Interactions between the West African Monsoon and the Eastern Tropical Atlantic Ocean. J. Clim. 2009, 22, 2591–2604. [Google Scholar] [CrossRef]
- Caniaux, G.; Giordani, H.; Redelsperger, J.-L.; Guichard, F.; Key, E.; Wade, M. Coupling between the Atlantic cold tongue and the West African monsoon in boreal spring and summer. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Wang, L.-C.; Jin, F.-F.; Wu, C.-R.; Hsu, H.-H. Dynamics of Upwelling Annual Cycle in the Equatorial Atlantic Ocean. Geophys. Res. Lett. 2017, 44, 3737–3743. [Google Scholar] [CrossRef]
- Zebiak, S.E.; Cane, M.A. A model El Niño–Southern Oscillation. Mon. Weather Rev. 1987, 115, 2262–2278. [Google Scholar] [CrossRef]
- Wang, L.-C.; Jin, F.-F.; Wu, C.-R. Dynamics of simulated Atlantic upwelling annual cycle in CMIP5 models. J. Geophys. Res. Ocean. 2017, 122, 3737–3743. [Google Scholar] [CrossRef]
- Balmaseda, M.A.; Vidard, A.; Anderson, D.L.T. The ECMWF Ocean Analysis System: ORA-S3. Mon. Weather Rev. 2008, 136, 3018–3034. [Google Scholar] [CrossRef]
- Zhai, F.; Hu, D. Revisit the interannual variability of the North Equatorial Current transport with ECMWF ORA-S3. J. Geophys. Res. Ocean. 2013, 118, 1349–1366. [Google Scholar] [CrossRef]
- Jin, F.-F.; Boucharel, J.; Lin, I.-I. Eastern Pacific tropical cyclones intensified by El Niño delivery of subsurface ocean heat. Nature 2014, 516, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Munoz, E.; Kirtman, B.; Weijer, W. Varied representation of the Atlantic Meridional Overturning across multidecadal ocean reanalyses. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2011, 58, 1848–1857. [Google Scholar] [CrossRef]
- Nnamchi, H.C.; Li, J.; Kucharski, F.; Kang, I.-S.; Keenlyside, N.S.; Chang, P.; Farneti, R. Thermodynamic controls of the Atlantic Niño. Nat. Commun. 2015, 6, 8895. [Google Scholar] [CrossRef]
- Nnamchi, H.C.; Li, J.; Kucharski, F.; Kang, I.-S.; Keenlyside, N.S.; Chang, P.; Farneti, R. An Equatorial–Extratropical Dipole Structure of the Atlantic Niño. J. Clim. 2016, 29, 7295–7311. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Wyrtki, K. An Estimate of Equatorial Upwelling in the Pacific. J. Phys. Oceanogr. 1981, 11, 1205–1214. [Google Scholar] [CrossRef]
- McGregor, S.; Holbrook, N.J.; Power, S.B. Interdecadal Sea Surface Temperature Variability in the Equatorial Pacific Ocean. Part I: The Role of Off-Equatorial Wind Stresses and Oceanic Rossby Waves. J. Clim. 2007, 20, 2643–2658. [Google Scholar] [CrossRef]
- Bunge, L.; Clarke, A.J. Seasonal Propagation of Sea Level along the Equator in the Atlantic. J. Phys. Oceanogr. 2009, 39, 1069–1074. [Google Scholar] [CrossRef]
- Ding, H.; Keenlyside, N.S.; Latif, M. Seasonal cycle in the upper equatorial Atlantic Ocean. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Li, G.; Du, Y.; Xu, H.; Ren, B. An Intermodel Approach to Identify the Source of Excessive Equatorial Pacific Cold Tongue in CMIP5 Models and Uncertainty in Observational Datasets. J. Clim. 2015, 28, 7630–7640. [Google Scholar] [CrossRef]

| Model Name | Modeling Center |
|---|---|
| ACCESS1-0 | The Centre for Australian Weather and Climate Research, Australia |
| ACCESS1-3 | The Centre for Australian Weather and Climate Research, Australia |
| bcc-csm1-1 | Beijing Climate Center, China Meteorological Administration, China |
| bcc-csm1-1-m | Beijing Climate Center, China Meteorological Administration, China |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada |
| CCSM4 | National Center for Atmospheric Research, US |
| CESM1-BGC | National Center for Atmospheric Research, US |
| CESM1-CAM5 | National Center for Atmospheric Research, US |
| CESM1-FASTCHEM | National Center for Atmospheric Research, US |
| CESM1-WACCM | National Center for Atmospheric Research, US |
| CMCC-CESM | Centro Euro-Mediterraneo per I Cambiamenti Climatici, Italy |
| CMCC-CM | Centro Euro-Mediterraneo per I Cambiamenti Climatici, Italy |
| CMCC-CMS | Centro Euro-Mediterraneo per I Cambiamenti Climatici, Italy |
| FGOALS-g2 | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences, China |
| GFDL-ESM2M | NOAA Geophysical Fluid Dynamics Laboratory, US |
| GISS-E2-R | NASA Goddard Institute for Space Studies, US |
| GISS-E2-R-CC | NASA Goddard Institute for Space Studies, US |
| HadGEM2-CC | Met Office Hadley Centre, UK |
| HadGEM2-ES | Met Office Hadley Centre, UK |
| IPSL-CM5A-LR | Institut Pierre-Simon Laplace, France |
| IPSL-CM5A-MR | Institut Pierre-Simon Laplace, France |
| IPSL-CM5B-LR | Institut Pierre-Simon Laplace, France |
| MRI-CGCM3 | Meteorological Research Institute, Japan |
| NorESM1-M | Norwegian Climate Centre, Norway |
| NorESM1-ME | Norwegian Climate Centre, Norway |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.-C.; Yu, J.-Y. Dynamics of Upwelling Annual Cycle in the Equatorial Pacific Ocean. Sustainability 2019, 11, 5038. https://doi.org/10.3390/su11185038
Wang L-C, Yu J-Y. Dynamics of Upwelling Annual Cycle in the Equatorial Pacific Ocean. Sustainability. 2019; 11(18):5038. https://doi.org/10.3390/su11185038
Chicago/Turabian StyleWang, Li-Chiao, and Jia-Yuh Yu. 2019. "Dynamics of Upwelling Annual Cycle in the Equatorial Pacific Ocean" Sustainability 11, no. 18: 5038. https://doi.org/10.3390/su11185038
APA StyleWang, L.-C., & Yu, J.-Y. (2019). Dynamics of Upwelling Annual Cycle in the Equatorial Pacific Ocean. Sustainability, 11(18), 5038. https://doi.org/10.3390/su11185038






