Abstract
To improve the heat dissipation performance of power batteries in electric racing cars in the Formula Student Electric China (FSEC), a battery cooling system was researched. A battery thermal model and a temperature experimental platform were established. The thermal model was verified by comparing the results of the ANSYS/Workbench simulations with the experimental results, and the maximum error was 7.2%. Based on the FSEC dynamic conditions, the cooling demand was analyzed according to the heat transfer theory. Then, an orthogonal method was used to optimize the position of the cooling fan and the arrangement of the cells, and a parameterized battery simulation model based on ANSYS/Icepak was established. The simulation results show that the maximum temperature difference was optimized by 38.35%. The results of the simulation were in good agreement with the experimental results, and the maximum error was less than 2 °C. This indicates that this design can ensure a car battery system that has a good heat dissipation performance in the FSEC; thus, the intended goal was achieved.
1. Introduction
The Formula Student Electric China (FSEC) was first held in China in 2013 and gradually became popular. As the only energy source for an electric car, the battery affects the racing performance, and temperature has a significant influence on the battery [1,2]. Owing to the complex acceleration and deceleration in the FSEC dynamic conditions, the battery easily overheats with the rapid changes in the current. Moreover, the safety and reliability requirements as per the rules of the FSEC, are considerable [3].
There have been previous studies on the battery thermal management: Zhao et al. [4] provided a basis for the improvement of the existing battery technology; Chen et al. [5] improved the heat dissipation performance by changing the inclination angle of the collector plate and the width of the ventilation channel; Mahamud et al. [6] effectively improved the non-uniformity of the temperature and proposed a method that changes the flow direction of the battery’s internal heat transfer; Fan et al. [7] applied an air parallel ventilation cooling battery box structure in the FSEC electric car; the Electric Power-driven Racing Car absorbed the heat generated by the battery pack continuously through a liquid flow in a small channel based on the compactness of the cold plate; Jin et al. [8] proposed the placement of a silicone thermal material between the heat pipes and batteries to increase the contact surface; and Zhao et al. [9] proposed a PCM/Al foam matrix for cooling the battery. In addition, new materials such as aluminum foam were proposed and copper foam applications have emerged, with a subsequent improvement in the thermal performance [10].
However, in these existing studies, the FSEC dynamic conditions were not studied in-depth. We analyzed the previous research results and have taken the FSEC dynamics into account for designing a suitable battery box cooling system for lithium batteries for improving the energy efficiency.
2. Thermal Model Establishment and Validation
2.1. Thermal Model Establishment
According to the common assumptions of previous research [11,12], the internal heat is generated evenly and loaded as a body heat source in the center of the cell, the thermal parameters do not change with the temperature, and the cell electrolyte flow is poor. Based on the above, the three-dimensional temperature field model of the interior of the square cell [13] is
where T is the temperature (K); ρ is the average cell density (kg/m3); Cp is the cell specific heat capacity (J/(kg·K)); λx, λy, and λz are the thermal conductivities in the x, y, and z directions, respectively (W/(m·K)); and q is the volume heat generation rate (W/m3).
2.1.1. Thermal Parameters
The battery thermal parameters include density, specific heat capacity, and thermal conductivity. The specific heat capacity can be measured or obtained by theoretical calculation [14]. To obtain the equivalent specific heat capacity, we took the weighted average of the specific heat capacity of the various materials in the battery.
It was difficult to directly measure the thermal conductivity because of the complicated internal heat transfer in the battery. Thus, in this paper, the thermal conductivity of the battery in different directions was estimated using the heat transfer parallel and series connection thermal resistance principle [15].
The equivalent thermal parameters for the cell were obtained based on the data from the battery supplier. In this paper, the lithium battery rated capacity was 8.3 Ah, the nominal voltage was 3.7 V, the cutoff charge and discharge voltages were 3.0 V and 4.2 V, respectively, and the maximum discharge current was 15C (124.5 A, −20–60 °C, the maximum discharge current was 150 A). Finally, the lithium battery thermal physical parameters were obtained (Table 1); the z direction was the direction of the battery thickness, perpendicular to the battery tab.

Table 1.
Thermal physical parameters of the battery.
2.1.2. Heat Generation Rate
This paper uses the classic heat model proposed by Bernardi [16]. Considering the reversible reaction heat, even if the battery limits a high current with the 10C condition discharge process, it does not exceed 5% of the total heat. To calculate the battery heat rate, the model is as follows:
where I is the working current of the battery (A); Vb is the cell volume (m3); Rr is the equivalent internal resistance of the battery (Ω); and kt is the heat correction coefficient, when the battery discharges at 1.35 and charges at 1.15.
In addition, the high current and internal resistance of the battery were taken into account, and the heat generation rate was based on the ohmic resistance heat generation model
2.1.3. Internal Resistance Test
The battery equivalent resistance includes the ohmic resistance and the polarization resistance, and is affected by the state of charge (SOC) and other factors. The equivalent resistance was important in establishing an accurate and effective battery thermal model.
We used five lithium batteries of 3.7 V/8.3 Ah as experimental samples to build the equivalent battery internal resistance testing platform, as shown in Figure 1a. Based on the hybrid pulse power characterization (HPPC) method [17] for obtaining the internal resistance for different SOCs, the test was done with battery testing system from the Jinfan company. The experiment was conducted under a constant temperature of 22 °C. According to the test rebound voltage, the equivalent resistance was calculated under different SOCs, as shown in Figure 1b; the figure shows that the equivalent resistance was 5–8 mΩ.
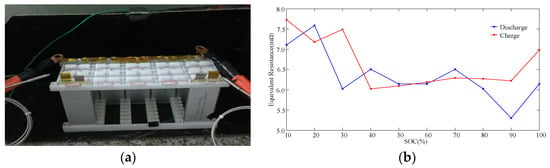
Figure 1.
(a) Battery internal resistance test. (b) Battery internal resistance curve.
2.2. Thermal Model Validation
2.2.1. Battery Temperature Test
Before the test, the battery was fully charged, and the acquisition circuit was designed to measure the surface temperature with a K-type thermocouple for a cell in real time. The test for the surface temperature of the battery platform was established as shown in Figure 2a, and the environmental temperature was controlled strictly; the battery cooling was by air natural convection with the ambient. Four temperature sensors were arranged on the surface of the cell, as shown in Figure 2b.
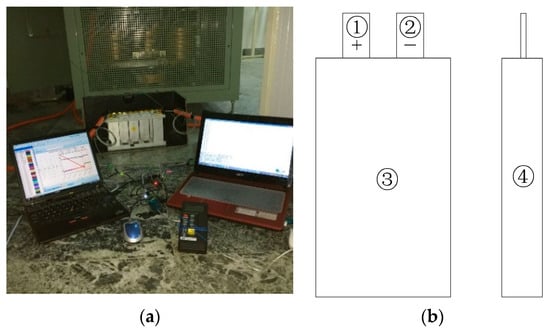
Figure 2.
(a) Battery surface temperature test. (b) Schematic diagram of the temperature sensor; the numbers 1–4 indicate sensor positions.
2.2.2. Validation Model
In order to verify the accuracy of the thermal model, the heat dissipation of the battery was simulated under FSEC conditions. The test was carried out three times, and the average results were compared with the simulation results, as shown in Figure 3. Tests T1–T4 were experimental results of the sensor location shown in Figure 2b, and simulation T1 to T4 were the simulation results in the four regions.
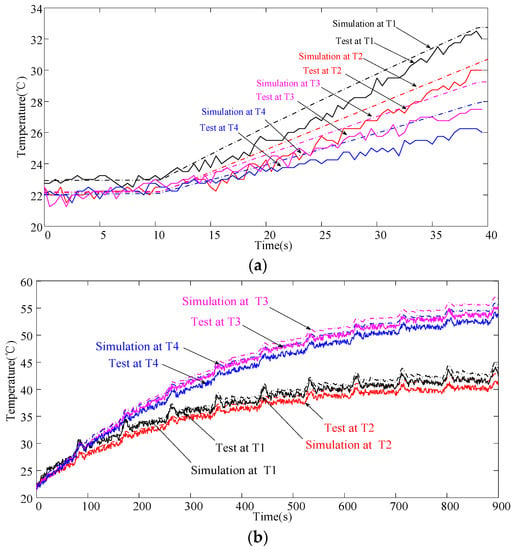
Figure 3.
(a) Comparison of simulation and experiment with a 10C (83 A) discharge for 30 s. (b) Comparison of simulation and experiment with the cycle condition.
As seen from Figure 3, the temperature change trend between simulation and experiment in the discharge process was similar, and the maximum error was not more than 2 °C and less than 8%, within an acceptable error range.
Errors exist, on one hand, owing to the thermal battery model that was simplified for the actual battery thermogenesis of a complex chemical reaction. On the other hand, the self-designed temperature test system also has some errors, including those in the thermocouple thermal response time, thermocouple contact, etc.
3. Heat Dissipation for Battery Pack
Based on the balance principle between the generation of the battery heat and the dissipation, the arrangement of the battery pack and the cooling structure of the battery box were designed. The heat generated in the internal battery was transferred to the surface of the battery shell by heat conduction and was transferred by convection in air, eventually achieving the heat dissipation effect by internal air flow.
Based on the parameters of the electric racing car, the battery pack was determined to be 2P110S (parallel, serial) by capacity estimation and parameter matching of the power system. Considering the actual battery box that was symmetrically placed on both sides in the car, one side of the battery box was designed for thermal management in this paper, and the battery cooling demand was calculated taking the FSEC dynamic conditions into account. The structure of battery pack is shown in Figure 4a.
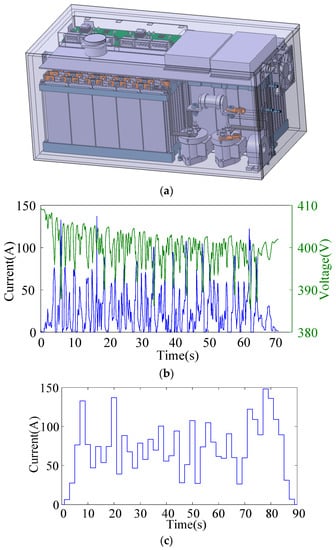
Figure 4.
(a) Battery pack. (b) Collected data. (c) Autospeed data in the Formula Student Electric China (FSEC).
In order to simulate the FSEC competition conditions, two major categories were defined: battery discharge with a limited constant current for 30 s and a cycle endurance condition. Considering the precision of the instruments for the battery charge and discharge test, an auto speed cycle condition is shown in Figure 4b, with the green curve indicating the change in total battery voltage, and the blue curve showing the change in current, which is simplified and enlarged in Figure 4c.
3.1. Heat Dissipation under FSEC Conditions
3.1.1. Limited High Constant Current Condition
Considering that the electric motor can withstand a maximum current of 160 A in the FSEC, the maximum discharge current of the cell was limited to 80 A when the battery pack was 2P. In this paper, the limited constant current condition was a 10C battery discharge for 30 s. According to the battery heat generation model and cell geometry, each battery generates heat as the electric core and the tab heat.
Assuming that the temperature of the battery box was stable at 35 °C and the initial temperature of the air and battery, TB, was 25 °C, ∆T was 10 °C, and the heat transfer coefficient was 30 W/(m2·K). The battery heat was transferred as per the Fourier heat transfer law from the inside to the surface of the aluminum-plastic film, and the cell surface heat was transferred to the surface air by Newton’s law of cooling. The air flow in the battery box was for a cooling effect.
The required air layer thickness for cooling was 5.436 mm; hence, the required amount of air and the air volume of the 110 cells in the battery box were 0.1071 × 10−3 m3 and 1.1781 × 10−2 m3, respectively. Therefore, the air flow was different for different discharge times, and different cooling conditions were required to obtain a cooling effect. The air flow rate of the heat dissipation requirement under the condition of a constant current discharge of the limited current is shown in Figure 5; it can be seen that the maximum air flow demand is 11.781 × 10−3 m3/s.
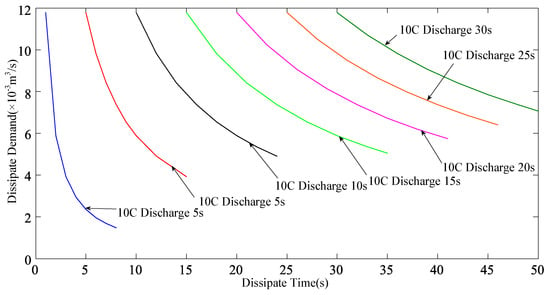
Figure 5.
Air flow demand under limited, high constant current discharging conditions.
3.1.2. Cycle Condition
Considering the similarities in the battery system working current between the autospeed condition and the endurance in the FSEC, and referring to the autospeed condition data in Figure 6, an 8C-constant current discharge calculation was considered according to the simplified 90-s cycle, and the detailed calculation process was consistent with that in 3.1.1. It was seen that the maximum air flow demand was 11.68 × 10−3 m3/s.
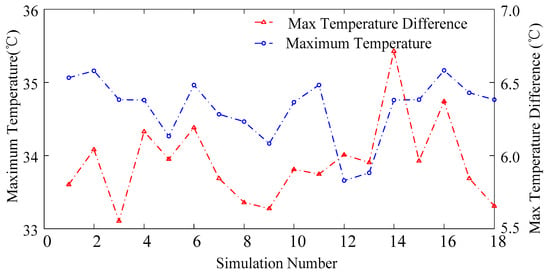
Figure 6.
Results of the L18 (37) orthogonal design.
3.2. Flow for Fan
According to 3.1, the maximum air cooling demand for the battery under the FSEC dynamic conditions can be determined, and the cooling fan air volume was obtained using the following equation:
where CFM is the air flow(m3/s); Qp is the heat power (W); ρ is the density of air (kg/m3); Cp is the specific heat of air (J/(kg·K)); ΔT is the change in temperature.
When the battery was working at the maximum current (10C), considering the BMS and the other electrical heating in the battery system, the air flow demand for the fan can be calculated as 0.526 m3/min using Equation (3). A DC fan can meet the cooling requirements, with a maximum volume of 0.533 m3/min and a static pressure of 29.969 Pa. Considering the effects of the pressure on the inlet and outlet, the fan was placed for a forced cooling.
4. Battery Cooling System Design
Based on the calculated air cooling demand of the FSEC and the electric racing car’s dynamic system, which has a certain number of cells that should be designed as a detached stack according to the FSEC rules, the maximum voltage should be less than 120 VDC, and the energy should be less than 1.67 kW·h. Combined with the layout of the racing car, three stacks were placed in one battery box, one pack with 2P15S cells in the preliminary design, and the other two with 2P20S. Considering the other necessary electrical units, the battery size was designed to be 0.4675 m × 0.2322 m × 0.21 m. This paper mainly considers the battery heat dissipation in the discharge condition combined with the FSEC dynamic working conditions.
4.1. Optimization Design
Under a precondition of the FSEC rules, the battery box heat dissipation effect was simulated to design a suitable battery box heat dissipation structure and determine the key factor’s optimum design and the combination, which will impact the battery box’s heat dissipation effect. The key factors include the battery arrangement modes and the fan position. Each factor was selected for three levels. L18 (37) was selected as the orthogonal array and the factor levels are shown in Table 2. The fan position’s y- and z- axes shown in Table 2 were set by the ANSYS/Icepak parametric model.

Table 2.
Factors and levels of the battery cooling simulation.
Considering the maximum temperature and the maximum temperature difference as the simulation standards, a parametric simulation model was established with ANSYS/Icepak to simulate the limited constant current discharge 30-s condition, and the simulation results of the orthogonal array are shown in Figure 6.
According to the calculation of the average and range for each factor, and the level index, the priority of the factors was A > B 2> B1 > C1 > C2 (1 was the inlet, 2 the outlet). The optimal combination was A2 (Lateral wind) B13 (0.16) C12 (0.11) B23 (0.16) C21 (0.06).
In order to select better optimal parameters, the orthogonal experiments were repeated to optimize the cooling structure of the battery box. Owing to space limitations, they are not presented in detail in this paper. Eventually, the most optimal parameter combinations were a battery lateral wind, (0.13 0.11) as the inlet locations for the fan, and (0.15, 0.08) as the outlet locations for fan.
Finally, based on the above optimized results, the optimization results of the simulation of the battery box with the ANSYS/Icepak parametric model were established. The optimized results are shown in Table 3.

Table 3.
Comparison of the results before and after optimization.
4.2. Verification Test
According to the optimized results by the orthogonal design, the battery heat dissipation structure was designed, and the heat dissipation performance in the FSEC dynamic conditions was analyzed with ANSYS/Icepak. The thermal analysis results of the limited constant current (10C) discharge for 30 s and the end temperature field analysis results with the condition in Figure 4c are shown in Figure 7.
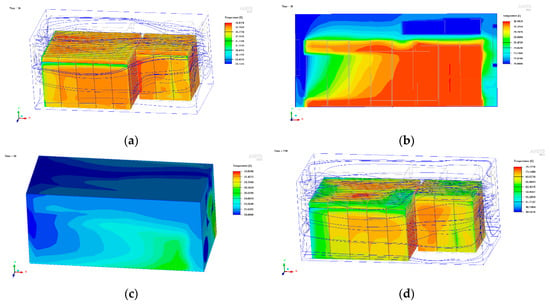
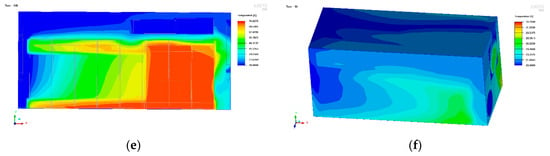
Figure 7.
(a) Temperature field and air flow of the battery at the end of the limited high current discharging. (b) Temperature field of the cut plane for the battery system at the end of the limited high current discharging. (c) Temperature field for the battery box at the end of the limited high current discharging. (d) Temperature field and air flow of the battery at the end of cycle discharging condition. (e) Temperature field of the cut plane for the battery system at the end of cycle discharging condition. (f) Temperature field for the battery box at the end of cycle discharging condition.
Figure 7a shows that the maximum temperature of the battery box was 31.533 °C, and the minimum temperature was 27.847 °C; the maximum temperature difference was 3.686 °C in this condition. Therefore, the difference in the temperature for a single cell was smaller than the total maximum temperature difference. From Figure 7b, it can be seen that the distribution of the temperature of the battery had a significant relationship with the air flow. The highest temperature of 31.072 °C for the battery box air occurred in the gap in the battery pack, and the other higher temperatures were close to the battery owing to air heat transfer with the battery. In Figure 7c, it can be seen that the temperature distribution of the battery box was also related to the opening position and the air flow, and the highest temperature was 28.304 °C in the vicinity of the outlet fan.
Figure 7e shows that the maximum temperature of the battery was 66.652 °C, the minimum temperature was 44.276, and the maximum temperature difference was 22.376 °C; the temperature difference between the cells was still lesser than the total maximum difference. From Figure 7f, it can be seen that the z section temperature distribution for the battery system and the maximum temperature of air at 33.466 °C also occurred in the gap in the battery pack. From Figure 7g, it can be seen that the highest temperature of the battery box was 31.543 °C in the vicinity of the exit fan.
In addition, a sandwich structure of glass fiber, carbon fiber, and moss foam was used in the battery box, which had good insulation and heat dissipation performance; the weight was reduced by more than 50% compared to aluminum, and the structural strength also met the basic requirements of the FSEC rules.
In general, Figure 7 show that the battery box cooling structure had good heat dissipation in the FSEC dynamic conditions. The experiment was tested to verify the credibility of the simulation. The temperature sensor arrangement on the battery pack in the test is shown in Figure 8a. The comparison between the experiment and simulation results is shown in Figure 8b,c.
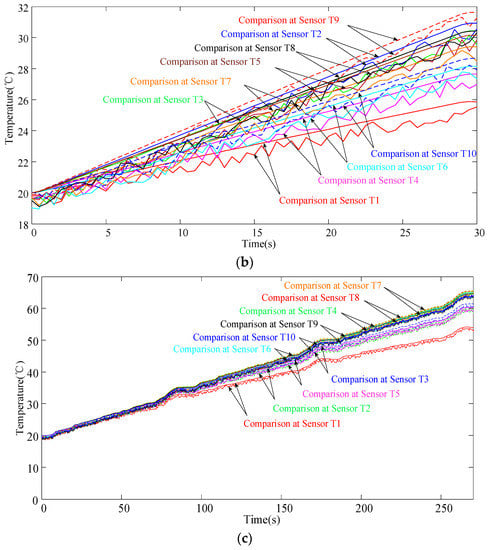
Figure 8.
(a) Schematic diagram of the temperature sensor measurement points in the battery system. (b) Limited high current discharging condition. (c) Cycle discharging condition.
According to the optimization results, the process design and assembly for the battery cooling system were completed, as shown in Figure 9. The battery cooling system was also successfully applied to the HRT-15E racing car as shown in Figure 10, and the phenomenon of local overheating and poor heat dissipation did not occur during the real racing car testing or debugging, further demonstrating that the battery cooling system designed in this paper achieved the desired cooling effect, ensuring the safety of the racing car to a certain extent.

Figure 9.
Power battery system product.

Figure 10.
HRT-15E electric racing car.
5. Conclusions
(1) Simplified Bernardi and battery tab thermal models were established in this paper, and the accuracy of the thermal model verified by the ANSYS/Workbench simulation analysis was consistent with the test results.
(2) The battery cooling system structure was optimized by an orthogonal design method and the simulation analysis was in good agreement with the experimental data. This shows that the method was feasible and effective for predicting the heat dissipation performance of a battery system in the FSEC.
(3) The battery cooling system designed in this paper was applied to an electric car, and overheating did not occur during real racing car testing, indicating that the cooling system design achieved the desired objectives.
Author Contributions
L.Z. designed the experiment; J.W. designed the system and wrote the paper; Y.L. analyzed the data; Q.L. done the FEM; W.L. reviewed and all authors revised manuscript.
Funding
This study was funded in part by the Foundation of Chinese State Key Laboratory of Robotics and Systems, grant number SKLRS201602B. This research received no external funding.
Conflicts of Interest
The authors declare that there was no conflict of interests regarding the publication of this paper.
References
- Kim, E.; Shin, K.G.; Lee, J. Real-Time Battery Thermal Management for Electric Vehicles. In Proceedings of the ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS), Berlin, Germany, 15–17 April 2014; IEEE Computer Society: Washington, DC, USA, 2014; pp. 72–83. [Google Scholar]
- Sabbah, R.; Kizilel, R.; Selman, J.R.; Al-Hallaj, S. Active (Air-Cooled) vs. Passive (Phase Change Material) Thermal Management of High Power Lithium-ion Packs: Limitation of Temperature Rise and Uniformity of Temperature Distribution. J. Power Source 2008, 182, 630–638. [Google Scholar] [CrossRef]
- Weinert, J.X.; Burke, A.F.; Wei, X. Lead-acid and Lithium-ion Batteries for the Chinese Electric Bike Market and Implications on Future Technology Advancement. J. Power Source 2007, 172, 938–945. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, S.; Liu, J.; Gu, J. A Review of Thermal Performance Improving Methods of Lithium-ion Battery: Electrode Modification and Thermal Management System. J. Power Source 2015, 299, 557–577. [Google Scholar] [CrossRef]
- Chen, L.T.; Xu, S.C.; Chang, G.F. A Study on the Flow Field Characteristics of HEV Battery Thermal Management System. Automot. Eng. 2009, 31, 224–227. [Google Scholar]
- Mahamud, R.; Park, C. Reciprocating air flow for Li-ion battery thermal management to improve temperature uniformity. J. Power Source 2011, 196, 5685–5696. [Google Scholar] [CrossRef]
- Fan, J.W.; Meng, Z.P. Design Method for the Forced-air Cooling Structure of Battery Box and Its Application on Electric Power-driven Racing Car. Auto Engineer 2014, 45–47. [Google Scholar]
- Jin, L.W.; Lee, P.S.; Kong, X.X.; Fana, Y.; Choua, S.K. Ultra-Thin Minichannel LCP for EV Battery Thermal Management. Appl. Energy 2014, 113, 1786–1794. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. An Experimental Study of Heat Pipe Thermal Management System with Wet Cooling Method for Lithium-ion Batteries. J. Power Source 2015, 273, 1089–1097. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Amiruddin, S.; Farid, M.; Selman, J.R.; Al-Hallaj, S. Thermal Management of Li-ion Battery with Phase Change Material for Electric Scooters: Experimental Validation. J. Power Source 2005, 142, 345–353. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Influence of operating conditions on the optimum design of electric vehicle battery cooling plates. J. Power Source 2014, 245, 644–655. [Google Scholar] [CrossRef]
- Wu, M.; Hung, Y.; Wang, Y.; Wan, C. Heat Dissipation Behavior of the Nickel/Metal Hydride Battery. J. Electrochem. Soc. 2000, 147, 930–935. [Google Scholar] [CrossRef]
- Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K. Thermal Behavior of small lithium-ion battery during rapid charge and discharge cycles. IEEJ Trans. Power Energy 2004, 124, 535–542. [Google Scholar] [CrossRef]
- Chen, S.C.; Wan, C.C.; Wang, Y.Y. Thermal Analysis of Lithium-ion Batteries. J. Electrochem. Soc. 1996, 143, 111–124. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wu, W.J.; Liu, H.W.; Shen, S.; Li, C.-Y.; Geng, H.-L. Thermal characteristics of battery for pure electric vehicles. J. Jilin Univ. (Eng. Technol. Ed.) 2014, 44, 925–932. [Google Scholar]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Guo, H.G.; Jiang, J.C.; Wang, J.S.; Lou, T.; Li, X. Characteristic on Internal Resistance of Lithium-ion Power Battery. J. Beijing Jiaotong Univ. Nat. Sci. Ed. 2011, 35, 119–123. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).