Characteristics of Cyclical Fluctuations in the Development of the Chinese Construction Industry
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
3.1. H-P Filtering Theory Model
3.2. Verification Model
3.2.1. Random Test
3.2.2. Test of Self-Correlation Coefficient
- (1)
- The self-correlation coefficient of the economic growth series and its series of 1–12 lag periods rk (k = 1, 2, …, 12).
- (2)
- The standard deviation of each self-correlation coefficient is obtained.
- (3)
- The comparison of the absolute value of rk with the value of 1.96 rk (with the significance level of 0.05) helps to determine whether the series can pass the statistical tests of significance. If the absolute value of rk is greater than 1.96 rk, it can pass the statistical significance test. If the absolute value of rk is less than or equal to 1.96 rk, it would fail the statistical significance test.
3.3. Samples and Data Sources
3.4. Measurements Steps
- (1)
- Eliminate the impacts of price changes on output values. The first measurement step is to treat the time series of the gross output values of the construction industry with the price index of retail commodity in order to eliminate the impacts of price changes on output values. The results from this step will obtain the constant-price, gross output values (CP-GOV) sequence of the construction industry. The price in 1978 will be the base price.
- (2)
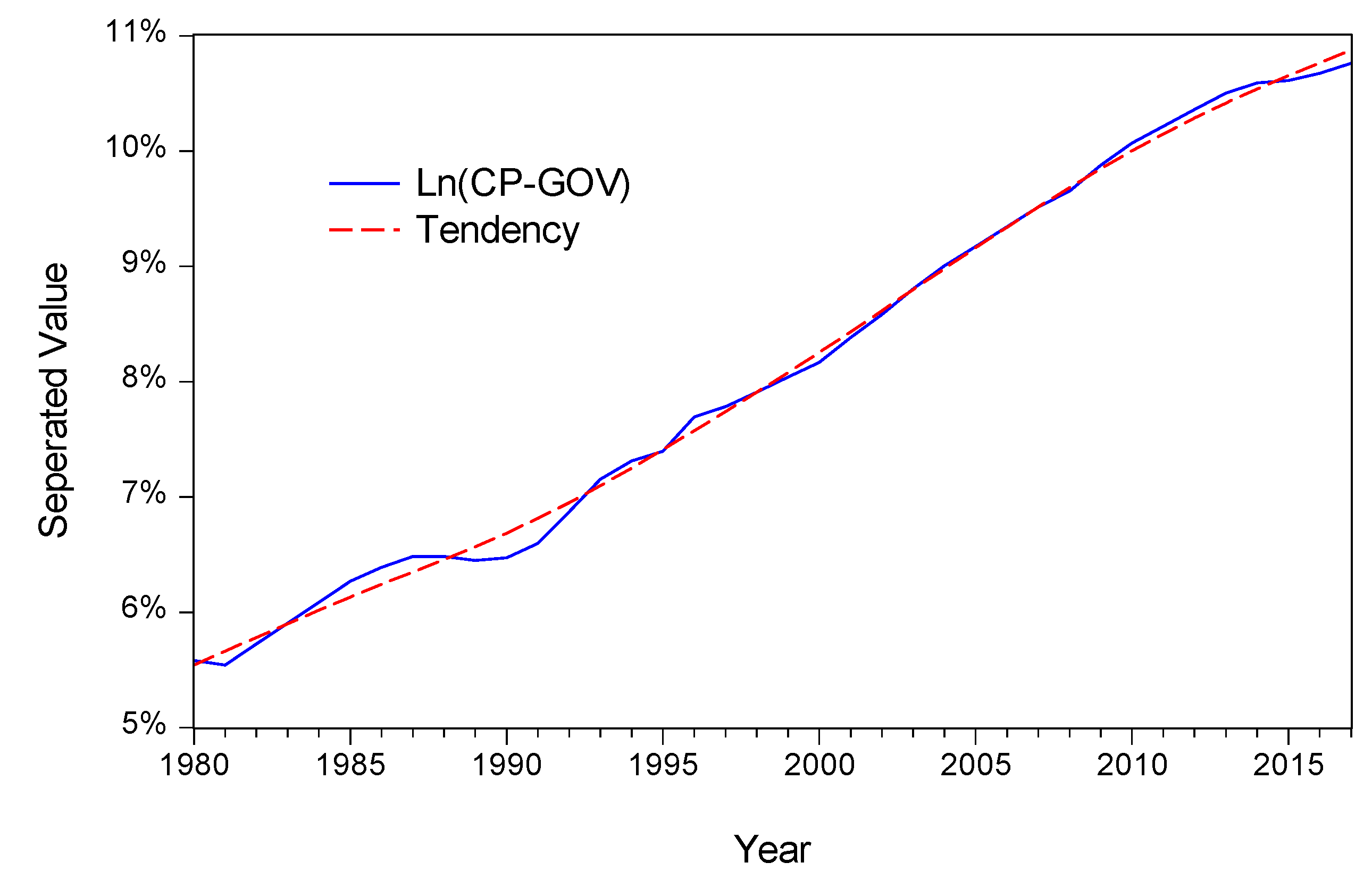
- Take natural logarithm process on the CP-GOV sequence of the construction industry in order to eliminate the influence of the different variance in 1980–2017.
- (3)
- Seasonal adjustment. Since the data used in this research is annual data, the time series of the construction industry does not need to be seasonally adjusted.
- (4)
- H-P Filtering Method. Using EVIEWS7.2 measurement analysis software, the authors analyzed the logarithmic sequence of the CP-GOV of the construction industry by using H-P Filtering Method. The value of λ is 100, as recommended by Hodrick & Prescott (1980) [35].
- (5)
- Determination of the cycles of economic fluctuations in the construction industry. Burns and Mitchell (1946) used the National Bureau of Economic Research (NBER)’s division method, which stated that a complete economic fluctuation could be determined from one wave to the next wave, from a trough to the next trough, or from an average value of some years to the value in the next time period in the same state (i.e., peak-to-peak, trough-to-trough or the entire cycles). In addition, an economic cycle should include four stages of recovery, prosperity, recession, depression in strict sense. According Burns and Mitchell (1946) [39], an economic cycle was observed when the economy runs from a peak to the next peak or from a trough to the adjacent trough, and the fluctuation time should last for more than 15 months. Meanwhile, the contraction or expansion of an economic cycle should continue for more than 5 months. Otherwise, it can only be considered as a temporary or irrelevant derailment of general economic activities. The same method was used by the United States Department of Commerce.
4. Results and Analyses
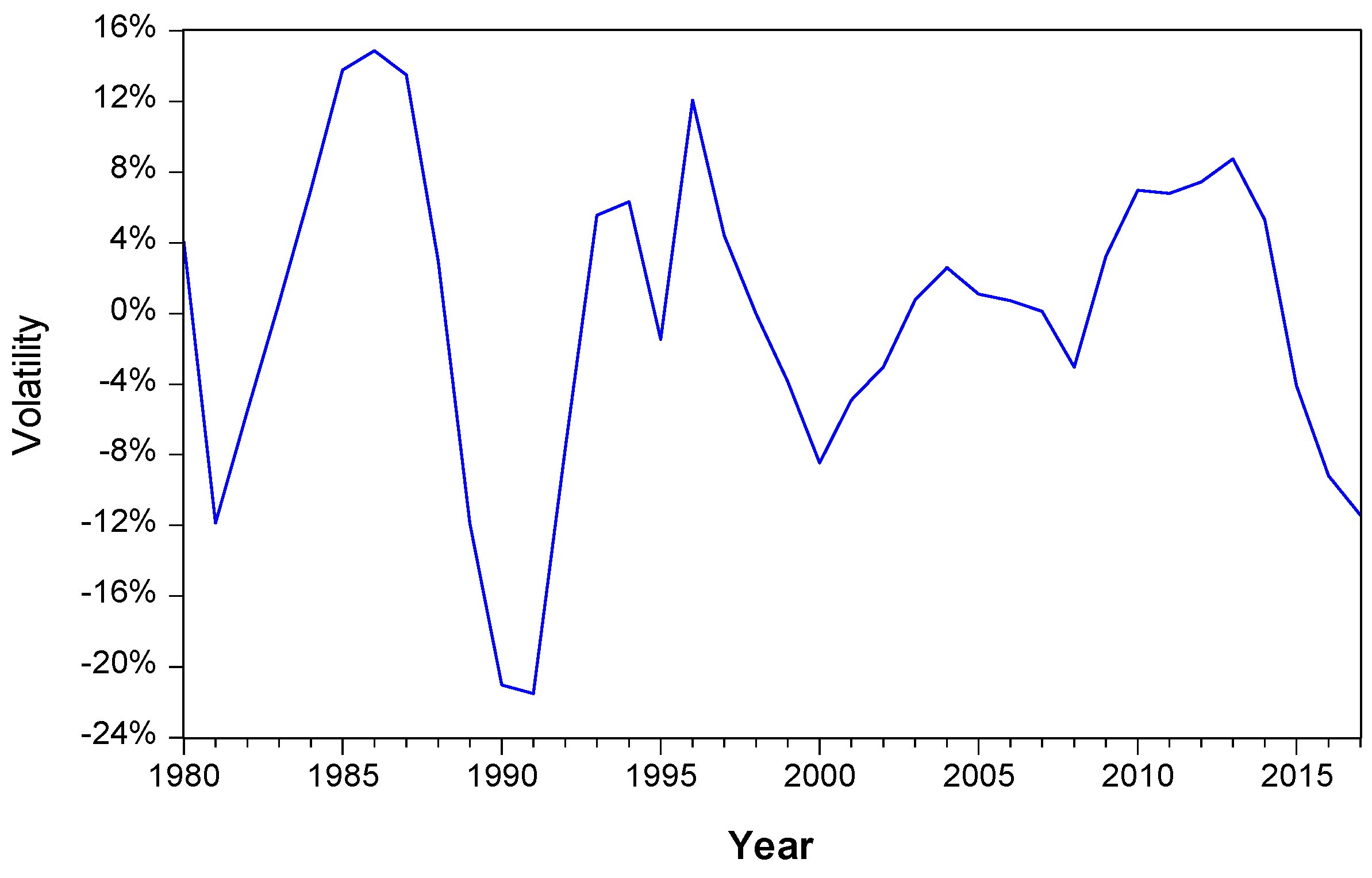
4.1. Results of Cycle Division
4.2. Test Result
4.2.1. Random Test Result
4.2.2. Test Result of Self-Correlation Coefficient
4.3. General Characteristics of Cyclical Fluctuations
- (1)
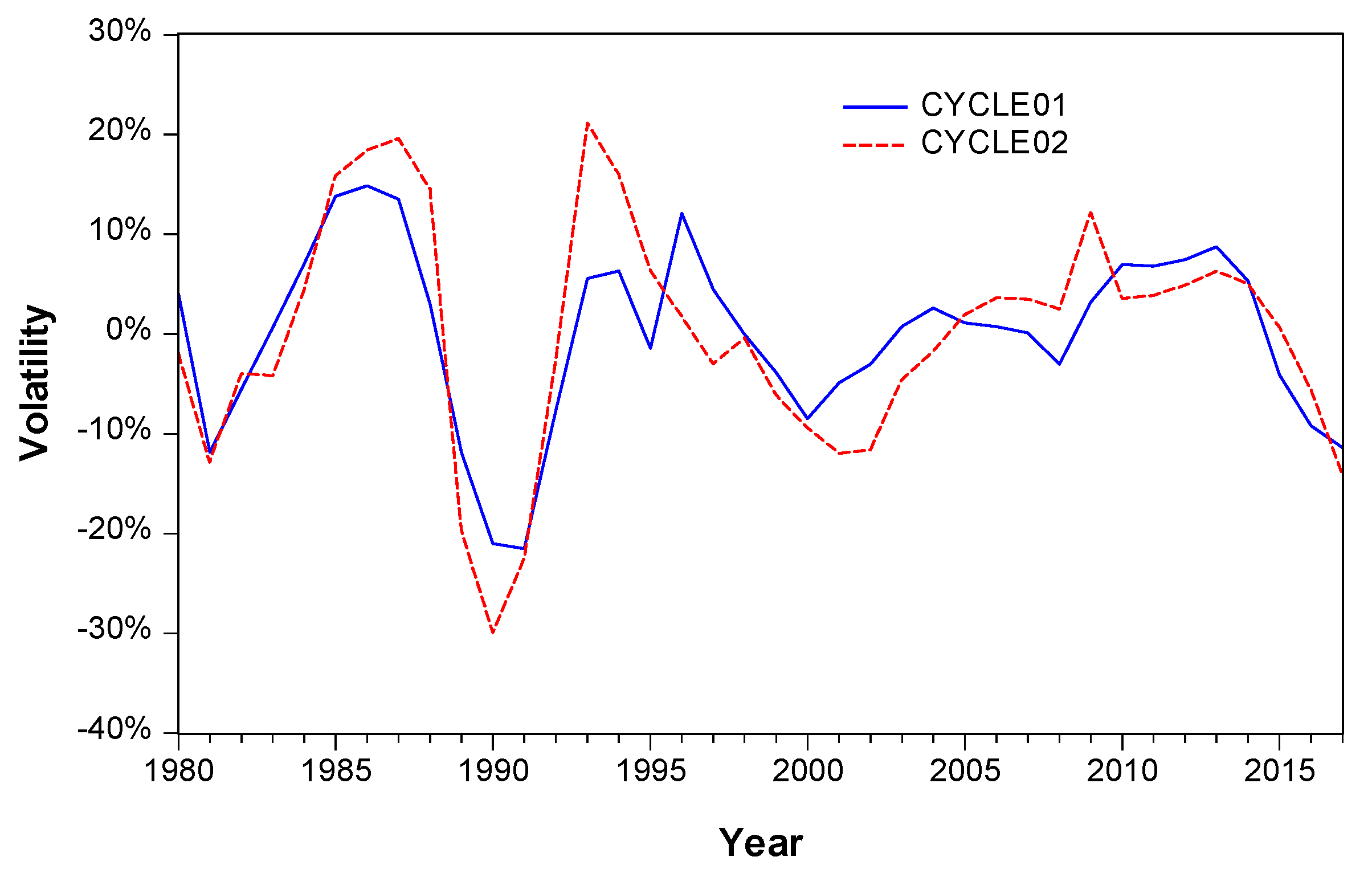
- The construction industry has experienced a total of five economic fluctuations in 1980–2017. The corresponding cycles in turn are 1981–1991, 1991–1995, 1995–2000, 2000–2008, and 2008–now. The longest fluctuation period is 10 years and the shortest is 4 years in the five rounds of economic fluctuations. The average cycle length is 6.75 years, which is slightly longer than the national macroeconomic cycle length (about 5 years). The cycle of 2008–2017 is the fifth incomplete cycle. No two cycles are exactly the same. The periodic fluctuations change irregularly.
- (2)
- The waveforms and amplitudes of the cycles show that the amplitudes of the first two cycles are relatively large. The maximum amplitude was 36.42%. The height of the wave reached 14.84%. The depth of the wave reached −21.58%. The first two rounds of the cyclical fluctuations presented the feature of steep rise and steep drop. The fluctuation amplitudes of the later three cycles are obviously reduced. These phenomena show that the construction industry has experienced rapid growth and its stability began to gradually increase.
- (3)
- According to the time sequence, the standard deviations of the fluctuation logarithmic sequence of CP-GOV of the construction industry in turn are 13.56, 6.57, 7.68, and 2.87. The standard deviation of the third round of fluctuation is slightly larger than the standard deviation of the second round. The overall trend of the standard deviations of the fluctuations is decreasing. It shows that the fluctuation range of the actual economic growth of the construction industry is gradually decreasing in deviations from the long-term trend. Currently, the economic growth of the construction industry is relatively stable.
- (4)
- The average potential of the economic growth of the construction industry has gradually increased in 1980–2017, which shows that the overall level of economic growth in each cycle continues to improve. This also reflects that the economic growth of the construction industry rises gradually and is relatively stable. Cyclical fluctuations in the construction industry are typical in its growth path during this period.
- (5)
- Judging from the expansion durations of the economic cyclical fluctuations of the construction industry, the first, second, and fourth cycles of fluctuations are long-expansion cycles (L > 1). The third and fifth cycles belong to short-expansion type (L < 1). These also show that the driving force of each expansion phase is not the same.
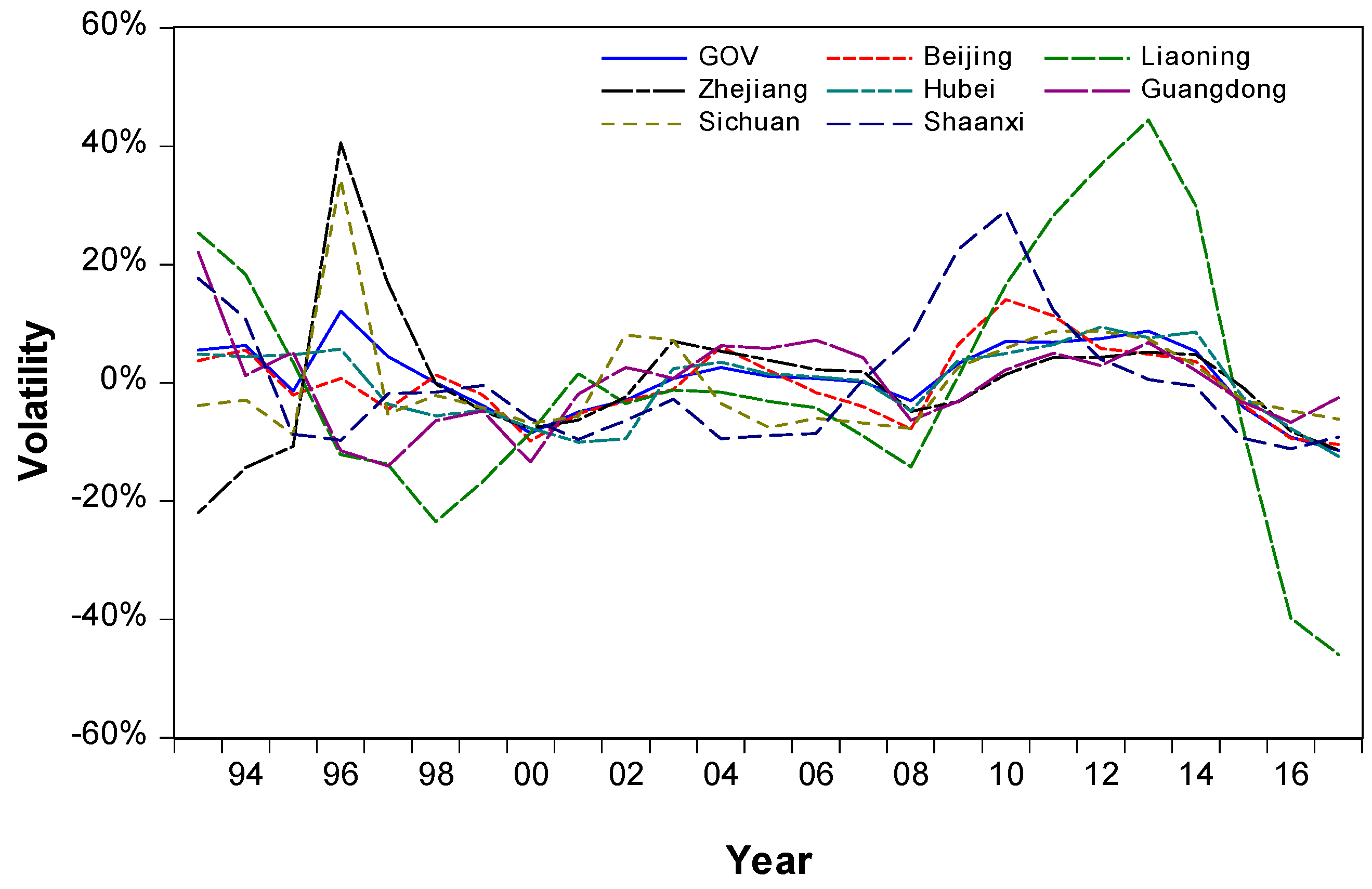
4.4. Comparison with Regional Provinces
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barras, R.; Ferguson, D. Dynamic modelling of the building cycle: 1. theoretical framework. Environ. Plan. A 1987, 19, 353–367. [Google Scholar] [CrossRef]
- Leitner, H. Capital markets, the development industry, and urban office market dynamics: Rethinking building cycles. Environ. Plan. A 1994, 26, 779–802. [Google Scholar] [CrossRef]
- Czerny, M. Recovery of European construction industry. Wifo Mon. 2006, 79, 113–120. [Google Scholar]
- Li, Y.; Ding, R.; Sun, T. The Drivers and Performance of Environmental Practices in the Chinese Construction Industry. Sustainability 2019, 11, 614. [Google Scholar] [CrossRef]
- Jones, T.; Shan, Y.; Goodrum, P.M. An investigation of corporate approaches to sustainability in the US engineering and construction industry. Constr. Manag. Econ. 2010, 28, 971–983. [Google Scholar] [CrossRef]
- Loosemore, M.; Lim, B.T.H. Linking corporate social responsibility and organizational performance in the construction industry. Constr. Manag. Econ. 2016, 35, 90–105. [Google Scholar] [CrossRef]
- Pham, H.; Kim, S.Y.; Luu, T.V. Managerial perceptions on barriers to sustainable construction in developing countries: Vietnam case. Environ. Dev. Sustain. 2019, 2, 1–25. [Google Scholar] [CrossRef]
- Tokbolat, S.; Karaca, F.; Durdyev, S.; Calay, R.K. Construction professionals’ perspectives on drivers and barriers of sustainable construction. Environ. Dev. Sustain. 2019, 6, 1–18. [Google Scholar] [CrossRef]
- Bon-Gang, H.; Ming, S.; Jun-Ming, L. Adoption of sustainable construction for small contractors: Major barriers and best solutions. Clean Technol. Environ. Policy 2018, 20, 2223–2237. [Google Scholar] [CrossRef]
- Ernst, E.; Saliba, F. Are House Prices Responsible for Unemployment Persistence? Open Econ. Rev. 2018, 29, 795–833. [Google Scholar] [CrossRef]
- Bilal, K. Interaction between the economic growth and the construction industry: A time series analysis on Turkey (2000–2012). Emerg. Mark. J. 2013, 3, 20–34. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, X. Thinking about the relationship between the cyclical fluctuation of construction industry and the economic cycle fluctuation. Econ. Probl. 2005, 24–26. [Google Scholar] [CrossRef]
- Chia, F.C.; Skitmore, M.; Runeson, G.; Bridge, A. Economic development and construction productivity in Malaysia. Constr. Manag. Econ. 2014, 32, 874–887. [Google Scholar] [CrossRef]
- Barras, R. A Simple theoretical model of the office-development cycle. Environ. Plan. A 1983, 15, 1381–1394. [Google Scholar] [CrossRef]
- Rosen, K.T. Toward a Model of the office building sector. Real Estate Econ. 1984, 12, 261–269. [Google Scholar] [CrossRef]
- Wheaton, W.C. The cyclic behavior of the national office market. Real Estate Econ. 1987, 15, 281–299. [Google Scholar] [CrossRef]
- Xue, J. Discussion on the building period. Nankai J. Philos. Soc. Sci. Ed. 1987, 5, 47–53. [Google Scholar]
- Cheng, L. The Macro thinking of the economic cycle fluctuation of China’s construction industry. Mod. Constr. Manag. 1995, 4, 33–34. [Google Scholar]
- Alagidede, P. On the temporary and permanent components of global construction. Appl. Econ. Lett. 2016, 23, 284–289. [Google Scholar] [CrossRef]
- Kuznets, S. Secular Movement of Production and Price; Houghton Mifflin Company: Boston, MA, USA; New York, NY, USA, 1930; pp. 99–133. [Google Scholar]
- Gottlieb, M. Long Swings in Urban Development; National Bureau of Economic Research: New York, NY, USA, 1976; pp. 137–187. [Google Scholar]
- Harvey, D. The urban process under capitalism: A framework for analysis. Int. J. Urban Reg. Res. 1978, 2, 101–131. [Google Scholar] [CrossRef]
- Barras, R.; Ferguson, D. A spectral analysis of building cycles in Britain. Environ. Plan. A 1985, 17, 1369–1391. [Google Scholar] [CrossRef]
- Wheaton, W.C.; Torto, R.G.; Evans, P. The cyclic behavior of the greater London office market. J. Real Estate Financ. Econ. 1997, 15, 77–92. [Google Scholar] [CrossRef]
- Gornig, M.; Michelsen, C. German construction industry: New residential construction at cyclical peak-public construction gaining ground. DIW Econ. Bull. 2015, 3, 23–31. [Google Scholar]
- Shi, B.; Wan, S. Analysis on the economic cycle of China’s construction industry. Situat. Stat. Henan Prov. 1997, 6, 33–35. [Google Scholar]
- Zhu, X. Review and prospect of the development of China’s construction industry. J. Cent. South Univ. 2004, 6, 326–330. [Google Scholar]
- Yang, Y.Z. An empirical analysis of regional economic fluctuations in Chinese construction industry. World Manag. 2009, 12, 178–179. [Google Scholar]
- Yang, Y.Z. An empirical analysis of industrial structure economic fluctuations in the construction industry. J. Shanxi Univ. Financ. Econ. 2011, S3, 112–113. [Google Scholar]
- Grebler, L.; Burns, L.S. Construction cycles in the United States since World War II. Real Estate Econ. 1982, 10, 123–151. [Google Scholar] [CrossRef]
- Lopes, J. The construction industry and macroeconomy in Sub-Saharan Africa Post 1970. Constr. Manag. Econ. 1998, 16, 637–649. [Google Scholar] [CrossRef]
- Barras, R.; Ferguson, D. Dynamic modelling of the building cycle: 2. empirical results. Environ. Plan. A 1987, 19, 493–520. [Google Scholar] [CrossRef]
- Kuznets, S. Long swings in the growth of population and in related economic variables. Proc. Am. Philos. Soc. 1958, 102, 25–52. [Google Scholar]
- Nistorescu, T.; Ploscaru, C. Impact of economic and financial crisis in the construction industry. Manag. Mark. 2010, 8, 25–36. [Google Scholar]
- Hodrick, R.; Prescott, E.C. Post-war U.S. business cycles: An empirical investigation. J. Money Credit Bank. 1997, 29, 1–16. [Google Scholar] [CrossRef]
- Baxter, M.; King, R.G. Measuring business cycles: Approximate band-pass filters for economic time series. Rev. Econ. Stat. 1999, 81, 575–593. [Google Scholar] [CrossRef]
- Christiano, L.J.; Fitzgerald, T.J. The band pass filter. Int. Econ. Rev. 2003, 44, 435–465. [Google Scholar] [CrossRef]
- National Bureau of Statistics of the People’s Republic of China (NBSPRC). 2018 China Statistical Yearbook; National Data: Beijing, China, 2019.
- Burns, A.F.; Mitchell, W.C. Measuring Business Cycles, NBER Studies in Business Cycles; National Bureau of Economic Research: New York, NY, USA, 1946; Volume 2. [Google Scholar]
| Author | Method and Implementation Area/Country | Time Scope | Cycle Length (years) | Explanation |
|---|---|---|---|---|
| Kuznets (1930) [20] | Moving average method was used in the United States; Portland; United Kingdom; Germany; France; Belgium; and Other countries | 1782–1922 | 15–25 | To study the markets of wheat, corn, potatoes, cotton, anthracite coal, bituminous coal, petroleum, pig iron, steel |
| Barras and Ferguson (1985) [23] | Spectral analysis; Turning point analysis; and Dynamic modeling were used to study British | 1945–1980 | 4–5 (demand cycle) 9 (supply cycle) | Industrial, commercial and residential; Different sectors of construction exhibit cycles with different lengths. |
| Gottlieb (1976) [21] | Europe and North America (eight countries) | Varies | 15–25 | |
| Harvey (1978) [22] | Theoretical model was used to study Britain, United States, and France | 1800s–1930s | 15–25 | Investment cycles to the cycle of building |
| Wheaton (1987) [16] | Structural econometric model was used to study the United States | Mid-1960 to mid-1980 | 10–12 | Office building construction (Supply is more responsive to market conditions than demand) |
| Leitner (1994) [2] | Three-year moving averages and Autocorrelation coefficient were used to study Dallas, Houston, Los Angeles Minneapolis; St Paul; San Francisco | 1963–1985 | 4–5 | Urban office cycle |
| Wheaton et al. (1997) [24] | Structural economic model was used in London office market | 1970–1995 | 20 | 2 large swings in office rental rates in the last 20 years; only 1 building boom |
| Cheng (1995) [18] | Net output value growth rate of the construction industry in China | 1953–1992 | Long (8) Short (2) Average 4 | 9 cycles |
| Shi (1997) [26] | Annual growth rate of gross output value of the construction industry China | 1953–1992 | 5.57 | 7 cycles |
| Zhu (2004) [27] | Qualitative analysis of China | 1949–2003 | 10.5 | 4 stages |
| Yang (2009; 2011) [28,29] | Growth rate of gross output value of the construction industry in China | 1991–2007 | 6.4 |
| Number | Section | Cycle Duration (Years) | Extension (year) | Contraction Duration (year) | Type |
|---|---|---|---|---|---|
| 1 | 1981–1991 | 10 | 5 | 5 | Long |
| 2 | 1991–1995 | 4 | 3 | 1 | Long |
| 3 | 1995–2000 | 5 | 1 | 4 | Short |
| 4 | 2000–2008 | 8 | 4 | 4 | Long |
| 5 | 2008-now | 5 | ─ | Short | |
| Average value | 6.75 | ─ | ─ | ─ |
| Lag Phase k | Self-Correlation Coefficient rk | Standard Deviation sk | 1.96 sk | Absolute Value |rk| | If |rk| > 1.96 sk |
|---|---|---|---|---|---|
| 1 | 0.921 | 0.069 | 0.135 | 0.921 | Greater |
| 2 | 0.835 | 0.099 | 0.194 | 0.835 | Greater |
| 3 | 0.749 | 0.121 | 0.237 | 0.749 | Greater |
| 4 | 0.665 | 0.139 | 0.272 | 0.665 | Greater |
| 5 | 0.583 | 0.154 | 0.301 | 0.583 | Greater |
| 6 | 0.505 | 0.166 | 0.326 | 0.505 | Greater |
| 7 | 0.430 | 0.177 | 0.347 | 0.430 | Greater |
| 8 | 0.355 | 0.187 | 0.366 | 0.355 | Less than |
| 9 | 0.278 | 0.196 | 0.384 | 0.278 | Less than |
| 10 | 0.198 | 0.204 | 0.401 | 0.198 | Less than |
| 11 | 0.117 | 0.212 | 0.415 | 0.117 | Less than |
| 12 | 0.038 | 0.218 | 0.427 | 0.038 | Less than |
| ID | Section | Cycle Length (Years) | Wave Height (%) | Wave Depth (%) | Fluctuation Range (%) | Standard Deviation σ | Average Potential | Extension Length | L |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1981–1991 | 10 | 14.84 | −21.58 | 36.42 | 13.56 | 6.24 | 5 | |
| 2 | 1991–1995 | 4 | 6.29 | −1.44 | 7.73 | 6.57 | 7.18 | 3 | >1 |
| 3 | 1995–2000 | 5 | 12.15 | −7.88 | 20.03 | 7.68 | 7.91 | 1 | <1 |
| 4 | 2000–2008 | 8 | 3.94 | −2.42 | 6.36 | 2.87 | 9.05 | 4 | =1 |
| 5 | 2008-now | - | 5 | <1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Xie, H.; Niu, X. Characteristics of Cyclical Fluctuations in the Development of the Chinese Construction Industry. Sustainability 2019, 11, 4523. https://doi.org/10.3390/su11174523
Sun Y, Xie H, Niu X. Characteristics of Cyclical Fluctuations in the Development of the Chinese Construction Industry. Sustainability. 2019; 11(17):4523. https://doi.org/10.3390/su11174523
Chicago/Turabian StyleSun, Yanfang, Haiyan Xie, and Xirong Niu. 2019. "Characteristics of Cyclical Fluctuations in the Development of the Chinese Construction Industry" Sustainability 11, no. 17: 4523. https://doi.org/10.3390/su11174523
APA StyleSun, Y., Xie, H., & Niu, X. (2019). Characteristics of Cyclical Fluctuations in the Development of the Chinese Construction Industry. Sustainability, 11(17), 4523. https://doi.org/10.3390/su11174523





