A Hybrid Model Based on Principal Component Analysis, Wavelet Transform, and Extreme Learning Machine Optimized by Bat Algorithm for Daily Solar Radiation Forecasting
Abstract
1. Introduction
- The factors affecting solar radiation contain meteorological indicators and historical data on solar radiation in this paper;
- ELM is a new type of neural network that has been applied in solar radiation prediction, which avoids the shortcomings of slow learning, large training samples, and over-fitting in previous studies;
- The BA-optimized ELM application further improves the robustness and prediction accuracy of the model;
- Implementation of WT greatly reduces the difficulty of solar radiation prediction;
- This paper focuses on the correlation between influencing factors and uses PCA to reduce the dimensionality to improve computational efficiency and prediction accuracy;
- This may be the first paper to study solar radiation prediction methods that can be applied to different parts of the world at the same time.
2. Methodology
2.1. Wavelet Transform
2.2. Bat Algorithm
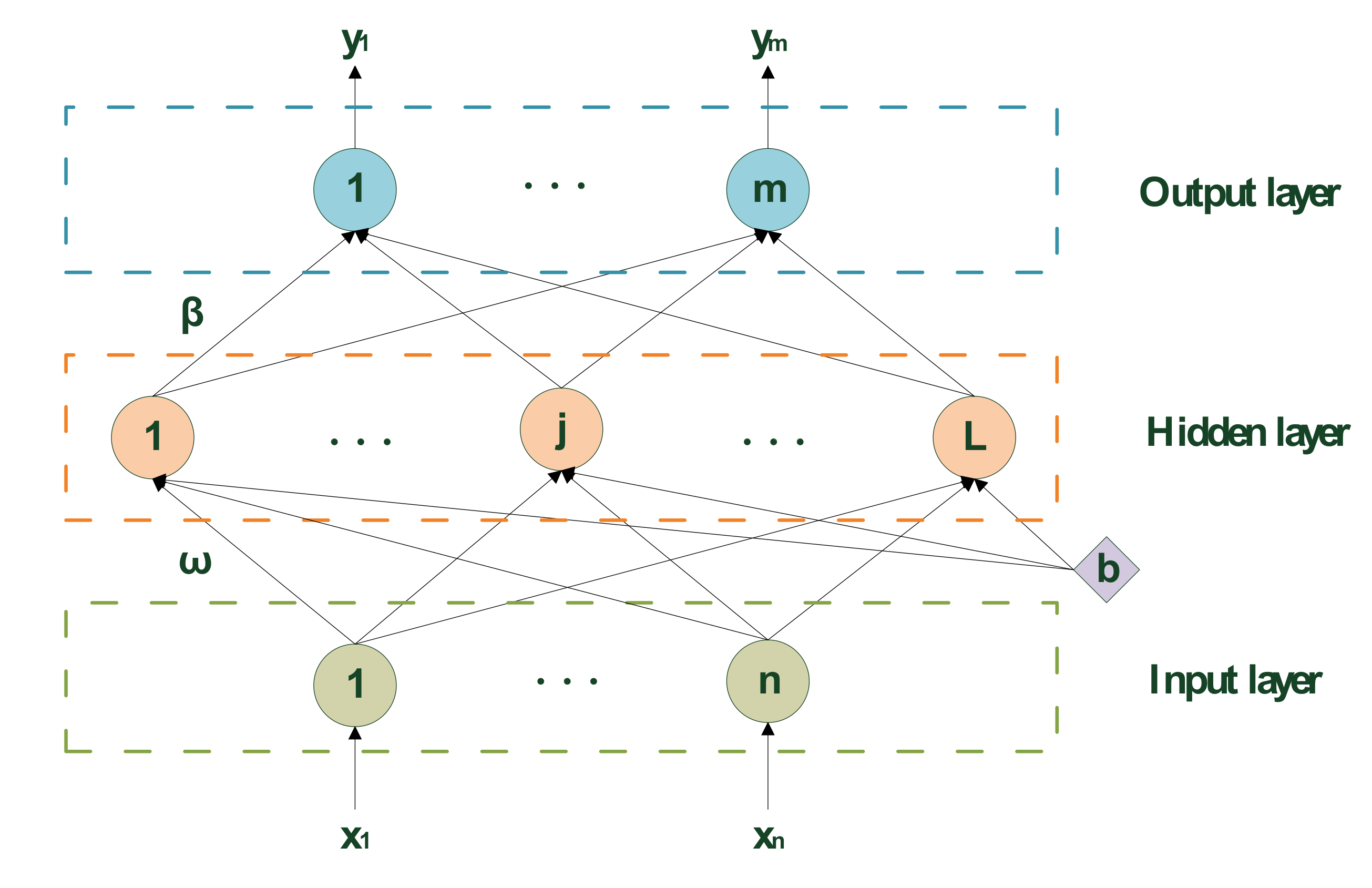
2.3. Extreme Learning Machine
2.4. The Proposed Model
3. Empirical Analysis
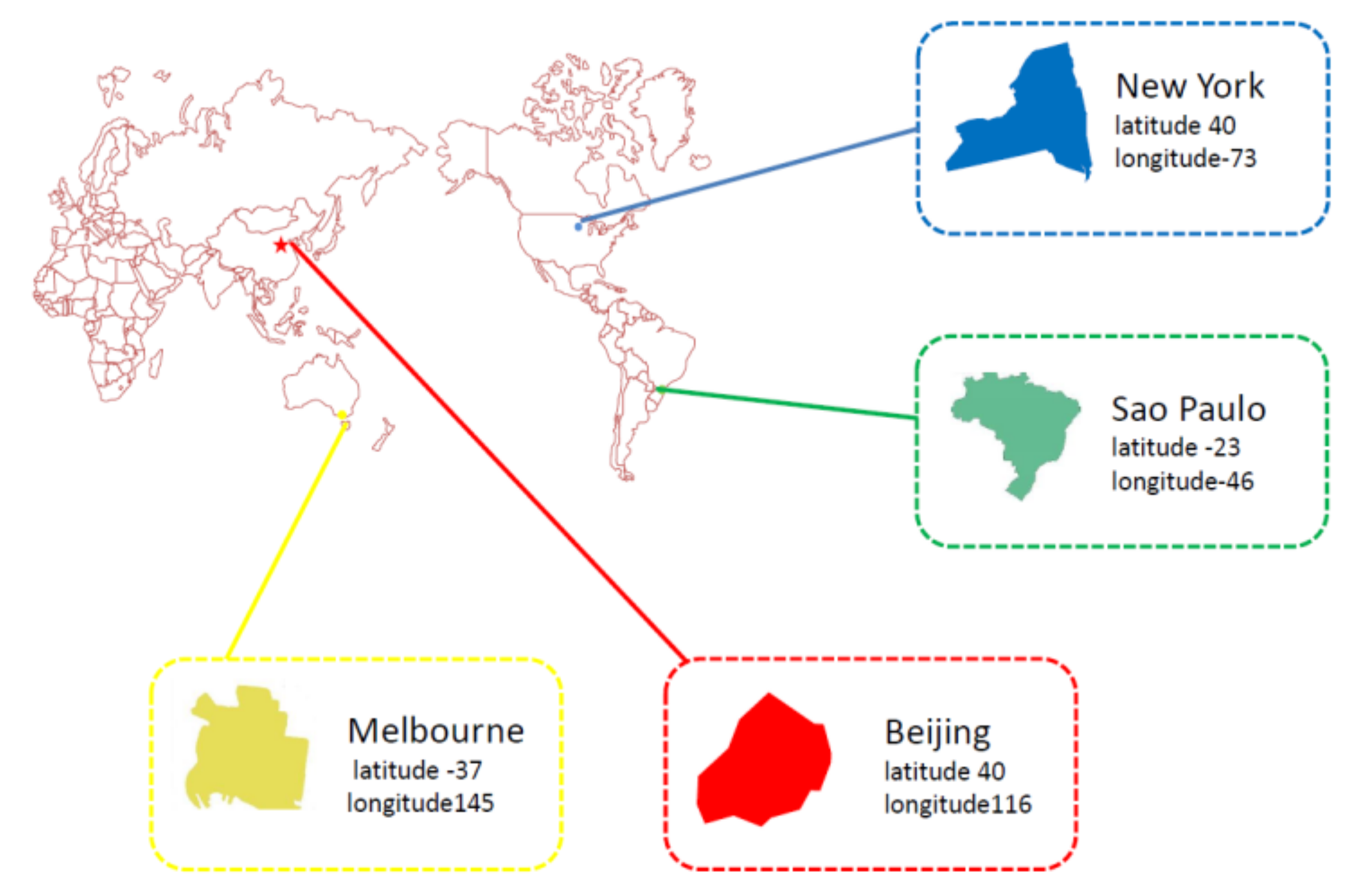
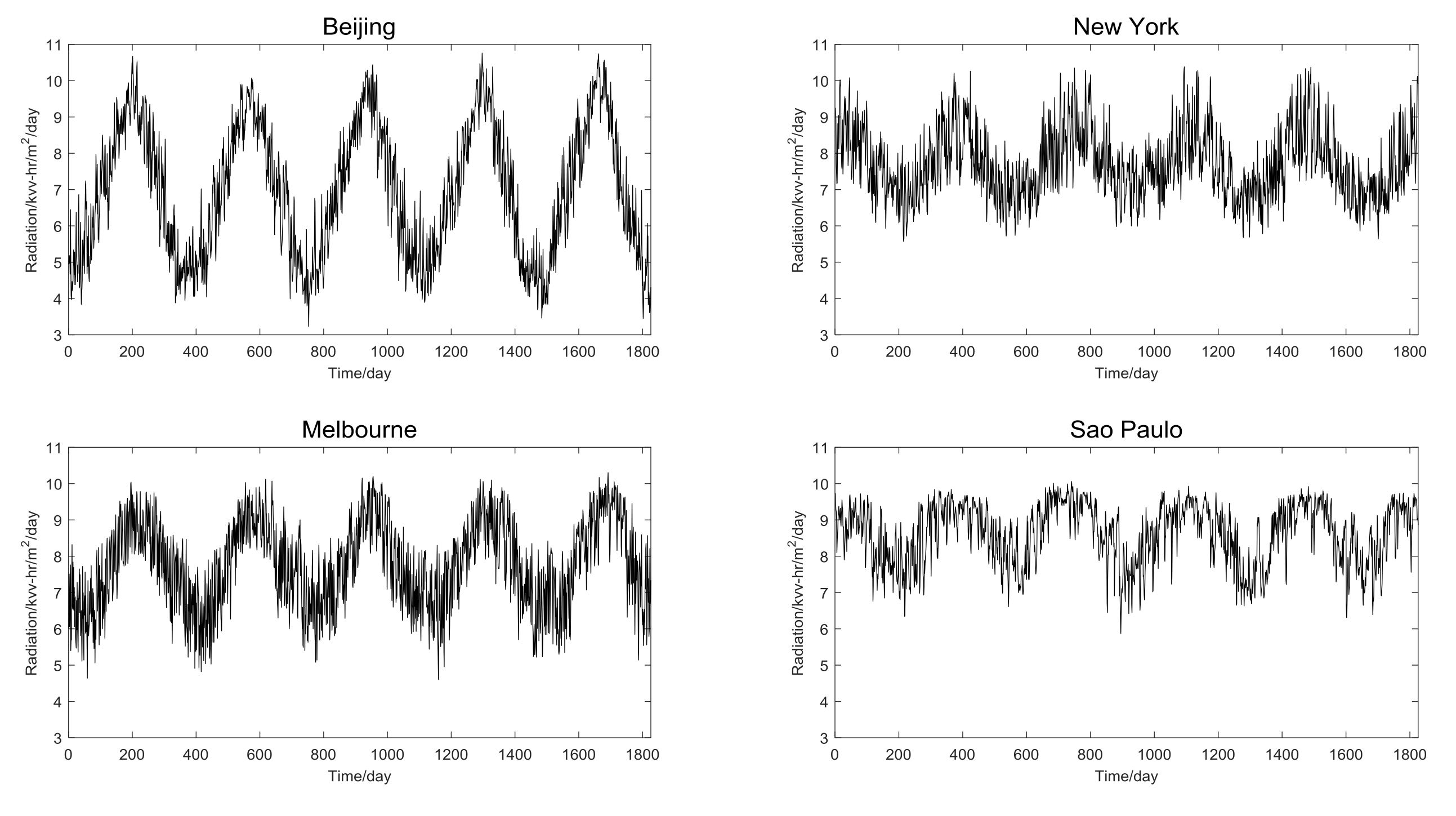
3.1. Data
3.2. Input Selection
3.2.1. Selection of Meteorological Indexes by Pearson Coefficient Test
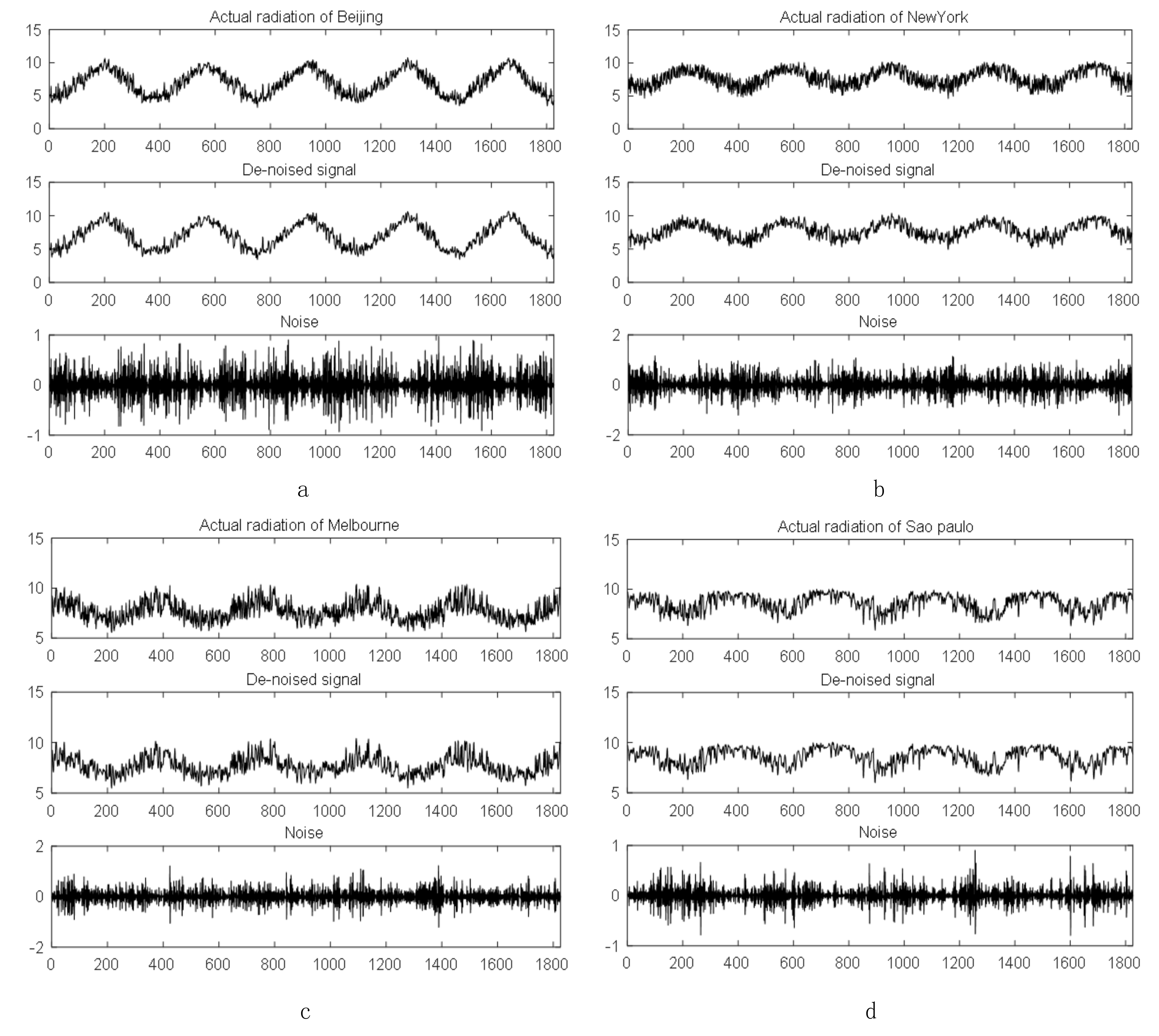
3.2.2. Decomposition of Solar Radiation Series by WT
3.2.3. Determination of the Lags by PACF
3.2.4. Reduction of Dimensionality by PCA
3.3. Parameters Setting and Forecasting Evaluation Criteria
3.4. Solar Radiation Forecasting
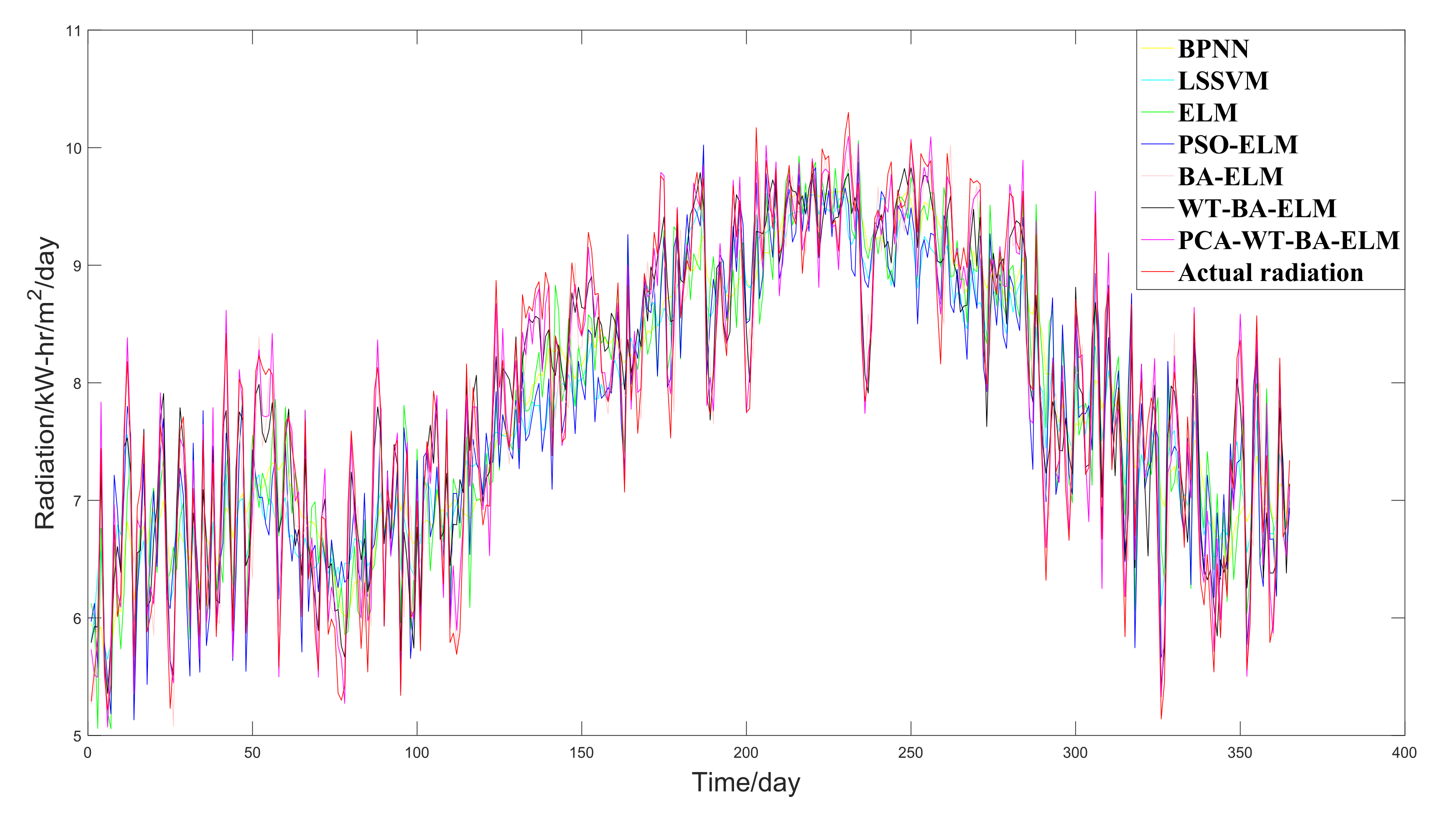
3.4.1. The Case of Beijing
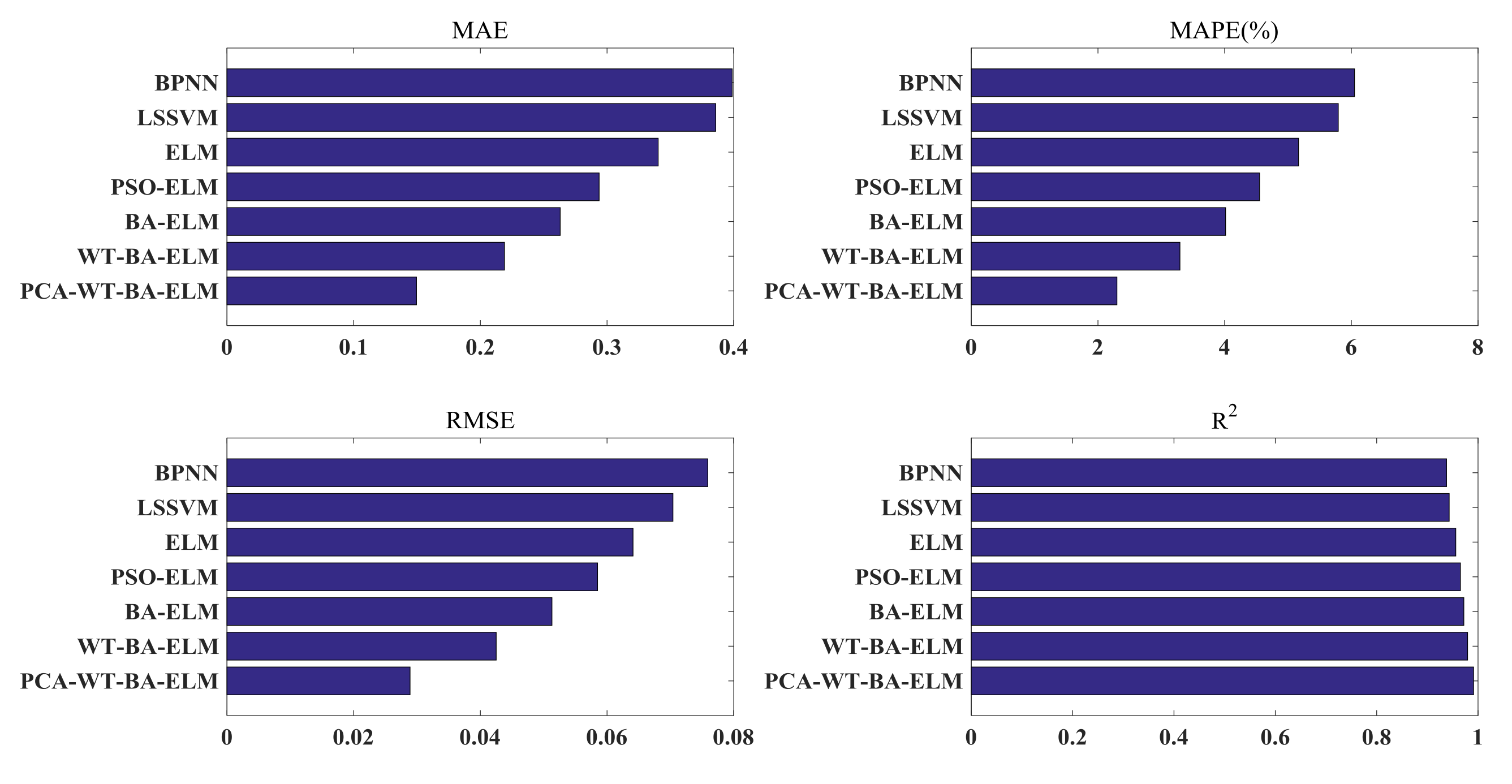
- (a)
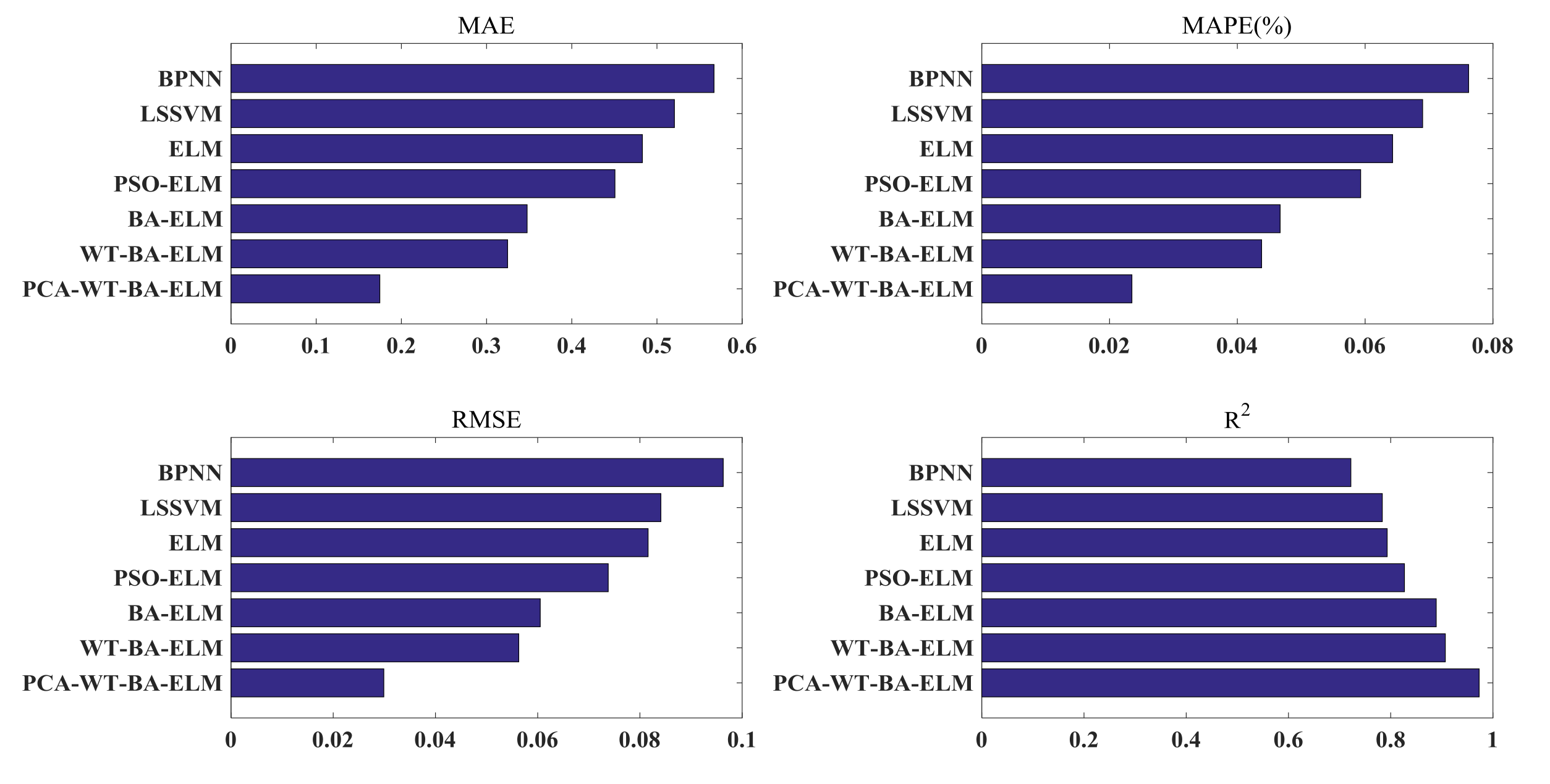
- The MAE, MAPE, and RMSE of PCA-WT-BA-ELM are the minimum and the R2 is the maximum, which demonstrates its performance sufficiently;
- (b)
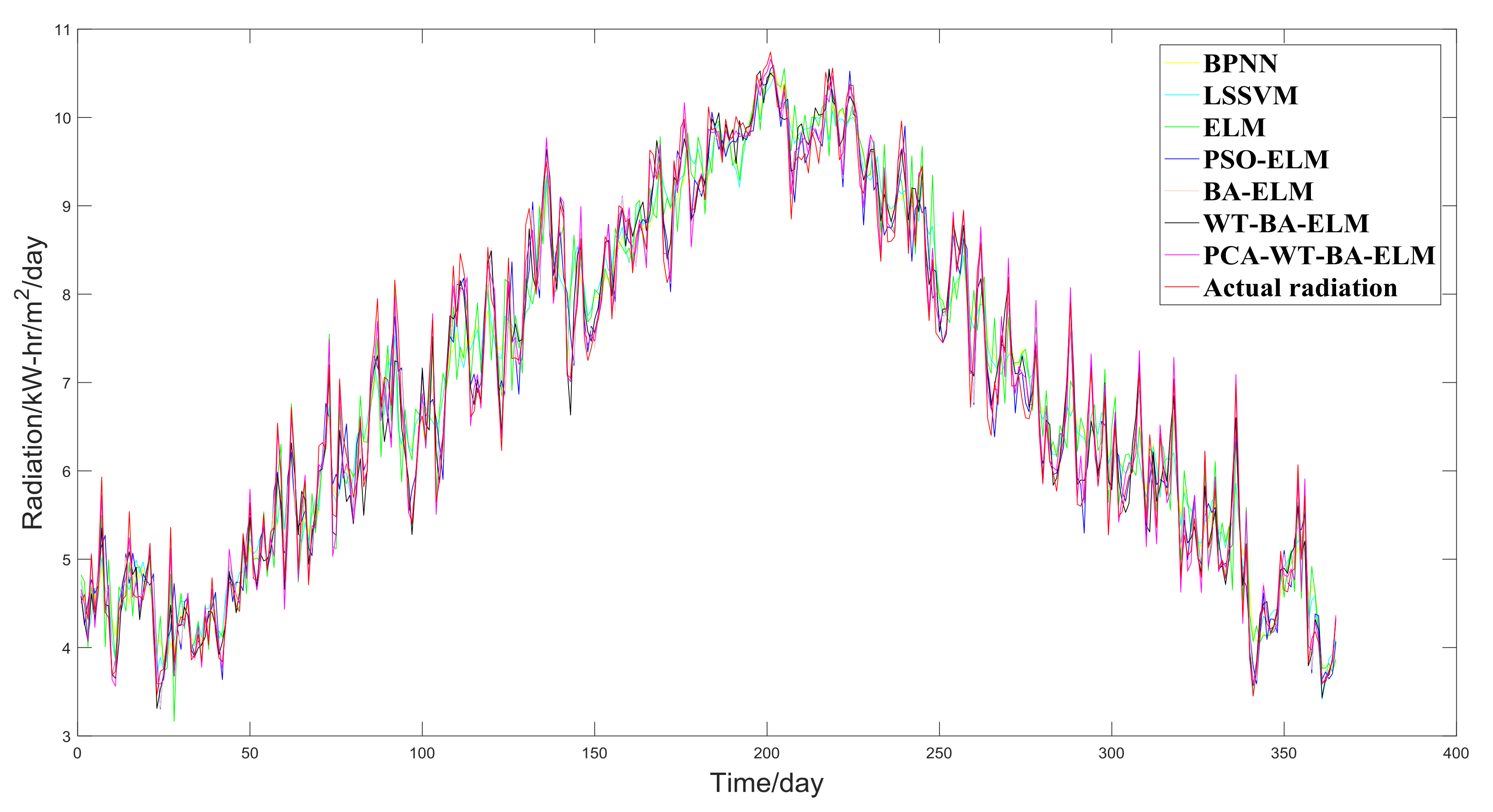
- The predicted carbon price curve is closest to the actual carbon price curve, which is better than the Single-LSSVM and Single-BPNN. Single ELM’s MAE, MAPE, RMSE and R2 surpasses Single-LSSVM and Single-BPNN, showing that Single-ELM has the best predictive performance. In addition, as can be discovered in Table 6, the learning speed of Single-ELM is the shortest, reflecting that in the part of prediction accuracy and learning speed, Single-ELM exceeds Single-LSSVM and Single-BPNN;
- (c)
- When Comparing with single ELM, hybrid models (including PSO-ELM and BA-ELM) have smaller MAE, MAPE, RMSE, and larger R2, which shows that it makes sense to optimize the ELM parameters. BA-ELM′s MAE, MAPE, and RMSE are smaller, and BA-ELM’s R2 is larger than PSO-ELM’s R2, reflecting that BA-ELM is more precious in the whole, and BA is superior to PSO in the part of optimizing the parameter of ELM;
- (d)
- After the comparison with BA-ELM, the predicted solar radiation curve of WT-BA-ELM is closest to the actual one. For that the solar radiation series is highly uncertain, nonlinear, dynamic, and complex, it may not be appropriate to predict straight without decomposition. It can therefore be seen that the MAE, MAPE, RMSE, and R2 of WT-BA-ELM are better than BA-ELM;
- (e)
- The predicted solar radiation curve of PCA-WT-BA-ELM is closer to the actual solar radiation curve than that of WT-BA-ELM. The MAE, MAPE, RMSE, and R2 of PCA-WT-BA-ELM are better than WT-BA-ELM. All of this can verify the need to use PCA to reduce the dimensions of the BA-ELM input.
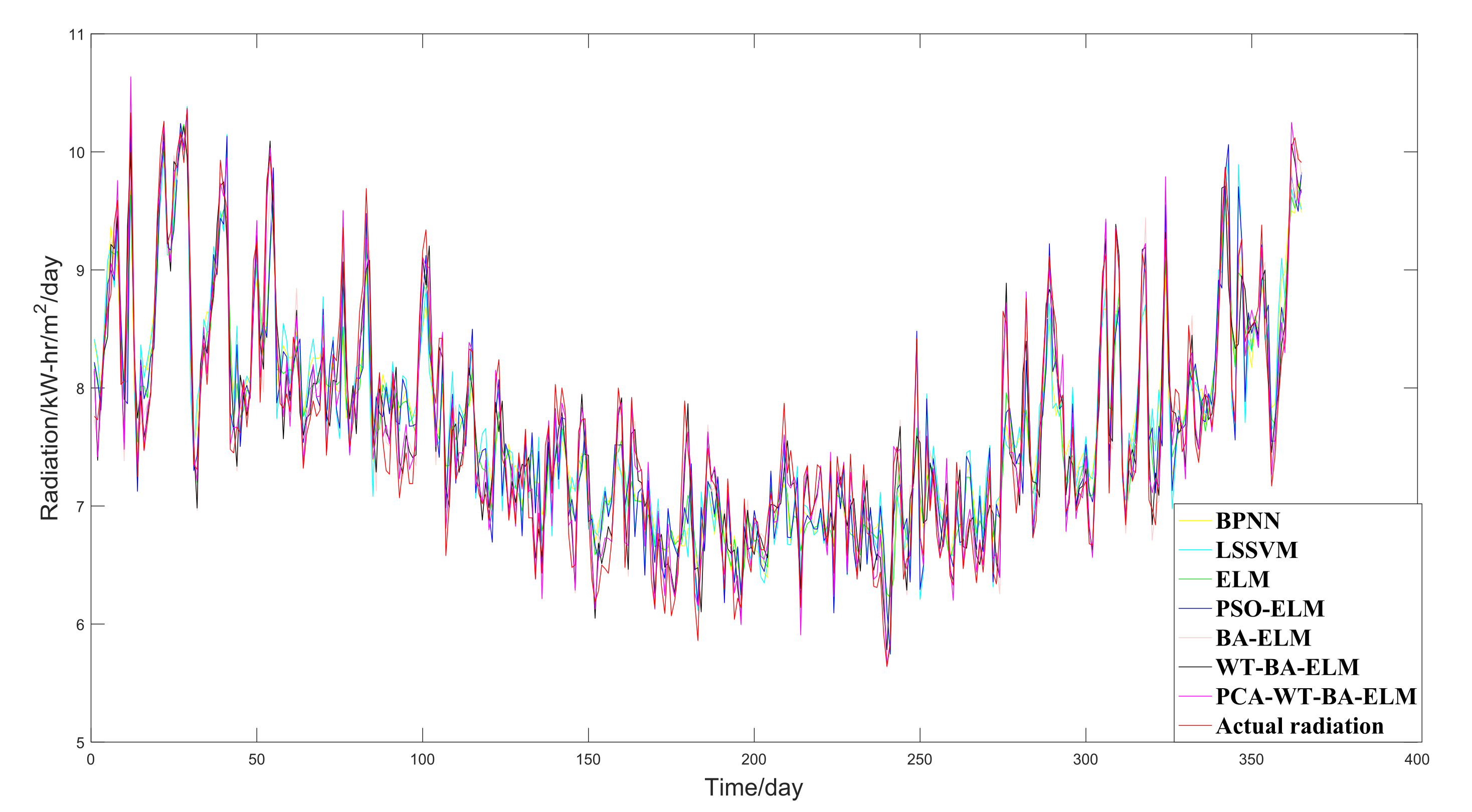
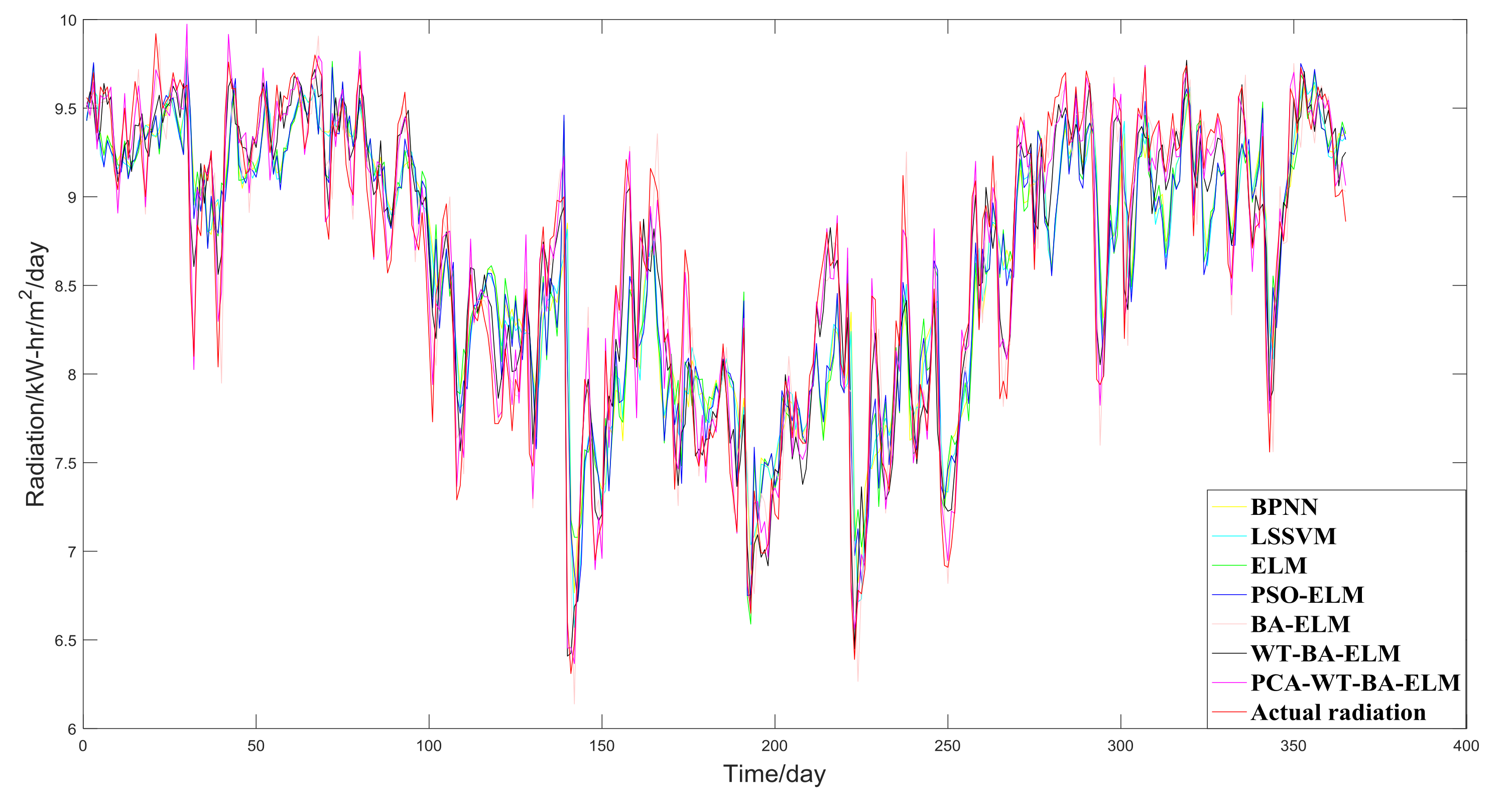
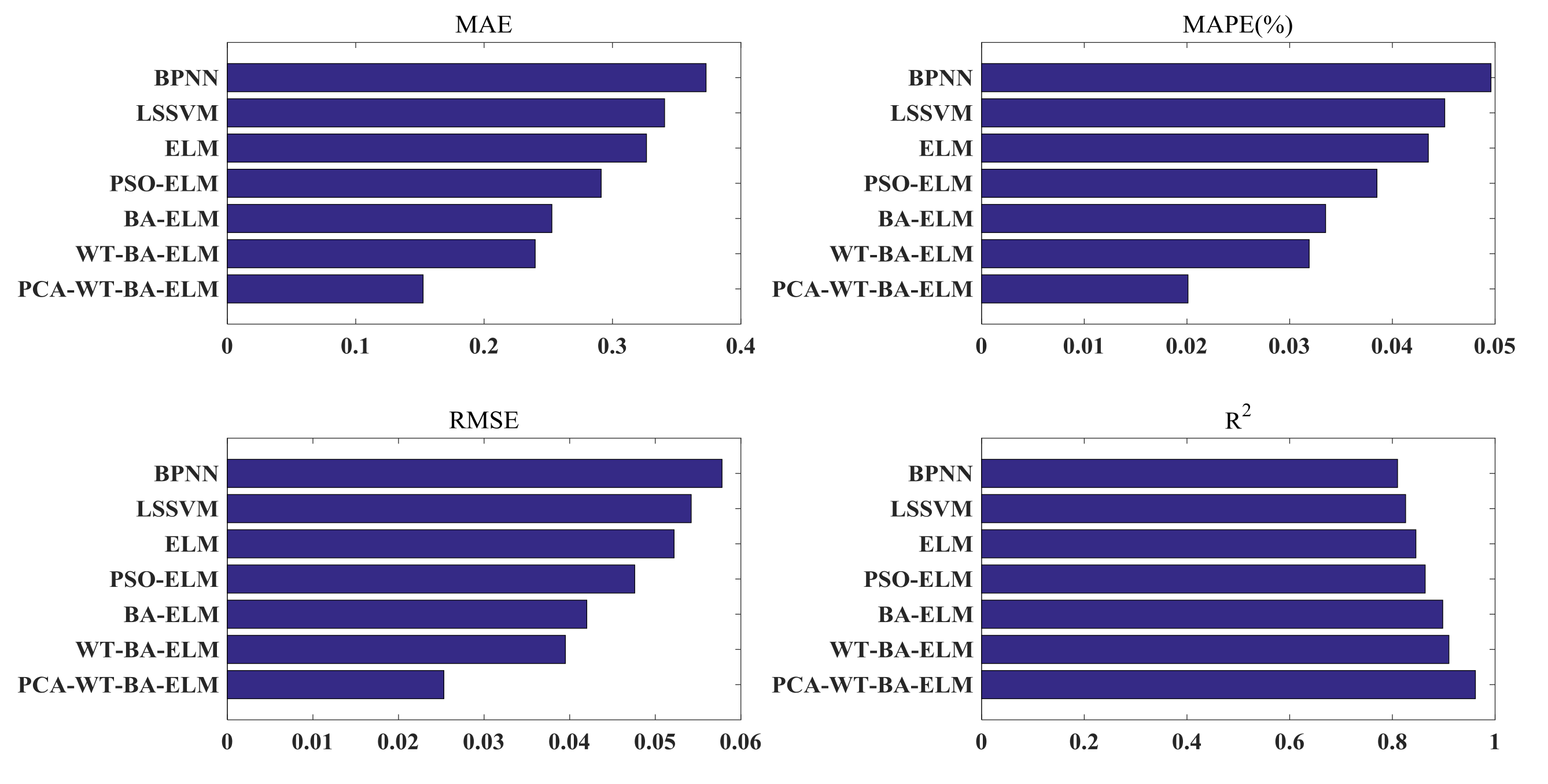
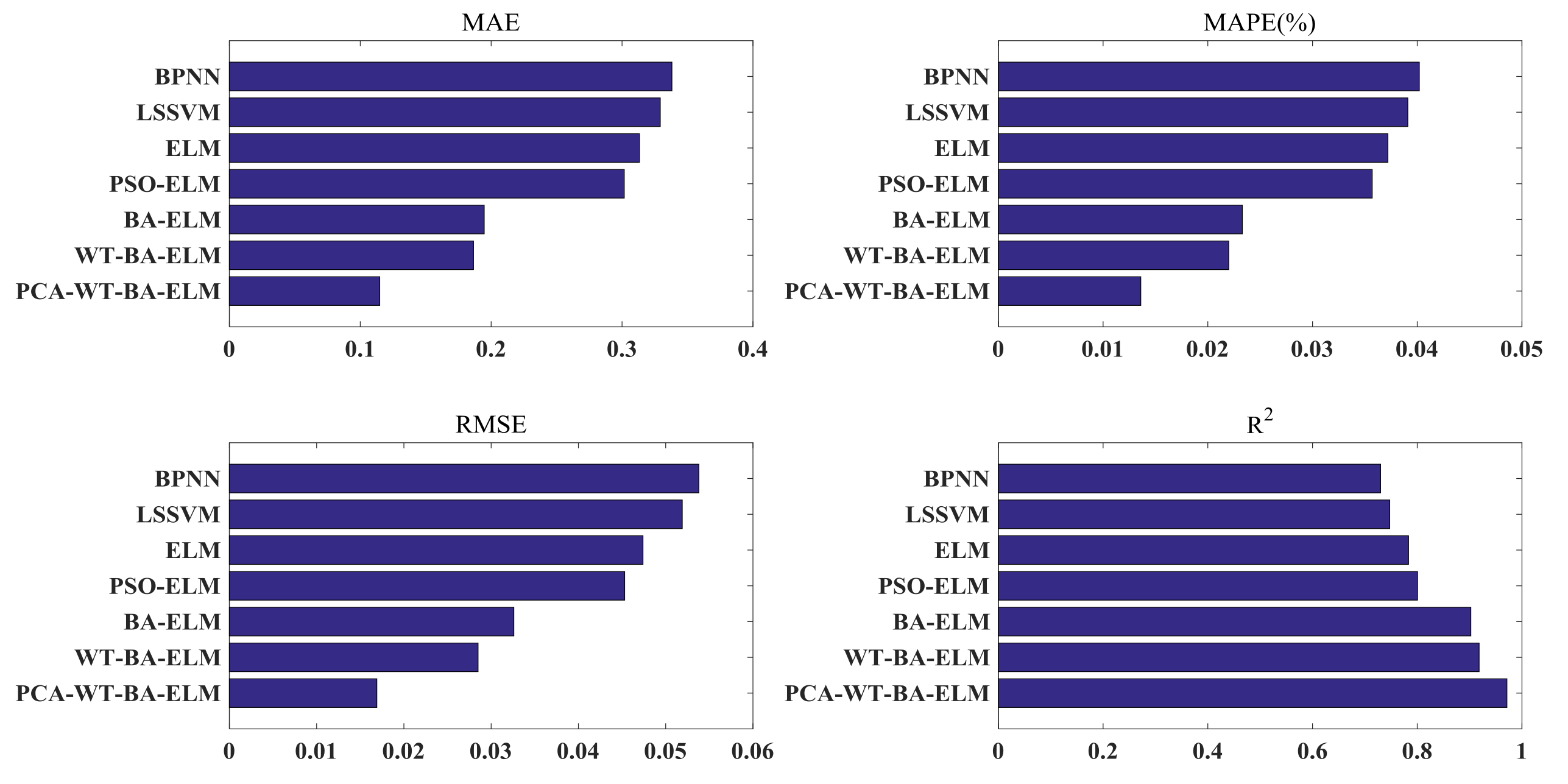
3.4.2. The Case of New York, Melbourne, and São Paulo
4. Conclusions
- (a)
- ELM is superior to BPNN and LSSVM in predicting accuracy and learning speed. Because the ELM parameter, which the users have to make appropriate adjustments of, is the just number of hidden nodes. After stochastically installing the input weight and the hidden layer deviation, the output weight of the ELM can be analytically determined by solving the linear system according to the Moore-Penrose (MP) generalized inverse idea.
- (b)
- In terms of prediction precision, both BA-ELM and PSO-ELM are superior to ELM, and BA-ELM is better than PSO-ELM. Therefore, it makes sense to optimize the parameters of the ELM through optimization method, and BA is more competitive than PSO;
- (c)
- The model using decomposition method WT-BA-ELM performs better than that without it, which means that the decomposition method is able to ameliorate the forecasting performance, and it is essential to denoise the solar radiation sequence through WT as its uncertain, nonlinear, dynamic and complex features;
- (d)
- Compared with the model not using dimensionality reduction method WT-BA-ELM, the model with PCA-WT-BA-ELM is superior. It shows that the dimension reduction method is able to enhance the forecasting performance, and it is a necessity to decrease the dimension of many input indicators of BA-ELM through PCA;
- (e)
- The PCA-WT-BA-ELM model is superior to other methods in solar radiation prediction in Beijing, New York, Melbourne, and São Paulo. It can therefore be inferred that the proposed hybrid model can be utilized to predict solar radiation in different parts of the world at the same time, and it greatly expands the application of the model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gouda, S.G.; Hussein, Z.; Luo, S.; Wang, P.; Cao, H.; Yuan, Q. Empirical models for estimating global solar radiation in Wuhan City, China. Eur. Phys. J. Plus 2018, 133, 517. [Google Scholar] [CrossRef]
- Zhu, C.H. The calculating and distributing of solar diffuse irradiance in China. Acta Energy Sol. Sin. 1984, 5, 242–249. (In Chinese) [Google Scholar]
- Audi, M.S. Simple hourly global solar radiation prediction models. Renew. Energy 1991, 1, 473–478. [Google Scholar] [CrossRef]
- Collares-Pereira, M.; Rabl, A. The average distribution of solar radiation correlations between diffuse and hemispherical and between daily and hourly insulation values. Sol. Energy 1979, 22, 155–164. [Google Scholar] [CrossRef]
- Trapero, J.R.; Kourentzes, N.; Martin, A. Short-term solar irradiation forecasting based on dynamic harmonic regression. Energy 2015, 84, 289–295. [Google Scholar] [CrossRef]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a coupled autoregressive and dynamical system (CARDS) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Voyant, C.; Paoli, C.; Muselli, M.; Nivet, M. Multi-horizon solar radiation forecasting for Mediterranean locations using time series models. Renew. Sustain. Energy Rev. 2013, 28, 44–52. [Google Scholar] [CrossRef]
- Fidan, M.; Hocaoğlu, F.O.; Gerek, Ö.N. Harmonic analysis based hourly solar radiation forecasting model. IET Renew. Power Gen. 2014, 9, 218–227. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Solar radiation forecast based on fuzzy logic and neural networks. Renew. Energy 2013, 60, 195–201. [Google Scholar] [CrossRef]
- Olcan, C.; Mahmudov, E. Hybrid Fuzzy Time Series Methods Applied to Solar Radiation Forecasting. J. Mult.-Valued Log. Soft Comput. 2016, 27, 89–116. [Google Scholar]
- Akarslan, E.; Hocaoğlu, F.O.; Edizkan, R. A novel MD (multi-dimensional) linear prediction filter approach for hourly solar radiation forecasting. Energy 2014, 73, 978–986. [Google Scholar] [CrossRef]
- Amrouche, B.; Le Pivert, X. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Convers. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Paoli, C.; Voyant, C.; Muselli, M.; Nivet, M. Forecasting of preprocessed daily solar radiation time series using neural networks. Sol. Energy 2010, 84, 2146–2160. [Google Scholar] [CrossRef]
- Adel, M.; Massi, P.A. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar]
- Gala, Y.; Fernández, Á.; Díaz, J.; Dorronsoro, J.R. Hybrid machine learning forecasting of solar radiation values. Neurocomputing 2016, 176, 48–59. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Ekici, B.B. A least squares support vector machine model for prediction of the next day solar insolation for effective use of PV systems. Measurement 2014, 50, 255–262. [Google Scholar] [CrossRef]
- Sun, S.; Wang, S.; Zhang, G.; Zheng, J. A decomposition-clustering-ensemble learning approach for solar radiation forecasting. Sol. Energy 2018, 163, 189–199. [Google Scholar] [CrossRef]
- Meenal, R.; Selvakumar, A. Immanuel. Assessment of SVM, empirical and ANN based solar radiation prediction models with most influencing input parameters. Renew. Energy 2018, 121, 324–343. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feed forward neural networks. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Li, S.; Goel, L.; Wang, P. An ensemble approach for short-term load forecasting by extreme learning machine. Appl. Energy 2016, 170, 22–29. [Google Scholar] [CrossRef]
- Syed, M.; Sivanagaraju, S. Short Term Wind Speed Forecasting using Hybrid ELM Approach. Indian J. Sci. Technol. 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Abdoos, A.A. A new intelligent method based on combination of VMD and ELM for short term wind power forecasting. Neurocomputing 2016, 203, 111–120. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Panigrahi, B.K. A hybrid wavelet-ELM based short term price forecasting for electricity markets. Int. J. Electr. Power Energy Syst. 2014, 55, 41–50. [Google Scholar] [CrossRef]
- Sun, W.; Wang, C.; Zhang, C. Factor analysis and forecasting of CO2 emissions in Hebei, using extreme learning machine based on particle swarm optimization. J. Clean. Prod. 2017, 162, 1095–1101. [Google Scholar] [CrossRef]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 267–289. [Google Scholar] [CrossRef]
- Guo, J.; White, J.; Wang, G. A genetic algorithm for optimized feature selection with resource constraints in software product lines. J. Syst. Softw. 2011, 84, 2208–2221. [Google Scholar] [CrossRef]
- Stelios, P.; Maria, M. An in depth economic restructuring framework by using particle swarm optimization. J. Clean. Prod. 2019, 215, 329–342. [Google Scholar]
- Liu, Q.; Wu, L.; Xiao, W.; Wang, F.; Zhang, L. A novel hybrid bat algorithm for solving continuous optimization problems. Appl. Soft Comput. 2018, 73, 67–82. [Google Scholar] [CrossRef]
- Gupta, D.; Arora, J.; Agrawal, U.; Khanna, A.; De Albuquerque, V.H.C. Optimized Binary Bat algorithm for classification of white blood cells. Measurement 2019, 143, 180–190. [Google Scholar] [CrossRef]
- Wulandhari, L.A.; Komsiyah, S.; Wicaksono, W. Bat Algorithm Implementation on Economic Dispatch Optimization Problem. Procedia Comput. Sci. 2018, 135, 275–282. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Kalogirou, S.A. An adaptive wavelet-network model for forecasting daily total solar-radiation. Appl. Energy 2006, 83, 705–722. [Google Scholar] [CrossRef]
- Monjoly, S.; André, M.; Calif, R.; Soubdhan, T. Hourly forecasting of global solar radiation based on multiscale decomposition methods: A hybrid approach. Energy 2017, 119, 288–298. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, J.; Wang, J.; Xu, J. Day-ahead electricity price forecasting using wavelet transform combined with ARIMA and GARCH models. Appl. Energy 2010, 87, 3606–3610. [Google Scholar] [CrossRef]
- Sun, W.; Sun, J. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm. J. Environ. Manag. 2017, 188, 144–152. [Google Scholar] [CrossRef]
- Mallet, Y.; De Vel, O.; Coomans, D. Fundamentals of Wavelet Transforms. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2000; Chapter 3; Volume 22, pp. 57–84. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Alves Barata, J.C.; Hussein, M.S. The Moore-Penrose Pseudoinverse: A Tutorial Review of the Theory. Braz. J. Phys. 2012, 42, 146–165. [Google Scholar] [CrossRef]
- Salaken, S.M.; Khosravi, A.; Nguyen, T.; Nahavandi, S. Extreme learning machine based transfer learning algorithms: A survey. Neurocomputing 2017, 267, 516–524. [Google Scholar] [CrossRef]
- Solar Radiation Data and Meteorological Data. Available online: http://eosweb.larc.nasa.gov/sse/ (accessed on 31 December 2018).

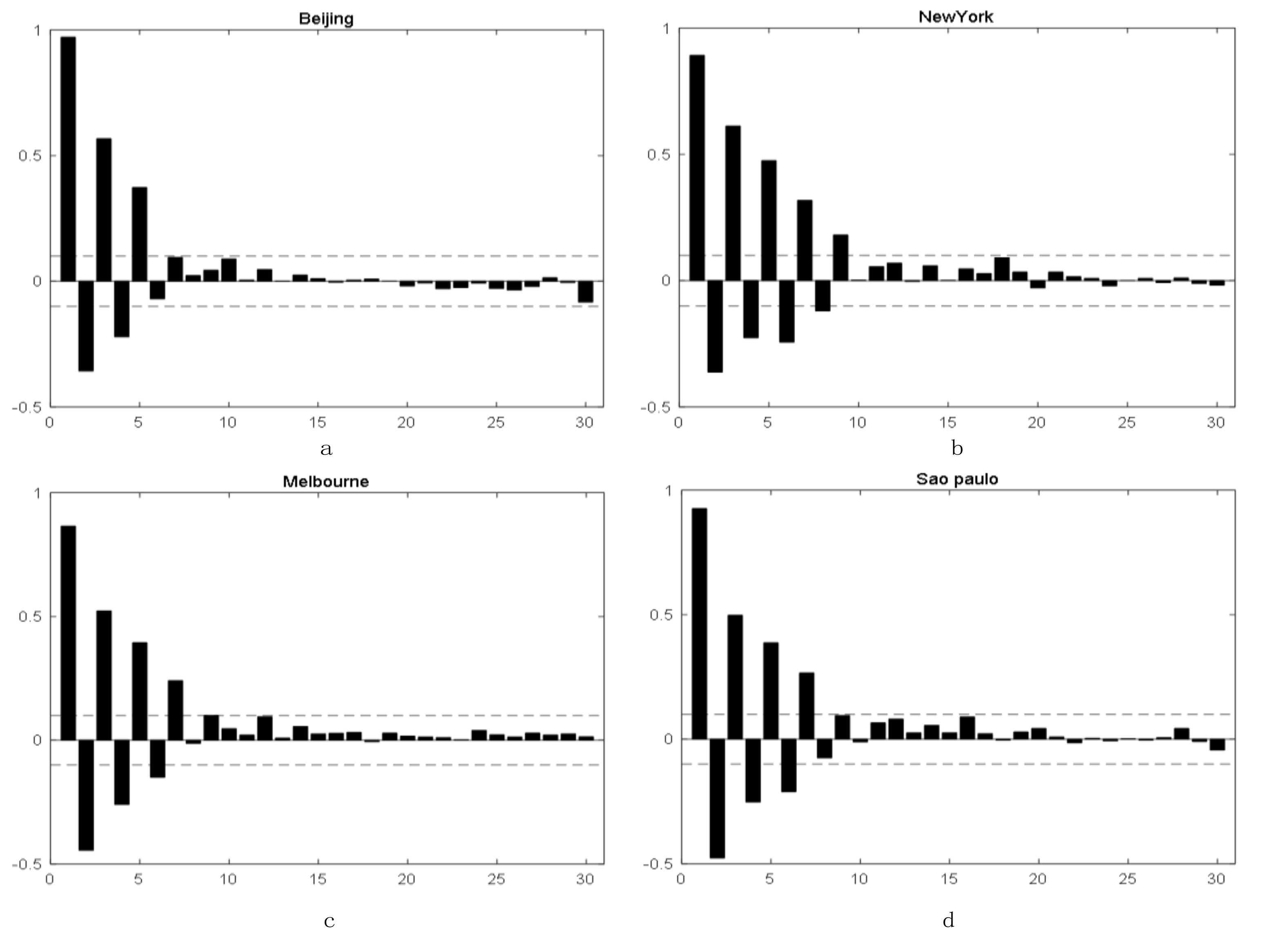
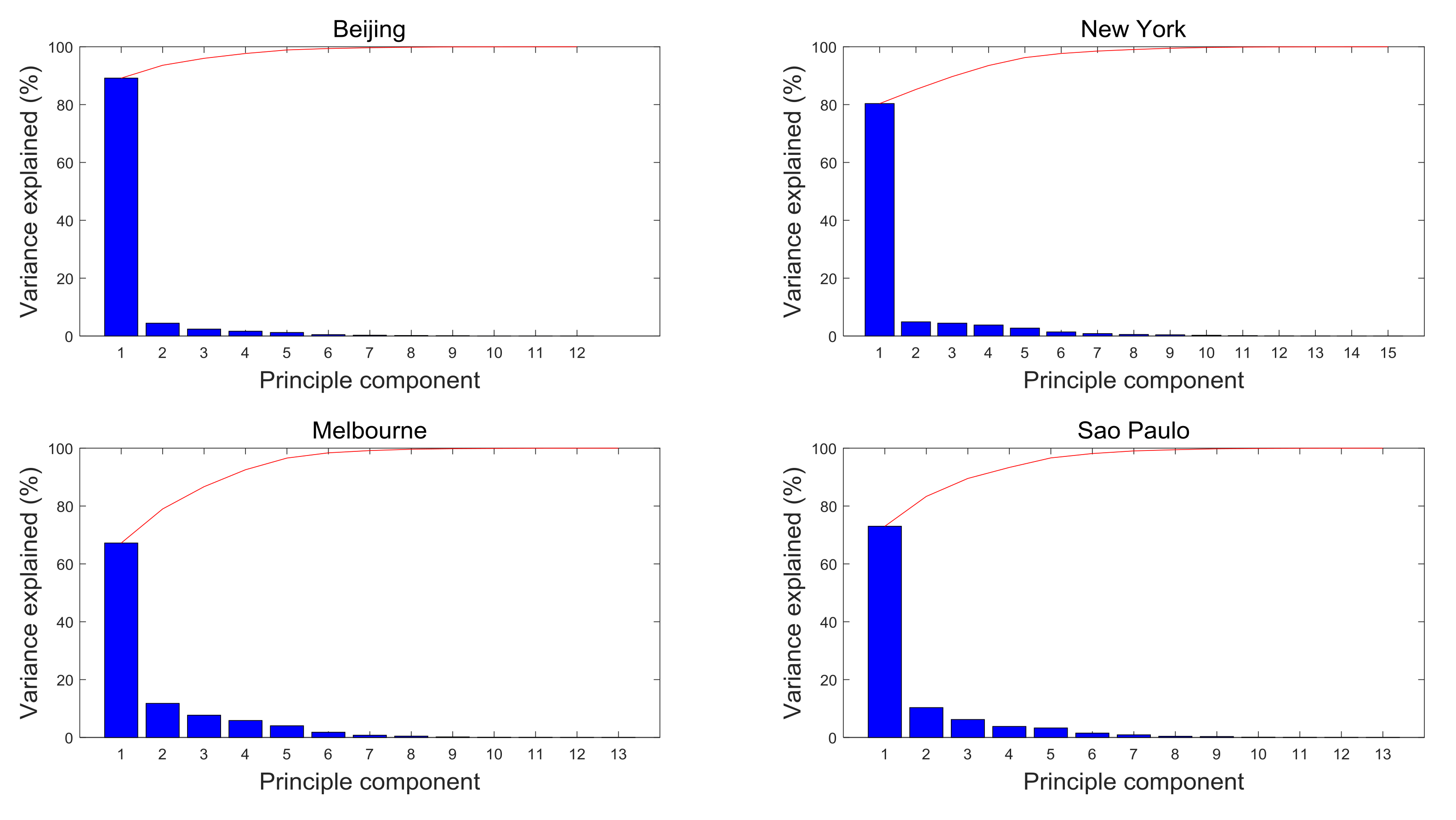
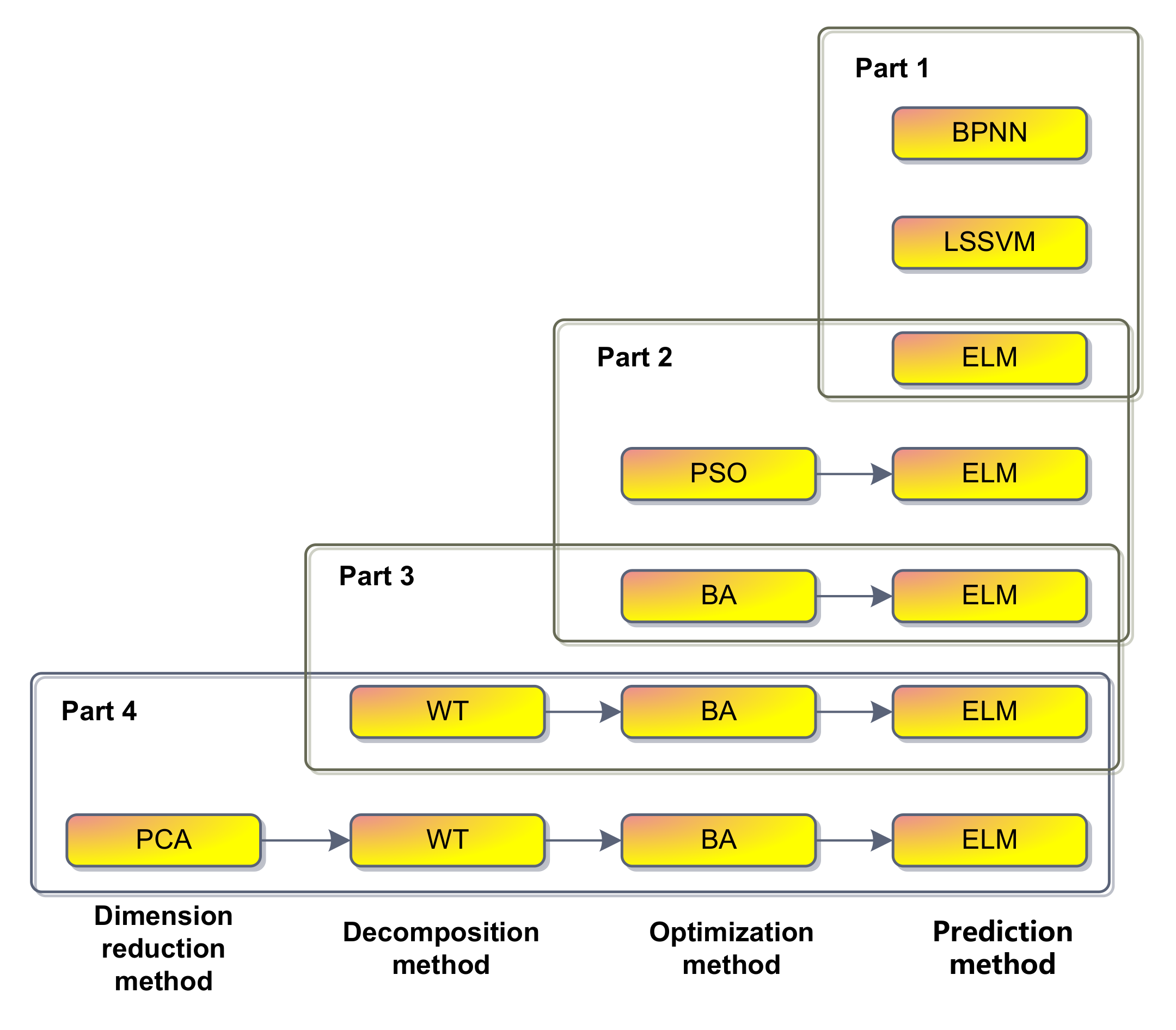
| Indicator | Abbreviation | Unit | Beijing | New York | Melbourne | São Paulo |
|---|---|---|---|---|---|---|
| Precipitation | PRECTOT | Mm/day | 0.118 ** | 0.089 ** | −0.020 | 0.101 ** |
| Specific Humidity at 2 M | SH2M | kg/kg | 0.911 ** | 0.883 ** | 0.834 ** | 0.895 ** |
| Relative Humidity at 2 M | RH2M | % | 0.446 ** | 0.562 ** | −0.446 ** | 0.502 ** |
| Surface Pressure | SP | kPa | −0.779 ** | −0.290 ** | −0.568 ** | −0.658 ** |
| Temperature Range at 2 M | T2M_RANGE | C | −0.162 ** | -0.449 ** | 0.237 ** | −0.572 ** |
| Earth Skin Temperature | EST | C | 0.922 ** | 0.768 ** | 0.800 ** | 0.691 ** |
| Dew/Frost Point at 2 M | T2M_DEW | C | 0.967 ** | 0.906 ** | 0.828 ** | 0.901 ** |
| Maximum Temperature at 2 M | T2M_MAX | C | 0.858 ** | 0.840 ** | 0.713 ** | 0.285 ** |
| Temperature at 2 M | T2M | C | 0.926 ** | 0.844 ** | 0.893 ** | 0.868 ** |
| Minimum Temperature at 2 M | T2M_MIN | C | 0.963 ** | 0.849 ** | 0.815 ** | 0.667 ** |
| Wind Speed Range at 50 M | WS50M_RANGE | m/s | −0.139 ** | −0.167 ** | 0.361 ** | 0.042 |
| Wind Speed Range at 10 M | WS10M_RANGE | m/s | −0.147 ** | −0.175 ** | 0.397 ** | 0.176 ** |
| Minimum Wind Speed at 50 M | WS50M_MIN | m/s | −0.408 ** | −0.119 ** | −0.076 ** | −0.085 ** |
| Minimum Wind Speed at 10 M | WS10M_MIN | m/s | −0.417 ** | −0.195 ** | −0.081 ** | −0.154 ** |
| Maximum Wind Speed at 50 M | WS50M_MAX | m/s | −0.422 ** | −0.234 ** | 0.224 ** | −0.035 |
| Maximum Wind Speed at 10 M | WS10M_MAX | m/s | −0.345 ** | −0.302 ** | 0.261 ** | 0.063 ** |
| Wind Direction at 50 M | WD50M | m/s | −0.471 ** | −0.368 ** | −0.041 | 0.194 ** |
| Wind Direction at 10 M | WD10M | m/s | −0.481 ** | −0.364 ** | −0.032 | 0.190 ** |
| Wind Speed at 50 M | WS50M | m/s | −0.457 ** | −0.197 ** | 0.109 ** | −0.053 * |
| Wind Speed at 10 M | WS10M | m/s | −0.426 ** | −0.278 ** | 0.154 ** | −0.073 ** |
| Insolation Clearness Index | ICI | 0.048 * | 0.001 | 0.000 | −0.013 |
| Region | Selected Indexes | Indexes Number |
|---|---|---|
| Beijing | SH2M, EST, T2M_DEW, T2M_MAX, T2M, T2M_MIN | 6 |
| New York | SH2M, EST, T2M_DEW, T2M_MAX, T2M, T2M_MIN | 6 |
| Melbourne | SH2M, EST, T2M_DEW, T2M_MAX, T2M, T2M_MIN | 6 |
| São paulo | SH2M, SP, EST,T2M_DEW, T2M, T2M_MIN | 6 |
| City | Lag |
|---|---|
| Beijing | (xt-1, xt-2, xt-3, xt-4, xt-5) |
| New York | (xt-1, xt-2, xt-3, xt-4, xt-5, xt-6, xt-7, xt-8, xt-9) |
| Melbourne | (xt-1, xt-2, xt-3, xt-4, xt-5, xt-6, xt-7) |
| São Paulo | (xt-1, xt-2, xt-3,xt-4, xt-5, xt-6, xt-7) |
| Beijing | New York | Melbourne | São Paulo | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Component | PC1 | Component | PC1 | Component | PC1 | PC2 | PC3 | Component | PC1 | PC2 |
| SH2M | 0.899 | SH2M | 0.87 | SH2M | 0.847 | −0.298 | 0.198 | SH2M | 0.902 | −0.162 |
| EST | 0.973 | EST | 0.861 | EST | 0.81 | −0.056 | 0.458 | SP | 0.906 | −0.005 |
| T2M_DEW | 0.954 | T2M_DEW | 0.854 | T2M_DEW | 0.782 | 0.22 | 0.513 | EST | 0.881 | 0.21 |
| T2M_MAX | 0.932 | T2M_MAX | 0.856 | T2M_MAX | 0.774 | 0.415 | 0.321 | T2M_DEW | 0.857 | 0.38 |
| T2M | 0.975 | T2M | 0.859 | T2M | 0.765 | 0.518 | 0.004 | T2M | 0.84 | 0.459 |
| T2M_MIN | 0.985 | T2M_MIN | 0.861 | T2M_MIN | 0.741 | 0.517 | −0.255 | T2M_MIN | 0.816 | 0.455 |
| Lag 1 xt-1 | 0.966 | Lag 1 xt-1 | 0.862 | Lag 1 xt-1 | 0.704 | 0.4 | −0.324 | Lag 1 xt-1 | 0.78 | 0.383 |
| Lag 2 xt-2 | 0.96 | Lag 2 xt-2 | 0.854 | Lag 2 xt-2 | 0.779 | −0.451 | 0.034 | Lag 2 xt-2 | 0.928 | −0.152 |
| Lag 3 xt-2 | 0.954 | Lag 3 xt-2 | 0.834 | Lag 3 xt-2 | 0.927 | −0.115 | −0.22 | Lag 3 xt-2 | −0.713 | 0.214 |
| Lag 4 xt-4 | 0.95 | Lag 4 xt-4 | 0.93 | Lag 4 xt-4 | 0.776 | −0.459 | 0.021 | Lag 4 xt-4 | 0.813 | −0.417 |
| Lag 5 xt-5 | 0.941 | Lag 5 xt-5 | 0.959 | Lag 5 xt-5 | 0.869 | −0.077 | −0.291 | Lag 5 xt-5 | 0.923 | −0.153 |
| Lag 6 xt-6 | 0.938 | Lag 6 xt-6 | 0.924 | −0.259 | −0.15 | Lag 6 xt-6 | 0.922 | −0.311 | ||
| Lag 7 xt-7 | 0.961 | Lag 7 xt-7 | 0.92 | −0.148 | −0.241 | Lag 7 xt-7 | 0.795 | −0.448 | ||
| Lag8 xt-8 | 0.962 | |||||||||
| Lag 9xt-9 | 0.965 | |||||||||
| Model | Parameters |
|---|---|
| BPNN | L = 10; learning rate = 0.0004 |
| LSSVM | L = 10; γ = 50; σ2 = 2 |
| ELM | L = 10; g(x) = ‘sig’; |
| PSO-ELM | N = 10; N_iter = 500; c1 = c2 = 2; w = 1.5; rand = 0.8 |
| BA-ELM | N = 10; N_iter = 500; A = 1.5; γ = θ = 0.9; R = 0.0001; F = [0, 2] |
| Training Time (s) | Test Time (s) | |
|---|---|---|
| BPNN | 2621.112 | 0.265 |
| LSSVM | 1784.593 | 0.153 |
| ELM | 19.341 | 0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wei, Z. A Hybrid Model Based on Principal Component Analysis, Wavelet Transform, and Extreme Learning Machine Optimized by Bat Algorithm for Daily Solar Radiation Forecasting. Sustainability 2019, 11, 4138. https://doi.org/10.3390/su11154138
Zhang X, Wei Z. A Hybrid Model Based on Principal Component Analysis, Wavelet Transform, and Extreme Learning Machine Optimized by Bat Algorithm for Daily Solar Radiation Forecasting. Sustainability. 2019; 11(15):4138. https://doi.org/10.3390/su11154138
Chicago/Turabian StyleZhang, Xing, and Zhuoqun Wei. 2019. "A Hybrid Model Based on Principal Component Analysis, Wavelet Transform, and Extreme Learning Machine Optimized by Bat Algorithm for Daily Solar Radiation Forecasting" Sustainability 11, no. 15: 4138. https://doi.org/10.3390/su11154138
APA StyleZhang, X., & Wei, Z. (2019). A Hybrid Model Based on Principal Component Analysis, Wavelet Transform, and Extreme Learning Machine Optimized by Bat Algorithm for Daily Solar Radiation Forecasting. Sustainability, 11(15), 4138. https://doi.org/10.3390/su11154138




