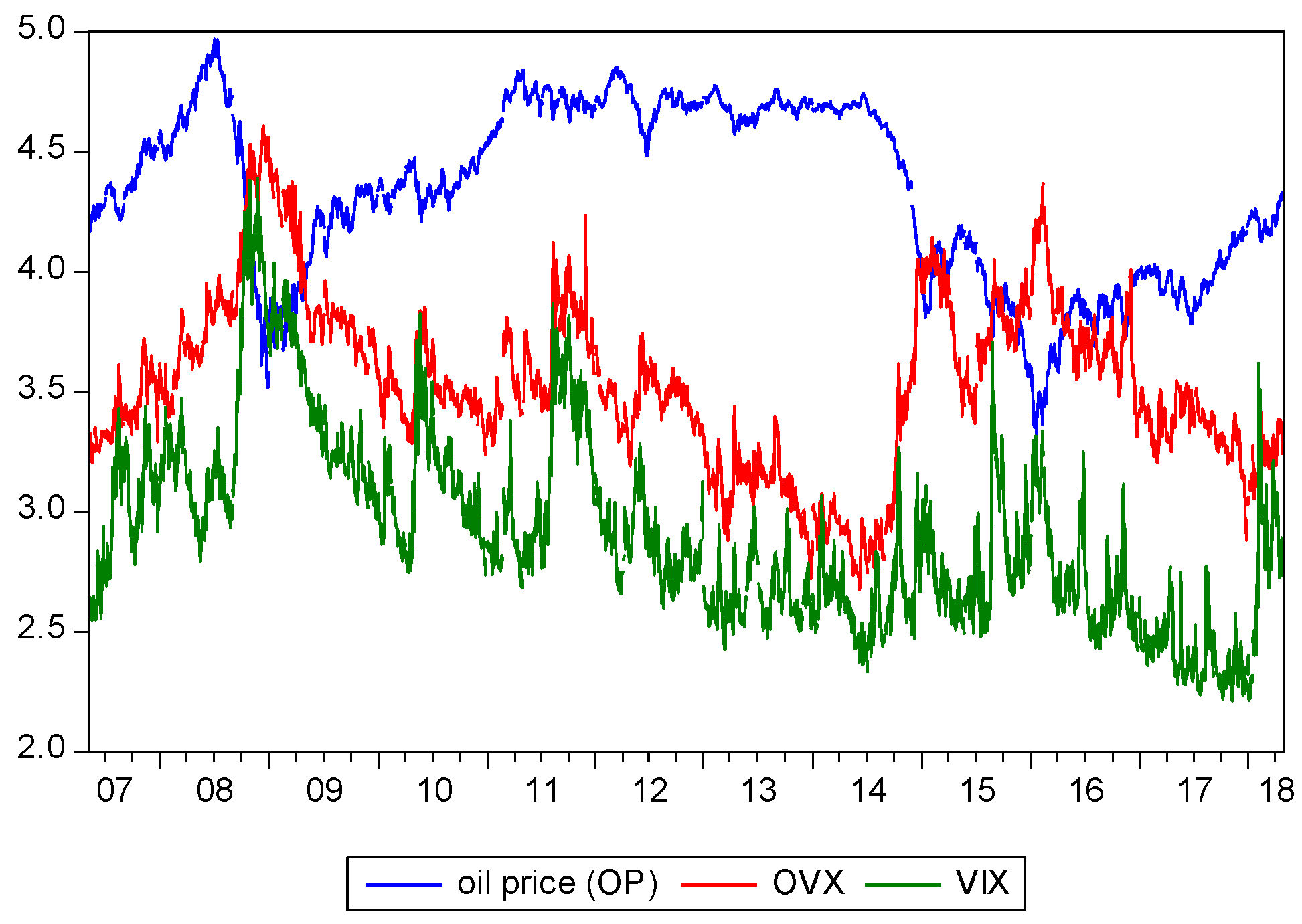
1. Introduction
Dramatic fluctuations in oil prices have had a major impact on various commodity markets, especially the severe financial crisis in mid-September 2008 that led to structural changes in the crude oil market [
1,
2] making the system of the entire market more vulnerable. Oil market participants have become more sensitive to external information such as oil price or stock price volatility and may change their trading strategies.
The statement at the website [
3] claims that the Chicago Board Options Exchange (CBOE) Crude Oil ETF Volatility Index (OVX) measures the market’s expectation of 30-day volatility of crude oil prices by applying the stock index options volatility index (VIX) methodology to United States Oil Fund, LP (USO) options spanning a wide range of strike prices. Although many studies have suggested that the performance of the volatility model can be significantly improved by including VIX [
4], it is surprising that crude oil OVX did not attract much attention in predicting oil price changes. Because OVX is a market-determined forecast, it is very similar to the stock market’s implied volatility index [
1]. For example, ref. [
5] pointed out that OVX is a measure of uncertainty in the oil market and can directly predict market expectations for future 30-day crude oil price volatility. In ref. [
6], the authors argued that since volatility comes from market option prices, these prices are forward-looking and, therefore, represent a market consensus on expected future uncertainties. Furthermore, in the literature on oil prices and related volatilities, authors in [
7] indicated that oil price volatility positively influences stock returns, but the impact of implied volatility index of crude oil (OVX) is negative, which means the rise in future oil price uncertainty has caused the stock prices to fall. Using the implied volatility index (VIX) provided by Chicago Board Options Exchange (CBOE) to study the relationship between oil price and the US energy stock returns, authors in [
8] showed that a long-run relationship exists between the oil and VIX. Also in the causality test, there was a short-run leading effect between the OVX and the US energy stock returns. Authors in [
9] found that the lead–lag relation between the oil price and its volatility is central to any type of trading strategy based on futures and options on the OVX. Authors in [
10] further pointed out that there is a negative and asymmetric relationship between OVX changes and crude oil price returns. Authors in [
11] also documented that there is a significant, negative relationship between OVX changes and West Texas Intermediate (WTI) returns, and that the asymmetry relationship between them means the OVX has a greater predictive effect of gauging an investor’s fear rather than risk preference.
Furthermore, scholars in the economics and finance field have been very concerned about the issue of how oil price changes have been caused by structural changes in the crude oil market. Authors in [
1] found that during the three different structural periods the main drivers of oil price changes had significantly different effects on them. After accounting for structural breaks in the generalized autoregressive conditional heteroskedasticity (GARCH) model, authors in [
12] demonstrated that a strong volatility spillover effect exists between the oil price and the US stock market. Authors in [
13] indicated that the oil price has a one-way, nonlinear Granger causal relation with the US dollar exchange rate, and the short-run US dollar exchange rate has a more significant, negative impact on oil prices. If the structural changes are ignored during the financial crisis, the volatilities of the oil price and the US dollar exchange rate can increase with a negative correlation between them. Authors in [
14] found that oil prices are linearly co-integrated with OVX (VIX) during some sample periods. If structural changes during periods of economic recession are considered, only a one-way, linear Granger causality relationship exists between oil prices and these two volatilities.
Accurate prediction in the fluctuation magnitude and trend of oil prices by using updated economic data is considerably challenging for academics and industries who have adopted traditional linear models. Especially with structural changes, the fluctuation and speed of oil prices are more confusing. Authors in [
14,
15] indicated that linear models with structural changes may not be able to detect the cointegration relationship between oil price and its volatility. Authors in [
16] studied the conditional volatility of oil spot prices and future prices in various GARCH models, and they found that the fractionally integrated generalized autoregressive conditionally heteroskedastic (FIGARCH) model significantly reduced the degree of volatility persistence during the adjustment period after structural changes occurred. Authors in [
17] used a nonlinear cointegration model with thresholds and found that, due to endogenous structural changes, there was no long-run equilibrium linear relationship between oil and Indian stock markets, while the short-run Granger causality relation held during some subperiods. We, therefore, question whether the structural change in oil prices leads to nonlinear behavior.
For example, authors in [
18] found a nonlinear interaction between the oil market and the stock market in the Middle East and North Africa in nonlinear and asymmetrical causality tests. Authors in [
17] showed that the nonlinear relationship between the oil market and the Indian stock market was significant after the global financial crisis in 2008 based on the results of the nonlinear cointegration test. Authors in [
19] used a nonlinear autoregressive distributed lag (ARDL) model with panel data to find that oil price changes asymmetrically affect the stock markets of oil exporting and importing countries. Authors in [
20] reported that the implied volatility of gold and oil has a nonlinear, positive cointegrated relationship with the implied volatility of Indian stocks. Authors in [
21] conducted a nonlinear Granger causality test and found that there was a bidirectional, nonlinear relationship between oil prices and gold prices, and the results of the nonlinear ARDL test revealed that a positive shock in oil prices had a more pronounced effect than negative shocks on gold prices.
Straightforwardly, the literature on the nonlinear dynamic relationship between oil prices and its volatilities has lacked this kind of work. This paper aims to fill the gap in such a study. In other words, the purpose of this paper is to analyze the nonlinear long-run and short-run dynamic relationship between oil prices and its volatilities (VIX and OVX), representing the investor sentiment of stock and oil markets, to further understand how the structural change of oil prices, which might be caused by major international events, affect oil price behaviors.
Furthermore, in the short-run methodology, the linear Granger causality test may be unable to characterize the nature of nonlinear causality. Authors in [
22] proposed a nonlinear Granger causality testing method (hereafter, HJ), but there was a problem of over-rejection of the null hypothesis in large samples. Authors in [
23] modified the HJ model to effectively solve the shortcomings of large sample over-rejection (hereafter, DP). Since then, the DP model has been very popular in economics and finance fields [
13,
24,
25,
26,
27]. On the other hand, in the long-run methodology, traditional cointegration methods, including Engle and [
28,
29], might have a problem with a weak testing power of the unit root if two series are not integrated on the same order. Authors in [
30] therefore proposed the autoregressive distributed lag (ARDL) model to solve the problem of different integrated orders. However, this linear ARDL model still has the disadvantage of estimating bias when facing nonlinear relationships among variables. Authors in [
31] proposed a nonlinear ARDL (NARDL) model to detect nonlinear long-run equilibrium relations among variables, which allows long-run and short-run asymmetry in testing variables and is robust to small samples [
21]. Many related studies such as [
21,
32,
33,
34,
35] all use this method in their empirical studies. Along with this reason, this paper adopts this method to examine the nonlinear long-run relationships between oil prices and two fear gauges (VIX and OVX).
The rest of the paper is organized as follows.
Section 2 presents the methodology and data sources.
Section 3 shows the empirical results and analysis. Finally,
Section 4 concludes this paper.
4. Discussion
This paper employed a linear/nonlinear ARDL-bounds test to characterize the long-run cointegration of oil prices with two implied volatilities (OVX and VIX), representing panic gauges, and the short-run linear/nonlinear Granger causality between them. The results showed that the linear ARDL-bounds test method can only detect a long-run equilibrium relationship, while the NARDL-bounds test not only detected the long-run equilibrium relationship between oil price and OVX (VIX) but also found that the rising OVX (VIX) had a greater negative influence on the oil price than the declining OVX (VIX), thus indicating that a long-run, asymmetric cointegration exists between them. The results of linear Granger causality found that OVX (VIX) led the oil price in one direction. However, the nonlinear Granger causality test results showed that the oil price had a bidirectional nonlinear causality with OVX (VIX). Similarly, [
21] showed strong evidence of a bidirectional, nonlinear relation between oil and gold prices. The nonlinearity and asymmetry of the interactive mechanism between oil and gold prices was also shown by using the nonlinear Granger causality test from [
22]. Authors in [
59] indicated the presence of cointegration relationships, a nonlinear and positive impact of the implied volatilities, and an inverse bidirectional causality between gold and oil on the implied volatility of the Indian stock market. Authors in [
32] further found that the nonlinear ARDL models successfully captured the long-term linkages between oil and precious metal markets, and a bidirectional and symmetric effect presented between crude oil and gold markets using the nonlinear Granger causality test.
Meanwhile, we also saw that when major international political and economic events occur, such as government policies, geopolitical risks, investor sentiments, and natural disasters, structural changes in oil prices would change the behavior of oil prices and, thus, panic indices, which switched from a linear relationship to a nonlinear one. Therefore, the empirical results of this study investigating the long-run and short-run nonlinear relationships between oil prices and the two implied volatilities provide market participants with more valuable information (Recently, the nature of the nonlinear relationships between crude oil prices and other variables has led to increased interest in multiscale modelling approaches such as mode decomposition techniques (EMD). The interested readers may refer to the original paper of [
60,
61,
62]).