1. Introduction
The trend in inequalities shows that disparities in per capita income between Mediterranean economies increased until 1970, stabilised until the mid-1980s, and then increased again [
1]. The factors that characterize the economic differences between countries have been analyzed from different perspectives: social, legal and political [
2]. Less attention has been paid to the energy implications of inequalities and to the interconnection between financial and environmental flows, which can affect the pollution of the Mediterranean countries in various ways. As stated within the report from the UN Intergovernmental Panel on Climate Change 2014 Report, a growing share of CO
2 emissions from fossil fuel combustion in developing countries is released in the production of goods and services exported, notably from upper-middle-income countries to high-income countries [
3]. The literature devoted to transboundary pollution problems uses a game theoretical framework to express important strategic interactions between countries in addressing the problem of climate change [
4,
5,
6,
7,
8]. Along the same lines, the broad literature focused on environmental and climate justice has advocated for a reduction in inequality as a tool to address environmental problems [
9,
10]. Boyce [
11], in analysing the phenomenon of the unequal exchange of environmental resources between rich and poor countries, wonders who the winners are and, above all, why they can impose the relative costs on the losers. The last question has three possible answers. One is that losers do not yet exist. They belong to future generations, and therefore are not here to defend themselves. The second possibility is that losers already exist, but they do not know it. They lack information on the costs of environmental degradation. The third possibility is that losers exist and know it, but they do not have the power to prevent winners from imposing costs on them.
Our research has as its first objective that of verifying whether the possible balance of power between rich and emerging countries in the Mediterranean area exists and how it can be quantified. We analyze how financial and virtual environmental flows (environmental emissions embodied in goods) have been redistributed within the ten main Mediterranean countries, with particular reference to pollution. Six types of virtual environmental flows and three kinds of financial flows can generate a very large number of interactions’ patterns and a complex, enveloping structure. The nexus between resources’ or virtual flows (layers) in this complex system can be studied with several methodologies [
12,
13]—in a few cases, these flows have been associated with financial flows [
14,
15]. Applying advanced methods of correlation and network analysis [
16], we verify the dynamics of transfer processes with the aim of assessing whether the link between economic and financial inequality and the hypothesis that rich countries export environmental emissions to poor ones are confirmed. Our research questions may be stated as follows: are financial flows correlated and linked with virtual energy flows? Are Southern Mediterranean countries importing pollution from Northern ones? The allocation of emissions embodied in international trade and in financial flows is crucial to evaluate the real impact that each country has on environmental pollution and its sustainability. Therefore, the attribution of emissions becomes a crucial issue when we want to reveal the redistribution of pollution.
The analysis on environmental bilateral flows presented here is based on data drawn from multiregional input-output (MRIO) Eora database, which is a consumption-based accounting method. This method, in contrast to the production-based approach which estimates emissions released within a specific geographical area, attributes emissions to the final consumers of goods and services. The rest of the paper is organized as follows. In
Section 2, we describe data and methodology, which encompasses features of international pollution stock, emission technology, and financial flows countries. In
Section 3, we present our results and in
Section 4 we discuss our results. Finally, we offer concluding comments and suggestions.
2. Data and Materials and Methods
2.1. Data
Our analysis focuses on the Mediterranean area and covers the top 10 countries on all sides for which there is a coherent set of bilateral environmental and financial trade information: Cyprus, Egypt, France, Greece, Italy, Israel, Lebanon, Malta, Spain and Turkey. In the analysis of the network, all of these countries represent the nodes, while the borders are represented by cross-border environmental and financial flows. In particular, our observations contain six environmental dimensions (emissions of , , , equivalent emissions and water footprint in gigagrams (Gg), Energy in tera joules (TJ)) and three financial dimensions (Equity, Long-Term Debt and Short-Term Debt). The observation period is from 2002 to 2015. Data on environmental impacts come from Eora’s multi-regional input–output table (MRIO) which provides a time series of high-resolution I/O tables with corresponding environmental and social satellite accounts for 190 countries. The Eora MRIO database reports the direct and indirect flows of resource footprints between producers and final consumers aggregated at a national level. The data describe in detail the countries of origin of each footprint, reporting the embedded flows from each country of origin/issuer to each country of destination/consumption. Referring to the environmental footprint associated with consumption in a given country, the embedded flows are to be understood as virtual for the resource footprint.
Most empirical studies on the determinants of international capital flows usually focus only on foreign direct investment (FDI) because the analyses find out more on capital flows than on stocks of foreign investment. In contrast, in our study, data on financial transactions are taken from the Coordinated Portfolio Investment Survey (CPIS) conducted by the IMF. The CPIS records portfolio investment data in the form of shares and units in investment funds, long-term debt securities and short-term debt securities vis-à-vis more than seventy counterparty economies. All financial data are in millions of US dollars. They refer to the end of the year of the periods and do not provide information on portfolio flows. This choice allows us to keep all financial variables consistent and avoid having a matrix of financial margins calculated differently, with a negligible impact on the correlation analysis and, therefore, on the analysis of the output network. This approach is supported by many recent studies [
17] suggesting that foreign direct investment and portfolio investment can be treated as substitutes.
Based on the above explanations, we calculated, as a proxy for financial flows from country
i to country
j, the difference between two consecutive total amounts on assets held by residents of country
i (
i to
j) [
18]. Although previous studies [
19,
20] have already highlighted the drawbacks of CPIS data in terms of incompleteness, a lack of strong data consistency and the risk of undervaluation arising from the voluntary nature of the survey, due to the simultaneity of the survey and the use of consistent definitions, data collection is homogeneous and the geographical breakdown is very large for a comprehensive analysis of capital flows.
2.2. Pearson Correlation Index for Multiplex Networks
A first method to investigate layers’ correlations in a multiplex framework was proposed by Garlaschelli and applied to the commodity-specific trades [
21]. Garlaschelli extended the Pearson correlation index to the multiplex by averaging over space instead of time. The Pearson correlation index between the layers A and B (at time
t) will thus be:
It is noteworthy that the above definition of correlation can be applied both to links going in the same direction (Equation (
1)) and to links going in opposite directions (Equation (
2)):
2.3. Second Correlation Measure: Multiplexity and Multireciprocity
Recently, a more refined measure of correlation across layers in a (weighted) multiplex has been proposed [
16]. This measure derives from the extension of concept of reciprocity in weighted networks (see [
22]) to the context of multiple layers networks, and reads as follows:
for flows in the same direction, and:
for flows in the opposite direction. Multiplexity (Equation (
3)) and multireciprocity (Equation (
4)) are both normalized measures, spanning from 0 to 1. In the former case layers,
A and
B never overlap across the entire network; in the latter, they perfectly overlap, meaning that
they are perfectly correlated. A multiplex features homogeneous layers—the same units, or heterogeneous—different units. When a multiplex is heterogeneous, all flows are normalized to the relative total flow
W and become unit-less (scalar).
Any measure of correlation across layers (inter-layers) is sensitively dependent on the internal topology of each layer (intra-layer). Put simply, if two layers share the same hubs, any correlation results trivially from the mere overlap the two internal structures.
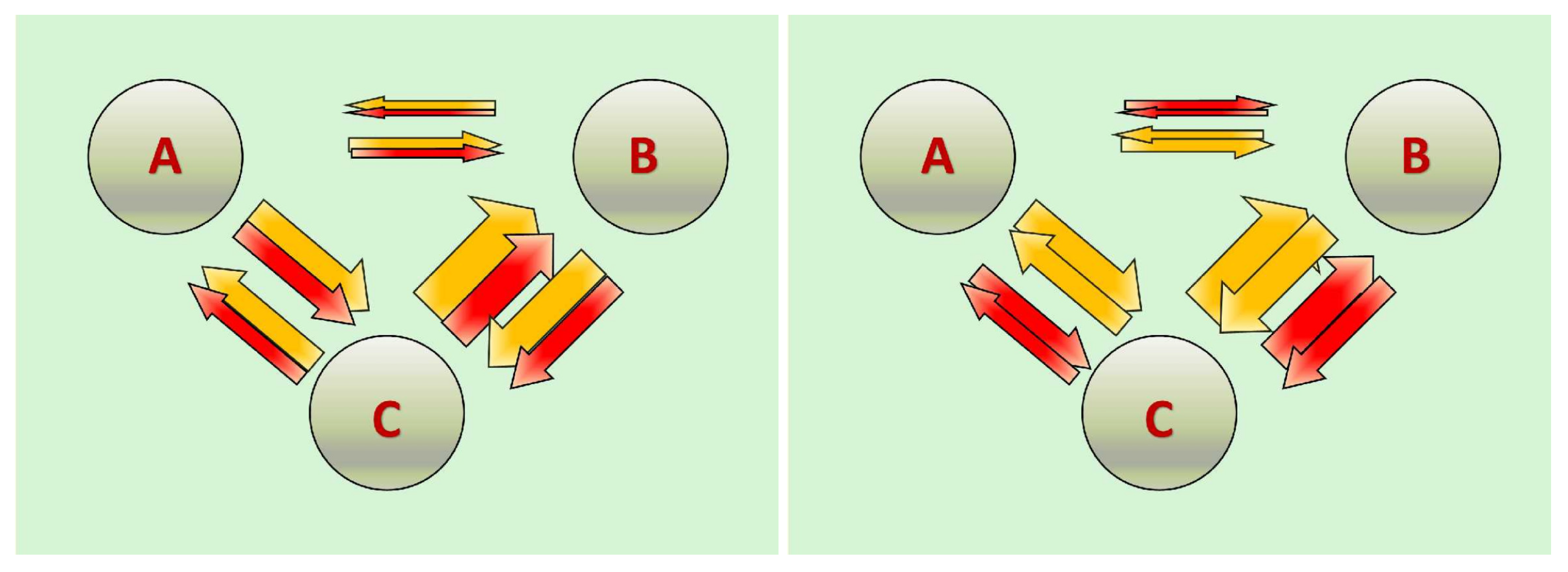
Figure 1 shows, by the means of a very simple and stylized multiplex with three nodes and two layers, to what extent the reciprocity structure within each layer can affect the observed correlation between layers (width of the arrows indicates the intensity of the flows).
Prima facie, the red and yellow layers seem to be very correlated when moving across nodes. Nevertheless, this is due the combined effect of the reciprocity level within each layer and the topology of the multiplex. For instance, node
C is a hub in both layers and thus node
A and
B tend to exchange with
C more than between each other.
Measures (
3) and (
4), differently from measure (
2) and (
1), permit the inclusion of suitable null models in the analysis and the development of an enhanced measure of correlation, cleaned by the intra-layer topological effects.
In [
16], the following enhanced measure of multiplexity between two generic layers
A and
B is proposed and denoted as
:
and enhanced multireciprocity
:
where
and
Both and can be positive or negative, indicating a positive or negative correlation in excess to the random correlation as captured by the null model and score 0 when the two layers are uncorrelated. It is noteworthy that and can vary freely without any upper or lower bound.
2.4. Models
A null model is meant to test the statistics significance of results, on the one hand, and to enhance the correlation analysis by clearing them from undesired side effects generated by the complexity of the interactions’ structure, on the other. In order to clear correlation measures across layers of the topological effects, we adopt the formalism of Exponential Random Graphs or models, which allow for obtaining maximally random ensembles of networks with specified constraints.
The method is composed by two main steps: the first one is the maximization of the Shannon entropy over a previously chosen set of graphs,
under a number of imposed constraints [
23], generically indicated as
(note the generality of the formalism, above:
G can be a directed, undirected, binary or weighted network). We can immediately choose the set
as the grandcanonical ensemble of binary directed graphs, i.e., the collection of networks with the same number of nodes of the observed one (say
N) and a number of links,
L, varying from zero to the maximum (i.e.,
). This prescription leads to the exponential distribution over the previously chosen ensemble
whose coefficients are functions of the Hamiltonian,
, which is the linear combination of the chosen constraints. The normalization constant,
, is the partition function [
23]. The second step prescribes how to numerically evaluate the unknown Lagrange multipliers
. Let us consider the log-likelihood function
and maximize it with respect to the unknown parameters. In other words, we have to find the value
of the multipliers satisfying the system
or that is the same,
i.e., a list of equations imposing the value of the expected parameters to be equal to the observed one. Note that the term “expected”, here, refers to the weighted average taken on the grandcanonical ensemble, the weights being the probability coefficients defined above. Thus, once the unknown parameters have been found, it is possible to evaluate the expected value of any other topological quantity of interest,
X:
Because of the difficulty to analytically calculate the expected value of the quantities commonly used in complex networks theory, it is often necessary to rest upon the linear approximation method:
, where
indicates the expected adjacency matrix, whose elements are
. For the weighted directed version of networks, a very useful null model is the
weighted directed configuration model (WDCM) that imposes the
and
strength sequence for every node (that is, the import and export sequence for every layer). The Hamiltonian will thus be:
2.5. z-Score and Statistical Validation
The transformed quantities defined in (
5) and (
6) capture the similarity (correlation) between layers in a multiplex by comparing the empirical values with the expected values under a null model (the WDCM, Equation (
15)). However, those quantities do not consider any information about the variances of the values of multiplexity and multireciprocity under the null model, thus giving no direct information about statistical significance. Given the absence of any parametric scale, it is difficult to disentangle, weak interlayer dependencies from pure noise. Put simply, if 0 signals that two layers are uncorrelated, what is the band of decimal values that are acceptable (i.e., significant) under the constraints we imposed? Moreover, the random fluctuations around the expectation values will in general differ for different pairs of layers, making our choice even more difficult and arbitrary. A way to solve this problem is to accept only those values that exceed a given number (threshold) of standard deviations of the mean value, more formally, for the multiplexity:
and for the multireciprocity:
For the explicit analytical expressions for these
z, see [
16]. The z-scores have the same signs as the corresponding quantities (see [
16] for demonstration), but in addition they allow us to test for statistical significance using, e.g., a threshold of
= 2 as in our case.
4. Discussion
Many studies focused on the worldwide increasing connection and environmental exchange [
31,
32]. The transfer of embodied emissions flows in commodity production affects the environmental system in trading area [
32,
33]. Xu et al. [
15] (2018) found that, over time, all flows between distant countries are increased more than those between adjacent countries. Furthermore, large increases in virtual resource flows also affect the financial capital flows between countries [
34]. Some empirical evidence has recently found that more financialised countries display higher correlations between outgoing financial flows and incoming environmental flows than from lower financialised countries [
14]. In
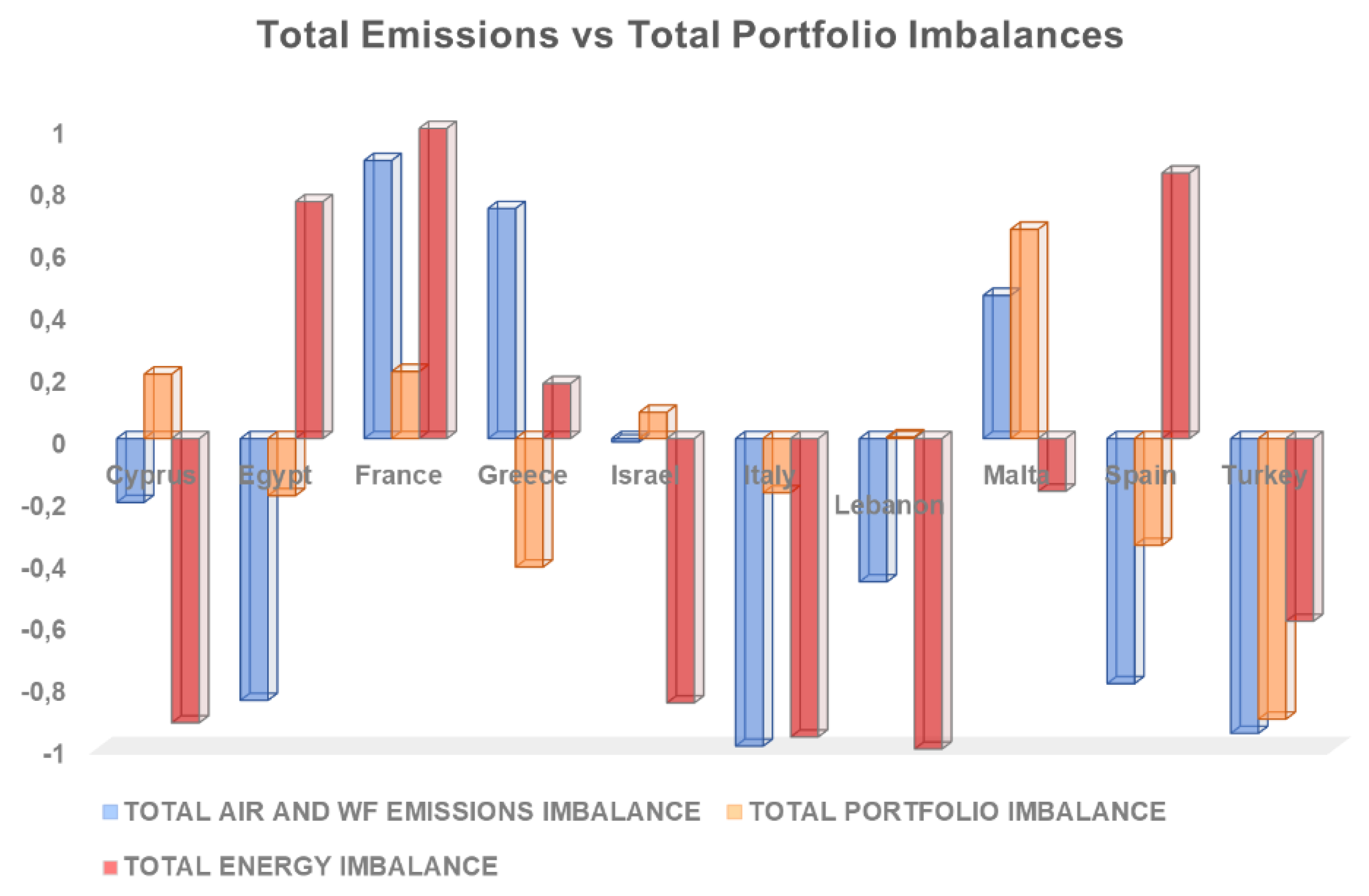
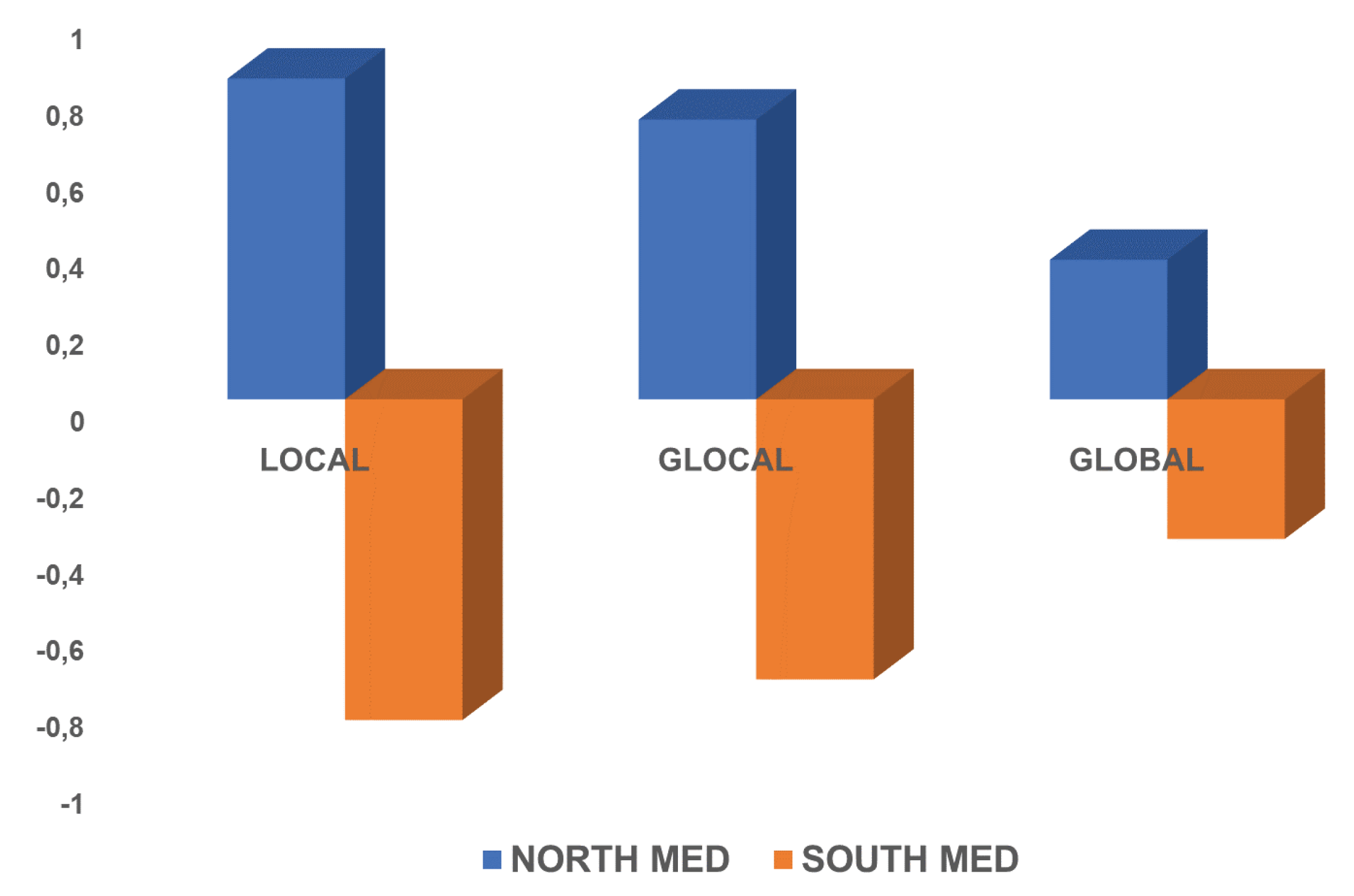
Figure 5, we show the imbalance of environmental emissions between the top 10 countries of the North and South Mediterranean areas. All of the EU countries of our sample (Cyprus, France, Greece, Italy, Malta and Spain) are classified as the North area, whereas Egypt, Israel, Lebanon and Turkey are within the South area. Interestingly, and consistent with the results in Ruzzenenti et al. [
14], data show an opposite pattern between North and South Mediterranean countries, suggesting that the former, generally more financial developed, are net exporters of energy and emissions, whereas the latter are net importers.
With regard to energy transfer, we have observed that the Mediterranean countries that are part of the EU export to other countries in our sample an average of 551,120 terajoules. The process of exporting energy from the north to the south, associated with that of financial flows, can be oriented towards boosting production in the less industrialised countries of the area. This hypothesis may be confirmed by the analysis of the flows of environmental emissions. We observe that the gap of exchange flows between the North and South Mediterranean decrease with the spatial dimension where the environmental factors are located. In more detail, the greatest imbalance affecting South Mediterranean countries refers to local impact emissions (
,
and water footprint) followed by nitrogen flows,
(i.e., glocal impact emissions) that show a strong and positive imbalance to the detriment of the same group of countries. The gap tends to be more balanced when global impact emissions (
) are considered. This is because all missions are highly connected and
represents the central node of the environmental network because all material processes generate
emissions [
35,
36,
37]. Therefore, each economy affects, and is affected, by these highly interconnected processes. This centrality also explains why
plays a crucial role in global warming.
Table 4 provides evidence about the emissions trend with regard to three typologies of environmental flows. In the last decade, data show that North Mediterranean countries have always been exporters of pollution. In contrast, South Mediterranean countries have been net importers of emissions and it has been observed for all environmental flows. Again, we found the greatest imbalance in local impact emissions whose trend has substantially been stable over the observation period.
We observe the same pattern with regards to the nitrogen emissions (glocal): differences between outgoing and incoming flows have substantially remained unchanged during the last two decades. South Med countries have steadily been importers of environmental flows, whereas Northern countries have always been net exporters. However, the gap is slightly lower compared to the local emissions. In contrast, data provide evidence of a steady increase of imported emissions by Southern countries. It is worth noting that, whereas local and glocal emissions show a reversal trend in 2015, data on suggest that North Mediterranean area have hardly increased their exports; specularly, Southern countries continue to be net importers.
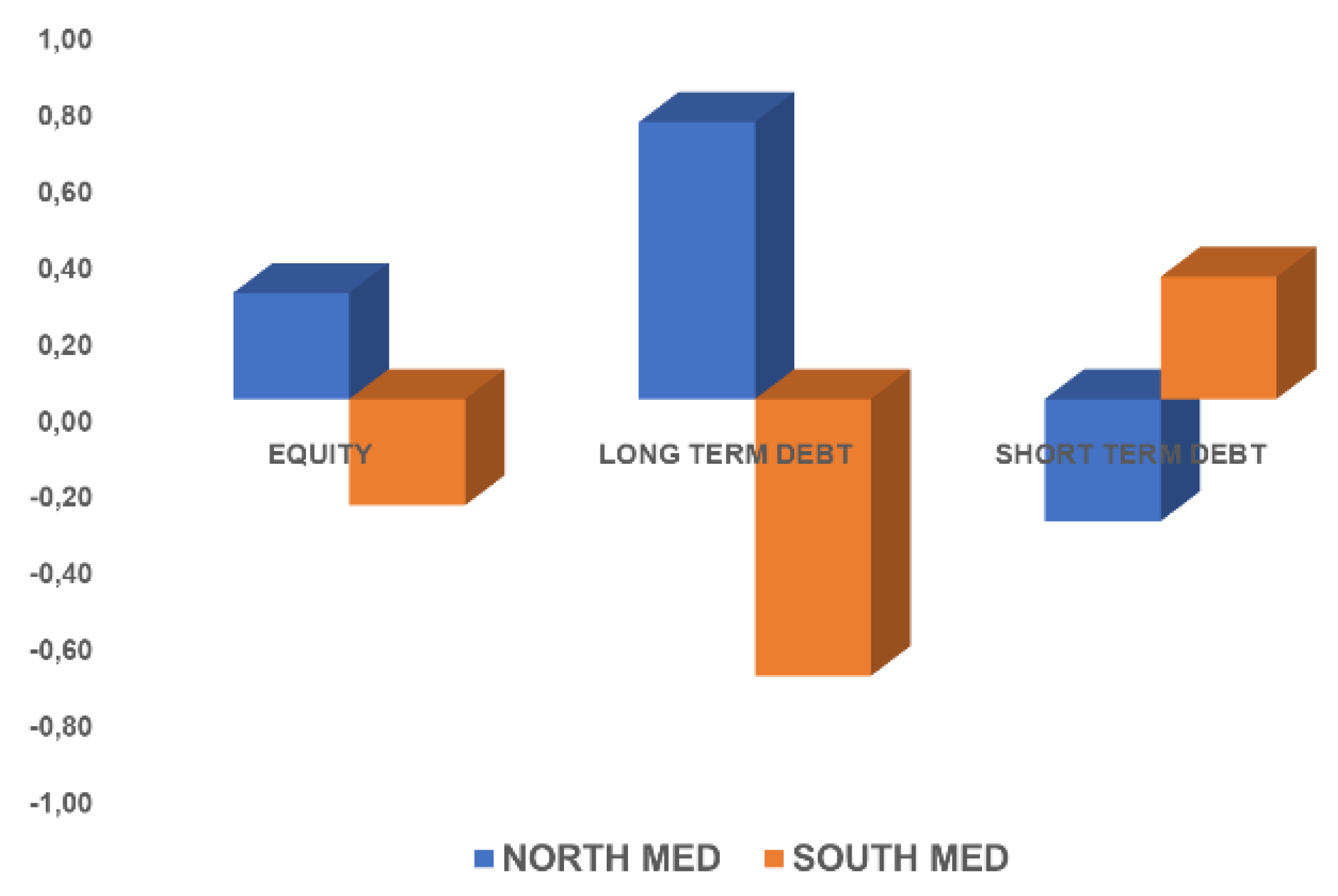
We run the same analysis for portfolio investment between the two Mediterranean macroarea.
Table 5 shows an unclear pattern of the financial flows direction. On average, North Med countries have been net exporters of equity and, more significantly, in long-term debt, whereas South Med countries have been net buyers of short term debt. The trend analysis highlights how assets of portfolio investments are characterized by different dynamic across the period. The attitude to act as importers or as exporters, although not particularly high, shows a certain variability for equity investment, whereas the graphic on long-term debt reveals that Northern and Southern Mediterranean countries are steadily net buyers and net sellers, respectively. It is worth highlighting that short-term debt, after an initial phase where both groups of countries behave both as importers and exporters, starting from 2010 shows a stable pattern with Northern as importers and Southern as exporters.
Overall, country-by-country analysis, for both financial and environmental flows, shows an uneven picture and the export of environmental emissions, by the more to less industrialized countries, does not seem confirmed. However, when the flows of incoming and outgoing countries are aggregated and the sample is split into North and South Mediterranean areas, data show a strong imbalance in environmental emissions to the detriment of the latter while a coherent pattern for financial flows is observed, where richer countries increase their equities and bond assets (
Figure 6).
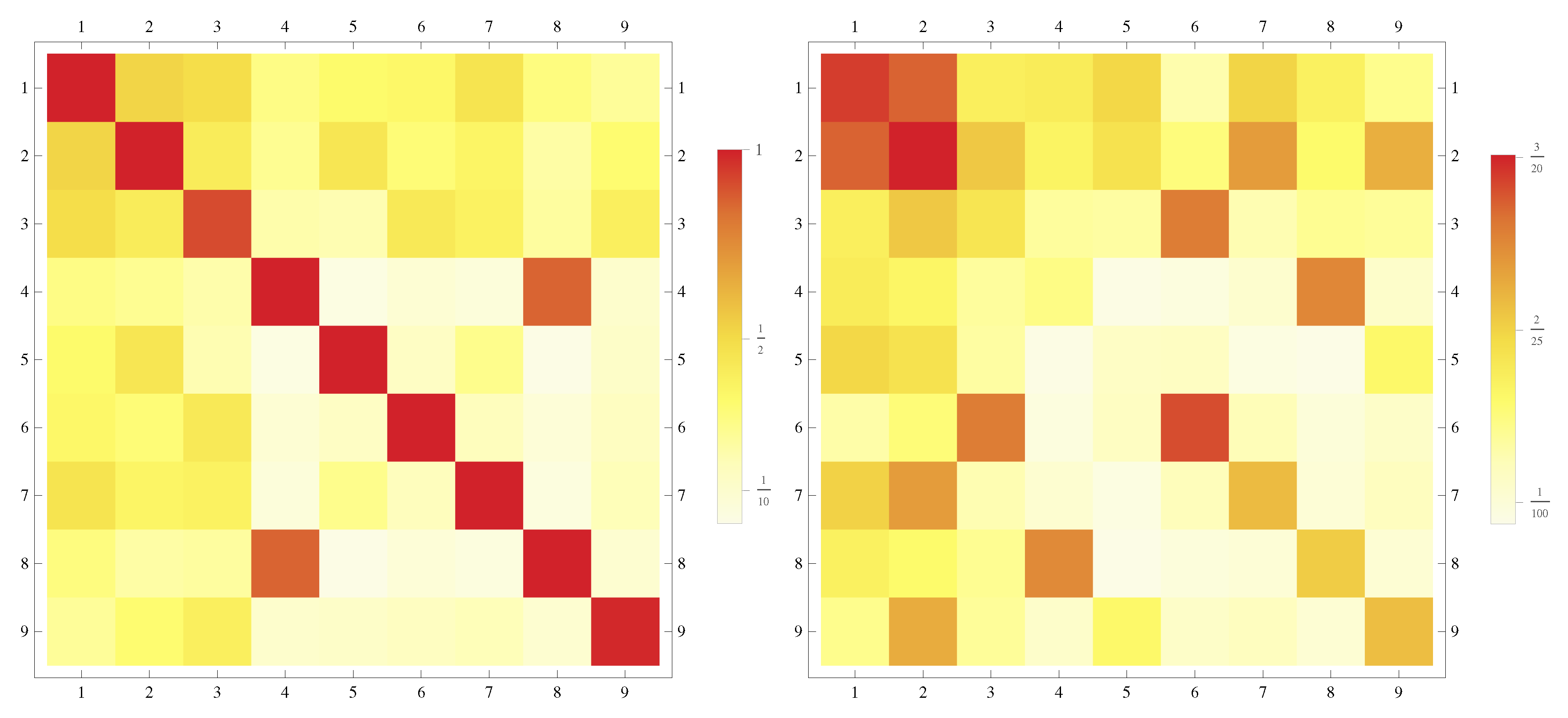
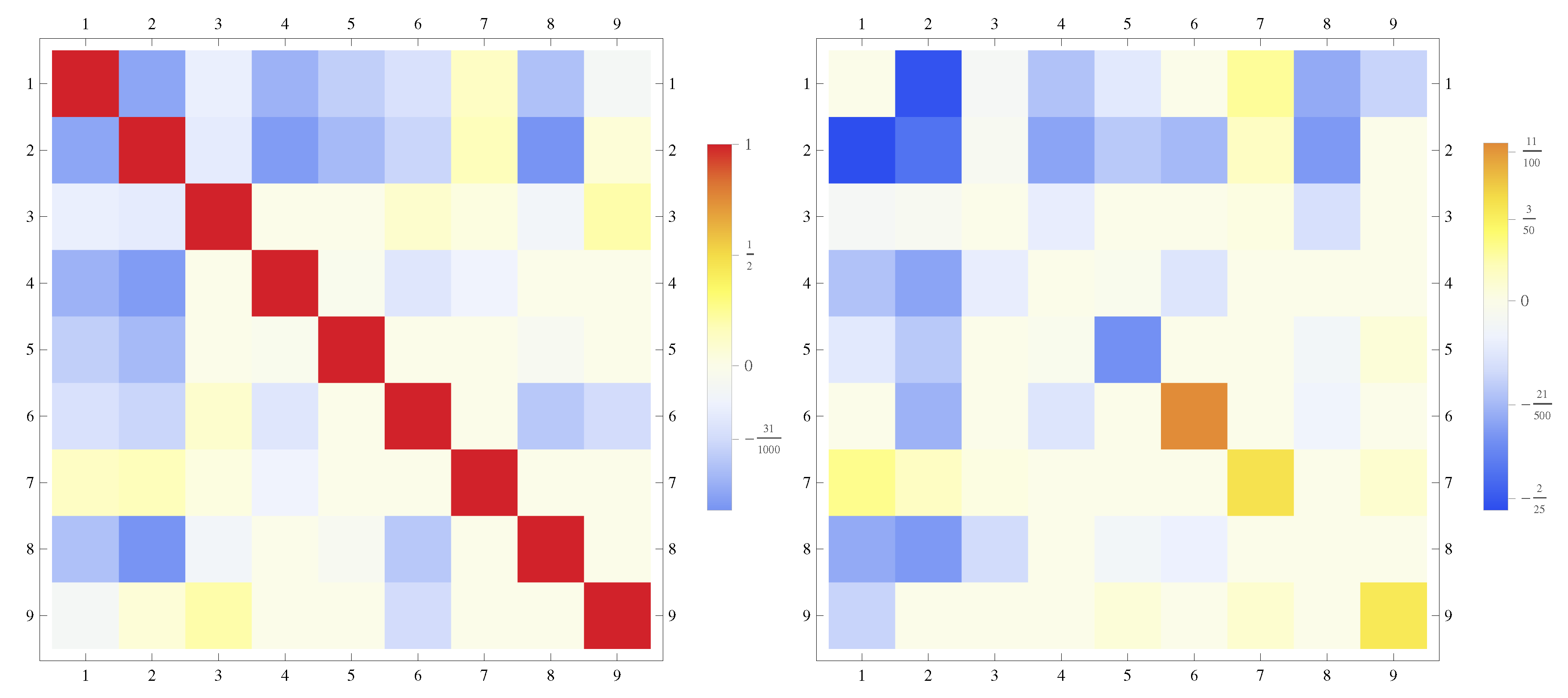
With regard to the embroilment of financial and environmental flows across the Mediterrean area, from the present analysis, no clear information emerges on the prominent role of equities in trading with environmental loads embodied in goods. These results contrasts with a previous study focusing on OECD countries [
14]. In one case, however, equity shows a significant, positive nexus with
. This is the strongest positive nexus observed, and it is more pronounced for opposite flows, suggesting that equity is exported to import coal-intensive products. The strongest negative nexus is exhibited by multiplex flows linking the long-term debt and water. As a matter of fact, water shows the strongest negative, reverse nexus with all financial layers, meaning that the more the network’s country tends to trade finance, the less trade embodied water and vice versa. Water is not exchanged for finance as coal intensive goods. It is also worth noting how environmental layers are mostly uncorrelated. Even
shows no significant correlation with energy, a result that contradicts previous studies on the global multiple virtual material flows network [
15]. On a global scale
and energy show the strongest nexus, foremost for flows in the opposite direction, with an increasing trend beginning with the 2000s. This nexus suggests that, in the world, from the beginning of the century, more and more countries began outsourcing carbon intensive energy and that this was not the case among Mediterranean countries.
5. Conclusions
The aim of this study was to identify whether financial and environmental flows have been redistributed within the main Mediterranean countries, with particular reference to pollution. Applying advanced methods of correlation and network analysis, we verify the dynamics of transfer processes for environmental flows, classified by pollution features.
Countries we have analysed show heterogeneous behaviour, both with regard to environmental and financial imbalances. However, when we focus on two macro-areas, the results confirm the hypothesis that the most financialised countries (which in our sample coincide with the countries of the north of the Mediterranean and which are part of the European Union) have carried out a process of transfer of financial, energy and environmental flows which constitutes the core of our work.
In particular, the countries of the Northern Mediterranean, typically characterized by a higher GDP, transfer financial and energy resources to the countries of the Southern Mediterranean. Capital and energy allow for increase fixed investments that produce polluting emissions. Our research has made it possible to highlight how the export component of emissions towards the south of the Mediterranean is concentrated in emissions with the greatest local impact. The result is consistent with the relationship between the surplus of the trade balance of the most industrialized countries and the method of accounting for consumption for the attribution of pollutant emissions.
This process is accompanied by a substantial increase in the financial activities of the countries of the North of the Mediterranean to the detriment of those of the South of the Mediterranean, which appear to be more indebted. Even if financial activities show a very weak, often negative, correlation with the environmental flows embodied and only in limited cases, we discover that the economic and financial development of the Nord Med go together with a growing impact on environmental sustainability measured by the various types of emissions covered by our study. After Boyce [
11], our study shows how most industrialized countries of the Mediterranean area are widening the economic and financial gap with the countries of the Southern Mediterranean.