Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China
Abstract
1. Introduction
2. Materials
2.1. Raw Materials
2.2. Preparation of Mixed Samples
2.3. Preparation of Test Samples
3. Methods
3.1. Testing Methods
3.2. Research Methods
3.2.1. Numerical Method in the Subgrade during Freeze-Thaw Cycles
3.2.2. The improved method of the specific heat capacity and thermal conductivity considering the effects of freeze-thaw cycles
3.2.3. Model Setup
4. Results and Discussion
4.1. Variations and Improved Calculation Model on Thermal Conductivity of MC and SC
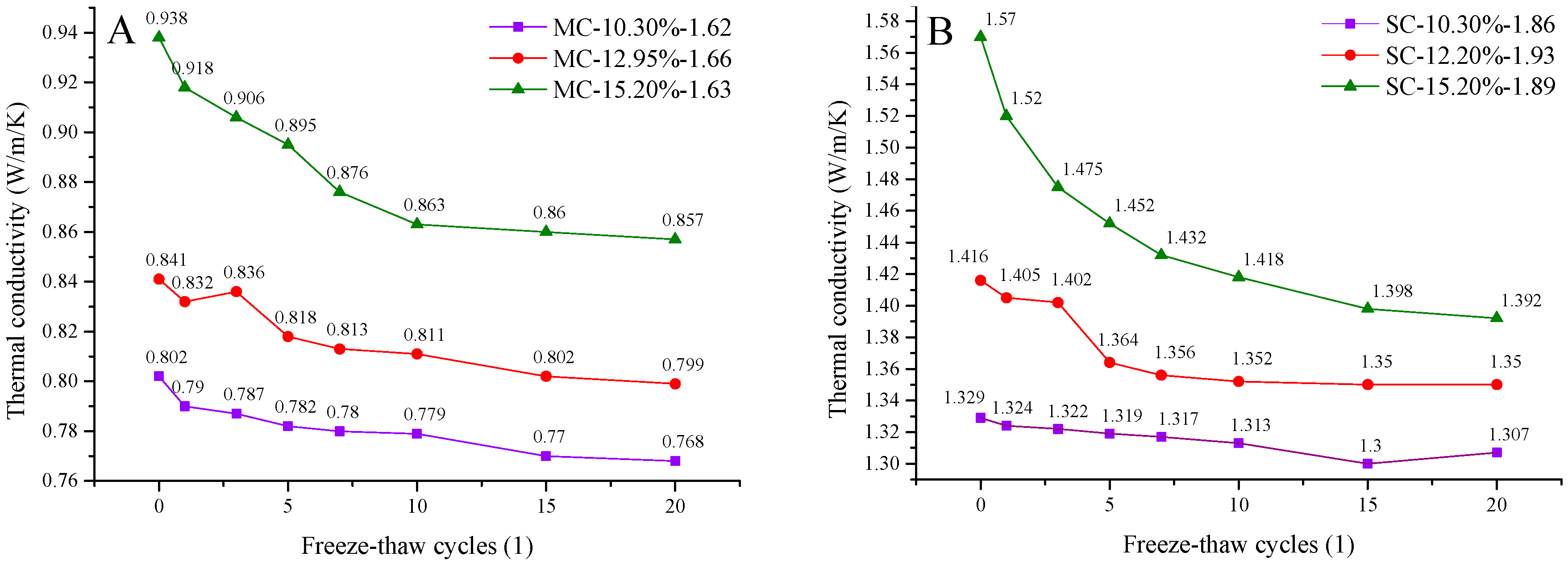
4.1.1. Variations on thermal conductivity of MC and SC
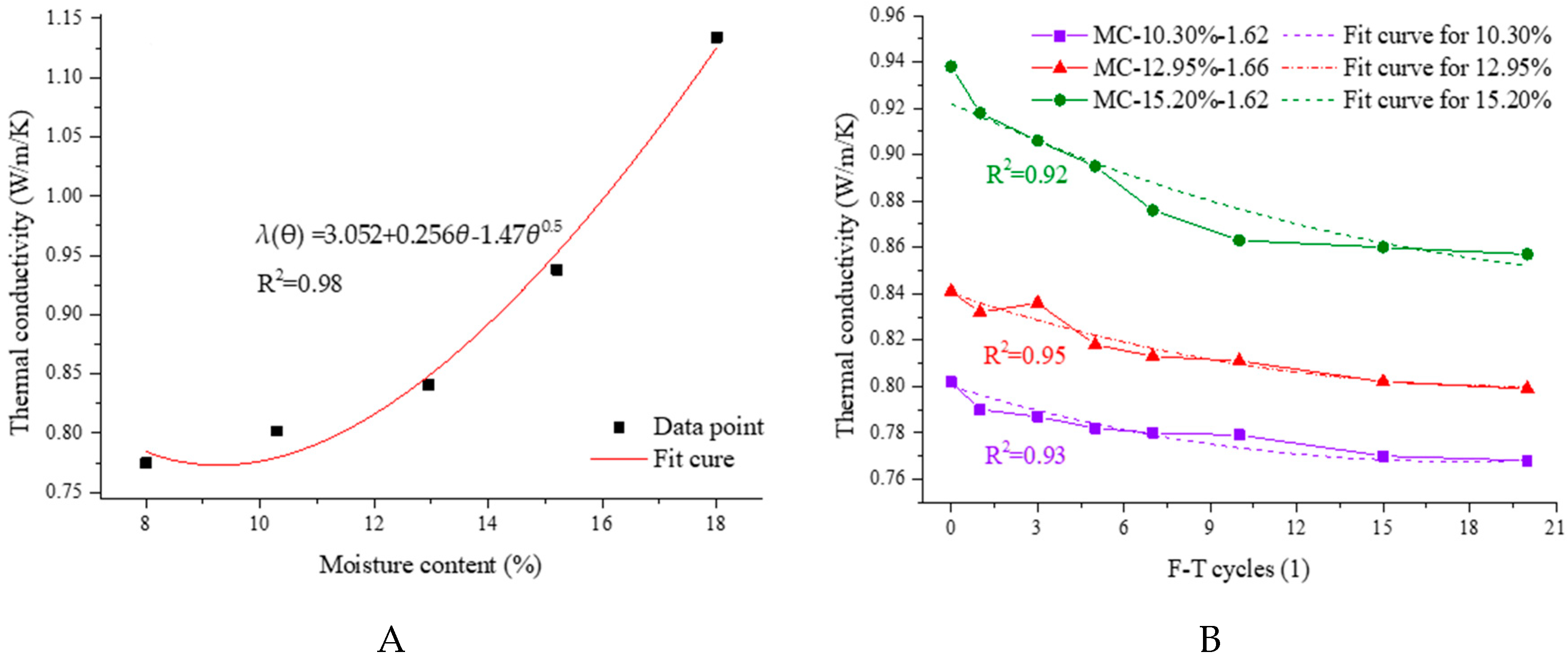
4.1.2. Improved Calculation Model on Thermal Conductivity of MC and SC
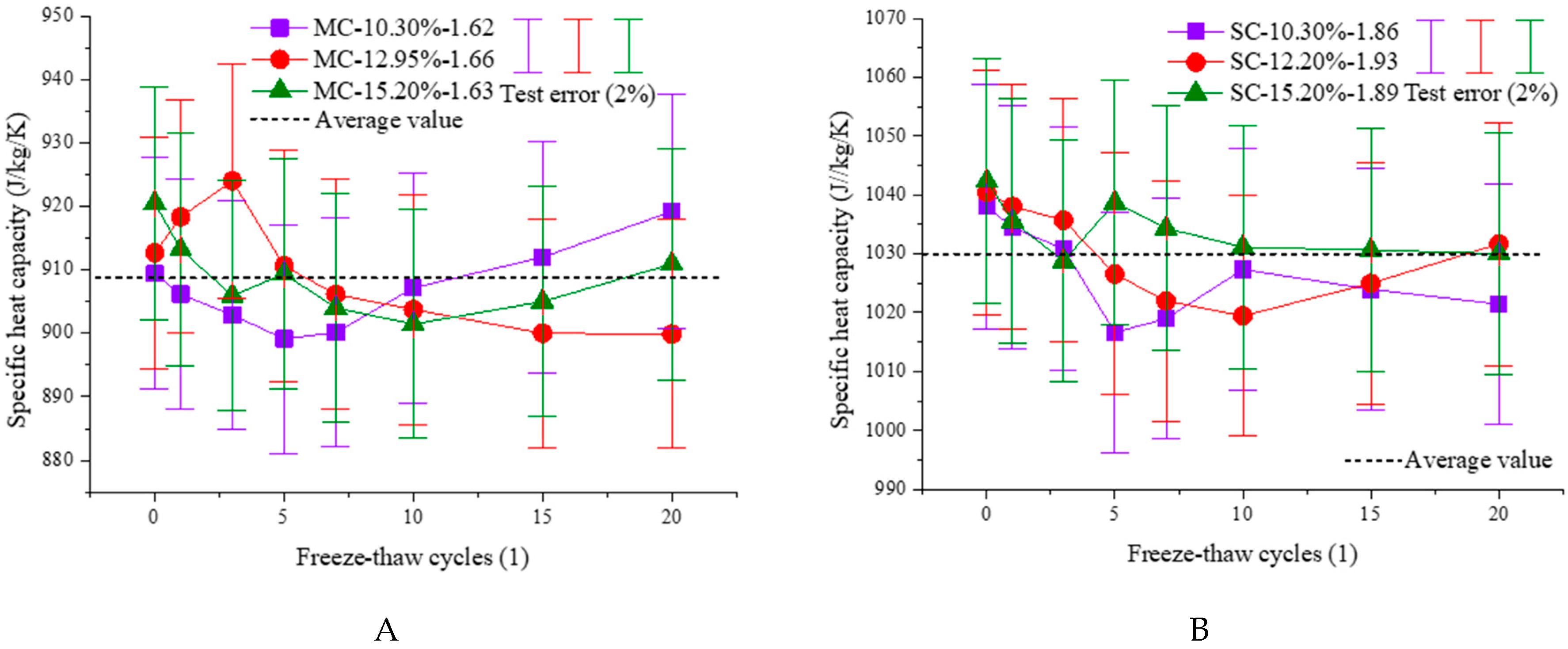
4.2. Variations on Specific Heat Capacity of MC and SC
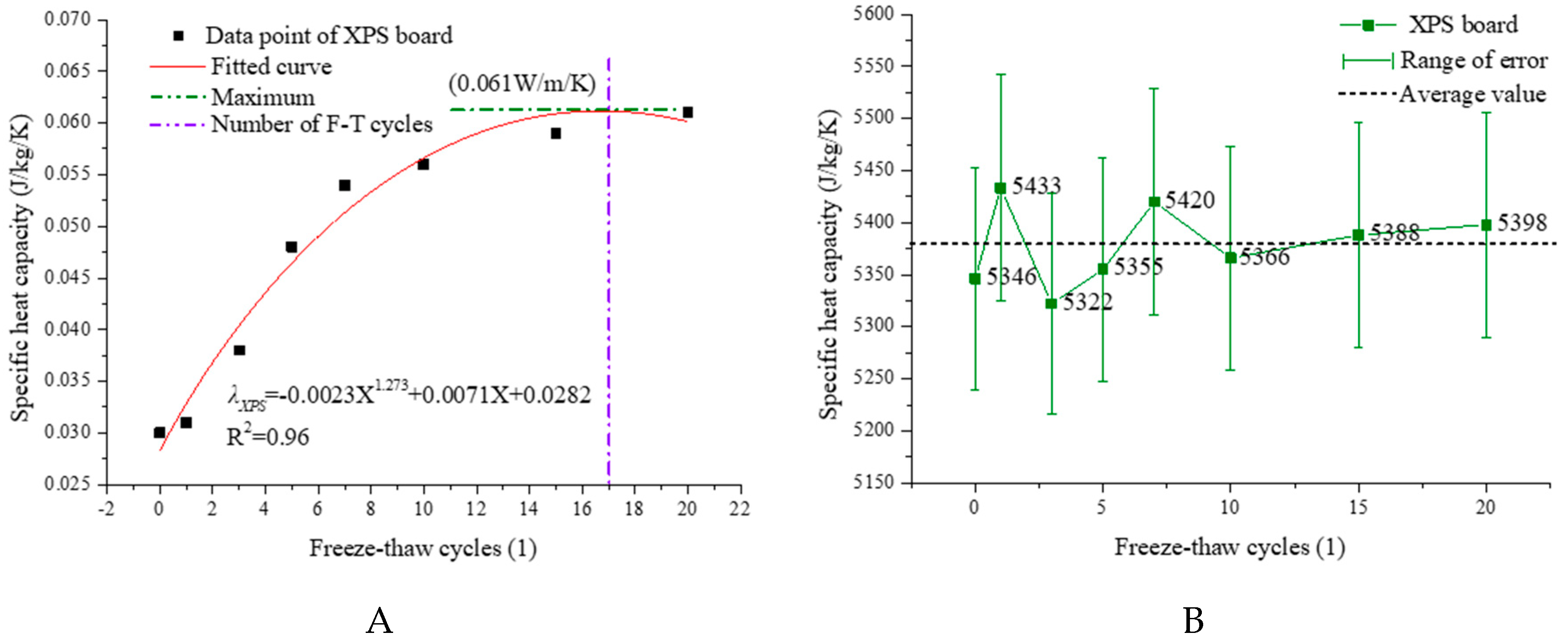
4.3. Variations on Thermal Conductivity and Specific Heat Capacity of the XPS board
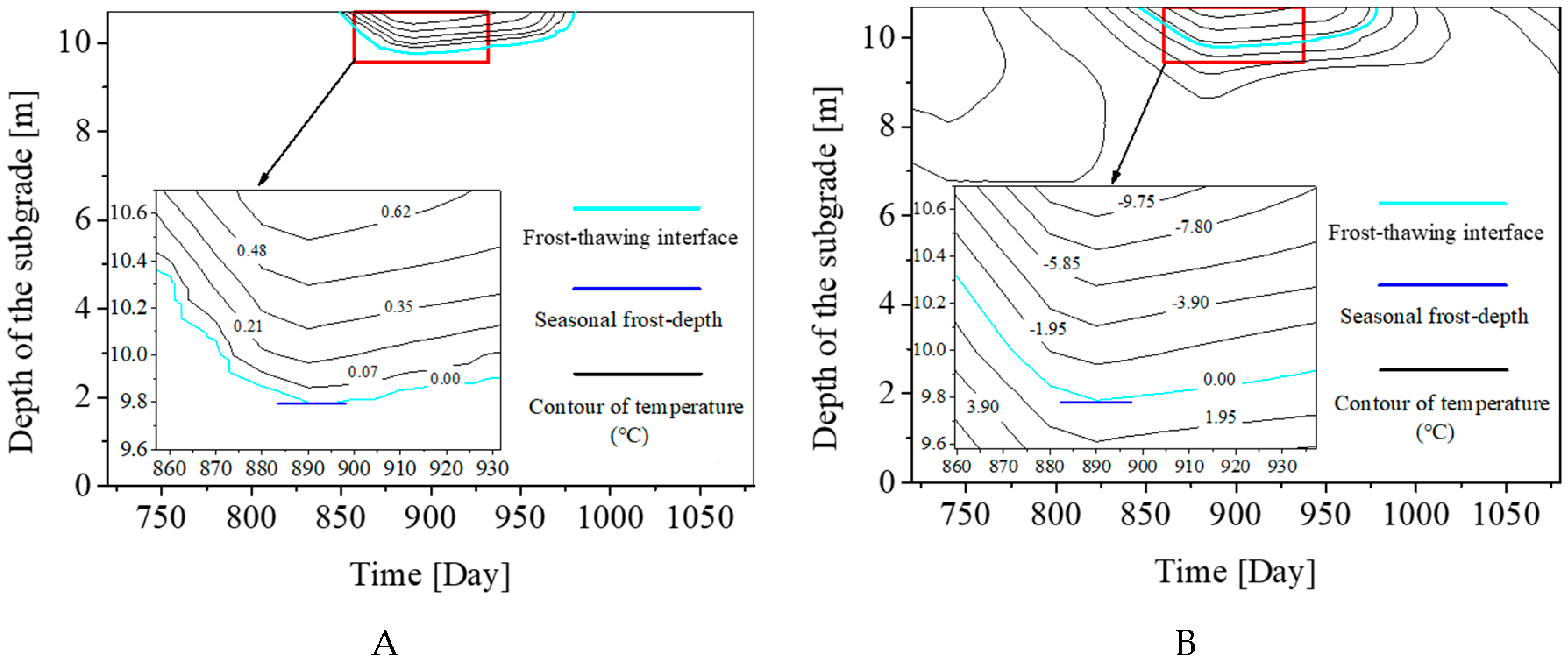
4.4. Simulation Results Considering the Effects of Freeze-Thaw Cycles on Thermophysical Properties for Structure I
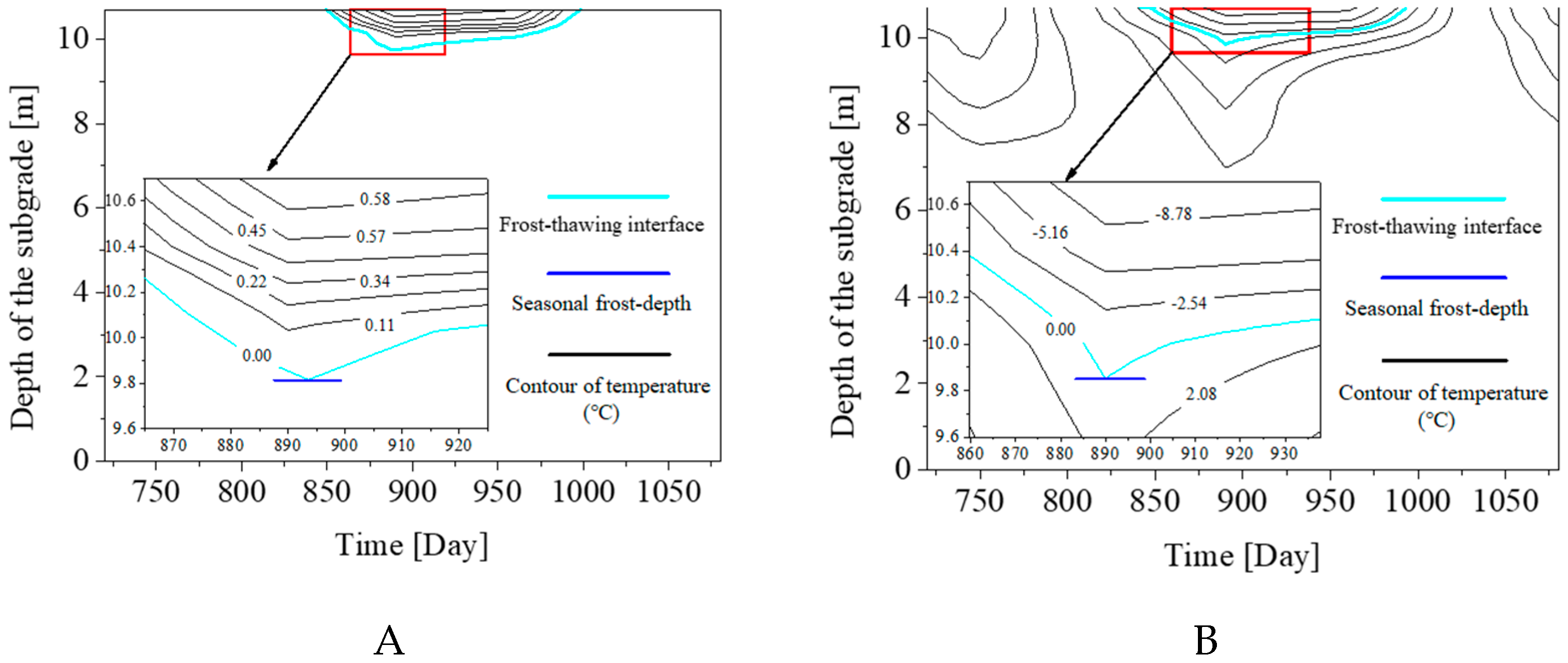
4.5. Simulation Results Considering the Effects of Freeze-Thaw Cycles on Thermophysical Properties for Structure II
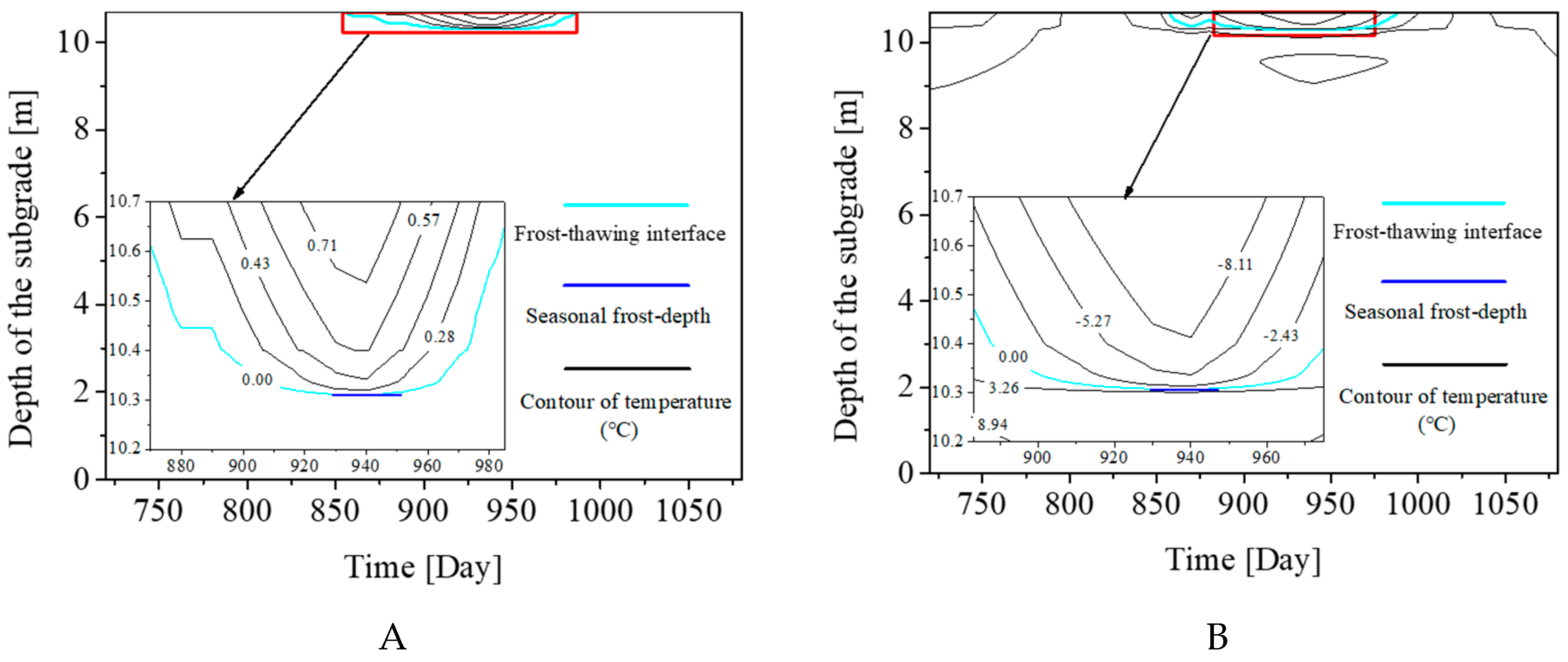
4.6. Simulation Results Considering the Effects of Freeze-Thaw Cycles on Thermophysical Properties for Structure III
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ran, Y.H.; Xin, L.; Cheng, G.D.; Zhang, T.J.; Wu, Q.B.; Jin, H.J.; Rui, J. Distribution of Permafrost in China: An Overview of Existing Permafrost Maps. Permafr. Periglac. Process. 2012, 23, 322–333. [Google Scholar] [CrossRef]
- Vaitkus, A.; Gražulytė, J.; Skrodenis, E.; Kravcovas, I. Design of frost resistant pavement structure based on road weather stations (RWSs) data. Sustainability 2016, 8, 1328. [Google Scholar] [CrossRef]
- Mahedi, M.; Cetin, B.; Cetin, K.S. Freeze-thaw performance of phase change material (PCM) incorporated pavement subgrade soil. Constr. Build. Mater. 2019, 202, 449–464. [Google Scholar] [CrossRef]
- Liu, Z.G.; Xu, F.M.; Cao, G.B. Study on cement concrete pavement treatment methods of common damage diseases. Appl. Mech. Mater. 2015, 716, 307–309. [Google Scholar] [CrossRef]
- Li, J.-P.; Sheng, Y.; Zhang, J. Study on diseases of cement concrete pavement in permafrost regions. Cold Reg. Sci. Technol. 2010, 60, 57–62. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, F.; Li, X.; Li, A.; Liu, M.; Luo, J.; Shao, Z. Characteristics and controlling factors of frost heave in high-speed railway subgrade, Northwest China. Cold Reg. Sci. Technol. 2018, 153, 33–44. [Google Scholar] [CrossRef]
- Haghi, N.T.; Nassiri, S.; Shafiee, M.H.; Bayat, A. Using field data to evaluate bottom ash as pavement insulation layer. Transp. Res. Rec. 2014, 2433, 39–47. [Google Scholar] [CrossRef]
- Nurmikolu, A.; Kolisoja, P. Extruded polystyrene (XPS) foam frost insulation boards in railway structures. In Proceedings of the International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–15 September 2005; Aa Balkema Publishers: Rotterdam, The Netherlands, 2005; p. 1761. [Google Scholar]
- Cai, D.; Yan, H.; Yao, J.; Cui, Y.; Chen, F. Engineering Test Research of XPS Insulation Structure Applied in High Speed Railway of Seasonal Frozen Soil Roadbed. Procedia Eng. 2016, 143, 1519–1526. [Google Scholar] [CrossRef][Green Version]
- Liping, Z. Study of Application of XPS Board in Frozen Subgrade Works. Master’s Thesis, University of Changan, Xi’an, China, 2009. [Google Scholar]
- Wei, H.; Zhang, Y.; Wang, F.; Che, G.; Li, Q. Experimental Research on Resilient Modulus of Silty Clay Modified by Oil Shale Ash and Fly Ash after Freeze-Thaw Cycles. Appl. Sci. 2018, 8, 1298. [Google Scholar] [CrossRef]
- Ahmaruzzaman, M. A review on the utilization of fly ash. Prog. Energy Combust. Sci. 2010, 36, 327–363. [Google Scholar] [CrossRef]
- Energy Administration of Jilin Province. The 13th Five-Year Plan for Energy Development of Jilin Province; Energy Administration of Jilin Province: Changchun, China, 2017. [Google Scholar]
- Zhang, F.-Q.; Li, W.-Q.; Guan, X.; Xu, X.-D. Application Research of Oil Shale Ash in Construction of Road. J. Jilin Inst. Archit. Civ. Eng. 2012, 2, 31–34. [Google Scholar]
- Li, Q.L.; Wei, H.B.; Han, L.L.; Wang, F.Y.; Zhang, Y.P.; Han, S.Y. Feasibility of Using Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability 2019, 11, 804. [Google Scholar] [CrossRef]
- Vallner, L.; Gavrilova, O.; Vilu, R. Environmental risks and problems of the optimal management of an oil shale semi-coke and ash landfill in Kohtla-Järve, Estonia. Sci. Total Environ. 2015, 524, 400–415. [Google Scholar] [CrossRef] [PubMed]
- Fulekar, M.H.; Dave, J.M. Disposal of fly ash—An environmental problem. Int. J. Environ. Stud. 1986, 26, 191–215. [Google Scholar] [CrossRef]
- Turner, J.P. Soil Stabilization Using Oil-Shale Solid Waste. J. Geotech. Eng. 1994, 120, 646–660. [Google Scholar] [CrossRef]
- Dahale, P.P.; Nagarnaik, P.B.; Gajbhiye, A.R. Utilization of Solid Waste for Soil Stabilization: A Review. Electron. J. Geotech. Eng. 2012, 17, 2443–2461. [Google Scholar]
- Horpibulsuk, S.; Phetchuay, C.; Chinkulkijniwat, A.; Cholaphatsorn, A. Strength development in silty clay stabilized with calcium carbide residue and fly ash. Soils Found. 2013, 53, 477–486. [Google Scholar] [CrossRef]
- Mir, B.A. Physical and Compaction Behaviour of Clay Soil–Fly Ash Mixtures. Geotech. Geol. Eng. 2013, 31, 1059–1072. [Google Scholar] [CrossRef]
- Mymrin, V.A.; Ponte, H.A. Oil-shale fly ash utilization as independent binder of natural clayey soils for road and airfield base construction. Part. Sci. Technol. 2005, 23, 99–107. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Cui, J.; Han, L.; Li, Z. Engineering and environmental evaluation of silty clay modified by waste fly ash and oil shale ash as a road subgrade material. Constr. Build. Mater. 2019, 196, 204–213. [Google Scholar] [CrossRef]
- Cui, J.H. Research on Stability of Subgrade Soil Modified by Oil Shale Waste Residue and Fly Ash; Jilin University: Chang Chun, China, 2018. [Google Scholar]
- MOT China. Specifications for Design of Highway Subgrades (JTG D30-2015); China Communications Press: Beijing, China, 2015; p. 7. [Google Scholar]
- MOT China. Test Methods of Soils for Highway Engineering (JTG E40-2007); China Communications Press: Beijing, China, 2007; p. 3. [Google Scholar]
- Simonsen, E.; Janoo, V.C.; Isacsson, U. Resilient properties of unbound road materials during seasonal frost conditions. J. Cold Reg. Eng. 2002, 16, 28–50. [Google Scholar] [CrossRef]
- Othman, M.A.; Benson, C.H. Effect of freeze-thaw on the hydraulic conductivity of three compacted clays from Wisconsin. Transp. Res. Rec. 1992, 1369, 118–225. [Google Scholar]
- Cassel, D.K.; Nielsen, D.R.; Biggar, J.W. Soil-Water Movement in Response to Imposed Temperature Gradients1. Soil Sci. Soc. Am. J. 1969, 33, 493–500. [Google Scholar] [CrossRef]
- Zi, W.Y.; Yan, J.Z.; Ping, G. Analysis of Impact of Moisture Content on Rock Thermal Conductivity Coefficient Using TCS Method. Adv. Mater. Res. 2015, 1095, 429–432. [Google Scholar]
- Slack, G.A. Thermal conductivity of ice. Phys. Rev. B 1980, 22, 3065–3071. [Google Scholar] [CrossRef]
- Dickinson, H.C.; Osborne, N.S. The specific heat and heat of fusion of ice. J. Frankl. Inst. 1915, 179, 489–491. [Google Scholar] [CrossRef][Green Version]
- Angell, C.; Sichina, W.; Oguni, M. Heat capacity of water at extremes of supercooling and superheating. J. Phys. Chem. 1982, 86, 998–1002. [Google Scholar] [CrossRef]
- Fei, Y.; Saxena, S. An equation for the heat capacity of solids. Geochim. Cosmochim. Acta 1987, 51, 251–254. [Google Scholar] [CrossRef]
- Sang-Ok, C.; Horton, R. Soil heat and water flow with a partial surface mulch. Water Resour. Res. 1987, 23, 2175–2186. [Google Scholar]
- El-Nabouch, R.; Bui, Q.-B.; Perrotin, P.; Plé, O. Shear parameters of rammed earth material: Results from different approaches. Adv. Mater. Sci. Eng. 2018, 2018, 8214604. [Google Scholar] [CrossRef]
- Nguyen, D.M.; Grillet, A.-C.; Bui, Q.-B.; Diep, T.M.H.; Woloszyn, M. Building bio-insulation materials based on bamboo powder and bio-binders. Constr. Build. Mater. 2018, 186, 686–698. [Google Scholar] [CrossRef]
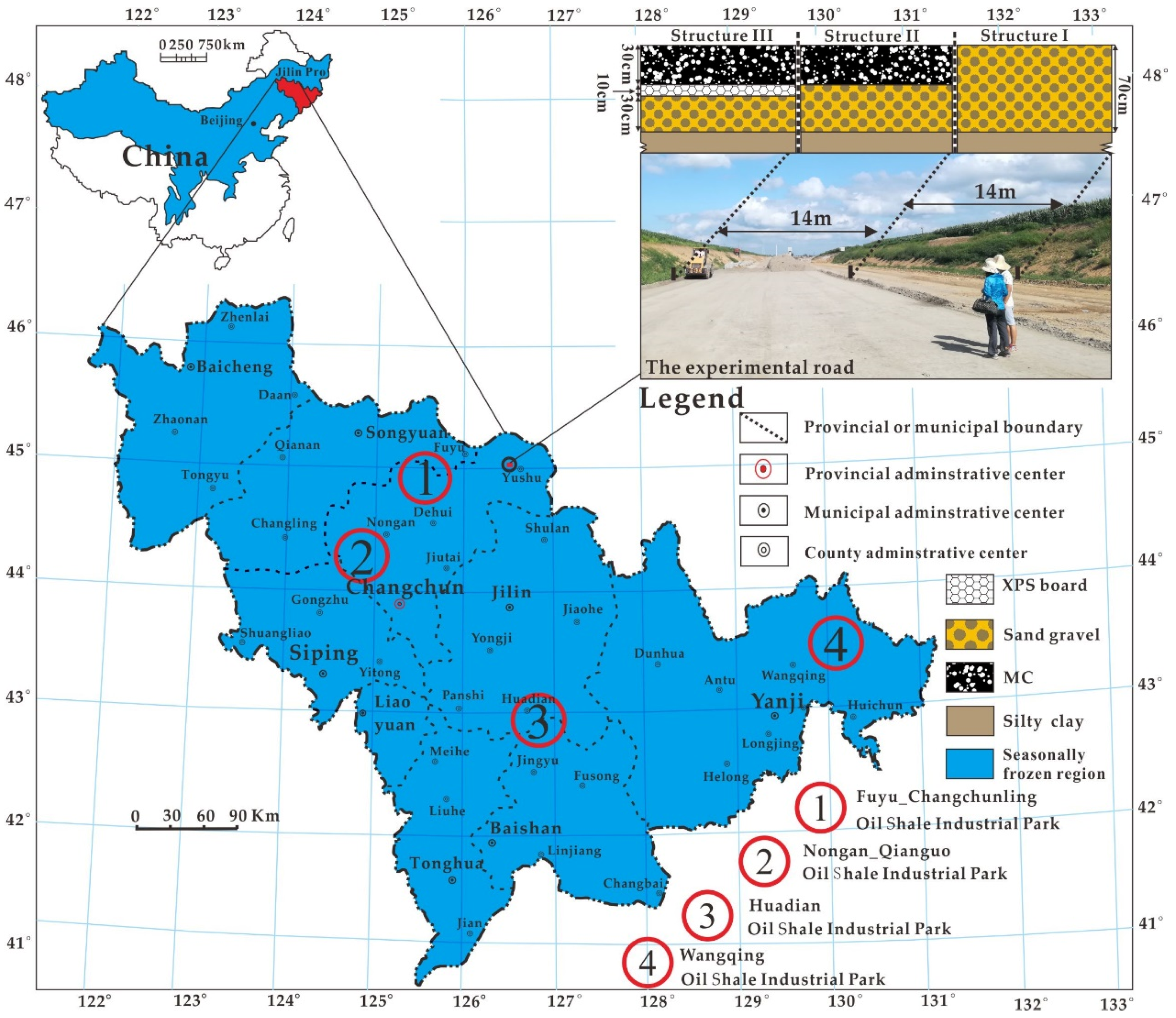

| Samples | Moisture (%) | Dry Density (g/cm3) | Number of F-T Cycle (1) | Samples | Moisture (%) | Dry Density (g/cm3) | Number of F-T Cycle (1) |
|---|---|---|---|---|---|---|---|
| MC | 8.00 | 1.59 | 0 | SC | 8.00 | 1.79 | 0 |
| 10.30 | 1.62 | 0, 3, 5, 10, 20 | 10.30 | 1.86 | 0, 3, 5, 10, 20 | ||
| 12.95 | 1.66 | 12.20 | 1.93 | ||||
| 15.20 | 1.63 | 15.20 | 1.89 | ||||
| 18.00 | 1.62 | 0, 20 | 18.00 | 1.85 | 0, 20 |
| Symbol | Units | Function | R2 | Reference | |
|---|---|---|---|---|---|
| Specific heat capacity | (Water) | J·kg−1 K−1 | 1020 + 30.637 × − 0.0627 × (274 ≤ ≤ 295 K) | 0.91 | Angell et al. [33] |
| (Ice) | 183.24 + 6.9712 × (100 ≤ ≤ 273 K) | 0.99 | Dickinson et al. [32] |
| Water Content w [%] | Permeability k [m2] | Density [kg m−3] | Specific Heat [J kg−1 K−1] | Thermal Conductivity [W m−1 K−1] | |
|---|---|---|---|---|---|
| MC | 15.6 | 6.5 × 10−14 | 1520 | ||
| XPS board | 0.3 | 1.0 × 10−19 | 45 | ||
| SC | 23.6 | 5.5 × 10−14 | 1640 | ||
| Sand Gravel | 16.0 | 5.5 × 10−12 | 1800 | 840 | 1.06 |
| Water | / | / | 980 | in Table 2 | in Table 2 |
| Ice | / | / | 917 | in Table 2 | in Table 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wei, H.; Zhou, P.; Zhang, Y.; Han, L.; Han, S. Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability 2019, 11, 3495. https://doi.org/10.3390/su11133495
Li Q, Wei H, Zhou P, Zhang Y, Han L, Han S. Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability. 2019; 11(13):3495. https://doi.org/10.3390/su11133495
Chicago/Turabian StyleLi, Qinglin, Haibin Wei, Peilei Zhou, Yangpeng Zhang, Leilei Han, and Shuanye Han. 2019. "Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China" Sustainability 11, no. 13: 3495. https://doi.org/10.3390/su11133495
APA StyleLi, Q., Wei, H., Zhou, P., Zhang, Y., Han, L., & Han, S. (2019). Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability, 11(13), 3495. https://doi.org/10.3390/su11133495





