Loss-Driven Adversarial Ensemble Deep Learning for On-Line Time Series Analysis
Abstract
:1. Introduction
2. Related Work
2.1. Ensemble Deep Learning
2.2. On-Line Learning
3. Proposed Method
3.1. Loss-Driven Adversarial Ensemble Deep Learning
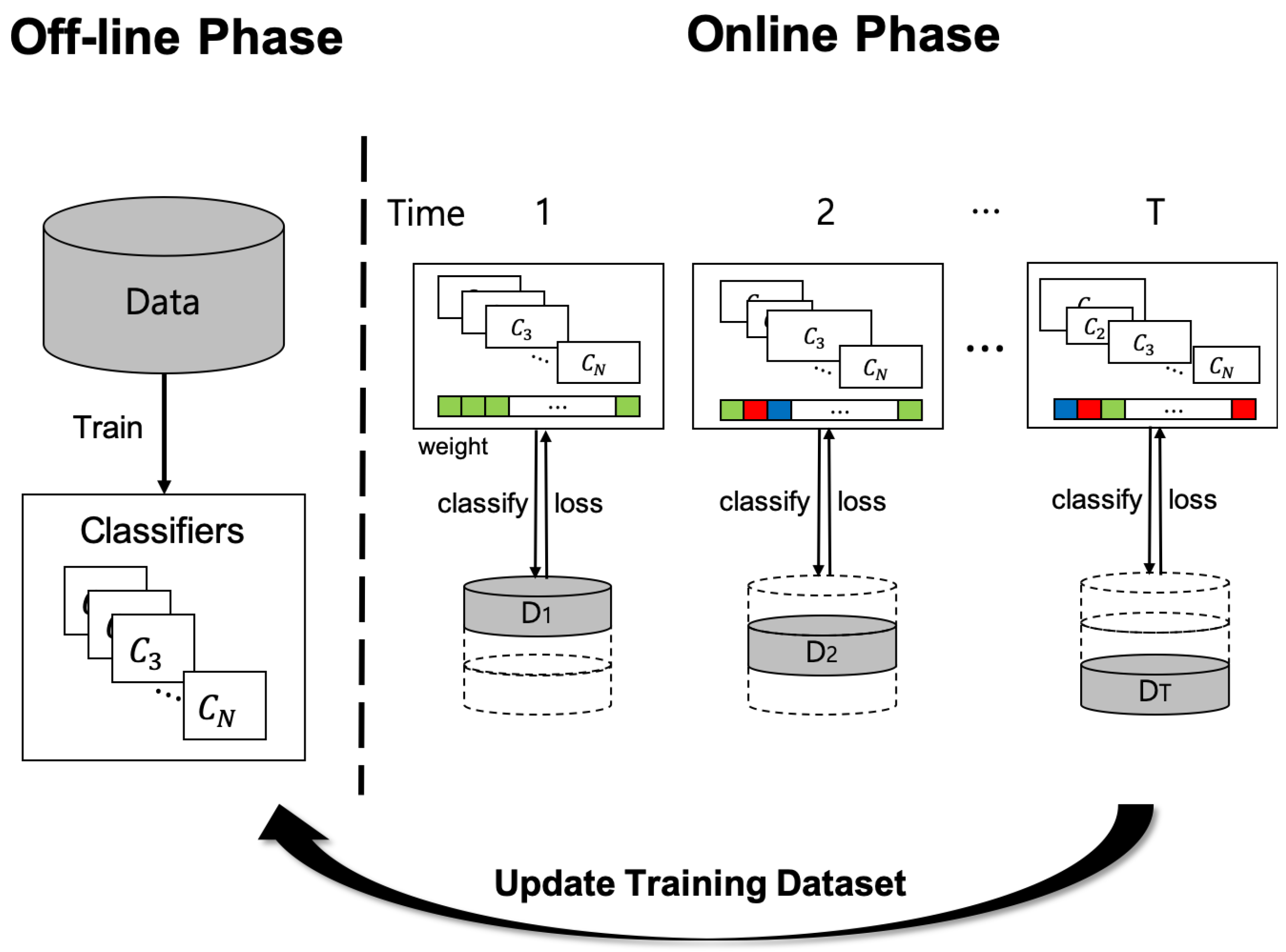
3.2. On-Line Time Series Analysis
4. Experiment
4.1. Experimental Design
4.2. Simulated Time Series Data
4.2.1. Data Description
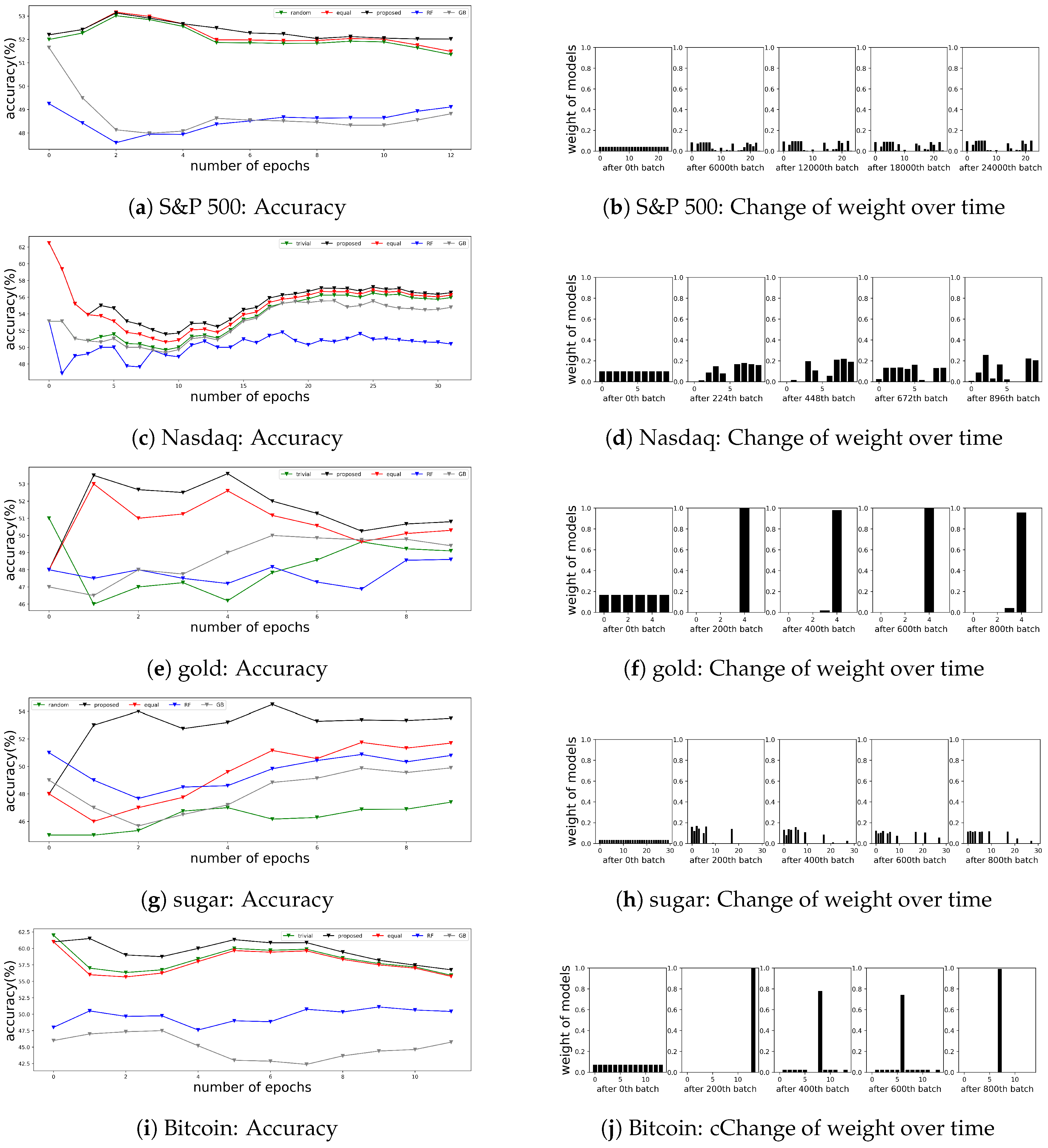
4.2.2. Results
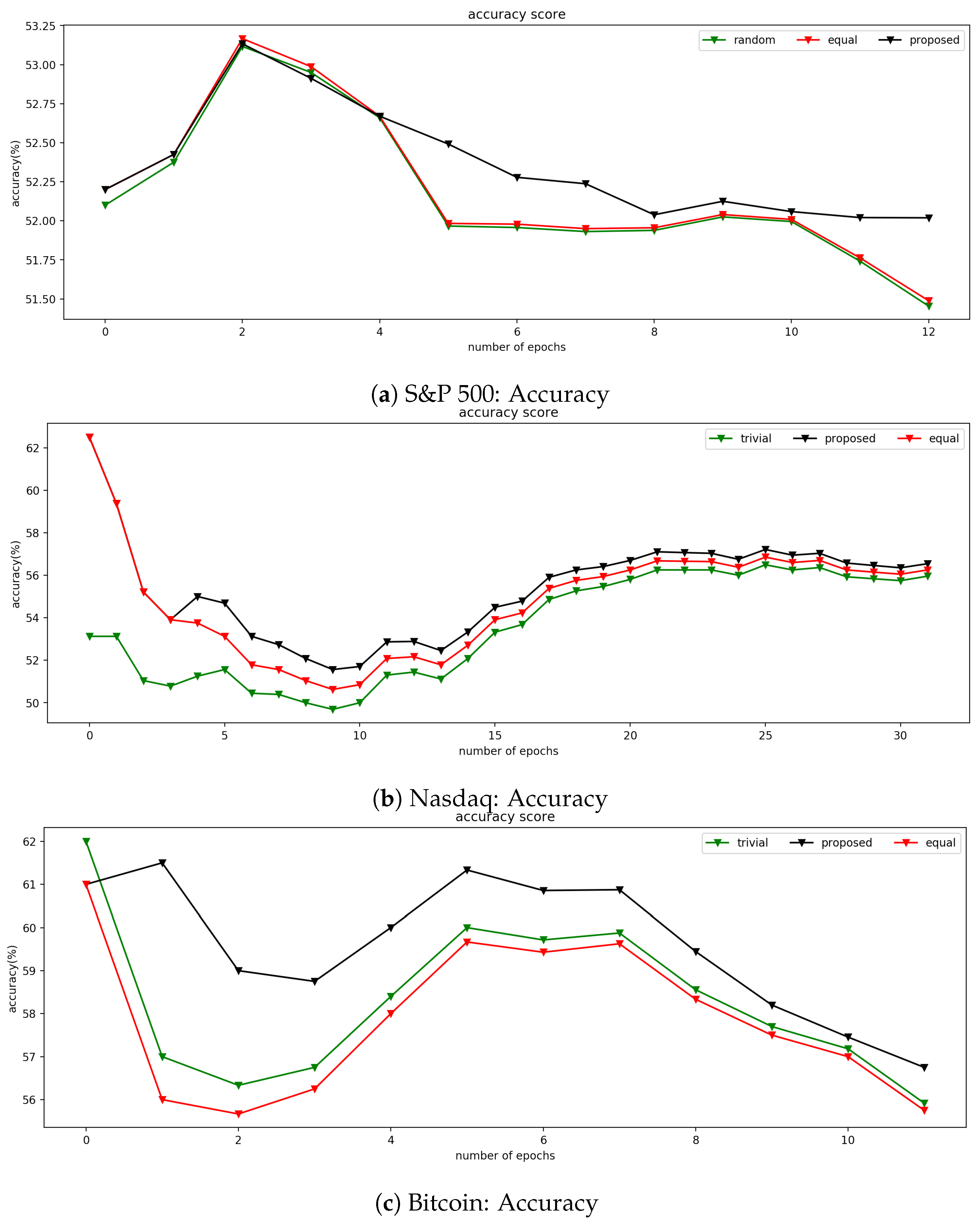
4.3. Financial Time Series Applications
4.3.1. Data Description
4.3.2. Results
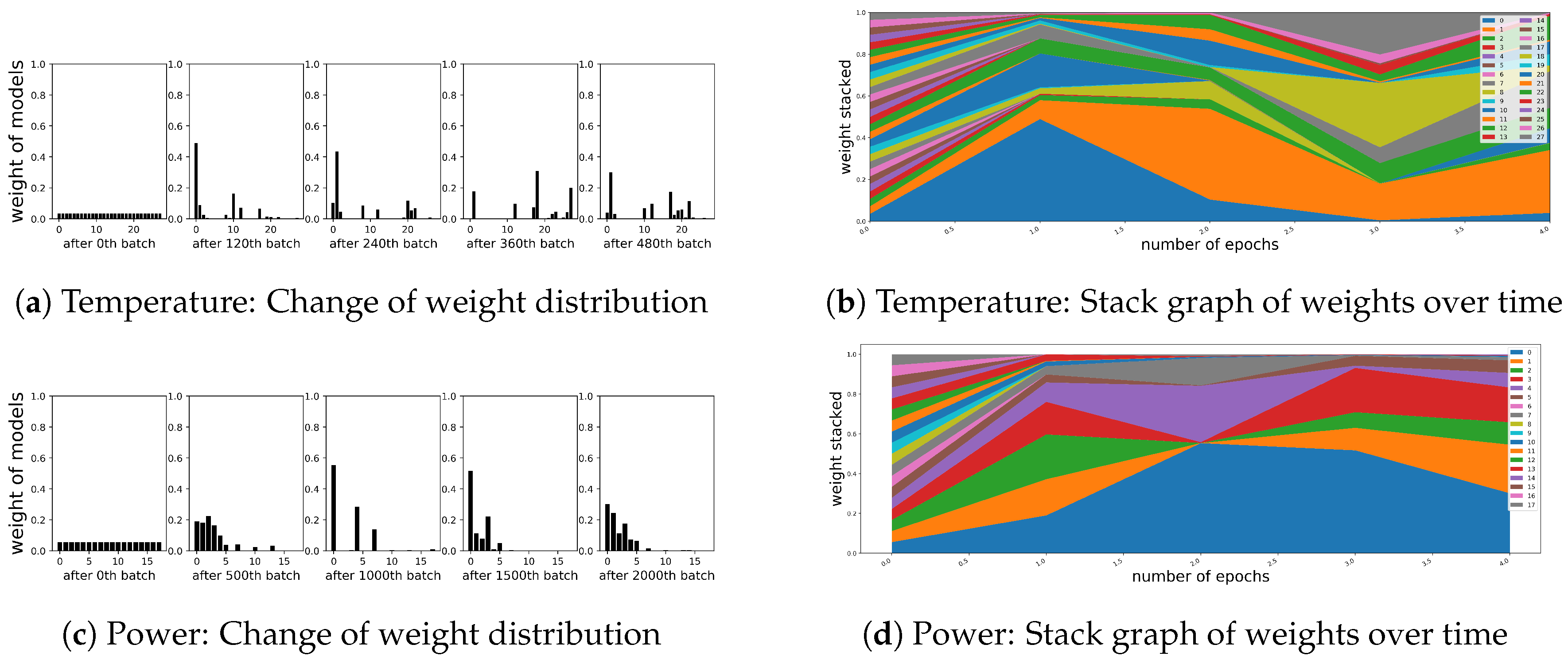
4.4. Non-Financial Time Series Applications
4.4.1. Data Description
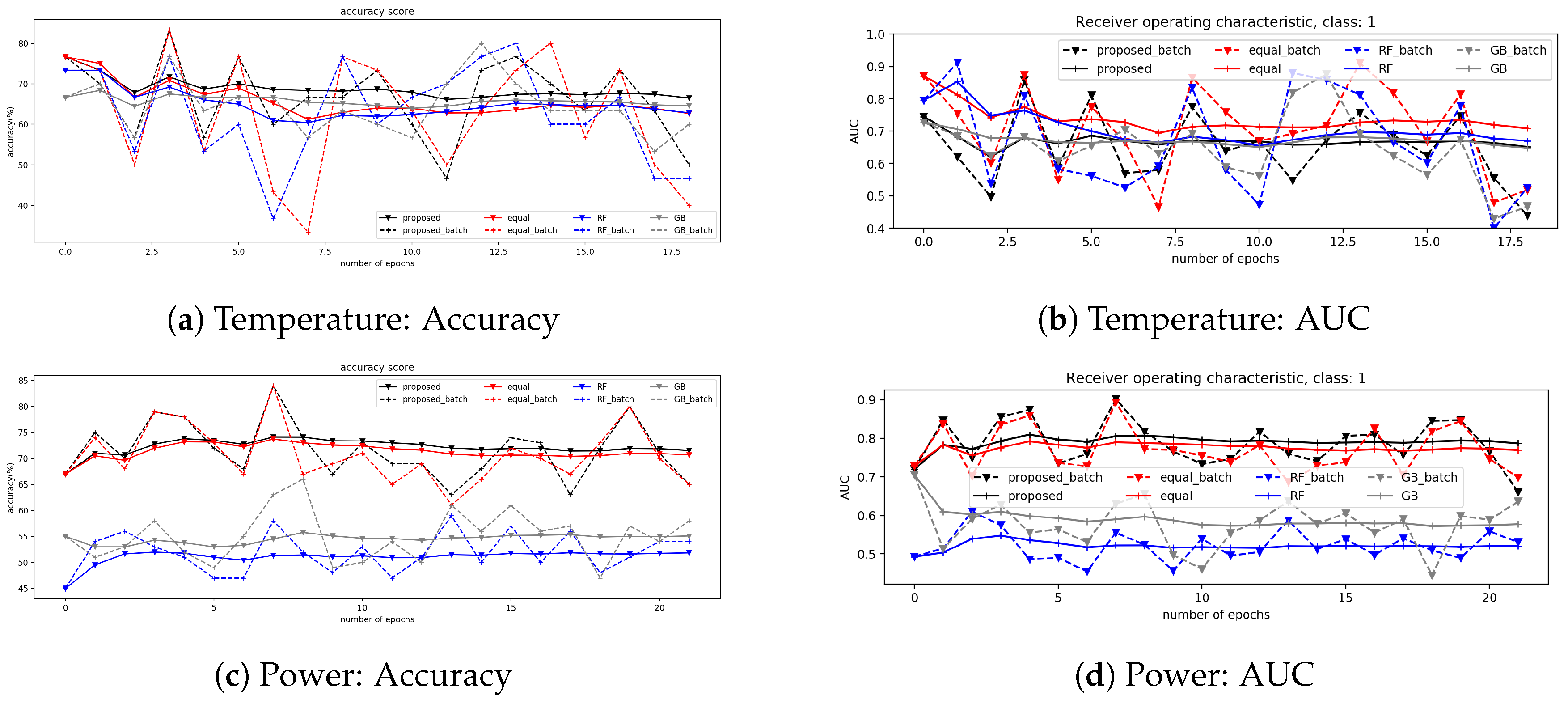
4.4.2. Results
5. Discussion
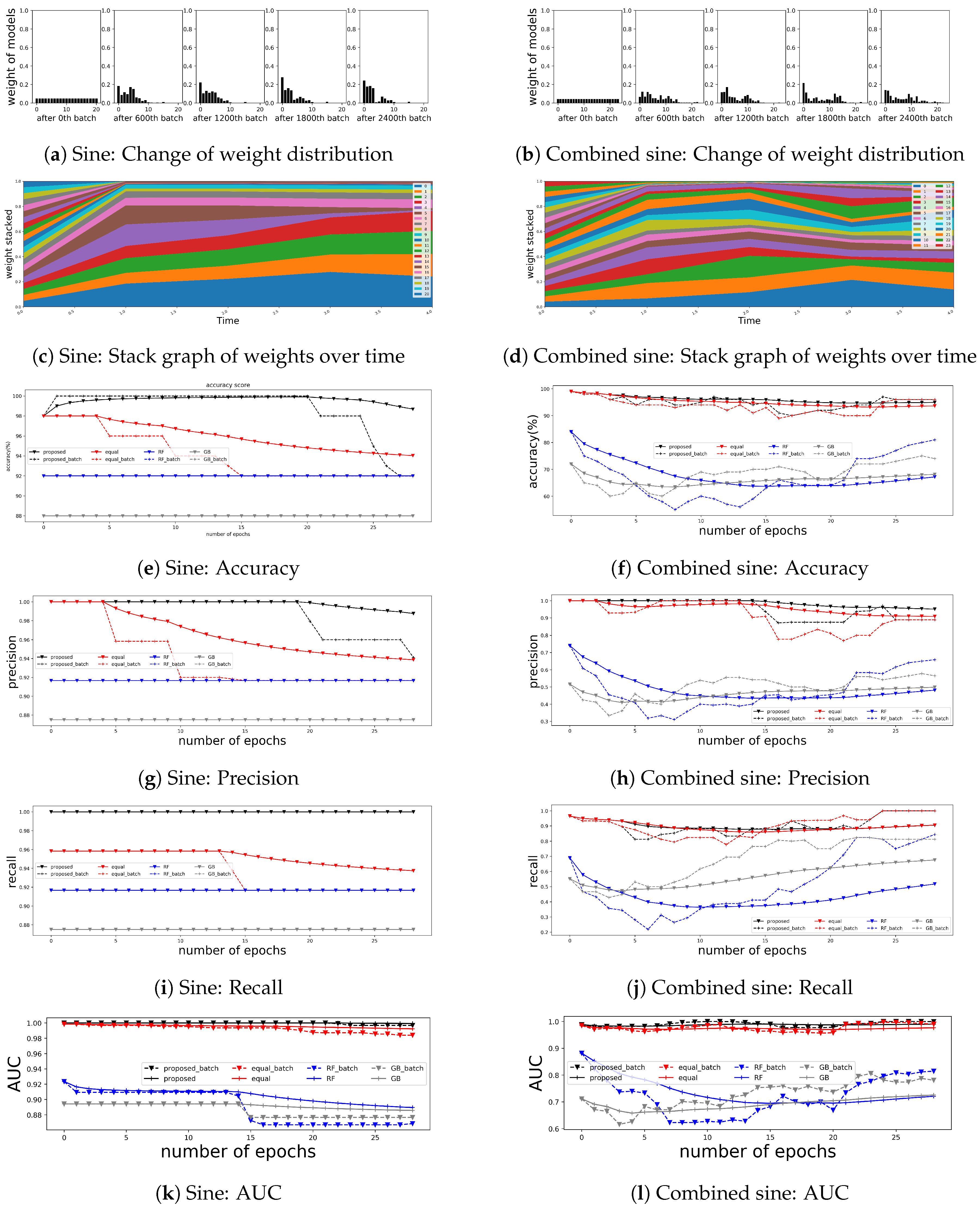
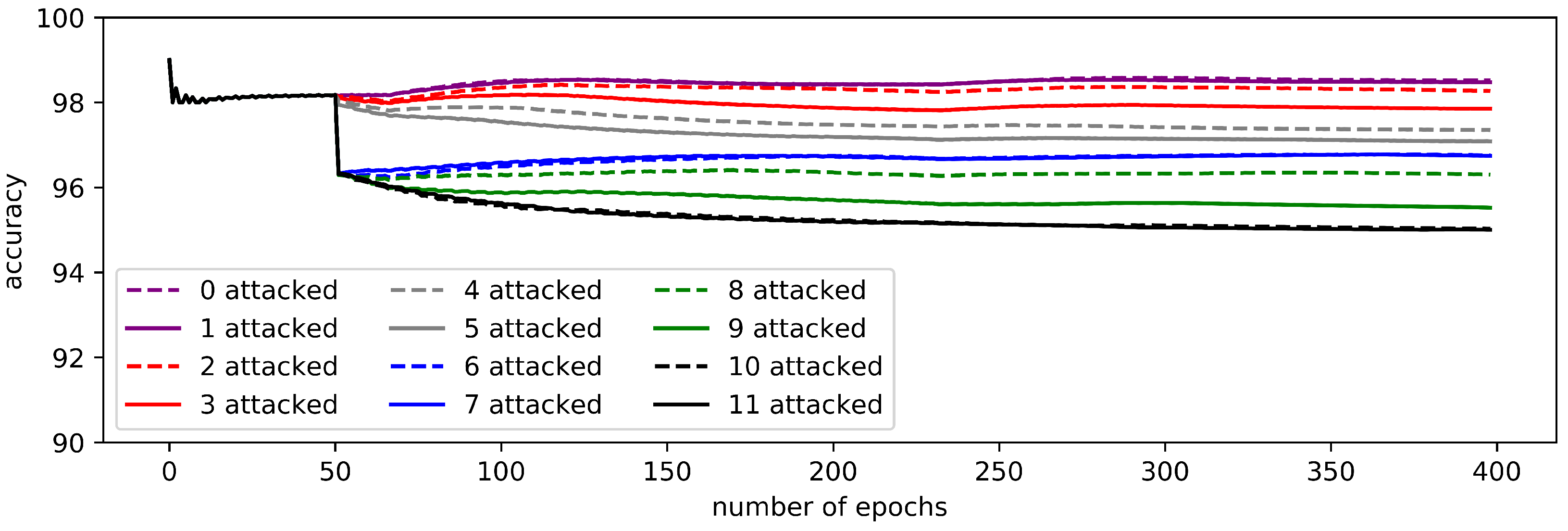
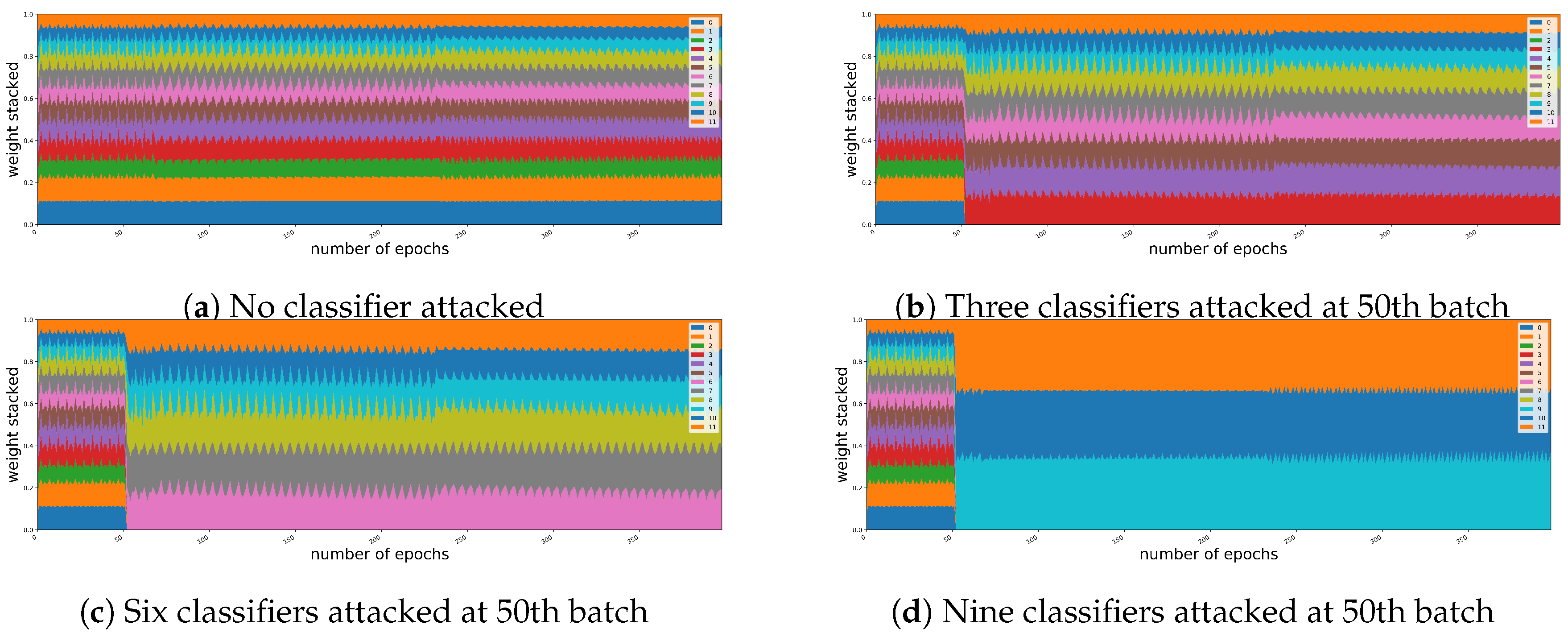
5.1. Robustness for the Intentional Attacks
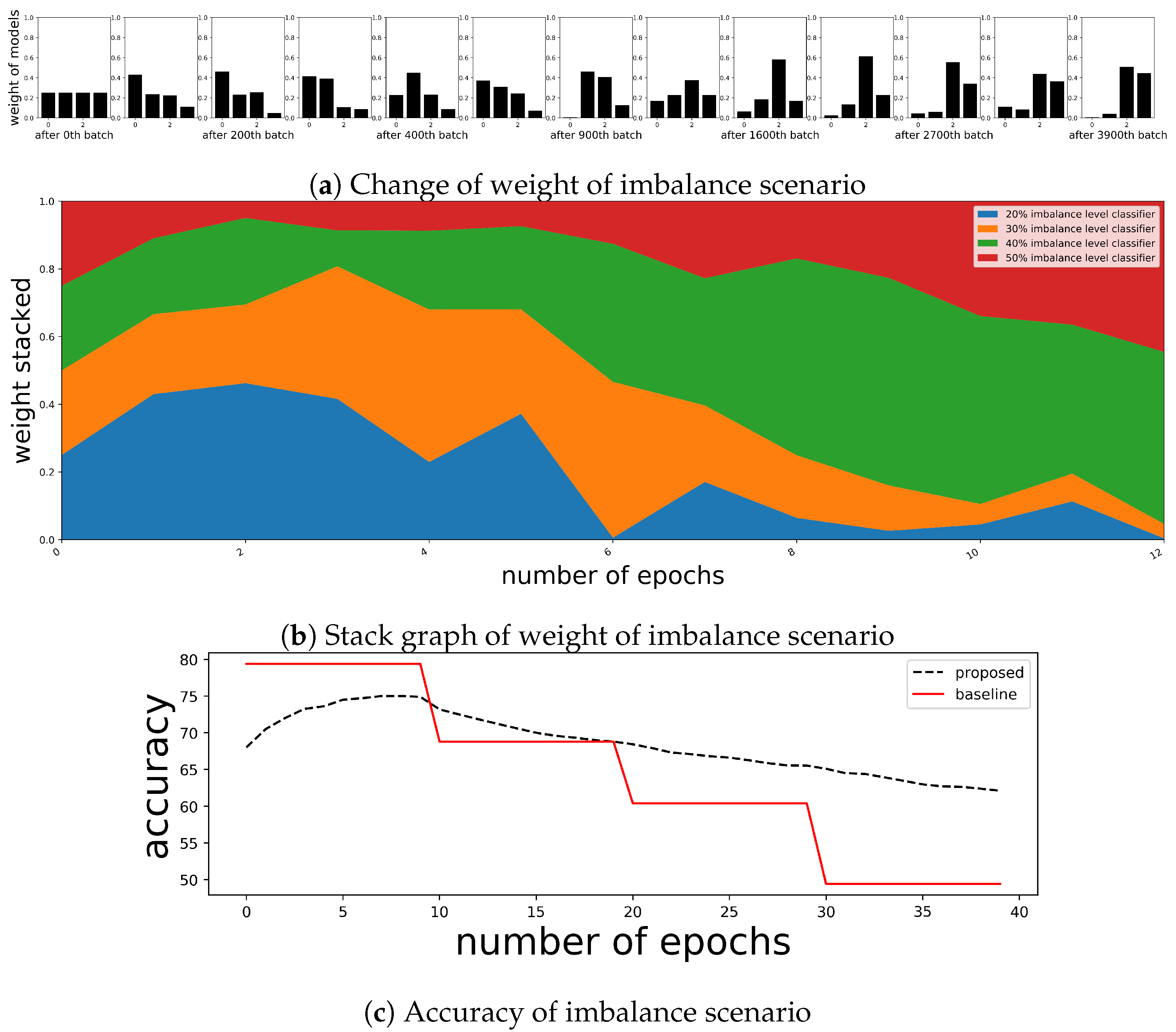
5.2. Sustainability for the Change of Target Distribution
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Predictive Variables
| Data | Predictors |
|---|---|
| S&P 500, gold, sugar | Open price, Low price, High price, Close price, Volume, RDP (−5), MA (5), MA (10), EMA (5), OSCP, EOSCP, DISP (5), EDISP (5) |
| Nasdaq | OBV, MA (5), BIAS (6), PSY (12), ASY (5), ASY (4), ASY (3), ASY (2), ASY (1) |
| cryptocurrency— Bitcoin | Crude oil, SSE, Gold, VIX, FTSE100,USD/CNY, USD/JPY, USD/CHF, Historical value of target variable, Trading volume, Average block size, Median confirmation time, Hash rate, Miners revenue, Cost per transaction, Confirmed transactions per day, The number of transaction excluding popular addresses |
| Savings bank data | Total credit, Total credit growth rate, Loan growth rate, Allowance for loan losses, Total subordinated loans to total loans, Allowance for bad debts to subordinated loans, Net non-performing loans ratio, Overdue ratio, Petty overdue ratio, Non-performing loans, Loan deposit ratio, Net loans to total assets, Net loans against liquid liabilities, Available funds ratio, Operating expenses to operating income, Operating return on assets, Current account ratio, BIS capital adequacy ratio, Net loan-to-equity, BIS simple capital adequacy ratio, Tangible common equity ratio, Total investment efficiency, Labor income share, Total asset growth rate, Tangible asset growth rate, Net income growth rate, Equity capital growth rate, Total net income, Return on assets, Return on equity, Interest coverage ratio, Capital ratio, Debt ratio, Liquidity ratio, Quick ratio, Payables dependency, Total assets, Debt repayment coefficient |
| Temperature | High temperature, Average temperature, Low temperature, Highest wind speed gust, High dew point, Low visibility, High wind speed, Average wind speed, Low sea level pressure, High visibility, Average visibility, Average dew point, Low dew point, High humidity, High sea level pressure, Low humidity, Average sea level pressure, Average humidity |
| Variables | Description | Formula |
|---|---|---|
| RDP () | Relative difference prices between k times before and now in percentage. | |
| MA (k) | Moving average of k times. | |
| EMA (k) | Exponential moving of k times. | where |
| DISP (k) | k-time disparity: the relative difference in percentage between k-time moving average and the current price. | |
| EDISP (k) | ]@c@k-time disparity with exponential moving average and the current price. | |
| OSCP | Price oscillator: the relative difference between 5-time moving average and 10-time moving average. | |
| EOSCP | Price oscillator with exponential moving average: the difference between 5-time exponential moving average and 10-time exponential moving average. | |
| RSI (k) | Relative strength index for k-times | where is 1 if there is upward-price change at time t and is 0 otherwise, and is 1 if there is downward -price change at time t and is 0 otherwise. |
| Variables | Description | Formula |
|---|---|---|
| OBV | On Balance Volume. is volume at time t | |
| Moving average of 5 times. | ||
| is close price at time t | ||
| The ratio of the number of rising periods over the n day. A is the number of rising days in the last n days. | ||
| The average return in the last 5 days. is log return | ||
| The average return in the last 4 days. | ||
| The average return in the last 3 days. | ||
| The average return in the last 2 days. | ||
| The average return in the last 1 days. |
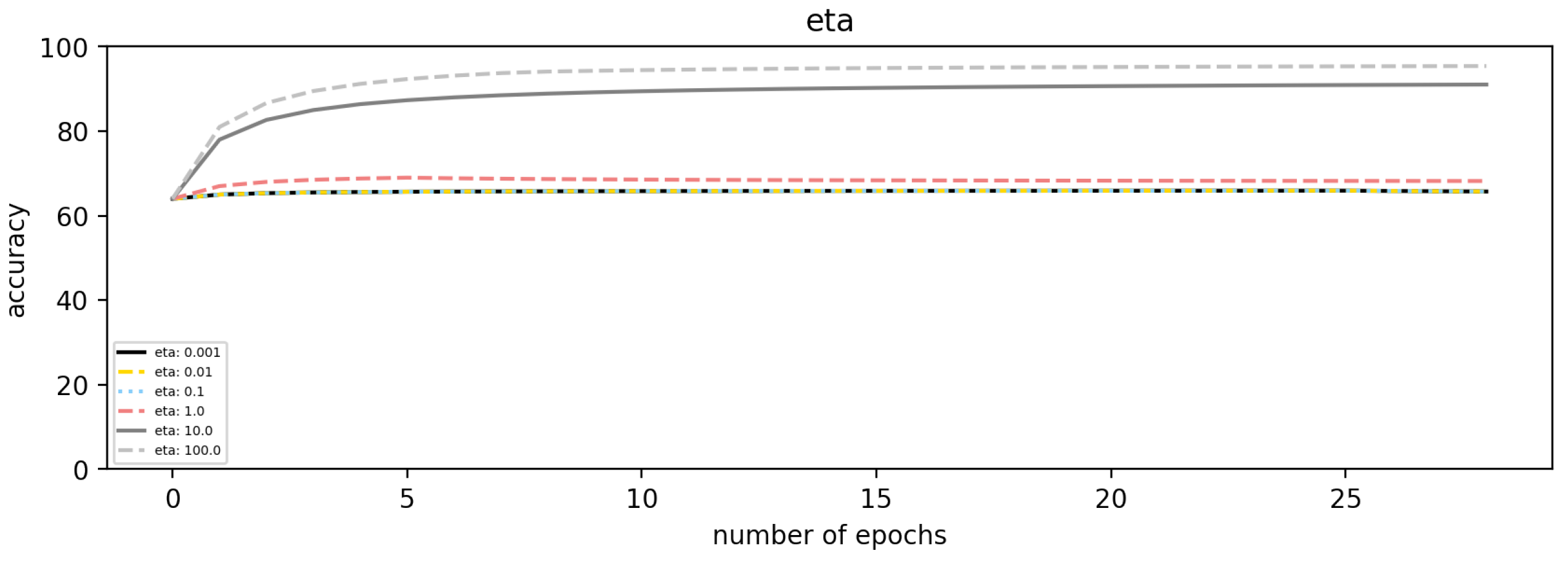
Appendix B. Additional Figures
References
- Ju, C.; Bibaut, A.; van der Laan, M. The relative performance of ensemble methods with deep convolutional neural networks for image classification. J. Appl. Stat. 2018, 45, 2800–2818. [Google Scholar] [CrossRef]
- Cruz, R.M.; Sabourin, R.; Cavalcanti, G.D. Dynamic classifier selection: Recent advances and perspectives. Inf. Fusion 2018, 41, 195–216. [Google Scholar] [CrossRef]
- Krawczyk, B.; Cano, A. Online ensemble learning with abstaining classifiers for drifting and noisy data streams. Appl. Soft Comput. 2018, 68, 677–692. [Google Scholar] [CrossRef]
- Krawczyk, B.; Minku, L.L.; Gama, J.; Stefanowski, J.; Woźniak, M. Ensemble learning for data stream analysis: A survey. Inf. Fusion 2017, 37, 132–156. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Park, S.; Hah, J.; Lee, J. Inductive ensemble clustering using kernel support matching. Electron. Lett. 2017, 53, 1625–1626. [Google Scholar] [CrossRef]
- Barbosa, J.; Torgo, L. Online ensembles for financial trading. In Practical Data Mining: Applications, Experiences and Challenges; ECML/PKDD: Berlin, Germay, 2006; p. 29. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Kolter, J.Z.; Maloof, M.A. Dynamic weighted majority: An ensemble method for drifting concepts. J. Mach. Learn. Res. 2007, 8, 2755–2790. [Google Scholar]
- Park, S.; Lee, J.; Son, Y. Predicting Market Impact Costs Using Nonparametric Machine Learning Models. PLoS ONE 2016, 11, e0150243. [Google Scholar] [CrossRef]
- Mosca, A.; Magoulas, G.D. Distillation of deep learning ensembles as a regularisation method. In Advances in Hybridization of Intelligent Methods; Springer: Berlin/Heidelberg, Germany, 2018; pp. 97–118. [Google Scholar]
- Choromanska, A.; Henaff, M.; Mathieu, M.; Arous, G.B.; LeCun, Y. The Loss Surfaces of Multilayer Networks; Artificial Intelligence and Statistics: New York, NY, USA, 2015; pp. 192–204. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P. Deep Neural Network Ensembles for Time Series Classification. arXiv 2019, arXiv:1903.06602. [Google Scholar]
- Fan, Z.; Song, X.; Xia, T.; Jiang, R.; Shibasaki, R.; Sakuramachi, R. Online Deep Ensemble Learning for Predicting Citywide Human Mobility. Proc. ACM Interact. Mob. Wearable Ubiquit. Technol. 2018, 2, 105. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Pineda, F.J. Generalization of back-propagation to recurrent neural networks. Phys. Rev. Lett. 1987, 59, 2229. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks IET, Edinburgh, UK, 7–10 September 1999. [Google Scholar]
- Mikolov, T.; Karafiát, M.; Burget, L.; Černockỳ, J.; Khudanpur, S. Recurrent neural network based language model. In Proceedings of the Eleventh Annual Conference of the International Speech Communication Association, Chiba, Japan, 26–30 September 2010. [Google Scholar]
- Benkeser, D.; Ju, C.; Lendle, S.; van der Laan, M. Online cross-validation-based ensemble learning. Stat. Med. 2018, 37, 249–260. [Google Scholar] [CrossRef] [PubMed]
- Van der Laan, M.J.; Polley, E.C.; Hubbard, A.E. Super learner. Stat. Appl. Genet. Mol. Biol. 2007, 6, 25. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Bubeck, S. Introduction to Online Optimization; Lecture Notes; Princeton University: Princeton, NJ, USA, 2011; pp. 1–86. [Google Scholar]
- Schapire, R.E.; Freund, Y. Boosting: Foundations and Algorithms; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 22 February 2019).
- Son, Y.; Noh, D.j.; Lee, J. Forecasting trends of high-frequency KOSPI200 index data using learning classifiers. Expert Syst. Appl. 2012, 39, 11607–11615. [Google Scholar] [CrossRef]
- Qiu, M.; Song, Y. Predicting the direction of stock market index movement using an optimized artificial neural network model. PLoS ONE 2016, 11, e0155133. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jo, K.; Ji, P. The analysis on the causes of corporate bankruptcy with the bankruptcy prediction model. Mark. Econ. Res. 2011, 40, 85–106. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]

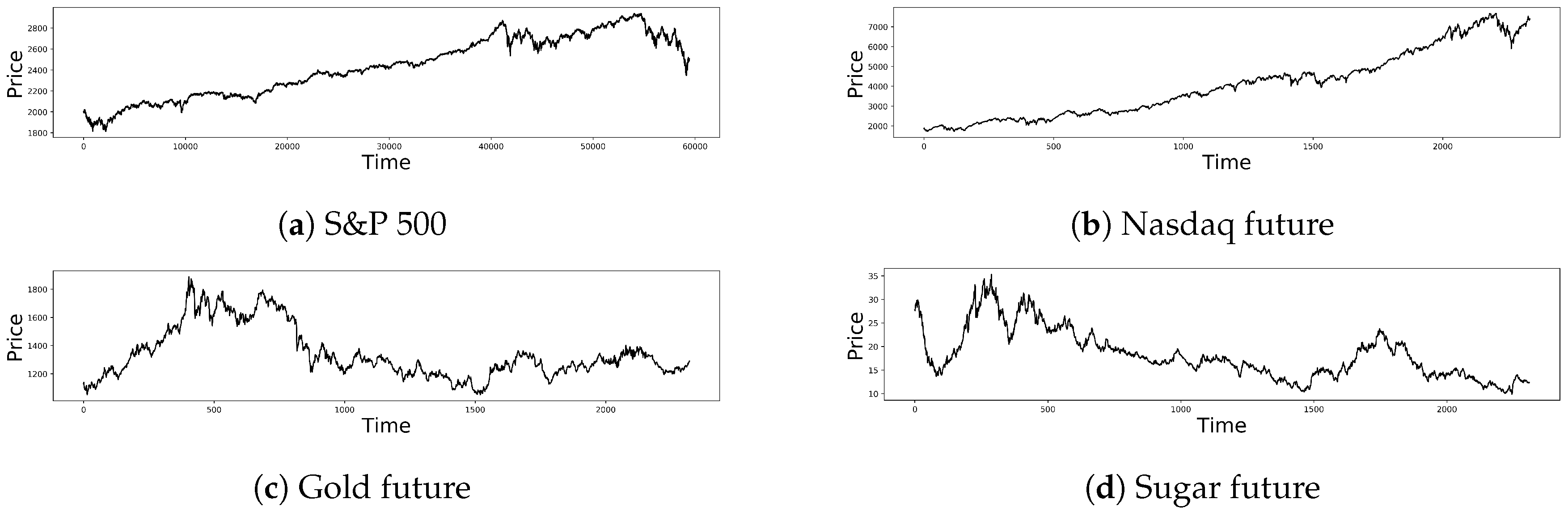
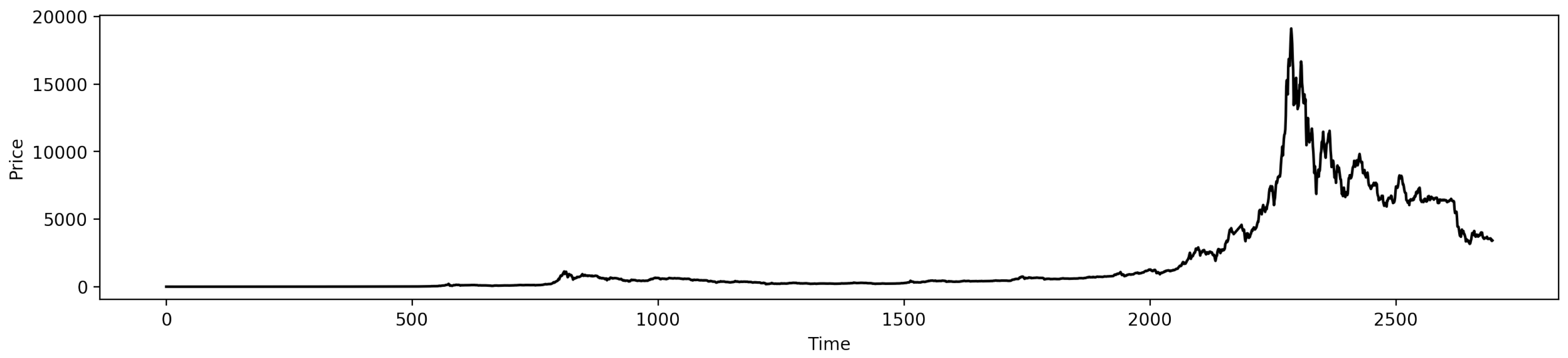

| Data | Predictor | Target | Freq | # of Data |
|---|---|---|---|---|
| S&P 500 | 13 variables in Appendix A | trend of price | 5 min | 59,453 |
| gold future | daily | 2246 | ||
| commodity—sugar future | 2252 | |||
| Nasdaq future | 9 variables in Appendix A | 2297 | ||
| cryptocurrency—Bitcoin | 17 variables in Appendix A | 2683 | ||
| bankruptcy—savings bank | 38 variables in Appendix A | default or not | quarterly | 4225 |
| Sine | Combination Sine | S&P 500 | Nasdaq | Gold | Sugar | Bitcoin | Temperature | Power Consumption | |
|---|---|---|---|---|---|---|---|---|---|
| proposed | 46.69 | 27.12 | 0.66 | 0.59 | 0.06 | 0.73 | 0.86 | 6.83 | 18.66 |
| equal | 42.03 | 25.81 | 0.13 | 0.29 | −0.44 | −1.07 | −0.14 | 2.97 | 17.8 |
| rf | 39.99 | −0.64 | −0.46 | −5.57 | −0.66 | −1.97 | −5.47 | 3.15 | −1.02 |
| bg | 35.99 | 0.33 | −0.17 | −1.17 | −0.14 | −2.97 | −1.64 | 4.9 | 2.21 |
| Data | Predictor | Target | Freq | # of Data |
|---|---|---|---|---|
| temperature | 18 variables in Appendix A | trend of temperature | daily | 1304 |
| power consumption | historical value | trend of consumption | 5055 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, H.; Lee, J.; Byun, J.; Son, B.; Park, S. Loss-Driven Adversarial Ensemble Deep Learning for On-Line Time Series Analysis. Sustainability 2019, 11, 3489. https://doi.org/10.3390/su11123489
Ko H, Lee J, Byun J, Son B, Park S. Loss-Driven Adversarial Ensemble Deep Learning for On-Line Time Series Analysis. Sustainability. 2019; 11(12):3489. https://doi.org/10.3390/su11123489
Chicago/Turabian StyleKo, Hyungjin, Jaewook Lee, Junyoung Byun, Bumho Son, and Saerom Park. 2019. "Loss-Driven Adversarial Ensemble Deep Learning for On-Line Time Series Analysis" Sustainability 11, no. 12: 3489. https://doi.org/10.3390/su11123489
APA StyleKo, H., Lee, J., Byun, J., Son, B., & Park, S. (2019). Loss-Driven Adversarial Ensemble Deep Learning for On-Line Time Series Analysis. Sustainability, 11(12), 3489. https://doi.org/10.3390/su11123489





