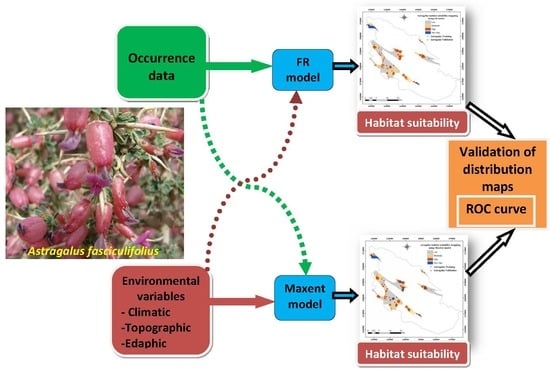
Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran
Abstract
1. Introduction
- (1)
- to quantify the relationship between A. fasciculifolius and the selected environmental variables;
- (2)
- to develop the habitat suitability index (HSI) and identify the additional and potential localities of A. fasciculifolius and targeting the marl soil conservation activities, as well as vegetation restoration planning; and,
- (3)
- to compare between FR and Maxent models for predicting the potential distribution of A. fasciculifolius in the study area.
2. Materials and Methods
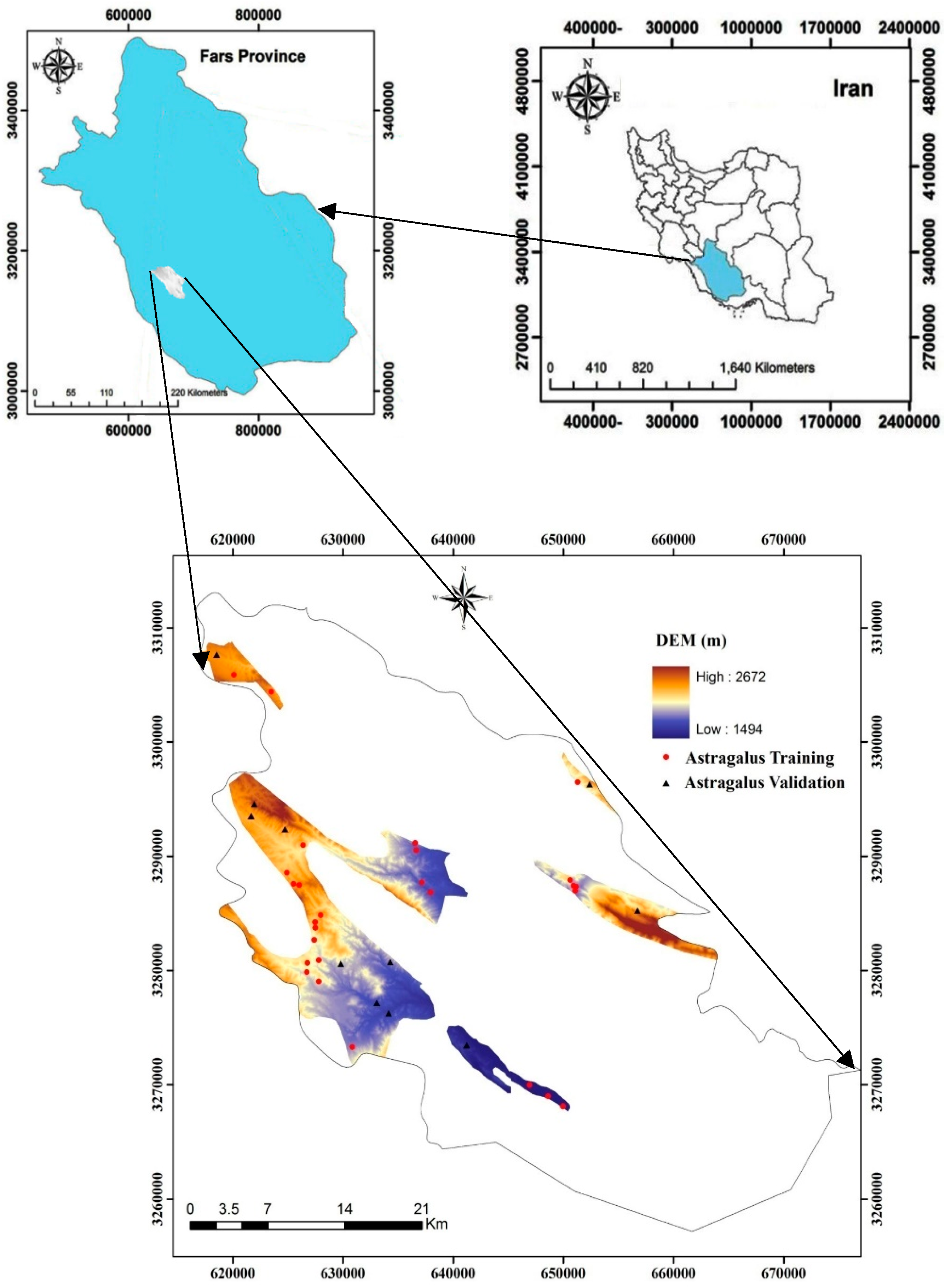
2.1. Study Area
2.2. Data Used
2.2.1. Species Description
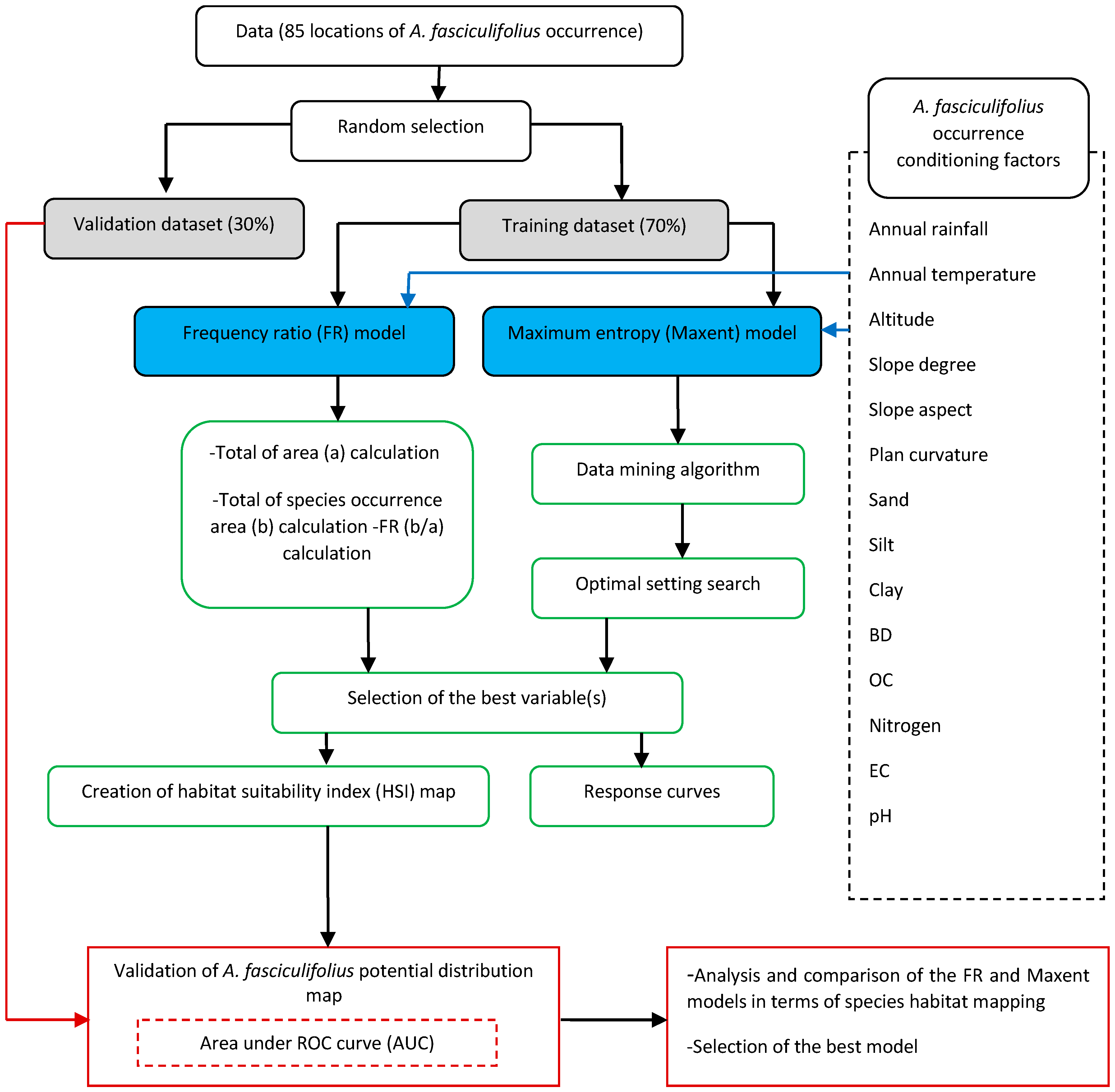
2.2.2. Species Occurrence Data
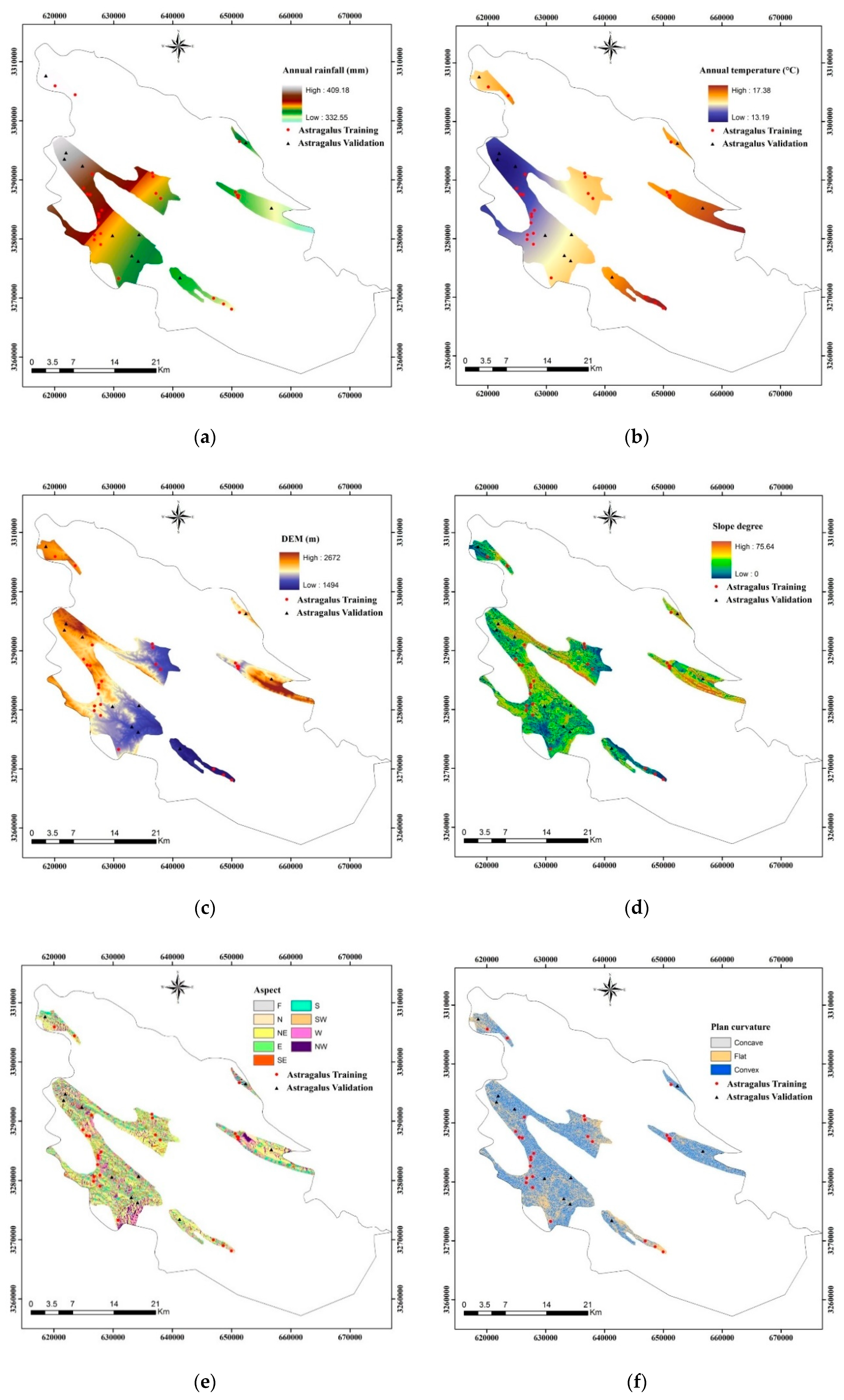
2.3. Geo-Environmental Variables
2.3.1. Climatic Data
2.3.2. Topographic Data
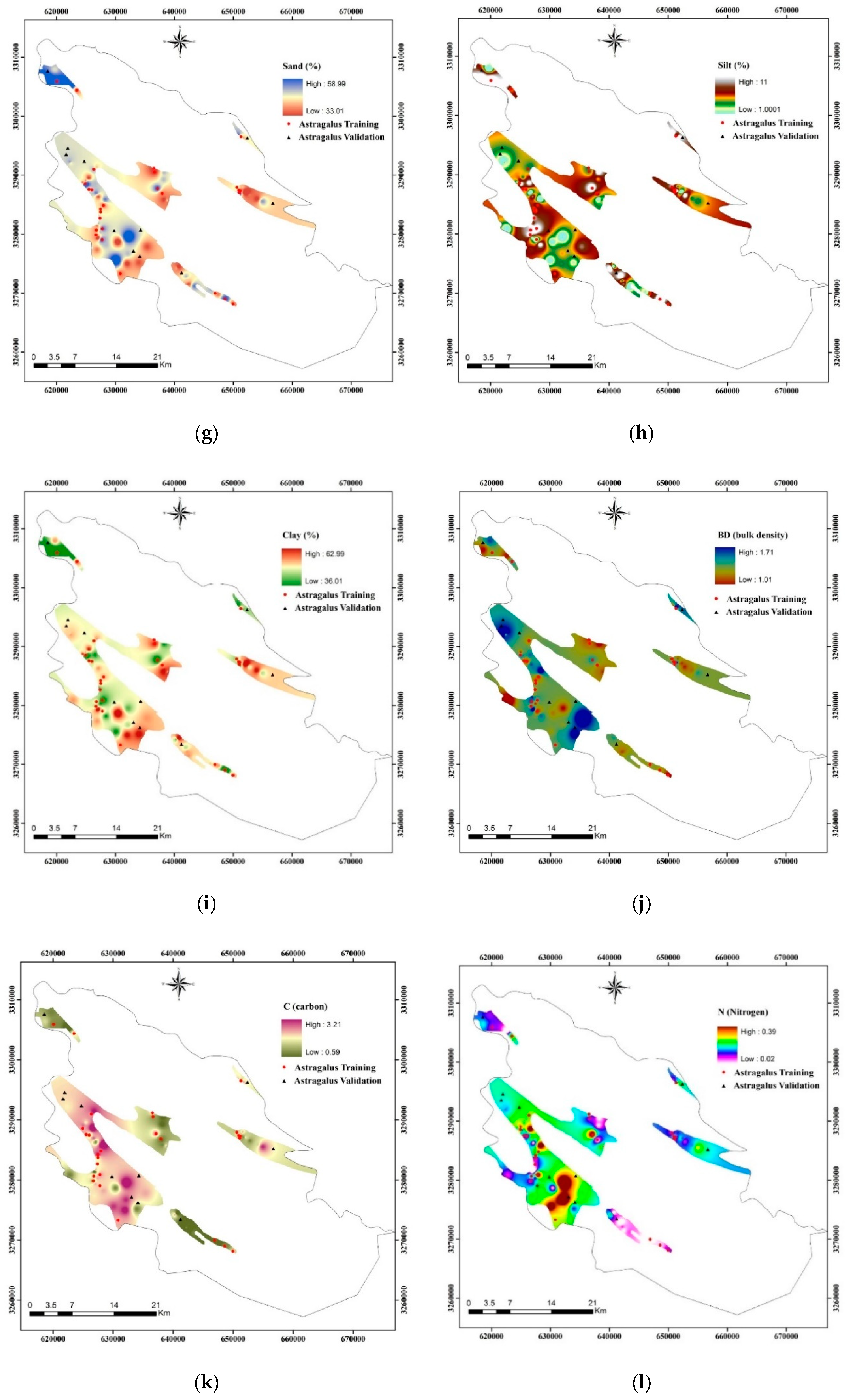
2.3.3. Soil Data Mapping
2.4. Models Description
2.4.1. Frequency Ratio (FR) Model
2.4.2. Maximum Entropy (Maxent) Model
2.5. Models Validation
3. Results and Discussion
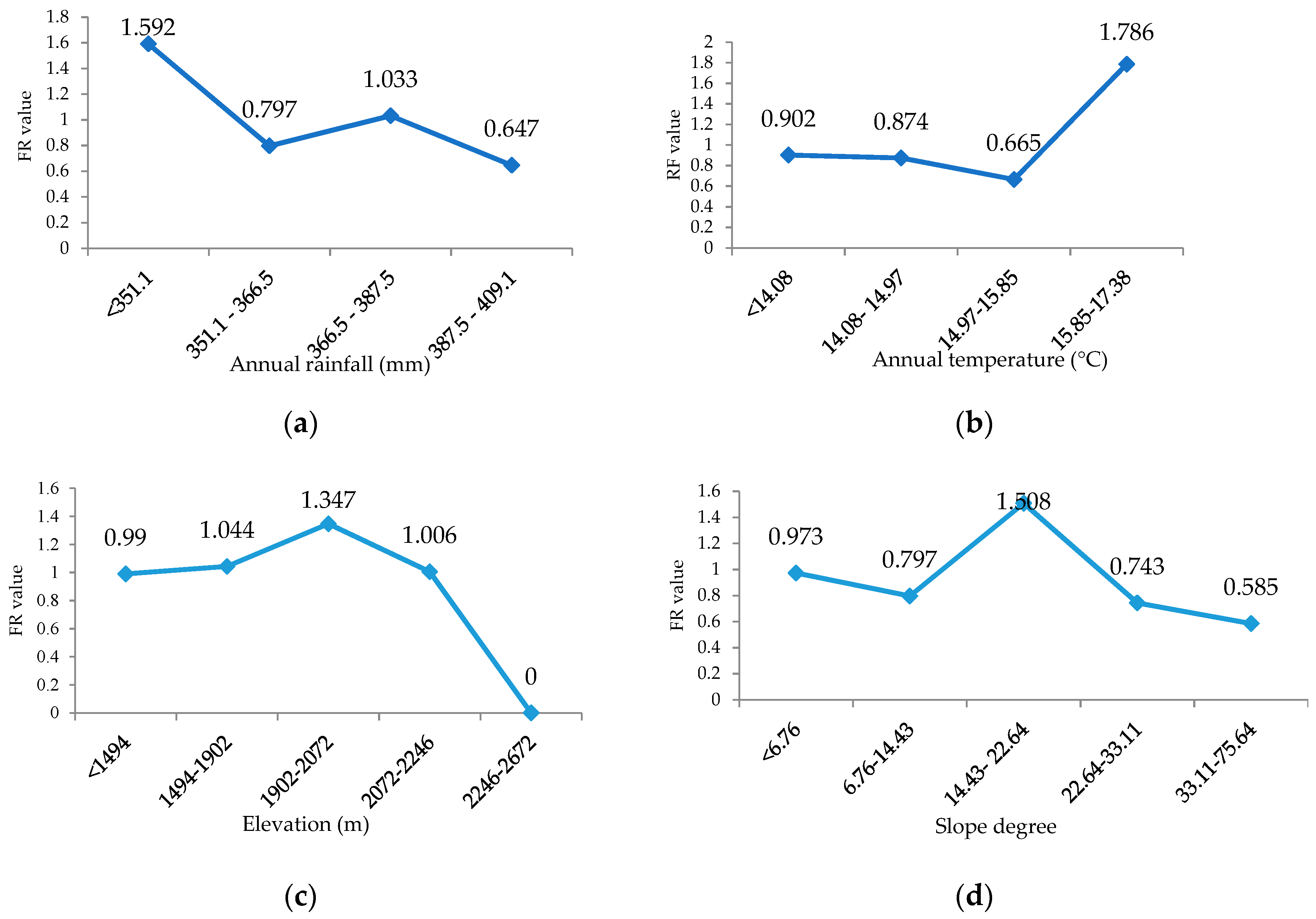
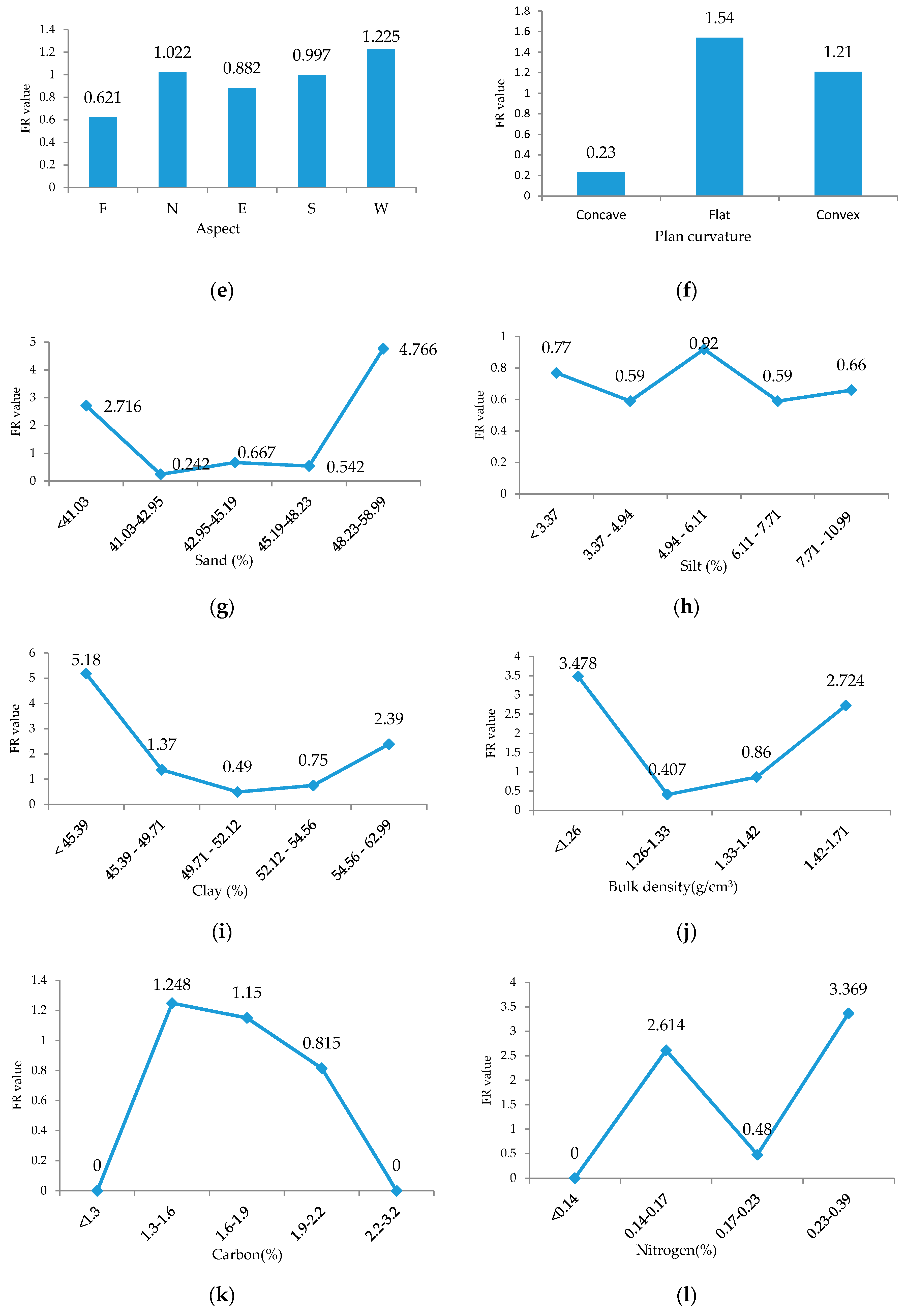
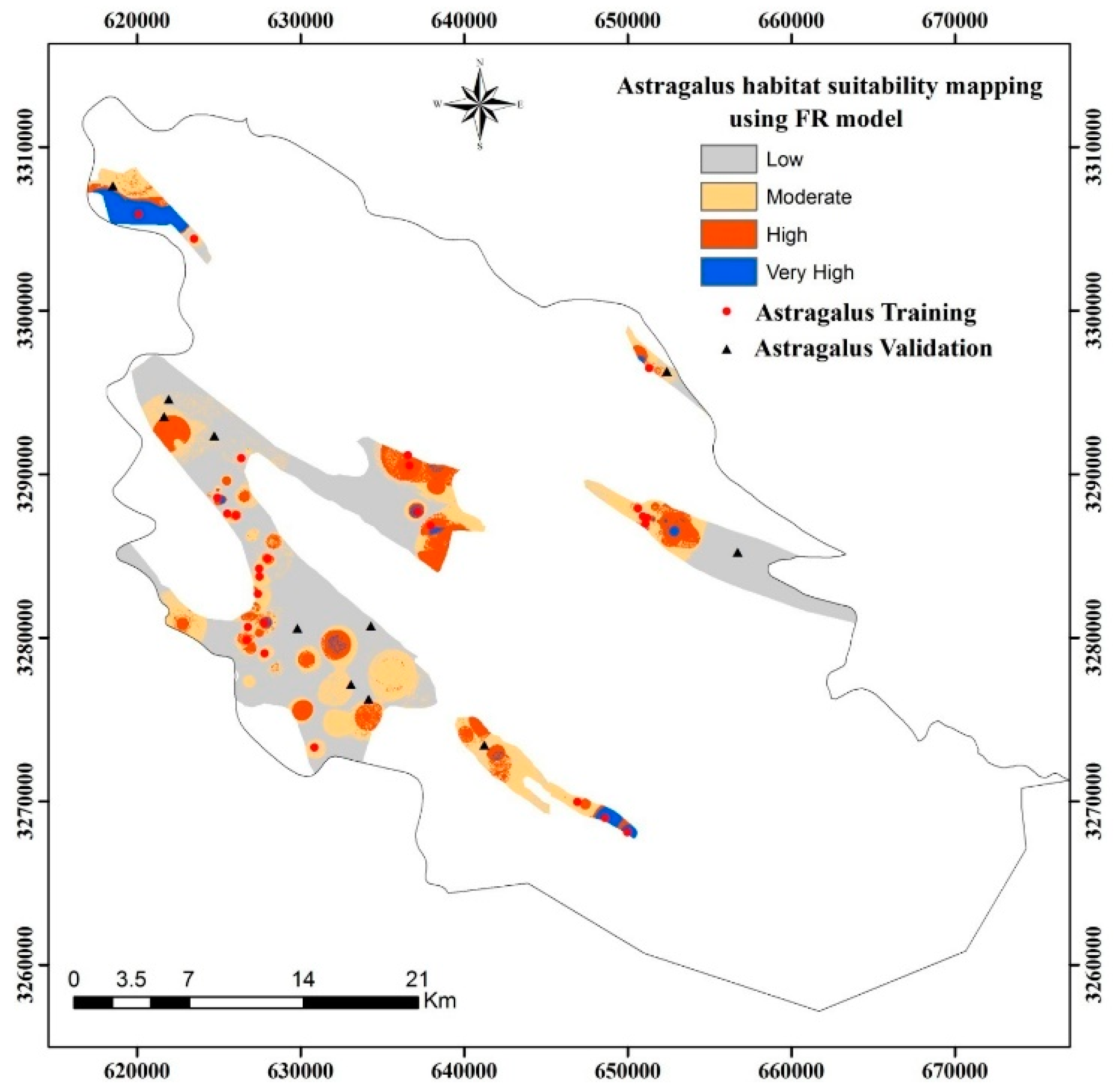
3.1. FR Model
3.2. Maxent Model
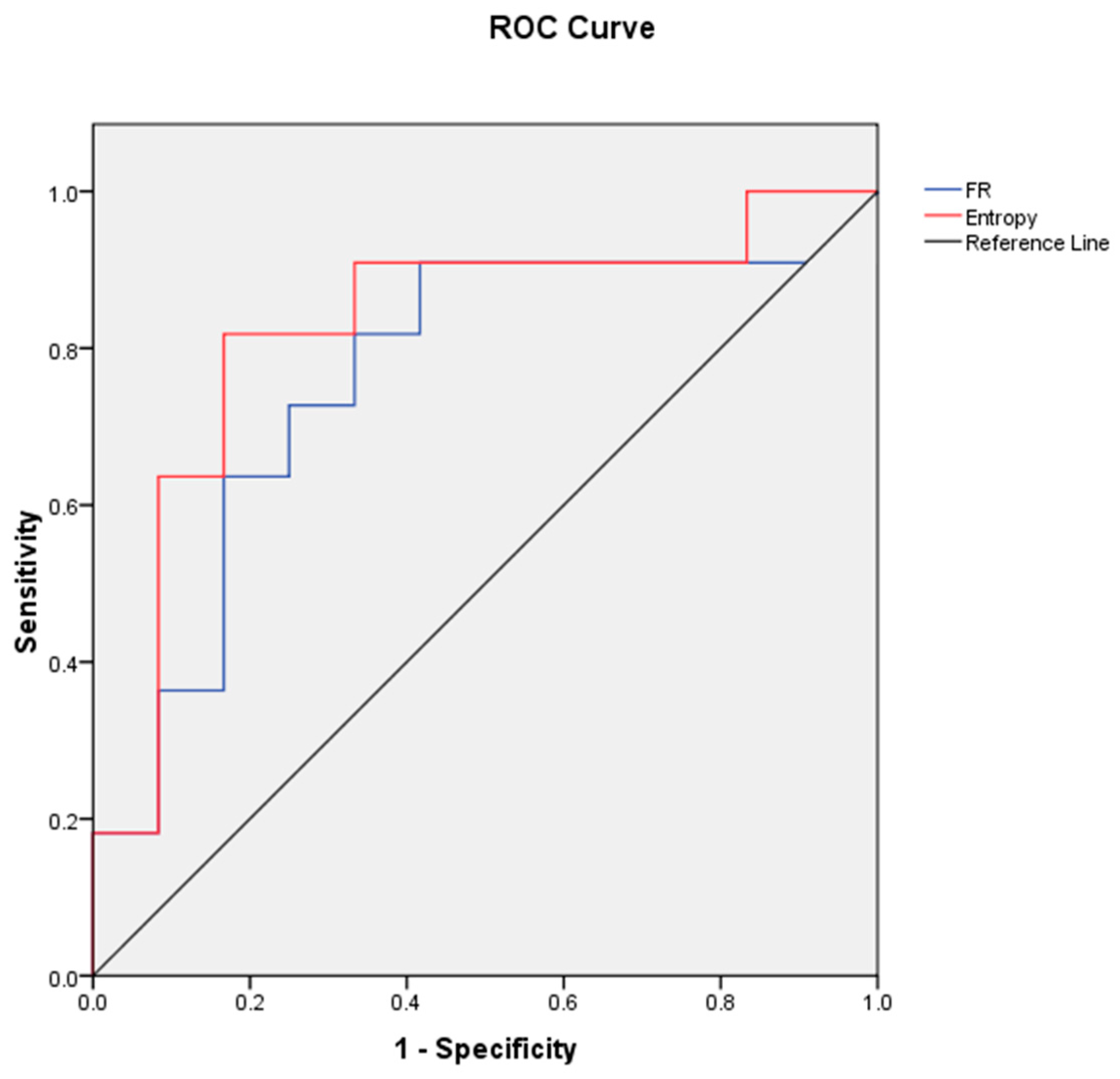
3.3. Validation of the HSI Maps and Comparison between FR and Maxent Models
3.4. Soil as a Key Factor
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Purves, D.W.; Dushoff, J. Directed seed dispersal and meta-population response to habitat loss and disturbance: Application to Eichhornia paniculata. J. Ecol. 2005, 93, 658–669. [Google Scholar] [CrossRef]
- Yi, Y.J.; Cheng, X.; Yang, Z.F.; Zhang, S.H. Maxent modeling for predicting the potential distribution of endangered medicinal plant (H. riparia Lour) in Yunnan, China. Ecol. Eng. 2016, 92, 260–269. [Google Scholar] [CrossRef]
- Thorn, J.S.; Nijman, V.; Smith, D.; Nekaris, K.A.I. Ecological niche modelling as a technique for assessing threats and setting conservation priorities for Asian slow lorises (Primates: Nycticebus). Divers. Distrib. 2009, 15, 289–298. [Google Scholar] [CrossRef]
- Wilson, C.D.; Roberts, D.; Reid, N. Applying species distribution modelling to identify areas of high conservation value for endangered species: A case study using Margaritifera margaritifera (L.). Biol. Conserv. 2011, 144, 821–829. [Google Scholar] [CrossRef]
- Qin, A.; Liu, B.; Guo, Q.; Bussmann, R.W.; Ma, F.; Jian, Z.; Xu, G.; Pei, S. Maxent modeling for predicting impacts of climate change on the potential distribution of Thuja sutchuenensis Franch., an extremely endangered conifer from southwestern China. Glob. Ecol. Conserv. 2017, 10, 139–146. [Google Scholar] [CrossRef]
- Pearson, R.G.; Raxworthy, C.J.; Nakamura, M.; Townsend, P.A. Predicting species distributions from small numbers of occurrence records: A test case using cryptic geckos in Madagascar. J. Biogeogr. 2007, 34, 102–117. [Google Scholar] [CrossRef]
- Elith, J.H.; Graham, C.P.; Anderson, R.; Dudík, M.; Ferrier, S.; Guisan, A.J.; Hijmans, R.; Huettmann, F.R.; Leathwick, J.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R. Species distribution models: Ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Hosseini, S.Z.; Kappas, M.; Chahouki, M.Z.; Gerold, G.; Erasmi, S.; Emam, A.R. Modelling potential habitats for Artemisia sieberi and Artemisia aucheri in Poshtkouh area, central Iran using the maximum entropy model and geostatistics. Ecol. Inform. 2013, 18, 61–68. [Google Scholar] [CrossRef]
- Khanum, R.; Mumtaz, A.S.; Kumar, S. Predicting impacts of climate change on medicinal asclepiads of Pakistan using Maxent modeling. Acta Oecol. 2013, 49, 23–31. [Google Scholar] [CrossRef]
- Yang, X.Q.; Kushwaha, S.P.S.; Saran, S.; Xu, J.; Roy, P.S. Maxent modeling for predicting the potential distribution of medicinal plant, Justicia adhatoda L. in Lesser Himalayan foothills. Ecol. Eng. 2013, 51, 83–87. [Google Scholar] [CrossRef]
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.S.S. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, A. GIS modeling of submerged macrophyte distribution using Generalized Additive Models. Plant Ecol. 1998, 139, 113–124. [Google Scholar] [CrossRef]
- Austin, M. Species distribution models and ecological theory: A critical assessment and some possible new approaches. Ecol. Indic. 2007, 200, 1–19. [Google Scholar] [CrossRef]
- Cassini, M.H. Ecological principles of species distribution models: The habitat matching rule. J Biogeogr. 2011, 38, 2057–2065. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Gastón, A.; García-Viñas, J.I. Modelling species distributions with penalised logistic regressions: A comparison with maximum entropy models. Ecol. Model. 2011, 222, 2037–2041. [Google Scholar] [CrossRef]
- Sahragard, H.P.; Chahouki, M.Z. An evaluation of predictive habitat models performance of plant species in Hozesoltan rangelands of Qom Province. Ecol Modell. 2015, 309, 64–71. [Google Scholar] [CrossRef]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2011, 17, 43–57. [Google Scholar] [CrossRef]
- Garcia, K.; Lasco, R.; Ines, A.; Lyon, B.; Pulhin, F. Predicting geographic distribution and habitat suitability due to climate change of selected threatened forest tree species in the Philippines. Appl Geogr. 2013, 44, 12–22. [Google Scholar] [CrossRef]
- Demir, G.; Aytekin, M.; Akgün, A.; Ikizler, S.B.; Tatar, O. A comparison of landslide susceptibility mapping of the eastern part of the North Anatolian Fault Zone (Turkey) by likelihood-frequency ratio and analytic hierarchy process methods. Nat. Hazards 2013, 65, 1481–1506. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, Northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at Al-Hasher area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Yan, S.; Wu, Y.; Pei, Y. GIS based frequency ratio and index of entropy models to landslide susceptibility mapping (Daguan, China). Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- GSI (Geological Survey of Iran). Geological Map of Shiraz, 1:250000; National Iranian Oil Company: Tehran, Iran, 1979. [Google Scholar]
- Nadal-Romero, E.; Petrlic, K.; Verachtert, E.; Bochet, E.; Poesen, J. Effects of slope angle and aspect on plant cover and species richness in a humid Mediterranean badland. Earth Surf. Process. Landf. 2014, 39, 1705–1716. [Google Scholar] [CrossRef]
- Gyssels, G.; Poesen, J.; Bochet, E.; Li, Y. Impact of plant roots on the resistance of soils to erosion by water: A review. Prog. Phys. Geogr. 2005, 29, 189–217. [Google Scholar] [CrossRef]
- Bochet, E.; García-Fayos, P.; Poesen, J. Topographic thresholds for plant colonization on semi-arid eroded slopes. Earth. Surf. Process. Landf. 2009, 34, 1758–1771. [Google Scholar] [CrossRef]
- García-Fayos, P.; García-Ventoso, B.; Cerdà, A. Limitations to plant establishment on eroded slopes in southeastern Spain. J. Veg. Sci. 2000, 11, 77–86. [Google Scholar] [CrossRef]
- Guerrero-Campo, J.; Palacio, S.; Montserrat-Martí, G. Plant traits enabling survival in Mediterranean badlands in northeastern Spain suffering from soil erosion. J. Veg. Sci. 2008, 19, 457–464. [Google Scholar] [CrossRef]
- Varavipour, M.; Asadi, T.; Arzjani, Z. Reletionship between the physico-chemical properties and different types of erosion on Marl soils south of Tehran, Iran. Asian J. Chem. 2010, 22, 5201–5208. [Google Scholar]
- Mozaffarian, V. Trees and Shrubs of Iran; Moaser Farhang Publications: Tehran, Iran, 2004. [Google Scholar]
- Shao, B.M.; Xu, W.; Dai, H.; Tu, P.; Li, Z.; Gao, X.M. A study on the immune receptors for polysaccharides from the roots of Astragalus membranaceus, a Chinese medicinal herb. Biochem. Biophys. Res. Commun. 2004, 320, 1103–1111. [Google Scholar] [CrossRef] [PubMed]
- Mosaddegh, M.; Naghibi, F.; Moazzeni, H.; Pirani, A.; Esmaeili, S. Ethnobotanical survey of herbal remedies traditionally used in Kohghiluyehva Boyer Ahmad province of Iran. J. Ethnopharmacol. 2012, 141, 80–95. [Google Scholar] [CrossRef] [PubMed]
- Shahid, M.; Rao, N.K. New records for the two Fabaceae species from the United Arab Emirates. J. New Biol. Rep. 2015, 4, 207–210. [Google Scholar]
- IRIMO. Climate Data-Base. Available online: http://www.weather.ir/English/ (accessed on 16 August 2017).
- Maassoumi, A.A. Astragalus in the Old World; Research Institute of Forests and Rangelands: Tehran, Iran, 1998. [Google Scholar]
- Rechinger, K.H. Flora Iranica, Vol. 175. Papilionaceae IV, Astragalus II; Akademische Verlagsgesellschaft: Salzburg, Austria, 1999. [Google Scholar]
- Frodin, D.G. History and concepts of big plant genera. Taxon 2004, 53, 753–776. [Google Scholar] [CrossRef]
- Podlech, D.; Zarre, S.; Ekici, M.; Maassoumi, A.A.; Sytin, A. A Taxonomic Revision of the Genus Astragalus L. (Leguminosae) in the Old World; Annalen des Naturhistorischen Museums in Wien. Serie B fürBotanik und Zoologie; Naturhistorisches Museum Wien: Wien, Austria, 2014. [Google Scholar]
- Mozaffarian, V. Flora of Khuzestan, Khuzestan Province; Animal Affairs and Natural Resources Research Center Publications: Tehran, Iran, 1999. [Google Scholar]
- Niknam, V.; Lisar, Y.S. Chemical composition of Astragalus: Carbohydrates and mucilage content. Pak. J. Bot. 2004, 36, 381–388. [Google Scholar]
- Sanchez, A.C.; Osborne, P.E.; Haq, N. Climate change and the African baobab (Adansoniadigitata L.): The need for better conservation strategies. Afr. J. Ecol. 2011, 49, 234–245. [Google Scholar] [CrossRef]
- Bouyoucos, G.J. Hydrometer method improved for making particle size analyses of soils. Agron. J. 1962, 54, 464–465. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. In Methods of Soil Analysis: Part 1—Physical and Mineralogical Methods; American Society of Agronomy, Inc.; Soil Science Society of America, Inc.: Madison, WI, USA, 1986. [Google Scholar]
- Bremmer, J.M.; Mulvaney, C.S. Regular Kjeldahl method. In Methods of Soil Analysis Part 2; American Society of Agronomy, Inc.; Soil Science Society of America, Inc.: Madison, WI, USA, 1982. [Google Scholar]
- Carter, M.R. Soil Sampling and Methods of Analysis; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Nosetto, M.D.; Jobbagy, E.G.; Paruelo, J.M. Carbon sequestration in semi-arid rangelands: Comparison of Pinus ponderosa plantations and grazing exclusion in NW Patagonia. J. Arid Environ. 2006, 67, 142–156. [Google Scholar] [CrossRef]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Bonham-Carter, G.E.; Cox, S.J.D. Geographic information systems for geoscientists: Modelling with GIS. Econ. Geol. 1995, 90, 1352–1353. [Google Scholar]
- Lee, M.J.; Song, W.; Lee, S. Habitat mapping of the leopard cat (Prionailurus bengalensis) in South Korea using GIS. Sustainability 2015, 7, 4668–4688. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Delineation of landslide hazard areas on Penang Island, Malaysia, by using frequency ratio, logistic regression, and artificial neural network models. Environ. Earth. Sci. 2010, 60, 1037–1054. [Google Scholar] [CrossRef]
- Mohammady, M.; Pourghasemi, H.R.; Pradhan, B. Landslide susceptibility mapping at Golestan Province, Iran: A comparison between frequency ratio, Dempster-Shafer, and weights-of-evidence models. J. Asian Earth Sci. 2012, 61, 221–236. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. A maximum entropy approach to species distribution modeling. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 83. [Google Scholar]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the Sibiciu Basin (Romania). Environ. Earth. Sci. 2011, 63, 397–406. [Google Scholar] [CrossRef]
- White, E.P.; Thibault, K.M.; Xiao, X. Characterizing species abundance distributions across taxa and ecosystems using a simple maximum entropy model. Ecology 2012, 93, 1772–1778. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.S.; Wei, Y.L.; Wang, X.G. Maxent modeling for predicting the potential distribution of Sanghuang, an important group of medicinal fungi in China. Fungal Ecol. 2015, 17, 140–145. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. Maxent Software for Modeling Species Niches and Distributions Version 3.4.0. Available online: http://biodiversityinformatics.amnh.org/open_source/maxent/ (accessed on 17 April 2018).
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Fielding, A.H.; Bell, J.F. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- Pearce, J.; Ferrier, S. Evaluating the predictive performance of habitat models developed using logistic regression. Ecol. Model. 2000, 133, 225–245. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Badano, E.I.; Cavieres, L.A.; Molina-Montenegro, M.A.; Quiroz, C.L. Slope aspect influences plant association patterns in the Mediterranean matorral of central Chile. J. Arid Environ. 2005, 62, 93–108. [Google Scholar] [CrossRef]
- Bennie, J.; Huntley, B.; Wiltshire, A.; Hill, M.O.; Baxter, R. Slope, aspect and climate: Spatially explicit and implicit models of topographic microclimate in chalk grassland. Ecol. Model. 2008, 216, 47–59. [Google Scholar] [CrossRef]
- Gong, X.; Brueck, H.; Giese, K.M.; Zhang, L.; Sattelmacher, B.; Lin, S. Slope aspect has effects on productivity and species composition of hilly grassland in the Xilin River Basin, Inner Mongolia, China. J. Arid Environ. 2008, 72, 483–493. [Google Scholar] [CrossRef]
- Jobbágy, E.G.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol. Appl. 2000, 10, 423–436. [Google Scholar] [CrossRef]
- Schenk, H.J.; Jackson, R.B. Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems. J. Ecol. 2002, 90, 480–494. [Google Scholar] [CrossRef]
- Cammeraat, E.; van Beek, R.; Kooijman, A. Vegetation succession and its consequences for slope stability in SE Spain. Plant Soil 2005, 278, 135–147. [Google Scholar] [CrossRef]
- Wezel, A.; Rajot, J.L.; Herbrig, C. Influence of shrubs on soil characteristics and their function in Sahelian agro-ecosystems in semi-arid Niger. J. Arid Environ. 2000, 44, 383–398. [Google Scholar] [CrossRef]
- Pei, S.; Fu, H.; Wan, C. Changes in soil properties and vegetation following exclosure and grazing in degraded Alxa desert steppe of Inner Mongolia, China. Agric. Ecosyst. Environ. 2008, 124, 33–39. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Qu, H.; Zuo, X.; Lian, J.; Tang, X.; Powers, R. Effects of shrub litter addition on dune soil microbial community in Horqin sandy land, northern China. Arid Land Res. Manag. 2011, 25, 203–216. [Google Scholar] [CrossRef]
- Masson-Boivin, C.; Giraud, E.; Perret, X.; Batut, J. Establishing nitrogen-fixing symbiosis with legumes: How many rhizobium recipes? Trends Microbiol. 2009, 17, 458–466. [Google Scholar] [CrossRef] [PubMed]
- Ranjbar, M.; Karamian, R. Some remarks on the genus Astragalus sect. Incani in Iran. Bot. J. Linn. Soc. 2003, 143, 443–447. [Google Scholar] [CrossRef][Green Version]
- Ranjbar, M. Astragalus sect. Trachycercis (Fabaceae) in Iran. Nord. J. Bot. 2009, 27, 328–335. [Google Scholar] [CrossRef]
- Ahmadi, A.; Shahmoradi, A.A.; Zarekia, S.; Ahmadi, E.; Nateghi, S. Autecological study of Astragalus effusus in rangelands of west Azarbaijan province, Iran. Iran J. Range Desert Res. 2013, 20, 172–181. [Google Scholar]
- Khormali, F.; Abtahi, A. Origin and distribution of clay minerals in calcareous arid and semi-arid soils of Fars Province, southern Iran. Clay Miner. 2003, 38, 511–527. [Google Scholar] [CrossRef]
- Ghanbarian, G.; Tayebi Khorrami, M. Ecological Regions of Iran: Vegetation Types of Jahrom Area; Technical Publication; Research Institute of Forest and Rangelands: Tehran, Iran, 2005. [Google Scholar]
- Manap, M.A.; Nampak, H.; Pradhan, B.; Lee, S.; Sulaiman, W.N.A.; Ramli, M.F. Application of probabilistic-based frequency ratio model in groundwater potential mapping using remote sensing data and GIS. Arab. J. Geosci. 2014, 7, 711–724. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Zharkikh, J.I.; Krasnoperov, R.I.; Nikolov, B.P.; Agayan, S.M. GIS-oriented solutions for advanced clustering analysis of geoscience data using ArcGIS platform. Russ. J. Earth Sci. 2016, 16. [Google Scholar] [CrossRef]
- Wong, K.C.; Peng, C.; Li, Y.; Chan, T.M. Herd clustering: A synergistic data clustering approach using collective intelligence. Appl. Soft Comput. 2014, 23, 61–75. [Google Scholar] [CrossRef]
- Barbosa, S.M.; Gouveia, S.; Scotto, M.G.; Alonso, A.M. Wavelet-based clustering of sea level records. Math. Geosci. 2016, 48, 149–162. [Google Scholar] [CrossRef]
- Jaafari, A.; Pourghasemi, H.R. Factors influencing regional scale wildfire probability in Iran: An application of random forests and support vector machines. In Spatial Modeling in GIS and R for Earth Science and Environmental; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 607–619. [Google Scholar]
- Pourghasemi, H.R.; Mohseni Saravi, M. Land-Subsidence Spatial Modeling using Random Forest Data Mining Technique. In Spatial Modeling in GIS and R for Earth Science and Environmental; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 147–159. [Google Scholar]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. Groundwater spring potential using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2018, 1–18. [Google Scholar] [CrossRef]
- Ljubomir, G.; Pourghasemi, H.R.; Drobnjak, S.; Bai, S. Testing a new ensemble model based on SVM and Random forest in forest fire susceptibility assessment and its mapping in Serbian National Park Tara. Forests 2019, 10, 408. [Google Scholar]
- Pourghasemi, H.R.; Rossi, M. Landslide susceptibility modeling in a landslide prone area in Mazandarn Province, North of Iran: A comparison between GLM, GAM, MARS, and M-AHP methods. Theor. Appl. Climatol. 2017, 130, 609–633. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth. Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Motevalli, A.; Zakeri, M.A. Gully Erosion Modeling Using GIS-Based Data Mining Techniques in Northern Iran: A Comparison Between Boosted Regression Tree and Multivariate Adaptive Regression Spline. Natural hazards GIS-based spatial modeling using data mining techniques. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques; Pourghasemi, H.R., Rossi, M., Eds.; Springer: Cham, Switzerland, 2019; pp. 1–26. [Google Scholar]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- Keesstra, S.; Mol, G.; de Leeuw, J.; Okx, J.; de Cleen, M.; Visser, S. Soil-related sustainable development goals: Four concepts to make land degradation neutrality and restoration work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Berendse, F.; van Ruijven, J.; Jongejans, E.; Keesstra, S. Loss of plant species diversity reduces soil erosion resistance. Ecosystems 2015, 18, 881–888. [Google Scholar] [CrossRef]
- Cerdà, A. The effect of patchy distribution of Stipa tenacissima L. on runoff and erosion. J. Arid Environ. 1997, 36, 37–51. [Google Scholar] [CrossRef]
- García-Fayos, P.; Bochet, E.; Cerdà, A. Seed removal susceptibility through soil erosion shapes vegetation composition. Plant Soil 2010, 334, 289–297. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerdà, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef]


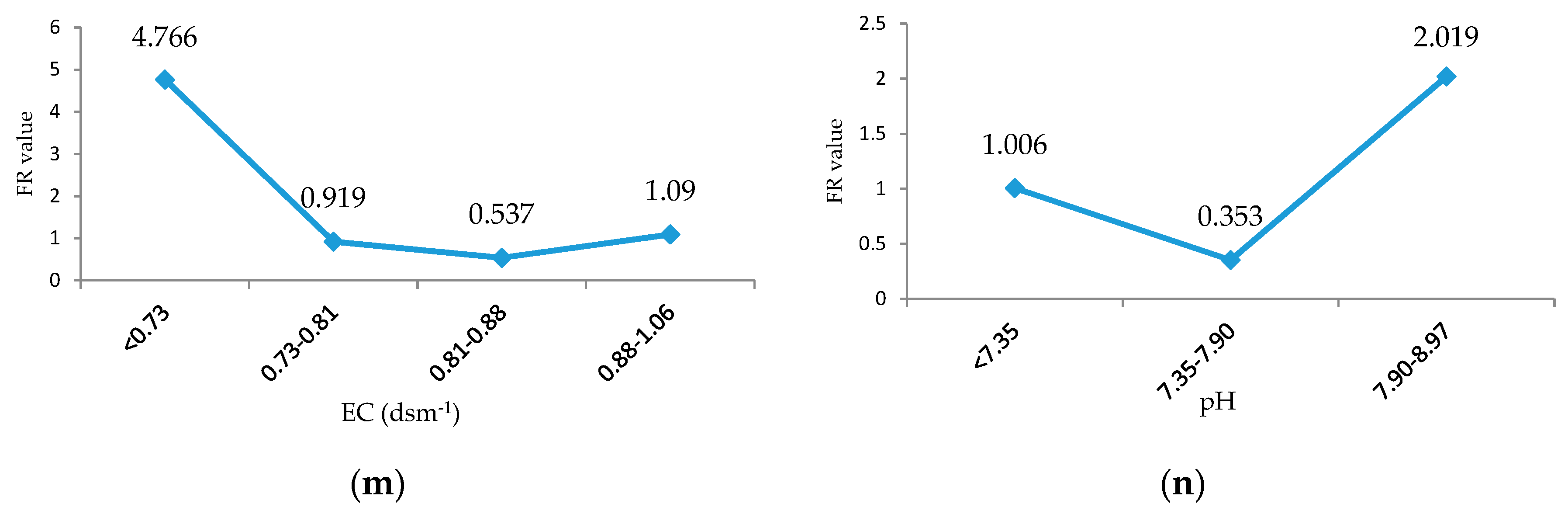

| Category | Predictor | Data Scale |
|---|---|---|
| Topography | Aspect | Categorical (9 classes) |
| Slope | Continuous | |
| Elevation | Continuous | |
| Plan curvature | Continuous | |
| Soil | EC | Continuous |
| Sand | Continuous | |
| Clay | Continuous | |
| Silt | Continuous | |
| Bulk Density | Continuous | |
| Organic Carbon | Continuous | |
| Nitrogen | Continuous | |
| PH | Continuous | |
| Climate | Rainfall | Continuous |
| Temperature | Continuous |
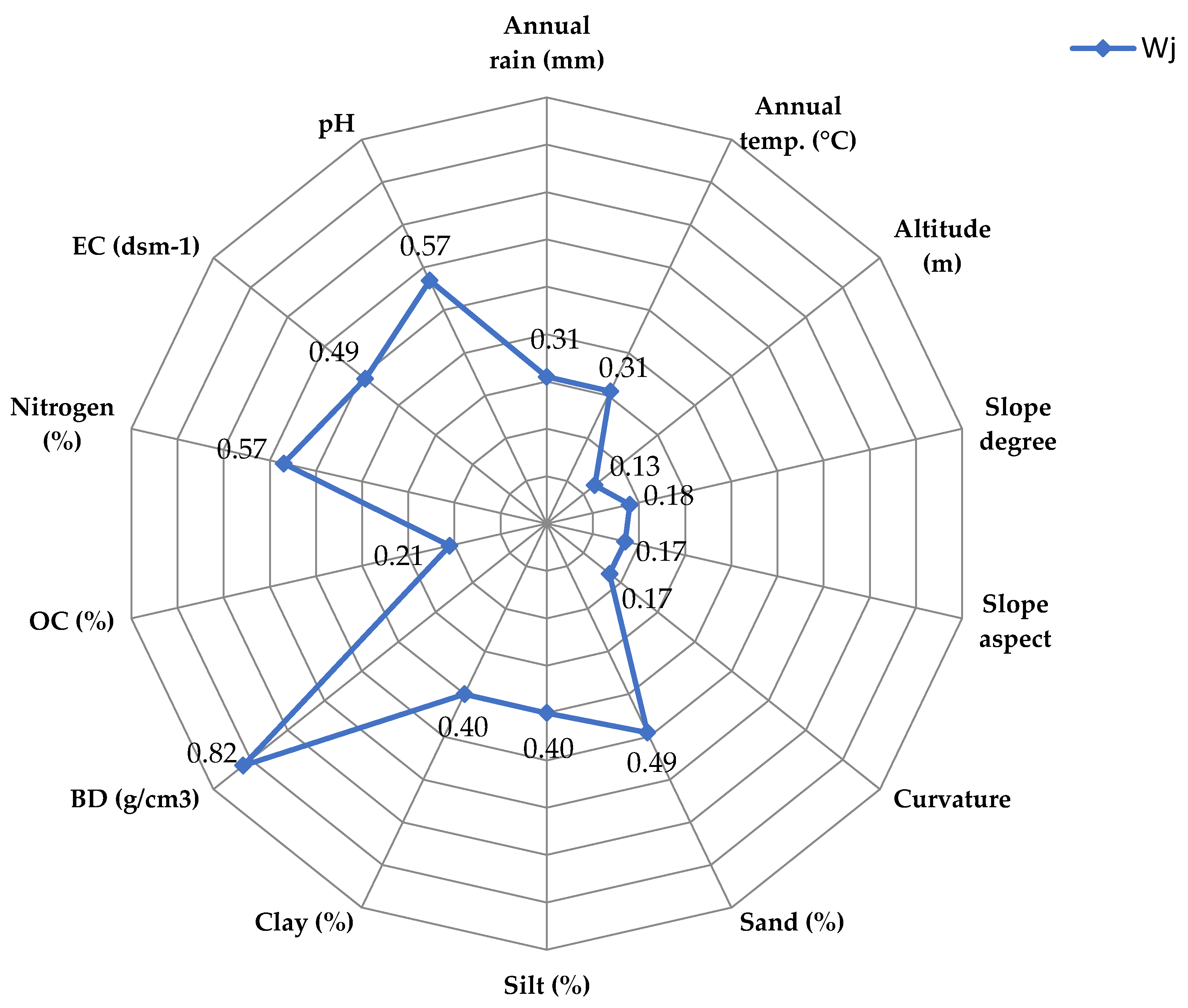
| Factor | Class | a | b | Pij | (Pij) | Hj | Hjmax | Ij | Wj |
|---|---|---|---|---|---|---|---|---|---|
| Annual rain (mm) | <351.18 | 21.43 | 34.12 | 1.59 | 0.39 | 1.38 | 2 | 0.31 | 0.31 |
| 351.18–366.50 | 44.23 | 35.29 | 0.79 | 0.19 | |||||
| 366.50–387.54 | 21.63 | 22.35 | 1.03 | 0.25 | |||||
| 387.54–409.18 | 12.71 | 8.24 | 0.65 | 0.16 | |||||
| Annual temperature (°C) | <14.08 | 16.95 | 15.29 | 0.9 | 0.21 | 1.42 | 2 | 0.29 | 0.31 |
| 14.08–14.97 | 24.22 | 21.18 | 0.87 | 0.21 | |||||
| 14.97–15.85 | 37.09 | 24.71 | 0.66 | 0.16 | |||||
| 15.85–17.38 | 21.73 | 38.82 | 1.79 | 0.42 | |||||
| Altitude (m) | <1725 | 11.22 | 11.11 | 0.99 | 0.22 | 1.99 | 2.32 | 0.14 | 0.13 |
| 1725–1902 | 28.37 | 29.63 | 1.04 | 0.24 | |||||
| 1902–2072 | 24.74 | 33.33 | 1.35 | 0.31 | |||||
| 2072–2246 | 25.76 | 25.92 | 1.01 | 0.23 | |||||
| 2246–2672 | 9.91 | 0 | 0 | 0 | |||||
| Slope degree | <6.76 | 30.22 | 29.41 | 0.97 | 0.21 | 1.86 | 2.32 | 0.2 | 0.18 |
| 6.76–14.43 | 26.54 | 21.18 | 0.79 | 0.17 | |||||
| 14.4–22.64 | 23.39 | 35.29 | 1.51 | 0.33 | |||||
| 22.64–33.11 | 15.82 | 11.76 | 0.74 | 0.16 | |||||
| 33.11–75.64 | 4.02 | 2.35 | 0.58 | 0.13 | |||||
| Slope aspect | F | 5.68 | 3.53 | 0.62 | 0.13 | 1.91 | 2.32 | 0.18 | 0.17 |
| N | 29.91 | 30.59 | 1.02 | 0.21 | |||||
| E | 23.98 | 21.18 | 0.88 | 0.19 | |||||
| S | 21.22 | 21.18 | 0.99 | 0.21 | |||||
| W | 19.2 | 23.53 | 1.22 | 0.26 | |||||
| Plan | Concave | 31.89 | 7.407 | 0.23 | 0.08 | 1.31 | 1.58 | 0.17 | 0.17 |
| curvature | Flat | 31.35 | 48.15 | 1.53 | 0.51 | ||||
| Convex | 36.75 | 44.44 | 1.21 | 0.41 | |||||
| Sand (%) | <41.03 | 13.63 | 37.04 | 2.72 | 0.3 | 1.67 | 2.32 | 0.28 | 0.49 |
| 41.03–42.95 | 30.51 | 7.41 | 0.24 | 0.03 | |||||
| 42.95–45.19 | 44.37 | 29.63 | 0.67 | 0.07 | |||||
| 45.19–48.23 | 6.82 | 3.7 | 0.54 | 0.06 | |||||
| 48.23–58.99 | 4.66 | 22.22 | 4.77 | 0.53 | |||||
| Silt (%) | <3.73 | 9.62 | 7.41 | 0.77 | 0.11 | 1.71 | 2.32 | 0.26 | 0.4 |
| 3.73–4.94 | 31.15 | 18.52 | 0.59 | 0.08 | |||||
| 4.94–6.11 | 40.29 | 37.04 | 0.92 | 0.12 | |||||
| 6.11–7.71 | 12.57 | 7.41 | 0.59 | 0.08 | |||||
| 7.71–11.00 | 6.36 | 29.63 | 0.65 | 0.62 | |||||
| Clay (%) | <45.39 | 4.29 | 22.22 | 5.18 | 0.51 | 1.86 | 2.32 | 0.2 | 0.4 |
| 45.39–49.71 | 8.11 | 11.11 | 1.37 | 0.13 | |||||
| 49.71–52.12 | 45.16 | 22.22 | 0.49 | 0.05 | |||||
| 52.12–54.56 | 34.68 | 25.92 | 0.75 | 0.07 | |||||
| 54.56–62.99 | 7.76 | 18.52 | 2.39 | 0.23 | |||||
| BD (g/cm3) | <1.26 | 11.84 | 41.18 | 3.48 | 0.46 | 1.12 | 2 | 0.44 | 0.82 |
| 1.26–1.33 | 60.67 | 24.7 | 0.41 | 0.05 | |||||
| 1.33–1.42 | 21.88 | 18.82 | 0.86 | 0.11 | |||||
| 1.42–1.71 | 5.61 | 15.29 | 2.72 | 0.36 | |||||
| OC (%) | <1.3 | 0.01 | 0 | 0 | 0 | 1.56 | 2.32 | 0.33 | 0.21 |
| 1.3–1.6 | 2.97 | 3.7 | 1.25 | 0.39 | |||||
| 1.6–1.9 | 51.53 | 59.26 | 1.15 | 0.36 | |||||
| 1.9–2.2 | 45.39 | 37.04 | 0.81 | 0.25 | |||||
| 2.2–3.2 | 0.09 | 0 | 0 | 0 | |||||
| Nitrogen (%) | <0.14 | 0.03 | 0 | 0 | 0 | 1.3 | 2 | 0.35 | 0.57 |
| 0.14–0.17 | 18.42 | 48.15 | 2.61 | 0.4 | |||||
| 0.17–0.23 | 77.15 | 37.04 | 0.48 | 0.07 | |||||
| 0.23–0.39 | 4.39 | 14.81 | 3.37 | 0.52 | |||||
| EC (dsm−1) | <0.73 | 5.44 | 25.93 | 4.77 | 0.65 | 1.46 | 2 | 0.27 | 0.49 |
| 0.73–0.81 | 36.25 | 33.33 | 0.92 | 0.12 | |||||
| 0.81–0.88 | 41.32 | 22.22 | 0.54 | 0.07 | |||||
| 0.88–1.06 | 16.99 | 18.52 | 1.09 | 0.15 | |||||
| pH | <7.35 | 34.1 | 34.31 | 1.01 | 0.29 | 0.78 | 1.58 | 0.5 | 0.57 |
| 7.35–7.90 | 40.45 | 14.31 | 0.35 | 0.11 | |||||
| 7.90–8.97 | 25.44 | 51.37 | 2.02 | 0.59 |
| Models | Area | Standard Error | Asymptotic Significant | Asymptotic 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||
| Frequency Ratio | 0.76 | 0.11 | 0.05 | 0.556 | 0.97 |
| Maximum Entropy | 0.83 | 0.09 | 0.01 | 0.63 | 1.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mousazade, M.; Ghanbarian, G.; Pourghasemi, H.R.; Safaeian, R.; Cerdà, A. Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran. Sustainability 2019, 11, 3452. https://doi.org/10.3390/su11123452
Mousazade M, Ghanbarian G, Pourghasemi HR, Safaeian R, Cerdà A. Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran. Sustainability. 2019; 11(12):3452. https://doi.org/10.3390/su11123452
Chicago/Turabian StyleMousazade, Marjaneh, Gholamabbas Ghanbarian, Hamid Reza Pourghasemi, Roja Safaeian, and Artemi Cerdà. 2019. "Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran" Sustainability 11, no. 12: 3452. https://doi.org/10.3390/su11123452
APA StyleMousazade, M., Ghanbarian, G., Pourghasemi, H. R., Safaeian, R., & Cerdà, A. (2019). Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran. Sustainability, 11(12), 3452. https://doi.org/10.3390/su11123452