Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts
Abstract
1. Introduction
- Multivariate Adaptive Regression Splines (MARS): MARS build linear relationships between predictors and a target (predictand) by segmenting predictor variables. Possible nonlinear relationships can be identified by integrating all segments [3].
- Kernel Quantile Regression (KQR): Use of kernel functions (weighting functions) to model dependencies non-parametrically, which allows modelling of both Gaussian and non-Gaussian data [6]. KQR is closely related to Support Vector Machines, but with different loss functions.
- Quantile Regression Forest (QRF): Based on decision tree models, a random forest is a tree-based algorithm, which builds several trees and combines their output by averaging each tree leaf in the forest, which helps to improve the generalization ability of the model. In quantile regression forests, all outcomes are stored, thus the quantiles from each tree leaf can be be calculated [7].
- Gradient Boosting Model (GBM): Also for the GBM, a decision tree model is chosen typically as a base model; however, ensembles of such prediction models are generated. The final GBM model is built iteratively by optimizing an arbitrary differentiable loss function [8].
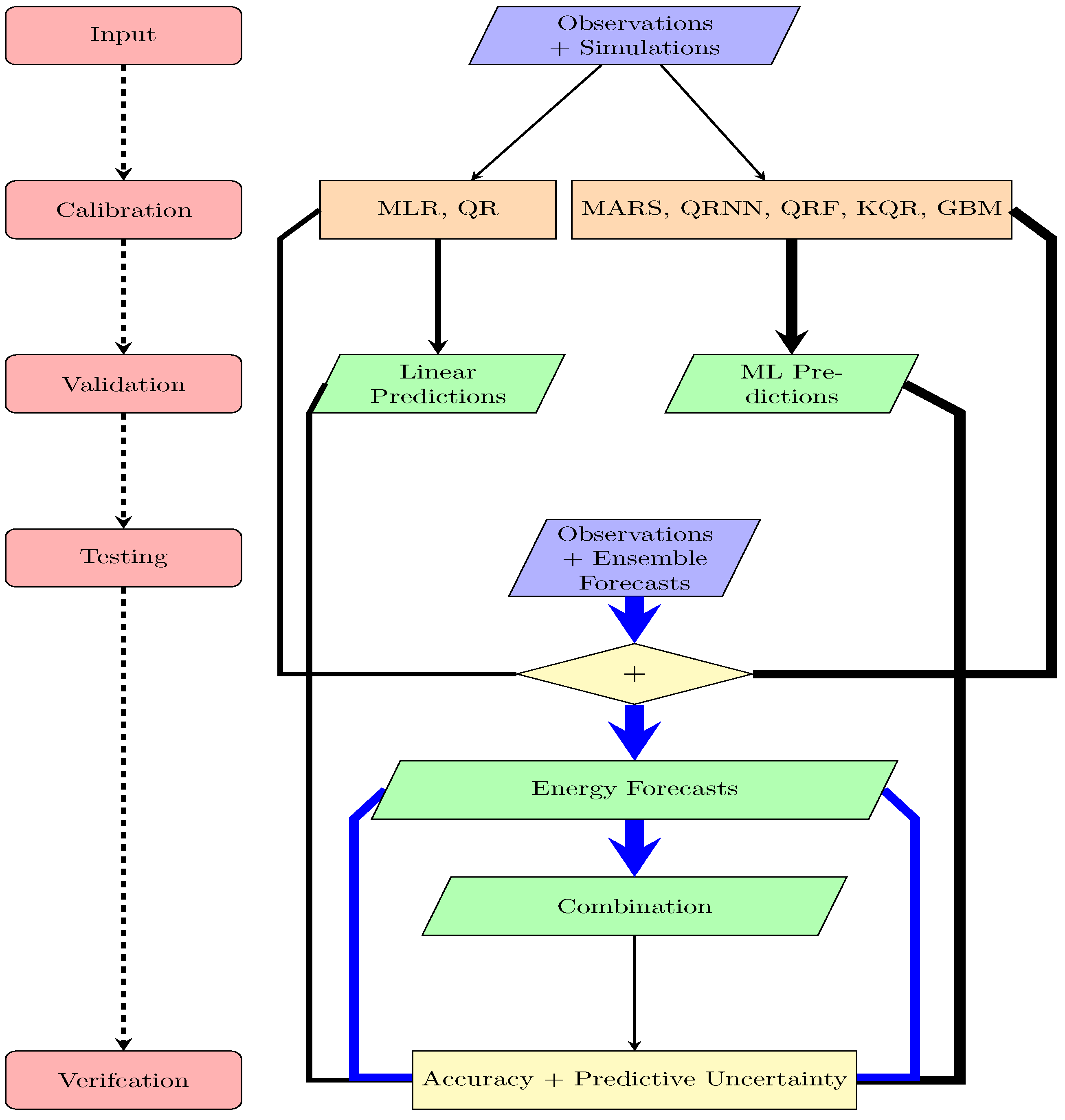
2. Materials and Methods
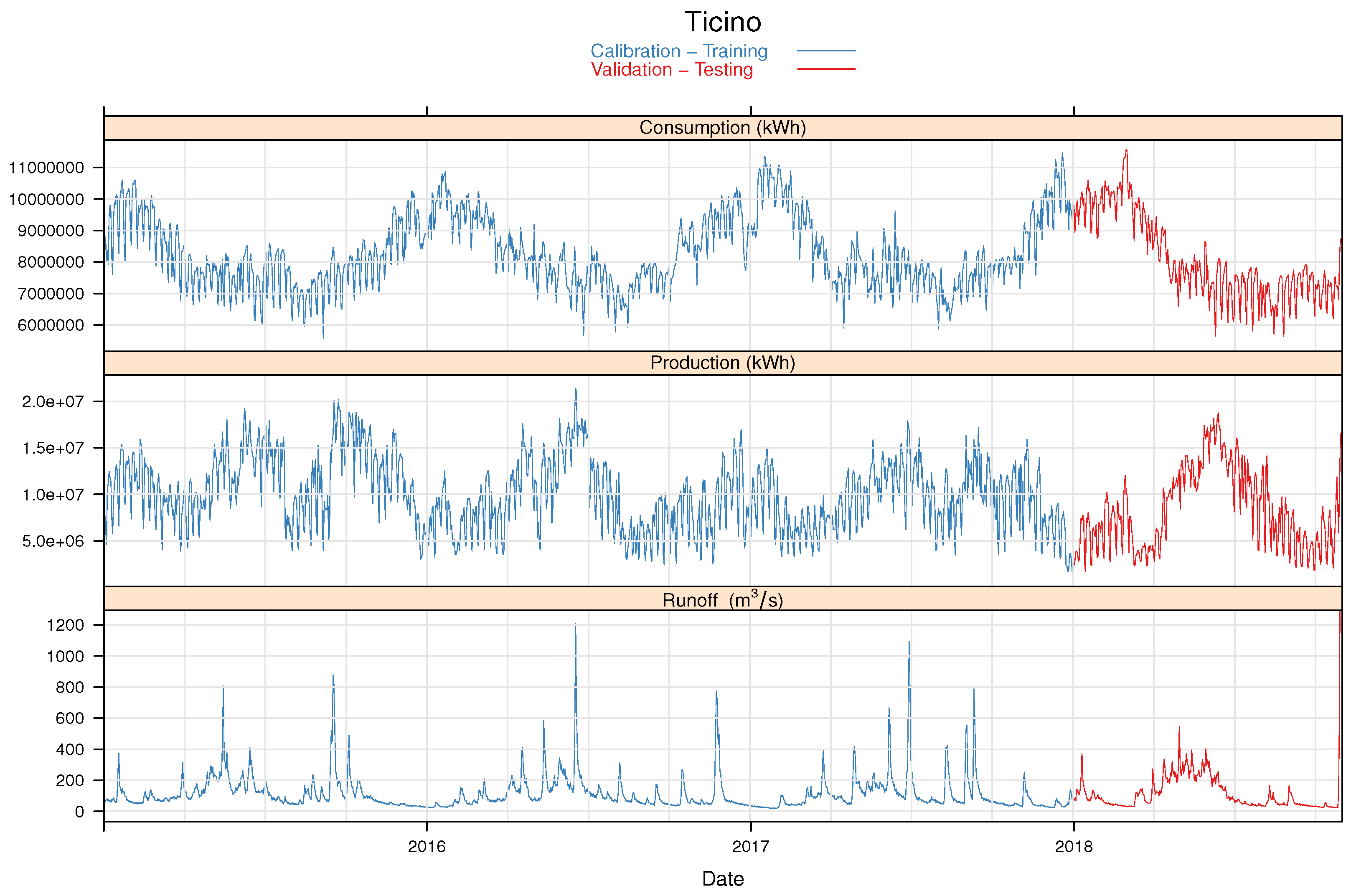
2.1. Data
2.2. Models
2.2.1. Multivariate Adaptive Regression Splines (MARS)
2.2.2. Quantile Regression (QR)
Quantile Regression Neural Network (QRNN)
Kernel Quantile Regression (KQR)
Quantile Regression Forest (QRF)
Gradient Boosting Machine (GBM)
- Computation of the negative gradient:
- Fitting a regression model, , predicting from the covariates
- Choosing a gradient descent step size as:
- Updating the estimate of as
2.3. Estimation of the Quantiles
2.4. Forecast Combination
2.5. Verification
3. Results and Discussion
3.1. Evaluation Based on Observed Meteorological Input Data
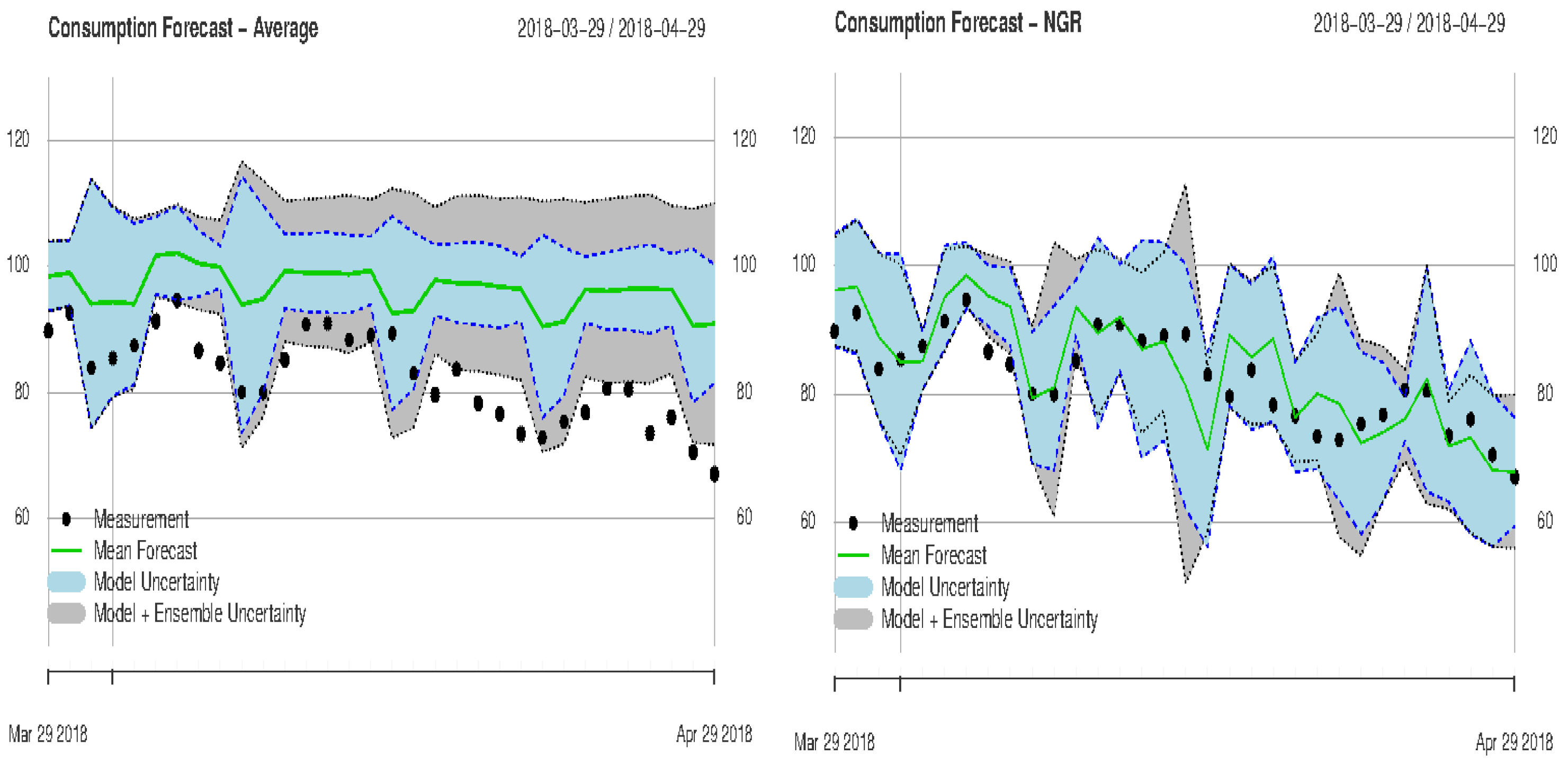
3.2. Monthly Forecasts
- The usage of hydro-meteorological data, even with low spatial resolution and high uncertainty, in combination with ML methods, will significantly improve the predictability of the energy consumption/production
- The time-scale decomposition of the most important variables (temperature, resp. runoff) enhances the quality of the predictions
- Monthly weather forecasts produce skillful energy forecasts and could be used gainfully for long-term planning (e.g., changes of the hydro-power management according to forecasts of dry summer periods and taking into consideration a potential increase of the PV production)
- The estimation and the verification of the predictive uncertainty lead to more reliable predictions and forecasts, which allow end-users to evaluate potential risks and losses, having more trustworthy information available
- The application of various models and ensembles and their optimal combination reduces biases and improves the overall forecast quality and reliability
- Since hydro-meteorological data are the most important drivers of the forecast models and are often publicly available, the proposed methods could be easily transferred to different locations, catchment or regions
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asbury, C.E. Weather load model for electric demand and energy forecasting. IEEE Trans. Power Appar. Syst. 1975, 94, 1111–1116. [Google Scholar] [CrossRef]
- Mirasgedis, S.; Sarafidis, Y.; Georgopoulou, E.; Lalas, D.; Moschovits, M.; Karagiannis, F.; Papakonstantinou, D. Models for mid-term electricity demand forecasting incorporating weather influences. Energy 2006, 31, 208–227. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Statist. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Takeuchi, I.; Le, Q.V.; Sears, T.D.; Smola, A.J. Nonparametric Quantile Estimation. J. Mach. Learn. Res. 2006, 7, 1231–1264. [Google Scholar]
- Meinshausen, N. Quantile Regression Forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Friedman, J. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.; Westveld, A., III; Goldman, T. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Karthik, A. A review of energy demand forecasting technologies. Int. J. Appl. Eng. Res. 2015, 10, 2443–2453. [Google Scholar]
- Li, Z.; Hurn, A.; Clements, A. Forecasting quantiles of day-ahead electricity load. Energy Econ. 2017, 67, 60–71. [Google Scholar] [CrossRef]
- Taylor, J.W.; Buizza, R. Using weather ensemble predictions in electricity demand forecasting. Int. J. Forecast. 2003, 19, 57–70. [Google Scholar] [CrossRef]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Bogner, K.; Liechti, K.; Zappa, M. Post-Processing of Stream Flows in Switzerland with an Emphasis on Low Flows and Floods. Water 2016, 8, 115. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bogner, K.; Pappenberger, F. Multiscale error analysis, correction, and predictive uncertainty estimation in a flood forecasting system. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Hu, J.; Liu, B.; Peng, S. Forecasting salinity time series using RF and ELM approaches coupled with decomposition techniques. Stoch. Environ. Res. Risk Assess. 2019. [Google Scholar] [CrossRef]
- Viviroli, D.; Zappa, M.; Gurtz, J.; Weingartner, R. An introduction to the hydrological modelling system PREVAH and its pre- and post-processing-tools. Environ. Model. Softw. 2009, 24, 1209–1222. [Google Scholar] [CrossRef]
- Monhart, S.; Spirig, C.; Bhend, J.; Bogner, K.; Schär, C.; Liniger, M.A. Skill of Subseasonal Forecasts in Europe: Effect of Bias Correction and Downscaling Using Surface Observations. J. Geophys. Res. Atmos. 2018. [Google Scholar] [CrossRef]
- Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression: Models, Methods and Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training, R Package Version 6.0-79; 2018. Available online: https://CRAN.R-project.org/package=caret (accessed on 1 February 2019).
- Zakeri, I.F.; Adolph, A.L.; Puyau, M.R.; Vohra, F.A.; Butte, N.F. Multivariate adaptive regression splines models for the prediction of energy expenditure in children and adolescents. J. Appl. Physiol. 2010, 108, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Zareipour, H.; Bhattacharya, K.; Canizares, C.A. Forecasting the hourly Ontario energy price by multivariate adaptive regression splines. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 7. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52, Special Issue: Progress of Machine Learning in Geosciences. [Google Scholar] [CrossRef]
- Friederichs, P.; Hense, A. Statistical Downscaling of Extreme Precipitation Events Using Censored Quantile Regression. Mon. Weather Rev. 2007, 135, 2365–2378. [Google Scholar] [CrossRef]
- Milborrow, S. Earth: Multivariate Adaptive Regression Splines, R Package Version 4.6.3; 2018. Available online: https://CRAN.R-project.org/package=earth (accessed on 1 February 2019).
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econ. J. Econ. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Robust tests for heteroscedasticity based on regression quantiles. Econ. J. Econ. Soc. 1982, 50, 43–61. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Estimating conditional quantiles with the help of the pinball loss. Bernoulli 2011, 17, 211–225. [Google Scholar] [CrossRef]
- White, H. Nonparametric Estimation of Conditional Quantiles Using Neural Networks. In Computing Science and Statistics; Page, C., LePage, R., Eds.; Springer: New York, NY, USA, 1992; pp. 190–199. [Google Scholar] [CrossRef]
- Taylor, J.W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 2000, 19, 299–311. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Tan, Y.; Hong, T.; Kirschen, D.S.; Kang, C. Combining Probabilistic Load Forecasts. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B.M.J. Quantile Regression in Regional Frequency Analysis: A Better Exploitation of the Available Information. J. Hydrometeorol. 2016, 17, 1869–1883. [Google Scholar] [CrossRef]
- Cannon, A.J. Non-crossing nonlinear regression quantiles by monotone composite quantile regression neural network, with application to rainfall extremes. Stoch. Environ. Res. Risk Assess. 2018, 32, 3207–3225. [Google Scholar] [CrossRef]
- Lang, B. Monotonic Multi-layer Perceptron Networks as Universal Approximators. In Artificial Neural Networks: Formal Models and Their Applications—ICANN 2005; Duch, W., Kacprzyk, J., Oja, E., Zadrożny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 31–37. [Google Scholar]
- Minin, A.; Velikova, M.; Lang, B.; Daniels, H. Comparison of universal approximators incorporating partial monotonicity by structure. Neural Netw. 2010, 23, 471–475. [Google Scholar] [CrossRef]
- Xu, Q.; Deng, K.; Jiang, C.; Sun, F.; Huang, X. Composite quantile regression neural network with applications. Expert Syst. Appl. 2017, 76, 129–139. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z. Feedforward networks with monotone constraints. In Proceedings of the IJCNN’99 International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999; Volume 3, pp. 1820–1823. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by support vector model. Appl. Math. Model. 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Oğcu, G.; Demirel, O.F.; Zaim, S. Forecasting Electricity Consumption with Neural Networks and Support Vector Regression. Procedia-Soc. Behav. Sci. 2012, 58, 1576–1585. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.; Olshen, R. Classification and Regression Trees; The Wadsworth and Brooks-Cole Statistics-Probability Series; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; p. 745. [Google Scholar] [CrossRef]
- Booker, D.J.; Whitehead, A.L. Inside or Outside: Quantifying Extrapolation Across River Networks. Water Resour. Res. 2018, 54, 6983–7003. [Google Scholar] [CrossRef]
- Taillardat, M.; Mestre, O.; Zamo, M.; Naveau, P. Calibrated Ensemble Forecasts Using Quantile Regression Forests and Ensemble Model Output Statistics. Mon. Weather Rev. 2016, 144, 2375–2393. [Google Scholar] [CrossRef]
- Meinshausen, N. quantregForest: Quantile Regression Forests, R Package Version 1.3-7; 2017. Available online: https://CRAN.R-project.org/package=quantregForest (accessed on 1 February 2019).
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification; Denison, D.D., Hansen, M.H., Holmes, C.C., Mallick, B., Yu, B., Eds.; Springer: New York, NY, USA, 2003; pp. 149–171. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Verbois, H.; Rusydi, A.; Thiery, A. Probabilistic forecasting of day-ahead solar irradiance using quantile gradient boosting. Sol. Energy 2018, 173, 313–327. [Google Scholar] [CrossRef]
- Kriegler, B. Cost-sensitive Stochastic Gradient Boosting Within a Quantitative Regression Framework. Ph.D. Thesis, University of California at Los Angeles, Los Angeles, CA, USA, 2007. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Glahn, H.; Lowry, D. The use of model output statistics (MOS) in objective weather forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Glantz, S.; Slinker, B. Primer of Applied Regression & Analysis of Variance; McGraw-Hill Education: New York, NY, USA, 2000. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Matheson, J.E.; Winkler, R.L. Scoring Rules for Continuous Probability Distributions. Manag. Sci. 1976, 22, 1087–1096. [Google Scholar] [CrossRef]
- Gneiting, T.; Ranjan, R. Comparing Density Forecasts Using Threshold- and Quantile-Weighted Scoring Rules. J. Bus. Econ. Stat. 2011, 29, 411–422. [Google Scholar] [CrossRef]
- Koenker, R.; Machado, J.A.F. Goodness of Fit and Related Inference Processes for Quantile Regression. J. Am. Stat. Assoc. 1999, 94, 1296–1310. [Google Scholar] [CrossRef]
- Laio, F.; Tamea, S. Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol. Earth Syst. Sci. 2007, 11, 1267–1277. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Shine, P.; Murphy, M.; Upton, J.; Scully, T. Machine-learning algorithms for predicting on-farm direct water and electricity consumption on pasture based dairy farms. Comput. Electron. Agric. 2018, 150, 74–87. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Aghaei, J.; Shafie-Khah, M.; Catalão, J.P.S. Probabilistic Load Forecasting Using an Improved Wavelet Neural Network Trained by Generalized Extreme Learning Machine. IEEE Trans. Smart Grid 2018, 9, 6961–6971. [Google Scholar] [CrossRef]
- Mosavi, A.; Bahmani, A. Energy Consumption Prediction Using Machine Learning; A Review. Preprints 2019. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Barbosa de Alencar, D.; De Mattos Affonso, C.; Limão de Oliveira, R.C.; Moya Rodríguez, J.L.; Leite, J.C.; Reston Filho, J.C. Different Models for Forecasting Wind Power Generation: Case Study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef]
- Bogner, K.; Liechti, K.; Zappa, M. Technical Note: Combining Quantile Forecasts and Predictive Distributions of Stream-flows. Hydrol. Earth Syst. Sci. 2017, 21, 5493–5502. [Google Scholar] [CrossRef]







| Dependent | Weekday | Holiday | Temp. | Precip. | Radiation | Wind | Runoff |
|---|---|---|---|---|---|---|---|
| Consumption [kWh] | 1–7 | 0–1 | [] | [mm] | [J/m] | [m/s] | |
| Production [kWh] | 1–7 | 0–1 | [] | [mm] | [J/m] | [m/s] | [m/s] |
| Emphasis | Quantile Weight Function |
|---|---|
| w1: center | |
| w2: tails | |
| w3: right tail | |
| w4: left tail |
| Consumption | MLR | MARS | QR | QRNN | QRF | KQR | GBM |
|---|---|---|---|---|---|---|---|
| Training | 0.68 | 0.84 | 0.69 | 0.87 | 0.82 | 0.89 | 0.89 |
| (0.62) | (0.76) | (0.62) | (0.76) | (0.75) | (0.82) | (0.78) | |
| Testing | 0.72 | 0.82 | 0.73 | 0.80 | 0.83 | 0.81 | 0.83 |
| (0.66) | (0.74) | (0.66) | (0.73) | (0.77) | (0.68) | (0.71) |
| Consumption | MLR | MARS | QR | QRNN | QRF | KQR | GBM |
|---|---|---|---|---|---|---|---|
| CRPS | 3.75 | 2.97 | 3.88 | 3.29 | 2.88 | 3.13 | 2.93 |
| w1 (center) | 0.77 | 0.61 | 0.79 | 0.65 | 0.60 | 0.64 | 0.59 |
| w2 (tails) | 0.64 | 0.54 | 0.71 | 0.67 | 0.49 | 0.58 | 0.56 |
| w3 (right tail) | 1.05 | 0.87 | 1.16 | 0.99 | 0.81 | 0.96 | 0.92 |
| w4 (left tails) | 1.14 | 0.89 | 1.14 | 0.98 | 0.88 | 0.89 | 0.83 |
| Production | MLR | MARS | QR | QRNN | QRF | KQR | GBM |
|---|---|---|---|---|---|---|---|
| Training | 0.45 | 0.62 | 0.44 | 0.73 | 0.72 | 0.70 | 0.75 |
| Testing | 0.45 | 0.61 | 0.43 | 0.51 | 0.54 | 0.59 | 0.61 |
| Production | MLR | MARS | QR | QRNN | QRF | KQR | GBM |
|---|---|---|---|---|---|---|---|
| CRPS | 16.92 | 13.83 | 17.16 | 15.86 | 16.06 | 15.10 | 15.02 |
| w1 (center) | 3.50 | 2.85 | 3.55 | 3.13 | 3.32 | 3.09 | 3.06 |
| w2 (tails) | 2.91 | 2.42 | 2.96 | 3.34 | 2.77 | 2.72 | 2.7 |
| w3 (right tail) | 5.01 | 4.04 | 5.14 | 4.46 | 4.68 | 4.36 | 4.21 |
| w4 (left tail) | 4.91 | 4.08 | 4.92 | 5.14 | 4.74 | 4.55 | 4.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogner, K.; Pappenberger, F.; Zappa, M. Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts. Sustainability 2019, 11, 3328. https://doi.org/10.3390/su11123328
Bogner K, Pappenberger F, Zappa M. Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts. Sustainability. 2019; 11(12):3328. https://doi.org/10.3390/su11123328
Chicago/Turabian StyleBogner, Konrad, Florian Pappenberger, and Massimiliano Zappa. 2019. "Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts" Sustainability 11, no. 12: 3328. https://doi.org/10.3390/su11123328
APA StyleBogner, K., Pappenberger, F., & Zappa, M. (2019). Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts. Sustainability, 11(12), 3328. https://doi.org/10.3390/su11123328





