Abstract
Comprehensive exergy and exergoeconomic assessments are reported for a proposed power producing system, in which an organic Rankine cycle is employed to utilize the waste heat from the fuel cell stack. A complete mathematical model is presented for simulating the system performance while considering water management in the fuel cell. The simulation is performed for individual components of the fuel cell system, e.g., the compressor and humidifiers. A parametric study is conducted to evaluate the effects on the system’s thermodynamic and economic performance of parameters, such as the fuel cell operating pressure, current density, and turbine back pressure. The results show that an increase in the fuel cell operating pressure leads to a higher exergy efficiency and exergoeconomic factor for the overall system. In addition, it is observed that the overall exergy efficiency is 4.16% higher than the corresponding value that is obtained for the standalone fuel cell for the same value of fuel cell operating pressure. Furthermore, the results indicate that the compressor and condenser exhibit the worst exergoeconomic performance and that the exergoeconomic factor, the capital cost rate and the exergy destruction cost rate for the overall system are 40.8%, 27.21 $/h, and 39.49 $/h, respectively.
1. Introduction
The reduction in fossil fuel resources and the environmental impacts that are associated with the use of these fuels influence the sustainability of future energy systems. Therefore, alternative energy sources and their more efficient utilization has been a major concern for researchers in recent years. Many consider fuel cells to be promising in this regard, as they use clean energy and have reduced greenhouse gas emission. In addition, the Carnot cycle efficiency does not limit their efficiency and they do not emit pollutants, such as sulfur dioxide and nitrous oxides [1]. Proton exchange membrane fuel cells (PEMFCs), among other types, are expected to play a major role in the future energy sector due to their high power density, quick starting, low operating temperatures, and simple stack design. However, reducing the capital costs, weight, and volume of these fuel cells is a challenge in making them competitive with traditional power producing systems like internal combustion engines [2]. In addition, it is necessary to have an appropriate and optimum value of water content inside PEMFCs to retain the durability of these fuel cells and the efficient operation of them. This can be achieved by humidifying the reactant gases before they enter the cell [3,4].
Semi-empirical and numerical models have been introduced in the literature in order to predict the variation of voltage with current density of a PEMFC and to understand and improve the performance of PEMFC systems. These models are also capable of predicting the fuel cell performance for engineering systems applications [5,6].
This section briefly reviews a selection of previously reported works that are related to the semi-empirical models. Amphlett [7] proposed a steady-state model for the Ballard Mark IV fuel cell produced by Ballard Power Systems Inc. when considering such operating parameters as the partial pressures at the electrodes, the operating temperature, and the fuel cell current. Some other researchers have used semi-empirical models for simulating PEM fuel cell performance [8,9,10]. The waste heat from these fuel cells is in the range of 50 °C to 100 °C, so that its recovery for performance enhancement is considered to be a technical challenge [11]. A few papers in the literature have dealt with the utilization of PEMFC waste heat [12,13]. Hwang et al. [14] proposed a combined heat and power (CHP) system that is based on a PEMFC for cogenerating electrical power and hot water and reported a maximum efficiency of 81% for the combined system. Zhang et al. [15] reported that such bottoming cycles as organic Rankine cycles (ORCs), Kalina cycles, and transcritical carbon dioxide cycles could conveniently use the waste heat from PEMFCs. Zhao et al. [16] proposed a hybrid power system and concluded that there are optimum values of fuel cell operating pressure at which the efficiencies of both PEMFC and overall system are maximized while using an ORC to recover waste heat from a PEMFC. However, they only carried out energy assessments of the system’s performance. He et al. [11] proposed an ORC/heat pump combined organic cycle for waste heat recovery from a PEMFC and concluded that an increase of approximately 4.7% in the thermal efficiency is possible for the recovery system. Ahmadi et al. [10] proposed a hybrid system consisting of liquefied natural gas and transcritical carbon dioxide cycles for waste heat recovery from a PEMFC to improve its performance. They concluded that the system efficiency could increase by 9% when compared to the standalone fuel cell. However, the water management of the PEMFC and the performance of the humidifiers were not separately considered in their work. Additionally, they did not analyze the system performance from the viewpoints of exergy and exergoeconomics. Chang et al. [17] designed a PEMFC–solar based residential combined cooling, heating, and power (CCHP) system and showed that the CCHP efficiency increases by up to 75.4% and 85.0% in the summer and winter times, respectively. However, the proposed system was not analyzed from the perspective of exergy and exergoeconomics. Chahartaghi et al. [18] reported energy and exergy efficiencies of 81.6% and 54.6%, respectively, for a CCHP system, but they did not address economic aspects, while using part of the heat rejected from a fuel cell for cooling production. Romdhane et al. [19] introduced a residential micro-CCHP system, including a low temperature PEMFC (LT-PEMFC) and a single effect lithium bromide-water (LiBr-H2O) absorption cycle. They only investigated the system from an energy viewpoint, and reported a maximum fuel saving ratio of about 35%. Ebrahimi et al. [20] carried out energy and exergy analyses for a micro-CCHP system that is based on a LT-PEMFC. A portion of the produced electric power is utilized to drive a thermoelectric cooler. Energy and exergy efficiencies of up to 76.9% and 53.9%, respectively, are calculated for the proposed system, but the economic aspects were not addressed. Arsalis [21] reviewed micro-CHP systems that are based on fuel cells, and concluded that PEMFCs are the most promising technology for cogeneration configurations.
Exergy analysis accounts for the quantity of energy and its quality, distinguishing it from energy analysis. Although exergy analysis provides a true measure of evaluating thermodynamic inefficiencies of systems, the cost of inefficiencies is an important issue in analyzing system performance. Exergoeconomic analysis assesses this parameter, which is as an exergy-aided method that provides important information regarding a system’s cost formation process [22]. In recent years, several studies have been carried out on the exergy analysis of the low temperature PEMFC (LT-PEMFC) [23,24]. Kazim [25] conducted an exergy analysis on the PEM fuel cell operating at voltages of 0.5 and 0.6 V. He investigated the effect of fuel cell parameters on exergy efficiency. However, the exergy destruction of the fuel cell and other auxiliary components was not evaluated in their work. Barelli et al. [26] conducted energy and exergy analyses for a CHP system that is based on a PEM fuel cell for residential applications and reported an exergy efficiency of 58% under optimum operating conditions. In another paper [27], Barelli et al. compared the energy and exergy performances of two micro CHP units that are comprised of solid oxide and PEM fuel cells. They concluded that the PEMFC based CHP system has higher exergy efficiency, due to its operation at atmospheric pressure and low temperature. Hanapi et al. [28] presented an exergy analysis for a PEM fuel cell that was employed in a mini urban car. Through a parametric study, they showed that an increase in operating temperature and pressure resulted in a higher value of exergy efficiency. However, they did not study the exergoeconomic performance of the system. Kalinci et al. [29] proposed a hybrid power system based on a PEMFC while using renewable energies to produce hydrogen and electricity. They performed a thermodynamic analysis using the energy and exergy approaches.
As mentioned earlier, much effort has been devoted to the exergy analysis of small scale LT-PEMFCs. Parametric studies have been performed to investigate the effects of the exergetic efficiency of various operating conditions. However, little data are available in the literature regarding the details of exergy destruction occurring in the various components of PEM hybrid systems. In addition, limited information is available in the literature on the exergoeconomic analysis of these fuel cells. Kazim [30] performed an exergoeconomic analysis for a 10 kW PEMFC and concluded that increasing the operating pressure and air stoichiometry can improve the fuel cell product exergy cost. In their work, the exergy destruction cost and exergoeconomic factors were not studied. Using a semi empirical model for simulating PEMFC performance, Mert et al. [2] presented an exergoeconomic analysis of a vehicular PEM fuel cell system. They reported that the fuel cell stack made the highest contribution to the overall cost. These authors did not present the exergy destruction and exergy cost of other components, such as humidifiers and compressor, separately. Suleiman et al. [31] carried out a thermoeconomic analysis for PEMFC systems that are fuelled with methanol and methane and showed that the system using methane exhibits comparatively lower capital cost. Sayadi et al. [32] performed an exergoeconomic analysis to address the trade-off among the advantageous and disadvantageous effects of incorporating an expander as part of a PEMFC system, to assist in selecting a proper design concept.
The use of ORC for the recovery of waste heat from energy conversion systems has been shown to be a promising technique in efficiency enhancement. As mentioned before, although the combination of an ORC and a LT-PEMFC has been reported in the literature, detailed exergy and exergoeconomic analyses of this combination are lacking, and inadequate attention has been paid to the modelling of the individual components. Water management in LT-PEMFCs is a crucial issue and it needs more attention. The present work addresses these gaps. A complete mathematical model is presented for simulating the overall system performance. In addition, the developed PEMFC model considers the multi-phase existence of water in the channels, thus more thoroughly investigating the fuel cell phenomena. A parametric analysis is conducted to evaluate the effects of several important parameters on the system’s thermodynamic and economic performances. The objectives are to understand the details of processes occurring in the proposed system and their impacts on its thermodynamic and economic performance.
2. System Description
Figure 1 shows a schematic of the proposed system. The proposed system includes an air compressor, a hydrogen tank, a pressure regulator, two humidifiers, a PEMFC stack, and an ORC with its components. Air is compressed in the compressor before it enters humidifier 2 and then passes to the cathode of fuel cell stack. The pressurized hydrogen is throttled through a pressure regulator, before being fed to the anode via humidifier 1. Afterwards, the air and hydrogen participate in electrochemical reactions to produce electric power and water. The unused hydrogen flows back to the PEMFC stack inlet to recycle it once the reaction is accomplished. The water exiting the stack also flows back to the humidifiers for reuse. The electrochemical reaction releases a considerable amount of heat in the stack. This heat is used to run the ORC, as shown in Figure 1. R123 is the working fluid in the ORC. It is evaporated at a constant sub-critical pressure as it is heated by the waste heat from PEMFC stack. The vapor then is expanded in the turbine to the condensing pressure to produce power. The superheated vapor exiting turbine flows to the condenser, where it rejects heat to the cooling water. Finally, the saturated liquid condensate is pumped to the subcritical pressure and the cycle is completed.
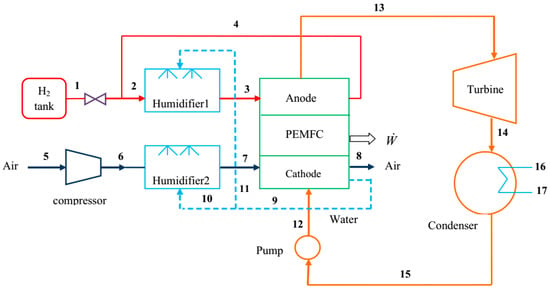
Figure 1.
Schematic diagram of the hybrid power system.
3. PEMFC Mathematical Modeling
The PEMFC modeling is presented in two sections.
3.1. LT-PEMFC Electrochemical Modeling
To simplify the PEMFC modeling, several assumptions are invoked, as follows [16,33]:
- System operation is at steady state.
- The inlet air contains 79% N2 and 21% O2 by volume.
- Constant and equal pressure is assumed for the gas flow channels in the fuel cell.
- Hydrogen at a relative humidity of 50% and humidified air at a relative humidity of 100% are supplied to the anode and cathode, respectively.
- The fuel cell operates at a temperature of 85 °C and a pressure of 300 kPa.
- The stream temperature at the channel exits is equal to that of the stack operating temperature.
- The heat losses from the system components to the surrounding environment are negligible.
- Pressure drops inside the fuel cell are neglected.
At the anode side, the hydrogen is ionized and electrons as well as H+ ions (protons) are produced:
Anode:
The released electrons are conveyed through an external circuit, while the hydrogen ions pass through the electrolyte. At the cathode side, water is produced as a reaction takes place among the oxygen, the electrons from the electrode, and the H= ions from the electrolyte:
Cathode:
The overall reaction in fuel cell is a combination of the above two reactions:
Overall reaction:
The reversible open circuit voltage that was generated by the fuel cell can be expressed by the Nernst equation [30]:
Here, and are the hydrogen and oxygen effective partial pressures at the anode and cathode, respectively, and they are defined as [8,16]:
In these equations, is the water molar fraction, which can be determined as [8,16]:
The saturation pressure of water vapor can be expressed as a function of temperature, via the following empirical equation [8,16]:
The in Equation (3) is the nitrogen molar fraction in the humidified air stream, calculated as:
where
and where and are the nitrogen molar fraction entering and exiting the fuel cell, respectively.
There are three kinds of irreversibility that reduce the value of the actual measured fuel cell voltage when compared to that of the reversible voltage. These irreversibilities are referred to as activation losses, concentration losses, and ohmic losses. Therefore, the actual voltage of PEMFC equals the Nernst voltage minus the mentioned losses [16,34]:
The activation overpotential is caused by the slowness of the reactions taking place on the electrode surfaces. It can be calculated by a semi-empirical equation, as [9,16]:
where denotes the oxygen concentration at the interface of cathode and membrane, as expressed as [8,9]:
and can be written as [16]:
where
The concentration overvoltage, or mass transport loss [35], occurs as the reactants concentrations at the electrodes surfaces are changed due to fuel consumption. In fact, insufficient reactants are transported to the electrode surfaces. The concentration overvoltage can be calculated as:
The ohmic loss occurs due to the electrical resistances that are associated with electrodes, bipolar plates, terminal connections, and the flow of ions in the electrolyte. This overvoltage can be calculated as [9,16]:
where represents the Nafion membrane resistance, expressed as:
Here, is the water content of membrane, the calculation of which is explained in the following section.
The real voltage of the fuel cell can be determined while using Equations (10)–(19). As the fuel cell stack consists of numerous connected single cells, the power generated by the fuel cell is calculated as:
3.2. Mass Balances
In the present work, spatial dependences are neglected for variables within the flow channels. For a specific current density, the mass balances for hydrogen and oxygen are expressed, on molar bases, as follows:
The second terms on the right side of the above two equations are the hydrogen and oxygen consumption rates, respectively. The entering hydrogen and air molar flow rates are calculated while using their respective stoichiometric rates. That is,
The entering and exiting nitrogen flow rates are equal, as this gas is not participating in the reaction:
In the present work, based on the model that was reported by Yi and Nguyen [36], the ratio of water molecules transferred per proton is calculated and considered for the water mass balance in the stack.
It is worth mentioning that several factors influence the water flow rate in the channels and the presence of its liquid and vapor phases. These factors are: (a) water production at the cathode because of the reaction among the oxygen, proton, and electron; (b) diffusion of water from cathode to anode; (c) transport of water from anode to cathode due to the electro-osmotic drag process; and, (d) the condensation and evaporation of water based on the partial pressure and saturation pressure of water [36,37].
In each flow channel, the liquid water flow rate, which is affected by condensation and evaporation, can be expressed as [37]:
This equation indicates that the difference between the partial pressure of the water and its saturation pressure at the corresponding temperature influences the condensation/evaporation rate. However, the equation is not valid when the water partial pressure is lower than the saturation pressure.
The water balances in the anode and cathode channels are expressed as [37]:
where is the ratio of water molecules per proton. This ratio can be written as [35,37]:
The following empirical equations are used for the physical parameters in the model [37,38]:
Determining the water content at the cathode and anode is somewhat complicated. In this regard, Equations (24) and (25) are suitable if the liquid and vapor in the channel are in equilibrium. This indicates that the liquid content of the channel exists either by partial evaporation of entering liquid or condensation. Rearranging Equations (24) and (25) results in the following:
This is a second order equation that can be easily solved. Two solutions are obtained for the water vapor content. If a positive and noncomplex solution is obtained from Equation (34), then the liquid water value is calculated using Equation (24). If a physical solution cannot be obtained, the liquid flow and the water vapor are calculated as:
The water migrating from the anode to the cathode is the difference between the inlet and outlet water flows:
In order to predict the cathode water content, Equation (26) is rearranged, as follows:
Equation (24) is used for calculating the liquid water flow in the cathode. If none of the results obtained from Equation (37) are physically meaningful, then no liquid flow exits the cathode channel, and the water vapor flow is calculated, as follows:
The solution method for and the calculation of water flows are summarized in the flowchart shown in Figure 2.
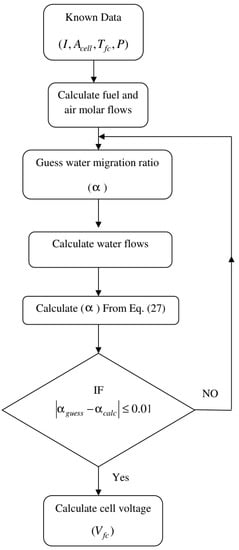
Figure 2.
Flowchart for the solution of and water flows.
Table 1 presents the parameter constants that were used in the modeling and the basic input overall system parameters used for the simulation and the parametric study.

Table 1.
Parameters considered in model and simulation of overall system.
4. Thermodynamic Analysis
Energy, exergy, and exergoeconomic analyses are performed in order to analyze the fuel cell system from the viewpoints of thermodynamics and economics. The methodology of each of these analyses is explained in the following sections.
4.1. Thermal Model of the System (First Law of Thermodynamics)
The thermodynamic assessment of the system considered is carried out while using a control volume approach. Therefore, the conservation of mass and energy for each system component as a control volume, under steady state conditions, can be written as:
The thermal models are presented for fuel cell and ORC separately, in the following subsections.
4.1.1. PEM Fuel Cell
The compressor actual power consumption can be written as:
The compressor isentropic efficiency is expressed as:
A large fraction of energy is dissipated as heat in the fuel cell. This heat is removed from the fuel cell and utilized in the ORC for additional power production in order to protect the fuel cell from overheating. The conservation of energy equation for the fuel cell can be written, as follows:
where and are the input heat rate to the system and the sensible heat rate, respectively.
In order to calculate , the fuel cell is considered as a separate control volume. Afterwards,
The PEMFC electrical efficiency is calculated as:
4.1.2. Organic Rankine Cycle
For simplification purposes, the heat interactions between the ORC system components and the surroundings, and also the pressure drop in the condenser and connecting pipes, are neglected. As mentioned before, the heat that is rejected from the fuel cell must be removed to bring about a specified operating temperature for the fuel cell under steady state condition.
The principle of energy conservation is invoked for the ORC components, with each treated as a control volume, resulting in the equations in Table 2. This table also includes the input heat to the ORC and the ORC thermal efficiency.

Table 2.
Energy balances and expressions for the organic Rankine cycles (ORC) components.
Finally, the system overall electrical efficiency can be defined as:
4.2. Exergy Analysis
Exergy is a useful concept for assessing the real thermodynamic inefficiencies that occur within a system [22]. Determining the exergy for each stream and also the exergy destruction for each system component is required for a detailed thermoeconomic analysis. The specific flow exergy of a stream can be written, while neglecting potential and kinetic forms of exergy, as the combination of physical and chemical components, as follows:
The specific physical exergy of the ith stream is given as [22]:
The chemical exergy of ideal gas mixtures is defined as [22]:
where and indicate the mole fractions of the ith component in the mixture at the restricted dead state and the dead state (environment state), respectively. In the present work, the restricted dead state condition is assumed as: T = 25 °C, p = 1 atm, whereas the unrestricted dead state condition is defined in Table 3 for a relative humidity of 60% [39].

Table 3.
Mole fractions of the components at dead state for a relative humidity of 60% [39].
The chemical exergy of hydrogen fuel is equal to 237,600 kJ/kmol [39]. As the air entering and exiting the cathode is humid, its chemical exergy is calculated while considering moist air as an ideal gas mixture. In practice, engineers often present the exergy of humid air per kg of dry air. The chemical exergy for humid air can be expressed as [39]:
where
Here, and are the humidity ratio at the given state and environmental dead state, respectively. The value of is calculated as 0.01912 for atmospheric air at 25 °C, 1 atm, and 60% relative humidity [39].
The exergy rate balance for a control volume under the steady state condition can be written as [22]:
or
The exergy efficiencies for the kth component () and the overall system () are expressed as:
where , , and indicate the rates of fuel exergy, product exergy of each system component and total exergy input of the H2, and air entering the system, respectively.
4.3. Exergoeconomic Analysis
Exergoeconomic analysis combines exergy concepts and the economic principles. This analysis provides useful information for designing more efficient systems by evaluating the costs of the inefficiencies. The specific costing (SPECO) method is followed in the present work. In this method, exergy and its unit cost balance are utilized for each system component with auxiliary cost relations, to provide a straightforward scheme to assess the system economic performance [40,41]. The cost balance equation for a system component is as follows [22]:
or
The cost associated with exergy destruction () is a hidden cost in Equation (58) [22]. This parameter can be expressed as:
where is the specific cost of the fuel exergy for the kth component, which is given as:
In the present work, the hydrogen and water costs are assumed to be 10 $/GJ and 1 $/m3, respectively. In addition, the fuel cell capital cost is taken to be 5000 $/kW and the humidifier capital cost is assumed to be 4% of the fuel cell cost [34]. Table 4 presents the capital cost functions for the other components.

Table 4.
Capital costs of the system components [41,42].
For each component of the system, the capital, and operating and maintenance cost rate, , is dependent on the capital cost [22,40]:
where is the operating and maintenance factor, taken as 1.06, N is the number of system operating hours in a year (8760 h/year) and CRF is the Capital Recovery Factor. The Capital Recovery Factor can be written as [22]:
where n is the system life (assumed to be 15 years) and i is the interest rate (taken as 10%).
Table 5 presents the cost balance and auxiliary equations for the system components. By simultaneously solving these equations, the specific cost and the corresponding cost rate of each exergy stream are calculated. Afterwards, the parameters for the exergoeconomic analysis are obtained [22].

Table 5.
Cost rate balances and auxiliary equations for components of the proton exchange membrane fuel cell-organic Rankine cycle (PEMFC-ORC) system.
The specific cost of the product exergy for the kth component can be expressed as:
The exergoeconomic factor (), which expresses the contribution of capital investment and operating and maintenance expenses on the total cost rate, is defined as:
The relative cost difference, rk, which indicates the relative increase between and , is defined as:
5. Results and Discussion
Energy, exergy, and exergoeconomic analyses are performed for the proposed system using the input data that are presented in Table 1 and Engineering Equation Solver (EES) software [43]. The electrochemical modeling of the PEMFC is validated while using the theoretical and experimental data of Miansari et al. [8]. The comparison is shown in Figure 3 and it indicates good agreement between the results in present work and those that are reported in literature. The slight difference between the results from the present model and the experimental data can be attributed to parameters, such as fuel cell voltage loss due to of cell coupling and heat loss, which are neglected in the present work.
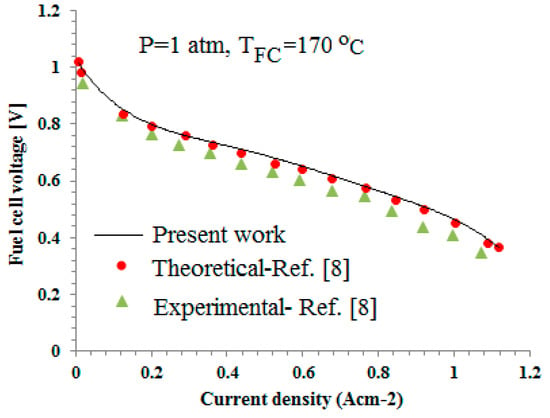
Figure 3.
Validation of simulation results for PEMFC performance using the theoretical and experimental data reported by Miansari et al. [8].
Parametric studies are performed to quantify the effects on the proposed system performance of decision parameters, such as the fuel cell current density, fuel cell operating pressure, and ORC turbine pressure. Figure 4a,b show the effects of current density on the fuel cell voltage and power density, respectively, for three values of fuel cell operating pressure. Referring to Figure 4a, the cell voltage decreases with an increasing current density. However, the slope of the variation is higher at lower and higher values of current density. This voltage-current density characteristic curve results from the combined effects of irreversibilities that are caused by activation, ohmic, and concentration overpotentials. Figure 4b indicates that, for a given value of cell operating pressure, the stack power density is a maximum at a particular value of current density, and the optimal value of current density is slightly higher at higher values of cell operating pressure. Figure 4b does not suggest the operation of fuel cell beyond the point at which power is a maximum, as the same output power may be achieved with a lower current density and consequently a higher voltage (see Figure 3). Figure 4a,b also show that a higher voltage and power density are achieved with a higher operating pressure. This is due to the improvements in the reversible thermodynamic potential (ENernst) and the reductions in the activation losses at the electrodes, especially at the cathode.

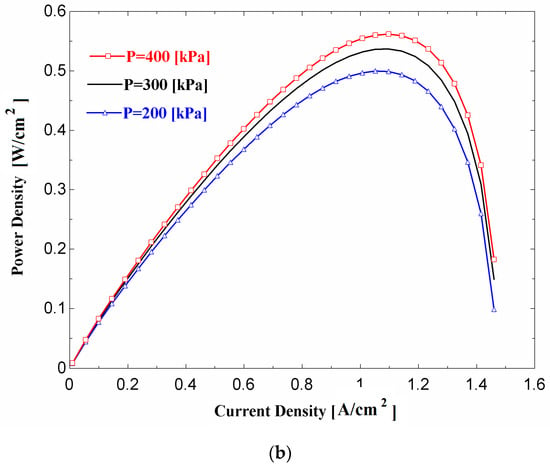
Figure 4.
Characteristic curves of the PEMFC with respect to current density at various operating pressures: (a) Polarization curve; (b) Power density.
Figure 5 shows the relation between fuel cell (as a standalone system) efficiency and power density. When referring to Figure 4b, the maximum power density is around 0.53 W/cm2 for an operating pressure of 300 kPa. With this value of power density, an efficiency of 33.5% is obtained from Figure 5. This efficiency is much lower than the maximum theoretical value, which is around 80%. Referring to Figure 5, much higher efficiencies may be obtained at significantly lower power densities. This indicates that, for a given value output power, choosing an appropriate point on the polarization curve (Figure 4a) could result in a larger fuel cell (with a larger active area) with higher efficiency or a compact fuel cell with less efficiency. In the literature, it has been reported that the maximum power density is not recommended in fuel cell sizing [44]. An operating point corresponding to a cell potential of around 0.65–0.7 V is common practice. Therefore, this results in a power density of 0.4 W cm−2 and an efficiency of around 44% for the proposed system at the operating condition.
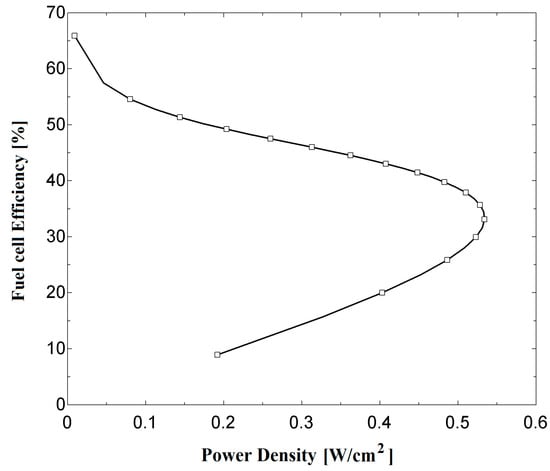
Figure 5.
Fuel cell efficiency vs. power density at P = 300 kPa.
The effects on the heat rejected from the fuel cell and the mole fraction of liquid water at the cathode outlet are shown in Figure 6 of the current density. It is observed that, with increasing current density, the considerably increases and the slightly decreases.
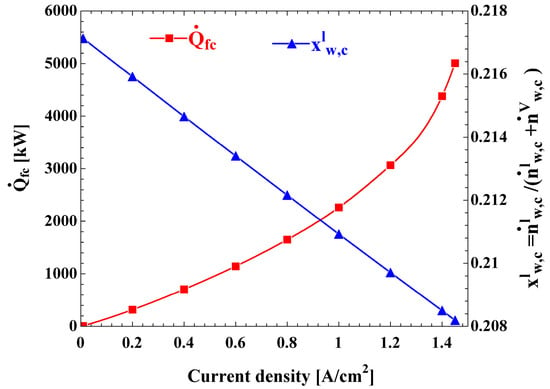
Figure 6.
The variation of heat rejected from the fuel cell and the mole fraction of liquid water at the cathode outlet with current density.
Figure 7 shows the effects of current density on exergy efficiency and net power output of the proposed system. Referring to Figure 7, the exergy efficiency drops as the current density increases. This trend can be explained by noting that, as the current density increases, the heat that is generated by fuel cell rises, so that the heat provided to the bottom cycle increases as more power is produced by the ORC. Additionally, referring to Figure 4b, there is a maximum value for the fuel cell output power as the current density changes. Therefore, as shown in Figure 7, the net output power is maximized at a particular value of current density. However, the amount of fuel input to the system and, subsequently the input exergy rate (), increases with increasing current density. In addition, the rate of increase in input exergy is higher than the rate of increase in system net power output at a current density less than the optimum value. Therefore, a decrease of exergy efficiency with current density is expected (see Equation (56)). For current densities that are higher than the optimum value, both and decrease, resulting in a reduction in exergy efficiency (see Equation (56)).
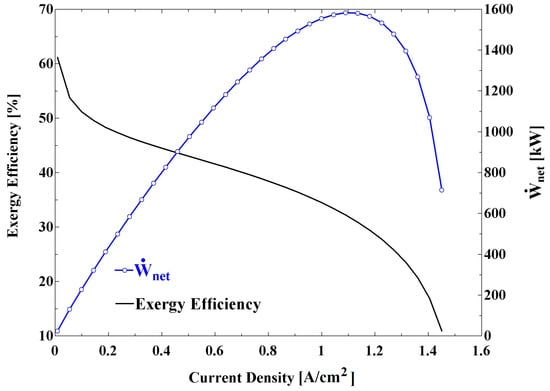
Figure 7.
Variation of overall exergy efficiency and system net power with current density at P = 300 kPa.
Figure 8 shows the influences on the overall and fuel cell exergy efficiencies of the fuel cell operating pressure. It is observed that an increase in the operating pressure increases the overall exergy efficiency. This is expected, as the increase in operating pressure results in an increased value of net output power. Figure 8 also indicates that the fuel cell exergy efficiency attains a maximum value at a particular operating pressure. Note that, at a fuel cell operating pressure of 300 kPa, the exergy efficiency of overall system is about four percent points greater than for a standalone PEM fuel cell system.
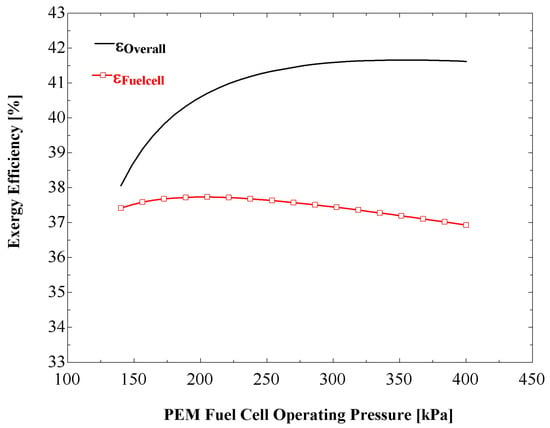
Figure 8.
Variations in overall and fuel cell exergy efficiency with the fuel cell operating pressure.
Figure 9 presents the effect of turbine back pressure on ORC exergy efficiency. It confirms the reduction of exergy efficiency with increasing turbine back pressure.
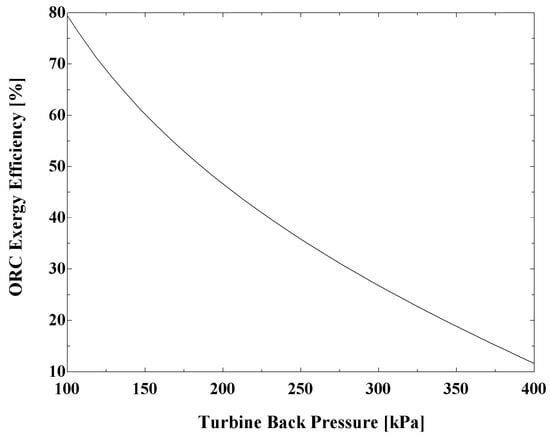
Figure 9.
Variation of ORC exergy efficiency with turbine back pressure.
Figure 10 shows the variations in cost per unit of electrical power produced by the turbine (), turbine power cost rate (), and the turbine generated power as the turbine back pressure changes. It is observed that the turbine power output and decrease as turbine back pressure increases. However, the decrease in is dominant, so that the net effect is an increase in as the pressure rises ().
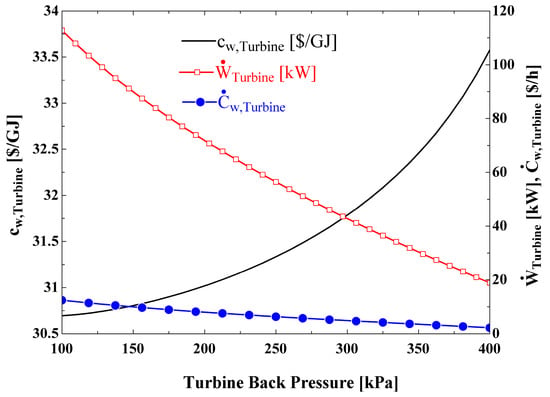
Figure 10.
Variation of the turbine power and cost per unit of turbine power with turbine back pressure.
Figure 11 shows the effect of current density on the unit cost of fuel cell net output power () and unit cost of the overall system net output power (), respectively, for three values of fuel cell operating pressure. It is observed that and increase with an increase in the current density. Referring to Figure 11, regardless of the operating pressure, little difference is observed between and when the current density is less than 0.8 A/cm2. At higher current densities, the addition of the ORC to the fuel cell results in a lower value of the product unit cost. The difference between the two product unit costs is more prominent at higher values of the fuel cell operating pressure. A comparison between the results in Figure 7 and Figure 10 shows that the operating pressure of 300 kPa is better than the other two pressure values that are indicated in Figure 11. The reasoning is as follows: comparing the results for the operating pressures of 300 kPa and 400 kPa it is observed that does not change much, but is higher for 400 kPa. In addition, although a lower value of is obtained for P = 200 kPa, for this operating pressure is much less than that for P = 300 kPa.
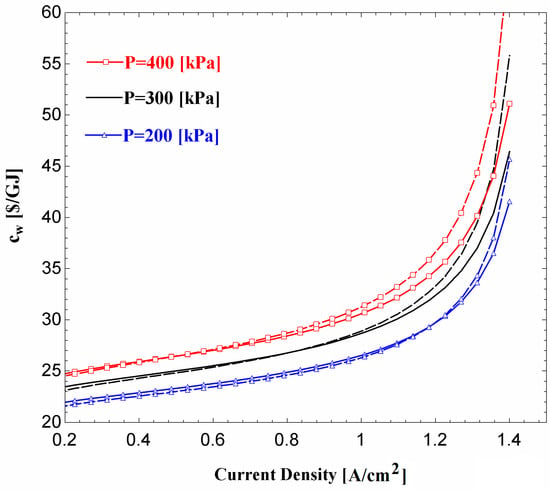
Figure 11.
Variation of unit cost of fuel cell net power output (dashed lines) and unit cost of overall system net output power (solid lines) with current density at various operating pressures.
Figure 12 depicts the variations in and with fuel cell current density, where it is observed that the increases with an increase in the current density and is maximized at a specific value of the current density. The increase in is due to the increase in exergy destruction and its associated cost for all of the components, particularly for the PEMFC component, which contributes the most to the overall exergy destruction. The trend of is similar to that of , since the contribution of PEMFC is very high in the overall capital cost rate.
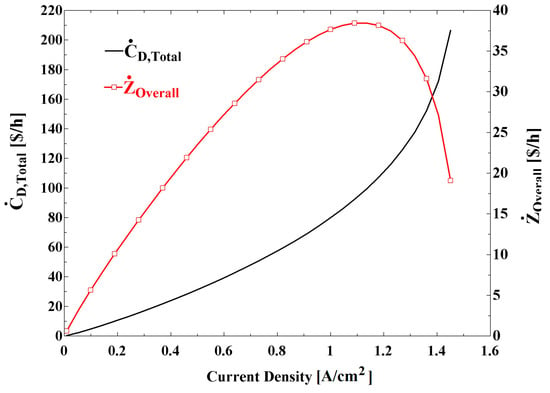
Figure 12.
Variation of exergy destruction cost rate and total capital cost rate vs. current density for the proposed system.
Figure 13 shows the variations in exergoeconomic factor,, with PEMFC operating pressure. An increase in the operating pressure is seen to lead to a higher value of , mainly due to the increase in owning and operating costs.
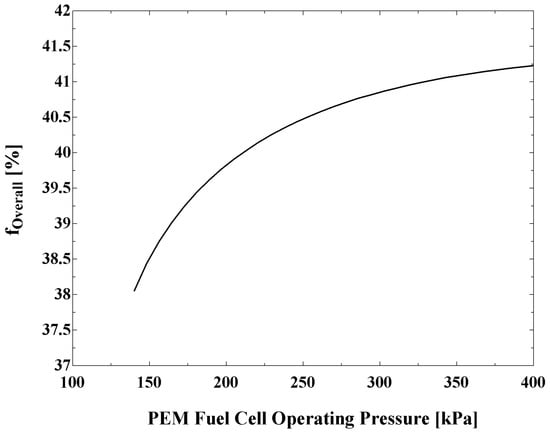
Figure 13.
Variation of overall exergoeconomic factor with PEM fuel cell operating pressure.
The solution to the system of cost balance and auxiliary equations determines the unit exergy cost at different points in the system. Table 6 gives the values of important exergy and exergoeconomic factors for the system. Referring to Table 6, the PEMFC stack, turbine, and air humidifier, among other system components, have the highest values of the sum and are, therefore, the most important components from a thermoeconomic viewpoint. The air compressor, condenser, and air humidifier exhibit the lowest f values. Therefore, regarding these components, selecting more expensive components are beneficial for better exergoeconomic system performance. In addition, the exergoeconomic factor of 41% that was obtained for the PEMFC indicates that the cost associated with exergy destruction for this component greatly exceeds the cost of its ownership and operation. The high exergy destruction in the fuel cell is mainly due to the irreversible nature of chemical reactions and voltage losses occurring in this component. An increase in the PEMFC operating pressure and air stoichiometry rate causes a decrease in the exergy destruction of the PEMFC and also in the associated cost, i.e., a higher operating pressure brings about a higher exergoeconomic factor for the PEMFC. For the turbine, the exergy efficiency is 86.0% and the exergoeconomic factor 52.1%. Therefore, the exergy and exergoeconomic performances of this component are satisfactory. The overall value of exergoeconomic factor for the proposed system is determined to be 40.8%. Thus, approximately 59% of the total cost rate of the system is due to exergy destruction. Therefore, in general, better exergoeconomic system performance is achieved with more expensive components.

Table 6.
Exergy and exergoeconomic parameters of the PEMFC-ORC system.
6. Conclusions
In the present work, a combined power producing system including a PEMFC stack and an ORC is proposed and investigated, in detail, from the viewpoints of exergy and economics. A parametric analysis is conducted in order to investigate the effects of the main parameters on the system’s thermodynamic and economic performance. The following conclusions are drawn from the exergoeconomic analysis and parametric study:
- An increase in the operating pressure results in an increase in the overall exergy efficiency. However, the fuel cell exergy efficiency is maximized at a specific value of operating pressure.
- The exergy efficiency for the hybrid power system can be higher than the corresponding value for the PEM fuel cell stack, as a standalone system, by up to 4.16%.
- Among the studied fuel cell operating pressures for the proposed system, it is observed that better thermodynamic and economic results are achieved with a pressure of 300 kPa.
- The combination of a PEMFC with an ORC is only economically justified at a specific value of current density, which depends on the fuel cell operating pressure.
- Among all the cycle components, the compressor and ORC condenser have the lowest exergoeconomic factors (less than 10%), which indicates that these components exhibit the worst exergoeconomic performances.
- Increasing the operating pressure of the PEMFC reduces its exergy destruction and also the cost associated with it.
- The overall exergoeconomic factor for the proposed system is observed to be 40.8%. Therefore, more expensive components are expected to enhance the exergoeconomic performance of the proposed system.
Author Contributions
All authors contributed equally to this paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Active surface area (cm2) | |
| Water activity | |
| Concentration at membrane surface (mol/cm3) | |
| Cost per unit exergy ($/kJ or $/GJ) | |
| Specific heat capacity (kJ/kmolK) | |
| Cost rate ($/s) | |
| CRF | Capital recovery factor |
| d | Channel height (cm) |
| D0 | Intradiffusion coefficient of water in membrane (cm2/s) |
| Diffusion coefficient of water in membrane (cm2/s) | |
| Specific exergy (kJ/kg) | |
| Exergy flow rate (kW) | |
| Exergoeconomic factor | |
| Faraday constant (C/mol) | |
| Change of Gibbs free energy () | |
| Specific enthalpy (kJ/kg) | |
| Higher heating value (kJ/kmol) | |
| heat of vaporization of water (kJ/kmol) | |
| Current density () | |
| Stack operating current (A) | |
| Limiting current density () | |
| Interest rate | |
| Condensation rate constant (1/s) | |
| Water permeability (cm2) | |
| Mass flow rate (kg/s) | |
| Molar flow rate (mol/s) | |
| Number of cells in stack | |
| Electro-osmotic drag coefficient (molecules/protons) | |
| Number of electrons | |
| Pressure (kPa) | |
| Heat transfer rate (kW) | |
| Relative cost difference | |
| Gas constant (kJ/(kg K)) | |
| Universal gas constant (kJ/(kmol K)) | |
| Total internal resistance (Ω) | |
| Membrane resistivity (Ω cm) | |
| specific entropy (kJ/(kg K)) | |
| Temperature (°C) | |
| Temperature (K) | |
| tm | Membrane thickness (cm) |
| Voltage (V) | |
| Power (kW) | |
| Mole fraction | |
| Mole fraction of water vapor | |
| Capital cost of a component ($) | |
| Capital cost rate ($/s) | |
| Greek letters | |
| Ratio of water molecules per proton flux (molecules/protons) | |
| Amplification constant (V(cm2/A)k) | |
| Exergy efficiency | |
| Efficiency | |
| Isentropic efficiency | |
| Stoichiometric rate | |
| Water viscosity (g/cm.s) | |
| Dry membrane density (g/cm3) | |
| Humidity ratio (kgv/kga) | |
| Empirical coefficient of activation overvoltage | |
| Membrane hydration | |
| Subscripts | |
| 0 | Dead (environmental) state |
| a | Anode, air |
| act | Activation, actual |
| C | Cathode |
| ch | Chemical |
| Cond | Condenser |
| Comp | Compressor |
| cv | Control volume |
| D | Destruction |
| elec | Electrical |
| F | Fuel |
| fc | Fuel cell |
| H2 | Hydrogen |
| H2O | Water |
| i | ith stream |
| in | Input |
| k | kth component |
| N2 | Nitrogen |
| O2 | Oxygen |
| Out | Output |
| P | Pump, Product |
| ph | Physical exergy |
| q | Heat |
| S,l | Sensible and latent heat |
| T | Turbine |
| th | Thermal |
| w | Water |
| v | Vapour |
| Superscripts | |
| l | Liquid |
| sat | Saturated |
| v | Vapour |
References
- Fallah, M.; Mahmoudi, S.M.S.; Yari, M. A comparative advanced exergy analysis for a solid oxide fuel cell using the engineering and modified hybrid methods. Energy Convers. Manag. 2018, 168, 576–587. [Google Scholar] [CrossRef]
- Mert, S.O.; Dincer, I.; Ozcelik, Z. Exergoeconomic analysis of a vehicular PEM fuel cell system. J. Power Sources 2007, 165, 244–252. [Google Scholar] [CrossRef]
- Chen, D.; Peng, H. A Thermodynamic model of membrane humidifiers for PEM fuel cell humidification control. J. Dyn. Syst. Meas. Control 2005, 127, 424–432. [Google Scholar] [CrossRef]
- Afshari, E.; Houreh, N.B. An analytic model of membrane humidifier for proton exchange membrane fuel cell. Energy Equip. Syst. 2014, 29, 83–94. [Google Scholar]
- Moreira, M.V.; Da Silva, G.E. A practical model for evaluating the performance of proton exchange membrane fuel cells. Renew. Energy 2009, 34, 1734–1741. [Google Scholar] [CrossRef]
- Saeed, W.; Warkozek, G. Modeling and analysis of renewable PEM fuel cell system. Energy Procedia 2015, 74, 87–101. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell. Electrochem. Sci. Technol. 1995, 142, 1–8. [Google Scholar] [CrossRef]
- Miansari, M.E.; Sedighi, K.; Amidpour, M.; Alizadeh, E.; Miansari, M.O. Experimental and thermodynamic approach on proton exchange membrane fuel cell performance. J. Power Sources 2009, 190, 356–361. [Google Scholar] [CrossRef]
- Sharifi Asl, S.M.; Rowshanzamir, S.; Eikani, M.H. Modelling and simulation of the steady-state and dynamic behavior of a PEM fuel cell. Energy 2010, 35, 1633–1646. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohammadi, A.; Pourfayaz, F.; Mehrpoya, M.; Bidi, M.; Valero, A.; Uson, S. Thermodynamic analysis of a waste heat recovery system for proton exchange membrane fuel cell using transcritical carbon dioxide cycle and cold energy of liquefied natural gas. J. Nat. Gas Sci. Eng. 2016, 34, 428–438. [Google Scholar] [CrossRef]
- He, T.; Shi, R.; Peng, J.; Zhuge, W.; Zhang, Y. Waste heat recovery of a PEMFC system by using organic Rankine cycle. Energies 2016, 9, 267. [Google Scholar] [CrossRef]
- Companari, S.; Valenti, G.; Macchi, E.; Lozza, G.; Ravida, N. Development of a micro-cogeneration laboratory and testing of a natural gas CHP unit based on PEM fuel cells. Appl. Therm. Eng. 2014, 71, 714–720. [Google Scholar] [CrossRef]
- Gandiglio, M.; Lanzini, A.; Santarelli, M.; Leone, P. Design and optimization of a proton exchange membrane fuel cell CHP system for residential use. Energy Build. 2014, 69, 381–393. [Google Scholar] [CrossRef]
- Hwang, J.J.; Zou, M.L. Development of a proton exchange membrane fuel cell cogeneration system. J. Power Sources 2010, 195, 2579–2585. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Lin, B.; Chen, J. Maximum equivalent efficiency and power output of a PEM fuel cell/refrigeration cycle hybrid system. Int. J. Hydrogen Energy 2011, 36, 2190–2196. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Gao, L.; Dai, Y. Parametric analysis of a hybrid power system using organic Rankine cycle to recover waste heat from proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2012, 37, 3382–3391. [Google Scholar] [CrossRef]
- Chang, H.; Wan, Z.; Zheng, Y.; Chen, X.; Shu, S.; Tu, Z.; Chan, S.H. Energy analysis of a hybrid PEMFC–solar energy residential micro-CCHP system combined with an organic Rankine cycle and vapor compression cycle. Energy Convers. Manag. 2017, 142, 374–384. [Google Scholar] [CrossRef]
- Chahartaghi, M.; Kharkeshi, BA. Performance analysis of a combined cooling, heating and power system with PEM fuel cell as a prime mover. Appl. Therm. Eng. 2018, 128, 805–817. [Google Scholar] [CrossRef]
- Romdhane, J.; Gualous, HL. Energy assessment of PEMFC based MCCHP with absorption chiller for small scale French residential application. Int. J. Hydrogen Energy 2018, 43, 19661–19680. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Derakshan, E. Design and evaluation of a micro combined cooling, heating, and power system based on polymer exchange membrane fuel cell and thermoelectric cooler. Energy Convers. Manag. 2018, 158, 346–355. [Google Scholar] [CrossRef]
- Arsalis, A. A comprehensive review of fuel cell-based micro-combined-heat-and-power systems. Renew. Sustain. Energy Rev. 2019, 105, 391–414. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Hussain, M.M.; Baschuk, J.J.; Li, X.; Dincer, I. Thermodynamic analysis of a PEM fuel cell power system. Int. J. Therm. Sci. 2005, 44, 903–911. [Google Scholar] [CrossRef]
- Leo, T.j.; Durango, J.A.; Navarro, E. Exergy analysis of PEM fuel cells for marine applications. Energy 2010, 35, 1164–1171. [Google Scholar] [CrossRef]
- Kazim, A. Exergy analysis of a PEM fuel cell at variable operating conditions. Energy Convers. Manag. 2004, 45, 1949–1961. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. An energetic–exergetic analysis of a residential CHP system based on PEM fuel cell. Appl. Energy 2011, 88, 4334–4342. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. An energetic–exergetic comparison between PEMFC and SOFC-based micro-CHP systems. Int. J. Hydrogen Energy 2011, 36, 3206–3214. [Google Scholar] [CrossRef]
- Hanapi, S.; Tijani, A.S.; Abdol Rahim, A.H. Exergy efficiency profile of a 1 kW open cathode fuel cell with pressure and temperature variations. Energy Procedia 2015, 79, 82–89. [Google Scholar] [CrossRef]
- Kalinci, Y.; Dincer, I.; Hepbasli, A. Energy and exergy analyses of a hybrid hydrogen energy system: A case study for Bozcaada. Int. J. Hydrogen Energy 2016, 42, 2492–2503. [Google Scholar] [CrossRef]
- Kazim, A. Exergoeconomic analysis of a PEM fuel cell at various operating conditions. Energy Convers. Manag. 2005, 46, 1073–1081. [Google Scholar] [CrossRef]
- Suleiman, B.; Abdulkareem, A.S.; Musa, U.; Mohammed, I.A.; Olutoye, M.A.; Abdullahi, Y.I. Thermo-economic analysis of proton exchange membrane fuel cell fueled with methanol and methane. Energy Convers. Manag. 2016, 117, 228–240. [Google Scholar] [CrossRef]
- Sayadi, S.; Tsatsaronis, G.; Duelk, C. Exergoeconomic analysis of vehicular PEM (proton exchange membrane) fuel cell systems with and without expander. Energy 2014, 77, 608–622. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Fuel Cell System Explained, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Ang, S.M.C.; Brett, D.J.L.; Fraga, E.S. A multi-objective optimization model for a general polymer electrolyte membrane fuel cell system. J. Power Sources 2010, 195, 2754–2763. [Google Scholar] [CrossRef]
- Yi, J.S.; Nguyen, T.V. An along-the-channel model for proton exchange membrane fuel cells. J. Electrochem. Soc. 1998, 145, 1149–1159. [Google Scholar] [CrossRef]
- Golbert, J.; Danial, R.L. Model-based control of fuel cells: (1) Regulatory control. J. Power Sources 2004, 135, 135–151. [Google Scholar] [CrossRef]
- Vincenzo, L.; Araya, S.S.; Olesen, A.C.; Nielsen, M.P.; Kaer, S.K. Modeling and experimental validation of water mass balance in a PEM fuel cell stack. Int. J. Hydrogen Energy 2016, 41, 3079–3092. [Google Scholar]
- Wark, K. Advanced Thermodynamics for Engineers; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Sarabchi, N.; Mahmoudi, S.M.S.; Yari, M.; Farzi, A. Exergoeconomic analysis and optimization of a novel hybrid cogeneration system: High-temperature proton exchange membrane fuel cell/Kalina cycle, driven by solar energy. Energy Convers. Manag. 2019, 190, 14–33. [Google Scholar] [CrossRef]
- Mohammadkhani, F.; Shokati, N.; Mahmoudi, S.M.S.; Yari, M.; Rosen, M.A. Exergoeconomic assessment and parametric study of a gas turbine-modular helium reactor combined with two organic Rankine cycles. Energy 2014, 65, 533–543. [Google Scholar] [CrossRef]
- Nami, H.; Mahmoudi, S.M.S.; Nemati, A. Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an organic Rankine cycle (GT-HRSG/SCO2). Appl. Therm. Eng. 2017, 110, 1315–1330. [Google Scholar] [CrossRef]
- Klein, S.A.; Alvarda, F. Engineering Equation Solver (EES); F-Chart Software: Madison, WI, USA, 2013. [Google Scholar]
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier: Waltham, MA, USA, 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).